«Информатика»

Вид материала

Учебное пособие

Содержание Позиционные системы счисления 10-ая система 8-ая система X - правильная дробь, заданная в 10-чной системе счисления и требуется перевести ее в систему счисления с основанием Q X в систему счисления с основанием Q X будет последовательность целых частей полученных произведений, изображенных одной Q

Подобный материал:

• Рабочая учебная программа по дисциплине «Информатика» Направление №230100 «Информатика, 91.73kb.
• Темы рефератов по курсу «Информатика», 10.55kb.
• Программа дисциплины Иностранный язык профессионального общения для направлений 080700., 259.96kb.
• Рабочая программа дисциплины: «Информатика с методикой преподавания» Для специальности:, 495.05kb.
• Рабочая программа «Основы микроэлектроники» для специальностей «Информатика и английский, 501.86kb.
• Учебно-методический комплекс по дисциплине б в дв. 01- цифровая обработка сигналов, 603.86kb.
• Учебно-методический комплекс по дисциплине педагогика направление подготовки, 1570.07kb.
• Программа пропедевтического курса «Информатика в играх и задачах», 125.46kb.
• Рабочая программа дисциплины для студентов магистратуры, обучающихся по направлению, 120.54kb.
• Метод Кругов Эйлера Аннотация. Логические задачи, представленные в данной рабочей тетради,, 456.39kb.

Позиционные системы счисления

При записи числа в позиционной системе счисления с основанием N используется N цифр, а каждая позиция в числе обозначает N в соответствующей степени. Используя такую запись можно перевести число из любой системы в десятичную.

10-ая система –>0,1,…,9

число 5202 –> 5*10³⁺2*10²+0*10¹⁺2*10⁰ = 5000+200+0+2

2-ая система. –> 0,1

число 1101₂ –> 1*2³+ 1*2²+0*2²⁺1* 2⁰= 8+4+0+1 = 13₁₀

8-ая система. –> 0,1,…,7

число 502₈ = 5*8²+0*8¹+2*8⁰ = 320+0+2 = 322₁₀

16-ная система. –>0,1,…,9,A,B,C,D,E,F

число E1₁₆ = 14*16¹+2*16⁰=224+2=226₁₀

При представлении чисел в компьютере основной системой счисления является двоичная. Числа в двоичной системе или в двоично–десятичном виде (10-ные цифры записываются их двоичным кодом). При работе в языках программирования или вычислительных пакетах используются десятичные числа в естественной или нормализованной форме. Числа в естественной форме (с фиксированной точкой): -30.57, 0.0245. Используется для записи целых чисел. Недостаток – ограниченный диапазон значений, много «лишних» знаков в числах 20000000000, 0.00004. Числа в нормализованной (экспоненциальной) форме (с плавающей точкой):

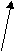–0.3057*10+02,	0.245*10–01		В 10-й системе A=M*10p, 0.1<=M<1 В позиционной системе с основанием Q A=M*Qp, 1/Q<=M<1
Мантисса
Порядок

Под число может быть отведено: 1 байт(8 бит), полуслово(2 байта=16 бит), слово(4байта=32 бита), двойное слово.

П


Рисунок 1 – Запись числа в ЭВМ

еревод десятичного числа D из десятичной системы в двоичную производится так:

1. Делим D на 2. Остаток - B0.

2. Частное снова делим на 2. Остаток - B1.

3. Повторяем, пока не получим 1/2=0 с остатком 1. Этот последний остаток и есть старшая единица.

Таблица 1- Пример перевода числа 154 из десятичной системы в двоичную.

Действие		остаток	Действие		остаток	Действие		остаток
1	154/2=77	B0=0	2	77/2=38	B1=1	3	38/2=19	B2=0
4	19/2=9	B3=1	5	9/2=4	B4=1	6	4/2=2	B5=0
7	2/2=1	B6=0	8	1/2=0	B7=1	Итак, 154=10011010

Перевод из двоичной системы исчисления в шестнадцатеричную состоит из двух этапов сначала двоичное число разбивается на комбинации по четыре двоичных цифры а затем каждая комбинация заменяется шестнадцатеричным числом (Таблица 2).

Таблица 2 – Соответствие двоичных и шестнадцатеричных чисел

2	16	2	16	2	16	2	16
0000	0	0001	1	0010	2	0011	3
0100	4	0101	5	0110	6	0111	7
1000	8	1001	9	1010	A	1011	B
1100	C	1101	D	1110	E	1111	F

Например: число 111010110 = 0001'1101'0110 = 1D6

Перевод дробных чисел из одной системы счисления в другую производится на основании следующих соображений. Пусть X - правильная дробь, заданная в 10-чной системе счисления и требуется перевести ее в систему счисления с основанием Q, т.е. найти цифры b_i для записи X=b_-1*Q^-1+b_-2*Q^-2+ ... +b_-m*Q^-m. Для определения bi умножим левую и правую части равенства на Q, причем в левой части умножение выполняется по правилам 10-чной арифметики. Имеем: X*Q=b_-1+b_-2Q^-1+...+b_-mQ^-m+1. Представим левую часть равенства как сумму целой и дробной частей X*Q=[X*Q]+{X*Q}и приравняем их с целой и дробной частями правой части равенства: [X*Q]=b_-1 и {X*Q}=b_-2Q^-1+...+b_-mQ^-m+1. Таким образом, цифра b_-1 является целой частью от умножения X на Q. Далее положим X₁=X*Q и повторим аналогичные действия для определения цифры b_-2 и других цифр (Таблица 3)

Таблица 3 - Алгоритм перевода правильной десятичной дроби X в систему счисления с основанием Q 

Рекуррентные формулы	Пояснения
b-i-1=[Xi*Q]	1) X умножить на Q, записанное в 10-чной системе счисления
Xi+1={Xi*Q}	2) дробную часть полученного произведения снова умножить на Q
Процесс продолжать до тех пор, пока последнее полученное произведение не станет равным нулю Xi+1=0, либо не будет достигнута требуемая точность изображения числа. (требуемое количество цифр после запятой).
Представлением числа X будет последовательность целых частей полученных произведений, изображенных одной Q-чной цифрой и записанных в порядке их получения

Примеры: Перевести число 0,36₁₀ в 2-чную систему счисления c 5 знаками после запятой. 0,36*2=0+0,72; 0,72*2=1+0,44; 0,44*2=0+0,88; 0,88*2=1+0,76; 0,76*2=1+0,52.

 Таким образом, 0,36₁₀=0,01011₂.

Перевести число 0,36₁₀ в 16-чную систему счисления c 2 знаками после запятой. 0,36*16=5+0,76; 0,76*16=12+0,16.

 Таким образом, 0,36₁₀=0,5С₁₆.