Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 85.92kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 101.07kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 129.5kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 107.65kb.
- Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию, 334.33kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 187.41kb.
- Рабочая программа учебной дисциплины ф тпу 21/01 Федеральное агентство по образованию, 307.9kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 217.64kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 236.22kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 266.17kb.
Р | Ф ТПУ 7.1- 21/01 |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Томский политехнический университет»
УТВЕРЖДАЮ
Декан ЭФФ
________________Евтушенко Г.С.
«___»__________________2009 г.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Рабочая программа по интегрированной образовательной программе «Электроника» для направления 200300 «Биомедицинская инженерия», специальности 200401- «Биотехнические и медицинские аппараты и системы», для направления 210100 «Электроника и микроэлектроника», специальности 210106- «Промышленная электроника», для направления 200200 «Оптотехника», специальности 200203- «Оптико-электронные приборы и системы».
Рабочая программа по интегрированной образовательной программе «Приборостроение» для направления 200100 «Приборостроение», специальностей: 200101- «Приборостроение», 200102- «Приборы и методы контроля качества и диагностики», 200106- «Информационно-измерительная техника и технология», для направления 200500 «Метрология, стандартизация и сертификация», специальности 200503- «Стандартизация и сертификация»,
Рабочая программа для специальности 220501- «Управление качеством».
Электрофизический факультет (ЭФФ)
Обеспечивающая кафедра «Высшей математики и математической физики» (ЕНМФ)
Курс I
Семестр 1
Учебный план набора 2009 года
Распределение учебного времени
-
Лекции
36
Практические занятия
44
Всего аудиторных занятий
80
Самостоятельная работа
80
Общая трудоемкость
160
Форма отчётности
экзамен
Томск-2009 г.
Предисловие
1. Рабочая программа составлена на основании ГОС ВПО по направлению приборостроение, утвержденных Министерством образования РФ № 686 от 02.03.2000 года, регистрационный номер 215.
РАССМОТРЕНА И ОДОБРЕНА на заседании обеспечивающей кафедры ВММФ, протокол № 121 от 28.08. 2009 года
- Разработчики –
доцент каф. ВММФ ______________ В.Ф. Зальмеж
доцент каф. ВММФ ______________ А.А. Михальчук
доцент каф. ВММФ ______________ Н.М. Филипенко
доцент каф. ВММФ ______________ И.А. Цехановский
3. Зав. обеспечивающей кафедры ВММФ А.Ю. Трифонов
- Рабочая программа соответствует действующему учебному плану и согласована c выпускающими кафедрами ЭФФ.
Председатель методической
комиссии ЭФФ Гормаков А.Н.
Аннотация
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
200300, 210100, 200200,
200100, 200500, 220501
Кафедра ВММФ ЕНМФ
доцент кафедры ВММФ, ЕНМФ, к.ф.-м.н., Зальмеж В.Ф.,
доцент кафедры ВММФ, ЕНМФ, к.ф.-м.н., Филипенко Н.М.
доцент кафедры ВММФ, ЕНМФ, к.ф.-м.н., Михальчук А.А.
доцент кафедры ВММФ, ЕНМФ, к.ф.-м.н., Цехановский И.А.
Цель: формирование знаний о математике, как особом способе познания мира и образе мышления, общности её понятий и представлений, дать опыт построения математических моделей и проводить необходимые расчёты в рамках построенных моделей; употребления математической символики для выражения количественных и качественных отношений объектов.
Содержание: Множества; вещественные числа; логическая символика; понятие функции и её свойства; числовые последовательности; предел функции и его свойства; бесконечно малые и бесконечно большие функции и их сравнение; непрерывность функции и классификация точек разрыва; замечательные пределы; производная и правила дифференцирования; дифференциал; правило Лопиталя; применение к исследованию функции; формула Тейлора; функция нескольких переменных; частные производные; экстремум функции нескольких переменных; скалярное поле и его геометрические характеристики; производная по направлению; градиент.
Рабочая программа курса «Дифференциальное исчисление», предназначенного для студентов первого курса всех специальностей ЭФФ, составлена в соответствии с государственными образовательными стандартами и образовательным стандартом Томского политехнического университета.
Курс 1 (1 семестр – экзамен )
Всего 160 ч., в т.ч.: ЛК – 36 ч., ПР – 44 ч., СР – 80 ч.
The developer - Filipenko N.M., faculty ENM
The developer - Zalmegh V.F., faculty ENM
The developer - Mikhalchuk A.A., faculty ENM
The developer - Thehanovskiy I.A., faculty ENM
The working program on discipline “Differential Counting” is intended for freshmen of 200300 and 200100 directions “Electrical Engineering”.
The program is composed in the correspondence with the impose requirements by the standard on formation of Tomsk polytechnic university.
The program contains exposition of the purposes of discipline, content of lectures, them of practical occupations, organization methods and form of monitoring of student independent work. In the end of the program provisional variant of tests, representation of entering monitoring are produced.
Цели и задачи преподавания дисциплины
«Дифференциальное исчисление»
Цели дисциплины:
В дисциплине «Дифференциальное исчисление» излагается материал, являющийся пререквизитом к изучению последующих курсов математики (понятия функции, предела, непрерывности, производной) : «Интегральное исчисление», «Ряды и комплексный анализ», «Дифференциальные уравнения». Изучаемый материал необходим также при изучении физики и специальных предметов.
Дисциплина базируется на знании школьного курса математики и курса «Линейная алгебра и аналитическая геометрия».
Целью изучения дисциплины студентами является приобретение знаний, предусмотренных программой, формированием умения и навыков применять полученные знания при решении конкретных задач.
Студент, изучив дисциплину «Дифференциальное исчисление» должен:
иметь представление:
- о математике, как особом способе познания мира и образе мышления,
- общности её понятий и представлений;
- о связи курса с другими дисциплинами;
уметь:
- использовать основные понятия и методы дифференциального исчисления.
- использовать математические модели для конкретных процессов и проводить необходимые расчёты в рамках построенных моделей;
- использовать полученные знания при усвоении учебного материала последующих дисциплин;
Знать и иметь опыт:
- употребления математической символики для выражения количественных и качественных отношений объектов,
- применения математических методов и элементов научных исследований в прикладных задачах и оценивания пределов применимости полученных результатов.
Задачи дисциплины:
В результате изучении дисциплины «Дифференциальное исчисление» студент обязан:
- Иметь представление:
- о математике, как особом способе познания мира и образе мышления, общности её понятий и представлений;
- о логической символике, используемой в данной и последующих дисциплинах;
- о множествах и операциях над ними;
- о функциональной связи переменных и её свойствах
- о математике, как особом способе познания мира и образе мышления, общности её понятий и представлений;
- Уметь:
использовать полученные знания при усвоении учебного материала последующих дисциплин;
применять методы дифференциального исчисления функций одной и нескольких переменных к отысканию физических и геометрических характеристик процессов; уметь устанавливать границы применимости изученных методов;
самостоятельно овладевать новыми математическими знаниями, опираясь на опыт, приобретённый в процессе изучения курса «Дифференциальное исчисление»;
- Знать и иметь опыт
работы с учебной и справочной литературой,
нахождения производных от функций одной и нескольких переменных,
исследование функций на экстремум и монотонность,
нахождение пределов,
применение методов, изученных в курсе «Дифференциальное исчисление» к решению физических задач.
Задачи изложения и изучения дисциплины
Для достижения целей, поставленных при изучении дисциплины, используется набор методических средств:
- лекции;
- практические занятия с опросом студентов и закреплением теоретического материала;
- индивидуальные задания;
- работа с учебниками в библиотеке по изучению разделов дисциплины, вынесенных на самостоятельное изучение
- индивидуальные и групповые консультации по теоретическим и практически вопросам курса;
Проверка приобретенных знаний, навыков и умений осуществляется посредством опроса студентов, текущих тестовых испытаний, контрольных работ, теоретических коллоквиумов и сдачи экзамена.
Содержание теоретического раздела
I. Введение в анализ (10 часов)
Понятие множества. Вещественные числа и их основные свойства. Логическая символика. Понятие модуля и его основные свойства.
Понятие функции: определение, четность, периодичность, монотонность, способы задания. Обратная функция. Классификация функций. Простейшие элементарные функции: свойства и графики.
Числовые последовательности: определение, свойства, арифметические действия над ними.
Бесконечно малые и бесконечно большие последовательности. Предел последовательности и его геометрическое истолкование. Свойства сходящихся последовательностей. Теорема о монотонной ограниченной последовательности. Число e.
Предел функции. Односторонние пределы. Теоремы о свойствах функций, имеющих предел.
Бесконечно малые и бесконечно большие функции: определение, свойства и их взаимная связь. Первый и второй замечательные пределы и их следствия.
Сравнения бесконечно малых величин. Свойства, таблица эквивалентно бесконечно малых величин и ее применение для вычисления пределов.
Непрерывность функции: определение, геометрическая интерпретация. Непрерывность в точке и на интервале. Теорема об арифметических действиях над функциями, имеющими предел. Теорема о непрерывности элементарных функций. Теорема о свойствах непрерывных функций.
Точки разрыва и их классификация. Схема исследования функции на непрерывность.
II. Дифференциальное исчисление функций одной переменной (16 часов)
Задачи, приводящие к понятию производной.
Определение и геометрический смысл производной. Уравнения касательной и нормали. Односторонние производные.
Понятие дифференцируемости функции. Связь дифференцируемых функций с функциями непрерывными.
Определение и геометрический смысл дифференциала.
Правила дифференцирования и таблица производных.
Теорема о производной обратной и сложной функций.
Дифференцирование показательно-степенной, неявной и параметрически заданной функции.
Производные и дифференциалы высших порядков. Формула Лейбница. Инвариантность.
Основные теоремы дифференциального исчисления: теоремы Ферма, Роля, Лагранжа, Коши и их геометрическая интерпретация.
Правила Лопиталя к раскрытию неопределенностей вида
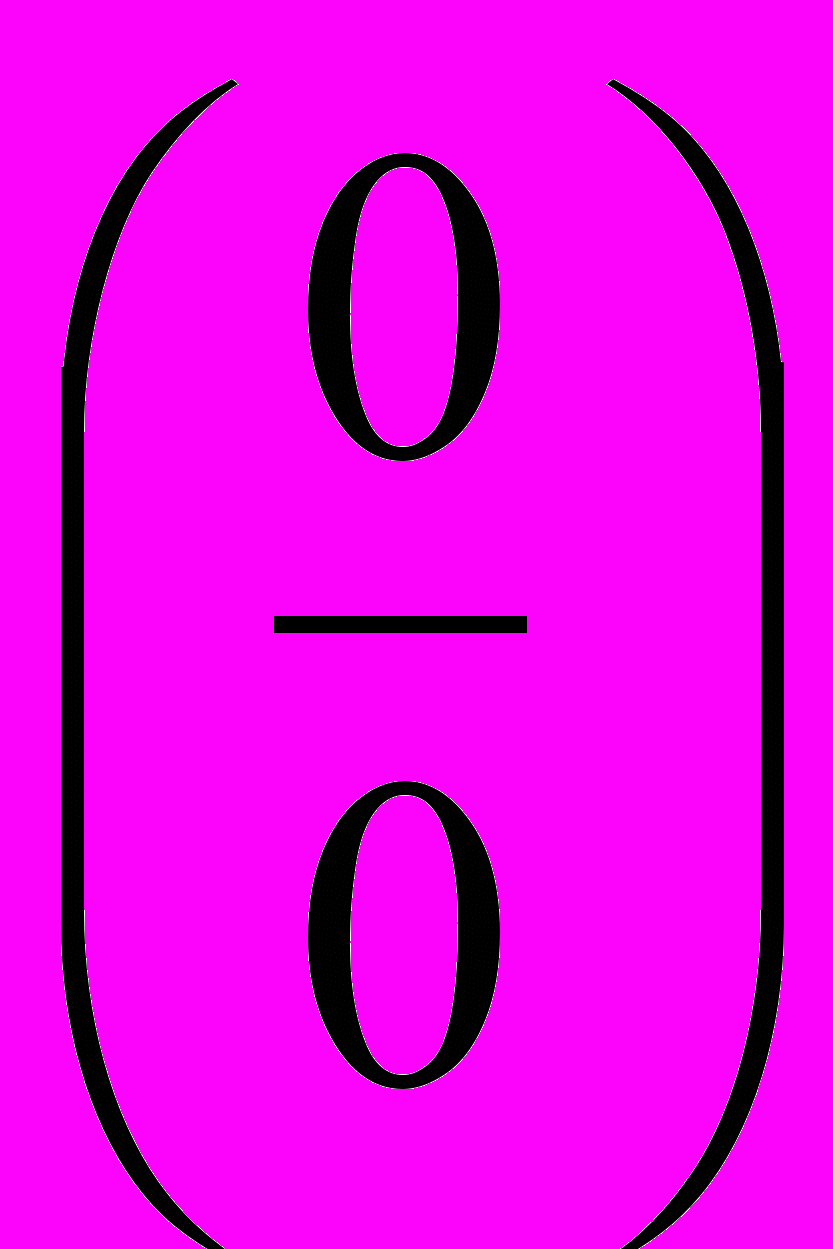 и
и 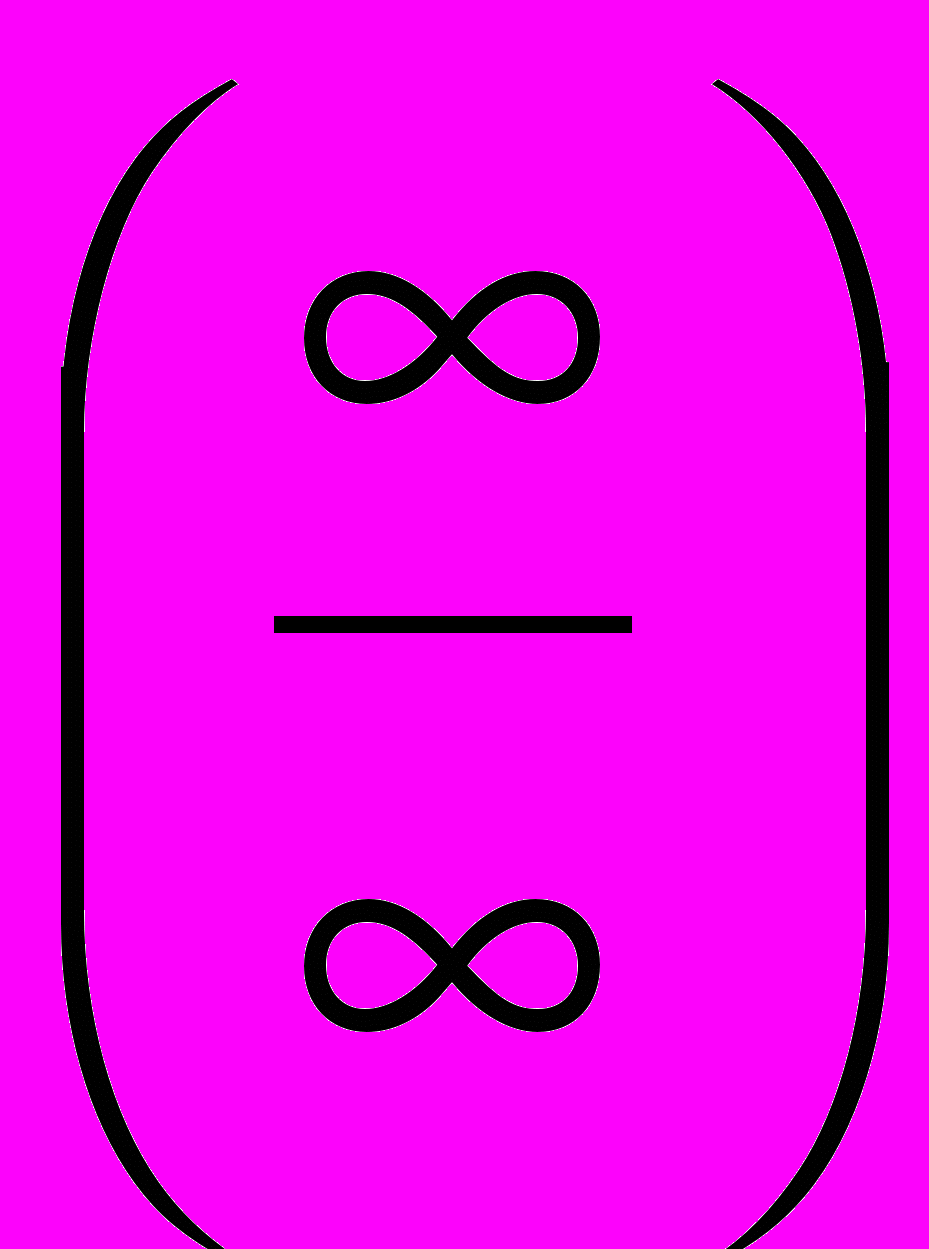 и их использование при раскрытии неопределенностей других видов.
и их использование при раскрытии неопределенностей других видов.Формула Тейлора. Формула Маклорена. Разложение элементарных функций по формуле Маклорена. Остаточный член в форме Лагранжа.
Монотонность функции. Точки экстремума. Теорема о необходимых и достаточных условиях существования экстремума. Схема исследования функций с помощью производных на экстремум.
Асимптоты: определение, виды (наклонная, вертикальная).
Выпуклость, вогнутость функции. Точки перегиба. Теорема о достаточных условиях существования точки перегиба.
Полная схема исследования функции и построения ее графика.
III. Дифференциальное исчисление функций нескольких переменных (10 часов)
Определение функции двух переменных. Область определения. Предел и непрерывность функции двух переменных.
Частные и полное приращение функции (геометрическая иллюстрация).
Свойства непрерывных функций двух переменных.
Частные производные функций нескольких переменных.
Полный дифференциал ФНП. Инвариантность формы первого дифференциала.
Производная сложной функции и функции заданной неявно.
Частные производные и дифференциалы высших порядков. Теорема Шварца.
Скалярное поле, линии и поверхности уровня. Градиент и производная по направлению. Свойства градиента.
Касательная плоскость и нормаль к поверхности.
Формула Тейлора для функции двух переменных.
Экстремум функции нескольких переменных (необходимое и достаточное условие).
Наименьшее и наибольшее значение функции в замкнутой области.
Условный экстремум функции нескольких переменных.
Содержание практического раздела
I. Введение в анализ (16 часов)
Понятие функции. Основные элементарные функции и их графики. Простейшее исследование и построение графиков функций. Последовательность (определение, свойства). Предел последовательности и его свойства.. (4 часа)
Вычисление пределов последовательностей. (2 часа)
Вычисление предела функции по определению. Вычисление пределов функции, содержащих неопределенности. Первый и второй замечательные пределы. (3 часа)
Бесконечно малые и их сравнение. Таблица эквивалентно бесконечно малых величин. Вычисление пределов с помощью таблицы. (2 часа)
Предел и непрерывность функции. Односторонние пределы. Классификация точек разрыва. Исследование функций на непрерывность с построением схематических графиков. (3 часа)
Контрольная работа. (2 часа)
II. Дифференциальное исчисление функций одной переменной (18 часов)
Задачи, приводящие к понятию производной. Техника дифференцирования функций, заданных явно. Правила дифференцирования. (2 часа)
Дифференцирование функций, заданных неявно и параметрически. Дифференциал и его геометрический смысл (2 часа)
Геометрический и физический смысл производной.. Производные и дифференциалы высших порядков. (2 часа)
Правило Лопиталя и его применение к вычислению пределов. Раскрытие неопределенностей вида
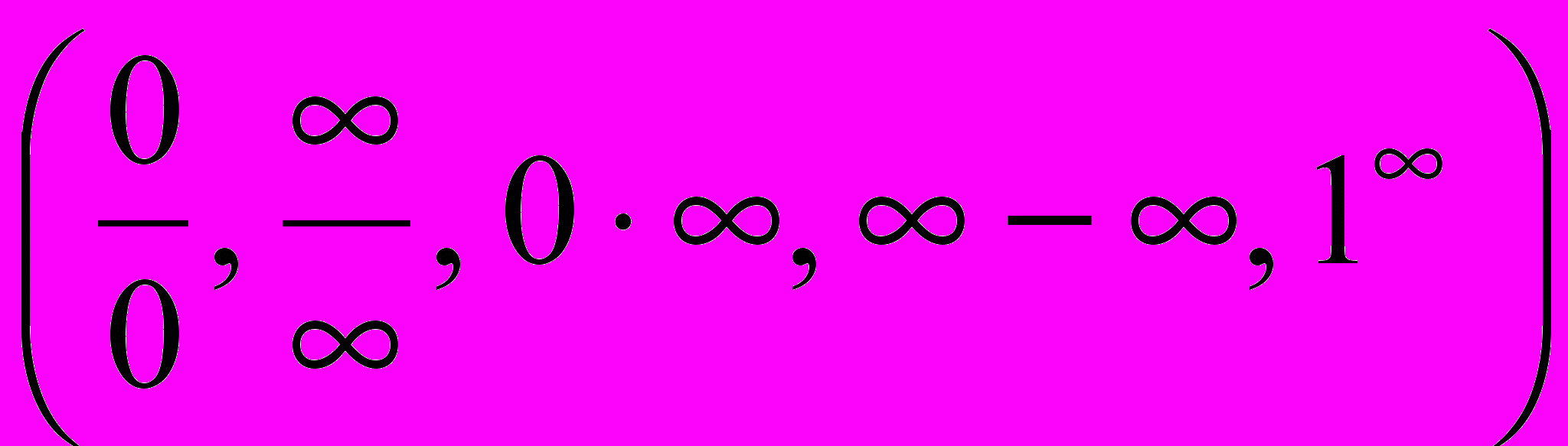 . (3 часа)
. (3 часа)Формулы Тейлора и Маклорена. Разложение элементарных функций по формуле Маклорена. (2 часа)
Применение производной к исследованию функций: возрастание и убывание функций; точки экстремума. Наибольшее и наименьшее значение функции на отрезке. Применение производной в задачах физики. (2 часа)
Выпуклость и вогнутость функции; точки перегиба; асимптоты. Полное исследование и построение графиков функций. (3 часа)
Контрольная работа. (2 часа)
III. Дифференциальное исчисление функций нескольких переменных (10часов)
Область определения, предел и непрерывность функции двух переменных. Частные производные первого и высших порядков для функции нескольких переменных. (2 часа)
Дифференцирование сложных функций, функций заданных неявно. Дифференциал функции нескольких переменных. Касательная плоскость и нормаль к поверхности. Производная по направлению. Градиент (3 часа)
Экстремум функции двух переменных. Условный экстремум. Отыскание наибольшего и наименьшего значения функции двух переменных в замкнутой области. (3 часа)
Контрольная работа. (1 час)
Календарный план
Содержание практических занятий и программа
самостоятельной (познавательной) деятельности по дисциплине
«Дифференциальное исчисление»
| № занятия | Тема | Домашняя и самостоятельная работа | С/Р час | ||||||||||
| 1 2 3 4 5 6 7 |
| Выполнение ИДЗ, работа с конспектом, обязательной и дополнительной литературой. Подготовка к к/р, повторение теоретического материала, завершение работы с ИДЗ-1. Анализ проверенной К\Р, работа над ошибками. | 4 4 4 4 4 4 | ||||||||||
| 8 9 10 11 12 13 14 15 16 17 |
| Выполнение ИДЗ, работа с конспектом, обязательной и дополнительной литературой. Подготовка к к/р повторение теоретического материала, завершение работы с ИДЗ-2. Анализ проверенной К\Р, работа над ошибками. | 4 4 4 4 4 4 4 4 4 4 | ||||||||||
| 18 19 20 21 22 |
| Выполнение ИДЗ, работа с конспектом, обязательной и дополнительной литературой. Подготовка к к/р повторение теоретического материала, завершение работы с ИДЗ-3. | 4 4 4 4 | ||||||||||
| Итого, время на самостоятельную работу студентов: выполнение ИДЗ, работу с основной и дополнительной литературой, подготовку к к\р | 80 | ||||||||||||
Текущий и итоговый контроль результатов изучения дисциплины
Целью текущего контроля знаний студентов является проверка ритмичности работы студентов, оценка усвоения теоретического, практического материала и приобретенных знаний, умений и навыков. Текущий контроль обеспечивается: --опросом студентов на практических занятиях; ---отображенной в рейтинг–плане, отчетностью студентов по результатам выполнения ИДЗ, самостоятельной работы в соответствии с программой , контрольными работами; --ежемесячной аттестацией студентов по результатам их работы на лекционных и практических занятиях, выполнения и защиты ИДЗ, опроса на практических занятиях, выполнения контрольных заданий по теоретическому и практическому материалу. По дисциплине составлен рейтинг–план, в соответствии с которым результаты текущей аттестации подаются в деканат ЭФФ. По дисциплине разработан комплект ИДЗ, состоящий из 4 заданий по 25 вариантов, комплект контрольных работ, 50 билетов для итоговой экзаменационной работы. Образцы контролирующих материалов прилагаются.
РЕЙТИНГ-ПЛАН
| № | Темы | Трудоёмкость в часах Ауд / сам | Рейтинг за практические занятия (баллы) | Промежуточный контроль работы студента | Рейтинг промежуточного контроля | Рейтинг темы (баллы) | |
| 1 | Введение в анализ | 26/26 | 5 | самостоятельная работа; ИДЗ-1 | 5 | 30 | |
| 1. контрольная работа | 20 | ||||||
| 2 | Дифференциальное исчисление функций одной переменной | 34/34 | 5 | самостоятельная работа, ИДЗ-2 | 5 | 40 | |
| 2.контрольная работа | 30 | ||||||
| 3 | Дифференциальное исчисление функций нескольких переменных | 20/20 | 5 | самостоятельная работа, ИДЗ-3 | 5 | 30 | |
| 3.контрольная работа | 20 | ||||||
| 4 | Итоговая экзаменационная работа | Экзамен 10 | | ||||
| | ВСЕГО | 80/80=160 | 100.Допуск к экзамену 55 балла | ||||
Учебно-методическое обеспечение дисциплины
Основная литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисление (в 2-х томах) - М. Наука, Математический анализ:1967, 1978, 1985, 1986 гг. – 1031 с. - 2710 экз.
2. Кудрявцев Л.Д. Курс математического анализа (в 3-х томах).- М. Наука, 1970, 1981, 1988 гг. – 1639 с. - 524 экз.
3. Никольский С.М. Курс математического анализа (в 2-х томах).- М. Наука, 1975, 1983, 1990 гг. - 822 с. - 360 экз.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М. Наука, 1980,1984,1988 гг. -432 с. - 268 экз.
5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. - М. Наука, 1981,1985,1988,1989 гг. -448 с. - 432 экз.
6. Берман Г.Н. Сборник задач по курсу математического анализа. - М. Наука, 1972, 1975, 1977, 1985 гг. - 416 с. - 1422 экз.
7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М. Высшая школа, 1980, 1986 гг. - 718 с. - 2790 экз.
8. Задачи и упражнения по математическому анализу (Под ред. Демидовича Б.П.) - М. Наука, 1972, 1978, 1990 гг. - 479 с. - 436 экз.
9. Минорский В.П. Сборник задач по высшей математике. - М. Наука, 1969, 1978, 1987 гг. - 352 с.
Дополнительная литература (учебные пособия и методические указания)
1 .Фихтенгольц Г.М. Основы математического анализа (в 2-х томах).- М. Наука, 1960, 1968 гг. - 903 с.
2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (в 3-х томах) - М. Наука,
1962, 1970 гг. - 2063 с. - 78 экз.
3. Шнейдер В.Е. и др. Краткий курс высшей математики (в 2-х томах ). - М. Наука, 1978. - 384 с.
4. Мантуров О.В., Матвеев Н.И. Курс высшей математики. - М. Наука,1980 г. - 480 с. - 299 экз.
5. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. - М. Наука , 1973 г. –720с.
6. ЗапорожецГ.Н. Руководство к решению задач по математическому анализу. - М. Высшая школа, 1966 г. –460 с. -256 экз.
7. Кузнецов Л.А. Сборник задач по высшей математике. – М. Наука, 1983г. -175 с. - 112 экз.
8. Сборник задач по математике для втузов (под ред. Ефимова А.В.) - М. Наука, 1981, 1986 гг. - 836 с.
9. Терехина Л.И., Фикс И.И. Дифференциальное исчисление. — Томск, Изд. ТПУ, 2004, - 224 с.
Образцы контролирующих материалов.
| Учебная дисциплина Дифференциальное исчисление |  | Ф ТПУ 7.1-21/01 |
ЭФФ Экзамен Курс 1
УТВЕРЖДАЮ
Декан ЭФФ
________________Евтушенко Г.С.
«___»__________________2009 г.

 Экзаменационный билет №1
Экзаменационный билет №1Дифференциальное исчисление
Семестр I Курс I 2009/2010 уч. год. ЭФФ
- Сформулировать и доказать теорему Лагранжа.
- Найдите пределы: а)
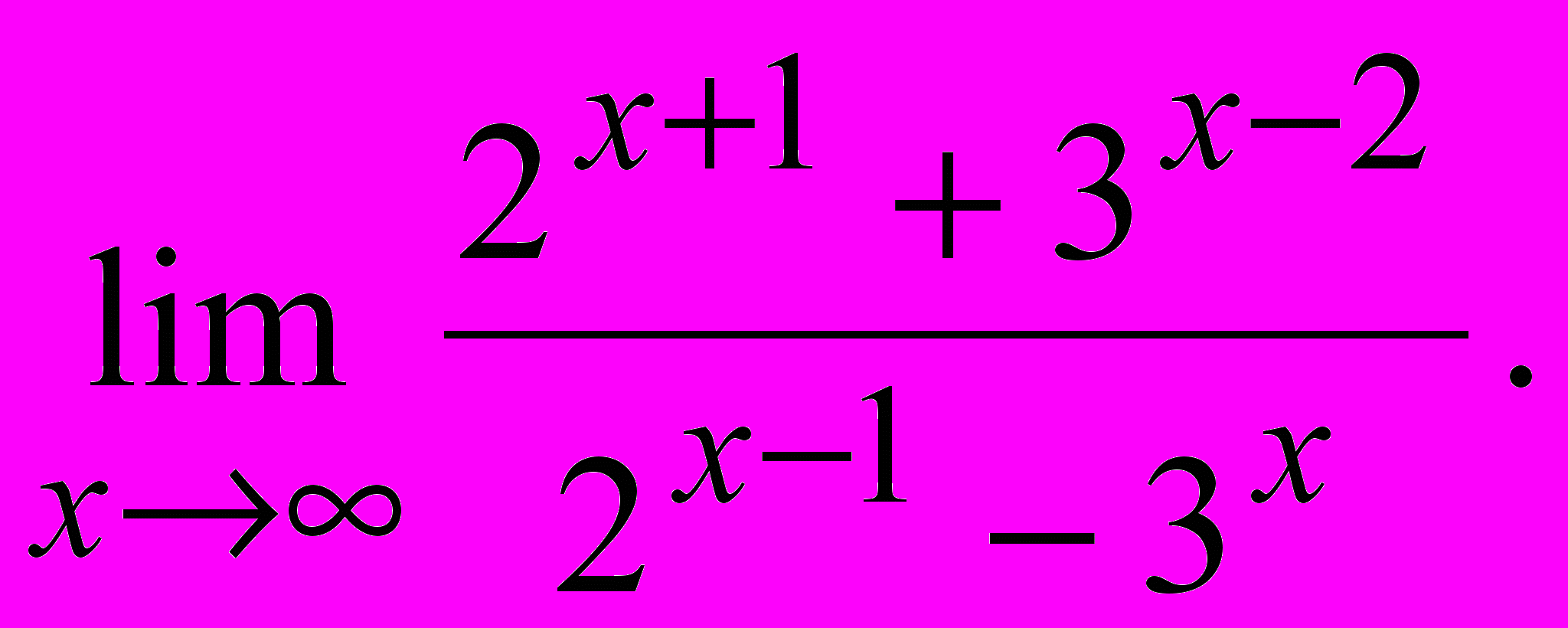 в)
в) 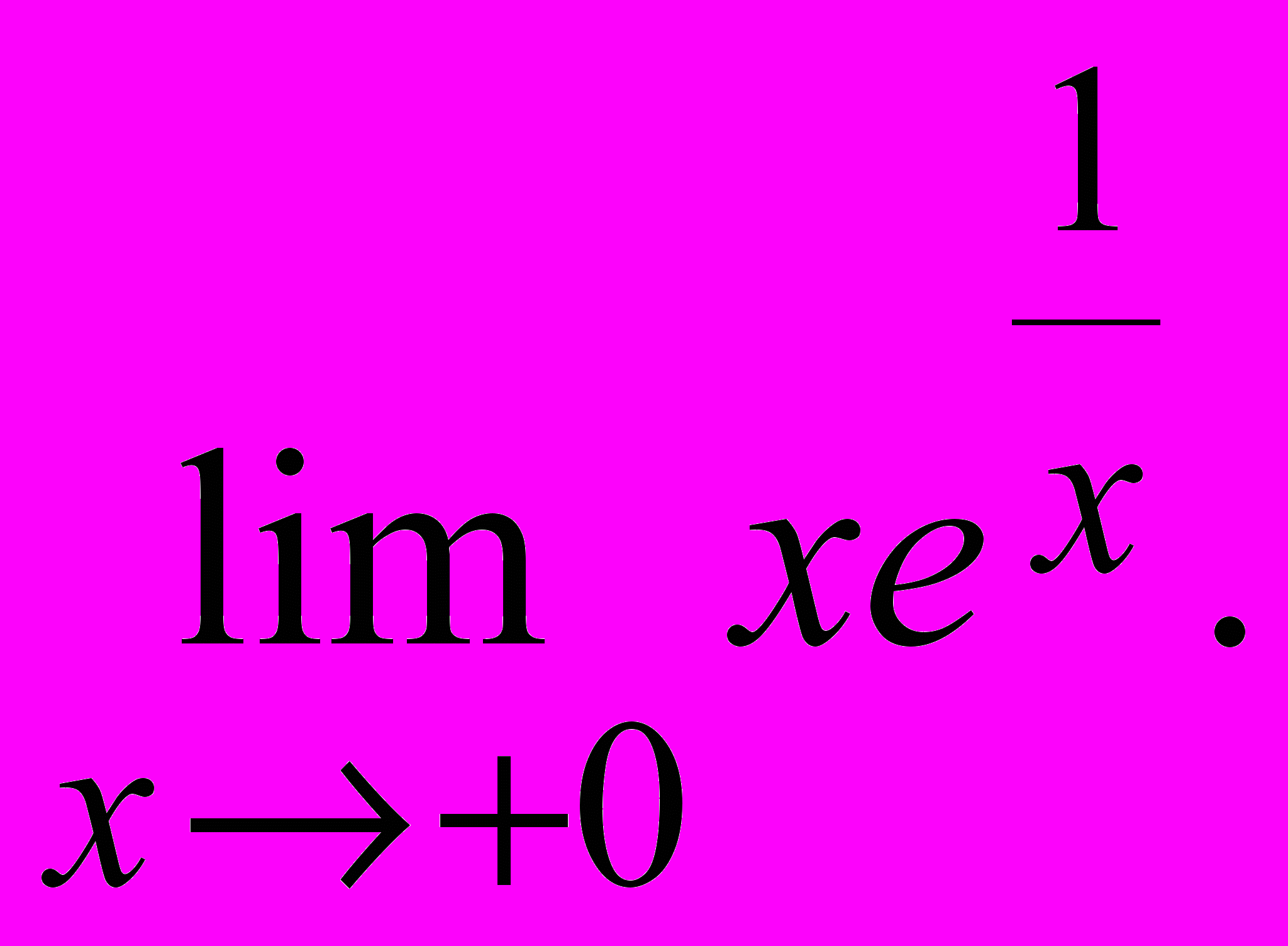
- Найдите а) производную функции
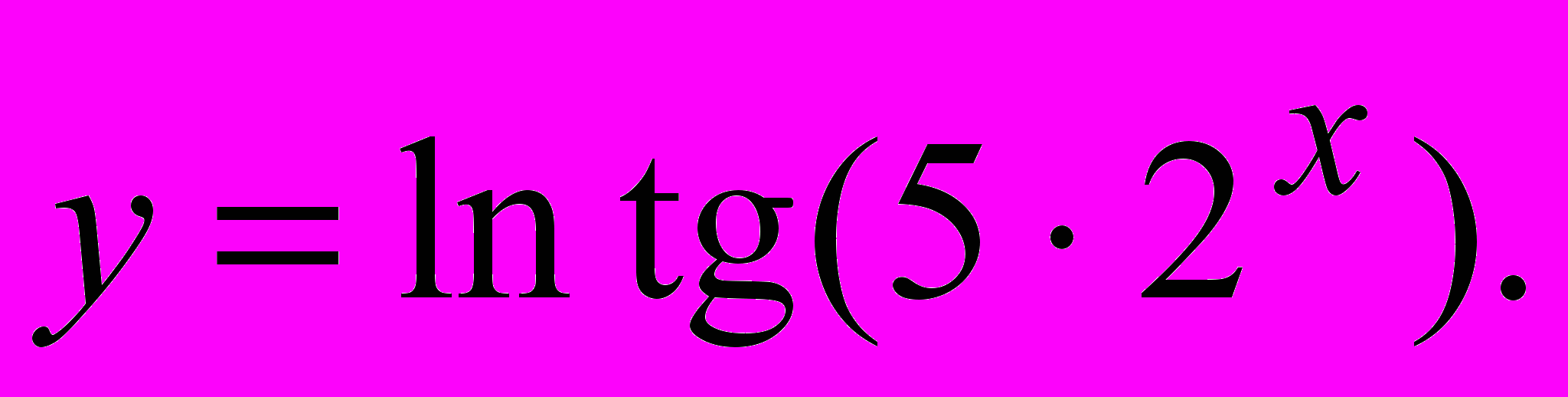
в) все частные производные первого порядка функции

- Определите точки перегиба и интервалы выпуклости и вогнутости функции
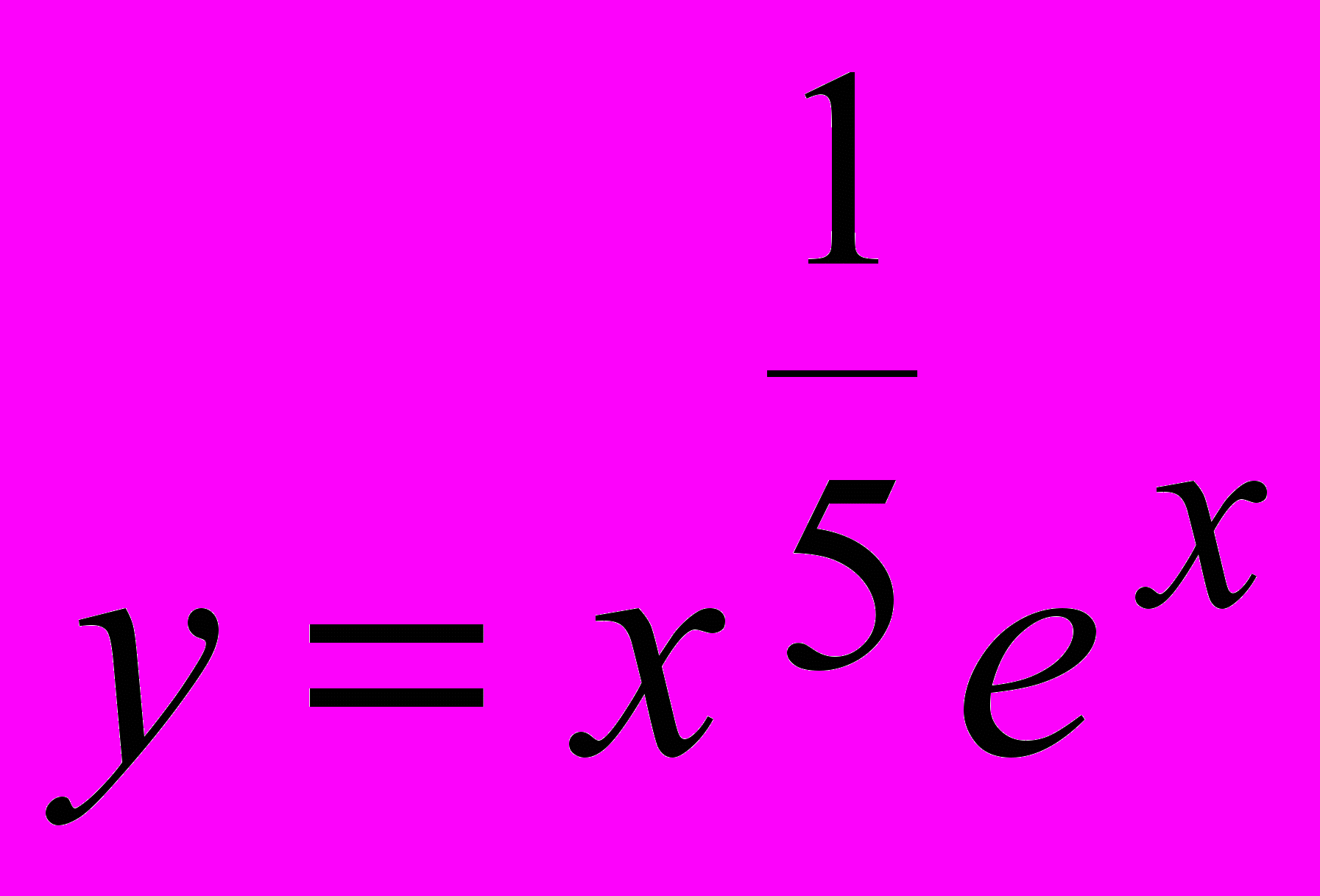 .
.
- Найти наибольшее и наименьшее значение функции:
 в замкнутой области, ограниченной линиями
в замкнутой области, ограниченной линиями 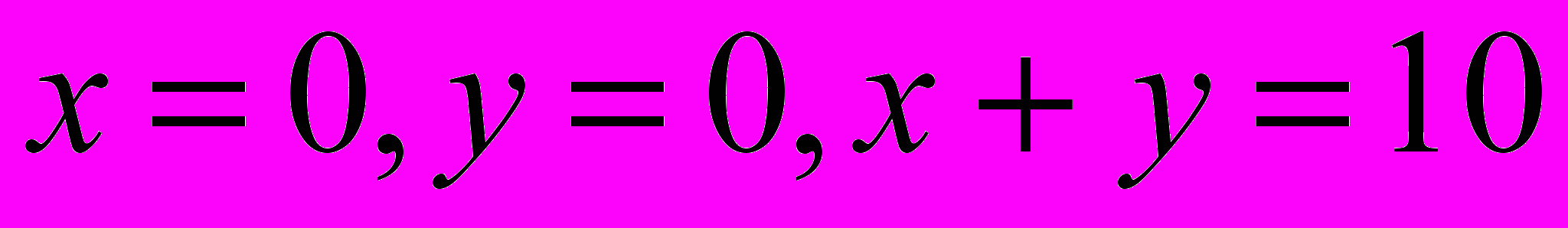 .
.
Составили - Зальмеж В.Ф.
Филипенко Н.М.
Утверждаю: Зав. кафедрой Трифонов А.Ю.
Контрольная работа №1 по теме «Введение в анализ»
ВАРИАНТ №1
Найти пределы
1.
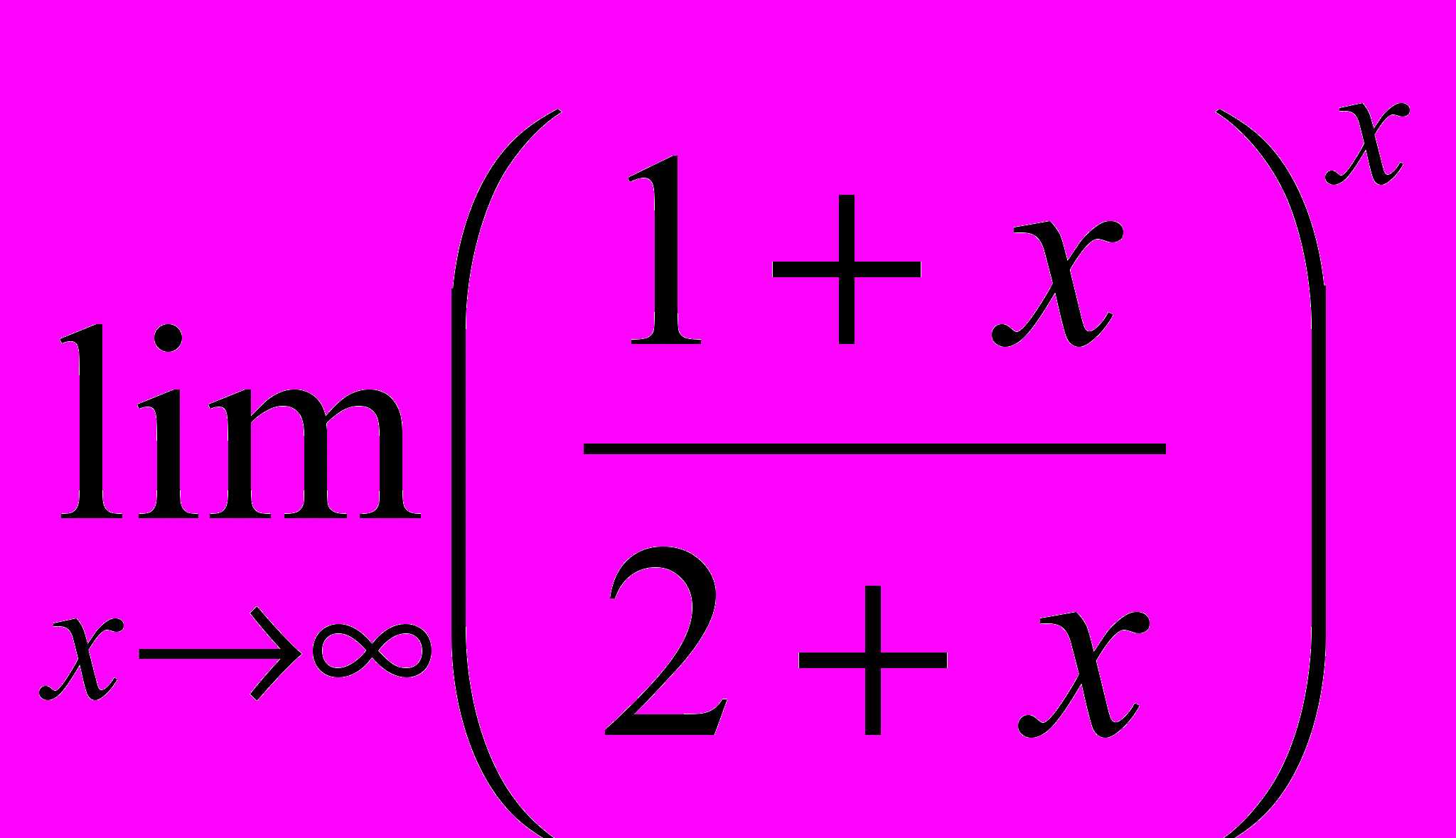 ; 1.
; 1. 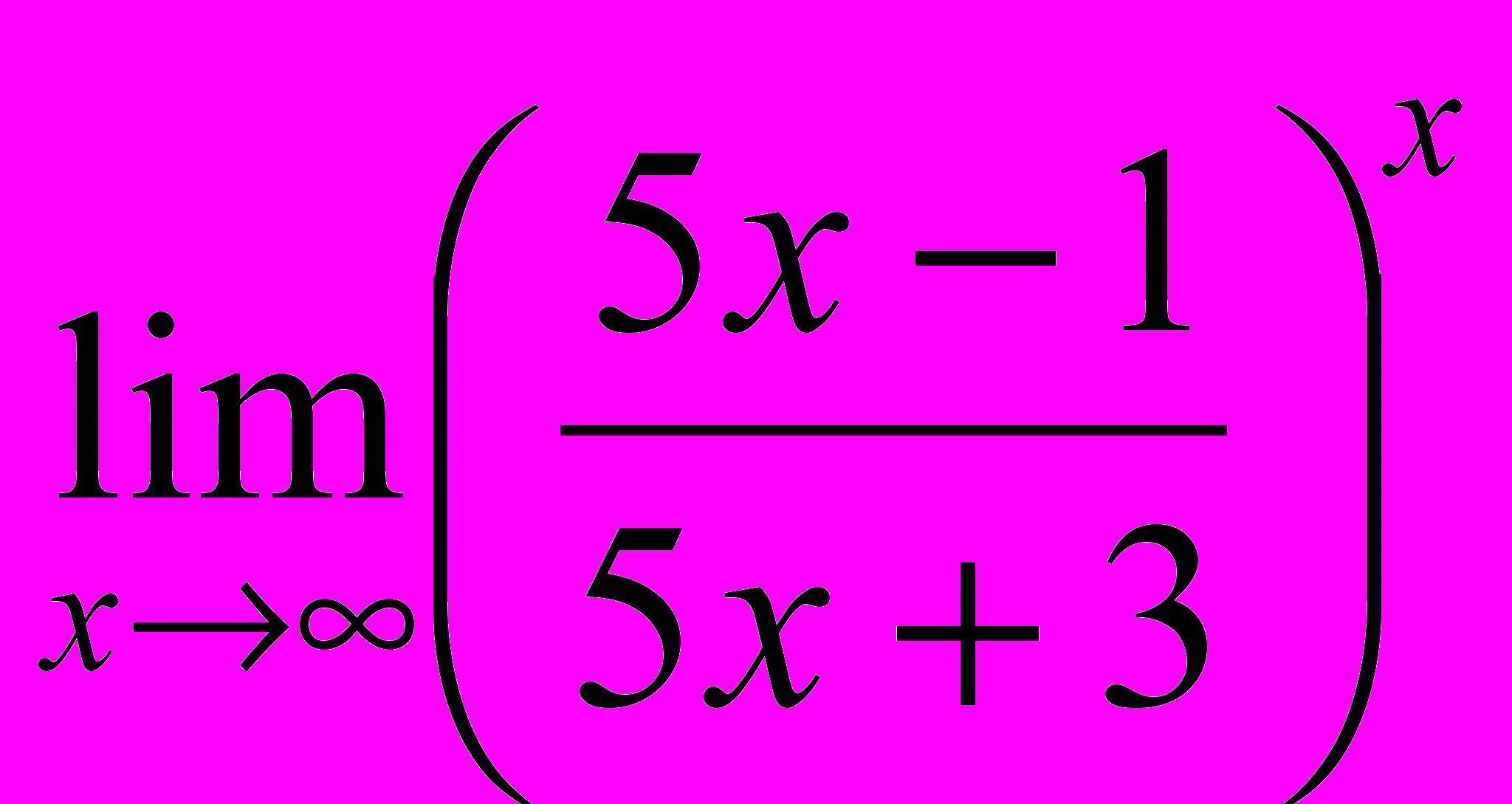 ;
;2.
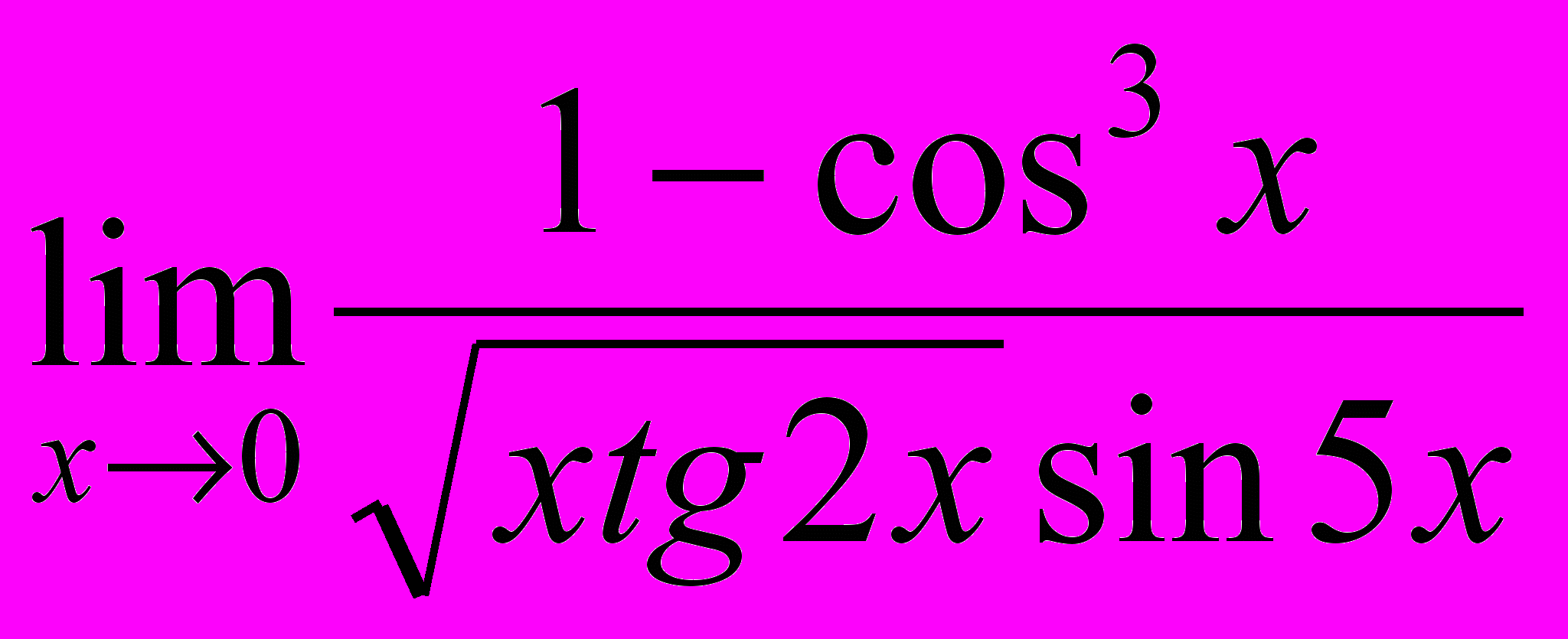 ; 2.
; 2. 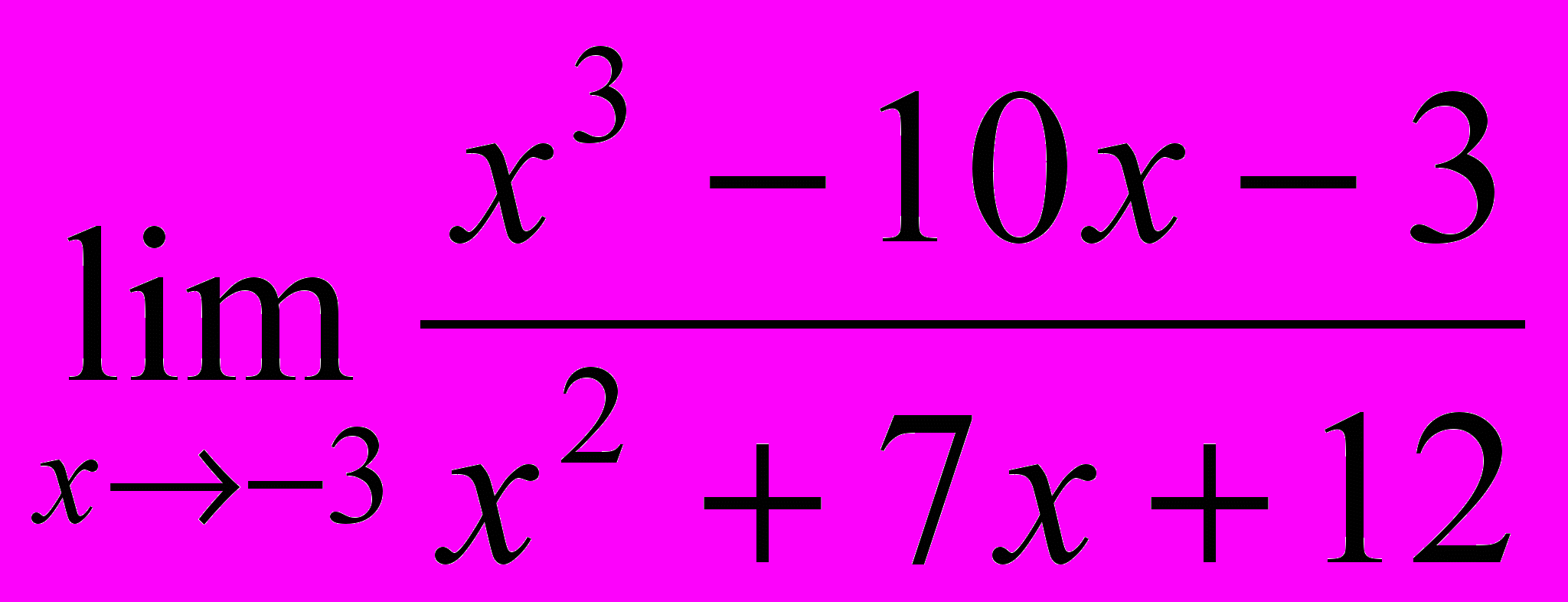 ;
;3.
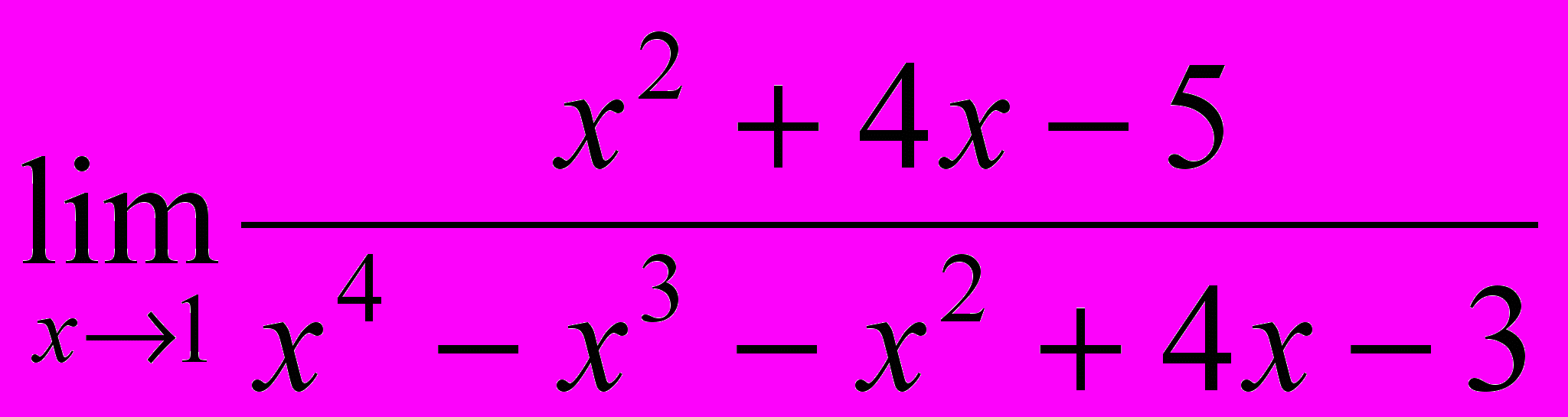 ; 3.
; 3. 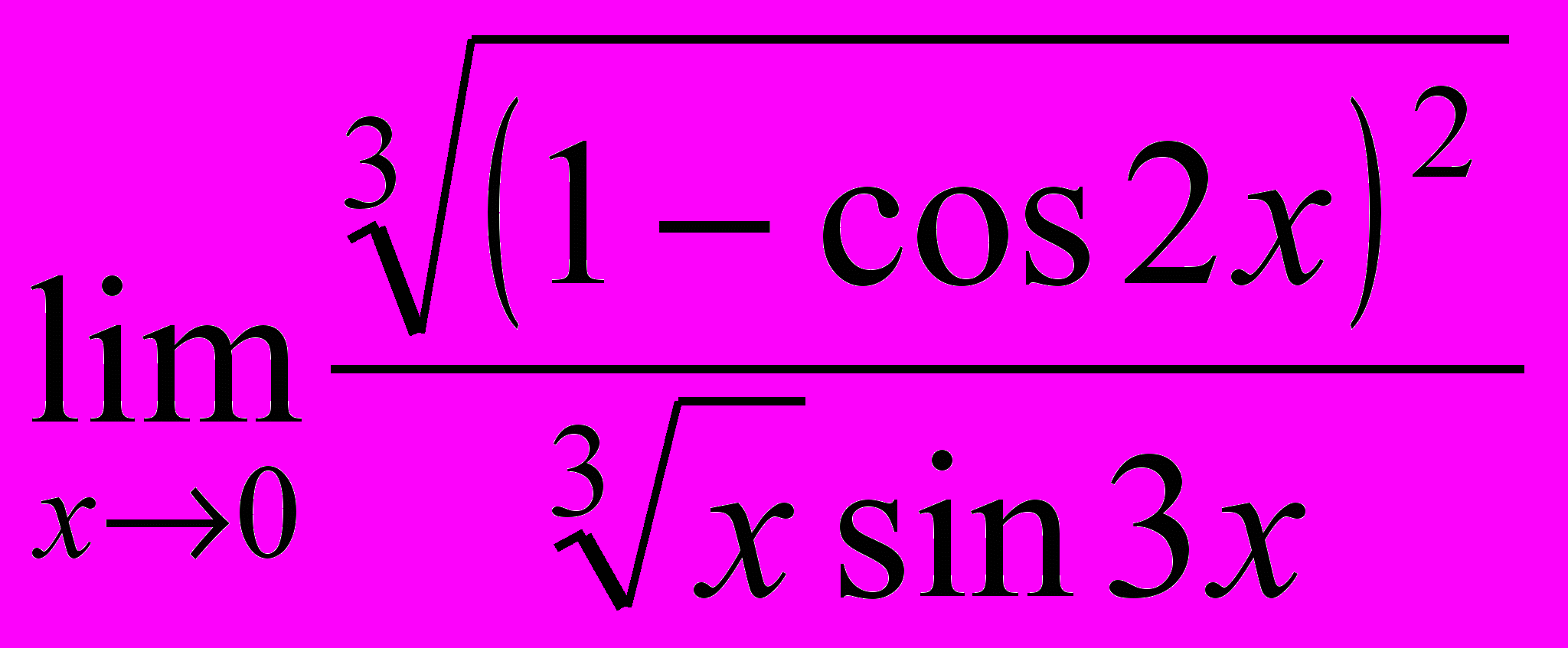 ;
;4.
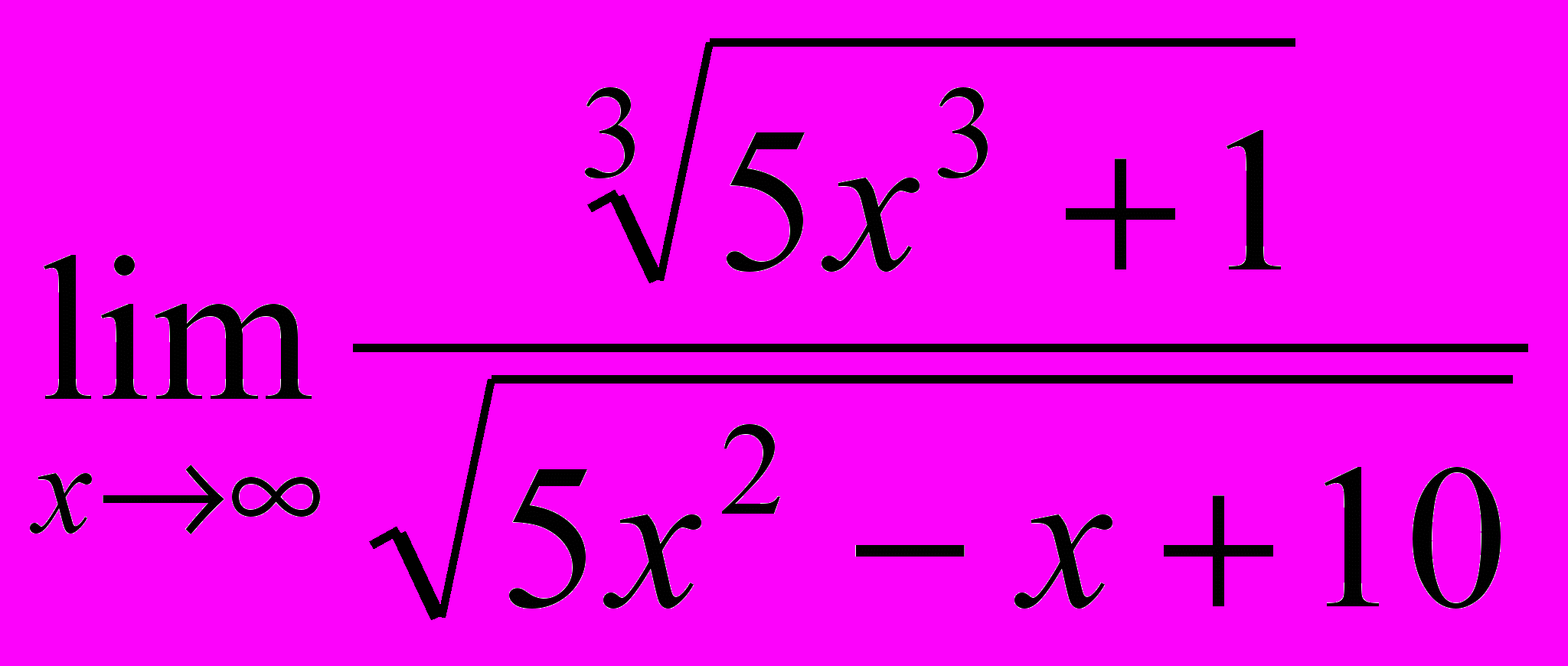 ; 4.
; 4. 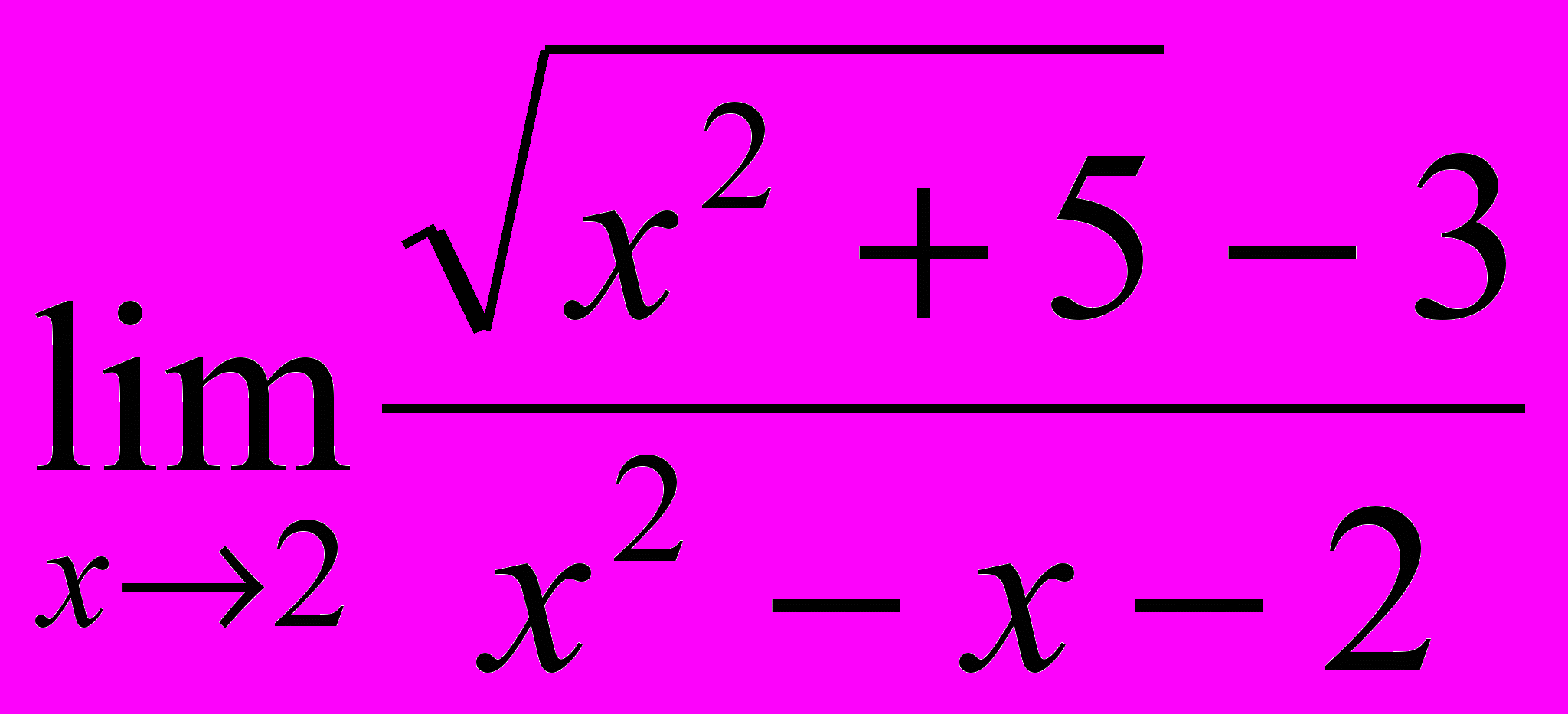 ;
;5.
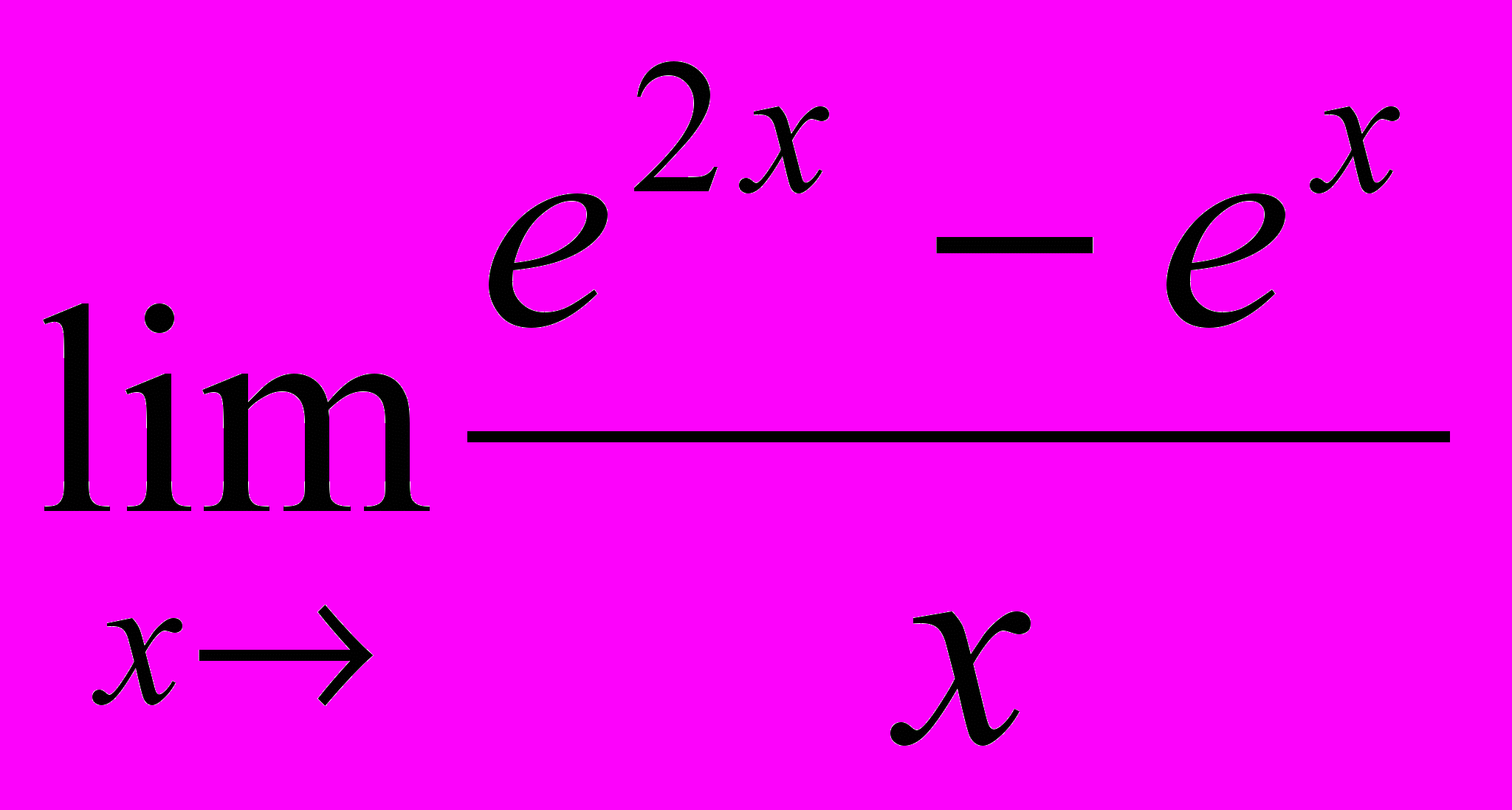 . 5.
. 5. 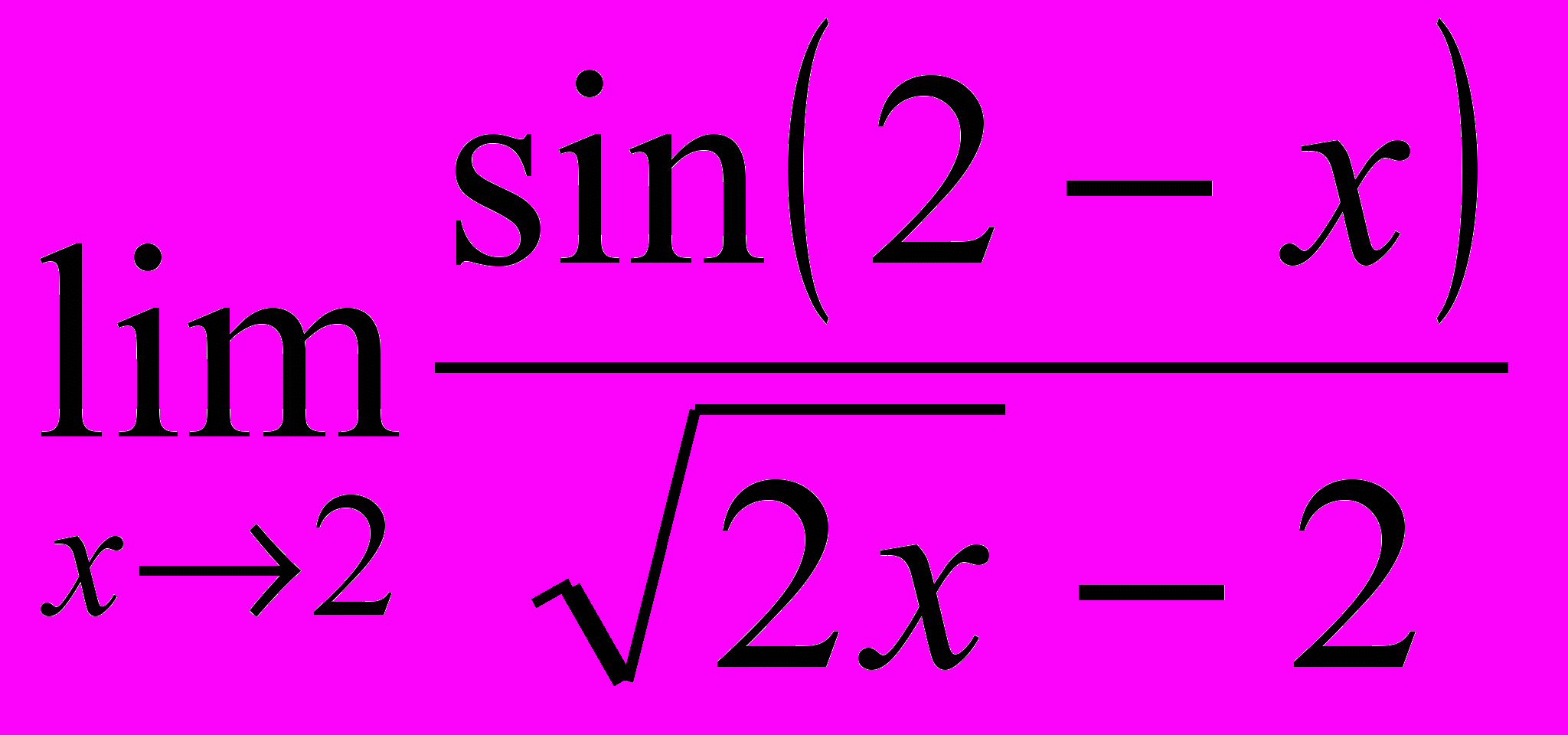 .
.II. Определить порядок малости
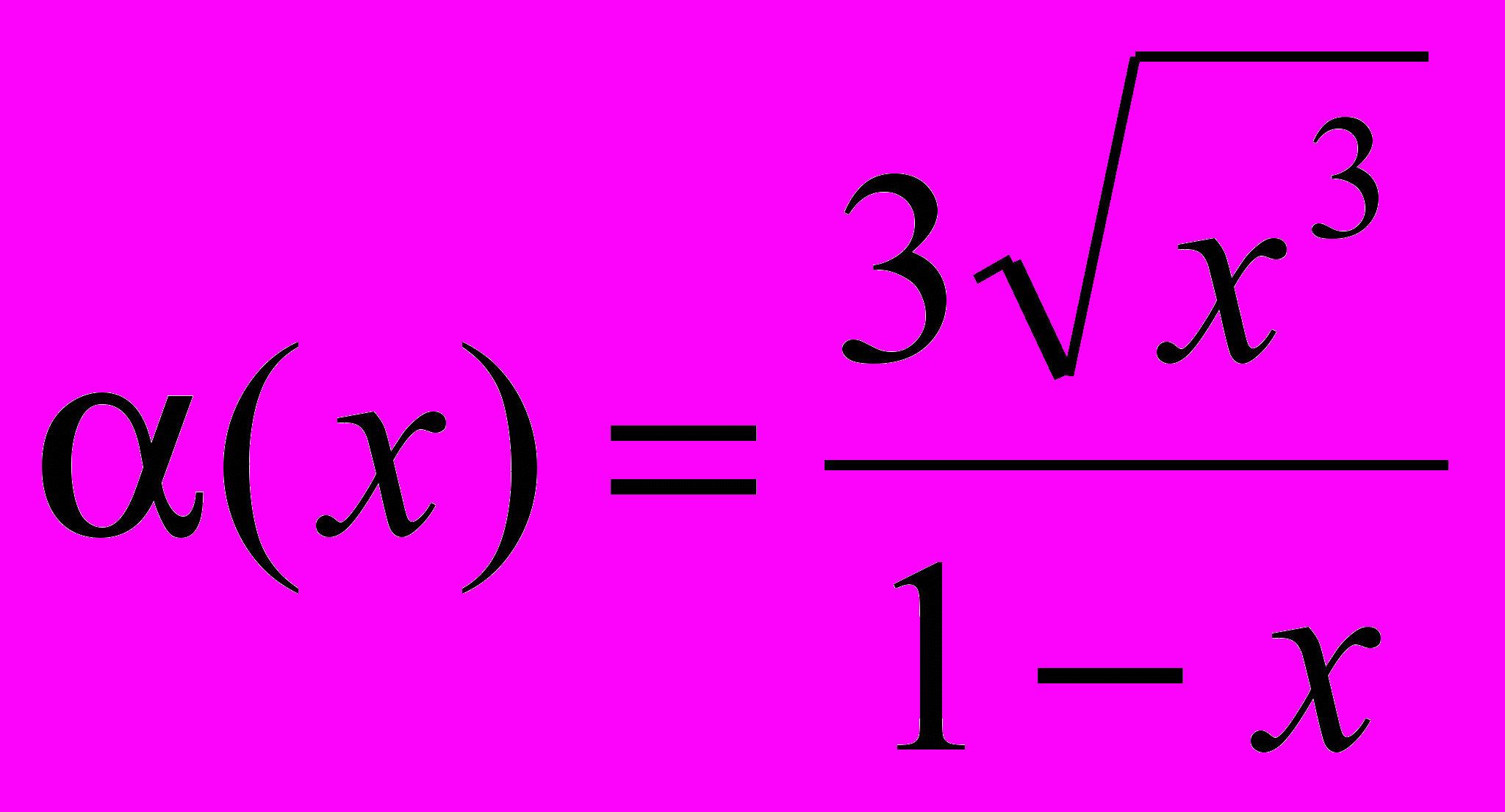 относительно x при
относительно x при  .
.Контрольная работа №2 по теме «Дифференциальное исчисление»
ВАРИАНТ №1
I. Найти производные следующих функций:
1.
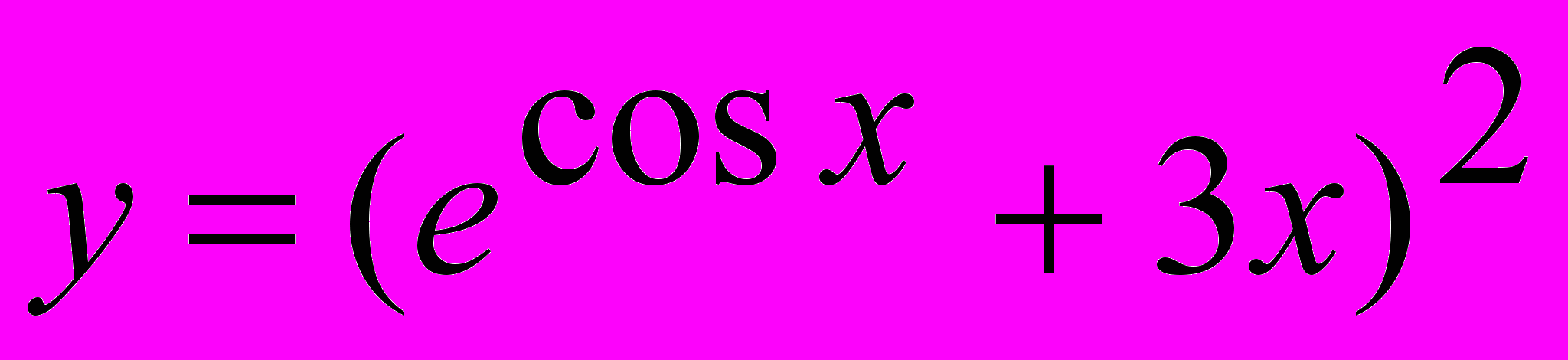 ; 2.
; 2. 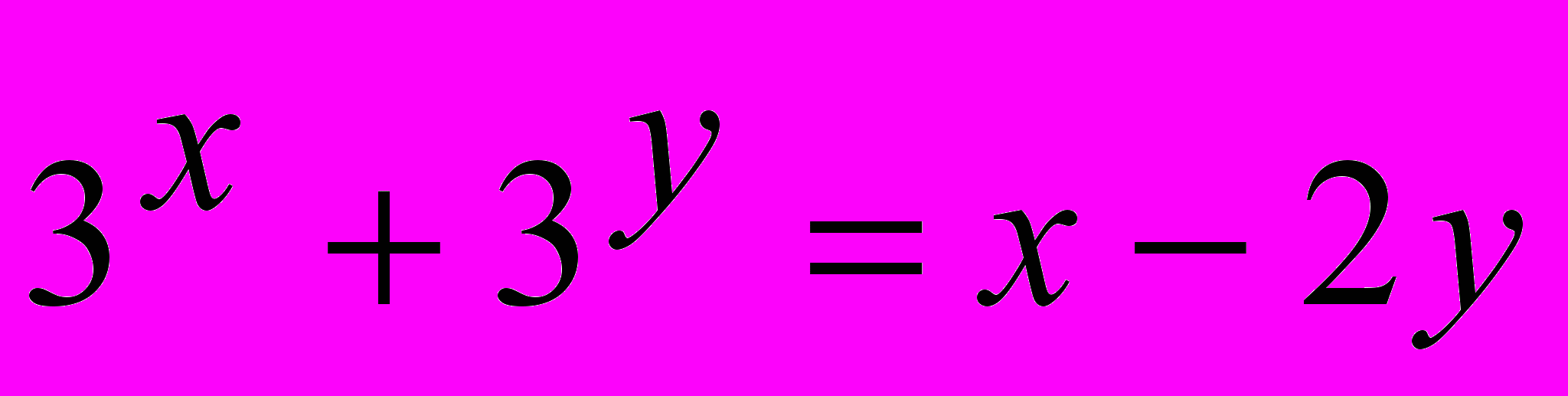 ; 3.
; 3. 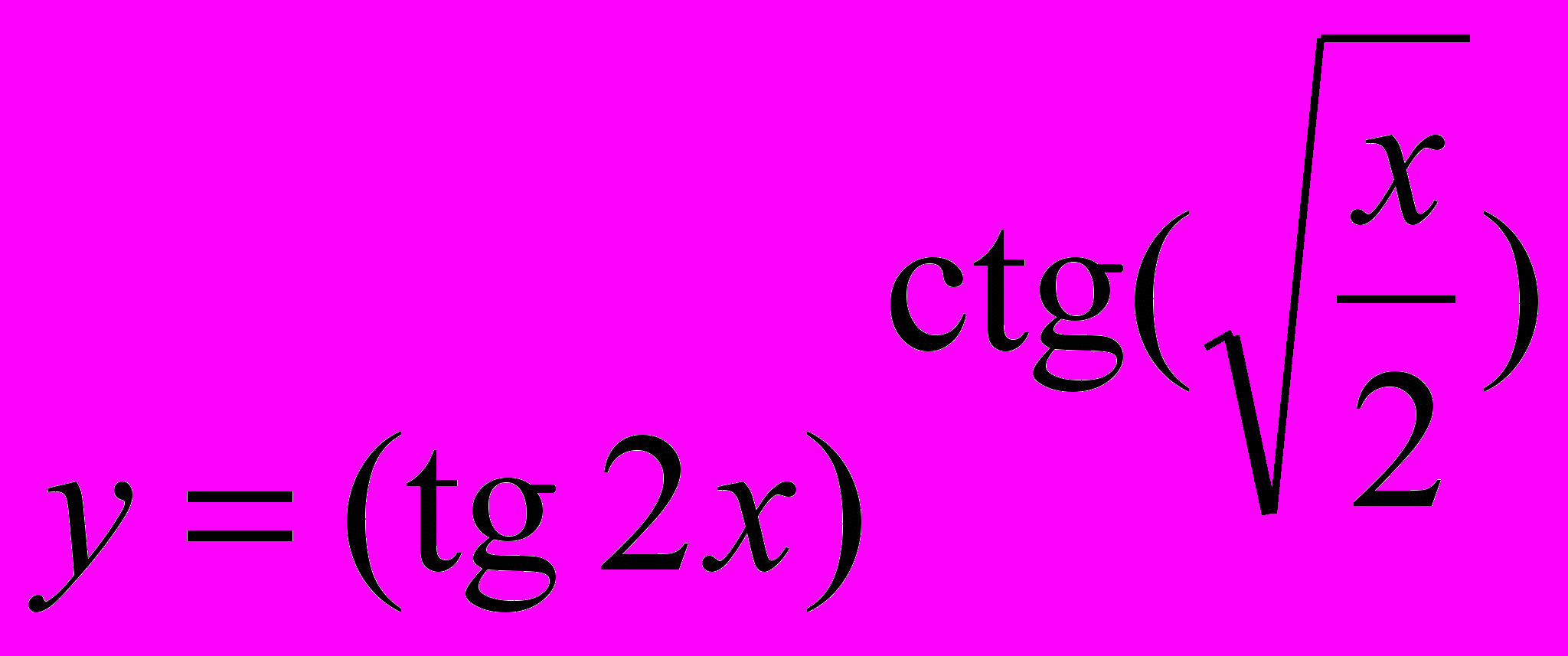 ;
; II. Найти вторую производную
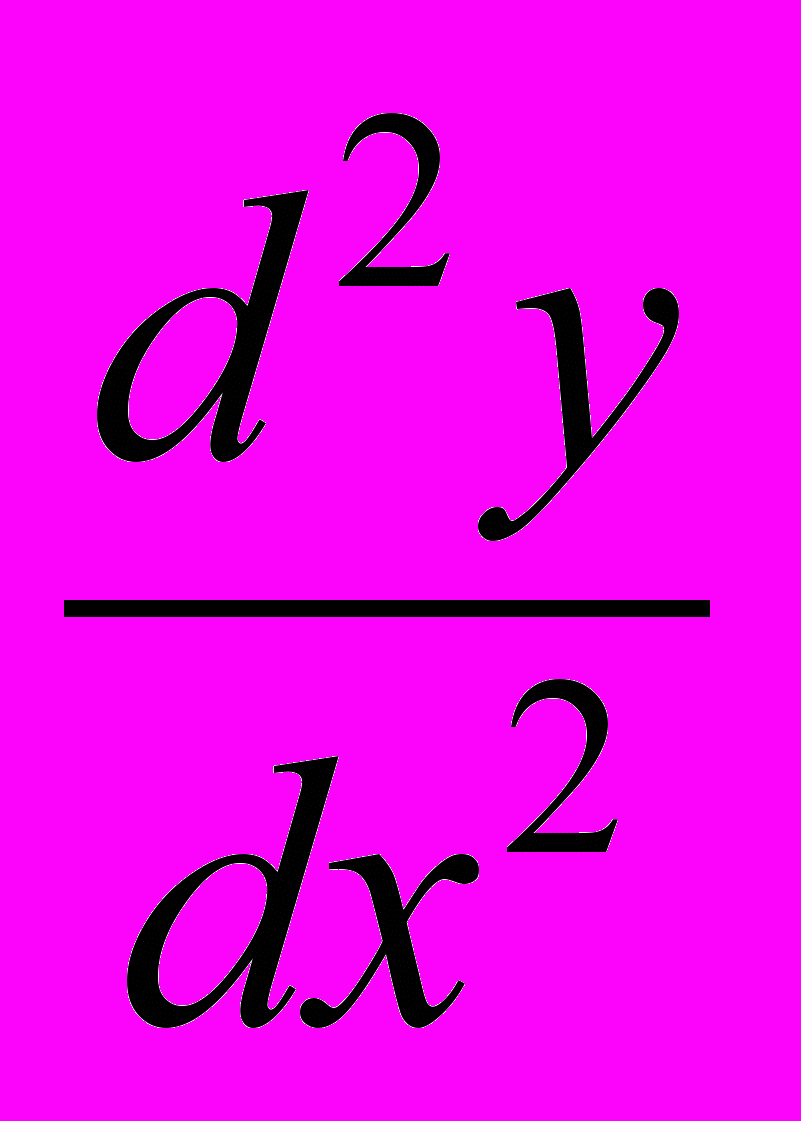 : 1.
: 1. 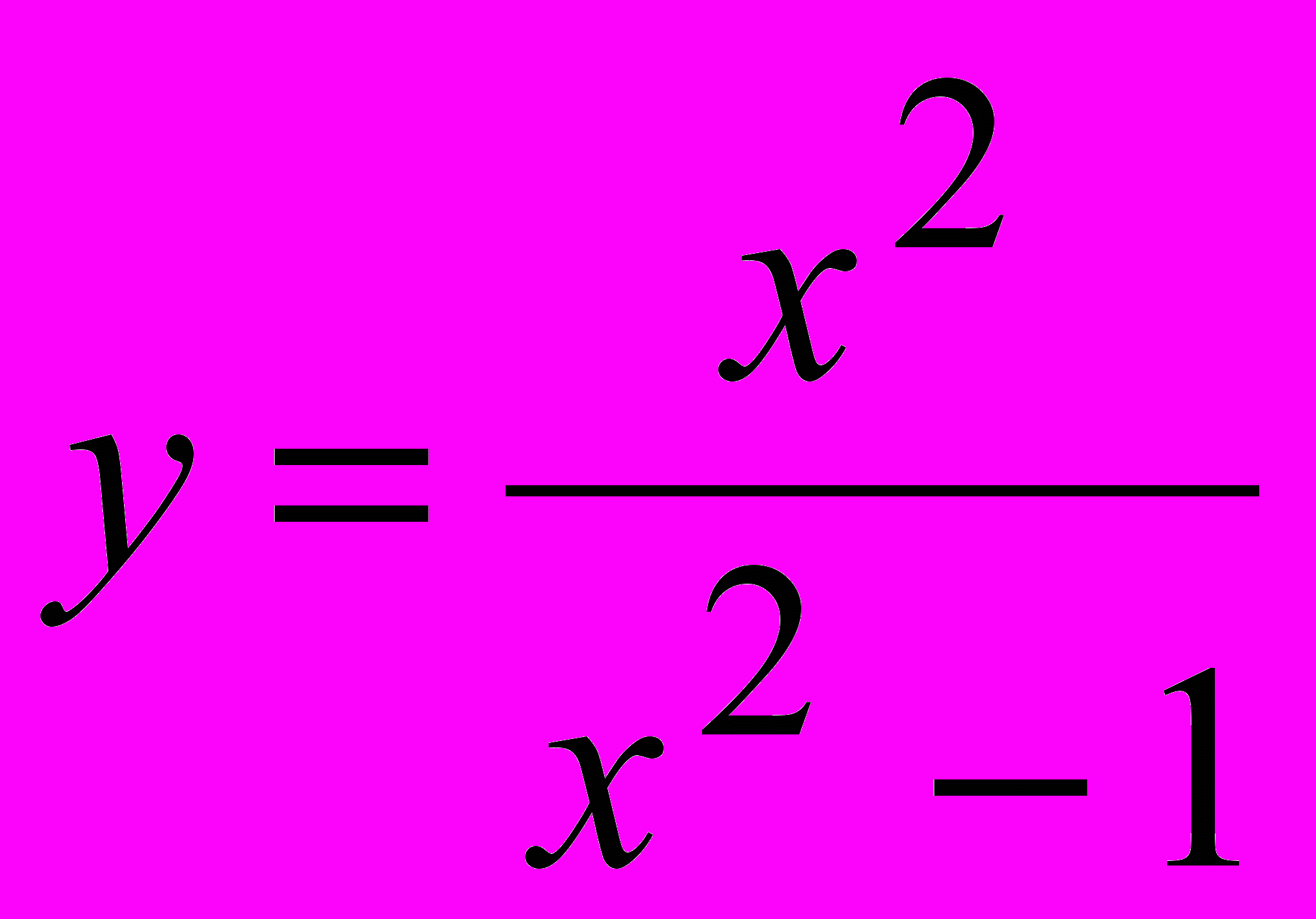 , 2.
, 2. 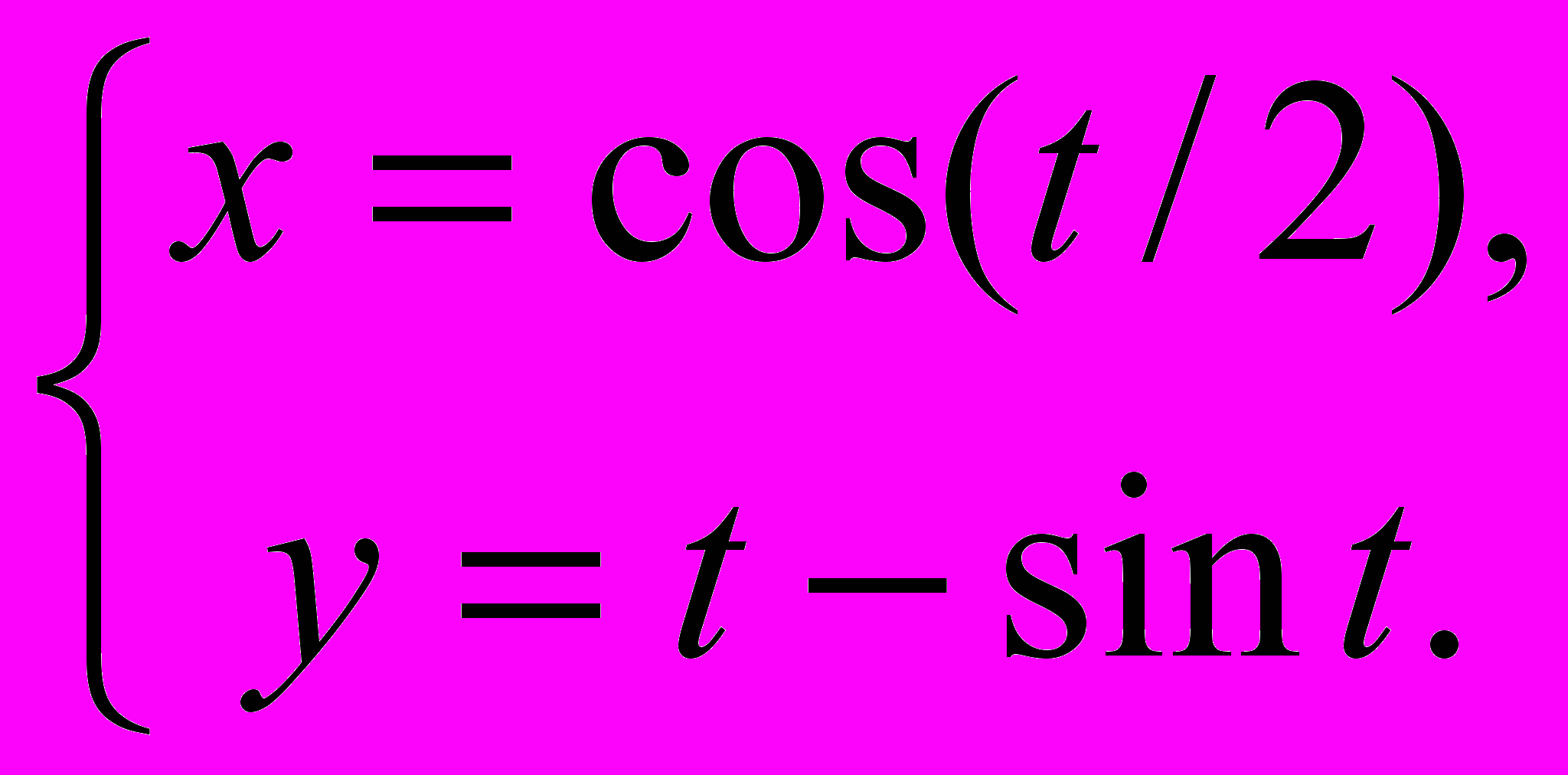
III. Пользуясь правилом Лопиталя найти пределы:
1.
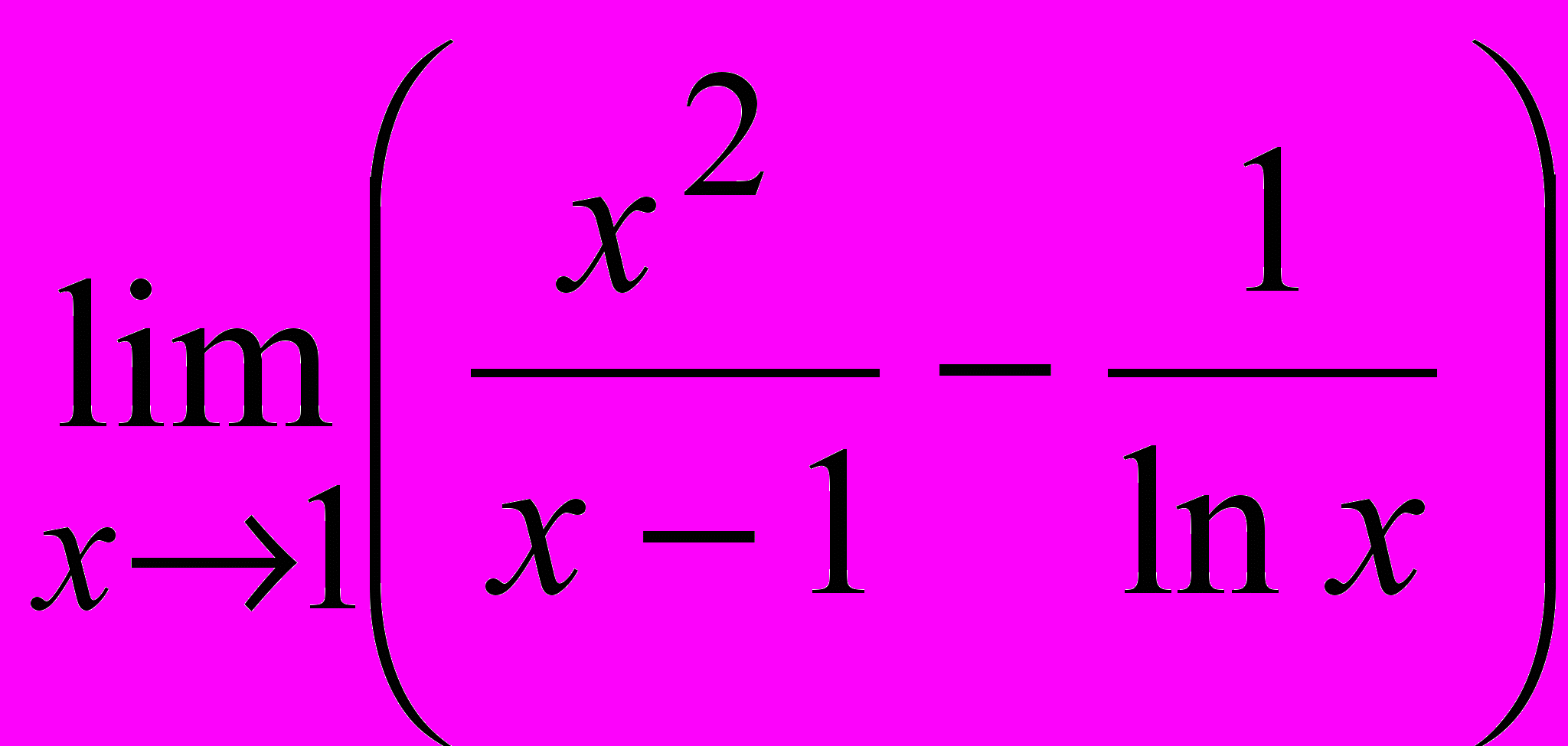 2.
2. 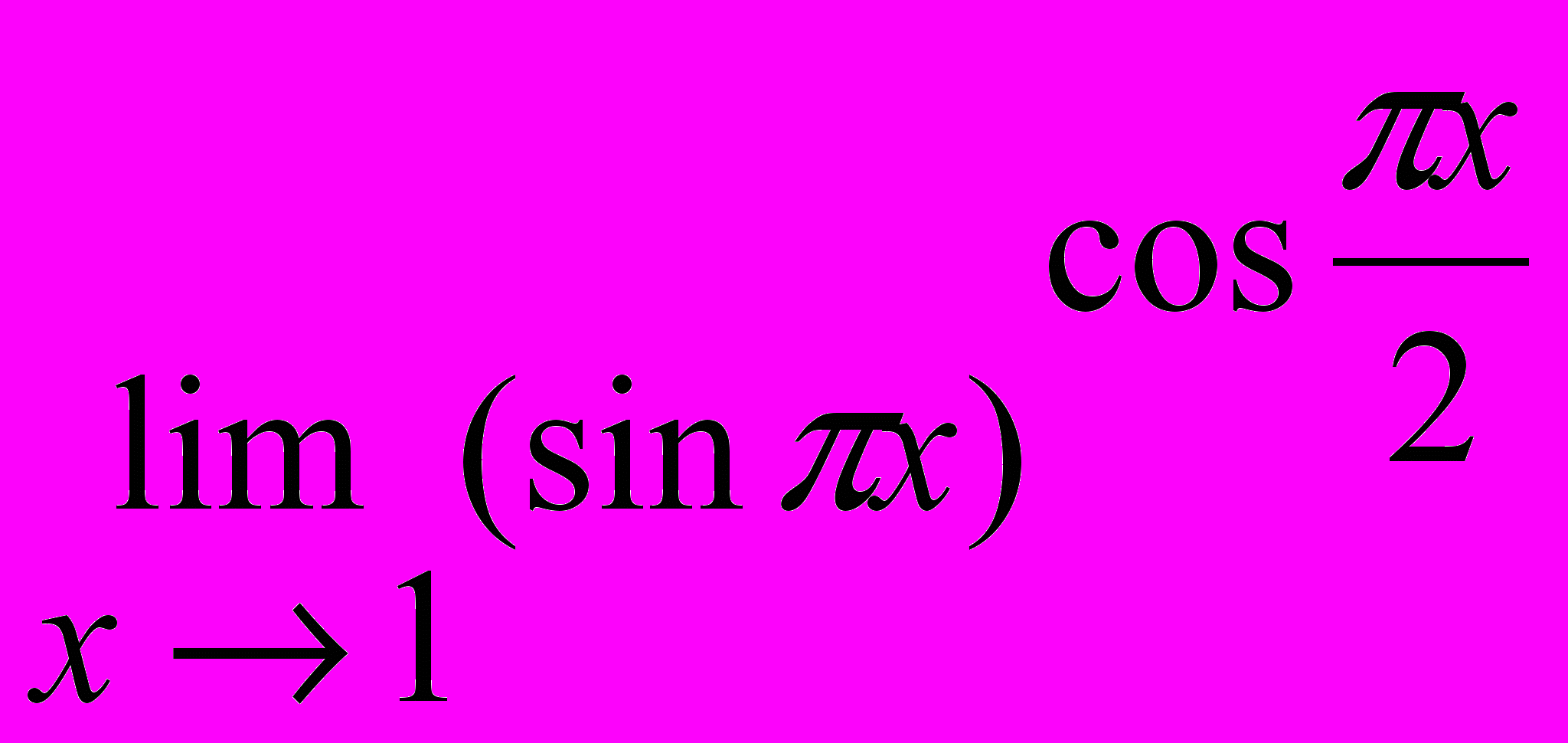
IV. Провести полное исследование функции и построить график функции :
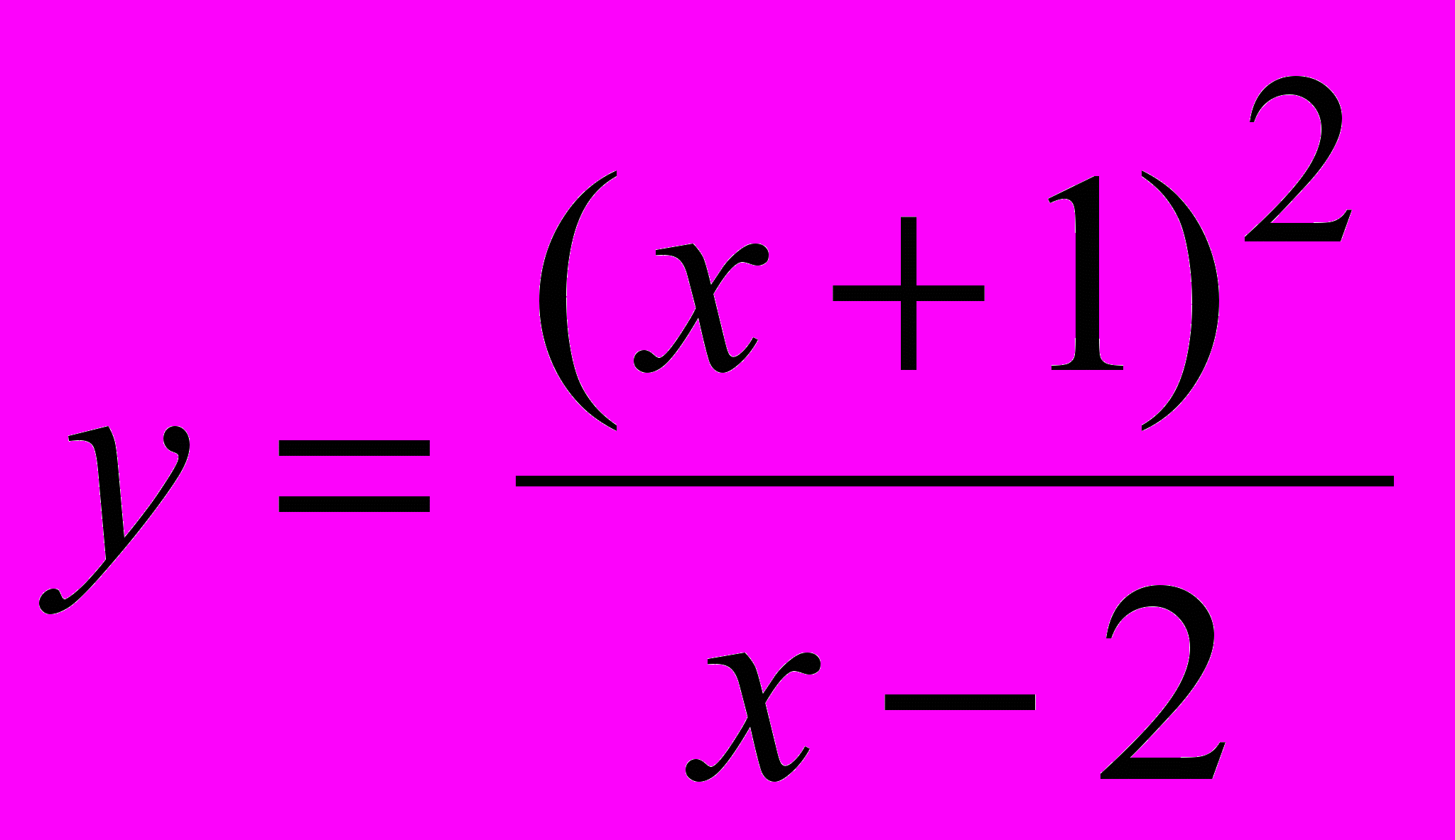 .
. Контрольная работа №3 по теме «Дифференциальное исчисление ФНП»
ВАРИАНТ №1
I. Найти и построить область определения следующих функций:
1.
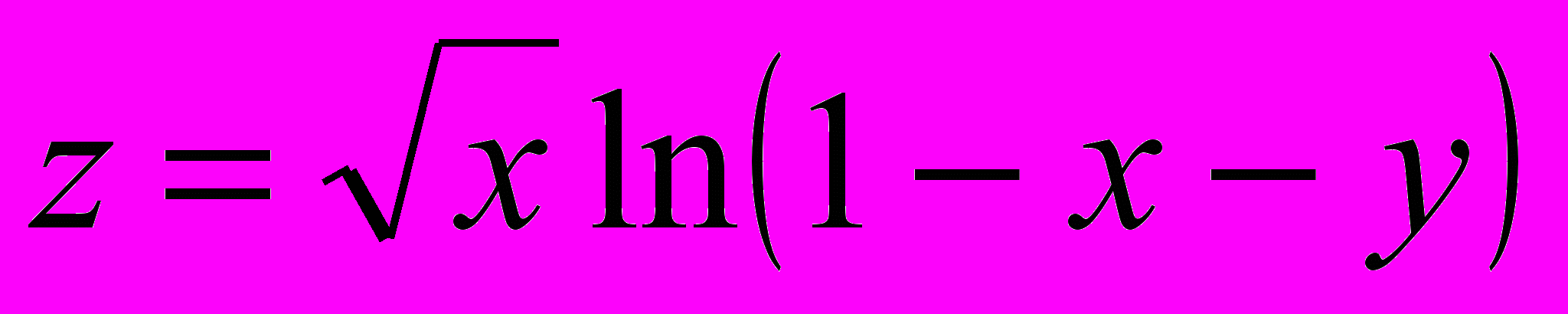 ; 1.
; 1. 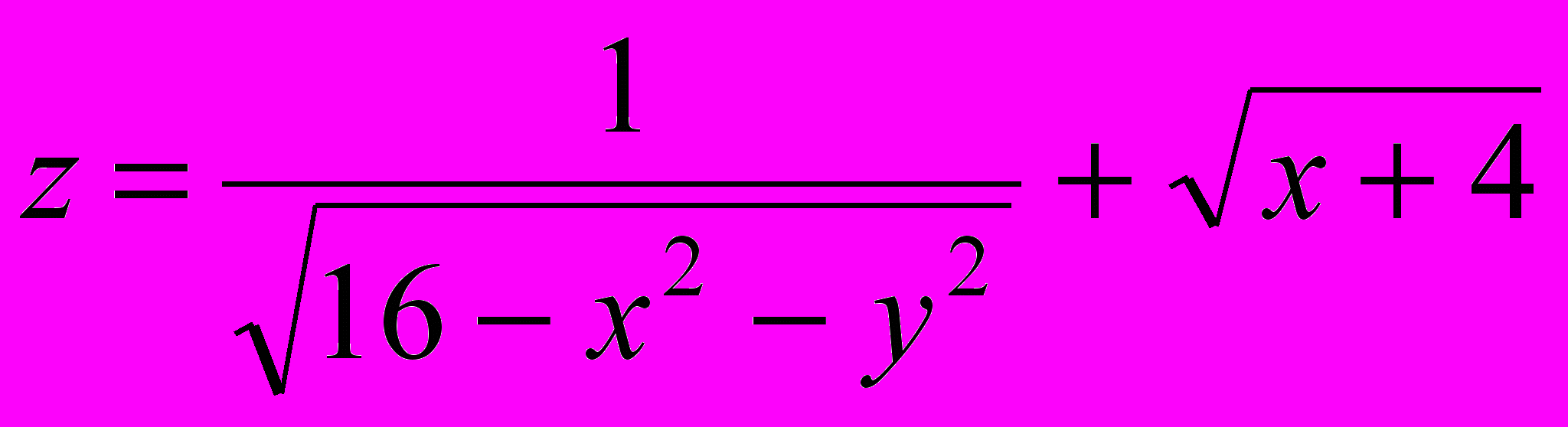 ;
;- Найти полный дифференциал функции
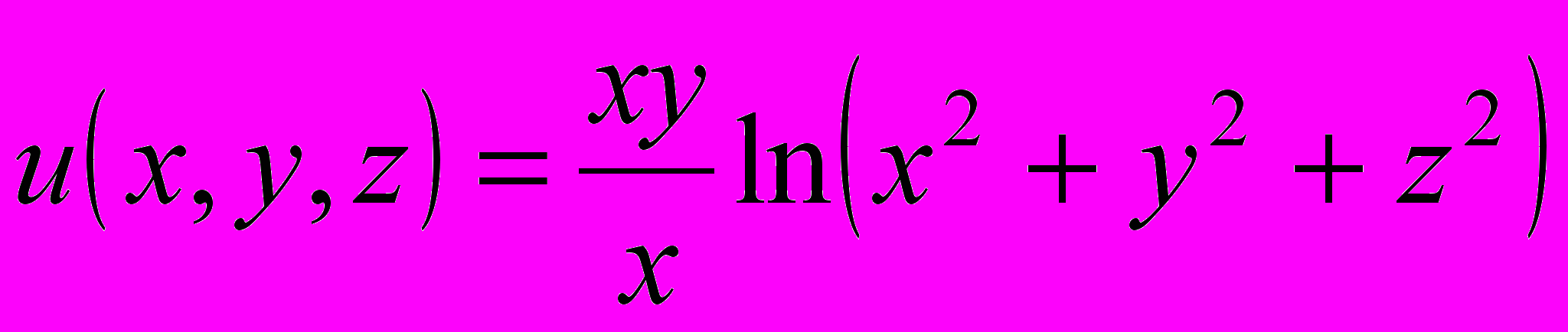 .
.
- Найти
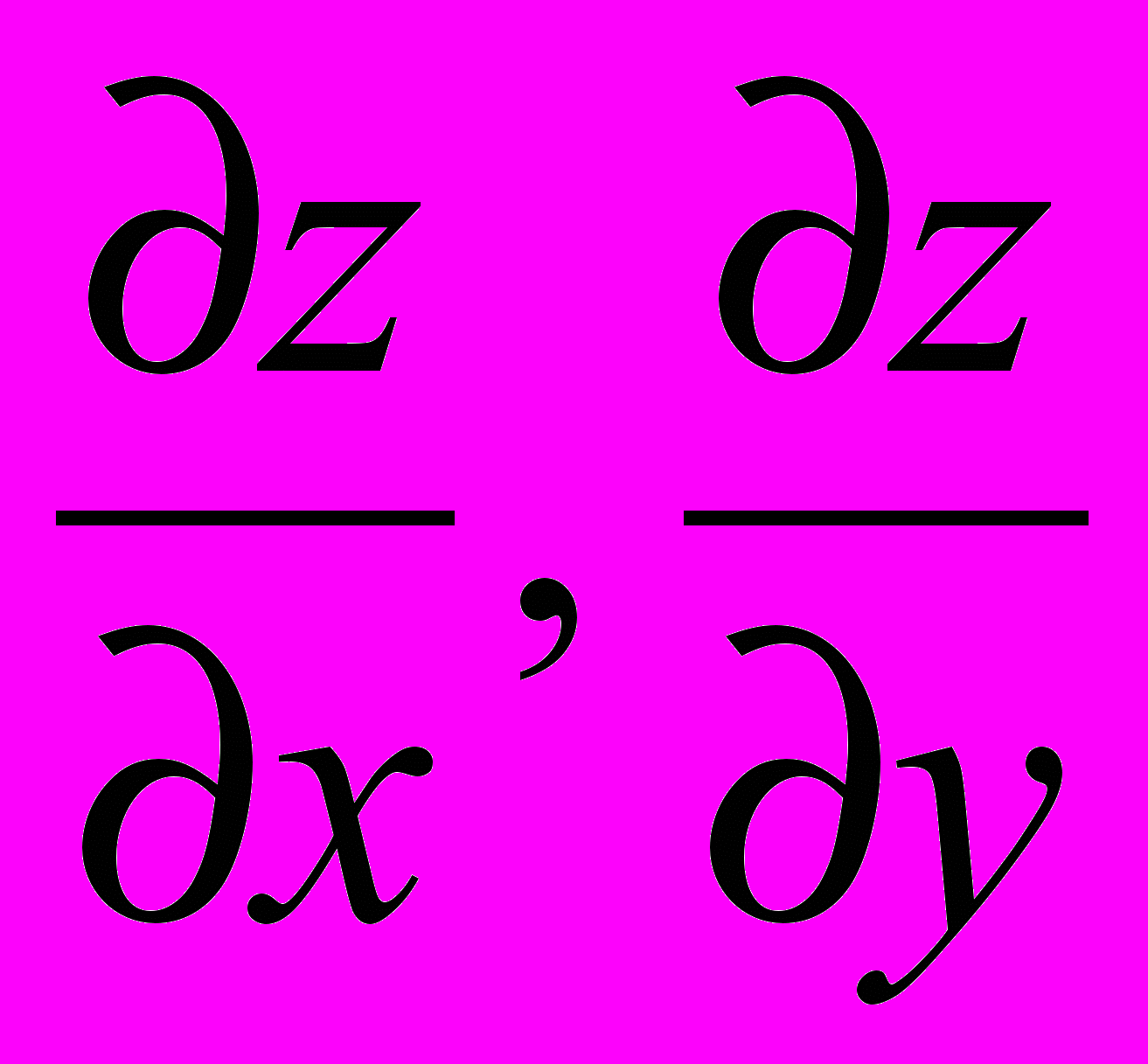 функции
функции 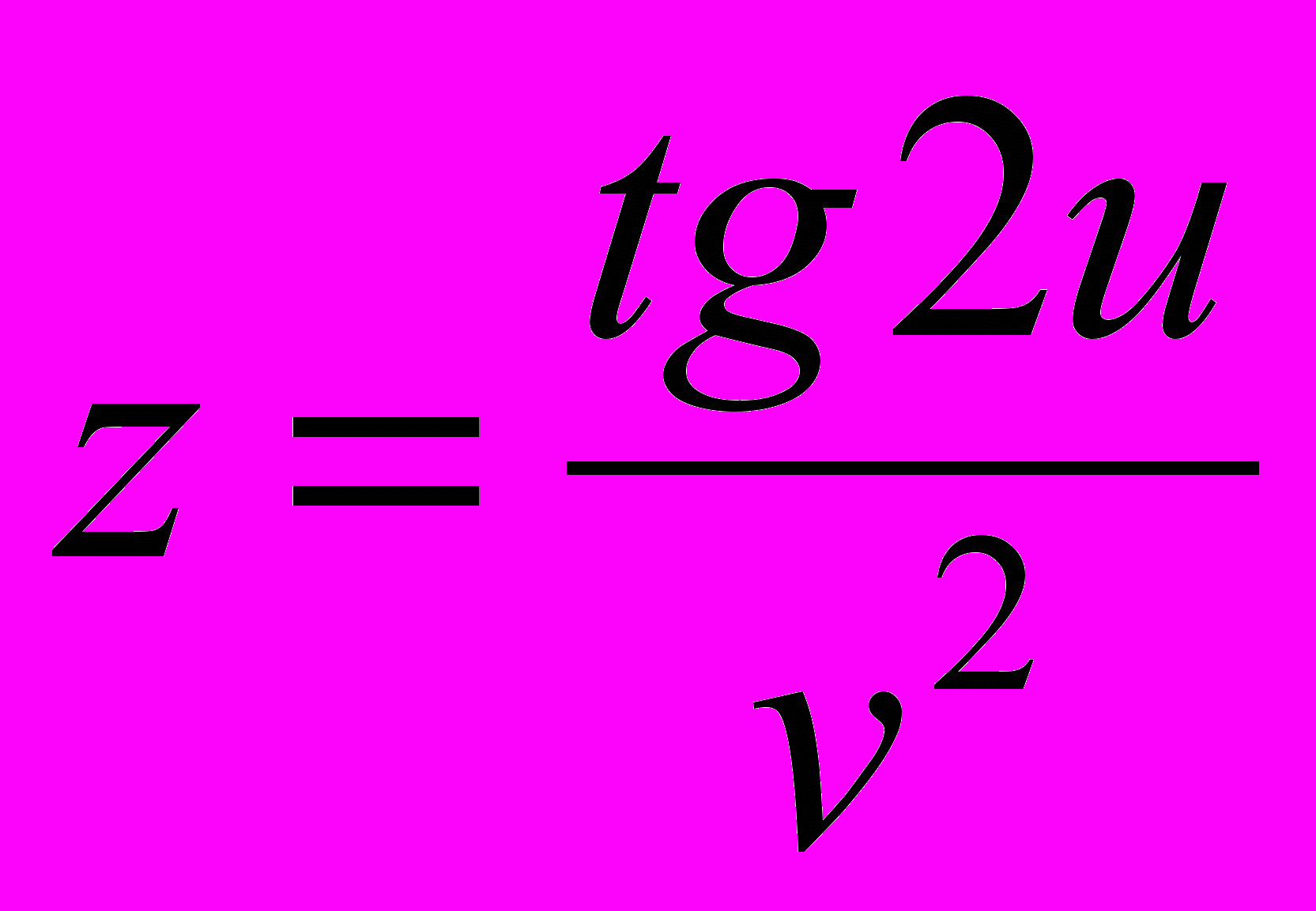 , если
, если 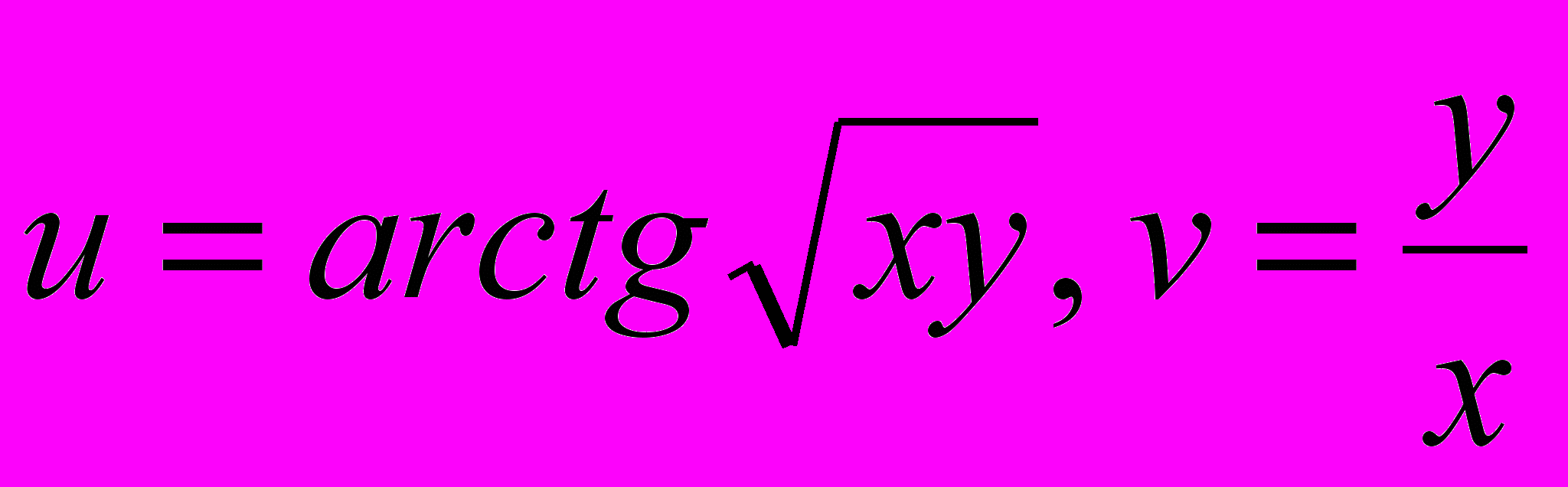 .
.
- Найти
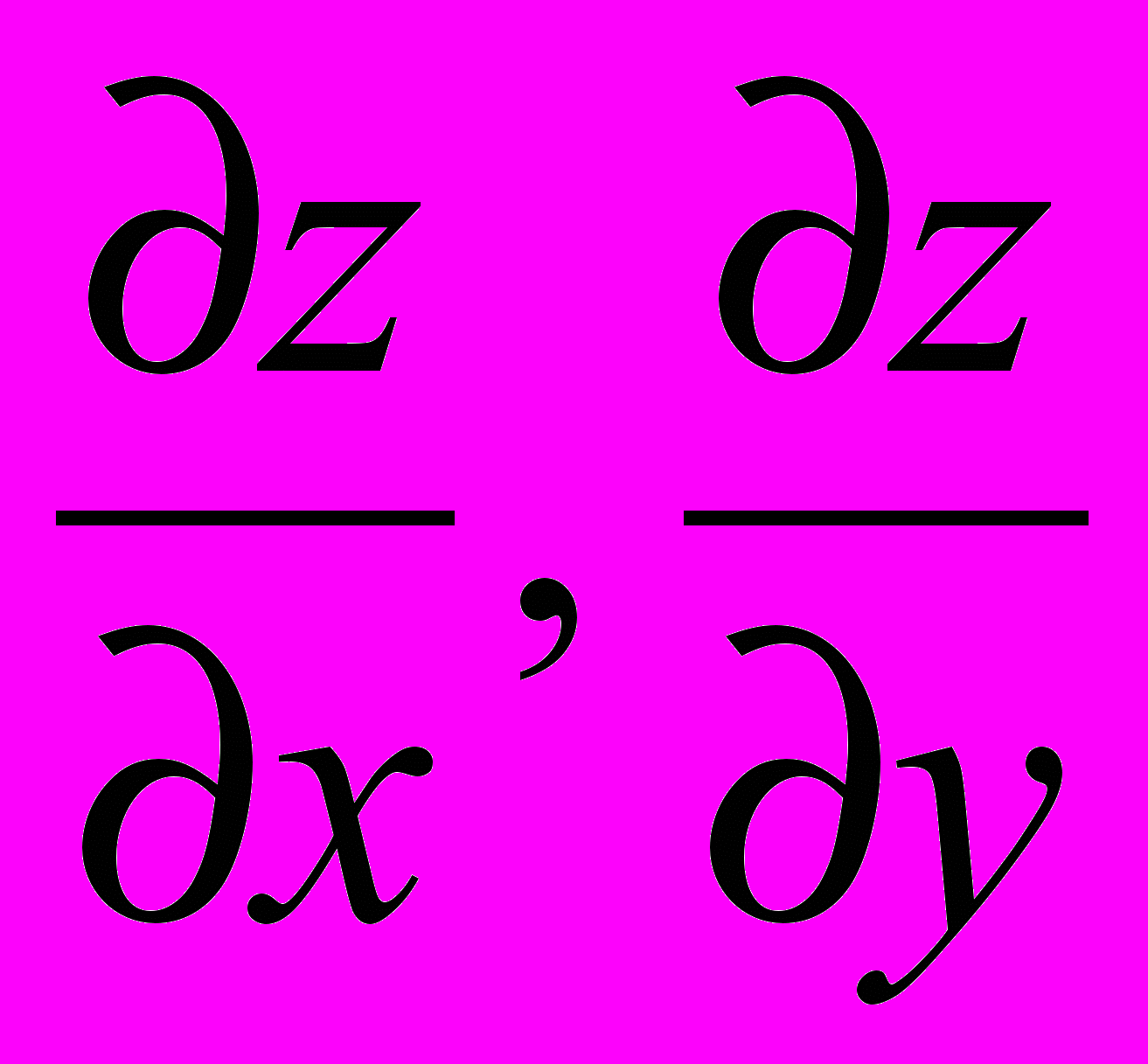 неявной функции
неявной функции 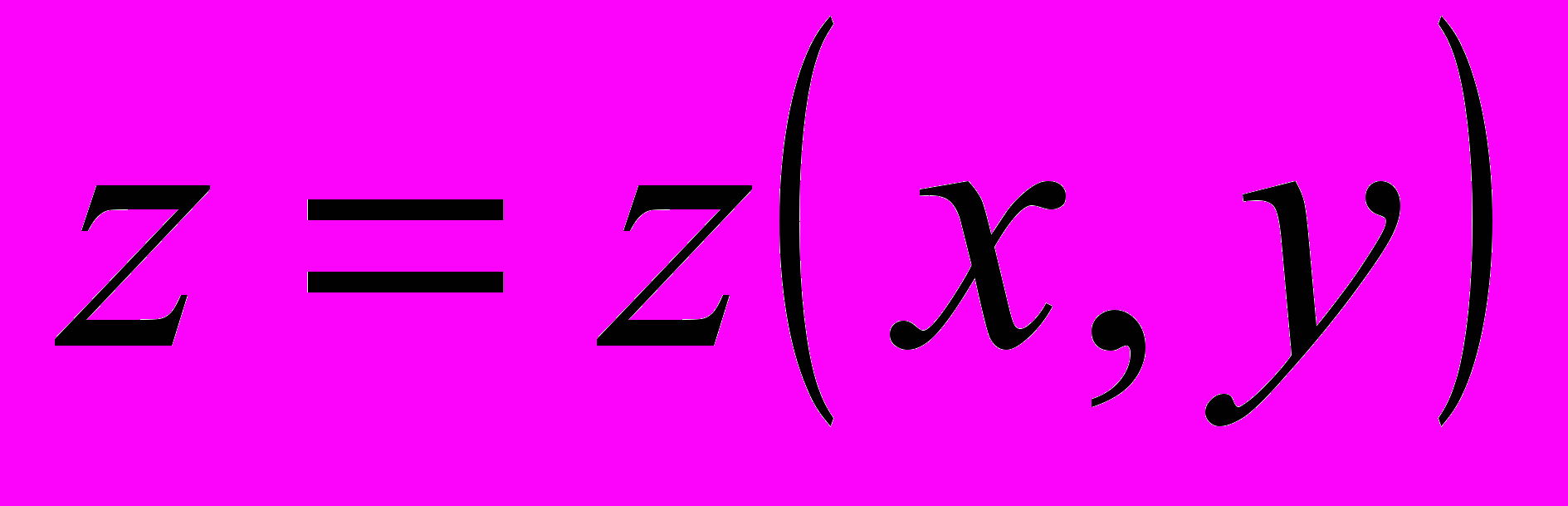 , заданной уравнением
, заданной уравнением 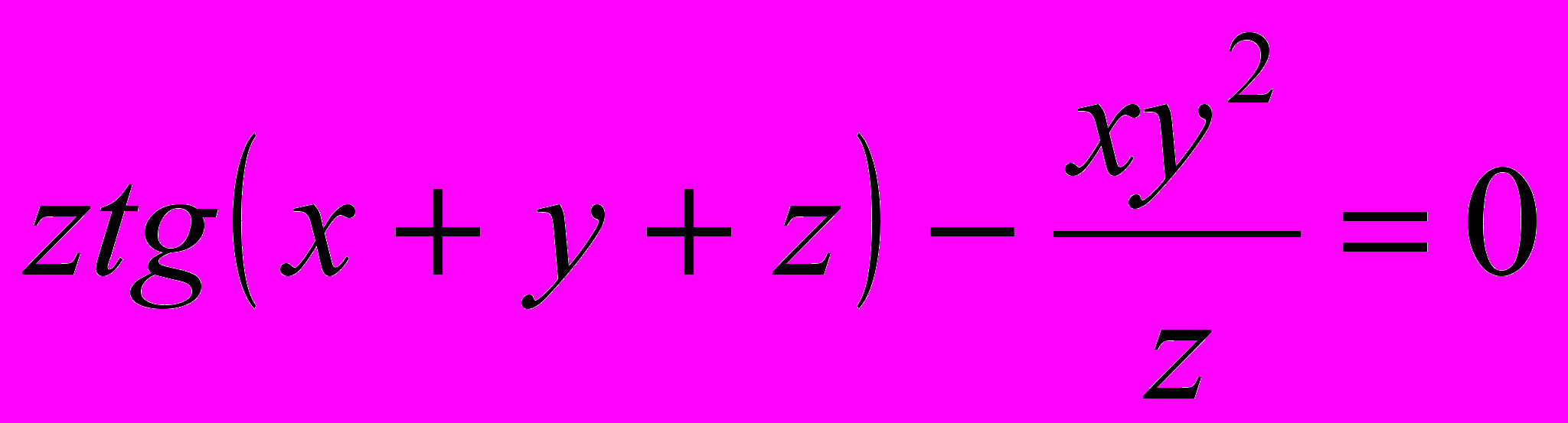 .
.
- Исследовать на экстремум функцию
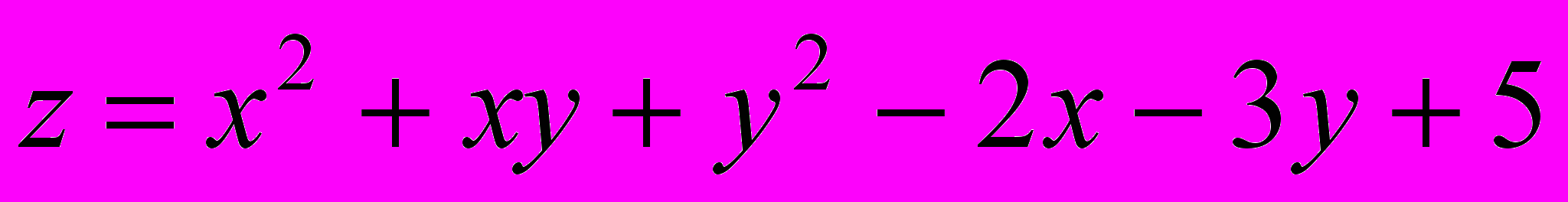 .
.
- Составить уравнение нормали к поверхности
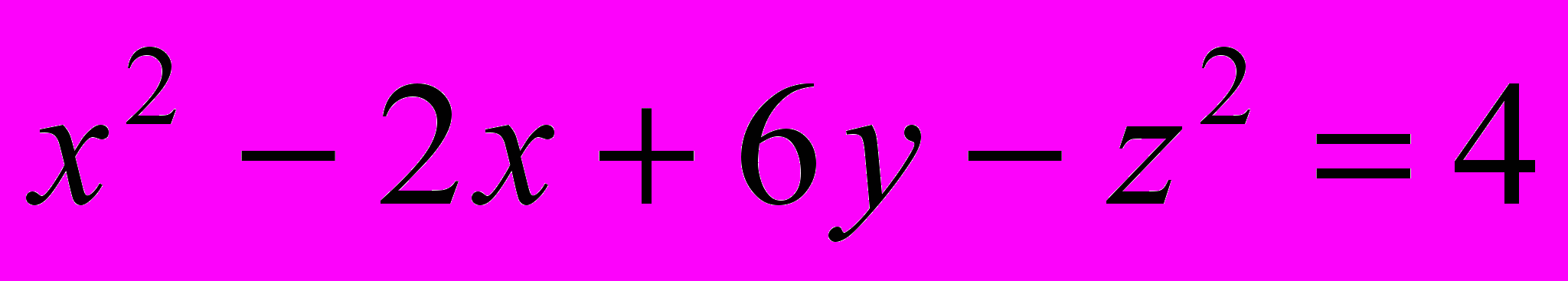 параллельно прямой
параллельно прямой 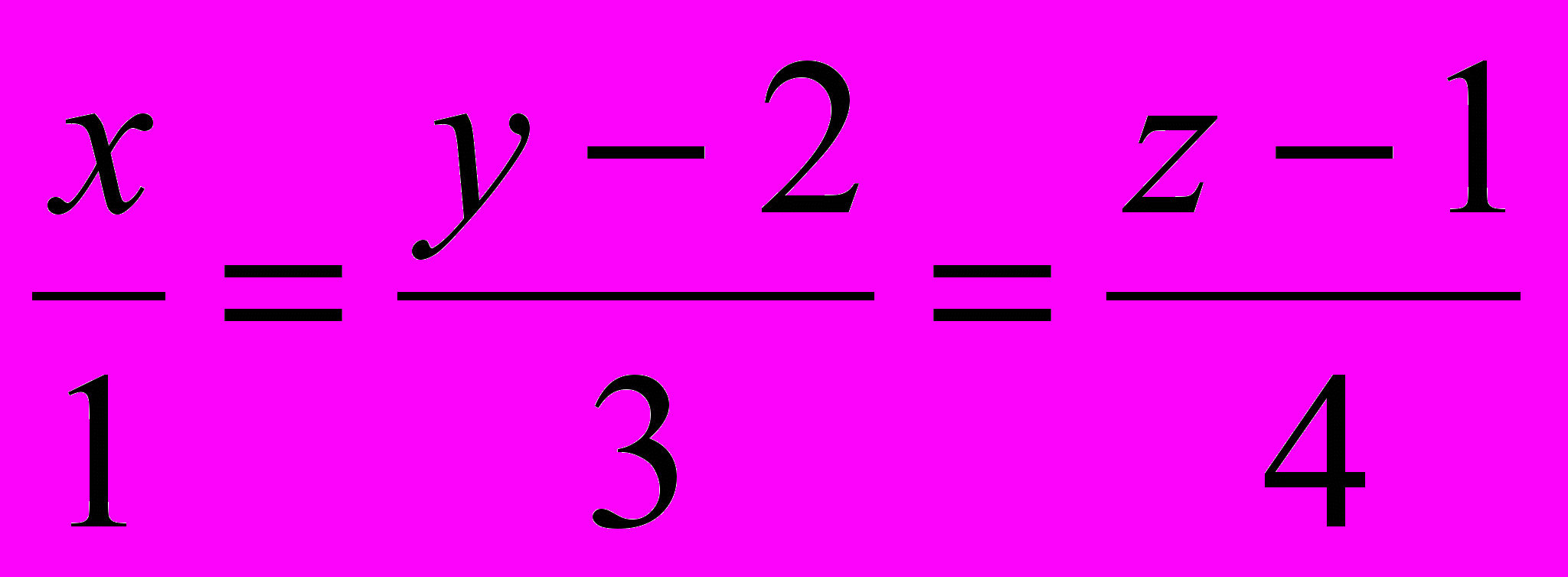 .
.
Документ:
Дата создания
