Урок по геометрии с применением икт
| Вид материала | Урок |
- Урок литературы с применением икт на тему "Любовная лирика С. А. Есенина", 80.95kb.
- Урок литературы в 9-м классе с применением икт по теме "Русская культура Серебряного, 112.76kb.
- Урок общественная лекция по теме : «Развитие геометрии как науки экскурс в историю», 48.39kb.
- Урок по геометрии и русскому языку на тему «Четырехугольники», 85.99kb.
- Урок окружающего мира с применением икт по теме "Почва, её состав и свойства" (3-й, 518.59kb.
- Урок алгебры в 8 классе с применением информационных технологий по теме «Решение квадратных, 94.17kb.
- Урок «Путешествие в музей геометрии» Тип, 151.51kb.
- Урок с применением икт «Индийские касты», 66.89kb.
- И. С. Тургенева «Отцы и дети» Цель урок, 54.88kb.
- Урок по музыке в 1-ом классе с применением икт по программе В. В. Алеева, Т. Н. Кичак, 42.39kb.
Аннотация проекта
Урок по геометрии с применением ИКТ
под редакцией А. В. Погорелова
Учитель МОУ Поназыревской основной общеобразовательной школы Поназыревского муниципального района Костромской области
Ярыгина Надежда Александровна
Тема: « Теорема Пифагора»
Цели:
- Познакомить учащихся с теоремой Пифагора и доказать её.
-Развивать логическое мышление учащихся;
- Прививать интерес к геометрии;
- Учить создавать презентации по изученному материалу;
Задачи:
- повторить соотношения между сторонами и углами в прямоугольном треугольнике.
- познакомить учащихся с биографией Пифагора и его открытиями
- доказать теорему Пифагора.
- решить простейшие задачи на применение теоремы Пифагора.
- показать применение теоремы, обратной теореме Пифагора.
Конспект урока
Тема: « Теорема Пифагора»
Цели:
- Познакомить учащихся с теоремой Пифагора и доказать её.
-Развивать логическое мышление учащихся;
- Прививать интерес к геометрии;
- Учить создавать презентации по изученному материалу;
Задачи:
- повторить соотношения между сторонами и углами в прямоугольном треугольнике.
- познакомить учащихся с биографией Пифагора и его открытиями
- доказать теорему Пифагора.
- решить простейшие задачи на применение теоремы Пифагора.
- показать применение теоремы, обратной теореме Пифагора.
Тип урока: Изучение нового материала
Вид урока: смешанный
Возраст детей: 13лет.
Программное обеспечение: Microsoft Word, Microsoft PowerPoint.
Наглядные пособия: портрет Пифагора, рисунки к теореме.
Межпредметные связи: история, информатика.
Оборудование: компьютеры, проектор, доска для фломастеров, экран, учебники, тетради, компьютерная презентация.
Прогнозируемый результат:
-
Знать зависимость между сторонами прямоугольного треугольника.- Уметь доказывать теорему Пифагора.
- Уметь применять теорему Пифагора к решению задач.
План урока:
- Организационный момент.
- Актуализация знаний.
- Сообщение учащихся о жизни Пифагора Самосского.
- Работа над теоремой.
- Значение теоремы Пифагора (рассказ ученика.)
- Решение задач с применением теоремы.
- Египетский треугольник
- Домашнее задание.
- Итог урока: Создание презентации по теме «ТЕОРЕМА ПИФАГОРА»
ХОД УРОКА:
1. Организационный момент (5 минут)
а) Сообщение темы урока «ТЕОРЕМА ПИФАГОРА»
( Слайд 1)
Сегодня на уроке мы приступаем к изучению одной из важнейших теорем геометрии- теоремы Пифагора. Она является основой решения множества геометрических задач и базой изучения теоретического материала.
б) Вопрос к учащимся: Какие вопросы возникли у вас в связи с темой урока?
(выслушиваю учеников)
в) А теперь попробуйте сформулировать цель урока
( говорят учащиеся)
Учитель сам четко формулирует цель
2.Актуализация знаний.
Прежде, чем приступить к изучению нового материала, вспомним определение косинуса угла и решим несколько устных задач
- Дайте определение косинуса острого угла прямоугольного треугольника.
- Чему равен косинус угла А на рисунке 1?
-Чему равен cos В на рисунке 2?
-
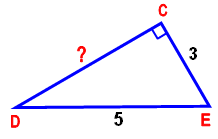
Чему равны косинусы острых углов СДЕ на рисунке 3? (Слайд 2)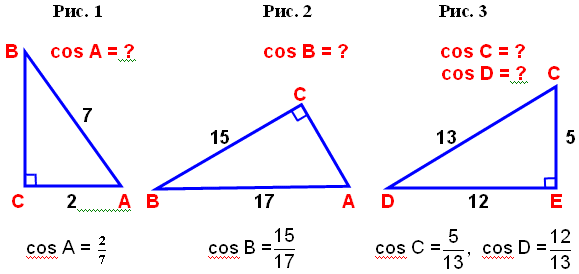
3. Итак, кто такой Пифагор? Чем он прославился?
На экране появляется портрет Пифагора (Слайд 3и 4)
Слово предоставляется учащимся ------------------ (5 минуты)
а)ПИФАГОР САМОССКИЙ
(
ок. 580 – ок. 500 г . до н.э.) О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.
Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки.
Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки.
Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду.
Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при сёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.
Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне.
Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
б) Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
- теорема о сумме внутренних углов треугольника;
- построение правильных многоугольников и деление плоскости на некоторые из них;
- геометрические способы решения квадратных уравнений;
- деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
- доказательство того, что
не является рациональным числом;
- создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.
Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.
Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.
После его смерти ученики окружили имя своего учителя множеством легенд.
4.Откройте тетради, запишите число … и тему урока «Теорема Пифагора».
- Ребята, может быть, вы что-нибудь слышали о теореме Пифагора?
- А ещё? (Пифагоровы штаны во все стороны равны.)
Действительно, это шуточная формулировка теоремы.
В современных учебниках теорема сформулирована так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». (Слайды 5и 6)
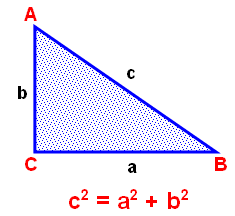
- Как записать теорему Пифагора для прямоугольного треугольника D АВС с катетами а , b и гипотенузой с (рис. 4)?
Рис. 4 9Слайд 7) Рис 5
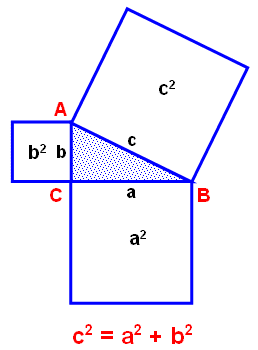
Предполагают, что во времена Пифагора теорема звучала по-другому: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Действительно,
с 2 – площадь квадрата, построенного на гипотенузе, а 2 и b 2 – площади квадратов, построенных на катетах (рис. 5).
Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка 6 видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.
Рис. 6
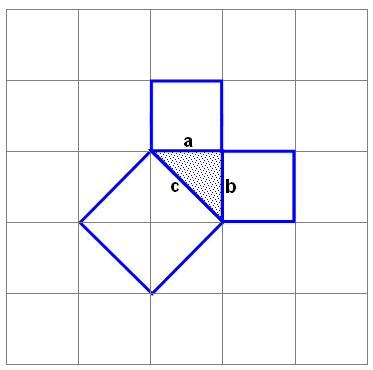Рис. 7\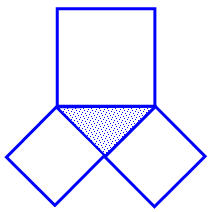
Смотрите, а вот и «Пифагоровы штаны во все стороны равны» (Слайд 9).
Такие стишки придумывали учащиеся средних веков при изучении теоремы; рисовали шаржи. Вот, например, такие (рис. 8, рис. 9): (Слайд8)
Рис 9
Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». В связи с этим более правдоподобной можно считать следующую запись: «… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».
На протяжении последующих веков были найдены другие доказательства теоремы Пифагора. В настоящее время их насчитывается более ста. Большинство способов её доказательства сводятся к разбиению квадратов на более мелкие части.
А сейчас докажем теорему Пифагора в современной формулировке.
Т е о р е м а. «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Начертите треугольник АВС с прямым углом С (рис. 13).
Рис. 10
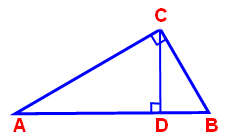
Д а н о: тр АВС, С = 99о.
Д о к а з а т ь: АВ 2 = АС 2 + ВС 2.
Д о к а з а т е л ь с т в о.
Проведём высоту CD из вершины прямого угла С.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе, поэтому
в тр ACD cos A
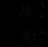, а в тр АВС cos А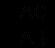 
Так как равны левые части этих равенств, то равны и правые, следовательно,
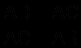. Отсюда, по свойству пропорции, получаем: АС 2 = AD* АВ . (1)
Аналогично, в тр В CD cos В
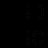, а в тр АВС cos В 
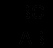Так как равны левые части этих равенств, то равны и правые, следовательно, 
. Отсюда, по свойству пропорции, получаем: ВС 2 = В D * АВ . (2) Сложим почленно равенства (1) и (2), и вынесем общий множитель за скобки:
АС 2 + ВС 2 = AD * AB + BD * AB = AB (AD + BD) = AB * AB = AB 2.
Получили, что
АВ 2 = АС 2 + ВС 2 .
.
Чтобы запомнить доказательство теоремы, предлагаю рисунок - опорный сигнал (рис. 14) и, думаю, он надолго останется в вашей памяти.
Рис . 11 (Слайд 10)
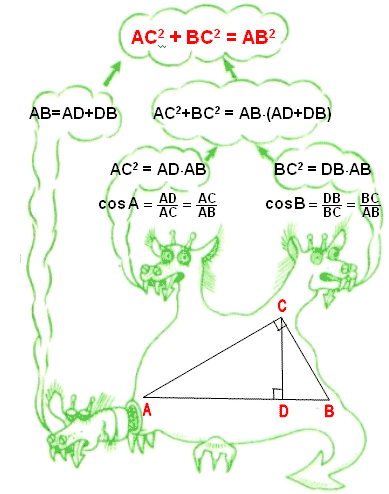
Отрубил Иван-царевич дракону голову, а у него две новые выросли.
На математическом языке это означает: провели в D АВС высоту CD, и образовалось два новых прямоугольных треугольника ADC и BDC .
Вспомнив этот рисунок, вы вспомните дополнительное построение и начало доказательства теоремы.
Теорема Пифагора – одна из главных теорем геометрии, потому что с её помощью можно доказать много других теорем и решить множество задач.
Особенностью теоремы Пифагора является то, что она неочевидна. Например, свойства равнобедренного треугольника можно увидеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что его стороны находятся в соотношении
с 2 = а 2 + b 2 .
5. О значении теоремы Пифагора расскажет ученик ---------------------------
6. Решение задач с применением теоремы Пифагора
Задача № 1 (Слайд 11)
Рис. 12
Д
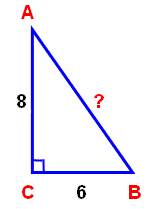ано:трАВСпрямоугольныйСА=8,СВ=6
Найти:АВ
Р е ш е н и е.
АВС - прямоугольный с гипотенузой АВ ,
по теореме Пифагора: АВ 2 = АС 2 + ВС 2,
АВ 2 = 8 2 + 6 2,
АВ 2 = 64 + 36,
АВ 2 = 100,
АВ =
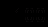, АВ = 10 .
Задача № 2 (Слайд 12)
Рис. 13
Р е ш е н и е.
Тр DCE - прямоугольный с гипотенузой DE (рис. 13), по теореме Пифагора:
DE 2 = D С 2 + CE 2,
DC 2 = DE 2 - CE 2,
DC 2 = 5 2 - 3 2,
DC 2 = 25 - 9,
DC 2 = 16,
DC = 4 .
7Получили прямоугольный треугольник со сторонами 3, 4 и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Что это за треугольник, расскажет ученик ------------------------------
Обратная теорема (слайды 13 и 14)
Нетрудно убедиться, что теорема, обратная к теореме Пифагора, также справедлива. Она позволяет проверить, является ли тот или иной треугольник прямоугольным. Например, если стороны треугольника имеют длины в 3, 4 и 5 единиц, то такой треугольник прямоугольный, так как 52 = 32 + 42. Этим пользовались землемеры и строители Древнего Египта: они размечали прямые углы с помощью веревки, разделенной узлами на 12 равных кусков.
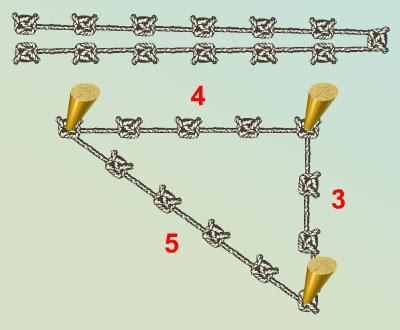
Прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским», а тройки (a, b, c) натуральных чисел, удовлетворяющие уравнению c2 = a2 + b2, т. е. служащие длинами сторон прямоугольных треугольников, Пифагоровыми. С изучения пифагоровых троек началась история великой теоремы Ферма, давшей мощнейший импульс развитию алгебры и, наконец, доказанной совсем недавно.
8. Домашнее задание: Пункты 63, 64; №2(3), №3(3) (Слайд 15)
9. Итог урока: Создайте опорный конспект по теме «ТЕОРЕМА ПИФАГОРА»
( примерный вариант презентации) (Слайд 16)
теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
с2= а2 +в2
Итак, (Слайд 17)
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путём
К результату мы придём.
Приложение