«Переборные задачи»
| Вид материала | Доклад |
- Некорректные задачи, 36.86kb.
- О. А. Щербина University of Vienna,\\, 120.29kb.
- Решение задачи одним из математических методов, 440.71kb.
- Программа дисциплины Методы оптимизации Семестры, 21.07kb.
- Задачи математического и линейного программирования. Математическая модель задачи использования, 25.82kb.
- Тема и задачи образовательного учреждения., 1740.01kb.
- Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 24.28kb.
- Лекции 7 8, 31.73kb.
- Двойственность в линейном программировании, 54.17kb.
- Задачи урока. Уметь решать расчётные задачи; Научиться формулировать чёткие ответы, 103.07kb.
Министерство образования и науки Украины
Донецкий национальный университет
Кафедра компьютерных технологий
Доклад
Тема: «Переборные задачи»
Исполнитель:
студент 2 курса
специальности ИСПР
Самороков М. Г.
2007
СОДЕРЖАНИЕ
- Определение NP-полной задачи
- Класс сложности NP
- Классы P и NP
- Полиномиальное сведение
- Классы P и NP
- Труднорешаемые проблемы
- Проблема SAT
- Проблема IS
- Проблема 3-COL
- Проблема ILP
- Проблема SAT
- Алгоритмы решения на примере задачи коммивояжёра
- Метод ветвей и границ
- Метод муравьиной колонии
- Метод ветвей и границ
Выводы
Список ссылок
Приложение А. Условия переборных задач.
1. ОПРЕДЕЛЕНИЕ NP-ПОЛНОЙ ЗАДАЧИ
В теории алгоритмов NP-полные задачи — это класс задач, лежащих в классе NP (то есть для которых пока не найдено быстрых алгоритмов решения, но проверка того, является ли данное решение правильным, проходит быстро), к которым сводятся все задачи класса NP. Это означает, что если найдут быстрый алгоритм для решения любой из NP-полных задач, любая задача из класса NP сможет быть решена быстро.
Формальное определение: назовём языком множество слов над алфавитом Σ. Задачей здесь является определение того, принадлежит данное слово языку или нет. Язык L1 называется сводимым (по Карпу) к языку L2, если существует функция,
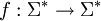 , вычислимая за полиномиальное время, обладающая следующим свойством: f(x) принадлежит L2 тогда и только тогда, когда x принадлежит L1. Язык L2 называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден и при этом сам лежит в классе NP. Таким образом, если будет найден алгоритм, решающий хоть одну NP-полную задачу за полиномиальное время, все NP-задачи будут лежать в классе P.
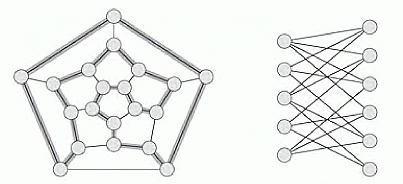
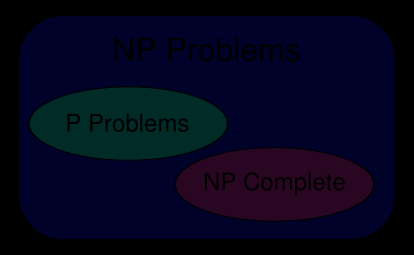
, вычислимая за полиномиальное время, обладающая следующим свойством: f(x) принадлежит L2 тогда и только тогда, когда x принадлежит L1. Язык L2 называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден и при этом сам лежит в классе NP. Таким образом, если будет найден алгоритм, решающий хоть одну NP-полную задачу за полиномиальное время, все NP-задачи будут лежать в классе P.Задача поиска гамильтонова цикла в графе изучается уже более ста лет. Гамильтоновым циклом в неориентированном графе G = (V, E) называется простой цикл, который проходит через все вершины графа. Графы, в которых есть гамильтонов цикл, называют гамильтоновыми. Задача о гамильтоновом цикле состоит в выяснении, имеет ли заданный граф G гамильтонов цикл. Формально говоря, HAM-CYCLE = {<G> | G — гамильтонов граф}. Задача о гамильтоновом цикле является NP-полной, и поэтому можно предполагать, что полиномиального алгоритма для нее вообще не существует. На рисунке ниже приведены примеры двух графов, левый из которых является гамильтоновым, правый же не обладает аналогичным свойством.
Рассмотрим проверку принадлежности к языку. Определить является ли граф гамильтоновым за полиномиальное время, скорее всего, не возможно, однако доказательство существования гамильтонова цикла в графе (состоящее в предъявлении гамильтонова пути) можно проверить за полиномиальное время. Назовем проверяющим алгоритмом алгоритм A с двумя аргументами; первый аргумент — входная строка, а второй — сертификат. A допускает вход x, если существует сертификат y, для которого A(x, y) = 1. Язык, проверяемый алгоритмом A: L = {x ∈ {0, 1}*: ∃ y ∈ {0,1}*, A(x, y) = 1}. Другими словами, алгоритм A проверяет язык L, если для любой строки x ∈ L найдется сертификат y, с помощью которого A может проверить принадлежность x к языку L, а для x ∉ L такого сертификата нет. Например, в задаче HAM-CYCLE сертификатом была последовательность вершин, образующая гамильтонов цикл.
2. КЛАСС СЛОЖНОСТИ NP.
Классом NP (от англ. non-deterministic polynomial) называют множество алгоритмов, время работы которых сильно зависит от размера входных данных, но если предоставить алгоритму некоторые дополнительные сведения (так называемых свидетелей решения), то он сможет достаточно быстро (за время, не превосходящее многочлена от размера данных) решить задачу. Проблема в том, что найти таких свидетелей бывает сложно, поэтому многие алгоритмы из класса NP считаются долгими.
Класс сложности NP определяется для множества языков, т.е. множеств слов над конечным алфавитом Σ. Язык L называется принадлежащим классу NP, если существуют двуместный предикат
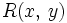 из класса P (т.е. вычислимый за полиномиальное время) и многочлен nc такие, что для всякого слова x условие «x принадлежит L» равносильно условию «найдётся y длины меньше nc такой, что верно
из класса P (т.е. вычислимый за полиномиальное время) и многочлен nc такие, что для всякого слова x условие «x принадлежит L» равносильно условию «найдётся y длины меньше nc такой, что верно 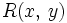 » (где n — длина слова x). Слово y называется свидетелем принадлежности x языку L. Таким образом, если у нас есть слово, принадлежащее языку, и ещё одно слово-свидетель ограниченной длины (которое бывает трудно найти), то мы быстро сможем удостовериться в том, что x действительно принадлежит L. Как видно, это определение является более общим, чем определения NP-полной задачи.
» (где n — длина слова x). Слово y называется свидетелем принадлежности x языку L. Таким образом, если у нас есть слово, принадлежащее языку, и ещё одно слово-свидетель ограниченной длины (которое бывает трудно найти), то мы быстро сможем удостовериться в том, что x действительно принадлежит L. Как видно, это определение является более общим, чем определения NP-полной задачи.Эквивалентное определение можно получить, используя понятие недетерминированной машины Тьюринга (т. е. обычной машины Тьюринга, у программы которой могут существовать разные строки с одинаковой левой частью). Если машина встретила «развилку», т. е. неоднозначность в программе, то дальше возможны разные варианты вычисления. Предикат R(x), который представляет данная недетерминированная машина Тьюринга, считается равным единице, если существует хоть один вариант вычисления, возвращающий 1, и нулю, если все варианты возвращают 0. Если длина вычисления, дающего 1, не превосходит некоторого многочлена от длины x, то предикат называется принадлежащим классу NP. Если у языка существует распознающий его предикат из класса NP, то язык называется принадлежащим классу NP. Такое определение эквивалентно верхнему: в качестве свидетеля можно взять номера нужных веток при развилках в вычислении. Поскольку, если x принадлежит языку, длина всего пути вычисления не превосходит многочлена, то и длина свидетеля тоже будет не превосходить многочлена от длины x.
Всякую задачу, принадлежащую NP, можно решить за экспоненциальное время (перебором всех возможных свидетелей длины меньше nc).
Легко видеть, что множество языков из NP не замкнуто относительно дополнения. Класс языков, дополнение которых принадлежит NP, называется классом co-NP.
Отношения класса NP с другими классами. Класс NP включает в себя класс P (даже точнее, известно включение
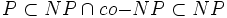 ). Однако ничего не известно о строгости этого включения. Задача о равенстве классов P и NP является одной из центральных открытых проблем теории алгоритмов. Если они равны, то любую задачу из класса NP можно будет решить быстро (за полиномиальное время). Однако научное сообщество склоняется в сторону отрицательного ответа на этот вопрос.
). Однако ничего не известно о строгости этого включения. Задача о равенстве классов P и NP является одной из центральных открытых проблем теории алгоритмов. Если они равны, то любую задачу из класса NP можно будет решить быстро (за полиномиальное время). Однако научное сообщество склоняется в сторону отрицательного ответа на этот вопрос.Класс NP включается в другие, более широкие классы, например, в класс PH. Существуют также открытые вопросы о строгости его включения в другие классы.
2.1. КЛАССЫ P И NP.
Язык L принадлежит классу P, если существует ДМТ M, которая допускает язык L и останавливается за полиномиальное время.
Язык L принадлежит классу NP, если существует НМТ M, которая допускает язык L и останавливается за полиномиальное время.
Приведем пример языка, принадлежащего классу P:
- Язык записей графов, в которых есть эйлеров цикл.
Соответствующая ДМТ несложна: она проверяет связность данного графа, и проверяет, что степени всех вершин — четные. Если оба условия выполнены, ДМТ возвращает ответ «да».
Приведем пример языка, принадлежащего классу NP:
- Язык записей графов, в которых есть гамильтонов цикл.
Соответствующую НМТ тоже придумать несложно. НМТ угадывает порядок обхода вершин в гамильтоновом цикле, после чего проверяет, что все соседние вершины (то есть идущие подряд в угаданном обходе) соединены ребром. Если хотя бы один порядок обхода является гамильтоновым циклом, то НМТ возвращает ответ «да», в противном случае, действительно, ответ: «нет».
П
 оскольку всякая ДМТ является частным случаем НМТ, ясно, что
оскольку всякая ДМТ является частным случаем НМТ, ясно, что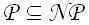
Важнейшим неразрешенным вопросом для Computer Science до сих является: верно ли, что
P ≠ NP
Ответ на вопрос о равенстве классов P и NP определил бы, действительно ли задачу легче проверить, чем решить ( P≠NP). Или решить столь же просто, что и проверить (P=NP).
Впервые вопрос о равенстве классов был поставлен независимо Куком и Левиным в 1971 г. В настоящее время большинство математиков считают, что эти классы не равны. Согласно опросу, проведённому в 2002 г. среди 100 учёных, 61 человек считает, что ответ — «не равны», 9 — «равны», 22 затруднились ответить и 8 считают, что вопрос не зависит от текущей системы аксиом и, таким образом, не может быть доказан или опровергнут.
В настоящий момент проблема равенства классов P и NP является одной из семи проблем, за решение которых Математический институт Клэя назначил премию в 1 млн. долларов США.
2.2. ПОЛИНОМИАЛЬНОЕ СВЕДЕНИЕ
Предположим, что про некоторый язык P1 не принадлежит классу P. То есть P1 — это некоторая заведомо сложная проблема. Предположим также, что имеется некоторый язык P2, и все попытки построить алгоритм, решающий P2 не увенчались успехом. В таком случае, возникает предположение, что P2 не принадлежит P. Для доказательства этого предположения используем метод полиномиального сведения:
Найдем полиномиальный алгоритм, строящий по экземпляру P1 экземпляр P2 с таким же ответом (сведем P1 к P2).
После этого приведем доказательство от противного: пусть P2 принадлежит P. Тогда, по определению, существует ДМТ M, допускающая язык P2. Зная это, построим следующую ДМТ M′:
 Эта ДМТ допускает язык P1. Язык P1 оказывается принадлежащим классу P. Получили противоречие, следовательно, P2 не принадлежит P, что и требовалось доказать.
Эта ДМТ допускает язык P1. Язык P1 оказывается принадлежащим классу P. Получили противоречие, следовательно, P2 не принадлежит P, что и требовалось доказать. 3
 . ТРУДНОРЕШАЕМЫЕ ПРОБЛЕМЫ.
. ТРУДНОРЕШАЕМЫЕ ПРОБЛЕМЫ.К классу NP-полных задач относится большое количество игр и головоломок. Например, такая известная всем головоломка как пятнашки…
Пятнашки — популярная головоломка, придуманная в 1878 году Ноем Чепменом. Существует вариант для восьми элементов. Представляет собой набор одинаковых квадратных костяшек с нанесёнными числами, заключённых в квадратную коробку. Длина стороны коробки в четыре раза больше длины стороны костяшек для набора из 15 элементов и в три раза больше для набора в 8 элементов, соответственно в коробке остаётся незаполненным одно квадратное поле. Цель игры — перемещая костяшки по коробке добиться упорядочивания их по номерам, желательно сделав как можно меньше перемещений.
Пятнашки представляют собой классическую задачу для моделирования эвристических ссылка скрыта. Обычно задачу решают через количество перемещений и поиск манхэттенского расстояния между каждой костяшкой и её позицией в собранной головоломке. Для решения используются алгоритмы наподобие волнового.
Нерешаемая комбинация, предложенная Ноем Чепменом на рисунке.
М
 ожно показать, что некоторые начальные положения пятнашек невозможно привести к собранному виду: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать ni = k, то есть если после костяшки с i-м числом нет чисел, меньших i, то k = 0. Также введем число e - номер ряда пустой клетки (считая с 1). Если сумма
ожно показать, что некоторые начальные положения пятнашек невозможно привести к собранному виду: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать ni = k, то есть если после костяшки с i-м числом нет чисел, меньших i, то k = 0. Также введем число e - номер ряда пустой клетки (считая с 1). Если сумма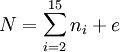 является нечётной, то решения головоломки не существует. Для вариантов пятнашек с большим, чем 15, количеством костяшек задача поиска кратчайшего решения является NP-трудной.
является нечётной, то решения головоломки не существует. Для вариантов пятнашек с большим, чем 15, количеством костяшек задача поиска кратчайшего решения является NP-трудной.3.1. ПРОБЛЕМА SAT.
Приведем пример очень важной для теории сложности NP–полной задачи. В англоязычной литературе для нее принято сокращение SAT (от англ. satisfiability — выполнимость), в русскоязычной, соответственно, ВЫП.
Пусть дана формула, содержащая булевы переменные, операторы «
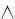 » («и»), «
» («и»), «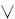 » («или») и «¬» («не»), и скобки. Формула называется выполнимой, если существует такой набор значений переменных, при подстановке которого формула принимает значение истина. SAT — это язык выполнимых формул. В 1971 году Стивен Кук доказал NP–полноту задачи SAT.
» («или») и «¬» («не»), и скобки. Формула называется выполнимой, если существует такой набор значений переменных, при подстановке которого формула принимает значение истина. SAT — это язык выполнимых формул. В 1971 году Стивен Кук доказал NP–полноту задачи SAT. Теорема (Кук): Проблема SAT NP-полна.
Доказательство:
Докажем сначала, что SAT
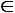 NP.
NP. Для этого достаточно привести недетерминированную машину Тьюринга, которая принимает язык SAT. Простейшая НМТ действует так:
Угадать значения всех переменных.
Подставить эти значения в формулу.
Если формула приняла значение истина, перейти в допускающее состояние.
Видно, что эта НМТ допускает формулу w тогда и только тогда, когда существует подстановка значений, выполняющая формулу w.
Рассмотрим любой язык Lиз NP. Необходимо теперь доказать, что существует полиномиальное сведение L к SAT, то есть по экземпляру L построить формулу для SAT с тем же ответом. При этом, поскольку Lпринадлежит NP, существует НМТ M, которая допускает язык L, совершая не более p(n) переходов, где p(n) — некоторый полином.
Искомая формула имеет следующую структуру:
( М начинает, имея на входе данный экземпляр L)
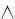 (Первый шаг M происходит по правилам)
(Первый шаг M происходит по правилам) 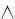 (…)
(…) 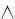 (Шаг M номер p(n) происходит по правилам)
(Шаг M номер p(n) происходит по правилам) 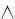 (М пришло в допускающее состояние)
(М пришло в допускающее состояние)К сожалению, технические детали этой формулы весьма громоздки, поэтому ограничимся лишь приведенным выше каркасом.
Предположим, что рассматриваемый экземпляр действительно принадлежит L. Значит, машина Тьюринга M, получив на вход этот экземпляр, может при определенном выборе переходов прийти в допускающее состояние. Тогда формула, описывающая процесс работы M, должна выполняться, поскольку все утверждения про работу M, закодированные в ней, верны.
И наоборот, если формула выполнима, то, анализируя значения переменных в каждой скобке, можно понять, какой переход был выбран на каждом шаге, и убедиться, что машина Тьюринга проделывала только разрешенные переходы и пришла в итоге в допускающее состояние, а значит, входной экземпляр принадлежит языку L.
Проблема 3-SAT
Если некоторая проблема является NP–полной, то любое ее обобщение тем более является NP–полной проблемой. В то же время, иногда частный случай NP–полной проблемы может сам по себе обладать NP–полнотой. Важный пример — задача 3-SAT. Это задача о выполнимости некоторого класса булевых формул, но не столь общего, как в задаче SAT. Для определения 3-SAT введем несколько простых определений.
Литералом называется выражение вида «x» или «¬x», где x — переменная.
3-дизъюнктом называется выражение вида «a
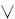 b
b 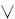 c», где a, b и c — литералы.
c», где a, b и c — литералы.Булева формула записана в 3-конъюнктивной нормальной форме, если она является логическим «и» произвольного количества 3-дизъюнктов. Например:
(x1
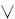 ¬x2
¬x2 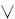 x3)
x3) 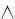 (¬x1
(¬x1 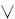 x2
x2 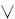 ¬x4)
¬x4) 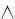 (x2
(x2 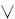 ¬x3
¬x3 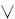 x4)
x4)Проблема 3-SAT формулируется так: является ли данная формула, записанная в 3-конъюнктивной нормальной форме, выполнимой.
Проблема 3-SAT также NP–полна, что чрезвычайно удобно использовать при доказательстве NP–полноты других задач.
3.2. ПРОБЛЕМА IS.
Следующая NP–полная проблема относится к теории графов. Сокращение IS расшифровывается как Independent Set — Независимое Множество, сокращенно — НМ.
Множество вершин графа называется независимым, если никакие две вершины из этого множества не соединены ребром.
Дан граф G и число k. Проблема IS такова: Существует ли в графе G независимое множество из k вершин?
Докажем NP–полноту проблемы IS.
Для начала убедимся, что IS
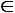 NP. Для этого представим недетерминированный алгоритм, допускающий язык IS. Его суть такова:
NP. Для этого представим недетерминированный алгоритм, допускающий язык IS. Его суть такова:Угадать про каждую вершину, принадлежит ли она искомому множеству.
Убедиться, что выбрано ровно kвершин.
Проверить, что нет двух выбранных вершин, соединенных ребром.
Если все проверки закончились удовлетворительно, перейти в допускающее состояние.
Теперь сведем 3-SAT к IS, чем докажем NP-полноту IS. Для формулы в 3-конъюнктивной нормальной форме приведем граф и число, принадлежащие языку IS тогда и только тогда, когда формула принадлежит языку 3-SAT, то есть является выполнимой.
Каждому дизъюнкту в булевой формуле (например, (x1
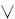 ¬x2
¬x2 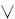 x3)) поставим в соответствие 3 смежные вершины, по одной вершине на литерал. Тем самым мы потребуем, чтобы в решении задачи про независимое множество из этих вершин было выбрано не более одной.
x3)) поставим в соответствие 3 смежные вершины, по одной вершине на литерал. Тем самым мы потребуем, чтобы в решении задачи про независимое множество из этих вершин было выбрано не более одной.Вершину, соответствующую литералу xi в одном дизъюнкте, и вершину, соответствующую литералу ¬xi в другом, соединим ребром. Тем самым мы удостоверимся, что в разных дизъюнктах не будут выбраны противоречащие друг другу литералы.
Положим k = количество дизъюнктов в формуле.
Поясним приведенные выше манипуляции на примере. Так выглядят формула и соответствующий ей граф (k = 3):
(x1
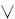 ¬x2
¬x2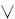 x3)
x3)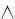 (¬x1
(¬x1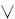 x2
x2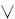 x4)
x4)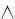 (¬x2
(¬x2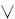 ¬x3
¬x3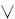 ¬x4)
¬x4) 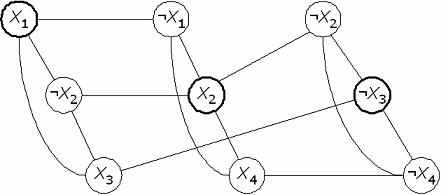
Вершины независимого множества соответствуют истинным литералам в формуле. В каждом дизъюнкте обязан оказаться хотя бы один истинный литерал (ведь k равно количеству дизъюнктов), и противоречий возникнуть не может благодаря ребрам, проведенным между дизъюнктами.
3.3. ПРОБЛЕМА 3-COL.
Еще одна красивая NP–полная задача из теории графов относится к раскраске графа или определению хроматического числа графа.
Дан граф G. Можно ли раскрасить вершины G в три цвета так, чтобы не было двух смежных вершин, раскрашенных в один цвет?
Проблема 3-COL NP–полна, как и любая проблема k-COL при условии k ≥ 3.
Обычно задача решается нахождением максимальных независимых множеств.
3.4. ПРОБЛЕМА ILP.
Следующая NP–полная задача имеет алгебраический вид. Сокращение ILP расшифровывается как Integer Linear Programming — Целочисленное Линейное Программирование.
Дан набор ограничений вида
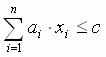
При этом aiи c — целые числа.
Существует ли целочисленный вектор x, удовлетворяющий всем неравенствам?
4. АЛГОРИТМЫ РЕШЕНИЯ NP-ПОЛНЫХ ЗАДАЧ НА ПОИМЕРЕ ЗАДАЧИ КОММИВОЯЖЁРА.
4.1. МЕТОД ВЕТВЕЙ И ГРАНИЦ.
Метод ветвей и границ — общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации, особенно дискретной и комбинаторной оптимизации. По существу, метод является комбинаторным (алгоритм перебора) с отсевом подмножеств множества допустимых решений, не содержащих оптимальных решений. Метод был впервые предложен Ленд и Дойг в 1960 г. для решения задач линейного программирования.
Общее описание
Общая идея метода может быть описана на примере поиска минимума и максимума функции f(x) на множестве допустимых значений x. Функция f и x могут быть произвольной природы. Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ).
Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Процедуру можно рекурсивно применять к подобластям. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти.
Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений.
В основе метода ветвей и границ лежит следующая идея (для задачи минимизации): если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева). Обычно, минимальную из полученных верхних оценок записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница которого больше значения m, может быть исключен из дальнейшего рассмотрения.
Если нижняя граница для узла дерева совпадает с верхней границей, то это значение является минимумом функции и достигается на соответствующей подобласти.
4.2. МЕТОД МУРАВЬИНОЙ КОЛОНИИ.
Муравьиные алгоритмы (Алгоритм оптимизации подражанием муравьиной колонии) — один из наиболее эффективных полиномиальных алгоритмов для «решения» NP-полной задачи коммивояжёра.
В основе алгоритма лежит поведение муравьиной колонии — маркировка более удачных путей большим количеством феромона. Работа начинается с размещения муравьёв в вершинах графа (городах), затем начинается движение муравьёв — направление определяется вероятностным методом, на основании формулы вида:
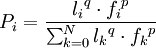 , где: Pi вероятность перехода по пути i, li длинна iого перехода, fi количество феромона на iом переходе,
, где: Pi вероятность перехода по пути i, li длинна iого перехода, fi количество феромона на iом переходе,q величина, определяющая «жадность» алгоритма, p величина, определяющая «стадность» алгоритма и q + p = 1
Решение не является точным и даже может быть одним из худших, однако, в силу вероятности решения, повторение алгоритма может выдавать (достаточно) точный результат.
ВЫВОДЫ.
Можно сказать, что все задачи – переборные, так как любую задачу можно решить полным перебором.
Эффективное решение переборных задач было бы прорывом в Computer Science, но поскольку пока его нет, переборные задачи решаются либо путём сокращения перебора, отбрасыванием заведомо ложных вариантов, либо находя приближённое решение искомой задачи.
СПИСОК ССЫЛОК.
- Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений. — М.: Вильямс, 2002.
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.
- An Annotated List of Selected NP-complete Problems, HTML-DOC, ссылка скрыта, 07.07.07, 10.30.
- Материалы свободной энциклопедии «Wikipedia», ссылка скрыта
ПРИЛОЖЕНИЕ А.
Задача 1.
Построить алгоритм, выдающий без повторений все перестановки N чисел.
Решение.
Этот алгоритм хорошо известен и достаточно подробно изложен. Опишем его (при N=5), от чего рассуждения не утратят общности. Алгоритм составлен так, что в процессе его исполнения перестановки N чисел располагаются лексикографически (в словарном порядке). Это значит, что перестановки сравниваются слева направо поэлементно. Больше та, у которой раньше встретился элемент, больше соответствующего ему элемента во второй перестановке. (Например, если S=(3,5,4,6,7),а L=(3,5,6,4,7), то S
Принцип работы алгоритма разъясним на примере. Допустим, необходимо воспpоизвести все перестановки цифр 3,4,5,6,7. Первой перестановкой считаем перестановку (3,4,5,6,7). Последней воспроизводимой перестановкой будет (7,6,5,4,3).
Предположим, что на некотором шаге работы алгоритма получена перестановка
P=(5,6,7,4,3).
Для того чтобы определить непосредственно следующую за ней перестановку, необходимо, пересматривая данную перестановку справа налево, следить за тем, чтобы каждое следующее число было больше предыдущего, и остановиться сразу же, как только это правило нарушится. Место останова указано стрелкой:
(5,6,7,4,3).
Затем вновь просматриваем пройденный путь ( справа налево ) до тех пор, пока не дойдем до первого числа, которое уже больше отмеченного. Ниже место второго останова отмечено двойной стрелкой.
(5,6,7,4,3).
Поменяем местами отмеченные числа:
(5,7,6,4,3).
Теперь в зоне, расположенной справа от двойной стрелки, упорядочим все числа в порядке возрастания. Так как до сих пор они были упорядочены по убыванию , то это легко сделать, перевернув указанный отрезок. Получим:
Q=(5,7,3,4,6).
Q и есть та перестановка, которая должна воспроизводиться непосредственно после P.
Действительно, P
Задача 2.
Сгенерировать все подмножества данного n-элементного множества {0,..., n-1}.
Решение.
Заведем массив B[0..n] из (n+1) элемента. B[i]=0, если i-ый элемент в подмножество не входит, и B[i]=1 иначе. Т.о. пустому подмножеству будет соответствовать набор из n нулей, а n-элементному подмножеству - набор из n единиц. Тут явно заметна связь подмножества с двоичным представлением числа.
Алгоритм: будем генерировать числа от 0 до 2n-1, находить их двоичное представление, и формировать подмножество из элементов с индексами единичных битов в этом представлении.
Но число 2n-1 может не поместиться в разрядную сетку машины. Поэтому генерацию будем проводить, используя массив B:
Сначала B[i]=0 для всех i, что соответствует пустому подмножеству.
Будем рассматривать массив B как запись двоичного числа
B[N]...B[1]B[0],
и моделировать операцию сложения этого числа с единицей. При сложении будем просматривать число справа налево заменяя единичные биты нулями до тех пор, пока не найдем нулевой бит, в который занесем 1. Генерация подмножеств заканчивается, как только B[N]=1
(предыдущая конфигурация была 1...12 = 2n-1).
while B[N]<>0 do begin i:=0; { индекс бита двоичного числа }
while (B[i]=1) do begin
B[i]:=0; { моделируем перенос в следующий разряд, }
i:=i+1 { возникающий при сложении }
end;
B[i]:=1;
{ Распечатываем индексы единичных элементов массива B -новое сгенерированное подмножество }
For i:=0 to N-1 do
if B[i]=1 then write(i);
writeln; { переход на новую строку при печати }
end;
Задача 3.
Сгенерировать все k-элементные подмножества множества A из N чисел, A={1, 2, ..., N}.
Пример: N=3, k=2,
подмножества {1,2}, {1,3}, {2,3}.
Решение.
Воспользуемся следующим алгоритмом генерации сочетаний по k элементов из множества A:
В массиве B будут находиться индексы используемых на данном шаге элементов из A (общее их число k). В качестве начальной конфигурацией возьмем следующую: B[j]=j, j=1,...,k.
Ищем B[j] с максимальным индексом j такое, что
B[j]
увеличиваем это B[j] на 1, а для всех m>j полагаем B[m]=B[m-1]+1 (B[j] растут с ростом j, и мы ищем и увеличиваем на 1 такое B[j] с максимальным номером j, чтобы при заполнении возрастающими значениями элементов массива B[m], m>j, последний элемент B[k] не превосходил бы n). Если такого B[j] не существует, то генерация сочетаний для данного k закончена.
Задача 4.
Дана строка S и набор A слов А[1], ..., A[k]. Разбить строку S на слова набора всеми возможными способами.
Пример: S=ABBC
A[1]=A, A[2]=AB, A[3]=BC, A[4]=BBC, A[5]=H, A[6]=B
S = A B BC
= A BBC
= AB BC
Решение.
Эта задача реализуется следующим рекурсивным алгоритмом поиска с возвращением (все слова набора A упорядочены по номерам):
а) Если строка пустая, то одна из возможных дешифровок найдена, иначе при разборе текста мы проверяем А[i] (при изменении i от 1 до n) на вхождение в начало дешифруемой в данный момент строки.
б) Если какое-то A[i] входит в строку как префикс, то запоминаем номер i этого слова, затем выделяем слово из строки, а с остатком текста производим операцию разбора по пункту а).
Если ни одно из A[i] не входит в качестве префикса в дешифруемую сейчас строку, то осуществляем возврат на пункт а), предварительно добавляя в начало строки последнее удаленное оттуда слово, и пытаемся выделить из текста слово с большим номером в A. Если возврат осуществить невозможно (т. к. мы находимся в начале исходной строки), то алгоритм заканчивает свою работу. Все возможные дешифровки найдены.
Задача 5.
Данные N косточек домино по правилам игры выкладываются в прямую цепочку, начиная с косточки, выбранной произвольно,в оба конца до тех пор, пока это возможно. Построить алгоритм, позволяющий определить такой вариант выкладывания заданных косточек, при котором к моменту, когда цепочка не может быть продолжена, "на руках" останется максимальное число очков.
Решение.
Перебор с возвратом.
Задача 6.
a) В написанном выражении ((((1?2)?3)?4)?5)?6 вместо каждого знака ? вставить знак одной из 4 арифметических операций +,-,*,/ так, чтобы результат вычислений равнялся 35 (при делении дробная часть в частном отбрасывается). Найти все решения.
б) Вводится строка не более чем из 6 цифр и некоторое целое число R. Расставить знаки арифметических операций ("+", "-", "*", "/"; минус не является унарным, т.е. не может обозначать отрицательность числа; деление есть деление нацело, т.е. 11/3=3) и открывающие и закрывающие круглые скобки так, чтобы получить в результате вычисления получившегося выражения число R. Лишние круглые скобки ошибкой не являются.
Например: Строка 505597, R=120: ((5+0)*((5*5)-(9/7)))=120.
Решение.
а) Всего может быть 4 арифметических операции - "+","-","*", "/". Занумеруем их от 0 до 3. Вместо каждого из пяти знаков "?" может стоять один из знаков операции. Заведем массив A из 5 целых чисел, в i-ом элементе массива будет храниться код соответствующей i-му знаку "?" операции, т.е. число от 0 до 3. Начальная конфигурация - все элементы массива нулевые, конечная - все они равны 3. Генерация очередной конфигурации знаков равносильна прибавлению единицы в четверичной системе счисления, в которой разрешается пользоваться только цифрами от 0 до 3 (подобный метод решения мы уже встречали в задаче 2).
Приведем программный фрагмент генерации конфигураций.
Для удобства возьмем массив A не из 5, а из 6 элементов.
О получении последней конфигурации знаков будет свидетельствовать появление 1 в шестом разряде (если к 333334 прибавить 1, то получим 1000004 ).
for i:=1 to 6 do A[i]:=0;
while A[6]=0 do
begin
....
{ проверка, получили ли мы нужный результат }
....
i:=1;
while A[i]=3 do { Перенос в следующий разряд при }
begin { прибавлении единицы }
A[i]:=0;
i:=i+1;
end;
A[i]:=A[i]+1;
end;
Задача 7.
Построить все слова длины n>0 в алфавите скобок "(" и ")", представляющие правильные скобочные записи.
Решение
Перебор.
Задача 8.
Составить программу, которая печатает все различные представление числа N в виде всевозможных произведений (сумм) K натуральных чисел (N, K-вводятся, 1
Решение.
Предложим простой способ построения всех разбиений числа
на слагаемые. Разбиения будут строится в порядке, обратном лексикографическому. Очевидно, что первым разбиением в таком порядке будет разбиение, содержащее одно слагаемое, равное, а последним - разбиение из слагаемых, равных 1.
Как выглядит разбиение, следующее непосредственно за разбиением
n=с[1]+...+с[к] (1)
Будем искать разбиение, которое имеет самое большое число начальных слагаемых, равных начальным слагаемым разбиения (1) - обозначим эти слагаемые а[1],...,а[t-1] - и оставшиеся слагаемые которого определяются разбиением, непосредственно следующим за разбиением
s=a[t]+a[t+1]+...+a[k].
Легко видеть, что эти условия однозначно определяют значение t
t=max{i:a[i]>1}.
Таким образом, задача свелась к нахождению разбиения, непосредственно следующего за разбиением s=a[t]+1+...+1, где a[t]>1, а количество единиц равно k-t.Таким разбиением является разбиение s1=p+p+...+p+(s mod p), где p=a[t]-1.
Задача 9.
Подсчитать количество слов длины К из данных N букв, не содержащих данное подслово
Решение.
Простой случай
Элементы исходной последовательности-алфавита различны, слово зависит от порядка букв. Если в исходной последовательности есть одинаковые буквы, то надо будет кое-что подкорректировать (их-то порядок не важен будет в слове, если стоят рядом). Это сделаем потом. Каждый элемент алфавита мы можем использовать в слове один раз.
По идее всего слов размера К из N букв будет... из 1-й буквы N возможных из двух N2... - для каждой первой буквы N возможных слов... в общем из К ->
(1) Nk.
Из этого надо вычесть все последовательности, содержащие данную подпоследовательность. Сколько таких?
Пусть длина плохой подпоследовательности m. Ищем все подпоследовательности длины к с фикс. частью длины m.
Пусть фикс. часть в начале
<--фиксированная часть слова--><--можем менять-->
m букв k-m
Возможностей для изменения - n(k-m). Далее можно сдвинуть k-m раз вправо сию фикс. часть, получив таким образом еще (k-m)*n(k-m) слов. Тогда всего возможно
(2) (k-m+1)*n(k-m)
слов длины К из Н букв, содержащих данную подпоследовательность длины м.
Вычитаем (2) из (1) - получаем искомое число.
Сложный случай
Если же есть одинаковые буквы, то подсчет будет посложнее. Тебе понадобится подсчитать количество групп одинаковых букв и их количество в каждой (например, 3 буквы «н» и 2 буквы «а» в исходной последовательности - это 2 группы: по 3 и 2 элемента), затем для простоты сначала получить число (В) - ВСЕХ подпоследовательностей из К букв содержащих первую группу - то есть в которых она фиксирована.
- поделить это число на число комбинаций элементов в группе - тогда увидишь число РАЗЛИЧНЫХ таких подпоследовательностей (то есть различных слов),
вычесть это число РАЗЛИЧНЫХ из числа (В) ВСЕХ с первой группой - получили лишние слова, а затем вычесть результат из (1) - вообще всех слов.
И так для всех групп. Окончательно получим нечто меньшее nk - число ВСЕХ РАЗЛИЧНЫХ слов из К букв N-буквенной последовательности-алфавита.
Аналогичным образом поступить с числом слов, содержащих плохую подпоследовательность, превратив это число в число РАЗЛИЧНЫХ слов.
И вычесть, как и в простом случае это число, уже меньшее (2) из всех чисел (1). Возможно, такое решение, где все подсчитывается отдельно несколько неоптимально, но оно просто, очевидно, а, главное, должно работать.
Задача 10.
Классической задачей, которая решается методом перебора с отходом назад считается задача о восьми ферзях: требуется перечислить все способы расстановки 8-ми ферзей на шахматной доске 8 на 8, при которых они не бьют друг друга. Эту задачу решил больше 200 лет тому назад великий математик Леонард Эйлер. Заметьте, что у него не было компьютера, но тем не менее он абсолютно верно нашел все 92 таких расстановки!
Решение.
Очевидно, на каждой из 8 вертикалей должно стоять по ферзю. Каждую такую расстановку можно закодировать одномерным массивом
X[1],...,X[8],
где X[i] - номер горизонтали для i-го ферзя. Поскольку никакие два ферзя не могут стоять на одной горизонтали (тогда они бьют друг друга), то все X[i] различны, т.е. образуют перестановку из чисел 1..8. Можно, конечно, перебрать все 8! таких перестановок и выбрать среди них те 92, которые нас интересуют. Hо число 8!=40320 довольно большое.
Поэтому мы воспользуемся алгоритмом перебора с отходом назад, который позволит значительно сократить перебор и даст ответ намного быстрее:
program Queens;
const N=8;
type Index=1..N;
Rasstanovka=array [Index] of 0..N;
var X:Rasstanovka;
Count:word;
function P(var X:Rasstanovka;k,y:Index):boolean;
var i:Index;
begin
i:=1;
while (i
P:=i=k
end;
procedure Backtracking(k:Index);
var i,y:Index;
begin
for y:=1 to N do
if P(X,k,y) then
begin
X[k]:=y;
if k=N then
begin
for i:=1 to N do write(X[i]);writeln;inc(Count)
end;
Backtracking(k+1)
end
end;
begin
Count:=0;
writeln('Расстановки ',N,' ферзей:');
Backtracking(1);
writeln('Всего ',Count,' расстановок')
end.


