Коломак Евгения Анатольевна анализ управления конкурентной средой на субфедеральном уровне в россии специальность 08. 00. 13 Математические и инструментальные методы экономики автореферат

Вид материала

Автореферат

Содержание Share in regional production Tax exemptions Шестая глава N товаров, каждый из которых производится различными предприятиями, предполагается, что N V – среднее благосостояние, w

Подобный материал:

• Многоуровневые модели зависимости экономического роста от инвестиций: эконометрический, 321.8kb.
• Инструментарий анализа качества ассортимента и оценки рейтингов товаров предприятий, 286.28kb.
• Программа вступительного экзамена по специальности 08. 00. 13 «Математические и инструментальные, 555.96kb.
• Реферата по специальности 08. 00. 13 «Математические и инструментальные методы экономики», 141.02kb.
• Рефератов по специальности 08. 00. 13 «Математические и инструментальные методы экономики», 114.15kb.
• Фрактальный метод анализа ценных бумаг и формирования портфелей активов, 315.65kb.
• Рабочая программа дисциплины «экономико-математические методы и модели», 129.59kb.
• Программа вступительного экзамена в аспирантуру по специальности 08. 00. 13 «Математические, 180.85kb.
• Программа для поступающих в магистратуру по специальности 1-25 80 08 «Математические, 100.45kb.
• Экономико-математические модели анализа и прогнозирования Конъюнктуры регионального, 259.88kb.

Для тестирования гипотез из-за ограниченности информации оценивалось две системы. Каждая из них является модификацией полной системы, которая в соответствии со структурой теоретической модели предполагает проведение эмпирического анализа, как по секторам, так и по регионам. Опишем исходную систему.

Пусть i=1,…,N является индексом отрасли, r =1,…,R является индексом региона, а t=1,…,T - индекс времени. Система предложенных гипотез формирует следующую систему регрессионных уравнений:

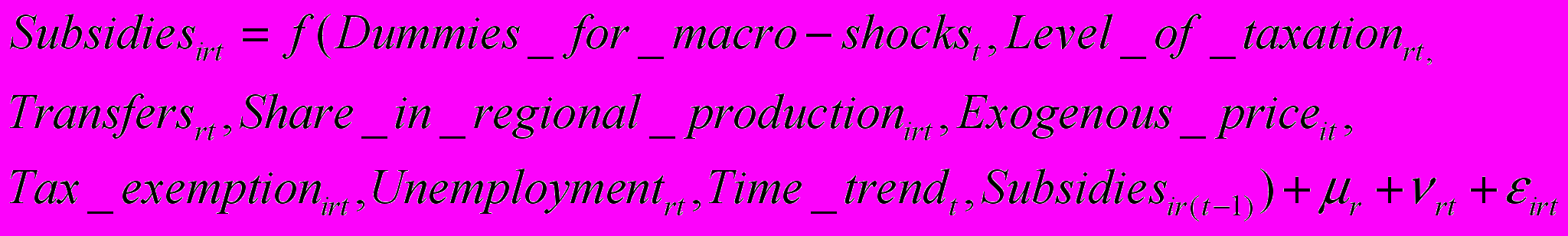
где:

 _r,  _r, _r – фиксированный региональный эффект;

_rt,  _rt, – случайная ошибка для региона;

_irt – случайная ошибка для отрасли;

Subsidies_irt – субсидии для отрасли i из бюджета региона r в году t;

Dummies for macro-shock_t – фиктивная переменная для макроэкономических ценовых шоков в году t;

Level of taxation_rt – налоговые доходы на душу населения в общих доходах бюджета региона r в году t;

Transfers_rt – доля трансфертов из федерального центра в доходах регионального бюджета в регионе r в году t;

Share in regional production_irt – доля отрасли i в производстве региона r в году t;

Exogenous price_it – средний уровень цен на продукцию отрасли i в году t;

Tax exemptions_irt – налоговые льготы, предоставленные сектору i в регионе r в году t;

Unemployment_rt – доля безработных в активном населении региона r в году t;

Time trend_t – временной тренд.

Количественные данные по субсидиям и налоговым льготам по отраслям были получены для одного региона, следовательно, ряд региональных переменных и региональных эффектов не могут быть оценены на основе располагаемой отраслевой информации. К числу таких региональных переменных относятся доля безработных, трансферты из федерального центра, уровень эффективного налогообложения в регионе. Эти региональные характеристики являются постоянными величинами для секторов по каждому году и оказываются составляющими временного эффекта для панельных оценках.

Модифицированная система, адаптированная для оценок по одному региону, приведена ниже.

Модификация 1

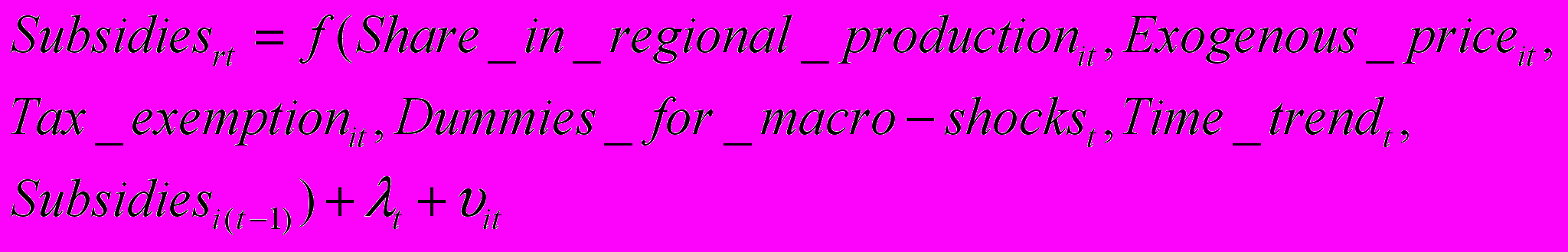
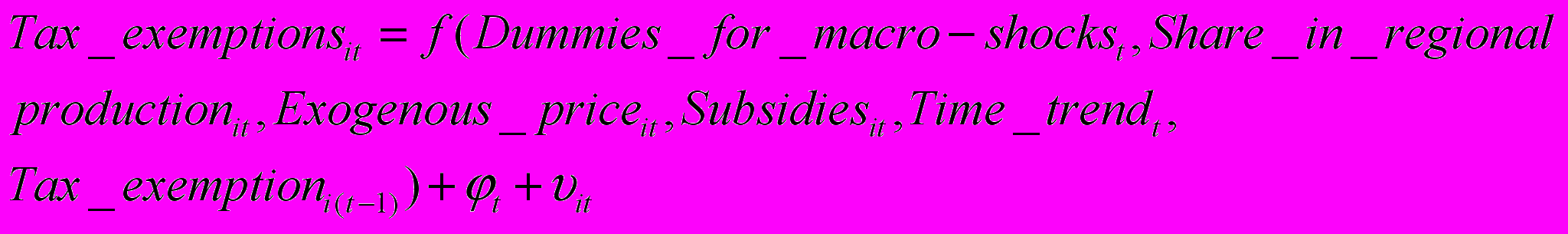
Индекс i идентифицирует сектор, t – год, λ_i и φ_i отражают особенности сектора.

Однако эффект региональных характеристик тоже представляет интерес. Для оценки их влияния оценивалась система на основе агрегированных по отраслям данных. Трактовка переменной по налоговым льготам в этих оценках отличается. Она отражает факт предоставления льгот и равна количеству решений по предоставлению налоговых льгот в регионе. Переменная доли сектора в региональном выпуске должна быть исключена, так как сумма долей всех секторов равна единице. Однако в качестве косвенной характеристики давления со стороны групп лоббирования в регионе введена фиктивная переменная, которая равна «1», если в регионе существует отрасль, производящая 1/3 и больше всего регионального промышленного выпуска, и равна «0» в противоположном случае. Переменная экзогенных цен для варианта агрегированных по секторам оценок совпадает с временным эффектом.

Модификация 2

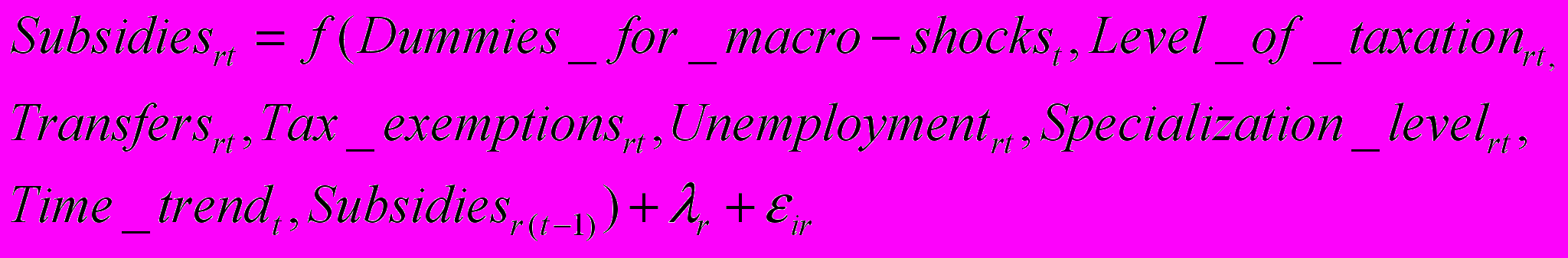
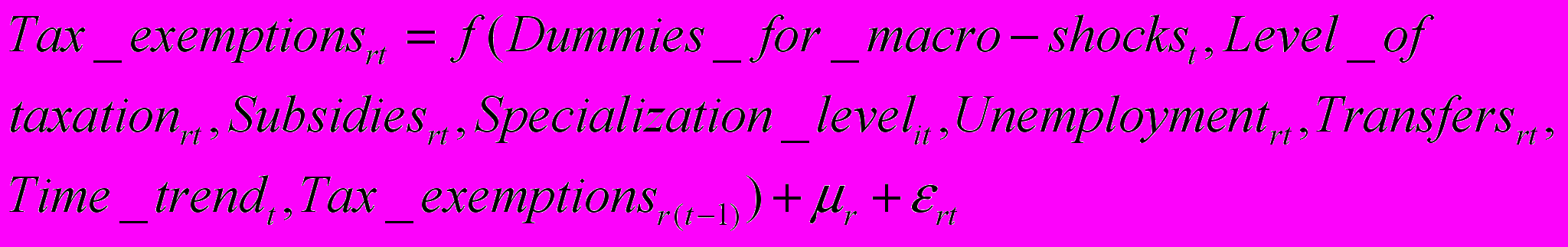
Введены следующие переменные:

Subsidies_rt – доля субсидий местным производителям в общих бюджетных затратах региона r в году t;

Specialization level_rt – фиктивная переменная, отражающая уровень специализации в регионе, которая принимает значение “1”, если в регионе существует отрасль промышленности, производящая более 1/3 общего регионального продукта промышленности в регионе r в году t;

Tax exemptions_rt – количество решений администрации по предоставлению налоговых льгот в регионе r в году;

λ_r, μ_r – переменные регионального эффекта.

Все уравнения относятся к классу динамических панельных регрессий с эндогенными переменными. Один из предлагаемых методов оценки таких регрессий – обобщенный метод моментов метод, предложенный Ареллано и Бондом, где в качестве инструментов используются лаговые значения переменных.

Эмпирические оценки показали, что размер деловой активности, представленной секторами, не имеет существенного значения для предоставления субсидий и налоговых льгот, более важно политическое лоббирование само по себе. Еще одним значимым фактором размера субсидий и налоговых льгот являются макроэкономические шоки. Оценки подтвердили также зависимость субсидий и налоговых льгот от уровня эффективного налогообложения в регионе и трансфертов из федерального центра. Высокий уровень налогов и трансфертов из бюджета более высокого уровня являются факторами, позволяющими региональным администрациям увеличивать субсидирование и налоговые льготы местным производителям. При этом социальные мотивы не влияют на решения региональных администраций при принятии решений о защите местных производителей.

Таким образом, субфедеральное субсидирование и налоговые льготы местным производителям являются результатом политического давления групп, лоббирующих интересы размещенных в регионе предприятий. При этом социальные факторы не находятся в фокусе внимания региональных политиков.

В пятой главе рассматриваются тенденции и эффекты методов прямого ценового контроля. Теоретической основой анализа, как и предыдущих главах, является политэкономический подход. Свойства равновесия модели регионального ценового регулирования затем тестируются на основе данных для регионов России.

Мы продолжаем рассматривать региональный рынок товаров i=0,1,…,n. Функция спроса населения региона на товары определена d_i(p_i). Пусть, если региональное правительство не вмешивается в рыночный механизм ценообразования, то экзогенными цены рынка равны: p₀^*, p₁^*,…, p_i^*,…, p_n^*. При этом для целей масштабирования примем p₀^*=1.

Функция предложения местных производителей зависит от экзогенных цен на факторы производства и готовую продукцию. Предположим, что региональная администрация может использовать ограничения на цены на готовую продукцию для регулирования рынка. Мы предполагаем, что производство в каждом секторе требует труд и специфический фактор производства, цены на который также регулируются. Следовательно, функция предложения местных производителей товара i зависит от цены товара, которая отличается от экзогенной рыночной цены, если местное правительство вводит ограничения на цены, и ограничения на цены на факторы производства: y_i(p_i, s_i,_i,_i), где p_i – уровень цены товара i, который необходимо получить, и который складывает в результате одновременного регулирования цены готовой продукции и цены фактора производства. Обозначим через p вектор регулируемых цен готовой продукции.

Население региона имеет предпочтения:



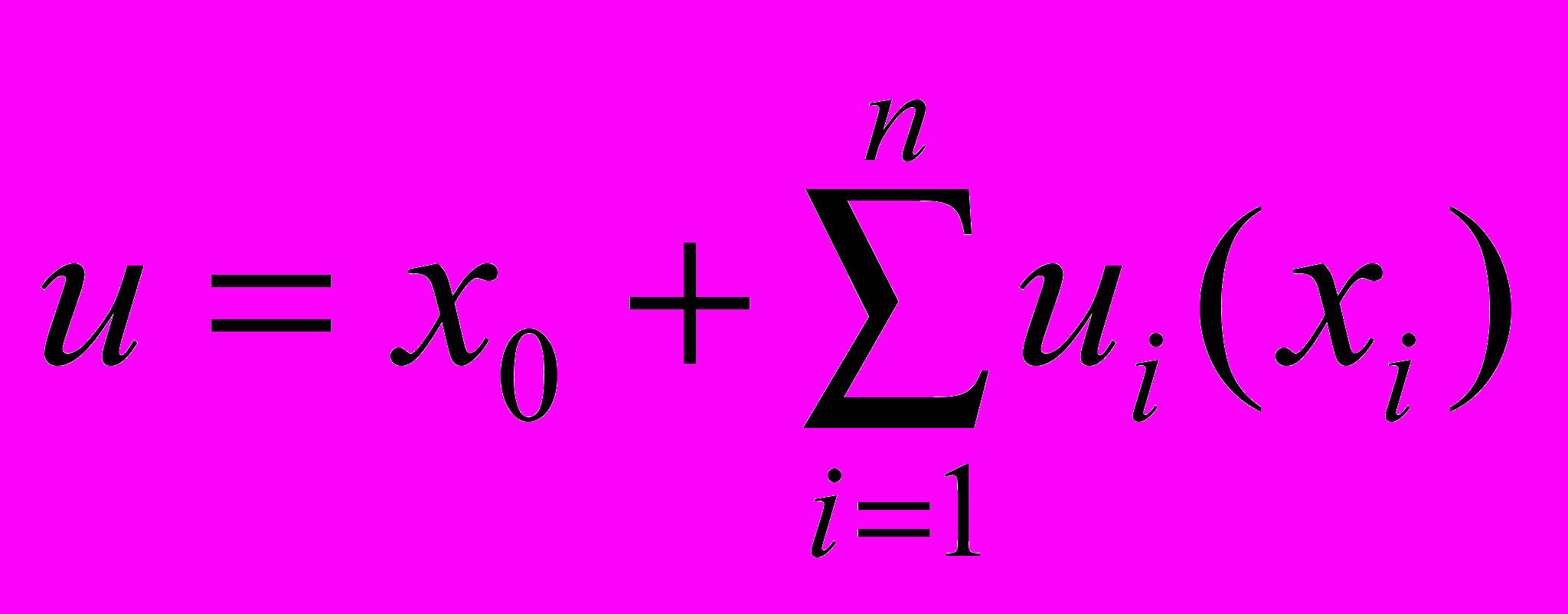
Выигрыш, который получает потребитель, равен



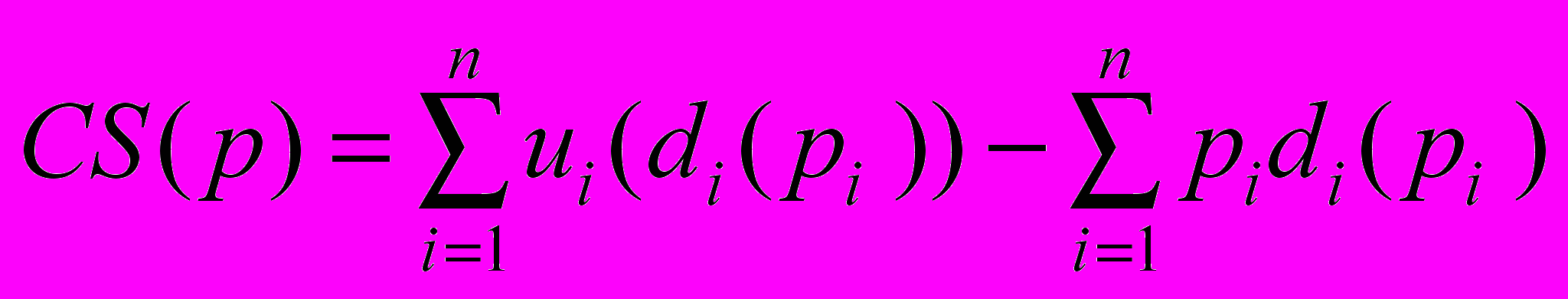
где p – вектор цен, которые определены региональной администрацией.

В данной постановке задачи не предполагается использование бюджетных средств для регулирования местного рынка, ценовые ограничения являются единственным инструментом в распоряжении местных властей, поэтому бюджетное ограничение теряет свой смысл. Тем не менее, бюджетные средства как производная от экономической активности в регионе и источник финансирования общественных благ продолжают фигурировать в задаче:



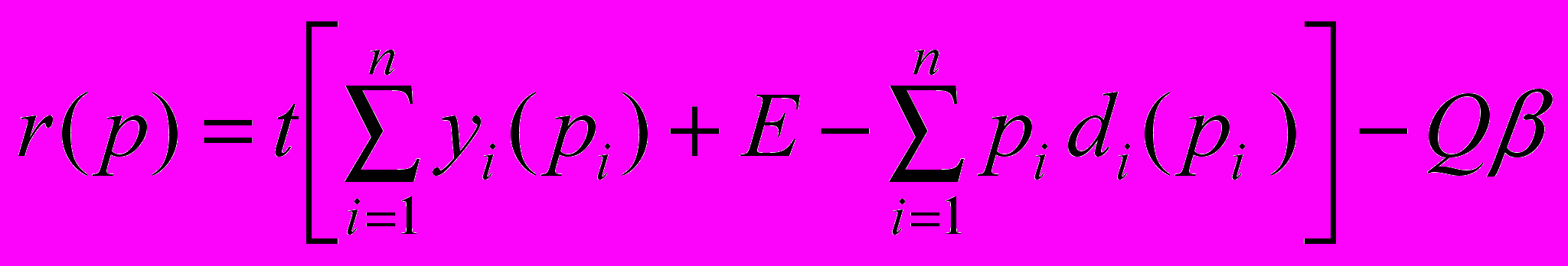
Где t - ставка налога, Q – минимальный набор бюджетных услуг,  - степень перераспределение местных издержек на другие бюджеты.

Производители заинтересованы в таком варианте ценового регулирования, которое соответствует их интересам, для этого они включаются в переговоры с местными властями. Лобби, представляющее интересы сектора i, делает предложения, которые связывают варианты ценовых ограничений с политической поддержкой. Пусть c_i(p_i) – поддержка от сектора i в зависимости от уровня цен. Лобби при формулировке своих предложений решает задачу максимизации благосостояния населения, занятого в секторе, которое равно:



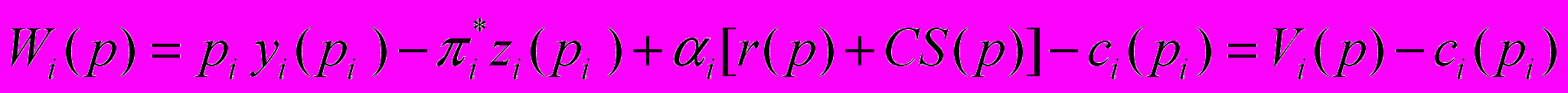
Где _l – ставка заработной платы; _i^* - экзогенная цена специфического фактора производства, используемого в секторе i; _i – доля голосующего на выборах населения, связанного с сектором i.

Правительство же при принятии решения в отношении ценовых ограничений максимизирует взвешенную сумму предложений от секторов и агрегированного благосостояния населения региона:



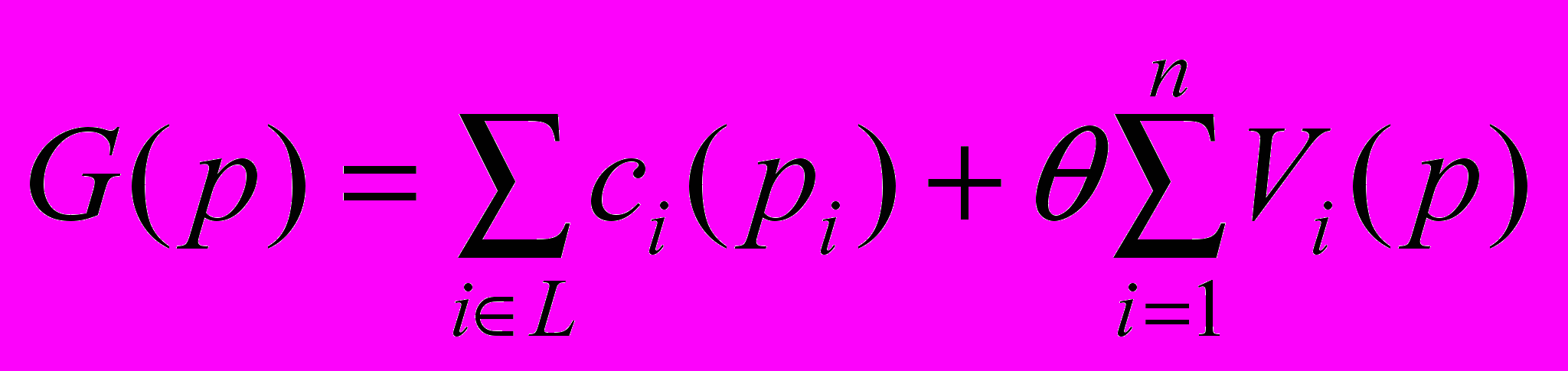
Где 01.

В соответствии с результатами Бернхайма и Винстона для рассматриваемой задачи верно следующее утверждение:

Утверждение 2. ({c_i⁰}_iL, {p⁰}) является равновесием региональной политики ценовых ограничений тогда и только тогда, когда:

(a) {c_i⁰} допустимы для всех iL;

(b) {p⁰} максимизирует G(p) для всех iL;

(c) {p⁰} максимизирует W_j(p)+ G(p) для всех jL;

(d) для каждого jL существует вариант (p^j), который максимизирует G(p) такой, что c_j⁰(p^j)=0.

Данные свойства позволяют определить равновесные цены, которые фиксирует правительство:

для всех j=1,…,n

Равновесия теоретической модели позволяют сформулировать ряд гипотез, которые могут быть протестированы на основе существующей информации.

Гипотеза 1. Ценовое регулирование на региональном уровне зависит от уровня экзогенных цен, следовательно, реагирует на макроэкономические шоки со стороны спроса и предложения.

Гипотеза 2. Регионы, демонстрирующие активный ценовой контроль имеют более низкий уровень налоговых доходов местного бюджета.

Гипотеза 3. Региональное ценовое регулирование - более активно в областях, где местные руководители имеют широкую поддержку населения.

Гипотеза 4. Концентрированный интерес производителей означает большую силу лоббирования и большую силу влияния на региональную власть для получения защиты.

Система предложенных гипотез формирует следующее регрессионное уравнение.



Для оценки уравнения использован панельный анализ с использованием моделей с фиксированным эффектом и со случайным эффектом. Оценки показали, что для ценового регионального регулирования значимым фактором были резкие макроэкономические ценовые изменения и поступления налоговых доходов в региональные бюджеты. Поддержка населения и уровень специализации не имели существенного значения при принятии решения о ценовых ограничениях на региональном уровне. Прямое ценовое регулирование использовалось субфедеральными органами власти для защиты населения территории от спекулятивных рыночных колебаний и для обеспечения социальной стабильности в регионе. Активность применения прямого ценового контроля определяли также внутренние условия развития регионов. Наблюдалась тенденция более интенсивного использования этого метода регулирования менее благополучными регионами страны.

Шестая глава посвящена вопросам теоретического и эмпирического анализа влияния рыночной инфраструктуры на характеристики конкурентной среды и динамику экономического развития регионов России.

Изложение материала начинается с теоретической модели влияния рыночной инфраструктуры на уровень конкуренции и эффективность экономического развития. В основе модели лежит постановка, предложенная Агийоном и Шанкерманом, которая дополнена политическими ограничениями.

В задаче рассматривается N товаров, каждый из которых производится различными предприятиями, предполагается, что N – достаточно большое. Потребители имеют одинаковые предпочтения, которые представлены функцией полезности:



Где x_j – потребление товара j; α – параметр, измеряющий возможности замещения одного товара другим, благодаря этому свойству, параметр α характеризует и обобщает в модели степень конкуренции на рынке товаров и эффект от инвестиций в инфраструктуру. Любые вложения в инфраструктуру, снижающие транзакционные издержки, имеют эффект увеличения степени конкуренции. Таким образом, коэффициент α является результатом инвестиций в рыночную инфраструктуру.

Выделяется группа производителей товаров, которые имеют высокие издержки на единицу продукции, их доля рынка равна q, и издержки - c_H. Остальная часть рынка (q-1) принадлежит фирмам с низкими удельными издержками . c_L (c_H>c_L). Фирмы конкурируют между собой, используя цены. В задаче ищется симметричное равновесие по Нэшу, в котором все фирмы, имеющие одинаковые издержки производства, устанавливают одинаковые цены p_i, 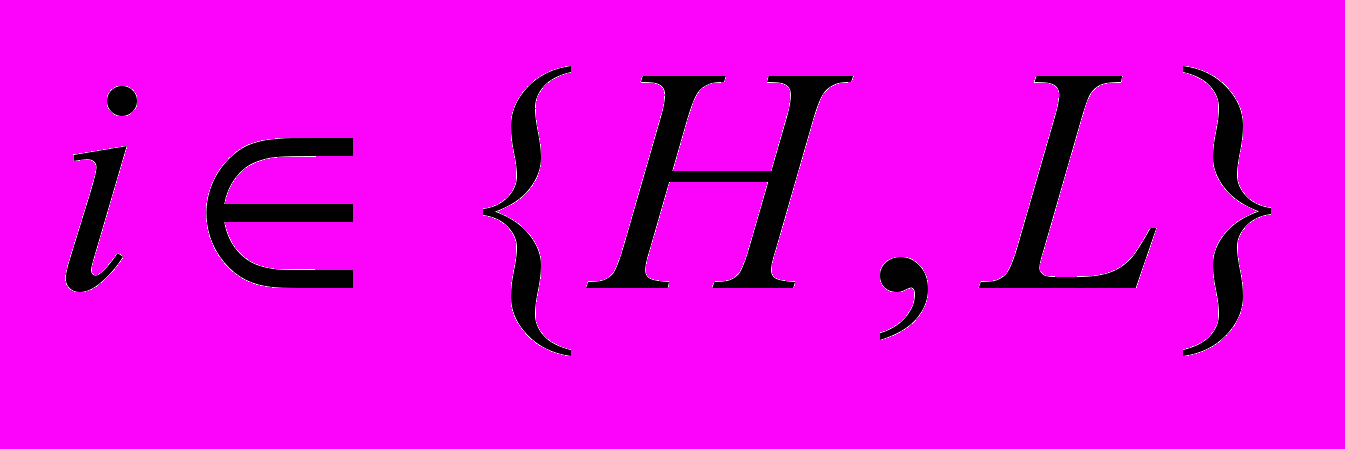. Фирмы максимизируют прибыль, предполагая, что другие участники рынка с издержками c_h (соответственно c_L) установят такую же цену p_h (соответственно p_L ) на свой товар: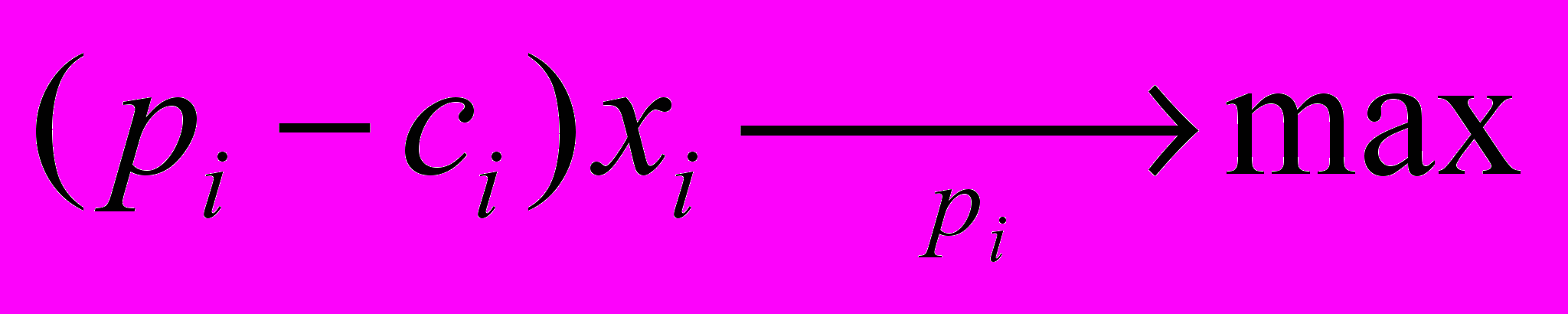



где x_i – спрос на продукцию фирмы i. Решение задачи проводит к следующему результату:



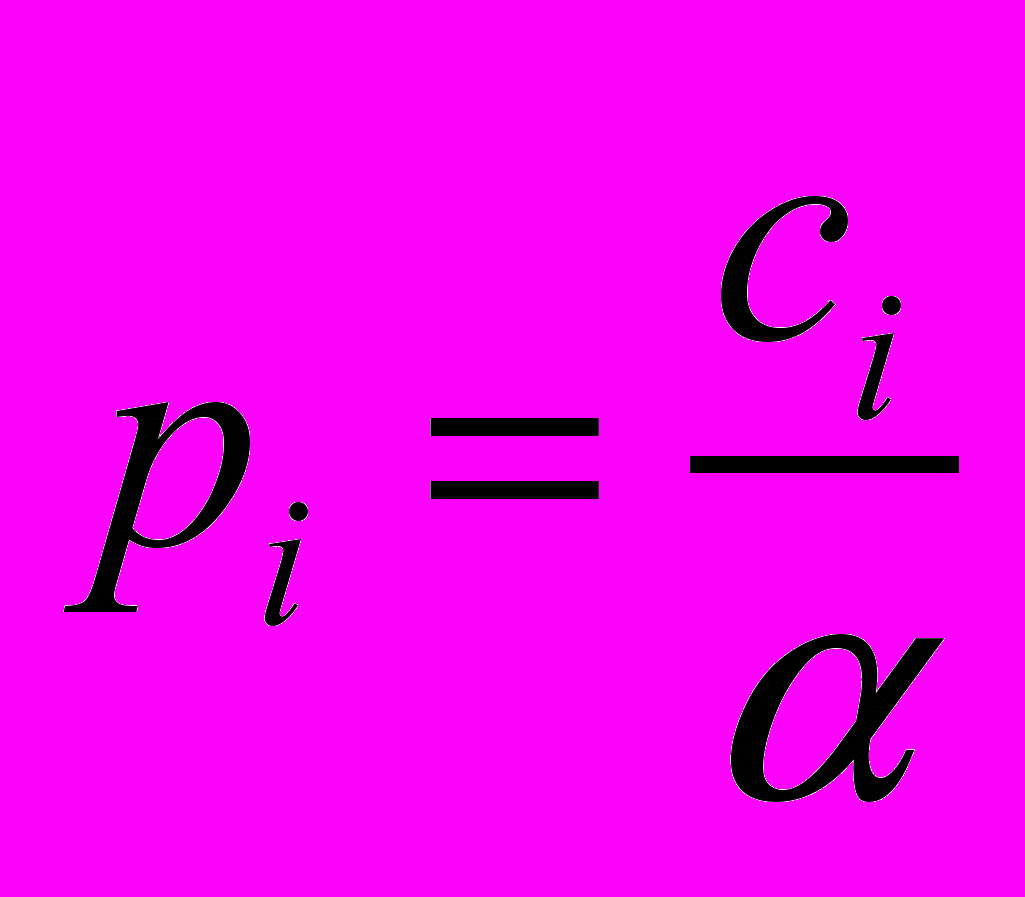
Таким образом, фирмы с низкими издержками устанавливают более низкую цену в равновесии, что позволяет им захватить большую часть рынка, причем цена снижается с ростом конкуренции.

Если мы обозначим через D_L и D_H равновесные объемы продаж предприятий соответственно с низкими и высокими издержками, то для них выполняется следующее соотношение:



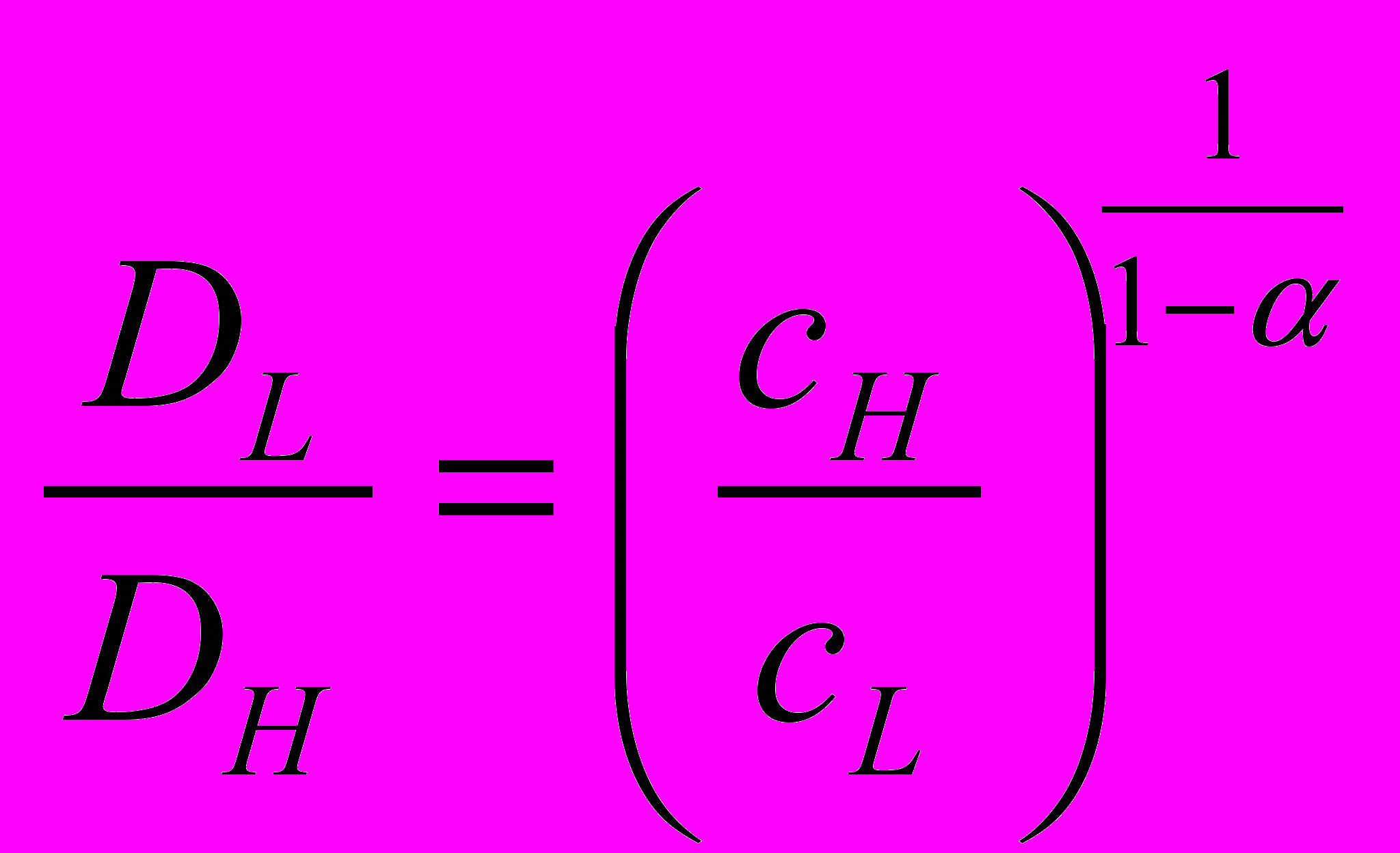
Из полученной пропорции следует, что доля рынка предприятий с низкими удельными издержками растет с ростом конкуренции и с ростом асимметричности издержек.

Предельный эффект инвестиций в инфраструктуру, снижающих транзакционные издержки и увеличивающих конкуренцию, для благосостояния вытекает из следующего соотношения:



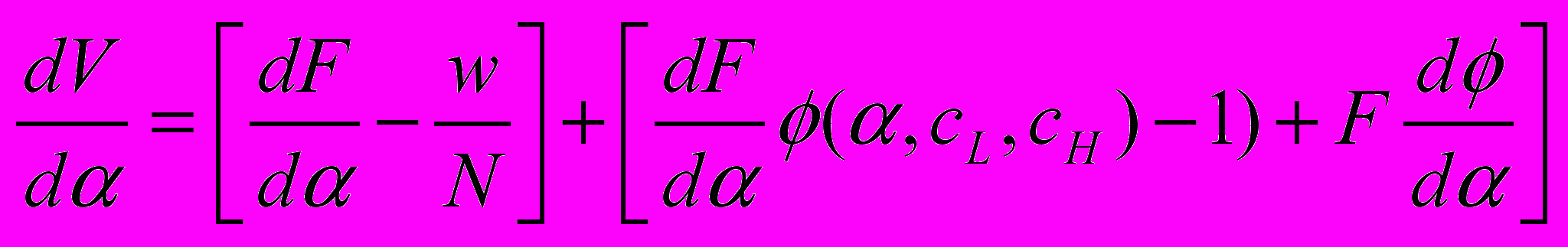
Где V – среднее благосостояние, w – доход репрезентативного потребителя, F(α)=D_s^α, D_s – равновесный спрос на продукцию фирмы в условиях равенства у всех фирм удельных издержек производства, 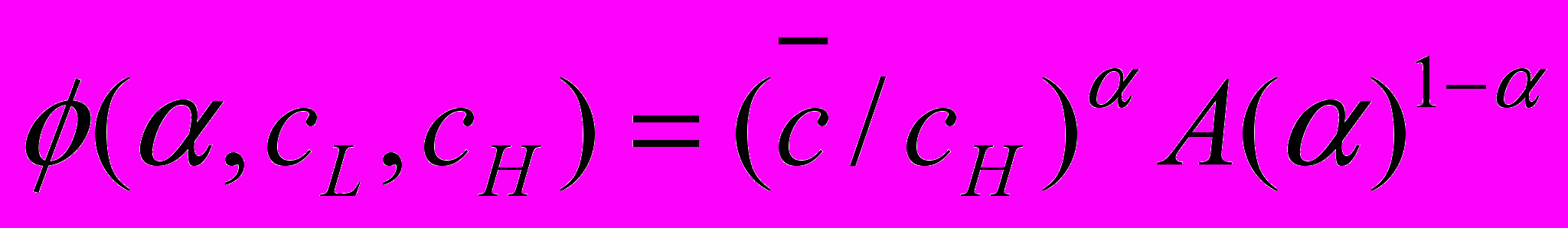, 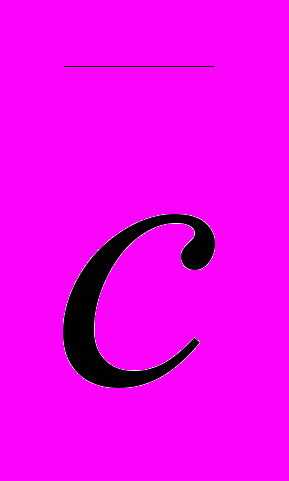- средние удельные издержки, .

Первое слагаемое предельного эффекта конкуренции характеризует эффект расширения общего выпуска, второе слагаемое отражает селекционный эффект. Эффект расширения связан с ростом выпуска и, соответственно, потребления и не зависит от неоднородности издержек производства в фирмах. Селекционный эффект отражает то, что в более конкурентной среде увеличивается доля производства фирм, имеющих более низкие издержки производства, в результате с одними и теми же общими издержками производится больше продукции, эффективность производства растет.

Учет влияния политических ограничений на размеры инвестирования в рыночную инфраструктуру означает введение в модель дополнительного участника – правительства, которое принимает решение о направлениях расходов общественных финансов и, в частности, о размерах той части, которая идет на развитие инфраструктуры.

Пусть производители с низкими и высокими издержками объединяются в соответствующие группы для создания политических лобби. Лоббирующие группы предлагают финансовую и нефинансовую поддержку (нефинансовая поддержка может быть оценена в денежном выражении) правительству, которое определяет объем инвестиций в инфраструктуру, в обмен на реализацию продвигаемого решения. В то время, как лоббирующие группы не рассматривают эффект их политического давления на вероятность перевыборов данного правительства, политики отдают себе отчет о существовании связи между размером поддержки, полученной от лобби, и собственными политическими перспективами. Поэтому правительство рассматривает не только сумму полученной поддержки от лобби, но и общественное благосостояние. Таким образом, целевой функцией политиков является взвешенная сумма этих двух составляющих.

Процесс лоббирования моделируется следующим образом. Каждая лоббирующая группа предлагает правительству объемы инвестирования в инфраструктуру, которым соответствуют варианты поддержки. Правительство определяет инвестиционную политику и получает соответствующую поддержку со стороны лобби.

Мы ищем равновесие двухэтапной некооперативной игры, в которой лобби одновременно выбирают свои варианты политических предложений правительству на первом этапе, и правительство выбирает политику для реализации на втором этапе. Фактически, в нашем случае каждый лобби определяет на первом этапе функцию предложения поддержки от объема инвестирования в инфраструктуру.

В задаче ищется равновесие по Нэшу, равновесием является:

1. Множество функций политических предложений (одно для каждой лоббирующей группы) такое, при котором группа максимизирует свой выигрыш в условиях заданных функций политических предложений со стороны других групп, и при котором максимизируется целевая функция правительства.

2. Объем инвестирования в инфраструктуру, который максимизирует целевую функцию правительства при заданных политических предложениях лобби.

Рассмотрим равновесия для двух крайних ситуаций, когда эффект отбора отсутствует (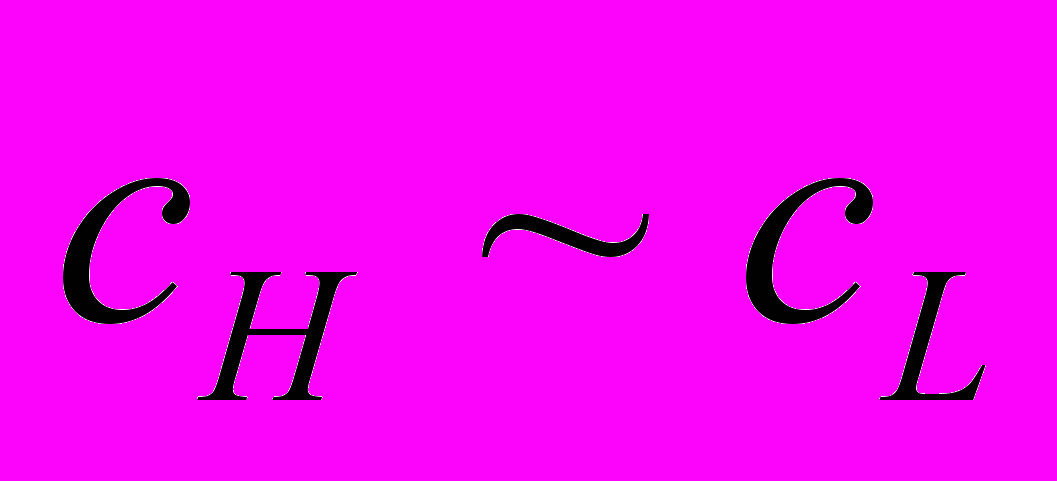), и когда эффект отбора максимален (, ).

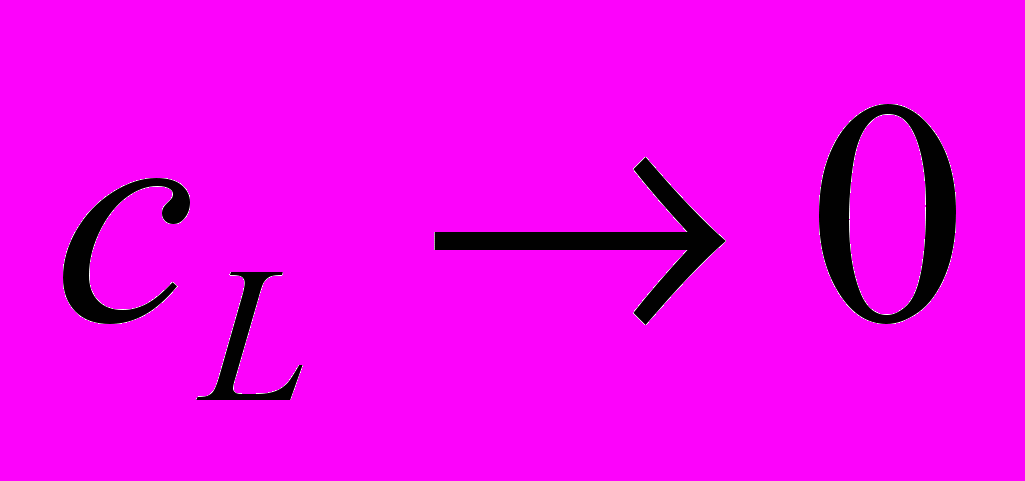В первом случае возможны три варианта решений. Первый вариант равновесия отражает ситуацию, когда правительство больше «ценит» поддержку, полученную от лоббирующих производителей, и не инвестирует в развитие инфраструктуры. Второй вариант соответствует ситуации доминирования общественных интересов в функции полезности правительства и максимальному объему инвестирования в инфраструктуру. В рамках третьего варианта решения правительству безразлично, чьи интересы удовлетворять, объем инвестиций в инфраструктуру может быть любым в рамках регионального бюджетного ограничения.

Во второй ситуации, когда 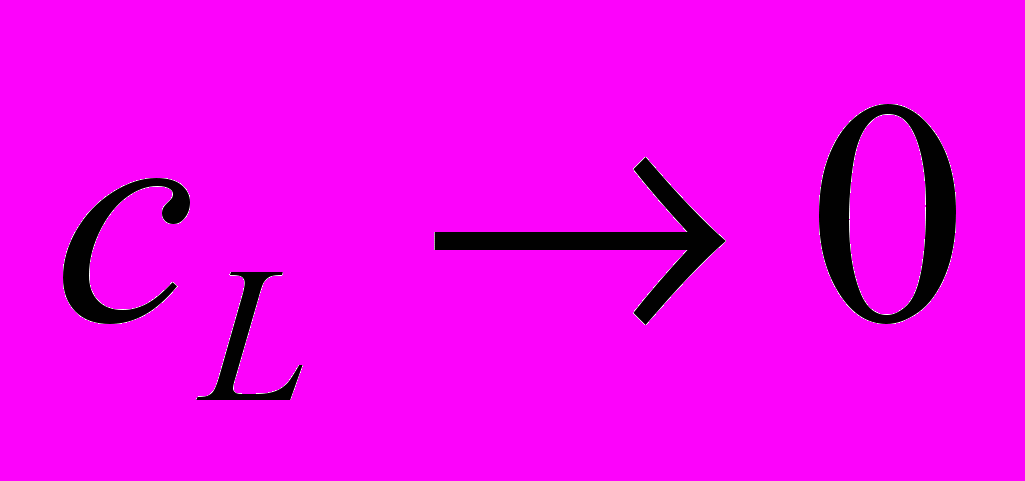, , равновесное значение близко к единице, что означает высокие инвестиции в развитие инфраструктуры рынка.

Полученные свойства равновесия задачи позволяют сформулировать следующие гипотезы для эмпирической верификации:

Гипотеза 1. Величина накопленных инвестиций в рыночную инфраструктуру имеет положительную корреляцию с уровнем благосостояния в регионе.

Гипотеза 2. Величина накопленных инвестиций в рыночную инфраструктуру, стимулируя конкуренцию, имеет в качестве следствия отрицательную корреляцию с уровнем затрат на производство продукции в регионах.

Изучение межрегиональных различия в уровне развития институциональной и физической рыночной инфраструктуры в России, тенденции в ее динамике, оценки влияния показателей развития инфраструктуры на уровень, динамику и показатели эффективности экономического развития территорий подтвердили выдвинутые гипотезы.

В седьмой главе работы выявляются тенденции в предоставлении налоговых льгот субфедерального уровня инвесторам, и оценивается их эффективность для привлечения инвестиций. Для этого сформирована следующая система гипотез:

Гипотеза 1. Субфедеральные налоговые льготы являются существенным фактором, определяющим межрегиональное распределение инвестиций в России. Более льготный налоговый режим привлекает больше инвестиций в регион.

Гипотеза 2. Субъективный фактор отсутствия доверия к команде региональной администрации, играет существенную роль в принятии инвестиционного решения, сдерживает приток инвестиций в регион.

Гипотеза 3. Регионы, имеющие более высокую долю добывающих и экспортно-ориентированных отраслей промышленности, привлекают больше инвестиций в нефинансовые.

Гипотеза 4. Инфраструктурная обеспеченность региона остается фактором, влияющим на решение инвесторов, предполагается положительная корреляция между уровнем развития региональной инфраструктуры и предложением инвестиций.

Гипотеза 5. Региональные власти, имеющие более высокие оценки недостатка инвестиций и относительно невыгодное сочетание индустриальных и инфраструктурных факторов развития, с большей готовностью используют законодательные меры, способные улучшить конкурентные позиции региона и привлечь инвестиции.

Гипотеза 6. Региональные законодательные инициативы в области налоговых льгот тем активнее распространяются, чем больше регионов такие инициативы уже поддержало.

Гипотеза 7. Величина и период предоставления льгот инвесторам, а также дополнительные льготы иностранным инвесторам находятся в прямой зависимости от оценок региональными администрациями дефицита инвестиционных ресурсов и от распространения инвестиционного законодательства по стране.

Гипотеза 8. Более активный контроль региональной администрации в предоставлении налоговых льгот инвесторам характерен для относительно благополучных регионов.

Первые четыре гипотезы связаны со свойствами функции предложения инвестиции, для их проверки оценивалось следующее уравнение:

Г