Geum.ru

Учебно-методический комплекс для специальностей: 080507 Менеджмент организации 080504 Государственное и муниципальное управление

Вид материалаУчебно-методический комплекс

Содержание


Цель лабораторной работы
Граница интервала
Обязательная литература
Типовые задачи контрольных работ
Подобный материал:
1   2   3   4

_____


ТЕМА СТАТИСТИЧЕСКАЯ ГИПОТЕЗА (2 ч)

Цель лабораторной работы – освоить технику проверки гипотезы о виде закона распределения генеральной совокупности, используя критерий Пирсона.

В результате выполнения работы студент должен научиться применять критерий Пирсона для проверки гипотез о нормальном законе распределения генеральной совокупности и законе распределения Пуассона. Уметь строить статистические таблицы в программной среде Excel для проведения необходимых расчетов и делать выводы по полученным результатам.


Вопросы для обсуждения:
  1. Статистические гипотезы и их прикладное назначение.
  2. Критическая область и область принятия решения.
  3. Ошибки первого и второго рода.
  4. Распределение . Критерий Пирсона.
  5. Эмпирические и теоретические частоты.
  6. Построение таблицы для проверки гипотезы о нормальном законе распределения генеральной совокупности.
  7. Построение таблицы для проверки гипотезы о распределении генеральной совокупности по закону Пуассона.
  8. Построение таблицы для проверки гипотезы о равномерном распределении генеральной совокупности.

Пример индивидуального задания.
  1. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с заданным эмпирическим распределением.




Номер интервала i

Граница интервала
Частота





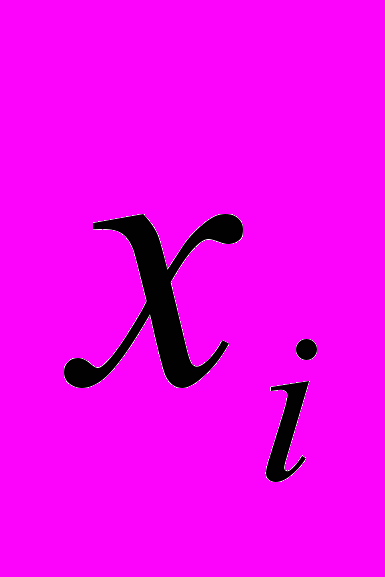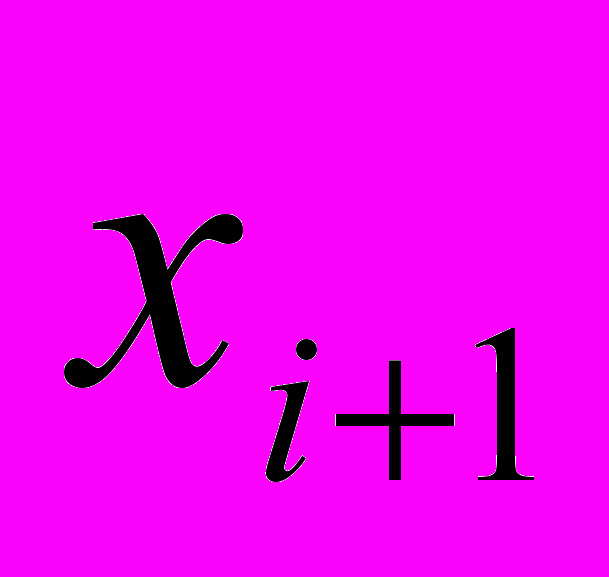1
-20
-10
20

2
-10
0
47

3
0
10
80

4
10
20
89

5
20
30
30

6
30
40
40

7
40
50
50



  1. В течение 10 часов регистрировали прибытие автомашин к бензоколонке и получили эмпирическое распределение, приведенное в таблице (в первом столбце указан интервал времени в часах, во втором столбце – частота, т.е. количество машин, прибывших в этом интервале). Всего было зарегистрировано 200 машин. Требуется при уровне значимости 0,01 проверить гипотезу о том, что время прибытия машин распределено равномерно.


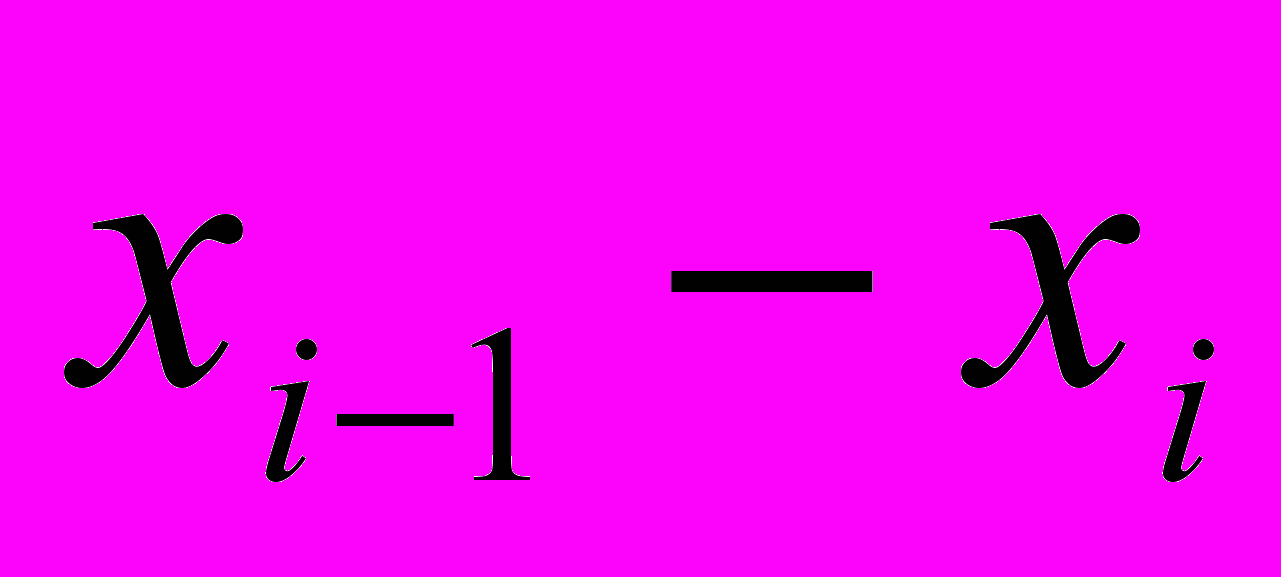8-9
12

9-10
40

10-11
22

11-12
16

12-13
28

13-14
6

14-15
11

15-16
33

16-17
18

17-18
14



  1. В итоге проверки на нестандартность 200 ящиков консервов получено следующее эмпирическое распределение (в первой строке указано количество 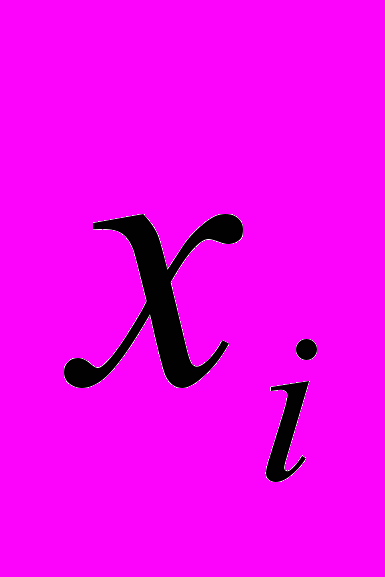нестандартных коробок консервов в одном ящике; во второй строке – частота , т.е. число ящиков содержащих 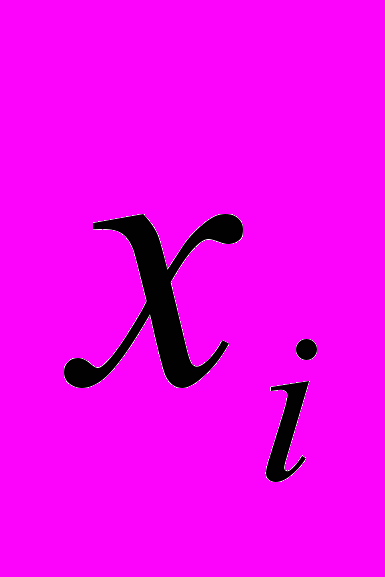коробок нестандартных консервов). Требуется при уровне значимости 0,05 проверить гипотезу о том, что случайная величина X – число нестандартных коробок – распределена по закону Пуассона.
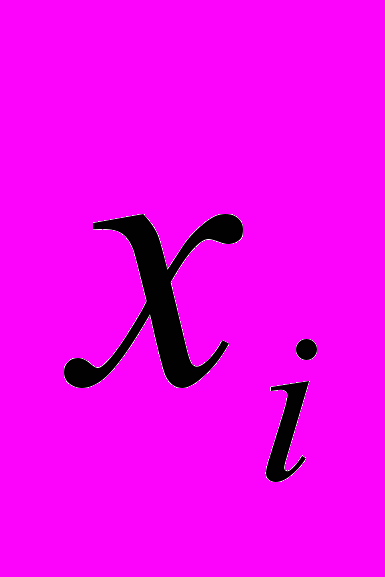0
1
2
3
4



132
43
20
3
2


Обязательная литература

Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2003, 480 с. Гл. 19, с. 181 – 185, с. 329 – 335.

Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М: «Высшая школа», 2004, 404 с. Гл. 13, с. 206 -207, с. 251 -259, с.275 -283.


ТИПОВЫЕ ЗАДАЧИ КОНТРОЛЬНЫХ РАБОТ

КОНТРОЛЬНАЯ РАБОТА №1
  1. Брошены две игральные кости. Какова вероятность того, что сумма очков на выпавших гранях делится на 2, причем на грани одной из костей появится 2?
  2. Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку, равна 0,1, второй - 0,15, третий - 0,2. Найти вероятность того, что при однократном измерении будет допущена ошибка хотя бы одним исследователем.
  3. Среди десяти документов три оформлены не по стандарту. Документы проверяют один за другим до выявления всех нестандартных. Какова вероятность того, что проверка закончится на 5 документе.
  4. Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2, 0,4, 1,3.
  5. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются).
  6. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0.4, независимо от других магазинов. Найти вероятность того, что число заявок в день не превысит двух. Найти среднее число заявок в день.
  7. Заряд охотничьего пороха отвешивается на весах, имеющих среднюю квадратическую ошибку взвешивания 150 мг. Номинальный вес порохового заряда 2.3 г. Определить вероятность повреждения ружья, если максимально допустимый вес порохового заряда 2.5 г.
  8. Концертный зал, рассчитанный на 1200 мест, имеет четыре буфета. Каждый зритель с равной вероятностью может посетить любой из буфетов. На сколько мест должен быть рассчитан каждый буфет, чтобы с вероятностью 0.9 каждый зритель мог быть обслужен в том буфете, который он посетил?
  9. При наборе книги на 300 страницах делают в среднем 6 опечаток. Найти вероятность того, что на 50 прочитанных страницах будет обнаружено не более трех опечаток.
  10. Вероятность того, что яблоко испортится при транспортировке 0,01. Яблоки упаковываются в коробки по 200 штук. Найти вероятность того, что в коробке окажется хотя бы одно испорченное яблоко.


Итоговая контрольная работа.
  1. Сумма событий. Совместные и несовместные события. Теорема сложения для классической модели. Следствия теоремы сложения.
  2. Доверительный интервал для среднего квадратического отклонения.
  3. Производителю электроламп известно, что средний срок работы лампы составляет 600 часов, среднее квадратическое отклонение срока работы- 40 часов. Какова вероятность, что срок работы от 550 до 700 часов. 2% ламп имеют минимальный срок работы. Какова его величина?
  4. В результате хронометража времени сборки узла различными сборщиками установлено, что дисперсия этого времени 2 мин2. Предполагая, что время сборки имеет нормальное распределение, найти минимальный объем выборки, при котором с надежностью 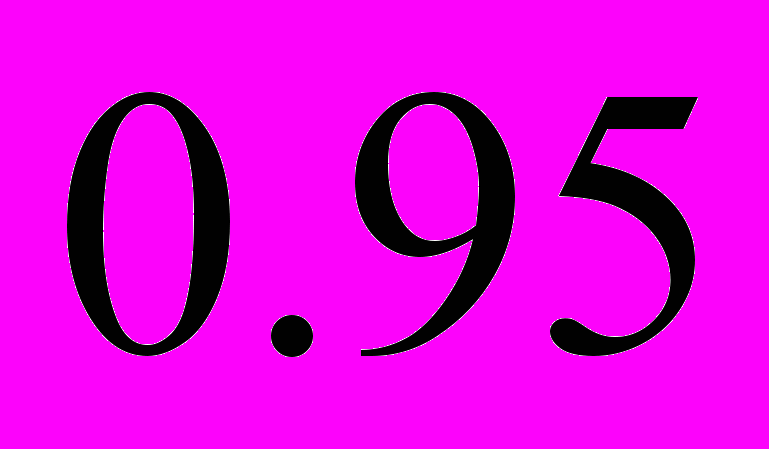точность оценки среднего времени сборки мин.

Система текущего и итогового контроля
знаний студентов


Общая оценка успеваемости студента по предмету выставляется за совокупный результат:

выполнения промежуточной контрольной работы №1 по первой части курса теории вероятностей (максимальное количество баллов – 25);

выполнения лабораторной работы №1 (максимальное количество баллов – 10);

выполнения лабораторной работы №2 (максимальное количество баллов – 10);

выполнения лабораторной работы №3 (максимальное количество баллов – 10);

выполнения итоговой контрольной работы (максимальное количество баллов – 45).

Максимально возможная сумма баллов, набираемых студентом в течение семестра, составляет 100 баллов. Соответствие между количеством выбранных баллов и оценкой представлено в следующей таблице:

Оценка

Набранные баллы

Неудовлетворительно

Удовлетворительно

Хорошо

Отлично

0-59

60-74

75-90

91-100

Набранная за семестр сумма является рекомендуемой оценкой для сдачи экзамена.


В случае неаттестации студента по курсу пересдача дисциплины осуществляется в форме экзамена. На экзамене каждому студенту предлагается ответить на два теоретических вопроса (см. контрольные вопросы) и решить одну задачу (см. типовые задачи итоговой контрольной работы).