Geum.ru

Discipline annotation “Systems Engineering”

Вид материалаДокументы
Supportive Materials
Discipline annotation
Aim of the Course
Discipline annotation
Methods of Teaching
Discipline annotation
Prior requirements
Aim of the course
Methods of Teaching
Подобный материал:
1   2   3   4   5   6   7   8   9   10

Assessment criteria:


Only those students who have got 35 % of the total amount of credits according to all forms of current control are admitted to an exam; students who have got no less than 91 % of the total amount of credits are free from the exam.

  1. Supportive Materials:
  • Program
  • Discipline schedule
  • Textbooks
  • Department manuals
  • Collected problems manuals
  • Set of individual tasks for current control
  • Tasks for rector tests
  • Examination cards
  1. Language of Instruction: Russian
  2. List of Recommended Literature


Basic Literature

  1. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика (Theory of Probability and Mathematical Statistics). К., Выща школа, 1979.
  2. Климов Г.П.. Теория вероятностей и математическая статистика (Theory of Probability and Mathematical Statistics). М., Издательство Московского университета, 1983.
  3. Коваленко И.Н., Гнеденко Б.В. Теория вероятностей (Theory of Probability). К., Выща школа ,1990.
  4. Розанов Ю.А. Теория вероятностей случайные процессы и математическая статистика (Theory of Probability, Casual Processes and Mathematical Statistics). М., Наука, 1985.
  5. Крамер Г. Математические методы статистики (Mathematical Methods of Statistics). М., Мир, 1975.
  6. Шметтерер Л. Введение в математическую статистику (Introduction to Mathematical Statistics). М., Наука, 1976.
  7. Закс Ш. Теория статистических выводов (Theory of Statistical Conclusions) . М., Мир,1975.
  8. Кендалл М.Д., Стюарт А. Статистические выводы и связи (Statistical Conclusions and Correlation). М., Наука, 1973.
  9. Боровков А.А. Математическая статистика (Mathematic Statistics). М., Наука, 1984.
  10. Леман Э. Проверка статистических гипотез (Check-up of the Statistical Hypotheses). М., Наука, 1979.
  11. Бикел П., Доксам К. Математическая статистика (Mathematic Statistics). М., Финансы и статистика, 1983.
  12. Ермаков С.М., Михайлов Г.А. Курс статистического моделирования (Course of Statistical Modeling). М., Наука, 1976.
  13. Сборник задач по теории вероятностей математической статистике и теории случайных функций (Collected Problems in Theory of Probability and Theory of Casual Functions). Под ред. А.А. Свешникова, М., Наука,1970.


Manuals and Methodological guidance

1. Учебно-методическое пособие “Теория вероятностей и математическая статистика” (Methodological guidance “Theory of Probability and Mathematical Statistics “). Сост. Рофе-Бекетов Ф.С., Подцыкин Н.С. – Харьков, 2001.

DISCIPLINE ANNOTATION

Mathematical Analysis and Differential Equations


Lecturer: Nikolenko Iryna Hennadiivna PhD (Physics and Mathematics), Associate Professor

Status: Normative


Courses, semesters: 1-2 courses, 1-3 semesters


Aim of the Course: is in providing future specialists with knowledge in the area of mathematical analysis and differential equations.


Prior Requirements: “Higher Algebra”, 1 semester, “Analytical Geometry”, 1 semester.


Tasks of the Discipline: following the completion of the course students must:


KNOW:
  • Features of infinitely small consecutive orders or functions;
  • Rules of differentiation;
  • Theories of Roll, Langrage, L’Hopital;
  • Necessary and sufficient conditions for extremum of functions;
  • Features of the anti-derivative and indefinite integral;
  • Rules of calculus of the Riemann integral;
  • Formulae for calculus of a shape area, quantities of lines, volumes of solids;
  • Formulae of differential of bivariate function, derivative of composite function;
  • LS method (least square method);
  • Linear operations on series;
  • Conditions of similarity and difference of numerical series;
  • the Leibniz's Theorem, Abel's theorem, Taylor and Maclaurin series;
  • Euler’s formula, a Fourier series for periodic function and Fourier integrals, Laplace formula;
  • Formulae for contour, double, triple integral calculus;
  • Green formulae;
  • Formulae of vector field current through the surface;
  • Taylor series;
  • Methods of solving the first-order equations;
  • Defining of discriminating polynomial of differential equation; application of the Wronskian, assignment and definition of Cauchy function;
  • Technology of reduction of the first degree linear equations system to the second degree equation;
  • Theorems about the existence of Laplace transform;
  • Formulae of figuring of derivative, convolution integral of originals;
  • Euler-Poisson equations, Ostrogradsky method;
  • Reasoning of heuristic formula of natural function according to the method of mathematical induction;
  • Verifying of the fundamental theorems.


BE ABLE TO:

  • Calculate borders and derivatives of simple and composite functions with one or a number of variables;
  • To trace functions, set distinctly, tacitly or with the help of parameters, to plot their graphs;
  • To find indefinite and defined integrals according to Riemann;
  • To calculate area of figures, length of lines, volume of solids;
  • To solve differential equations and systems of differential equations;
  • To apply differential or integral calculus to solving physical problems;
  • To trace numerical, consecutive and unusual integral conformity;
  • To explicate functions of vrai variable in Taylor, Maclaurin and Fourier series;
  • To find extremum of most functions variables;
  • To calculate contour; double and triple integrals;
  • To find the current of vector field through the surface;
  • To apply Stocks and Gauss-Ostrogradsky formulae;
  • To calculate integrals with the help of Euler beta and gamma functions.


Discipline Annotation:

Theory of limits: limit of sequence, limit of function, partial, superior and minimum limit of function. Continuity of function: local property of continuous functions, properties of continuous functions on interval. Differential calculus of one-variable function: derivatives and differentials of random order, properties of differential functions; Taylor’s function; extremum examination and plotting of function graphs. Indefinite integral: primary and indefinite integral, their properties; change of variable and integrating by parts; tabular interval; methods of integrating: rational functions; Ostrogradsky method; irrationalities, rational functions from trigonometric; some transcendental functions. Riemann integral: properties of integral functions; geometrical and physical application of integral; Riemann improper integral. Improper integrals; from infinite interval and from unbounded function on finite interval; convergence properties of improper integrals; absolute and conditional convergence. Numerical series; convergence properties of series, absolute and conditional convergence. Space 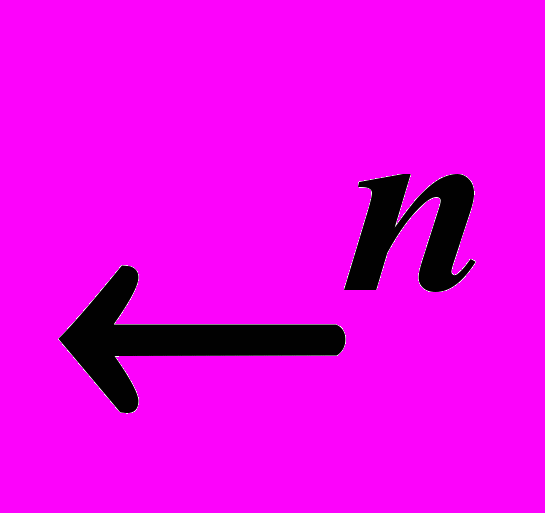; metric space, open and closed sets, their properties; compact sets in metric space and in 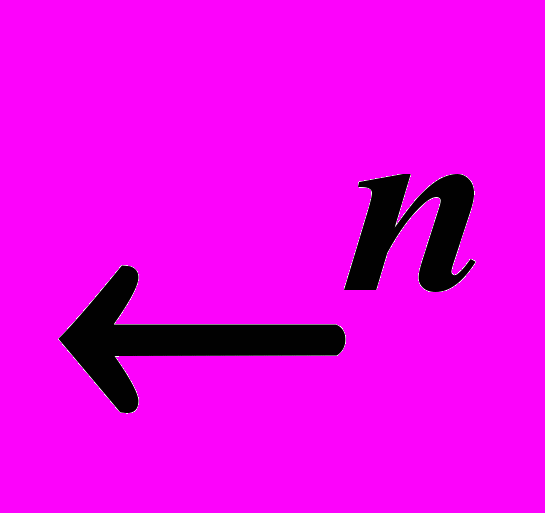; arrays in 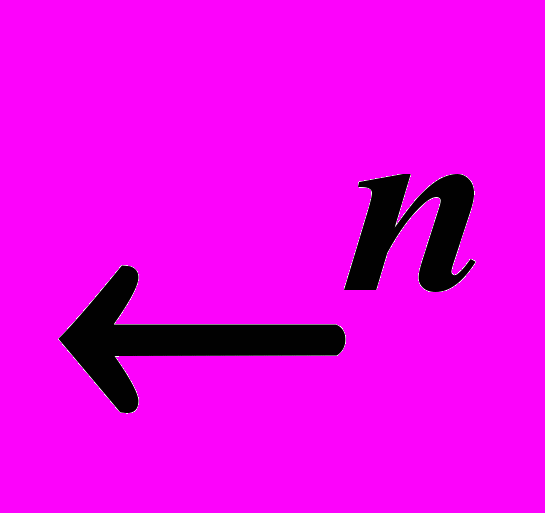, their convergence; properties of compactedness. Differential calculus of multivariable functions: variables and differentials of random order, properties of differential functions; Taylor function; the implicit function theorem; extremum examinations and extremum conditions. Functional consequence and series; conditions of proportional convergence of functional series; theorems about term-by-term differentiation and integration of functional series; formal power series and Taylor series. Riemann integrals depending on parameter: Euler’s integrals; Laplace method. Riemann multiple integral; properties of integral functions on sets, calculated by Jordan method; Fubini’s and change of variable theorem. Improper integrals; geometrical and physical application of multiple integral. Contour and surface integral: calculus of the first kind surface integrals and their properties, calculus of the second kind surface integrals; General Stock’s theorem and classic specific cases; elements of field theory. Fourier series: Fourier series relating to orthogonal vector system; trigonometrical Fourier series and their point convergence. Fourier integral: Fourier properties of change and point convergence of Fourier integral. Differential equations of n-power: Coachi’s differential equation; geometrical interpretation of the first-degree differential equation; normal system of differential equation; reduction of differential equation to normal system; Linear differential equations: first degree linear differential equations; methods of integrating factor and variations of arbitrary constant ; equations in total differentials; linear differential equations of higher order; linear differential equations with constant coefficients; Euler equation; method of certain constant variations; linear systems of differential equations: linear systems of differential equations with variable coefficients; linear systems of differential equations with constant coefficients. Laplace transform and application of operational calculus for differential equations.


Assessment Forms: calculus, tests, examination.


Supportive Materials: handbooks, methodological manuals and credit tasks.


List of Recommended Literature:

  1. Карташев А.П., Рождественский Б.Л. Математический анализ (Mathematical Analysis). - М.: Наука, 1984.
  2. Кудрявцев Л.Д. Краткий курс математического анализа (Brief Course of Mathematical Analysis). - М.: Наука, 1989.
  3. Зорич В.А. Математический анализ (Mathematical Analysis). - М.: Наука, 1984 (I, II т.).
  4. Фихтенгольц Г.М. Основы математического анализа (Principles of Mathematical Analysis) . - М.: Наука, 1964 (I, II т.).
  5. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу (Collected Problems in Mathematical Analysis). - М.: Наука, 1984. - I т. (Предел, непрерывность, дифференцируемость).
  6. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу ( Collected Problems in Mathematical Analysis). - М.: Наука, 1984. - II т. (Интегралы, ряды).
  7. Демидович Б.П. Сборник задач и упражнений по математическому анализу (Collected Problems in Mathematical Analysis). - М.: Наука, 1966.
  8. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений (Lectures in the Theory of Simple Differential Equations). М., Изд-во Моск. Ун-та, 1984.
  9. Степанов В.В. Курс дифференциальных уравнений (Course of Differential Equations). - М.: Гостехиздат, 1953.
  10. Понтрягин Л.С. Обыкновенные дифференциальные уравнения (Simple Differential Equations). - М.: Наука, 1974.
  11. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям (Collected Problems in Differential Equations). - М.: Наука, 1973(1979).



DISCIPLINE ANNOTATION


Discrete Mathematics

  1. Lecturer: Kabalyants Petro Stepanovych, Assistant Professor of Mathematical Modeling and Software Development Department
  2. Status: normative
  3. Course, semester: I course, 1and 2 semesters.
  4. Amount of Credits: 5, in total 162 academic hours; 52 hours of lectures, 52 hours of workshops, 58 hours of independent work.

1 semester—2,5 credits: chapters 1,2,3—written test + credit;

2 semester—2,5 credits: chapters 4,5,—written test + exam;
  1. Prior Requirements: school mathematics base
  2. Discipline Description (subject, aims, structure): the subject of the discipline is in methods of discrete mathematics: methods of the theory of sets, graph theory, combinatorics, logic, theory of numbers and theory of coding. Theory of sets and graph theory are studied in detail. Methods of the theory of sets and the theory of coding are studied throughout. A separate chapter is dedicated to the combinatorial analysis.

Aim of the course: to study principle methods of discrete mathematics: graph theory, the theory of sets, combinatorics, logic, the theory of automata and the theory of grammar. Great attention is paid to matrix, numerical and common algebraic methods which are effective in computer realization.

The program of the discipline consists of a schedule, thematic plan, containing 4 chapters which contain 45 topics and list of supportive materials.
  1. Methods of Teaching: lectures, workshops, independent work.

Elements of topical lectures, individual tasks for independent work.
  1. Assessment Forms: written control of individual tasks; written tests; written credit and written exam in the 1 and 2 semesters respectively.


Assessment Criteria:


Only those students who got 35 % of the total amount of credits according to all forms of current control are admitted to an exam; students who got no less than 91 % of the total amount of credits are free from exam.

  1. Supportive Materials:
  • Program
  • Discipline schedule
  • Textbooks
  • Department manuals
  • Collected problem textbooks (electronic copies for the chapter “Combinatorics)
  • Electronic version of the first semester notes
  • Set of individual tasks for current control
  • Tasks for rector tests
  • Examination cards
  1. Language of Instruction: Russian
  2. List of Recommended Literature


Basic Literature

  1. Берж К. Теория графов и ее применение (Graph Theory and its Application). – М.: ИЛИ, 1962. – 320с.
  2. Оре О. Теория графов (Graph Theory). – М.: Наука, 1968. – 352с.
  3. Сешу С., Рид М.В. Линейные графы и электрические цепи (Linear graphs and Electric Circuits). – М.: Высшая школа,1971. – 448с.
  4. Харари Ф. Теория графов (Graph Theory). – М.,Мир,1973. – 304с.
  5. Басакер Р.,Саати Т. Конечные графы и сети (Finite Graphs and Networks). – М.:Наука,1974. – 336с.
  6. Кристофидес Н. Теория графов (алгоритмический подход) (Graph Theory (Algorythmic Approach). – М.: Мир, 1978. – 432с.
  7. Майника Э. Алгоритмы оптимизации на графах и сетях (Graphs and Networks Algorithms Optimization on). – М.: Мир, 1981. – 323с.
  8. Свами М., Тхуласираман Н. Графы, сети и алгоритмы (Graphs, Networks and Algorithms). – М.: Мир, 1984. – 454с.
  9. Филлипс Д., Гарсиа-Диас А. Методы анализа сетей (Methods of Networks Analysis). – М.: Мир, 1984. – 496с.
  10. Кук Д., Бейз Г. Компьютерная математика (Computer Mathematics). – М.: Наука,1990. – 384с.
  11. Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику (Introduction into Logistics). Учеб. пособие для вузов. – М.: Изд.-во МГУ, 1982. – 120с.
  12. Сигорский В.П. Математический аппарат инженера (Mathematical Apparatus of an Engineer). – Киев, Техника, 1977. – 766с.
  13. Кузнецов ОЛ.П., Адельсон-Вельский Г.М. Дискретная математика для инженера (Discrete Mathematics for Engineers). – М.: Энергия, 1980. – 342с.
  14. Яблонский С.В. Введение в дискретную математику (Introduction into Discrete Mathematics) . – М.: изд. МГУ, 1986. – 384с.
  15. Виноградов И.М. Основы теории чисел (Principles of the Theory of Numbers). – М.: Наука 1965. – 172с.
  16. Гускин В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, язык, программирование (Algebra, Language, Programming). – К.: Наукова думка, 1978. – 318с.


Manuals and Methodical Guidance

  1. Руткас А.Г. Введение в теорию графов (Introduction into Graph Theory) . Учебное пособие . – Х.: ХГУ, 1993. – 63с.
  2. Дюбко Г.Ф. Введение в формальные системы (Introduction into Formal Systems). – Х.: ХИРЭ, 1992. – 170с.
  3. Бондаренко М.Ф., Білоус Н.В., Шубін І.Ю. Збірник тестових завдань з дискретної математики (Collected Tests in Discrete Mathematics) . – Х.: ХДТУРЕ, 2000. – 156с.
  4. Бондаренко М.Ф., Білоус Н.В., Руткас А.Г. Комп'ютерна дискретна математика: Підручник для ВУЗів. (Computer Discrete Mathematics. High School Textbook) – Х.: Компания СМІТ, 2004. – 479с.



DISCIPLINE ANNOTATION


Economic theory


Lecturer: Shedyakova Tetyana Evheniivna, Associate Professor of the Economic Theory Department.,

Status: normative

Course, semester: I course, 2 semester

Amount of Credits: 3, 108 academic hours in total; 32 hours of lectures; 32 hours of seminars, 44 hours of independent work.

Prior requirements: “Higher Mathematics”, “Philosophy”.

Discipline description: The subject of the discipline is studying of the economic principles of social industry development, reasoning of a choice made by housekeeping individuals in optimal usage of limited resources aimed at a complete meeting of growing people’s needs.

Aim of the course is in forming the system of knowledge about economic relations in the society, problems of effective usage of scarce resources, functioning of basic components of the economic system, development of students’ economic thinking and also preparation for the further study of other economic disciplines’ backgrounds and potential implementation of economic knowledge in future profession.


To know: basic stages of economic thinking development, problems and principles of functioning and development of social industry, property relations, economic systems,
commodity-money relations, basis of offer and demand in market economy, rational consumer choice, firm operation, market resources and market structures, principles of national economy functioning, monetary and financial system, forming of macroeconomic equilibrium and forms of macroeconomic instability, principles of economic state regulation and international economic relations. The theoretical material which is studied is divided into 16 topics.


Methods of Teaching: lectures, workshops, independent work.


Assessment Forms: current control in the form of module tests, shotgun quizes on a covered theoretical material, final control in the form of written exam.


Assessment Criteria:


Students’ assessment is brought about according to the Bologna System requirements. In all forms of work a student can get a maximum of 100 credits (points), 60 of which is obtained due to a current work in the semester and 40 can be got in the final control. The course is divided into 3 modules, each allows to obtain 1/3 of the total amount of credits in a current work. Students’ assessment is carried out on the basis of an average credit calculus separately in each module and exam with a following reassessment of these rates into a sum of obtained credits through special coefficients as a relation of a maximum amount of credits which can be obtained in a module or an exam to a maximum of the scale through which average rates are calculated. Average rates are calculated on the basis of the five-grade scale. For students’ assessment during the workshops a scale from 0 to 5 with a 0.5 division value is used. For a current module tests assessment the five-grade scale is also used, but the mark is given as the ration from the division of points, received by the student during the test, into the coefficient of recalculation which is defined as the ratio from the division of the amount of questions, that were set for the test, into 5. Writing of all tests is compulsory. A student gets a “0” if he/she hasn’t written a test. The calculus of an average rating for the current work in the semester is brought about due to the formula of arithmetic mean with a weight number 2 – for the module test; 1 or 0.5 (it depends on the wok done by the student o his/her activity) for workshop. The exam is assessed as the arithmetic mean separately for each question in the exam card. So the average rating is recalculated into the amount of points got at the exam following the procedure described.


Supportive Materials:

  • The program;
  • Textbooks and manuals in economic theory;
  • Legal documents justifying the current economic processes in the country;
  • Collected problems on micro- and macroeconomics;
  • Electronic materials which are given to the student at the beginning of the semester;
  • Tasks for the current assessment;
  • Examination cards.