Geum.ru

Тесты. Тема Основы теории рыночного спроса и предложения Закон спроса предполагает, что

Вид материалаТесты

Содержание


Тема 12. Общее равновесие и экономическая эффективность
Тема 13. Ценообразование в различных рыночных структурах
Подобный материал:
1   ...   5   6   7   8   9   10   11   12   13

Ставка процента составляет 10%.

Финансовые возможности фирмы (включая возможности получения

кредита) ограничены суммой 4 млн. долл.
  1. Какие проекты осуществит фирма?
  2. Какие проекты осуществит фирма, если финансовые возможности фирмы возрастут до 7 млн. долл.?



Тема 12. Общее равновесие и экономическая эффективность




  1. * Два потребителя А и В имеют функции полезности:

U(X, Y) = min{XY}; U(X, Y) = XY. Задано исходное распределение двух благ: X = 6, Y = 0; X = 0, Y= 9. Пусть цена блага Х равна 1, цена блага Y равна Р.
  1. Найдите функцию спроса на благо Y при достижении Парето-эффективности.
  2. Чему равна равновесная цена блага Y?
  3. Найдите оптимальные наборы благ для потребителей.

Покажите решение графически.

  1. В экономике имеется два типа потребителей. Первый тип имеет функцию полезности U(X, Y) = X + Y; второй тип - U(X, Y) = min{2X, Y}. При первоначальном распределении благ каждый имеет 1 ед. блага Х и 1 ед. блага Y. Найдите равновесные цены в условиях совершенной конкуренции и объемы по­требления благ для каждого типа потребителей.



  1. Предпочтения Робинзона Крузо заданы функцией U(C, R) = CR, где С – потребление кокосов, R – досуг. Робинзон Крузо распределяет 48 часов между трудом и работой. Если он работает L часов, то получает кокосы в количестве С = 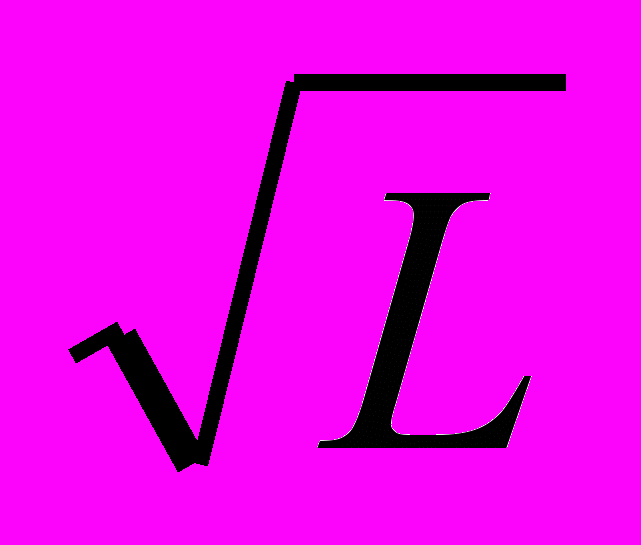. Сколько времени будет работать Робинзон Крузо?



  1. Робинзон Крузо тратит 4 часа в день на ловлю рыбы и сбор кокосов. Он может за час поймать 2 рыбы или собрать 3 кокоса. Его функция полезности имеет вид U(C, F) = CF, где F – количество рыбы, потребляемой за день, C – количество потребляемых за день кокосов. Какое количество рыбы будет потреблять Робинзон Крузо при оптимальном выборе?



  1. У Робинзона Крузо имеется 12 часов в день, которые он может потратить на сбор коко­сов или ловлю рыбы. Он может за час поймать 2 рыбы или собрать 6 кокосов. Его функция по­лезности имеет вид U(C, F) = CF, где F – потребление рыбы, C – потребление кокосов. Если он распределяет свое время наилучшим образом, то его потребление будет таким же, как при по­купке рыбы и кокосов на рынке совершенной конкуренции, где цена кокосов равна 1. Найдите доход Робинзона Крузо и цену рыбы.



  1. В некотором регионе производят только пшеницу (Х) и молоко (Y). Единственным огра­ниченным ресурсом является земля, площадь которой составляет 1000 кв. ед. На ед. пло­щади земли можно получить 13 ед. молока или 12 ед. пшеницы. Жители региона имеют функ­цию полезности U(X, Y) = XY. Найдите объем производства молока при Парето-опти­мальном распределении ресурса.



  1. Определите равновесные цены в экономике, которая состоит из двух отраслей с функ­циями спроса и предложения вида:

Q = 8 + 3P - 2P; Q = 10 - 2P + 2P;

Q = 14 + 2P - P; Q = 17 - P + 0,5P.
  1. Каким будет соотношение между объемами спроса и предложения в каждой из отраслей, если P= 1,5; P= 1,2?
  2. Восстановится ли при такой системе цен совместное равновесие на обоих рынках?

Тема 13. Ценообразование в различных рыночных структурах




  1. На большой территории, в центре которой размещается город, можно выращивать пше­ницу. Рыночная цена пшеницы в центре города равна 10 ден. ед. Издержки производства 1 ед зерна равны 5 ден. ед. Транспортировка 1 ед. продукции в центр города стоит 0,1 ден. ед. за км.
  1. Если ферма находится на расстоянии t км от центра города, то чему будет равна ее прибыль от продажи единицы зерна?
  2. Допустим, на этой ферме можно вырастить 1000 ед. пшеницы на 1 га земли. За какую плату фермер сдаст 1 га земли в аренду?



  1. Компания имеет монополию на осуществление воздушных перевозок. Функция спроса

Q = 160 - 2Р, где Q – число пассажиров в день, Р – цена услуги. Общие ежедневные издержки ТС = 2000 + 10Q.
  1. Найдите параметры рыночного равновесия.
  2. Если банковская ставка процента равна 10%, за какую сумму данная компания продала бы монопольное право на осуществление перевозок (предполагается, что спрос и издержки ни­когда не меняются)?
  3. Если другая фирма с теми же издержками войдет на данный рынок и отрасль станет дуопо­лией Курно, по какой цене будут предлагаться перевозки? Будут ли фирмы получать при­быль?



  1. Отрасль по производству велосипедов состоит из 100 фирм с долгосрочными функ­циями издержек TC(y) = 2 + y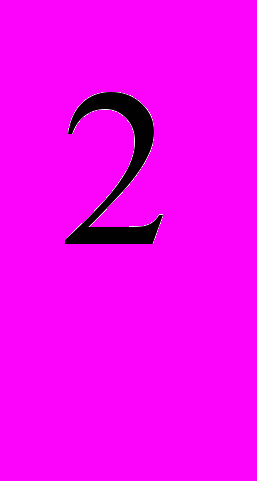/2 и 60 фирм, долгосрочные издержки которых TC(y) = y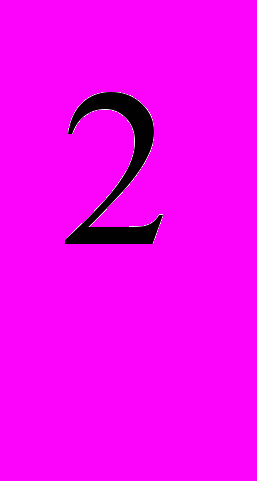/10. Ни одна новая фирма не может войти на рынок. Каково рыночное долгосрочное предложение, если цена велосипеда на рынке не меньше 2 ден. ед.?



  1. Отрасль состоит из двух фирм. Одна фирма имеет долгосрочную функцию издержек TC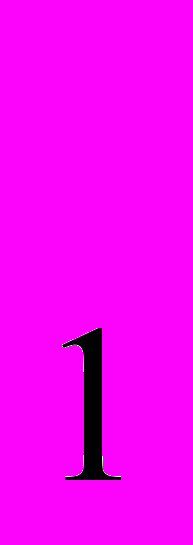(y) = 3 + 4у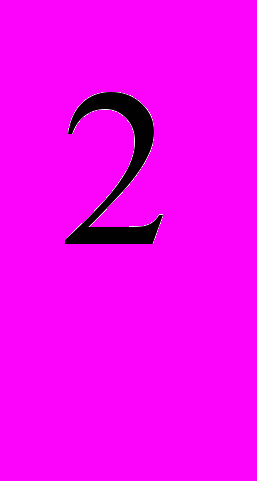/3, вторая фирма – ТС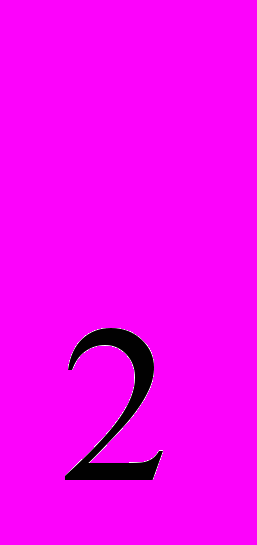(у) = 10 + y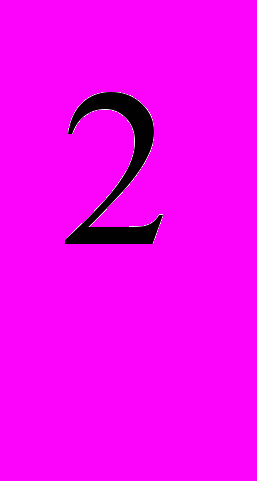/10. Если ни одна фирма не может войти на рынок, при какой цене на рынке будет действовать только одна фирма?



  1. На рынке могут работать 100 фирм, каждая из которых может произвести до 20 ед. про­дукции в год. Функция издержек i-ой фирмы имеет вид ТС(у) = 19 + iу, где i = 1, 2, ….100. Если цена продукции на рынке равна 25, сколько продукции будет произведено за год?



  1. *На рынке готовой продукции действует 8 фирм. Производственная функция одной фирмы равна q = 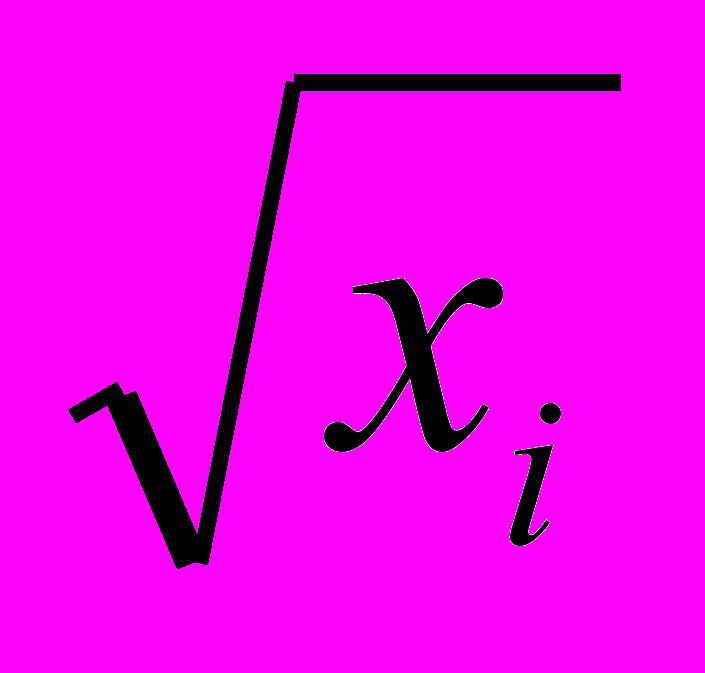, где х - количество затрачиваемого сырья i-ой фирмой. Рыночный спрос на продукцию Q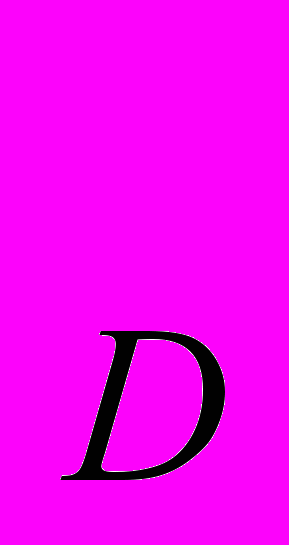 = . Предложение сырья имеет вид: Х= 8Р, где Р - цена еди­ницы сырья. Найдите равновесные значения цены готовой продукции и цены сырья (оба рынка являются совершенно конкурентными).

1 По Теме 1 решение задач не предусмотрено.

2) Значком * в тексте отмечены задачи повышенной сложности.