Тесты. Тема Основы теории рыночного спроса и предложения Закон спроса предполагает, что
| Вид материала | Тесты |
- Лекции по дисциплине «Микроэкономика», 563.24kb.
- Миссия выполнима. Твое призвание финансист, 66.53kb.
- Рыночное равновесие, 130.99kb.
- Концепция рыночного равновесия. Спрос и предложение. Факторы спроса и предложения., 1823.58kb.
- Лекция 4 основы теории спроса и предложения, 43.74kb.
- Для специальностей «Бухгалтерский учёт, анализ и аудит», 191.46kb.
- Принципы экономической науки, 13066.09kb.
- Альфред Маршалл "Принципы экономической науки", 784.69kb.
- Вопросы к экзамену по экономической теории для студентов 3 курса инженерного факультета:, 788.47kb.
- Реферат на тему "Законы спроса и предложения в системе рыночного механизма", 330.58kb.
 , x
, x ) = x
) = x
 x
x . Постройте кривую безразличия, проходящую через т. (3,4), и найдите предельную норму замещения в этой точке.
. Постройте кривую безразличия, проходящую через т. (3,4), и найдите предельную норму замещения в этой точке.3.6. Потребитель тратит имеющиеся у него деньги на покупку двух товаров - x и y. Функция полезности для него имеет вид: U(x, y) = min{4x, 2x + y}. Потребитель покупает 15 ед. товара x и 10 ед. товара y. Цена товара x равна 10 дол. Найдите доход потребителя. Каков наклон бюджетного ограничения в т.(15,10)?
3.7. Функция полезности некоторого потребителя имеет вид: U(x
 , x
, x )=4
)=4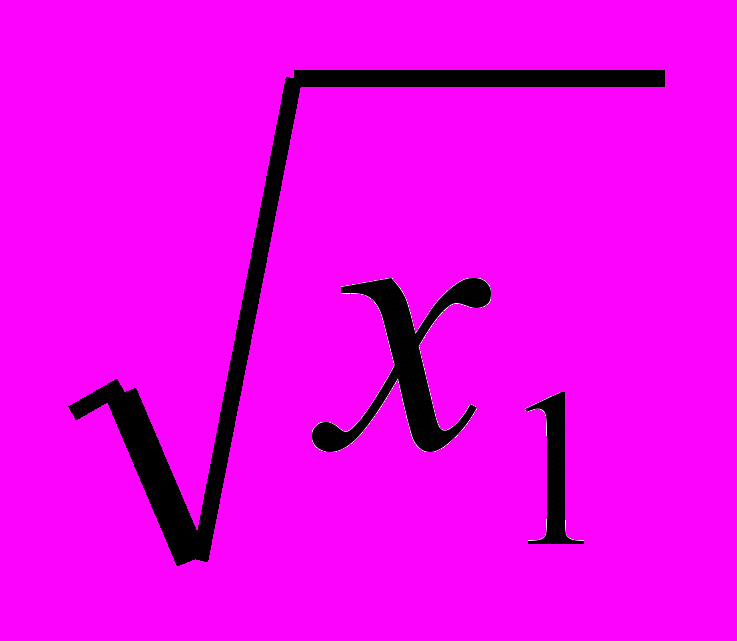 +x
+x , где x
, где x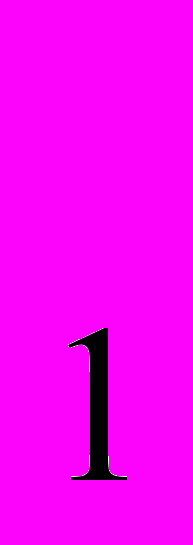 , x
, x - два взаимозаменяемых блага. Обычно потребитель потребляет эти блага в количестве x
- два взаимозаменяемых блага. Обычно потребитель потребляет эти блага в количестве x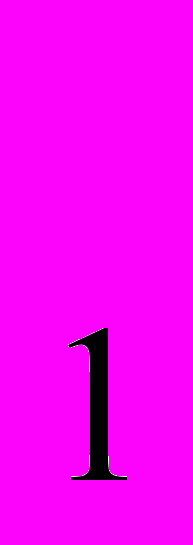 = 9, x
= 9, x = 10. Найдите предельную норму замещения в этой точке. Допустим, потребление первого блага сократилось до 4 ед. Как должно измениться потребление второго блага, чтобы значение функции полезности не изменилось?
= 10. Найдите предельную норму замещения в этой точке. Допустим, потребление первого блага сократилось до 4 ед. Как должно измениться потребление второго блага, чтобы значение функции полезности не изменилось?3.8. Потребитель имеет функцию полезности вида: U(х
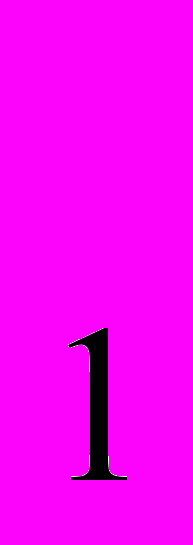 ,x
,x )=(x
)=(x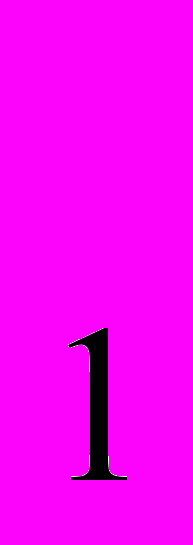 +2)
+2) (x
(x +6). Напишите уравнение касательной, проходящей через набор потребительских благ x
+6). Напишите уравнение касательной, проходящей через набор потребительских благ x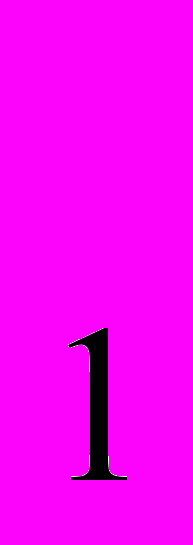 = 4, x
= 4, x = 6.
= 6.3.9. Функция полезности имеет вид U(x
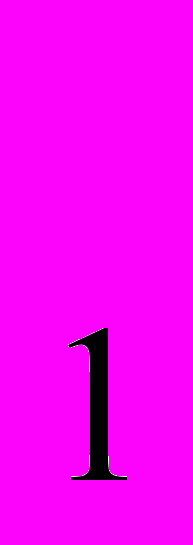 , x
, x ) = min{x
) = min{x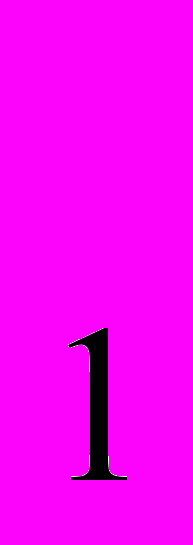 , 3x
, 3x }. Цена блага x
}. Цена блага x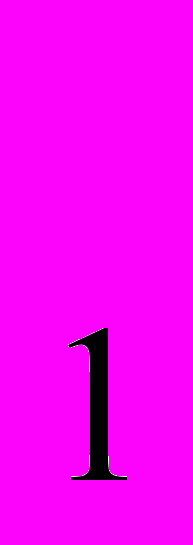 равна 2, цена блага х
равна 2, цена блага х равна 1. Доход потребителя равен 140. Определите координаты точки равновесия потребителя.
равна 1. Доход потребителя равен 140. Определите координаты точки равновесия потребителя.3.10. Некто потребляет два блага - яблоки (Х
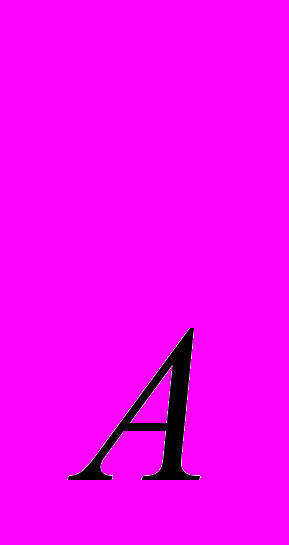 ) и бананы (Х
) и бананы (Х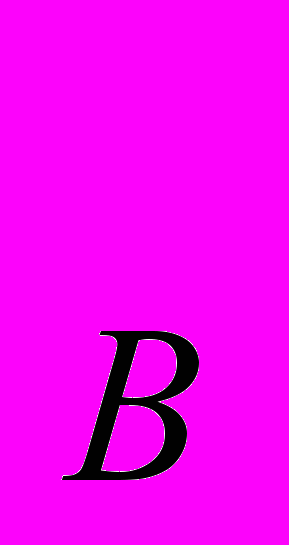 ). Целевая функция равна
). Целевая функция равна U(Х
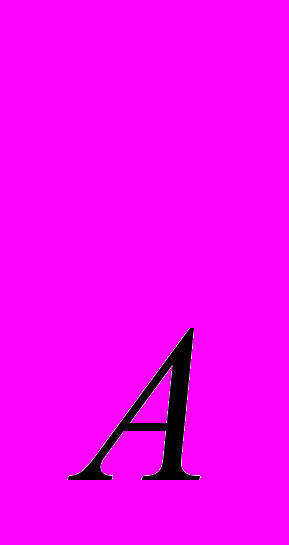 , Х
, Х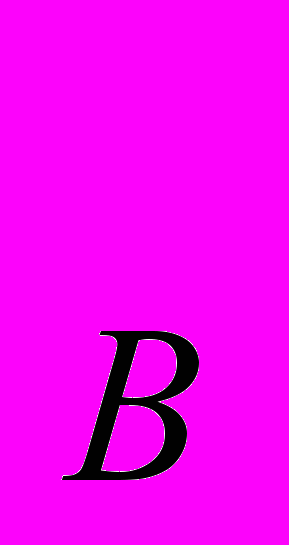 ) = Х
) = Х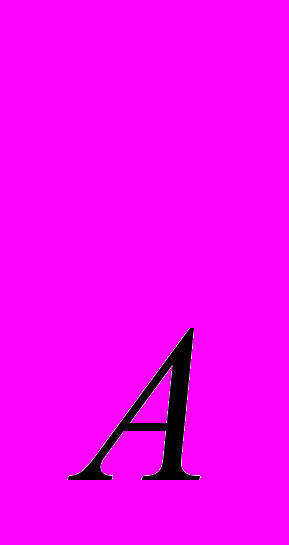
 Х
Х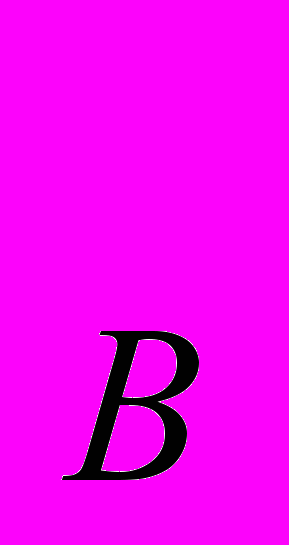 , P
, P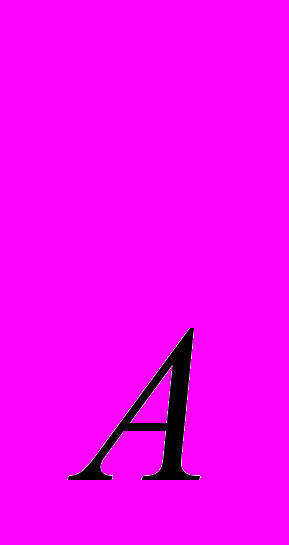 = 1, P
= 1, P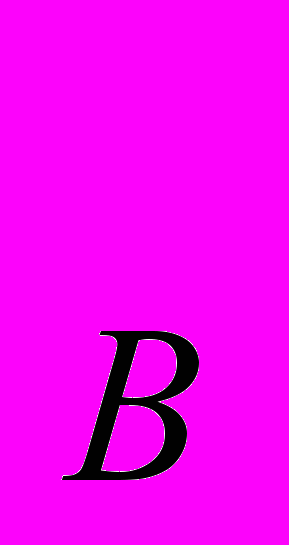 = 2, доход равен 40. Может ли значение целевой функции быть равно 150? 300? Обоснуйте свой ответ.
= 2, доход равен 40. Может ли значение целевой функции быть равно 150? 300? Обоснуйте свой ответ.3.11. Задана функция полезности некоторого потребителя U(x
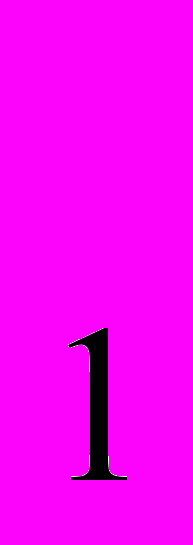 , x
, x ) = x
) = x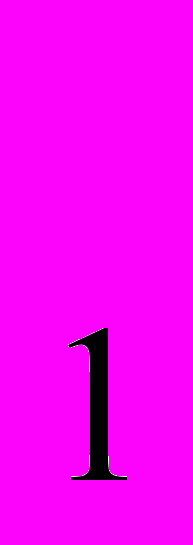
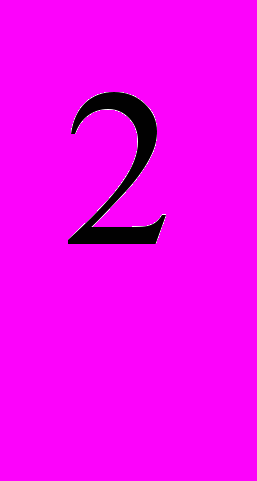
 x
x
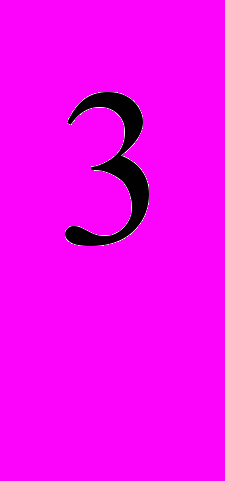 и цены двух благ - Р
и цены двух благ - Р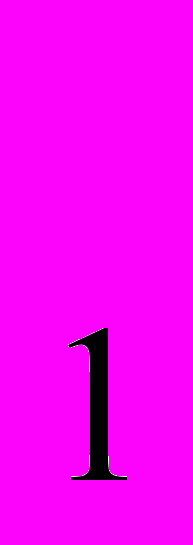 , Р
, Р .
.а) Найдите предельную норму замещения этих двух благ в т. (х
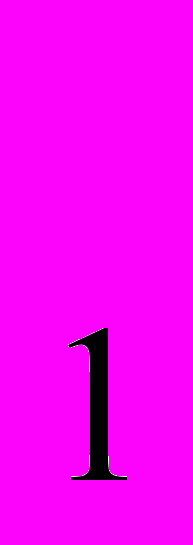 , х
, х ).
).б) Какую долю дохода потребитель расходует на первое благо, если он выбирает наилучшее сочетание товаров?
в) Если в общем виде U(х
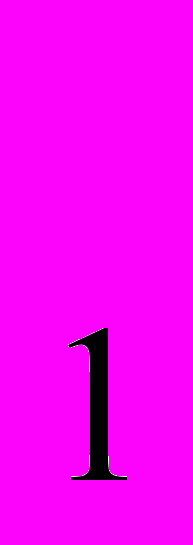 , х
, х ) = с
) = с х
х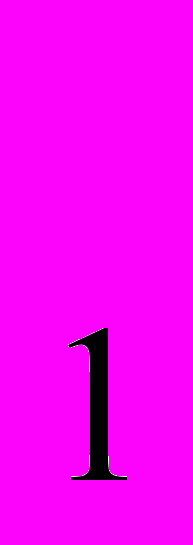

 х
х
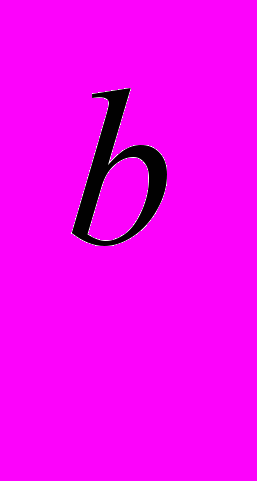 , где с, а, b - положительные числа, то какую долю дохода потребитель тратит на первый товар?
, где с, а, b - положительные числа, то какую долю дохода потребитель тратит на первый товар?3.12. У Кати есть выбор: съесть шоколадку или получить денежную компенсацию. Катя очень любит шоколад, но после 4-х шоколадок они превращаются для нее в "антиблаго", т.е. она согласна съесть еще одну шоколадку, если ей за это заплатят. Нарисуйте карту кривых безразличия для Кати.
3.13. В. любит приглашать гостей. Она также предпочитает, чтобы число мужчин на вечере равнялось числу женщин. Ее предпочтение можно представить в виде функции полезности
U(x, y) = min{2x - y, 2y - x}, где x – число женщин, y – число мужчин на вечере. Постройте кривую безразличия, если U(x, y) = 10.
3.14. В набор потребителя входят два товара: пиво и бананы, общая полезность которых характеризуется следующими данными:

 Количество кружек пива 1 2 3 4 5 6
Количество кружек пива 1 2 3 4 5 6  Общая полезность 10 18 24 28 31 33
Общая полезность 10 18 24 28 31 33 
Количество бананов 10 20 30 40 50 60

Общая полезность 7 13 18 22 25 27
Цена кружки пива - 10, цена одного банана - 0,5. Общий доход потребителя, который он тратит на эти два товара, равен 25. Найдите набор товаров в состоянии равновесия потребителя.
3.15. Функция полезности для данного потребителя имеет вид: U (х
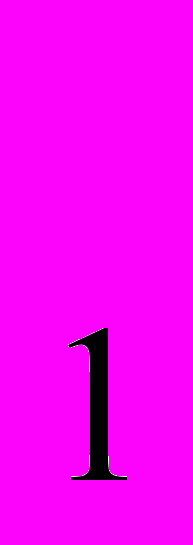 , х
, х ) = 4
) = 4 х
х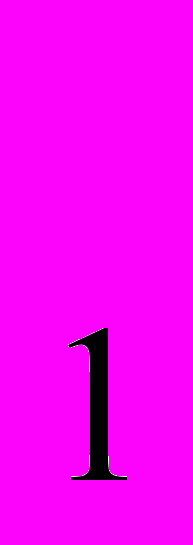
 х
х , а доход, выделенный им для покупки данных товаров, равен 24. В оптимальный набор вошли 2 ед. первого блага и 3 ед. второго блага. При каких ценах на товары потребитель сделал данный выбор?
, а доход, выделенный им для покупки данных товаров, равен 24. В оптимальный набор вошли 2 ед. первого блага и 3 ед. второго блага. При каких ценах на товары потребитель сделал данный выбор?3.16. На рис. 4 показана одна из кривых безразличия потребителя и его бюджетная линия. Цена товара Y равна 12.
а) Каков доход потребителя?
б) Какова цена товара Х?
в) Как изменится положение бюджетной линии при увеличении цены товара Y до 15?, снижении до 10?
г) Напишите уравнение бюджетной линии для каждого варианта.
Y

 45
45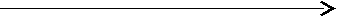
0 75 X
Рис. 4
3.17. Допустим, потребитель имеет месячный доход М = 200. На рис. 5 показаны две бюджетные линии и соответствующие им кривые безразличия.
а) Какова цена товара Y?
б) Определите координаты двух точек линии спроса данного потребителя на товар Х.
в) Зависит ли положение данной линии спроса от цены товара Y, от дохода потребителя?
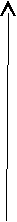
Y
4
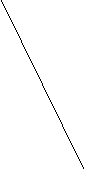
 0
0
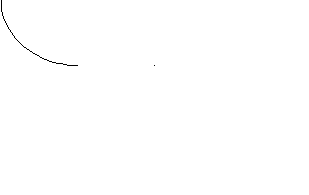
2
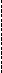
 0
01

 5
5

0 10 20 25 40 Х
Рис. 5
3.18. М выращивает яблони и другие культуры на площади 500 кв. футов. Каждая яблоня занимает 1 кв. ф., а другие культуры – по 4 кв.ф. Ее функция полезности имеет вид U(b, c) = b + 100c - c
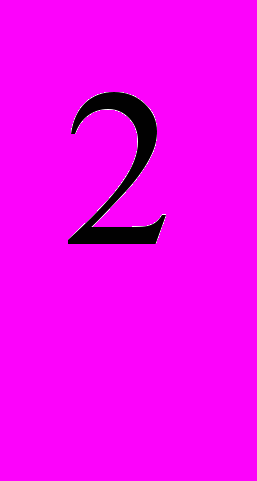 , где b – число яблонь, c – число других культур. Сколько яблонь и других деревьев посадит М., чтобы максимизировать полезность? Если площадь сада увеличится на 100 кв.ф., насколько изменятся посадки яблонь и других культур?
, где b – число яблонь, c – число других культур. Сколько яблонь и других деревьев посадит М., чтобы максимизировать полезность? Если площадь сада увеличится на 100 кв.ф., насколько изменятся посадки яблонь и других культур?3.19. Потребитель приобретает товары Х и Y. Товар Y продается по цене 2 дол. за единицу. Товар X продается по цене 10 дол. за единицу, если объем покупки не превышает 20 единиц, а за каждую следующую (сверх 20) единицу покупатель платит 5 дол. Пусть доход M = 300. Покажите графически бюджетное ограничение при этих условиях. Можно ли сказать, каким будет наиболее предпочтительный набор товаров X и Y для потребителя (X и Y - нормальные товары)?
3.20. Предположим, потребитель выбирает между двумя товарами, Х и Y. При заданных начальных ценах товаров и доходах потребитель, максимизирующий полезность, делает следующий выбор: X = 4 ед., Y = 5 ед. Допустим, цены товаров и доход изменились таким образом, что бюджетная линия описывается уравнением Y = 14 - 0,75X. Увеличилась ли для потребителя максимально достижимая полезность? Объясните ответ графически.
3.21. Проанализируйте график на рис. 6 и ответьте на вопросы:
а) Если доход потребителя равен 300, какова цена Р
 , P
, P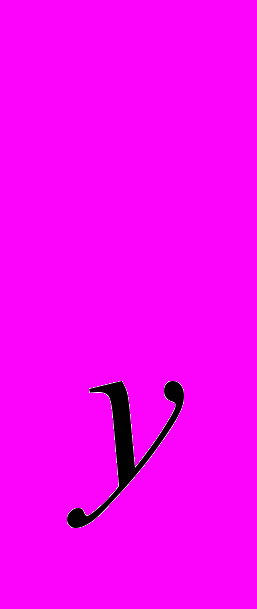 ?
?б) Чему равна предельная норма замещения в т. А?
в) Может ли предельная норма замещения в т. В равняться 5?
г) Если доход не меняется, как бы должны измениться цены Р
 и P
и P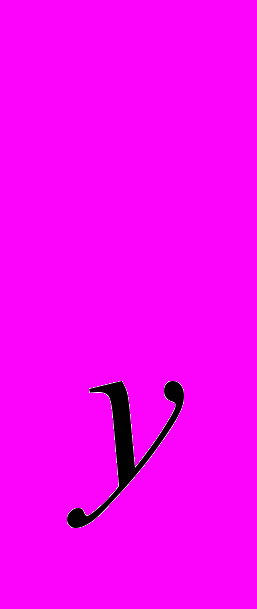 , чтобы т. В стала точкой равновесия потребителя?
, чтобы т. В стала точкой равновесия потребителя? Y
Y
 20
20
 12 А
12 А В
 0 4 10 Х
0 4 10 Х Рис. 6
3.22. Диаграмма изображает кривую «доход-потребление» товара Х для потребителя.
 Расходы на другие 600
Расходы на другие 600 товары, долл.

 400
400






 В
В А

 U
U
U
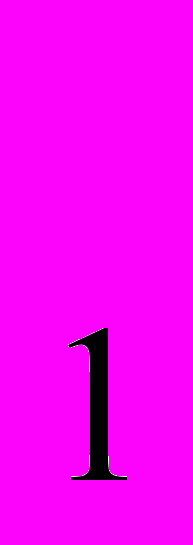
 0 30 40 45 60 Товар Х, шт.
0 30 40 45 60 Товар Х, шт.Ответьте на следующие вопросы:
А) Какова цена товара Х?
Б) Каковы координаты двух точек (А, В) на кривой Энгеля?
В) Может ли товар быть «некачественным» при уровне доходов в 600 д.? 2000 д.?
3.23. На рис. 7 кривые PC
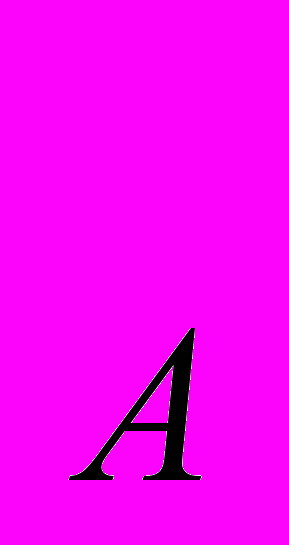 и PC
и PC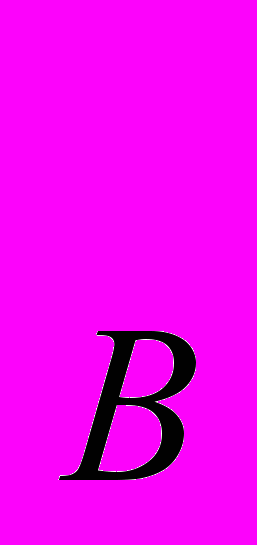 - кривые “цена-потребление” товара Х для двух покупателей А и В. Докажите, используя график, что у покупателя В спрос на товар Х больше при любой его цене?
- кривые “цена-потребление” товара Х для двух покупателей А и В. Докажите, используя график, что у покупателя В спрос на товар Х больше при любой его цене? М
М

 PC
PC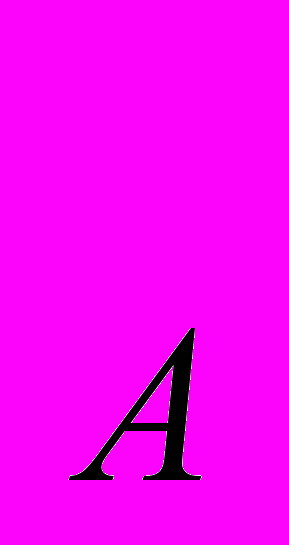

PC
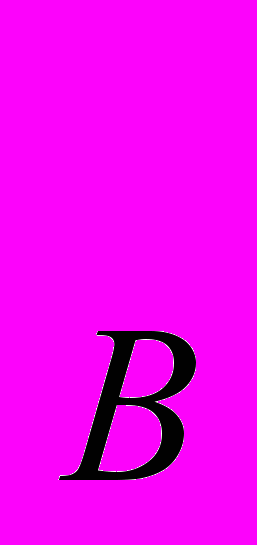
 0 Х
0 Х Рис. 7
3.24. Пусть функция полезности потребителя имеет вид U(x, y) =
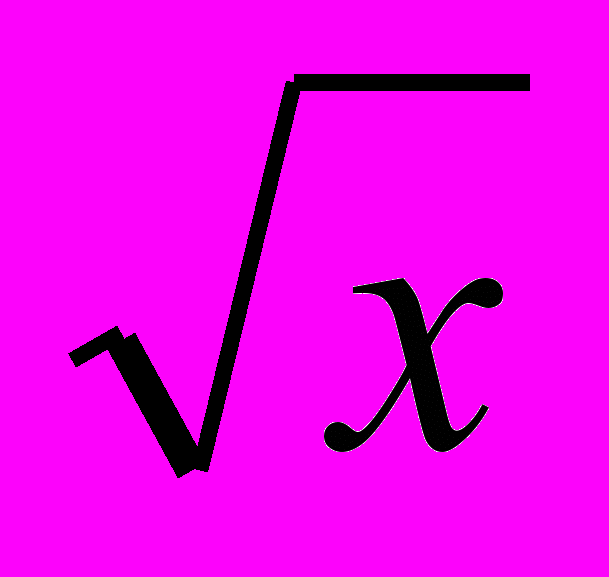 + y, где х – потребление лимонада, а y – расходы на все прочие товары. Потребитель имеет постоянный доход М, а цена лимонада – Р. Найдите кривую спроса на лимонад.
+ y, где х – потребление лимонада, а y – расходы на все прочие товары. Потребитель имеет постоянный доход М, а цена лимонада – Р. Найдите кривую спроса на лимонад.3.25. Целевая функция потребителя имеет вид U(x, y) = (х + а)(у + b), где а, b 0. Цены благ равны P
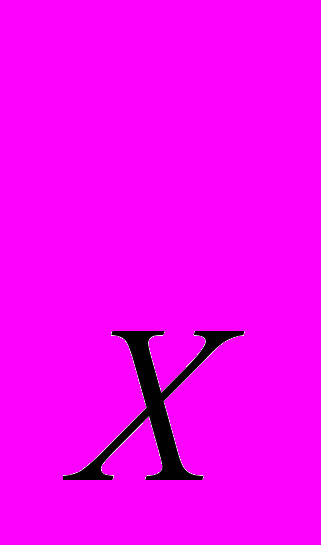 и P
и P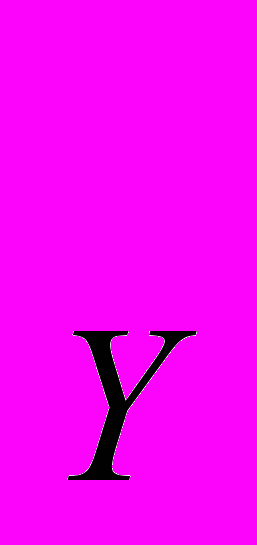 . Доход потребителя равен М. Найдите функцию спроса на благо Х и на благо Y. Какими благами являются товары Х и Y для данного потребителя?
. Доход потребителя равен М. Найдите функцию спроса на благо Х и на благо Y. Какими благами являются товары Х и Y для данного потребителя?3.26. Функция спроса на вино Q = 0,02
 M – 2Р, где М – доход, Р - цена бутылки вина, Q - количество бутылок вина. Пусть М = 7500, Р = 30.
M – 2Р, где М – доход, Р - цена бутылки вина, Q - количество бутылок вина. Пусть М = 7500, Р = 30.А) Если цена вина вырастет до 40, то каким должен стать доход, чтобы покупатель мог купить прежнее количество вина? При этом доходе и новой цене сколько бутылок вина будет куплено?
Б) Чему равен эффект замены и эффект дохода при повышении цены на вино до 40?
3.27. Задана функция спроса потребителя на благо Х: Q
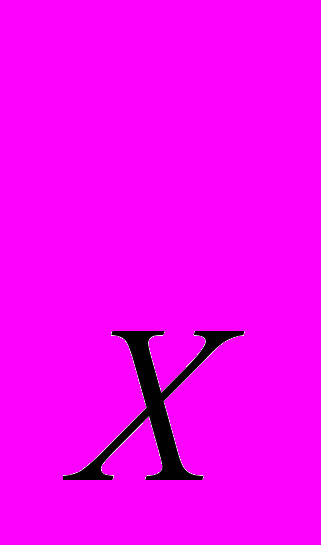 =
= 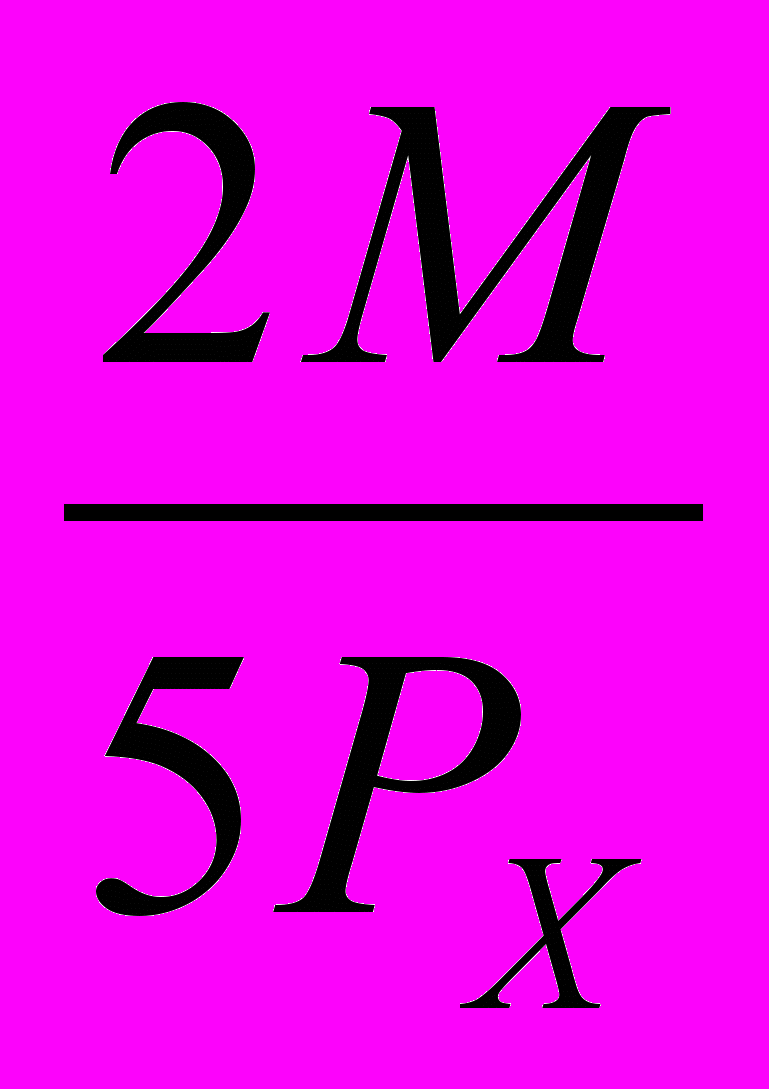 , где М – доход, P
, где М – доход, P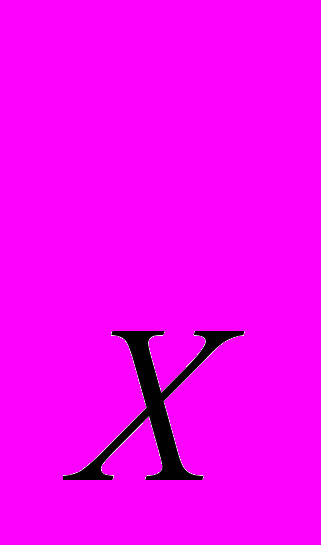 - цена блага Х. Известно, что потребитель весь доход тратит только на два блага – Х и Y, причем P
- цена блага Х. Известно, что потребитель весь доход тратит только на два блага – Х и Y, причем P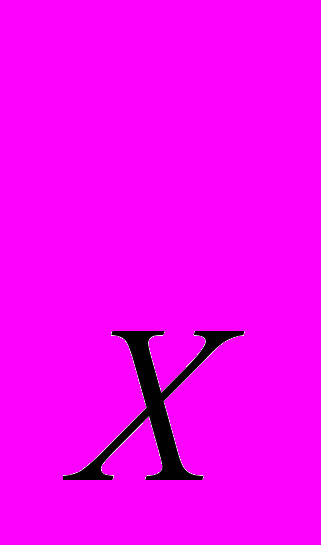 = 5, Р
= 5, Р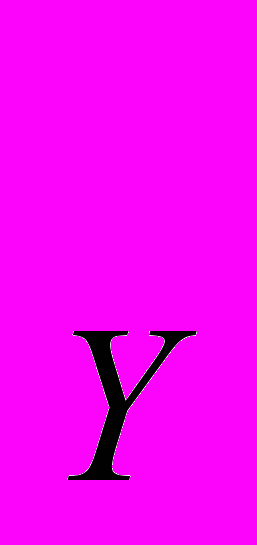 = 20, М = 1000.
= 20, М = 1000.1. Определите, как изменится спрос на благо Х, если его цена упадет до 4 ден. ед.?
2. Найдите эффект замены и эффект дохода в общем изменении спроса на товар Х.
3.28. Функция полезности потребителя имеет вид: U(Х, Y) =
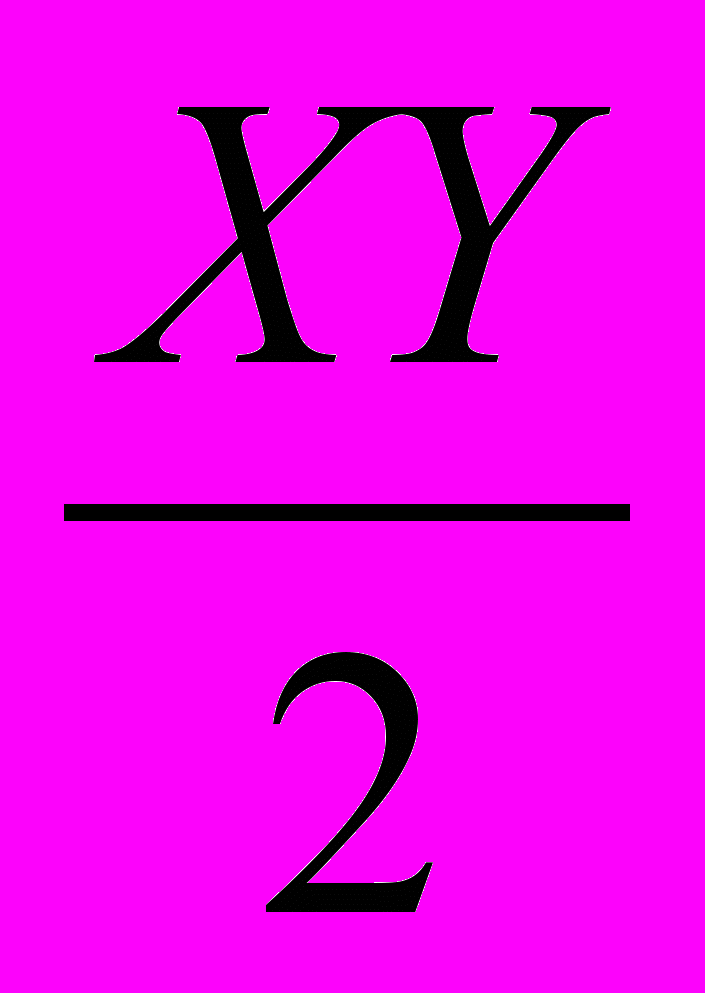 . Доход (М) потребитель тратит только на два товара - Х и Y, причем P
. Доход (М) потребитель тратит только на два товара - Х и Y, причем P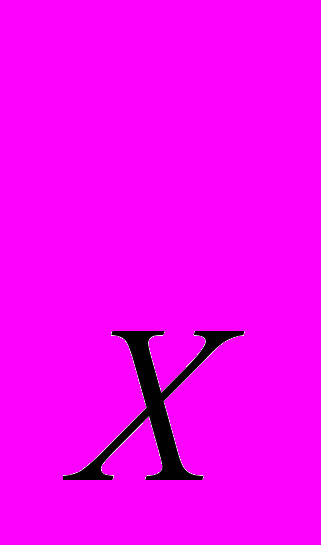 = 3, Р
= 3, Р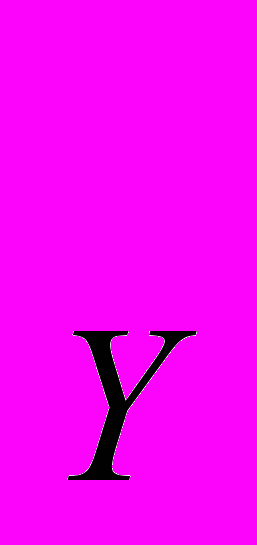 = 2, М = 24. Найдите эффект замены и эффект дохода в общем изменении спроса на товар Y, если цена на него увеличится до 3. Сравните разложение по Слуцкому и по Хиксу. Покажите решение графически.
= 2, М = 24. Найдите эффект замены и эффект дохода в общем изменении спроса на товар Y, если цена на него увеличится до 3. Сравните разложение по Слуцкому и по Хиксу. Покажите решение графически.3.29. Пусть потребитель потребляет только яблоки (Х
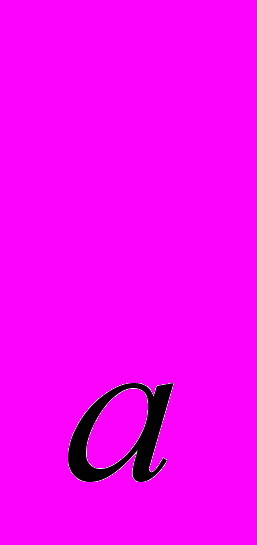 ) и бананы (Х
) и бананы (Х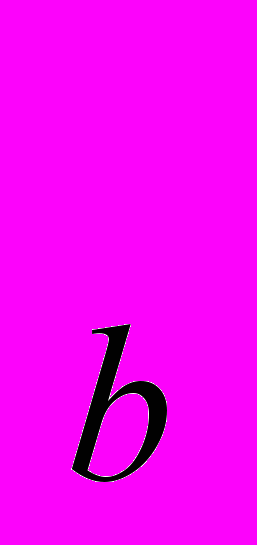 ) и его функция полезности: U(X
) и его функция полезности: U(X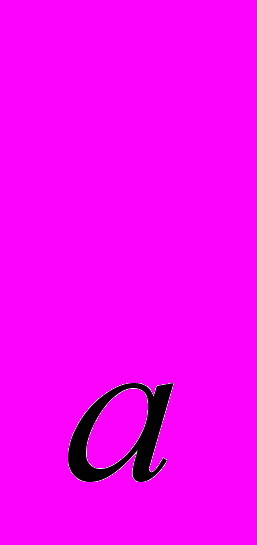 , X
, X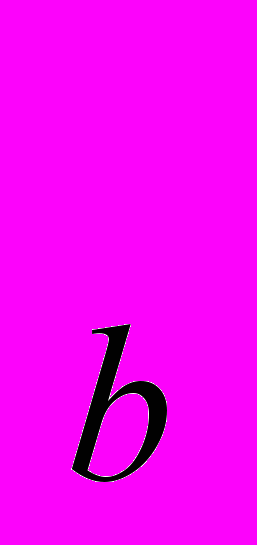 ) = X
) = X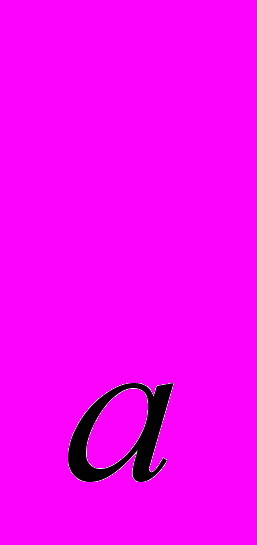 X
X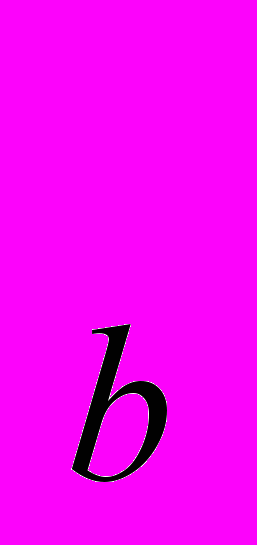 . Цена яблок равна 1, цена бананов равна 2. Доход составляет 40. Определите, как изменится спрос на бананы, если их цена упадет до 1? Чему равен эффект замены и эффект дохода в изменении спроса на бананы? Покажите решение графически.
. Цена яблок равна 1, цена бананов равна 2. Доход составляет 40. Определите, как изменится спрос на бананы, если их цена упадет до 1? Чему равен эффект замены и эффект дохода в изменении спроса на бананы? Покажите решение графически.3.30. Функция полезности потребителя U(x, y) = xy. P
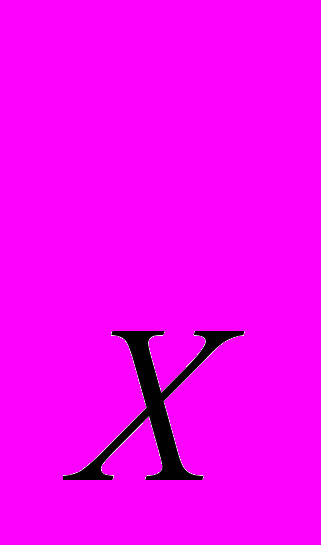 = 4, Р
= 4, Р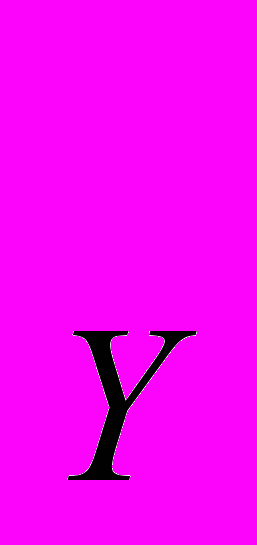 = 1. Доход потребителя равен 80. Цена товара Х увеличилась в 2 раза. Определите координаты равновесного состояния потребителя до и после изменения цены товара Х. Покажите решение графически. Найдите эффект замены и эффект дохода в общем изменении спроса на товар Х. Сравните разложение по Хиксу и по Слуцкому.
= 1. Доход потребителя равен 80. Цена товара Х увеличилась в 2 раза. Определите координаты равновесного состояния потребителя до и после изменения цены товара Х. Покажите решение графически. Найдите эффект замены и эффект дохода в общем изменении спроса на товар Х. Сравните разложение по Хиксу и по Слуцкому.3.31. Рассмотрите рис. 8 и ответьте на вопросы:
 Y
Y
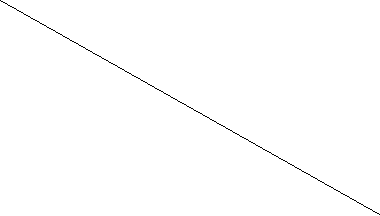
 30
30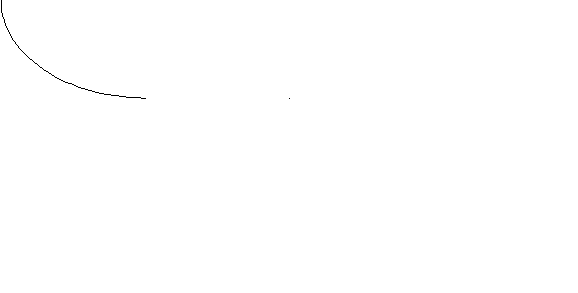
 22,5 С
22,5 С 
Е
F
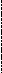

0 30 35 43 75 90 120
Рис. 8
а) Если доход М = 300, Р
 = 4, P
= 4, P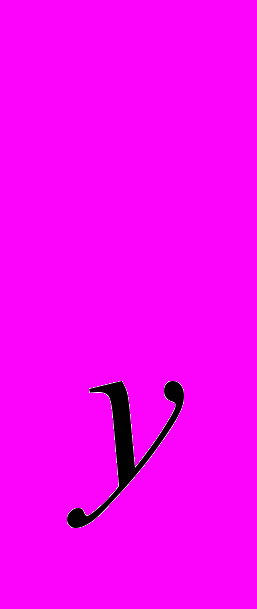 = 10, сколько товара Х потребляется при этих условиях?
= 10, сколько товара Х потребляется при этих условиях?б) Если цена товара Х упадет до 2,5 (при прочих неизменных условиях), каков будет спрос на товар Х?
в) Найдите эффект замены и эффект дохода в общем изменении спроса на товар Х.
г) Каким товаром - нормальным или низшим - является благо Х?
д) Нарисуйте на отдельном графике кривую Энгеля и кривую спроса для товара Х.
3.32. Целевая функция потребителя имеет вид U(x, y) = x -
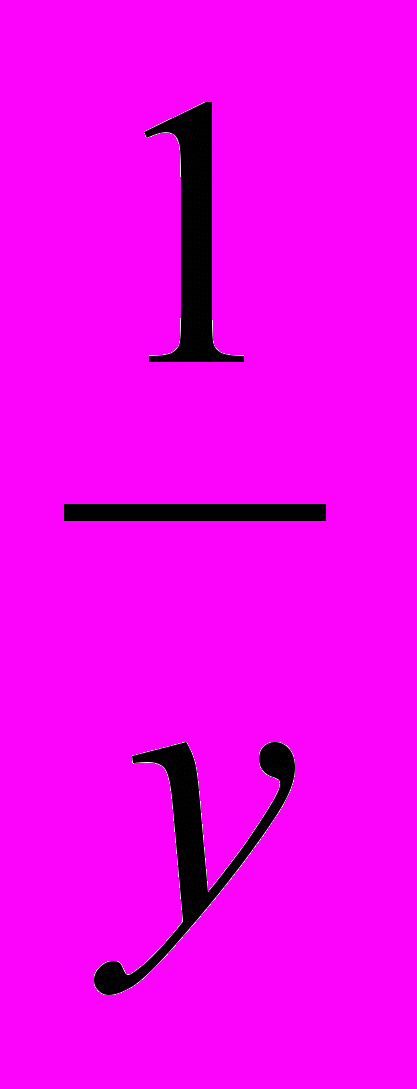 . Цена блага х равна 4, цена блага у равна 1.
. Цена блага х равна 4, цена блага у равна 1. а) Какое количество блага у купит потребитель при оптимальном выборе?
б) Если доход потребителя равен 30, чему равна максимально достижимая полезность?
Покажите решение на графике.
Тема 4: ПРОИЗВОДСТВО: ФАКТОРЫ И ИЗДЕРЖКИ ПРОИЗВОДСТВА
4.1. Объясните форму изоквант.
4.2. Почему предельная норма замещения труда капиталом (MRTS
 ) уменьшается по мере замещения труда капиталом?
) уменьшается по мере замещения труда капиталом?4.3. Выведите формулу для MRTS
 , не прибегая к дифференцированию производственной функции (логически).
, не прибегая к дифференцированию производственной функции (логически).4.4. Обоснуйте с помощью закона убывающей предельной производительности вид кривых совокупного, среднего и предельного продуктов переменного фактора.
4.5. Зависит ли средний, предельный и совокупный продукты труда от величины применяемого фирмой капитала? Если да, то каким образом?
4.6. Объясните, почему средний продукт труда продолжает увеличиваться после прохождения точки начала уменьшения предельной производительности.
4.7. Докажите, что кривая MP
