Тесты. Тема Основы теории рыночного спроса и предложения Закон спроса предполагает, что
| Вид материала | Тесты |
СодержаниеТема 11. РЫНОК ЗЕМЛИ. ЗЕМЕЛЬНАЯ РЕНТА Дополнительные задачи) Тема 3. Теория потребительского поведения Затраты труда |
- Лекции по дисциплине «Микроэкономика», 563.24kb.
- Миссия выполнима. Твое призвание финансист, 66.53kb.
- Рыночное равновесие, 130.99kb.
- Концепция рыночного равновесия. Спрос и предложение. Факторы спроса и предложения., 1823.58kb.
- Лекция 4 основы теории спроса и предложения, 43.74kb.
- Для специальностей «Бухгалтерский учёт, анализ и аудит», 191.46kb.
- Принципы экономической науки, 13066.09kb.
- Альфред Маршалл "Принципы экономической науки", 784.69kb.
- Вопросы к экзамену по экономической теории для студентов 3 курса инженерного факультета:, 788.47kb.
- Реферат на тему "Законы спроса и предложения в системе рыночного механизма", 330.58kb.
Тема 11. РЫНОК ЗЕМЛИ. ЗЕМЕЛЬНАЯ РЕНТА
11.1. Какое из утверждений является верным:
а) Цены товаров высоки, потому что землевладельцы берут высокую ренту.
б) Землевладельцы получают высокую ренту, потому что цены товаров, производимых с использованием земли, высоки. Обоснуйте свой ответ.
11.2. Какие факторы воздействуют на спрос на конкретный участок земли? Как могут спекулянты недвижимостью использовать эти знания для получения прибыли?
11.3. «Поскольку на конкурентном рынке земли цены выравниваются, дифференциальная рента в условиях долгосрочного равновесия должна быть равна нулю». Верно ли это высказывание?
11.4. Почему земельная рента называется чистой экономической рентой?
11.5. Может ли землевладелец переложить вводимый государством налог на арендатора, повышая ставку ренты?
11.6. Вся обрабатываемая земля состоит из участков лучшего, среднего и худшего качества. Производственная функция для каждого из участков:
Q
 = 40S
= 40S - 0,5 S
- 0,5 S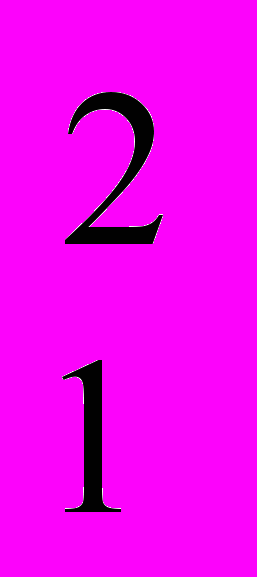 , Q
, Q = 35S
= 35S - 0,6S
- 0,6S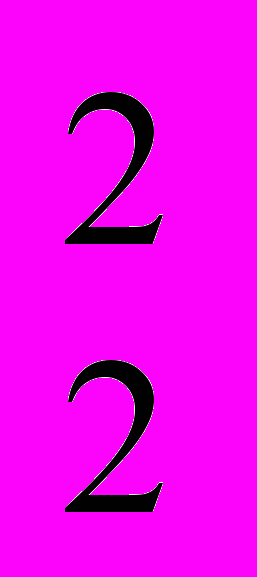 , Q
, Q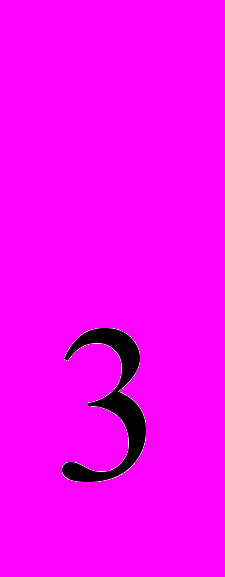 = 30S
= 30S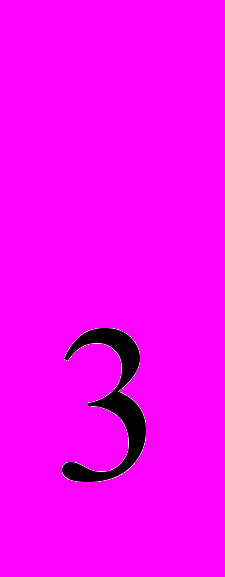 - 0,75S
- 0,75S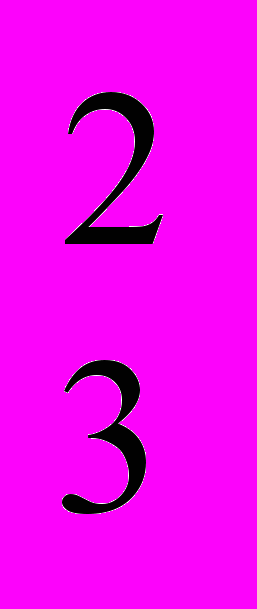 ,
, где S
 , S
, S , S
, S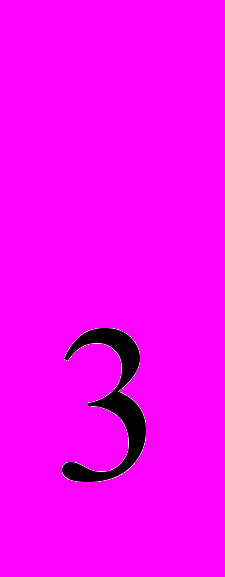 - площади, соответственно, лучшего, среднего и худшего участков. Допустим, что S
- площади, соответственно, лучшего, среднего и худшего участков. Допустим, что S = 15, S
= 15, S = 20, S
= 20, S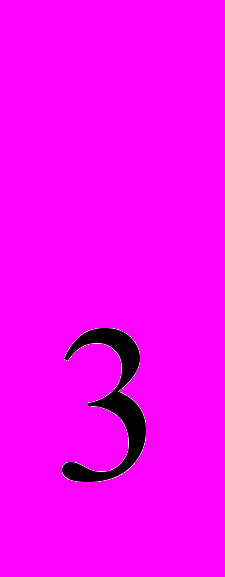 = 16. Рыночная цена продукта, производимого на этих участках, равна 4.
= 16. Рыночная цена продукта, производимого на этих участках, равна 4.а) Определите величину арендной платы за каждый из участков.
б) Найдите величину дифференциальной ренты для каждого участка.
Покажите решение графически.
11.7. Зависимость объема (Q) выращиваемой гречихи от используемых площадей (S) задана в виде Q = 100S - S
 . Цена тонны гречихи равна 10 ден.ед. Каков максимальный размер ренты, которую может заплатить фермер за пользование землей, если площадь участка составляет 25 га? Какова будет цена 1 га земли, если годовая ставка процента равна 2,5%?
. Цена тонны гречихи равна 10 ден.ед. Каков максимальный размер ренты, которую может заплатить фермер за пользование землей, если площадь участка составляет 25 га? Какова будет цена 1 га земли, если годовая ставка процента равна 2,5%?11.8. Предположим, участок земли продается по цене 50 тыс. дол. Вы оцениваете, что при сдаче земли в аренду рента составит 4 тыс. дол. в год. Земля будет приносить этот доход всегда. Считая, что сегодня ставка ссудного процента 10%, купите ли вы этот участок?
Тема 12. ОБЩЕЕ РАВНОВЕСИЕ И ЭКОНОМИЧЕСКАЯ ЭФФЕКТИВНОСТЬ
12.1. Каким образом участники обмена двух товаров в модели Эджуорта достигают Парето-эффективного распределения?
12.2. Каким образом граница возможных полезностей связана с кривой контрактов?
12.3. Всегда ли кривая производственных возможностей характеризуется возрастающей предельной нормой трансформации?
12.4. Может ли комбинация товаров Х и Y быть, с точки зрения общества, технически эффективной, но экономически неэффективной? А наоборот?
12.5. Докажите математически и объясните экономический смысл формулы предельной нормы трансформации товаров Х и Y:
MRРT
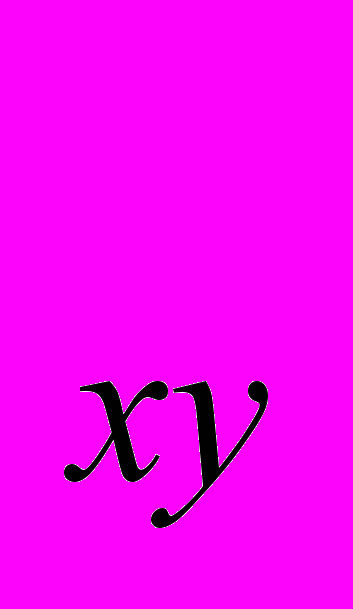 = -
= - 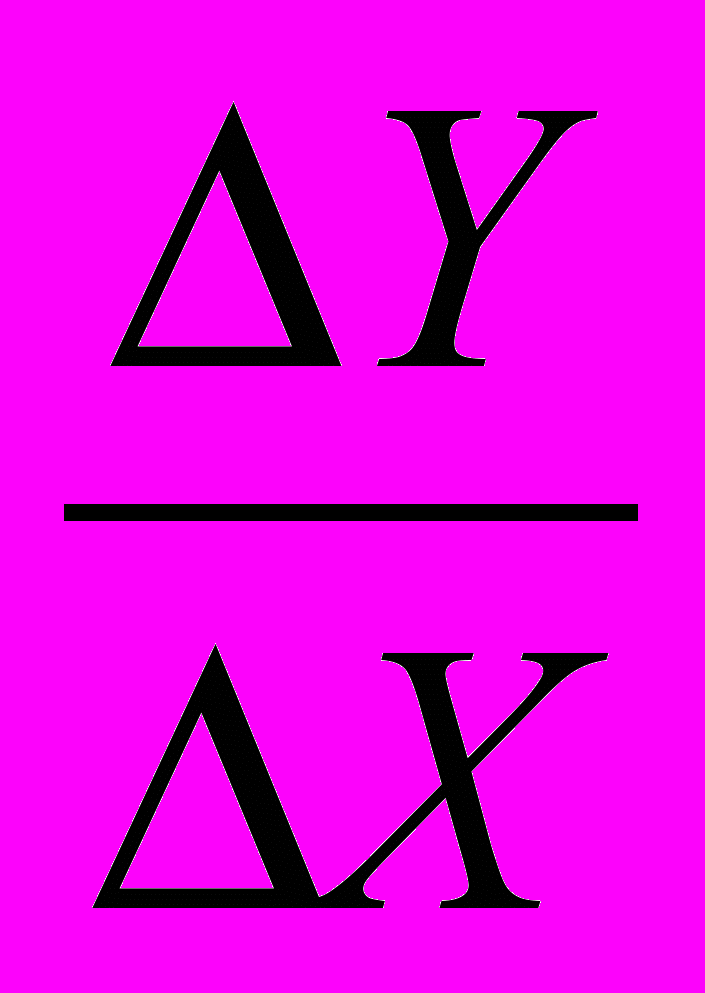 =
= 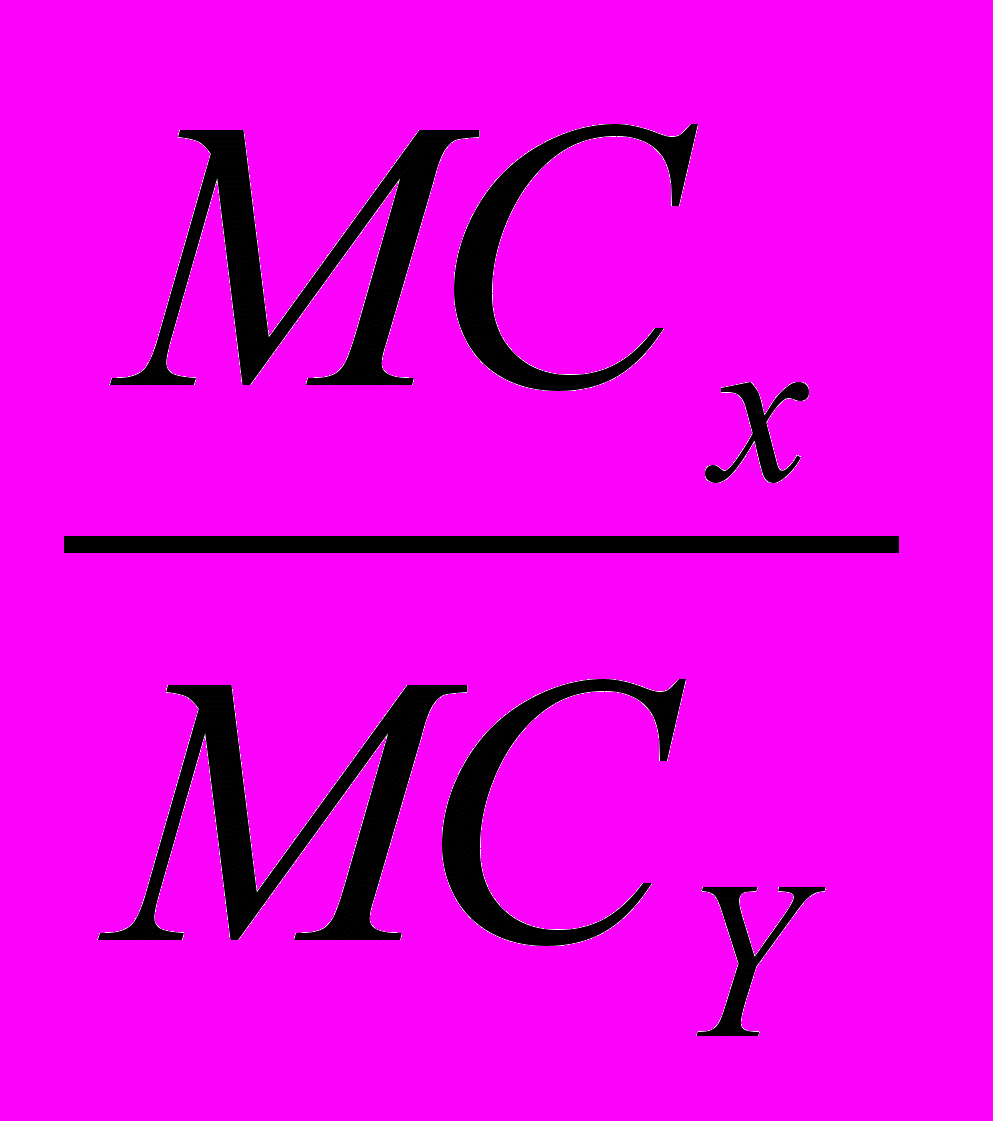
12.6. Почему система рынков с совершенной конкуренцией может достичь Парето-эффективности? Чем определяется распределение благосостояния в такой системе?
12.7. Почему существует множество вариантов распределения ресурсов, отвечающих критерию оптимальности по Парето? (Для объяснения используйте кривую потребительских возможностей).
12.8. Почему для достижения оптимальности по Парето необходимо, чтобы предельные нормы замещения для обоих потребителей равнялись предельной норме трансформации?
12.9. Покажите, каким образом монопольный контроль над ценами препятствует достижению эффективности. Как монополия влияет на распределение ресурсов в условиях общего равновесия?
12.10. На диаграмме Эджуорта представлен обмен двух благ Х и Y между двумя потребителями М и N.
А
В
D U
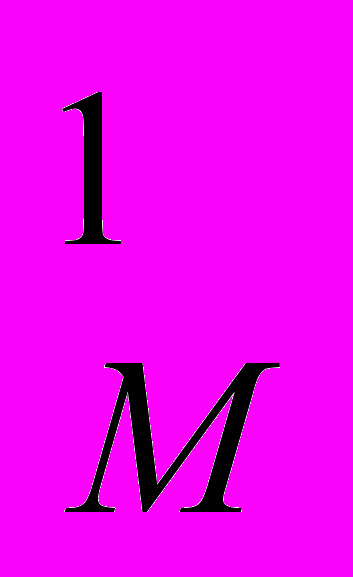
U
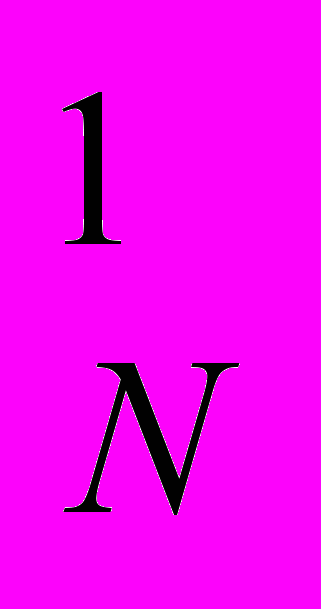 U
U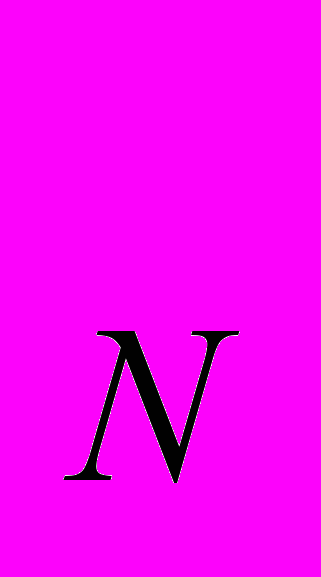 U
U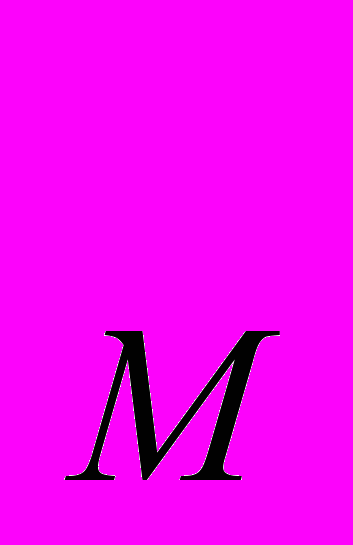
Y N


 50 ед.
50 ед.
Х
М 100 ед.
Ответьте на следующие вопросы:
а) Если первоначальный вариант распределения представлен т.В, захотят ли потребители перейти к варианту распределения, представленному т.С?
б) Захочет ли потребитель М перейти из т.В в т.D?
в) Объясните, почему оба потребителя выразят желание торговать между собой, если исходный вариант распределения представлен т.А? Может ли экономическая теория точно предсказать, каковы будут результаты обмена между ними?
12.11. Ограниченное число ресурсов (капитала – 50 ед., труда – 100 ед.) распределяется между производством продуктов А и В. Соответствующие производственные функции имеют вид: Q
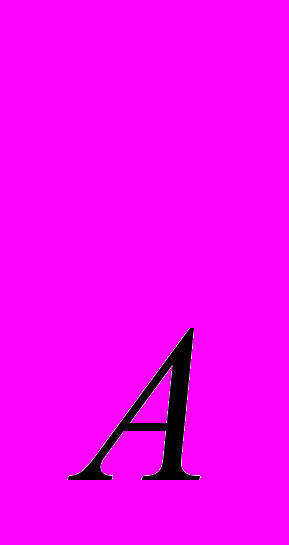 = K
= K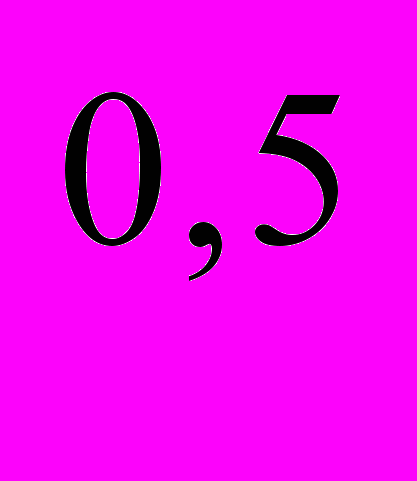 L
L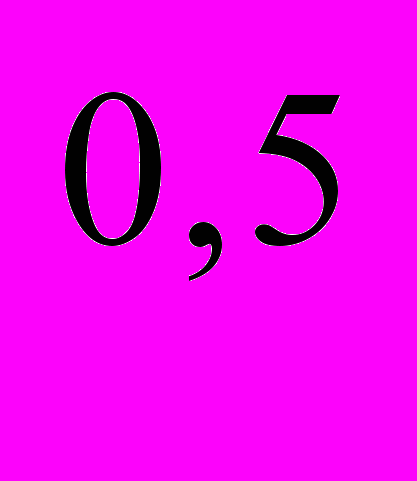 , Q
, Q = K
= K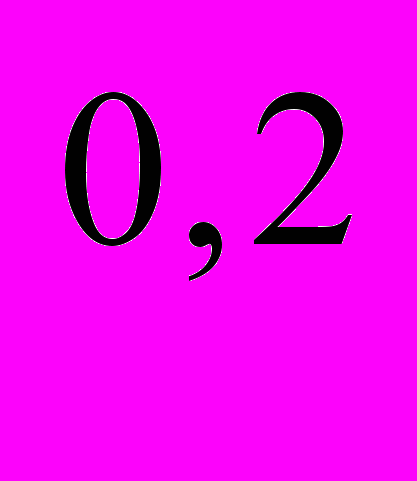 L
L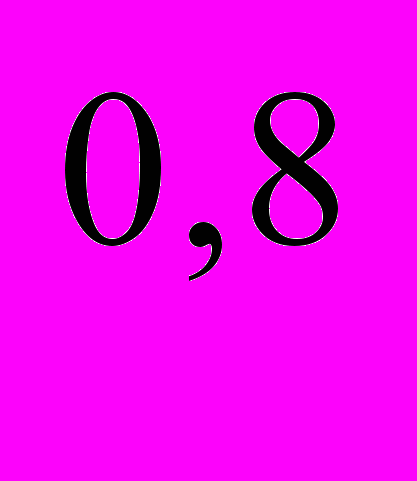 . Постройте кривую производственных контрактов и кривую производственных возможностей.
. Постройте кривую производственных контрактов и кривую производственных возможностей.12.12. Для двух потребителей товары Х и Y служат дополняющими товарами в пропорции 1:1. Общее количество товара Х – 20 шт., товара Y – 20 шт. Первоначальное распределение товаров таково: Х
 = 8, Y
= 8, Y = 4; Х
= 4; Х = 12, Y
= 12, Y = 16. Цена товара Х - 1 дол., цена товара Y - 3 дол. Будут ли меняться цены товаров и если да, то в каком направлении?
= 16. Цена товара Х - 1 дол., цена товара Y - 3 дол. Будут ли меняться цены товаров и если да, то в каком направлении? 12.13. Два потребителя А и В делят между собой 100 кг блага Х и 200 кг блага Y. Функции полезности: U
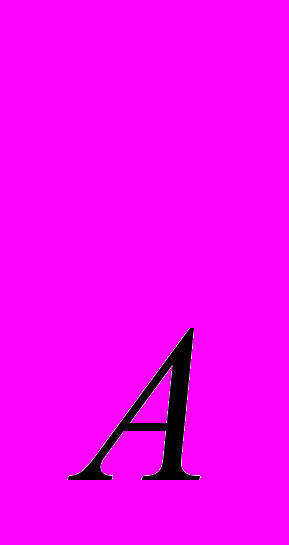 = (Х
= (Х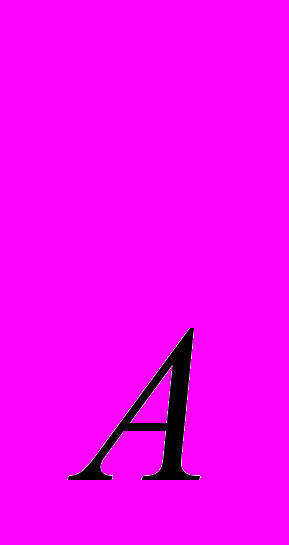 )
) Y
Y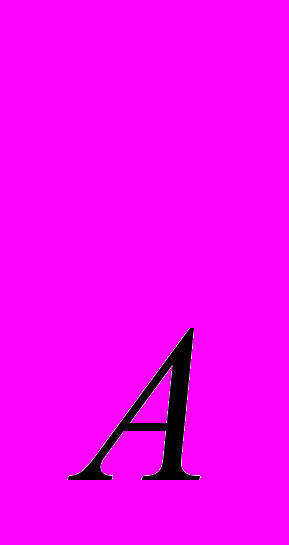 , U
, U = Х
= Х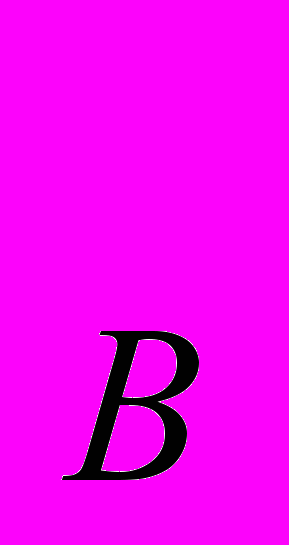 ( Y
( Y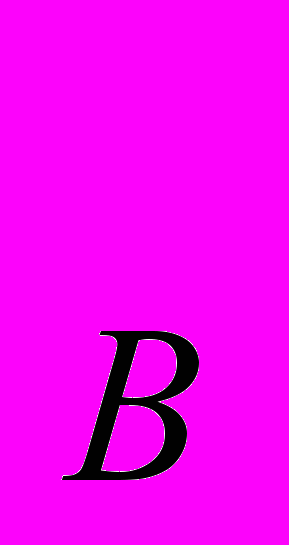 )
) .
.- Постройте кривую контрактов А и В.
- Постройте границу потребительских возможностей.
12.14. . Два потребителя А и В делят между собой 70 кг товара Х и 70 кг товара Y. Функции полезности: U
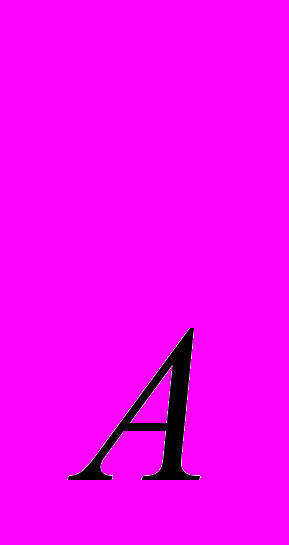 = (Х
= (Х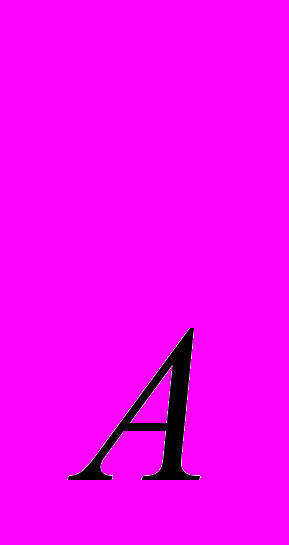 )
) Y
Y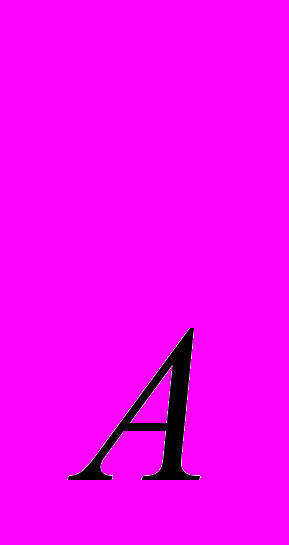 , U
, U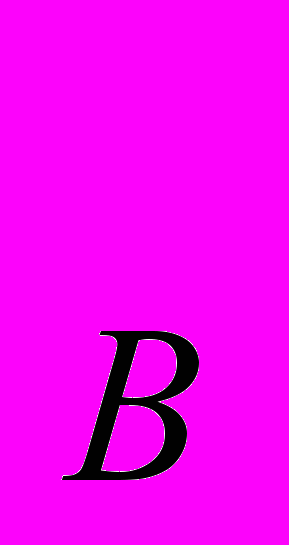 = Х
= Х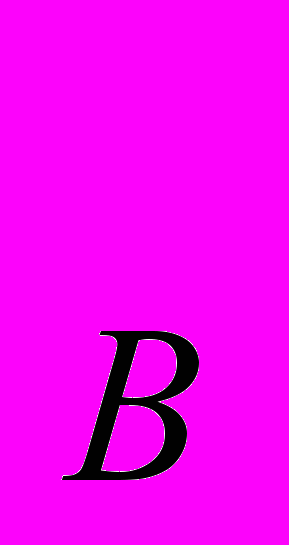 ( Y
( Y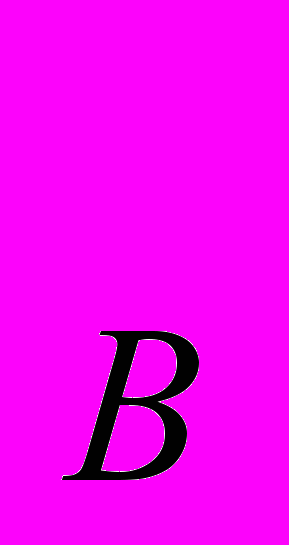 )
) . Первоначальное распределение товаров оказалось таким: Х
. Первоначальное распределение товаров оказалось таким: Х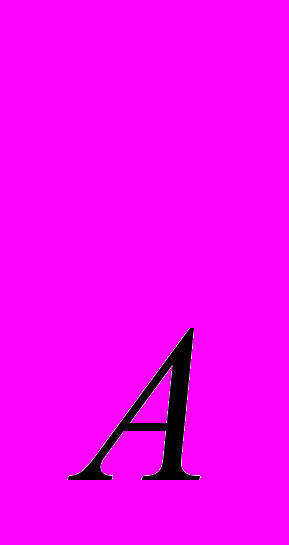 = 20, Y
= 20, Y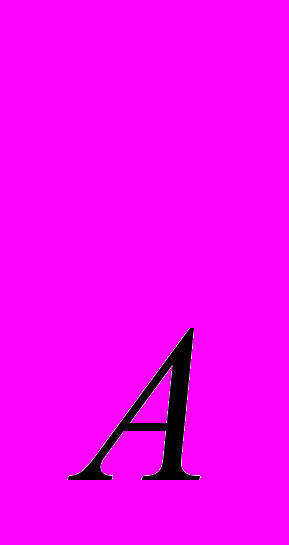 = 50; Х
= 50; Х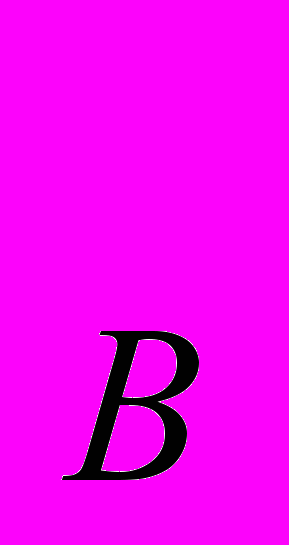 = 50, Y
= 50, Y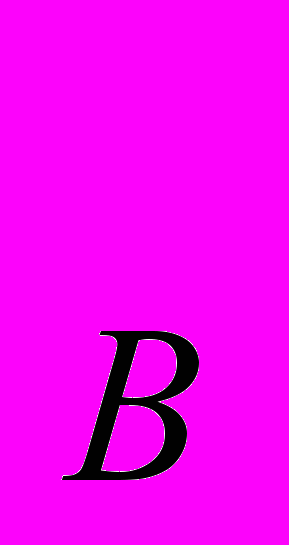 = 20 при ценах Р
= 20 при ценах Р = 10, Р
= 10, Р = 5.
= 5. - Является ли первоначальный выбор потребителей оптимальным?
- В каком направлении должны меняться цены товаров, чтобы распределение благ изменялось в направлении Парето-оптимальном?
Покажите решение графически.
12.15. Производственная функция общества описывается уравнением Q = 40L - 5L
 , где L – объем используемого труда. Функция полезности потребителей в экономике равна U = 2Q - 2L
, где L – объем используемого труда. Функция полезности потребителей в экономике равна U = 2Q - 2L . Какой объем продукции будет произведен в равновесии, какой объем труда будет использован? Покажите решение графически.
. Какой объем продукции будет произведен в равновесии, какой объем труда будет использован? Покажите решение графически.12.16. В двухпродуктовой экономике два потребителя обмениваются двумя благами – Х и Y. Оба имеют функцию полезности вида U(Х, Y) = Х
 Y
Y . Первоначально блага распределялись следующим образом: Х
. Первоначально блага распределялись следующим образом: Х = 16, Y
= 16, Y = 13; Х
= 13; Х = 59, Y
= 59, Y = 2. Допустим, что цена блага Х равна 1 (Р
= 2. Допустим, что цена блага Х равна 1 (Р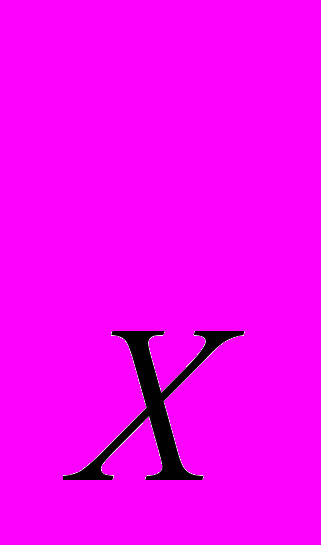 = 1). Найдите равновесную цену блага Y. Найдите оптимальное распределение благ между потребителями.
= 1). Найдите равновесную цену блага Y. Найдите оптимальное распределение благ между потребителями.12.17. Заданы функции полезности двух потребителей, обменивающихся двумя благами Х и Y: U
 ( Х
( Х , Y
, Y ) = Х
) = Х Y
Y ; U
; U (Х
(Х , Y
, Y ) = minХ
) = minХ , Y
, Y .
.Первоначально первый потребитель потребляет 3 ед. блага Х и 4 ед. блага Y. Второй потребитель потребляет 7 ед. блага Х и 6 ед. блага Y. Чему будет равно соотношение цен на эти блага в состоянии конкурентного равновесия?
- В экономике имеется только два потребителя с функциями полезности:
U
 ( Х
( Х , Y
, Y ) = Х
) = Х + 12
+ 12 ; U
; U (Х
(Х , Y
, Y ) = Х
) = Х + 3Y
+ 3Y .
.Первоначально первый потребитель имеет 6 ед. блага Х и 3 ед. блага Y. Найдите, какое количество блага Y будет иметь первый потребитель, если при обмене потребители стремятся к достижению эффективности по Парето? Покажите решение графически. Что представляет собой кривая контрактов?
12.19. Два потребителя А и В имеют функции полезности:
U
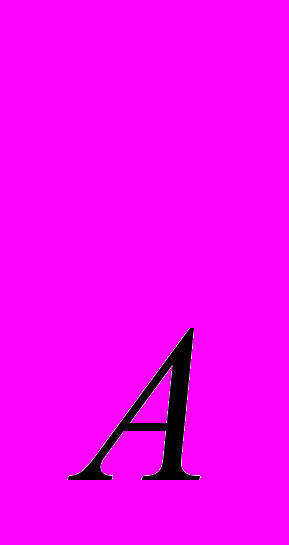 (Х
(Х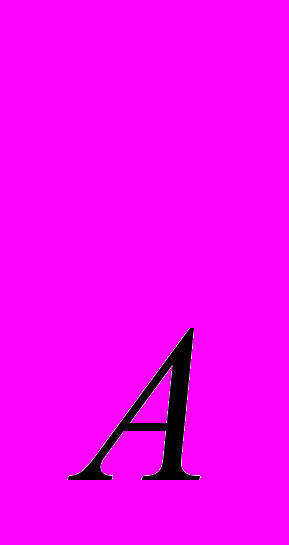 , Y
, Y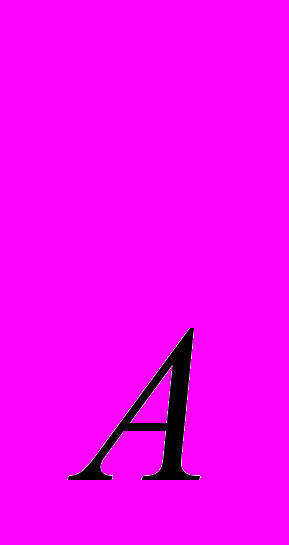 ) = Х
) = Х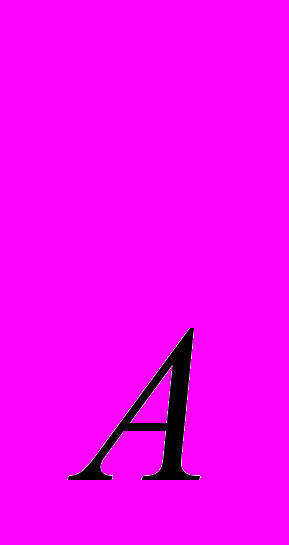 + 4
+ 4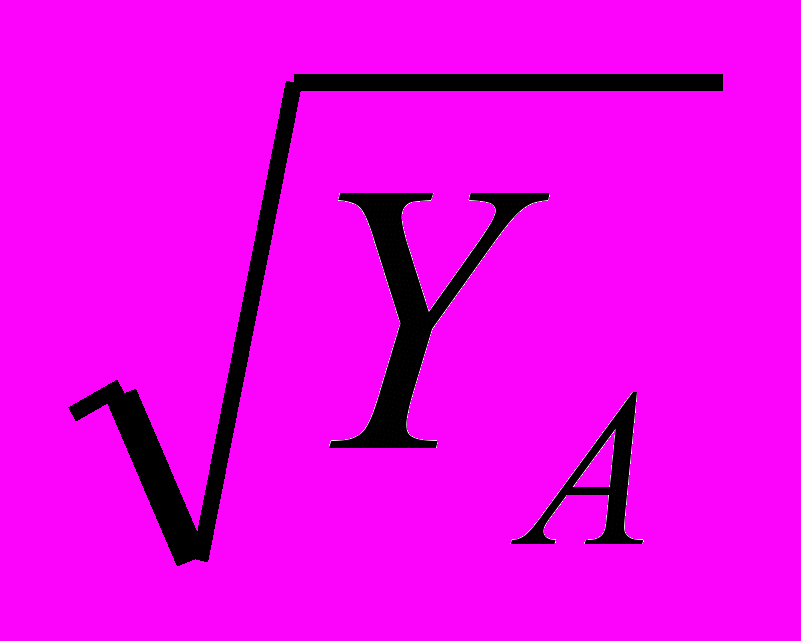 ; U
; U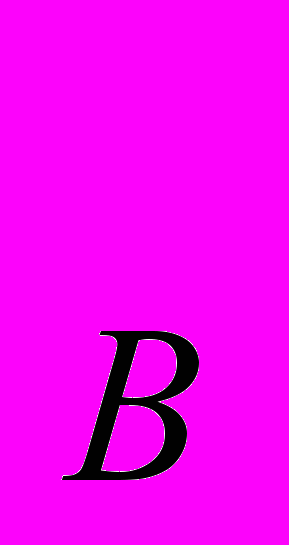 ( Х
( Х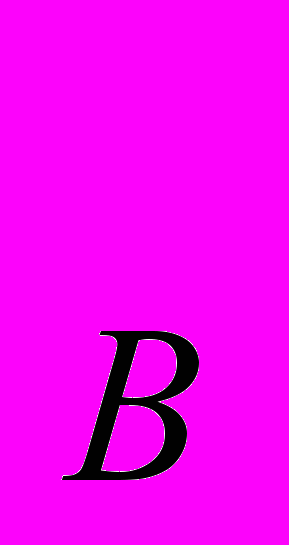 , Y
, Y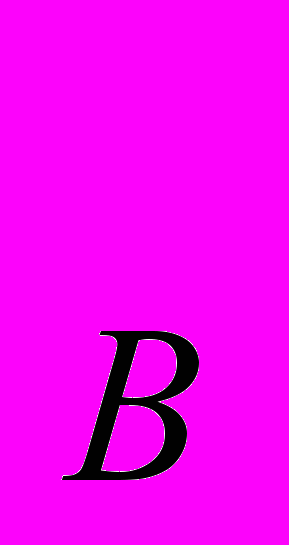 ) = Х
) = Х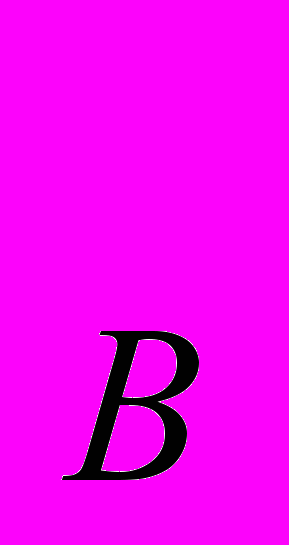 +2
+2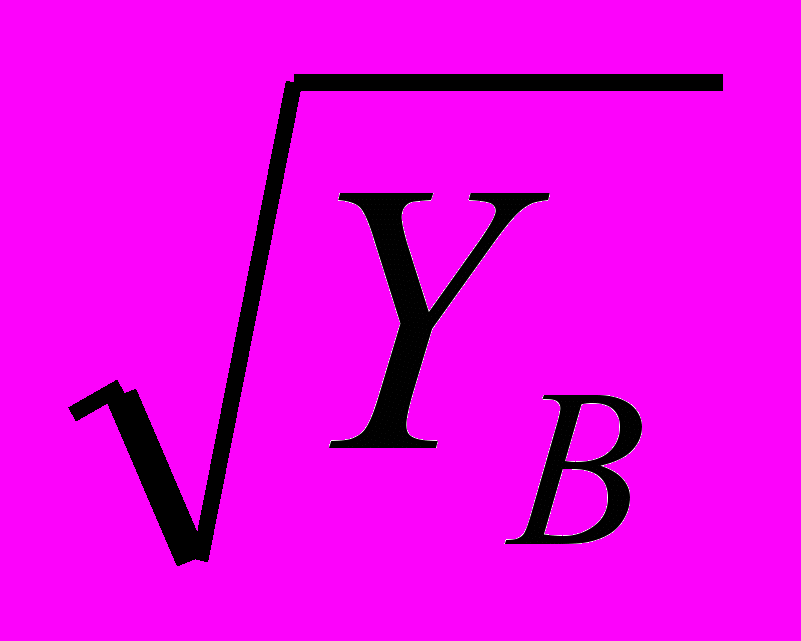 . Задано исходное распределение двух благ: Х
. Задано исходное распределение двух благ: Х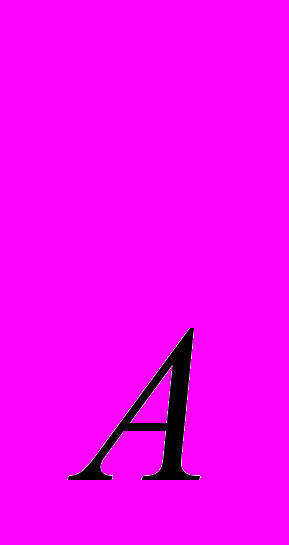 = 8, Y
= 8, Y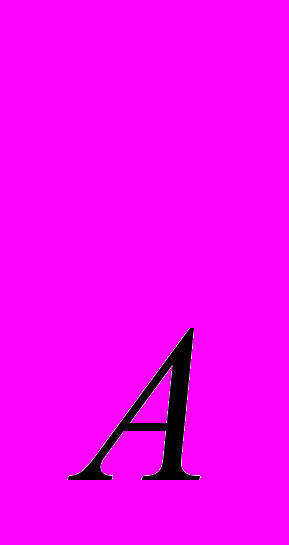 = 5; Х
= 5; Х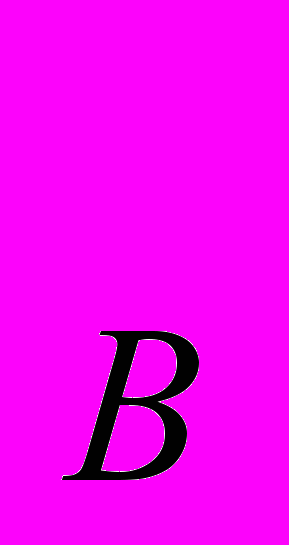 = 7, Y
= 7, Y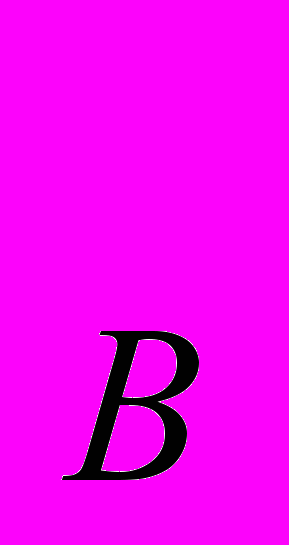 = 15. Какое количество блага Y будет иметь потребитель В, если участники обмена стремятся к Парето-эффективному распределению благ?
= 15. Какое количество блага Y будет иметь потребитель В, если участники обмена стремятся к Парето-эффективному распределению благ?12.20. В экономике обмена с двумя благами – яблоками и бананами – два потребителя стремятся к Парето-оптимальному распределению. Их функции полезности: U
 (А
(А , В
, В ) = А
) = А В
В ; U
; U (А
(А , В
, В ) = А
) = А В
В , где А – объем потребления яблок, В – объем потребления бананов. Первоначально блага распределялись следующим образом: А
, где А – объем потребления яблок, В – объем потребления бананов. Первоначально блага распределялись следующим образом: А = 8, В
= 8, В = 4; А
= 4; А = 16, В
= 16, В = 2. Определите, чему должно быть равно оптимальное соотношение в потреблении яблок и бананов у первого потребителя?
= 2. Определите, чему должно быть равно оптимальное соотношение в потреблении яблок и бананов у первого потребителя?ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ2)
Тема 2. Основы теории рыночного спроса и предложения
- На рынке совершенной конкуренции заданы функции спроса и предложения товара
Q
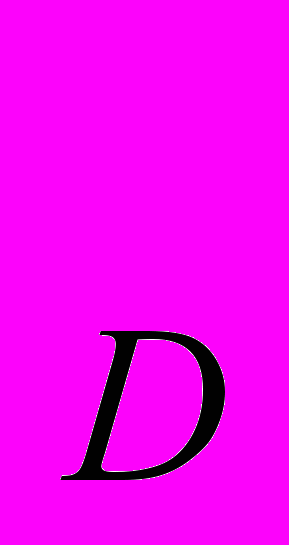 = 1200 – 100P, Q
= 1200 – 100P, Q = 100P.
= 100P. Допустим, власти решили сделать некоторый общегосударственный запас этого товара, введя натуральный налог на потребителей, следующим образом: покупая х ед. товара на рынке, потребители обязаны
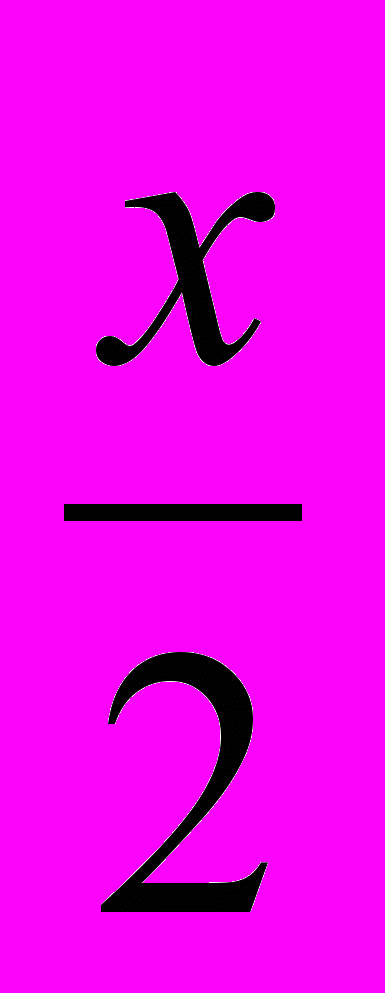 ед. товара отдать государству в виде налога.
ед. товара отдать государству в виде налога.Какая равновесная цена установится на рынке этого товара? Какое количество товара образует запас?
- На рынке заданы функции спроса и предложения: Q
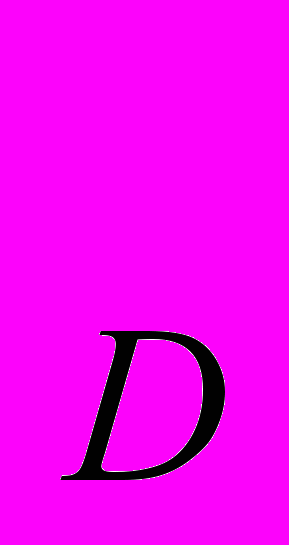 = 435 – 4Р, Q
= 435 – 4Р, Q = 15+ 8Р. Городские власти установили, что товар не может продаваться дороже 21 ден. ед. Чтобы избежать дефицита, власти ввели субсидию производителям за каждую единицу проданного товара. Найдите величину субсидии на единицу товара, при которой на рынке устанавливается равенство спроса и предложения.
= 15+ 8Р. Городские власти установили, что товар не может продаваться дороже 21 ден. ед. Чтобы избежать дефицита, власти ввели субсидию производителям за каждую единицу проданного товара. Найдите величину субсидии на единицу товара, при которой на рынке устанавливается равенство спроса и предложения.
- Функция спроса на товар Х имеет вид Q
 = 10 - Р
= 10 - Р + 0,1Р
+ 0,1Р . При цене товара Y = 8 ден. ед., было приобретено 6 ед. товара Х. Определите коэффициенты прямой и перекрестной эластичности спроса по цене на товар Х.
. При цене товара Y = 8 ден. ед., было приобретено 6 ед. товара Х. Определите коэффициенты прямой и перекрестной эластичности спроса по цене на товар Х.
- Определите коэффициент перекрестной эластичности спроса на товар Y по цене товара Х, если известно, что при цене товара Х равной 40 ден. ед. объем спроса на товар Y равен 200 шт., а при цене товара Х равной 70 ден. ед. объем спроса на товар Y = 140 шт. К какой группе относится данный товар?
- Функция спроса населения на данный товар имеет вид Q
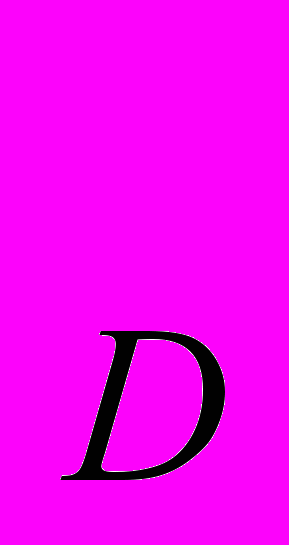 = 14 – 2P, функция предложения данного товара Q
= 14 – 2P, функция предложения данного товара Q = -4 + 2P. Определите ставку налога, при которой равновесный объем продаж составит 2 единицы.
= -4 + 2P. Определите ставку налога, при которой равновесный объем продаж составит 2 единицы.
- Функция спроса на данный товар Q
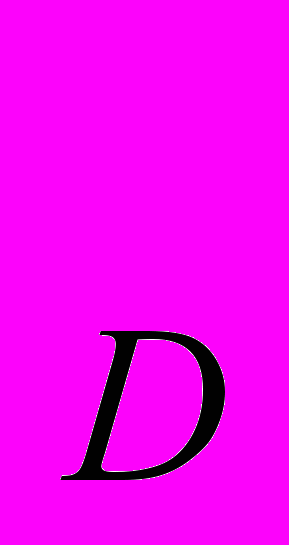 = 7 – P, функция предложения данного товара
= 7 – P, функция предложения данного товара
Q
 = -5 + 2P. При какой ставке налога общая сумма налога окажется максимальной?
= -5 + 2P. При какой ставке налога общая сумма налога окажется максимальной?- Функция спроса имеет вид Q
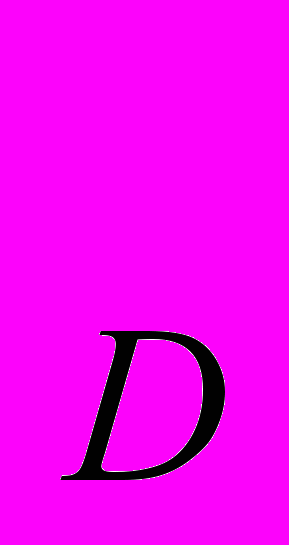 = 8 – P, функция предложения: Q
= 8 – P, функция предложения: Q = -4 + P. Рассчитайте размер потоварной дотации для достижения объема продаж в 4 единицы.
= -4 + P. Рассчитайте размер потоварной дотации для достижения объема продаж в 4 единицы.
Тема 3. Теория потребительского поведения
- Потребитель имеет функцию полезности U(x, y) = minx+2y, y+2x. Потребитель сделал выбор – купил 10 ед. блага х и 20 ед. блага у. Цена блага х равна 1. Какой доход имеет потребитель?
- N. изучает экономику и сдает два экзамена по этому предмету. Итоговая оценка курса (балл) определяется как минимум из двух полученных оценок. N. решила посвятить 1200 минут подготовке к экзамену. Она знает, что если она совсем не будет готовиться к первому экзамену, то получит 0 баллов. Каждые дополнительные 10 минут, потраченные на подготовку к 1-му экзамену, приносят дополнительно 1 балл. Если совсем не тратить время на подготовку ко 2-му экзамену, то N. получит 0 баллов. Каждые дополнительные 20 минут, потраченные на подготовку ко второму экзамену, увеличивают итоговую оценку на 1 балл. Найдите оптимальное распределение времени на подготовку к экзаменам, чтобы получить максимальный итоговый балл. Покажите решение графически.
- М также сдает два экзамена по курсу, но ее итоговый балл определяется как сумма баллов, полученных за два экзамена. М решила потратить 400 минут для подготовки к этим экзаменам. Если она тратит m
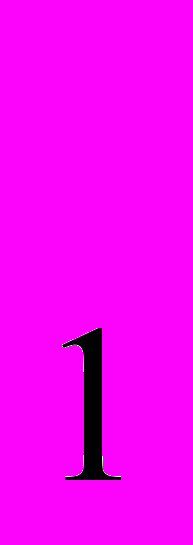 минут на первый экзамен, то ее балл будет x
минут на первый экзамен, то ее балл будет x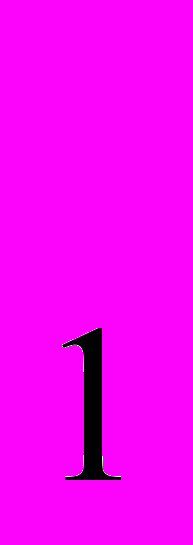 =
= 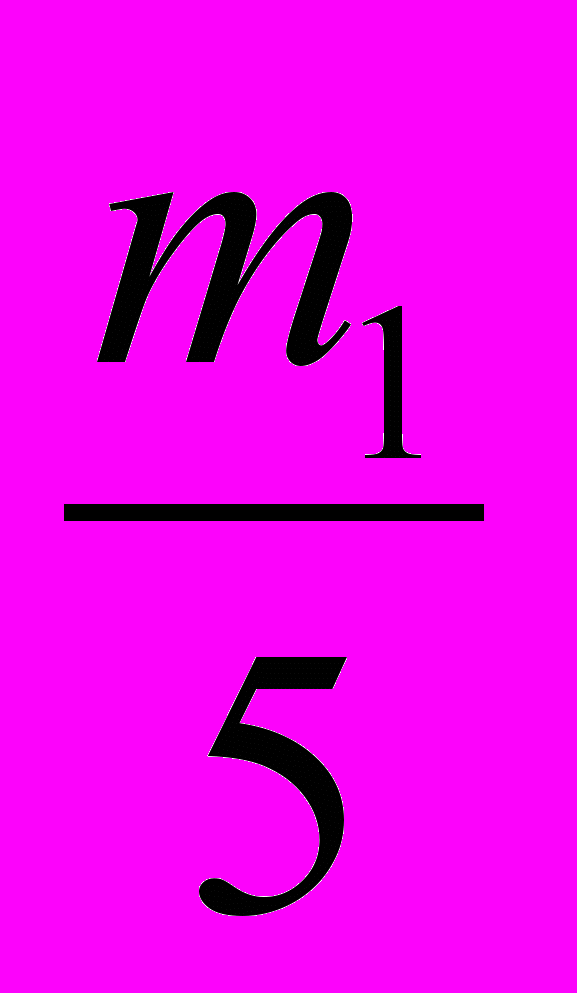 . Если она тратит m
. Если она тратит m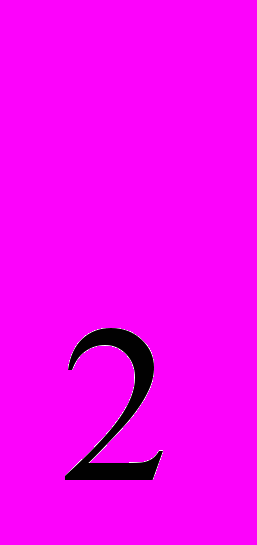 минут на второй экзамен, то ее оценка за этот экзамен будет x
минут на второй экзамен, то ее оценка за этот экзамен будет x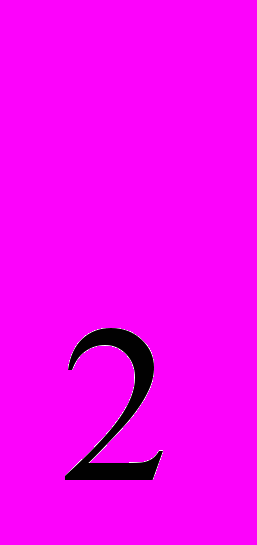 =
= 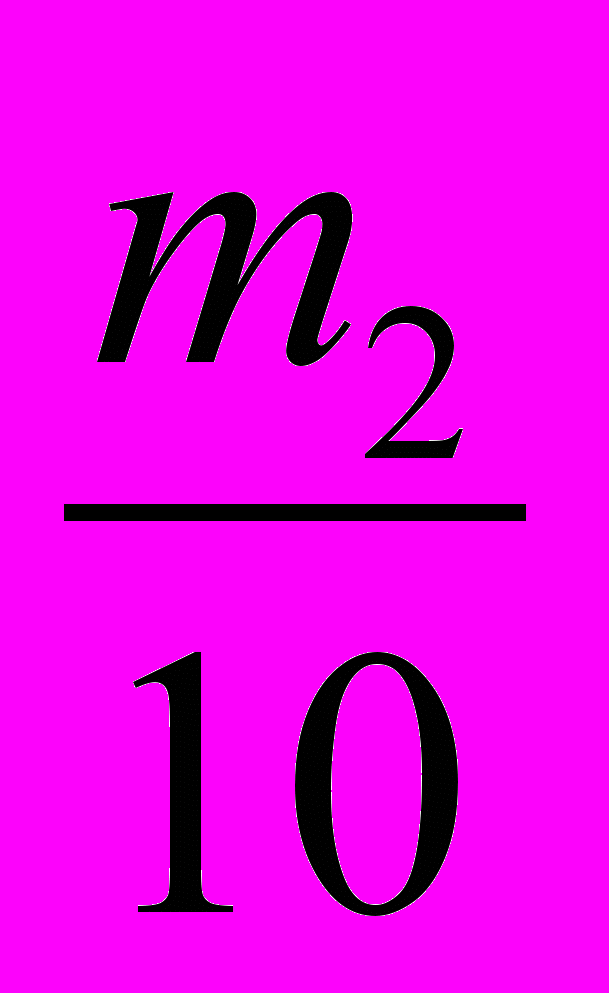 . Определите наибольший итоговый балл, который М может получить за курс. Покажите решение графически.
. Определите наибольший итоговый балл, который М может получить за курс. Покажите решение графически.
- Допустим, что два товара абсолютно дополняют друг друга в потреблении. Если цена одного товара изменилась, какая часть в изменении спроса данного товара вытекает из эффекта замещения, а какая – из эффекта дохода?. Покажите решение на графике.
- Предположим, функция полезности потребителя имеет вид U = X
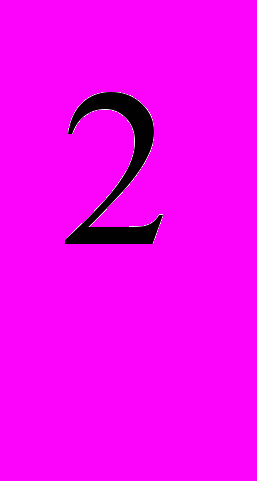 S, где S – часы отдыха (S
S, где S – часы отдыха (S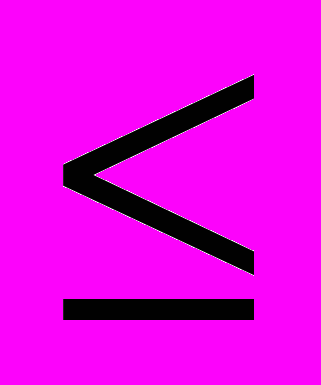 24), Х – ежедневное потребление других благ, определяемое временем работы и ставкой заработной платы w. Запишите в общем виде модель потребительского выбора. Зависит ли оптимальное количество часов ежедневного отдыха от ставки заработной платы?
24), Х – ежедневное потребление других благ, определяемое временем работы и ставкой заработной платы w. Запишите в общем виде модель потребительского выбора. Зависит ли оптимальное количество часов ежедневного отдыха от ставки заработной платы?
- Функция полезности потребителя Д имеет вид U(C, R) = C – (12-R)
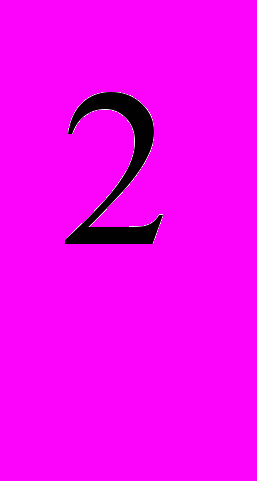 , где R – часы досуга в течение дня, С – объем потребления. Д должен распределить 16 часов в день между работой и досугом. Д имеет также нетрудовой доход, равный 20 ден. ед. в день.
, где R – часы досуга в течение дня, С – объем потребления. Д должен распределить 16 часов в день между работой и досугом. Д имеет также нетрудовой доход, равный 20 ден. ед. в день.
- Если почасовая ставка зарплаты равна 10 ден. ед., сколько часов Д предпочтет работать?
- Если нетрудовой доход Д сократится до 5 ден. ед. в день, сколько часов для работы выберет Д?
- Допустим, введен 20%-ный налог на весь доход, получаемый Д, ставка зарплаты 10, нетрудовой доход равен 20. Сколько часов Д будет работать?
- Функция полезности индивида имеет вид U(x, y) = 100x -
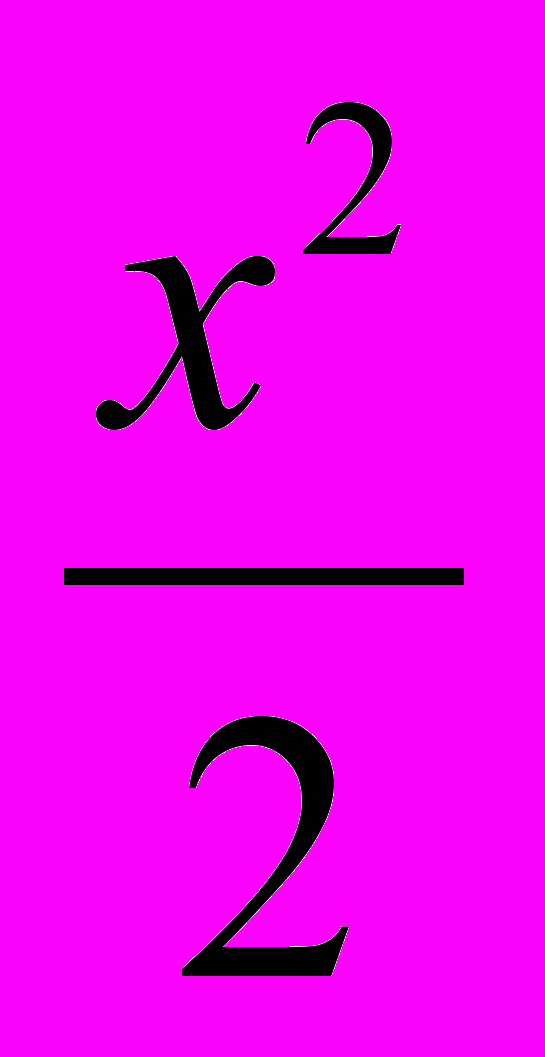 + y, где х – количество потребляемого данного блага, у – расходы на все другие товары.
+ y, где х – количество потребляемого данного блага, у – расходы на все другие товары.
- Какой функции спроса на благо х соответствует данная функция полезности?
- Определите, как изменится значение функции полезности, если цена блага х возрастет с 50 до 80 ден. ед., а доход потребителя остается неизменным и равен 4000?
- Насколько изменится выигрыш потребителя при таком росте цен?
- Предпочтения потребителя заданы функцией U(x, y) = minх, у, где х – количество данного блага, у – расходы на все другие блага. Доход потребителя равен 12, Р
 = 2.
= 2.
- Каким будет оптимальный выбор потребителя?
- Если цена блага х возрастет до 3 ден. ед. (при прочих неизменных условиях), насколько изменится значение функции полезности?
- Какую денежную компенсацию должен получить потребитель, чтобы при новой цене на благо х сохранить прежний уровень жизни?
Покажите решение графически.
- Предпочтения потребителя заданы функцией полезности U(x, y) = x -
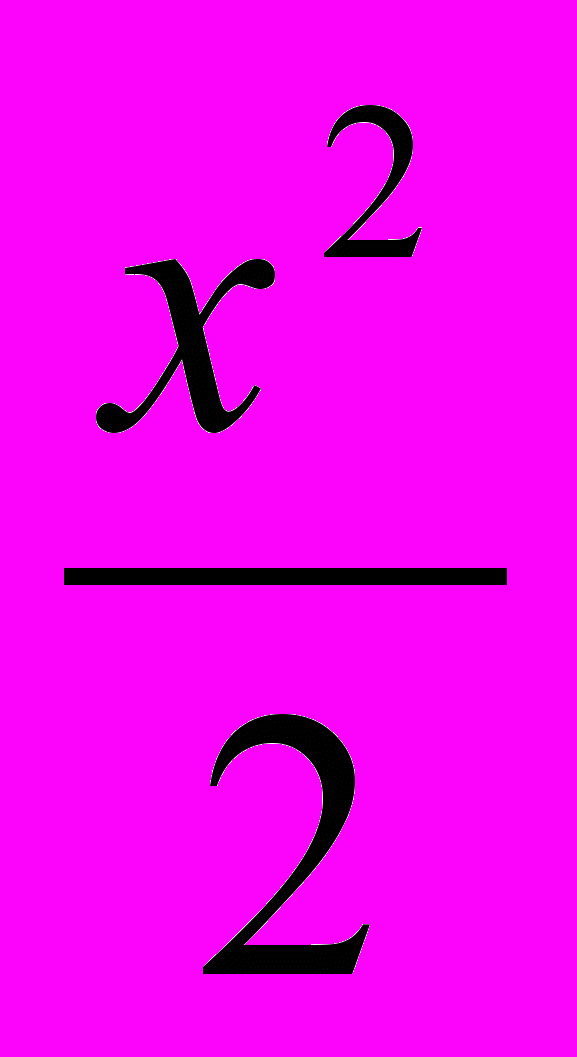 + y, где х, у – количества потребляемых благ. Доход, расходуемый только на эти два блага, равен m. Цена блага у всегда равна 1, цена блага х: 0 Р
+ y, где х, у – количества потребляемых благ. Доход, расходуемый только на эти два блага, равен m. Цена блага у всегда равна 1, цена блага х: 0 Р
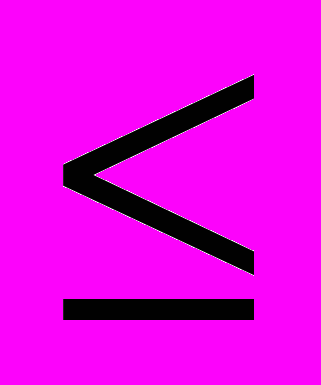 1.
1.
- Найдите функцию спроса на благо х.
- Каким будет значение функции полезности при оптимальном выборе потребителя?
- Как изменится оптимальный выбор потребителя, если при m=3 цена блага х возрастет с 0,5 ден. ед. до 1 ден. ед.
Покажите решение графически.
- Д. получила в подарок магнитофон. Ее функция полезности U(x, y, z) = x +
 f(y), где z – число кассет, которые она покупает, y – число имеющихся магнитофонов, f(y) = 0, если y 1 и f(y) = 24, если y 1, х – количество денег, которые она может потратить. Цена кассеты равна 3 ден. ед. Сколько кассет купит Д.?
f(y), где z – число кассет, которые она покупает, y – число имеющихся магнитофонов, f(y) = 0, если y 1 и f(y) = 24, если y 1, х – количество денег, которые она может потратить. Цена кассеты равна 3 ден. ед. Сколько кассет купит Д.?
- М. занимается баскетболом и теннисом. Ее предпочтения заданы функцией U(b, t) = bt, где b – число баскетбольных матчей, t – число теннисных матчей, которые она проводит в течение недели. Занятия являются платными. М. может потратить 24 ден. ед. в неделю на эти виды спорта. Одно занятие баскетболом и теннисом стоит 4 ден. ед. каждое. Одно занятие баскетболом занимает 4 часа, теннисом – 2 часа. Как изменится число еженедельных спортивных занятий, если М. решит тратить на эти виды спорта только 16 часов в неделю?
- Функция полезности потребителя U(x, y) = 3x + y. Если затраты на приобретение блага х равны х
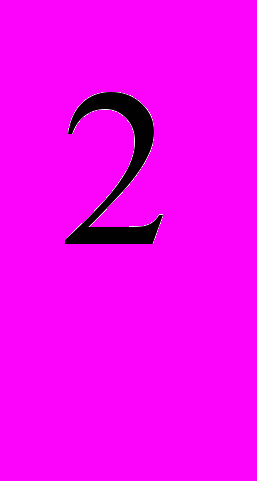 , Р
, Р = 6, доход равен 101, сколько единиц товара х купит потребитель?
= 6, доход равен 101, сколько единиц товара х купит потребитель?
- Потребитель потребляет два блага – Х и У. Функция спроса потребителя на товар Х имеет вид: Х = 0,02М – 3,64Р
 , где М – доход, равный 842, цена блага У равна 1. Если цена блага Х увеличится до 4, каким будет эффект замены и эффект дохода в изменении спроса на товар Х?
, где М – доход, равный 842, цена блага У равна 1. Если цена блага Х увеличится до 4, каким будет эффект замены и эффект дохода в изменении спроса на товар Х?
- Функция полезности потребителя U(X
 , X
, X ) = X
) = X X
X . P
. P = 1, P
= 1, P = 2, I = 30. Если цена блага В упадет до 1, как изменится потребление блага А? Найдите эффект замены и эффект дохода в изменении спроса на благо А.
= 2, I = 30. Если цена блага В упадет до 1, как изменится потребление блага А? Найдите эффект замены и эффект дохода в изменении спроса на благо А.
- *Р. любит сигареты. Его функция полезности U(x, c) = x + 10c – 0,5c
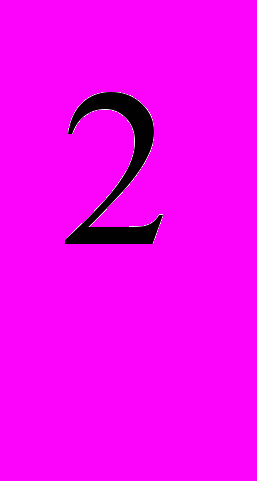 , где с – число сигарет, которые он выкуривает в неделю, х –затраты на потребление всех других товаров. Еженедельный доход равен 200 ден. ед. Цена сигарет увеличилась с 1 ден. ед. до 2-х ден. ед. Потере какого количества дохода эквивалентно это повышение цены? Покажите решение на графике.
, где с – число сигарет, которые он выкуривает в неделю, х –затраты на потребление всех других товаров. Еженедельный доход равен 200 ден. ед. Цена сигарет увеличилась с 1 ден. ед. до 2-х ден. ед. Потере какого количества дохода эквивалентно это повышение цены? Покажите решение на графике.
- Доход потребителя К равен 200 ден. ед. в неделю. Его целевая функция U(x, y) = 2x + y, где х, у – блага. Цена блага х Р
 = 4. В данный момент К не потребляет благо у. К получил приглашение за плату вступить в клуб, пропагандирующий потребление товара у. Если он вступит в клуб, то получит возможность покупать товар у по уменьшенной цене Р
= 4. В данный момент К не потребляет благо у. К получил приглашение за плату вступить в клуб, пропагандирующий потребление товара у. Если он вступит в клуб, то получит возможность покупать товар у по уменьшенной цене Р = 1 ден. ед. Какую максимальную цену заплатил бы этот потребитель за вступление в клуб? Дайте графическую иллюстрацию решения.
= 1 ден. ед. Какую максимальную цену заплатил бы этот потребитель за вступление в клуб? Дайте графическую иллюстрацию решения.
- Целевая функция потребителя U(x, y) = 2х + 5у. Цена блага х равна 4, цена блага у равна 15 ден. ед. Доход = 150. Если потребитель вступит в клуб любителей блага у, то он сможет покупать товар у по цене 10 ден. ед. Какой наибольший вступительный взнос заплатил бы этот потребитель?
Тема 4. Производство: факторы и издержки производства
- Производственная функция фирмы h = t + 2f , где h – объем выпускаемой продукции, t, f – количества используемых ресурсов. Пусть w
 , w
, w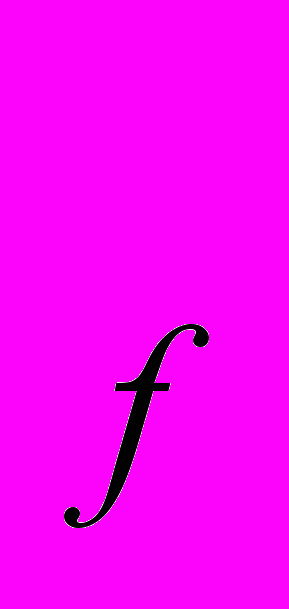 - заданные цены ресурсов. Чему равны минимальные издержки производства h ед. продукции? Дайте графическую иллюстрацию.
- заданные цены ресурсов. Чему равны минимальные издержки производства h ед. продукции? Дайте графическую иллюстрацию.
- Дайте графическое изображение следующих изоквант:
a) f(x, y) = min2x, x+y
b) f(x, y) = xy
c) f(x, y) = x + minx, y
d) f(x, y) = x + y
- Производственная функция фирмы f(x
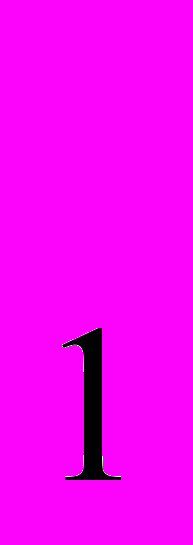 , x
, x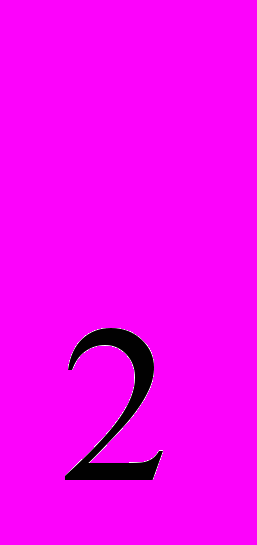 ) = 8x
) = 8x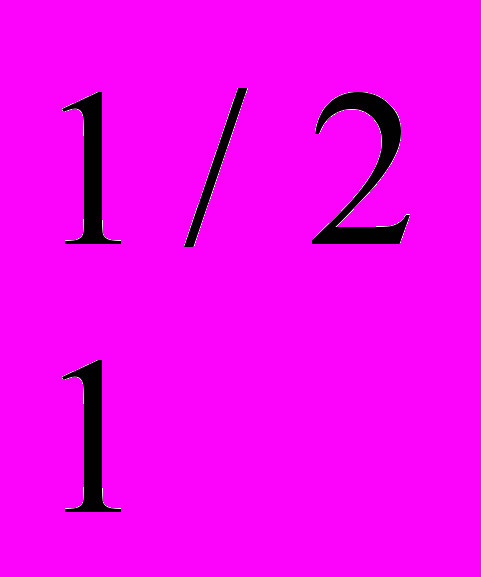 + 10x
+ 10x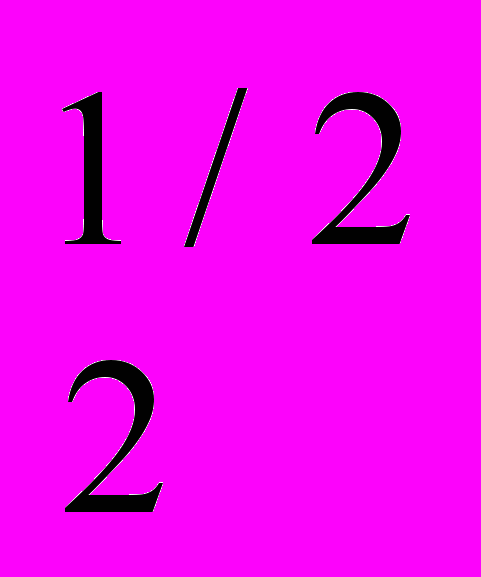 . Цена первого фактора равна 1, цена второго фактора равна 1. Цена выпуска равна 2. При каком выпуске прибыль фирмы максимальна?
. Цена первого фактора равна 1, цена второго фактора равна 1. Цена выпуска равна 2. При каком выпуске прибыль фирмы максимальна?
- Постоянные издержки фирмы равны 1000. Производственная функция в краткосрочном периоде у = 9х
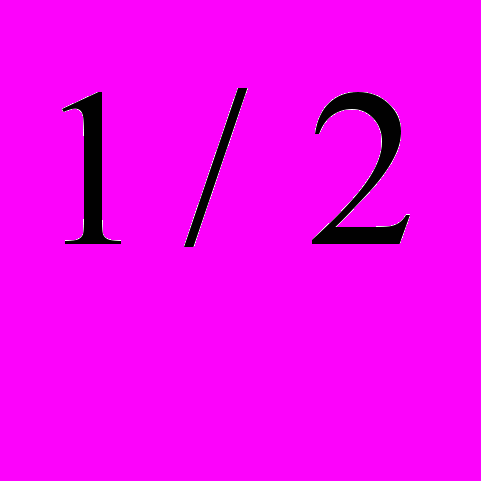 , где х –количество используемого переменного ресурса. Р
, где х –количество используемого переменного ресурса. Р = 4000. Найдите функцию общих издержек.
= 4000. Найдите функцию общих издержек.
- Допустим, необходимо разместить автомобильный завод в стране А либо в стране В. Производственная функция f(S, L) = S
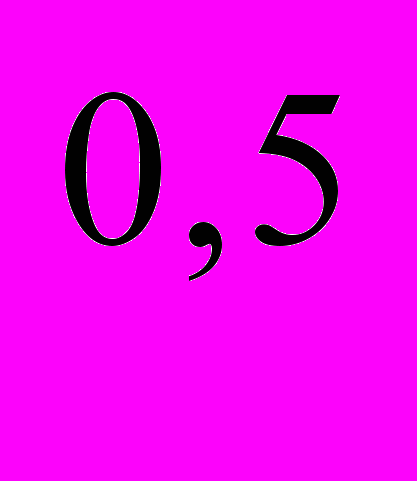 L
L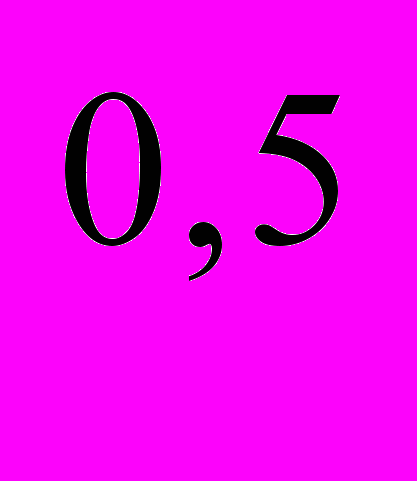 , где S – количество стали, L – количество труда. В стране А цена стали Р
, где S – количество стали, L – количество труда. В стране А цена стали Р = 7, цена труда Р
= 7, цена труда Р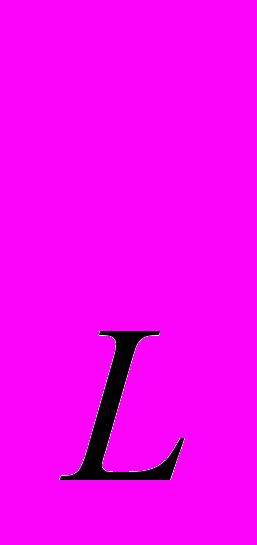 = 7. В стране В Р
= 7. В стране В Р = 8, Р
= 8, Р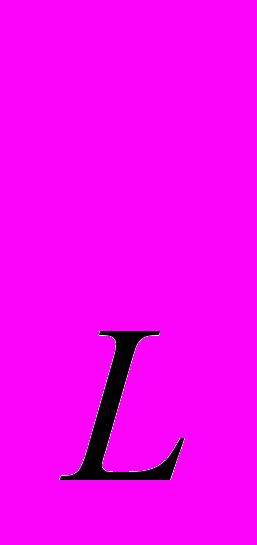 = 6. В какой стране нужно разместить завод, чтобы средние издержки производства автомобилей были минимальными?
= 6. В какой стране нужно разместить завод, чтобы средние издержки производства автомобилей были минимальными?
- Производственная функция фирмы, использующей два ресурса – х и у, имеет вид
f(x, y) =
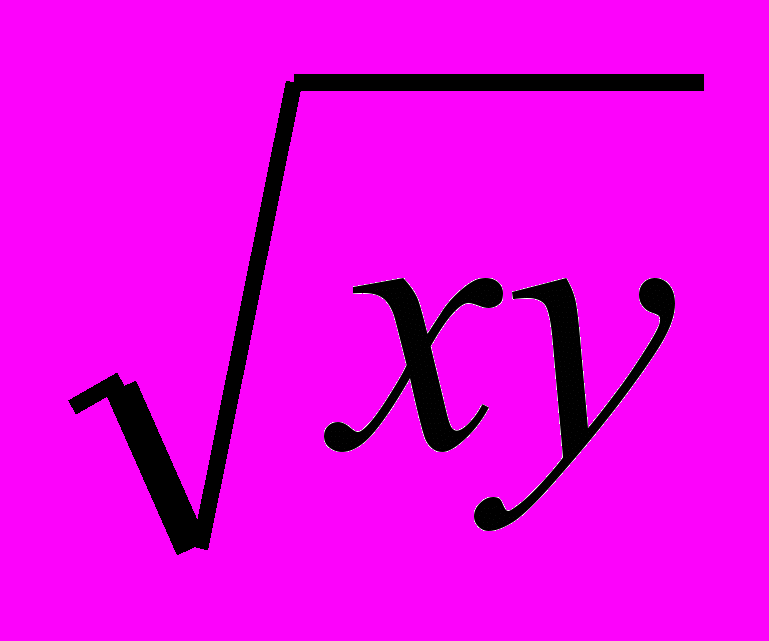 . Цена фактора х равна 17, цена фактора у равна 11. Фирма минимизирует средние издержки и тратит 517 ден. ед. на фактор х. Сколько денег тратит фирма на покупку фактора у?
. Цена фактора х равна 17, цена фактора у равна 11. Фирма минимизирует средние издержки и тратит 517 ден. ед. на фактор х. Сколько денег тратит фирма на покупку фактора у?- Фирма имеет производственную функцию Q = KL, где К – количество капитала, L – количество труда. Цена капитала Р
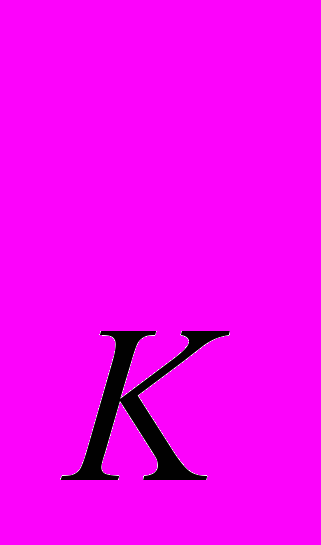 = r, цена труда Р
= r, цена труда Р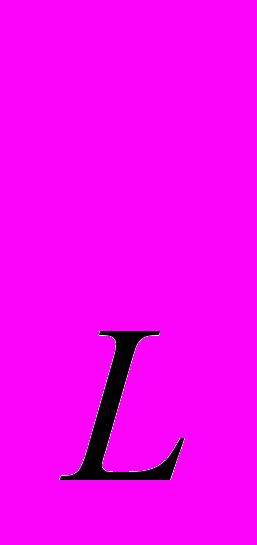 = w. Найдите функцию спроса на труд - L(Q, w, r).
= w. Найдите функцию спроса на труд - L(Q, w, r).
- Производственная функция f(x
 , x
, x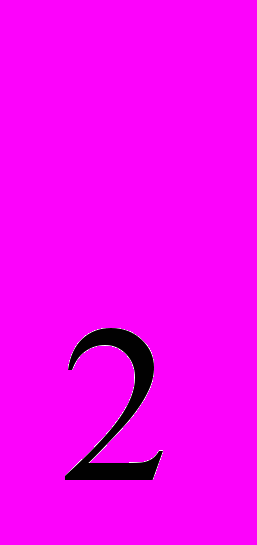 ) = [min{x
) = [min{x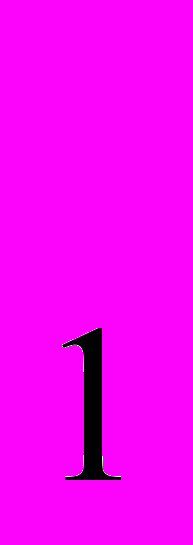 , 3x
, 3x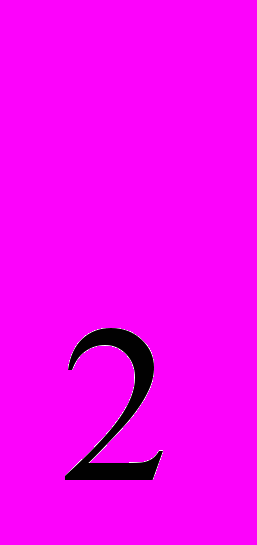 }]
}]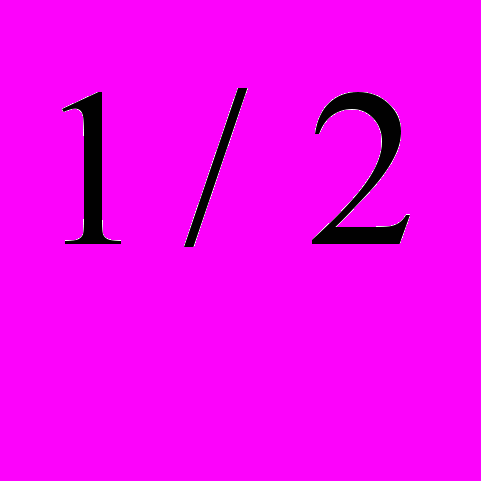 , где x
, где x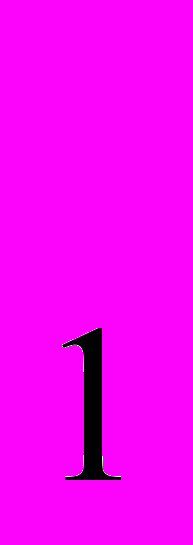 , x
, x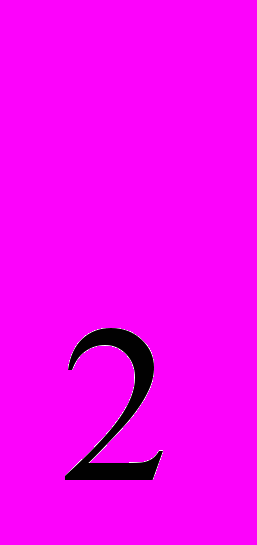 - затрачиваемые ресурсы. Цены факторов w
- затрачиваемые ресурсы. Цены факторов w 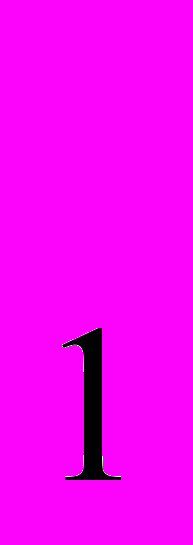 = w
= w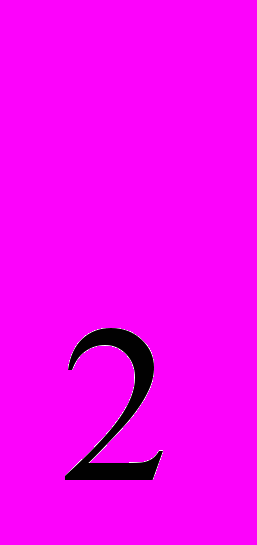 = 1. Найдите минимальные издержки производства Y ед. продукции.
= 1. Найдите минимальные издержки производства Y ед. продукции.
- Две фирмы А и В, производящие одну и ту же продукцию, имеют одинаковые производственные функции Y =
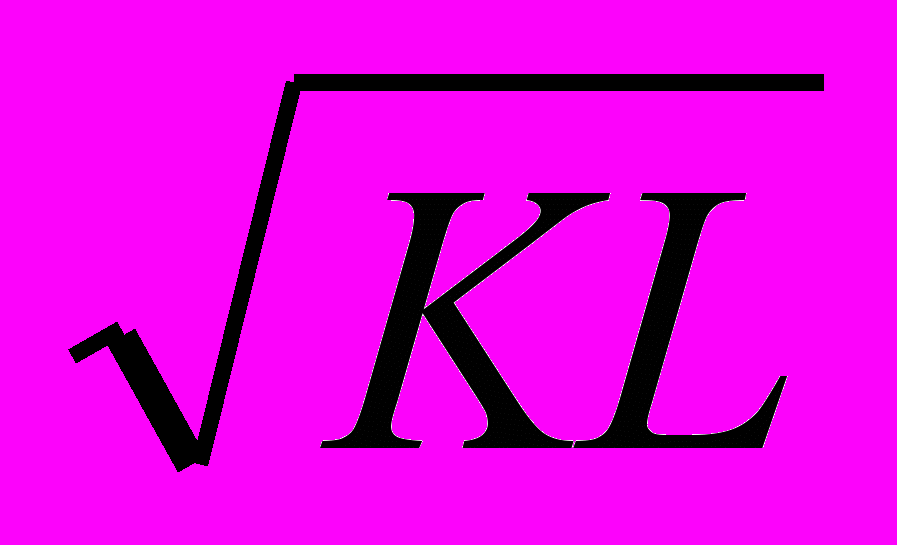 , где К – капитал, L – труд. Цена труда Р
, где К – капитал, L – труд. Цена труда Р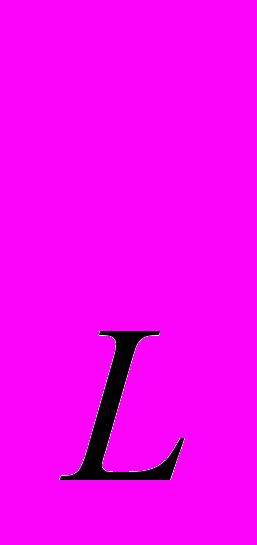 = 1, цена капитала Р
= 1, цена капитала Р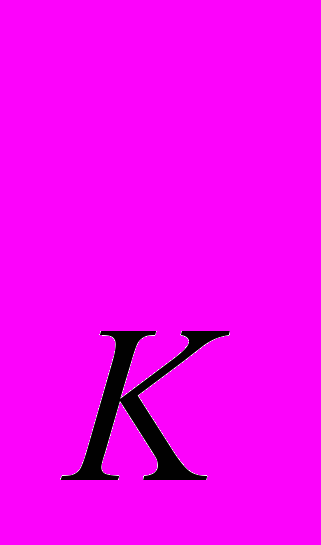 = 4. Каждая компания производит 40 ед. продукции в неделю. Компания А производит продукцию с минимальными издержками. Компания В затрачивает в 2 раза больше труда, чем А. Насколько общие издержки производства компании В больше, чем компании А? Покажите решение графически.
= 4. Каждая компания производит 40 ед. продукции в неделю. Компания А производит продукцию с минимальными издержками. Компания В затрачивает в 2 раза больше труда, чем А. Насколько общие издержки производства компании В больше, чем компании А? Покажите решение графически.
- Для получения 1 ед. сплава требуется 4 ед. меди и 3 ед. цинка. Цена меди равна 2, цена цинка равна 5. Запишите производственную функцию. Каковы средние издержки производства сплава?
- *Производство фруктового сока характеризуется функцией J = min{B, L}, где J – количество сока, B, L – затрачиваемые фрукты и труд. В свою очередь производство фруктов задано функцией B = S
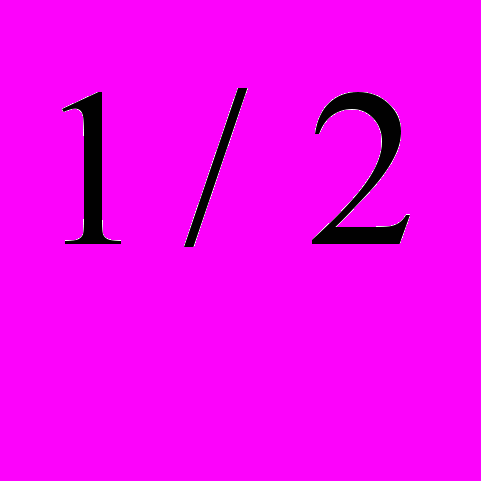 L
L 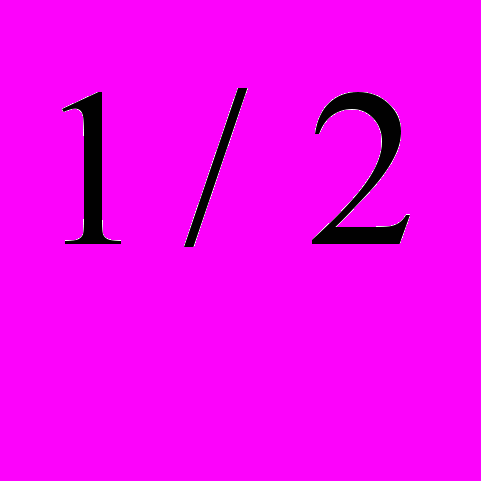 , где S – затраты семян, L – затраты труда. Если цена семян равна 1, цена труда равна 16, каковы средние издержки производства сока?
, где S – затраты семян, L – затраты труда. Если цена семян равна 1, цена труда равна 16, каковы средние издержки производства сока?
- Задана производственная функция f(L, M) = 4L
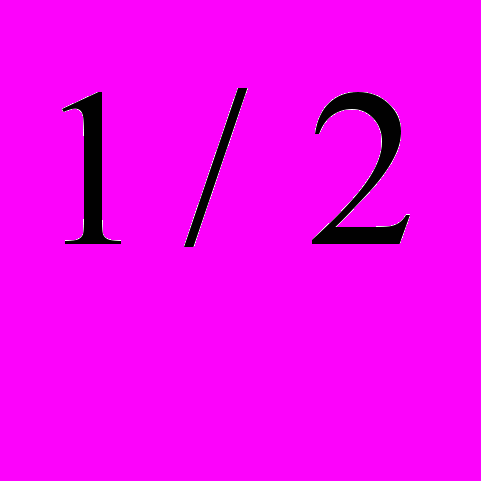 M
M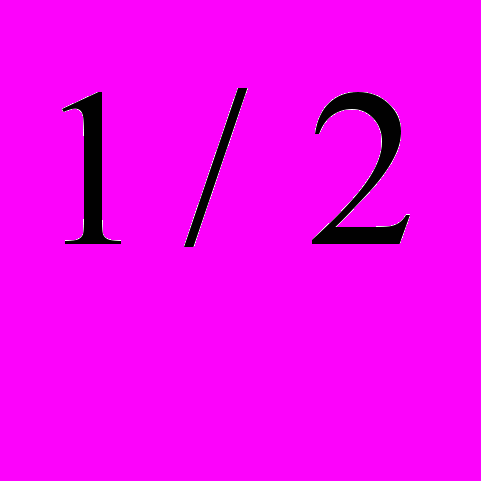 , где L – число единиц труда, М – число машин. Если Р
, где L – число единиц труда, М – число машин. Если Р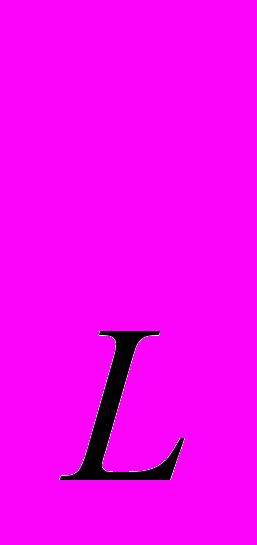 = 9, Р
= 9, Р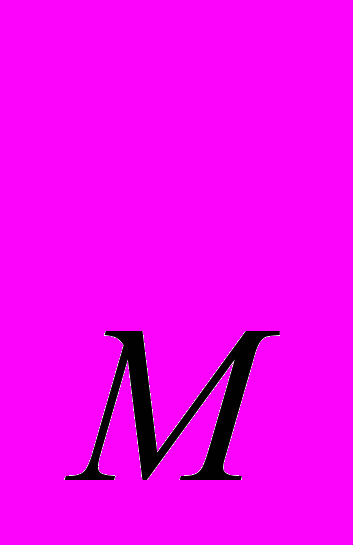 = 100, чему равны общие издержки производства 10 ед. продукции?
= 100, чему равны общие издержки производства 10 ед. продукции?
- Дана производственная функция y = max{10x
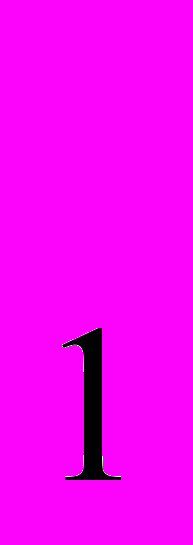 , 4x
, 4x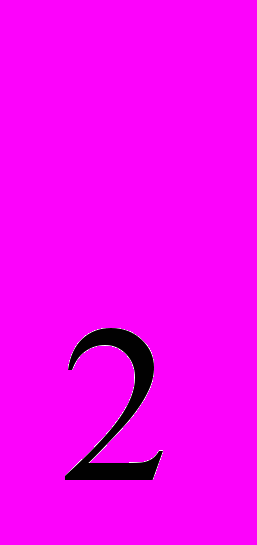 }, где x
}, где x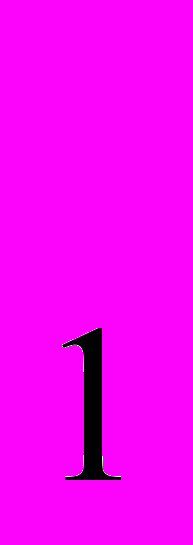 , x
, x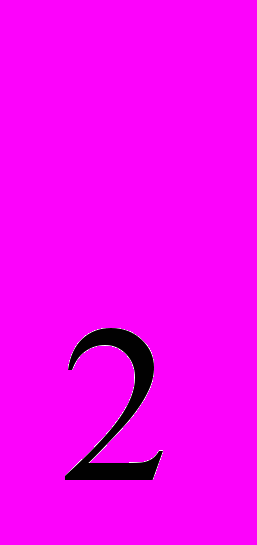 - количества используемых факторов. Найдите функцию затрат для выпуска продукции в количестве у, если Р
- количества используемых факторов. Найдите функцию затрат для выпуска продукции в количестве у, если Р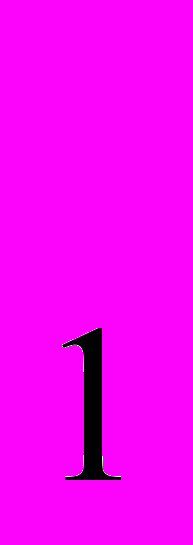 и Р
и Р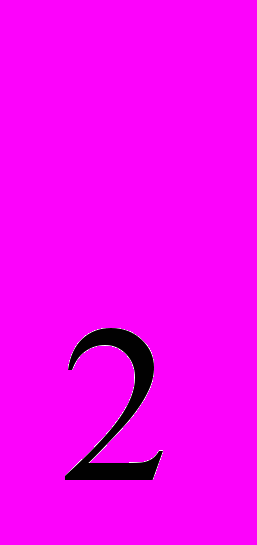 - цены факторов производства.
- цены факторов производства.
- Найдите функцию затрат для выпуска Y ед. продукции, если производственная функция Y = min{x
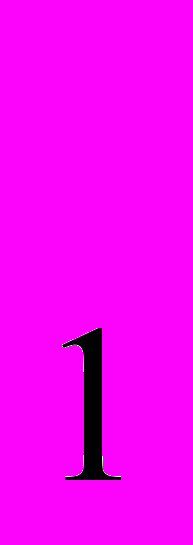 , x
, x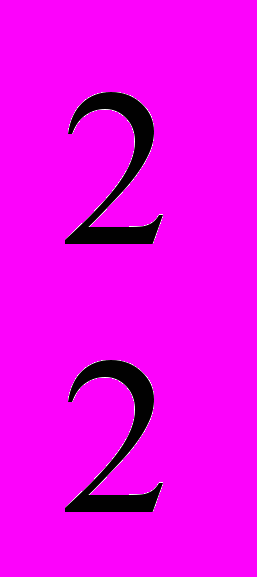 }, цены ресурсов соответственно w
}, цены ресурсов соответственно w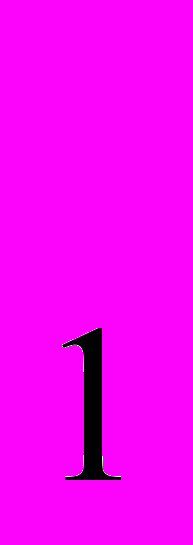 и w
и w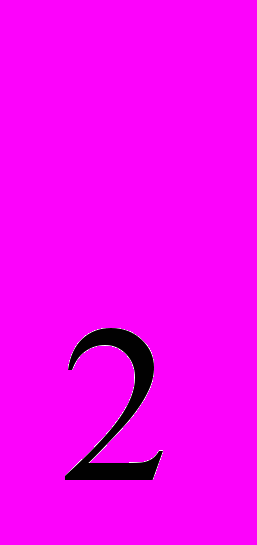 .
.
- Производственная функция конкурентной фирмы имеет вид у = 2х
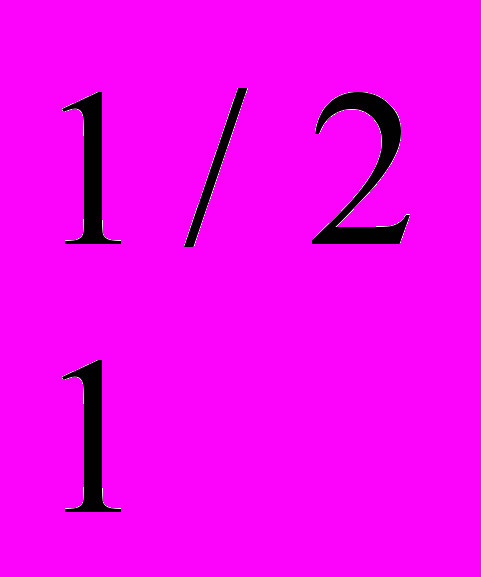 х
х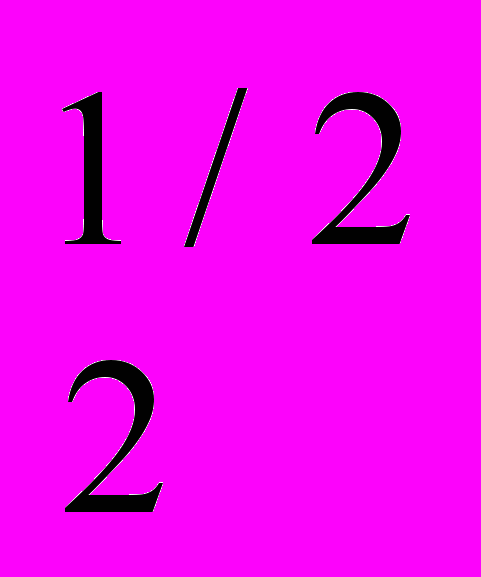 . Цены факторов производства Р
. Цены факторов производства Р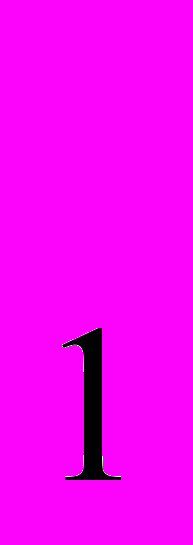 = 1, Р
= 1, Р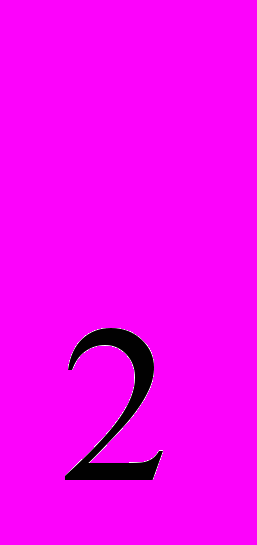 = 36. Фирма может покупать факторы производства в любом требуемом количестве по этим ценам. Найдите предельные издержки производства.
= 36. Фирма может покупать факторы производства в любом требуемом количестве по этим ценам. Найдите предельные издержки производства.
- Фирма имеет производственную функцию q = x
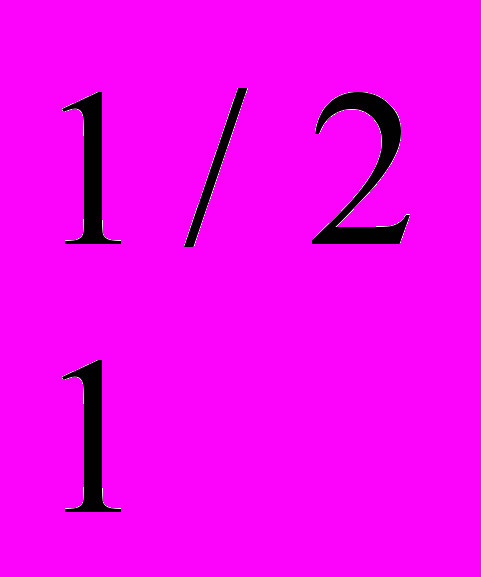 x
x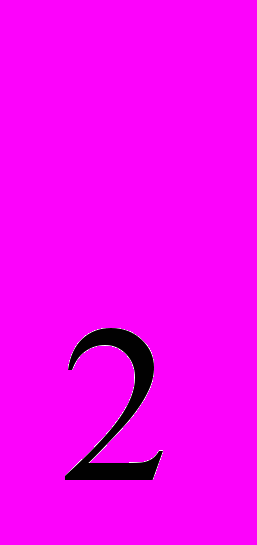 . В коротком периоде она должна использовать 50 ед. второго ресурса. Цена первого ресурса равна 250 ден. ед., цена второго ресурса равна 3 ден. ед. Найдите функцию предельных издержек фирмы.
. В коротком периоде она должна использовать 50 ед. второго ресурса. Цена первого ресурса равна 250 ден. ед., цена второго ресурса равна 3 ден. ед. Найдите функцию предельных издержек фирмы.
- Технология производства задана функцией Q = 0,1J
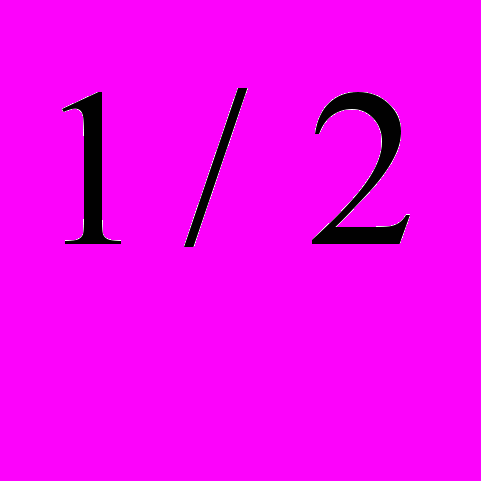 L
L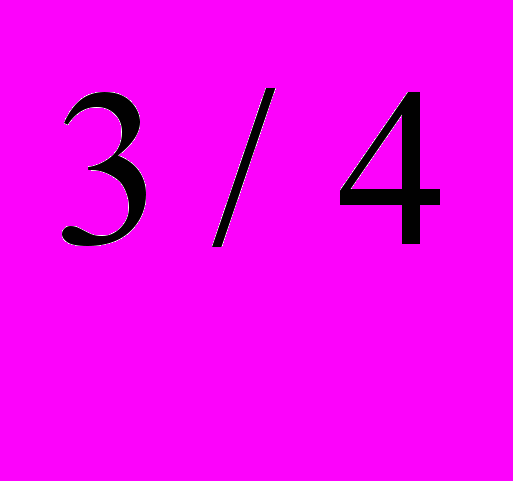 . Количество фактора вида J ограничено 100 ед., его цена Р
. Количество фактора вида J ограничено 100 ед., его цена Р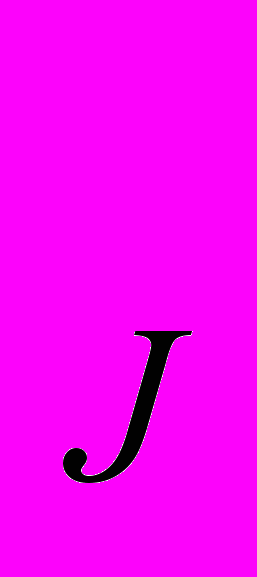 = 6. Цена труда Р
= 6. Цена труда Р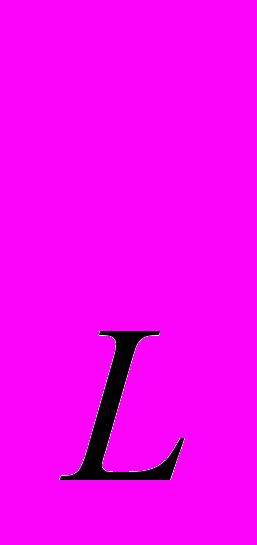 = 6. Найдите общие издержки производства 27 ед. продукции.
= 6. Найдите общие издержки производства 27 ед. продукции.
- Технология производства задана функцией q = min{M, L
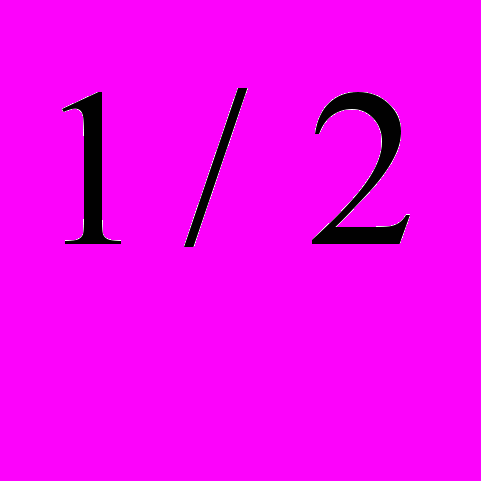 }. Цены ресурсов P
}. Цены ресурсов P = 2, Р
= 2, Р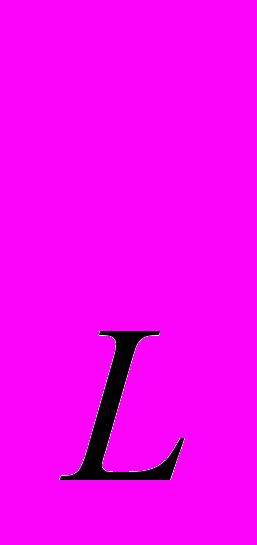 = 1.
= 1.
Найдите функцию долгосрочных предельных издержек фирмы.
- Производственная функция фирмы у = f(K, L) = KL
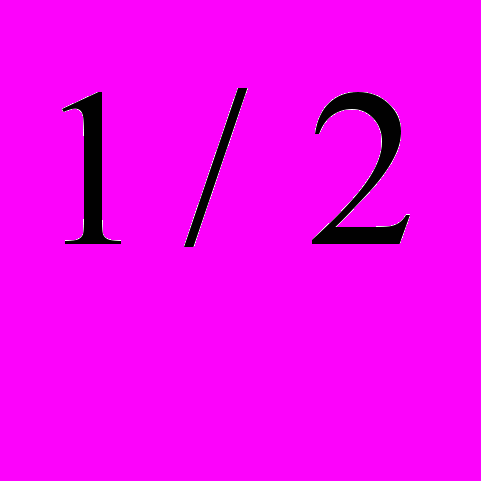 . Допустим, что Р
. Допустим, что Р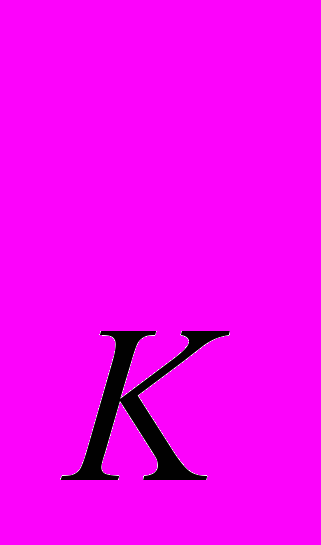 = r, P
= r, P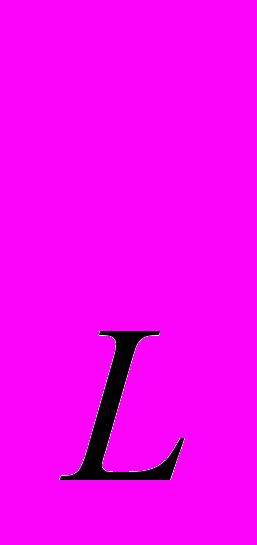 = w.
= w.
- Сколько труда наймет фирма, чтобы произвести у ед. продукции?
- Каково соотношение между спросом на труд и ценой капитала? Объясните.
- Фирма работает по технологии, отображаемой производственной функцией Q = L
 K
K . Цена труда составляет 8 ден. ед., а цена капитала – 16 ден. ед. Определите среднюю производительность труда при нахождении фирмы в состоянии равновесия.
. Цена труда составляет 8 ден. ед., а цена капитала – 16 ден. ед. Определите среднюю производительность труда при нахождении фирмы в состоянии равновесия.
- Производственная функция фирмы имеет вид Q =
 . Ставка заработной платы равна 3 ден. ед., а арендная плата за оборудование составляет 2 ден. ед. На основании этих данных постройте линию оптимального роста производства при следующих уровнях выпуска: Q
. Ставка заработной платы равна 3 ден. ед., а арендная плата за оборудование составляет 2 ден. ед. На основании этих данных постройте линию оптимального роста производства при следующих уровнях выпуска: Q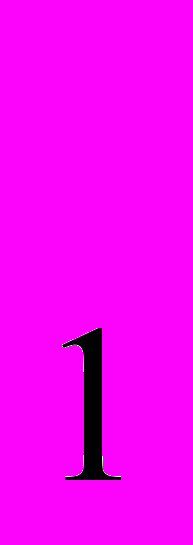 = 1; Q
= 1; Q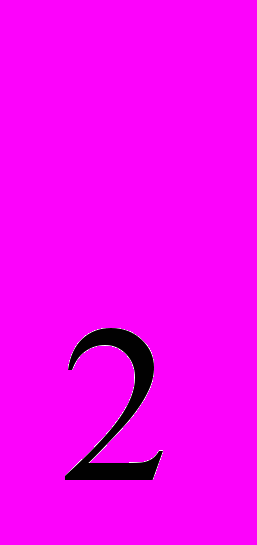 = 2; Q
= 2; Q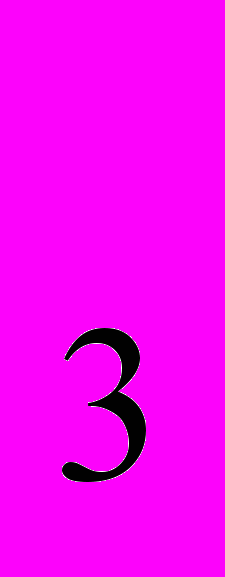 = 3. Рассчитайте уровни затрат на производство в точках оптимума производителя.
= 3. Рассчитайте уровни затрат на производство в точках оптимума производителя.
- Производственная функция фирмы имеет вид Q =
 . Затраты фирмы составляют 64 ден. ед. В начальный период ставка заработной платы равна 4 ден. ед., а ставка арендной платы – 8 ден. ед. В дальнейшем ставка арендной платы сократилась вдвое. Определите эффект замены и эффект выпуска.
. Затраты фирмы составляют 64 ден. ед. В начальный период ставка заработной платы равна 4 ден. ед., а ставка арендной платы – 8 ден. ед. В дальнейшем ставка арендной платы сократилась вдвое. Определите эффект замены и эффект выпуска.
- Постройте кривые общего, среднего и предельного продукта труда. Исходные данные:
Затраты труда | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| Объем выпуска | 10 | 30 | 60 | 80 | 95 | 108 | 112 | 112 | 108 | 100 |
