Гаврилов Андрей Владимирович, доцент нгавт 4 закон

Вид материала

Закон

Содержание 4. Задачи для самостоятельного решения

Подобный материал:

• Андрей Владимирович Курпатов Средство от депрессии, 2074.53kb.
• Ученого Совета Уральского государственного университета имени А. М. Горького программа, 481.82kb.
• Корляков Андрей Владимирович, к ф. м н, доцент область применения категории слушателей, 256.81kb.
• Фрагменты истории земской статистики, 182.52kb.
• Самостоятельная работа : 60 час. Преподаватели: доцент Наследов Андрей Дмитриевич,, 1089.06kb.
• Федеральный Закон «Об основах туристской деятельности в рф», 221.17kb.
• Методические указания по выполнению контрольной работы 6 Рекомендации по выполнению, 223.73kb.
• Программа курса система государственных закупок Преподаватель: Иванов Андрей Евгеньевич,, 179.08kb.
• Программа курса разработка управленческих решений Преподаватель: Иванов Андрей Евгеньевич,, 143.23kb.
• Родькина Елена Федоровна и председатель профсоюзного комитета Сисейкин Андрей Владимирович., 162.91kb.

3. Наблюдения

(3 балла за каждое выполненное задание)

Сейчас лето, пора школьных каникул. Можно не торопиться и оглянуться вокруг себя. Уверяем вас, что с высоты своих знаний, полученных в течение учебного года, вы увидите мир совершенно другими глазами.

1. Посадите на палочку или травинку каплю воды. Встаньте спиной к Солнцу и осторожно поднимайте каплю. Когда лучи Солнца образуют с направлением глаз угол около 42⁰, прозрачная капля вдруг вспыхнет чрезвычайно чистым по тону цветом. Если осторожно перемещать каплю по дуге окружности, можно увидеть все цвета радуги. Все цвета радуги – это сколько? И какие?
   
2. Понаблюдайте, при каком соотношении дневной и ночной температур воздуха утренняя роса на траве обильнее: при маленькой или большой разнице температур? Как можно объяснить ваше наблюдение?
   
3. Капелька росы на травинке или листике может служить маленьким микроскопом. Его очень просто сделать самому. Для этого нужно взять плотную бумагу, проколоть в ней иголкой дырочку и на нее аккуратно посадить каплю воды. Если теперь поднести капельку очень близко к газетному тексту, то вы увидите сильно увеличенную букву. Чем меньше капелька, тем больше увеличение. С помощью такого микроскопа можно рассматривать любые очень мелкие предметы. Кстати, в первом микроскопе, изобретенном Левенгуком, все было сделано именно так, только капелька была стеклянной. А как определить увеличение такого микроскопа?
   
4. Понаблюдайте за движением крыльев и положением лапок птиц во время взлета, полета, парения в воздухе и посадке. Что обеспечивает птице возможность держаться в воздухе? При всех ли погодных условиях возможно парение птицы? Если есть такая возможность, понаблюдайте за положением перьев в крыле птицы во время взлета и во время посадки. Сможете ли вы объяснить, почему крыло птицы состоит из отдельных перьев, а не является сплошной перепонкой?
   

5. Понаблюдайте, какого цвета тени отбрасывают цветные воздушные шарики в ясный солнечный день? Могут ли тени иметь цвет, и как объяснить ваши наблюдения?

6. В вашем отряде или в учебной группе обязательно найдется человек, который носит очки. Попытайтесь, глядя на этого человека в очках, определить, каким дефектом зрения он страдает: дальнозоркостью или близорукостью. По каким признакам вы смогли это установить?

7. Иногда может «ударить током», если просто пройтись по ковру. Може­те ли вы более подробно объяснить, что именно происходит? Почему, на­пример, «бьет током», когда вы идете по ковру, но ничего не слу­чается, если вы стоите на нем? Почему эти эффекты зависят от вре­мени года?

4. Задачи для самостоятельного решения

Задача 4.1. Винни-Пух и Пятачок одновремен­но отправились в гости друг к другу. Но поскольку Винни-Пух всю дорогу сочинял очередную «шумелку», а Пя­тачок считал пролетавших галок, они не заметили друг друга при встрече. После встречи Пятачок подошел к дому Винни-Пуха через четыре ми­нуты, а Винии-Пух подошел к дому Пятачка через одну минуту. Сколько минут был в пути каждый из них? (2 балла)


Задача 4.2. Однажды Красная Шапочка решила навестить бабушку. Путь ей предстоял не близкий. Сначала она треть пути неспешно шла по дорожке со скоростью υ. Затем, проголодавшись, села на пенек и съела несколько пирожков. Потратив на еду много времени, девочка загрустила, так как уже начало темнеть. Но тут из леса выбежал Серый Волк. Он любезно согласился подвезти её на себе до бабушки со скоростью 3υ. В результате получилось, что на всё путешествие девочка потратила столько же времени, сколько потребовалось бы при движении с постоянной скоростью υ. Сколько пирожков скушала Красная Шапочка во время отдыха на пеньке? На каждый пирожок она затрачивала одну девятую времени всего своего путешествия. (2 балла)


Задача 4.3. Ахиллес догоняет черепаху на прямой дороге. В начальный момент расстояние между ними 1 км. Начальные скорости Ахиллеса и черепахи равны 10 м/с и 10 см/с соответственно. Через каждую секунду их скорости скачком изменяются. Скорость Ахиллеса убывает на 1% от своего текущего значения, а скорость черепахи возрастает на 1% от своего текущего значения. На какое минимальное расстояние сможет приблизиться к черепахе Ахиллес и через сколько времени от начала погони? (3 балла)


Задача 4.4. Машина скорой помощи, спешащая к боль­ному с сердечным приступом, стоит у самого железнодорожного переезда, который станет свободным только через t_о=29 с из-за прохо­дящего мимо поезда. Через какое минималь­ное время, считая от момента освобождения поездом переезда, врач может прибыть к боль­ному? Расстояние от переезда до больного l =330 м, масса машины m = 1,8 т. Счи­тать, что максимальные значения силы тяги и силы торможения у машины не зависят от ско­рости, численно одинаковы и равны F = 1,8 кН. (3 балла)


Задача 4.5. За директором завода каждое утро в 8 часов приезжает машина и отвозит директора на завод, расположенный в нескольких километрах от его дома. Однажды директор вышел из дома в 7 часов и пошел по шоссе по направлению к заводу. Вскоре он встретил свою машину, сел в нее и приехал на завод на 12 минут раньше обычного. В котором часу директор встретил свою машину. (3 балла)

Задача 4.6. Два зайца состязаются в беге. Вначале стартовал первый заяц и бежал с постоянным ускорением. Второй заяц замеш­кался на старте на время х, но бежал с большим ускорением и догнал первого, причем в этот момент его скорость была в 2 раза больше, чем у первого зайца. Через какое время после выстрела стартового пистолета это произошло? (3 балла)


Задача 4.7. Группа индейцев племени Хитачи, двигаясь по тропинке со скоростью 3,6 км/ч, растянулась на 240 м. Вдруг замыкающий услышал звуки шагов бледнолицых. С этой вестью он посылает самого быстроногого индейца к вождю, который находится впереди группы. Индеец бежит со скоростью 7 м/с и, мгновенно выполнив приказ, возвращается к замыкающему группы с той же скоростью. Сколько времени индеец потратил на исполнение приказа? (3 балла)


Задача 4.8. Заяц убегает от Волка по прямой, двигаясь равномерно. В начальный момент времени расстояние между Зайцем и Волком s = 36 м, а скорость Волка v₀ = 14 м/с. Волк устает и через каждые Δt = 10 с (в моменты времени Δt, 2Δt, ЗΔt…, считая от начала движения) уменьшает свою скорость на Δv = 1 м/с. С какой скоростью v должен бежать Заяц, чтобы Волк его не поймал? (4 балла)




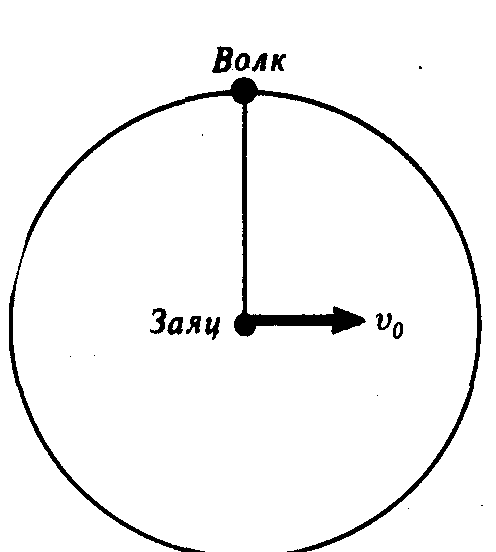
Задача 4.9. На горизонтальной поверхности льда на­рисована окружность радиусом R = 10 м. В цен­тре окружности находится заяц, а волк - на окружности (рис.). Заяц двигается по прямой с постоянной ско­ростью v₀ = 2 м/с. Волк должен двигаться по окружности так, чтобы расстояние между ним и зайцем все время оставалось равным началь­ному. До какой точки окружности волк сможет добраться, не нарушая правил игры? Коэф­фициент трения на льду μ = 0,06. Волк дви­жется строго по окружности, не подпрыгивая. (4 балла)


Задача 4.10. Муха заметила на столе каплю меда, пролетая точно над ней горизонтально со скоростью V₀ на высоте Н. Сколько времени необходимо мухе, чтобы как можно быстрее добраться до меда, если в любом направлении она может развивать ускорение а? (4 балла)


Задача 4.11. Неопознанный летающий объект (НЛО), который висел над Землей, начал двигаться и в течение 10 с летел по прямой с постоянным ускорением 100 м/с². Затем его ускорение упало до нуля, и еще столько же времени он летел по прямой с постоянной скоростью. Найти перемещение НЛО за 20 с и его среднюю скорость на первой половине пути. (4 балла)


Задача 4.12. Рассерженный бизнесмен вышел из налоговой инспекции, сел в джип, хлопнул дверью и дал полный газ. Дорога была ледяная, ну и колеса стали крутиться с постоянной скоростью n = 5 оборотов/с. Через сорок секунд гнев прошел. Где в этот момент окажется джип? Считайте, что диаметр колес d = 0.637 м, коэффициент трения скольжения резины по льду k = 0.051. (4 балла)




Задача 4.13. Однажды барону Мюнхгаузену понадобилось втащить на возвышенность ящик с пушечными ядрами. К его удивлению, скорость движения не изменилась после того, как ящик прошел край склона и стал двигаться горизонтально. Каков коэффициент трения между ящиком и землей? Мощность двигателя все время оставалась неизменной. Склон образует угол 45° с горизонтом. Трением между тросом и дорогой можно пренебречь. (4 балла)


Задача 4.14. Корабль злобных пришельцев из космоса представляет собой цилиндр высотой 100 м и диаметром 100 м, стоящий вертикально на плоской поверхности. Единственной уязвимой точкой корабля является маленький люк, находящийся в центре верхнего круга, да и то только в том случае, если попавший в него снаряд имеет скорость не меньше 20 м/с и прилетает под углом к вертикали не более чем 45° (данные получены из источника, заслуживающего полного доверия). В нашем распоряжении маленькая пушка, находящаяся на уровне земли. При какой минимальной скорости вылета снаряда из ствола пушки мы можем поразить корабль? Стрелять можно под любым углом и из любой точки на поверхности земли. (5 баллов)




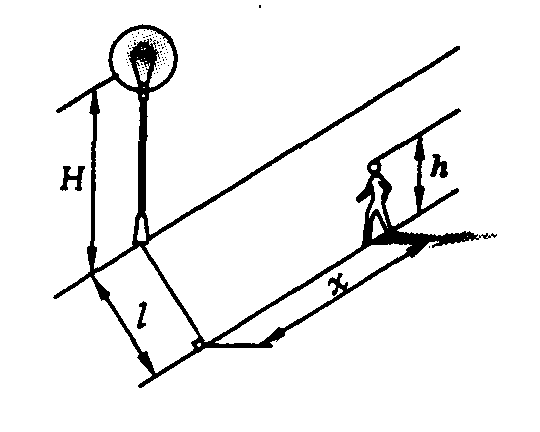
Задача 4.15. Поздним весенним вече­ром молодой человек ростом h возвращается домой по краю горизонтального пря­мого тротуара с постоянной скоростью v (рис.). На расстоянии l от края тротуа­ра стоит фонарный столб, на котором горит фонарь на вы­соте Н от поверхности зем­ли. Нарисуйте график зави­симости скорости тени голо­вы молодого человека от рас­стояния. (5 баллов)


Задача 4.16. Лягушка массой m сидит на листе кувшинки, масса которого в 3 раза меньше массы лягушки. С какой минимальной скоростью должна прыгнуть лягушка, чтобы перелететь этот лист, длина которого L? (5 баллов)


Задача 4.17. На гладкой горизонтальной поверхности расположены доски массы m₁. На первой доске сидит заяц массы m₂, который может прыгать с горизонтальной скоростью v₀ относительно доски. Вертикальную составляющую скорости он подбирает так, чтобы попасть на следующую доску. Заяц начинает перемещаться отдельными прыжками с первой доски на вторую, со второй на третью и т. д., при этом время отдыха на каждой доске равно времени предыдущего прыжка. Определите, какой максимальной средней скорости перемещения в горизонтальном направлении может достичь заяц, если число досок можно считать неограниченным. Трение между лапами зайца и досками очень велико. (5 баллов)


Задача 4.18. Камень массой М лежит на горизонтальной поверхности на расстоянии L от края пропасти. К камню прикреплена легкая нерастяжимая веревка, перекинутая через гладкий выступ на краю пропасти. Вверх по веревке лезет обезьяна массой m. С каким постоянным ускорением (относительно земли) она должна двигаться, чтобы успеть подняться рань­ше, чем начнет падать камень? Начальное расстояние обезьяны от выступа равно Н(Н <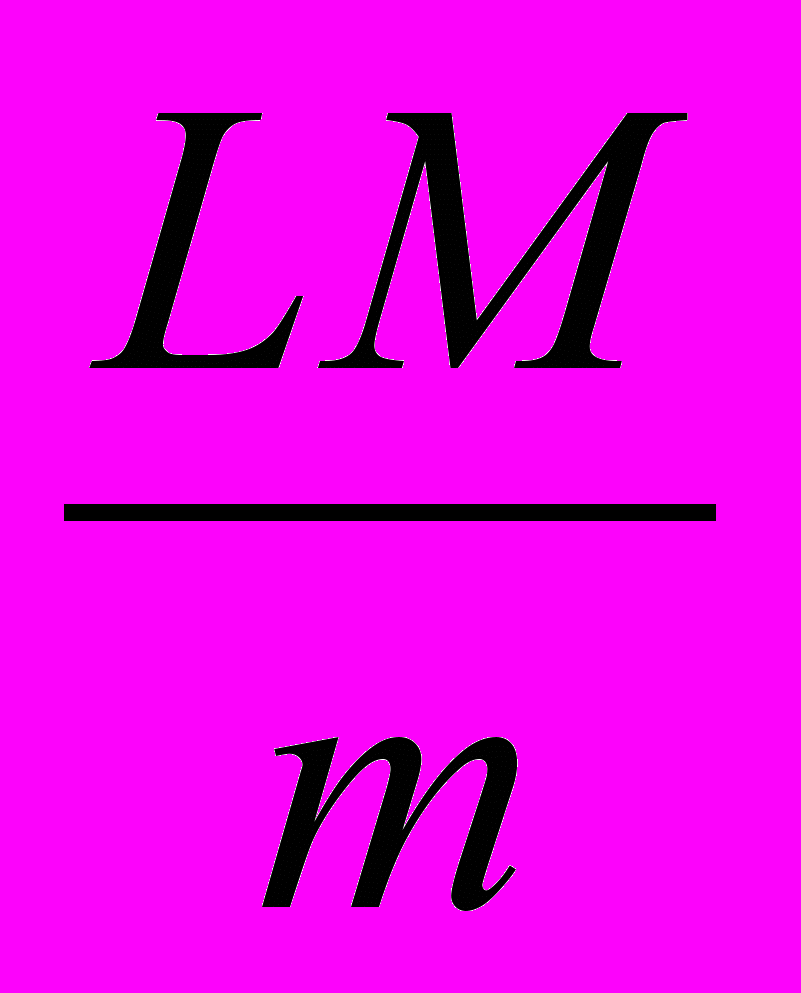). Коэффициент трения камня о поверхность равен μ, причем μ М < m. (5 баллов)


Задача 4.19. Обезьяна массой m висит на нижнем конце длинной лианы на высоте h над землей. Кусок лианы массой М обрывается. Обезьяна начинает карабкаться вверх, оста­ваясь все время на высоте А. Через какое время лиана коснется земли? (5 баллов)


З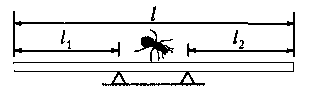адача 4.20. Муравей находится на середине соломинки длиной l (рис.). Соломинка лежит на двух опорах. Левая опора находится на расстоянии l₁ = 5l /12 от левого конца соломинки, а правая - на расстоянии /₂ = 13l /28 от её правого конца. На какие максимальные расстояния от середины соломинки влево и вправо может отползти муравей, чтобы соломинка при этом не перевернулась. Масса муравья в 6 раз меньше массы соломинки, а его размеры много меньше длины соломинки. Соломинку считать однородным стержнем. (5 баллов)


Задача 4.21. Для участия в Техничес­кой Олимпиаде Баренцева моря по подводному плава­нию Чебурашка изготовил радиоуправляемую модель Крокодила Гены. Однако мо­дель оказалась слишком тяжелой для своего объема - тонула в воде. Для поддержа­ния ее на плаву Чебурашка прикрепил к ней несколько герметичных полиэтиленовых пакетов с воздухом. Оказа­лось, что в соленом Баренце­вом море (плотность соленой воды ρ₁ = 1050 кг/м³) модель при погружении на глубину до h₁ = 7 м всплывает, а при погружении на большую глу­бину тонет. А в пресновод­ной дельте реки Печоры (плотность пресной воды ρ₂= 1000 кг/м³) аналогич­ная критическая глубина погружения составляет всего h₂ = 1 м. Найдите плотность модели Крокодила Гены. (5 баллов)