Geum.ru

Гаврилов Андрей Владимирович, доцент нгавт 4 закон

Вид материалаЗакон
Примеры решения задач
Задача №3.
Подобный материал:
1   2   3   4   5   6   7   8   9   10

Примеры решения задач


З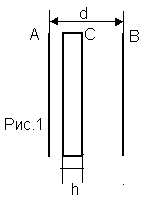адача №1. Две металлические пластины А и В находятся на расстоянии d = 10 мм друг от друга. Между ними находится металлическая пластина С толщиной h = 2 мм (рис.1). Потенциал пластины А = 50В, а пластины В = - 60В. Как изменится энергия конденсатора, если вынуть пластину С. Площадь поверхности пластины С , параллельной пластинам А и В равна 10 см2.

Решение. Напряженность электрического поля внутри проводника равна нулю, поэтому при удалении металлической пластины из поля в области пространства, ранее занятой пластиной, появиться электрическое поле, энергия которого W. Найдем связь между энергией поля, его напряженностью и объемом.

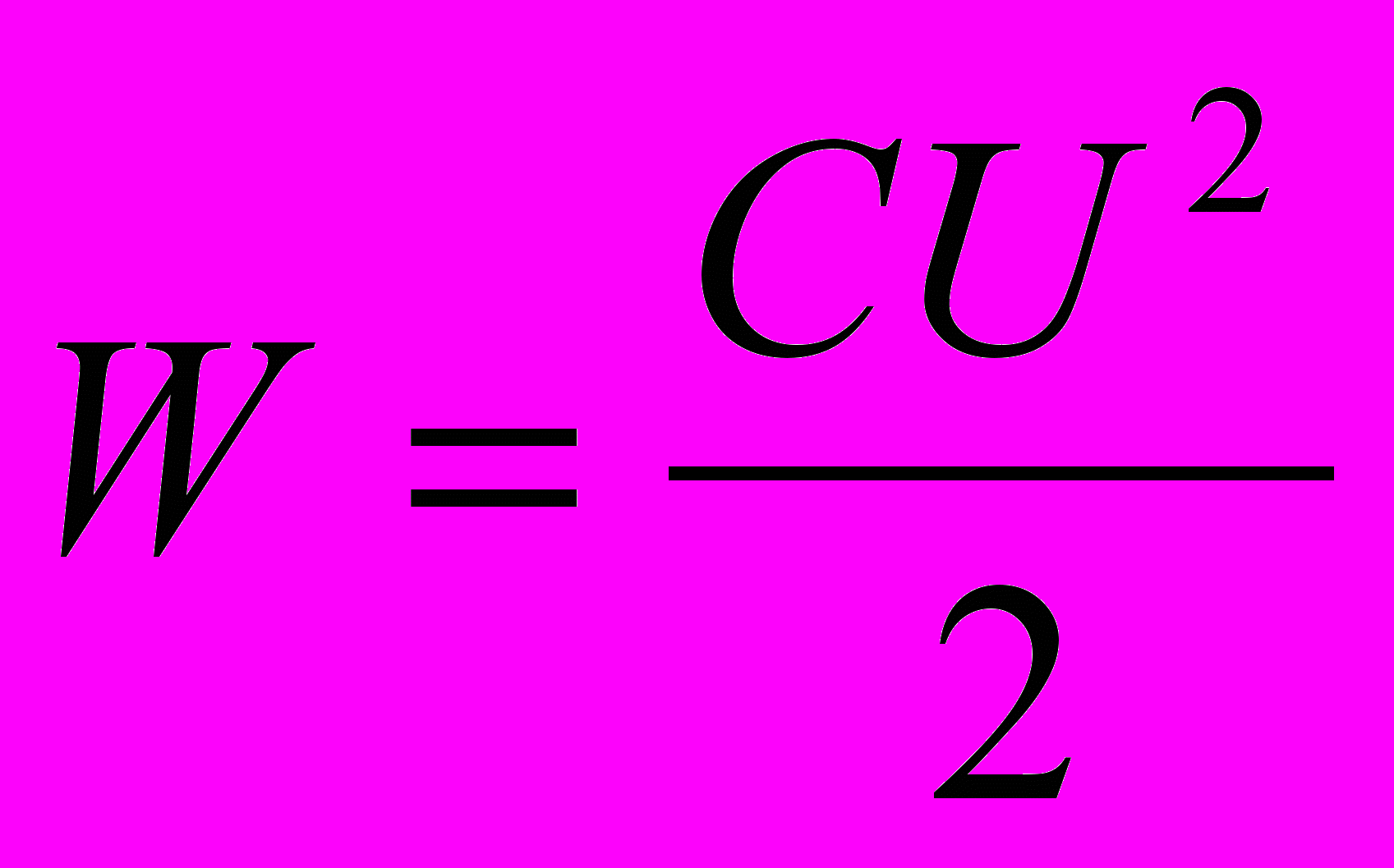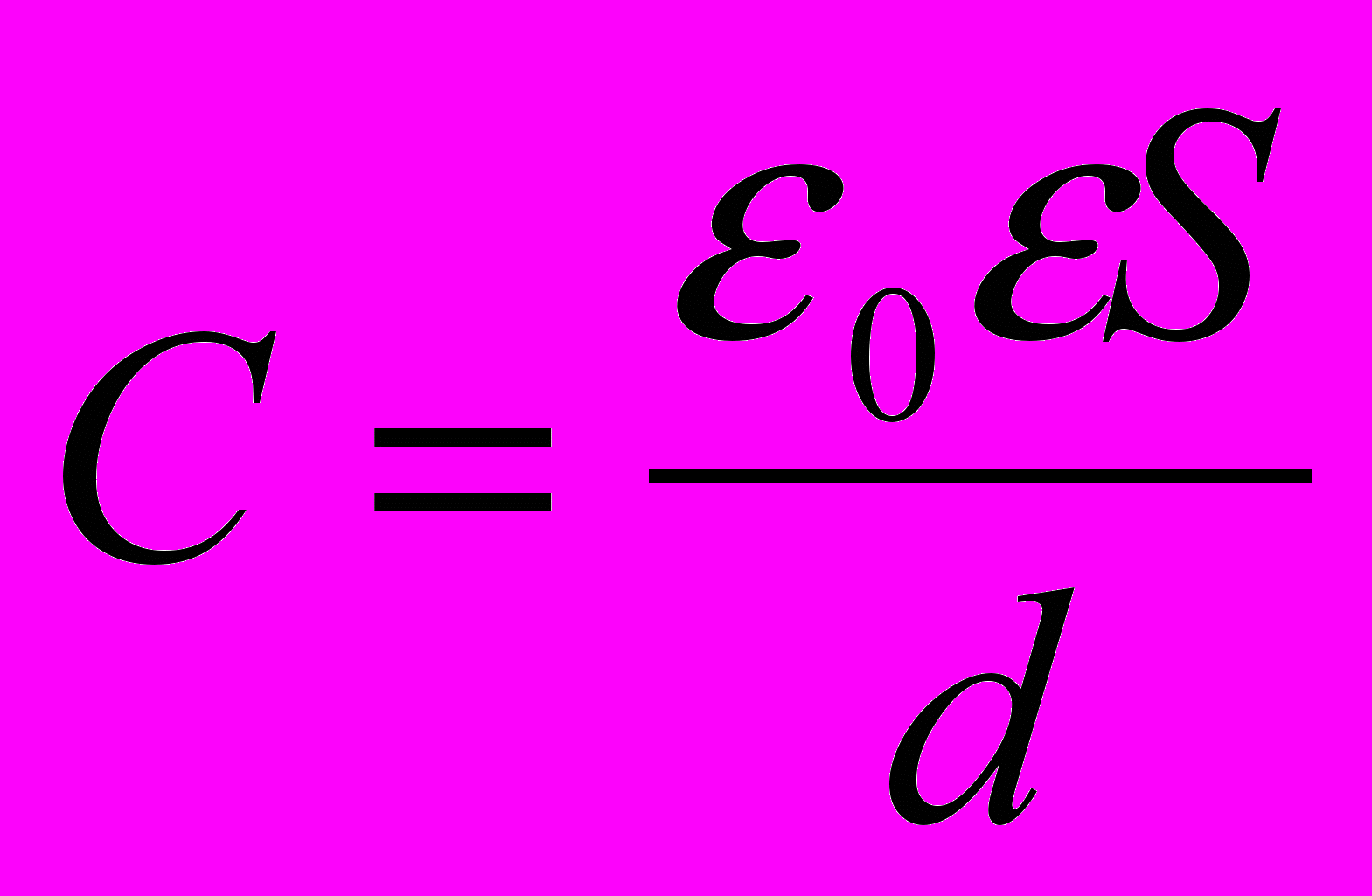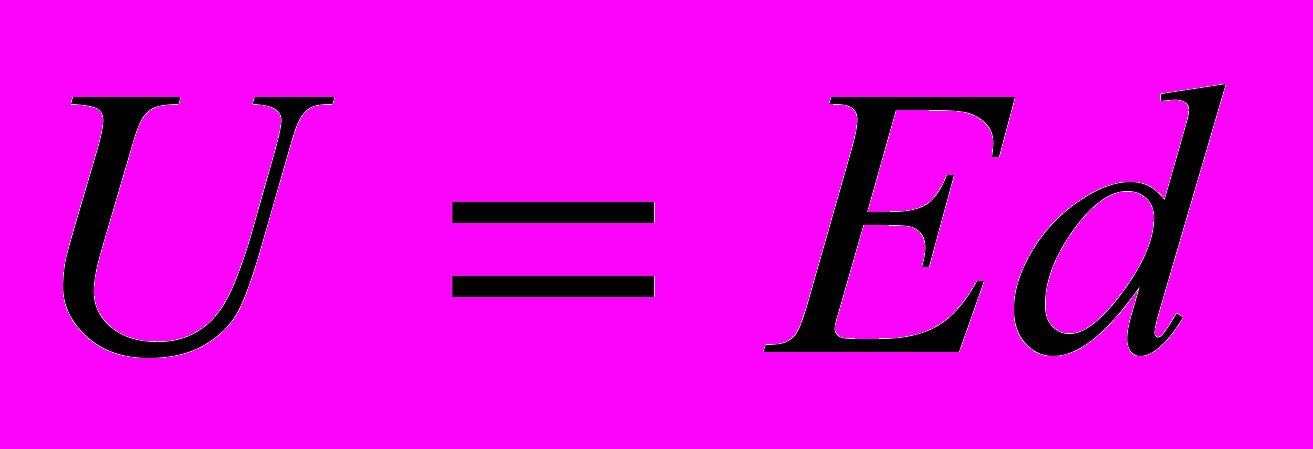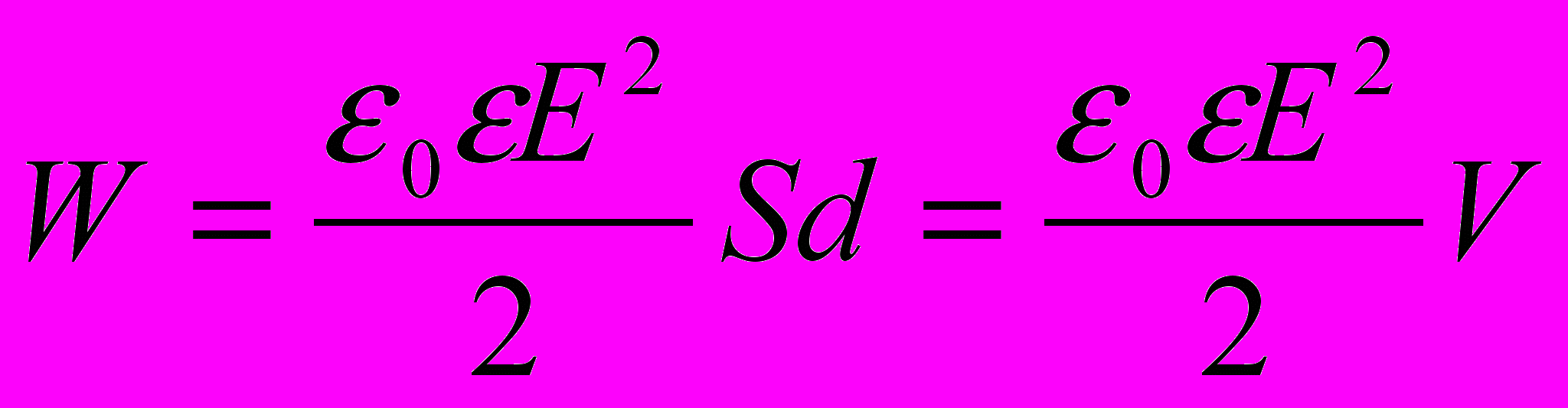; ; ; , где V – объем пластины. Так как в условии задачи не оговаривается вид диэлектрика, будем считать, что между пластинами А и В находится воздух или вакуум ε = 1.

С учетом принятых обозначений: 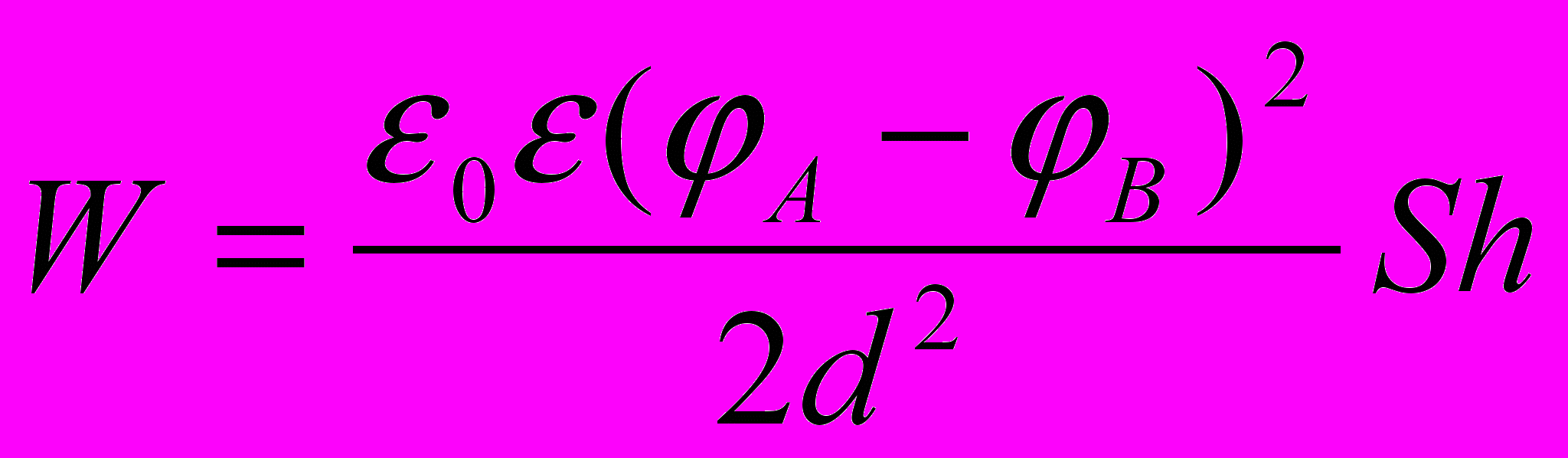= 2,68*10-7 Дж.

З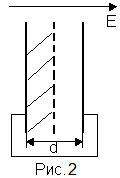адача №2. Две соединенные проводником пластины плоского конденсатора площадью S каждая, находятся на расстоянии d друг от друга (рис.1) во внешнем однородном электрическом поле, напряженность которого 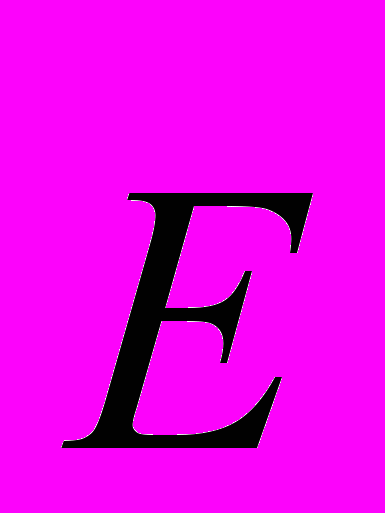. Какую работу надо совершить, чтобы медленно сблизить пластины до расстояния d/2?

Решение. Так как пластины замкнуты между собой проводником, то их потенциалы равны, а значит, равна нулю напряженность поля в пространстве между пластинами. После сближения пластин в области пространства, заштрихованной на рис.2, появится электрическое поле, энергия которого равна: . Исходя из закона сохранения энергии, можно записать: A=W.

Ответ: .

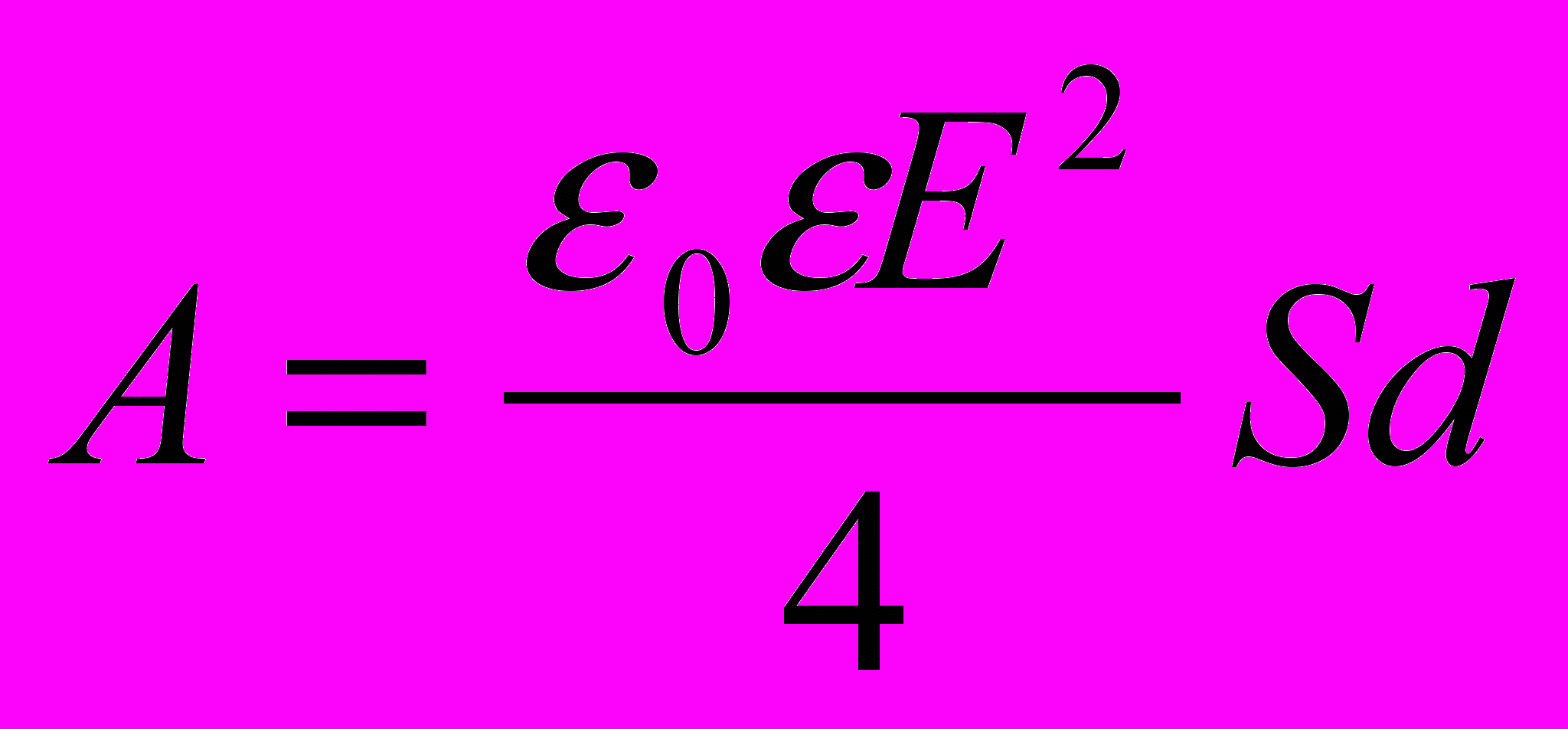З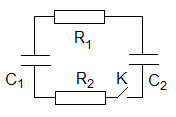адача №3. В схеме, изображенной на рисунке 1, найдите количество теплоты, выделившееся в каждом резисторе при замыкании ключа. Конденсатор, емкостью С1 заряжен до напряжения U1, а конденсатор емкостью С2 – до напряжения U2. Сопротивления резисторов R1 и R2.

Решение. Для рассматриваемой системы закон сохранения энергии имеет вид

0 = ΔW + Q или Q = Wнач - Wкон

Начальная энергия заряженных конденсаторов

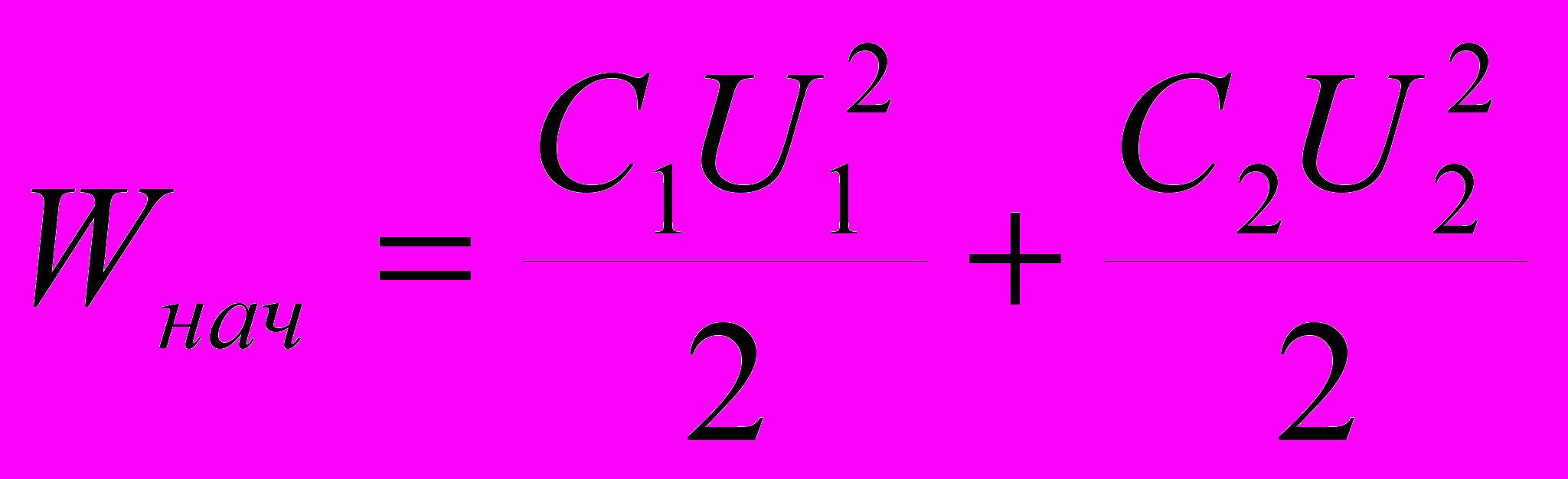
Для определения энергии системы в конечном состоянии воспользуемся законом сохранения заряда: суммарный заряд конденсаторов после замыкания ключа не изменяется. При соединении конденсаторов одноименно заряженными обкладками заряд равен 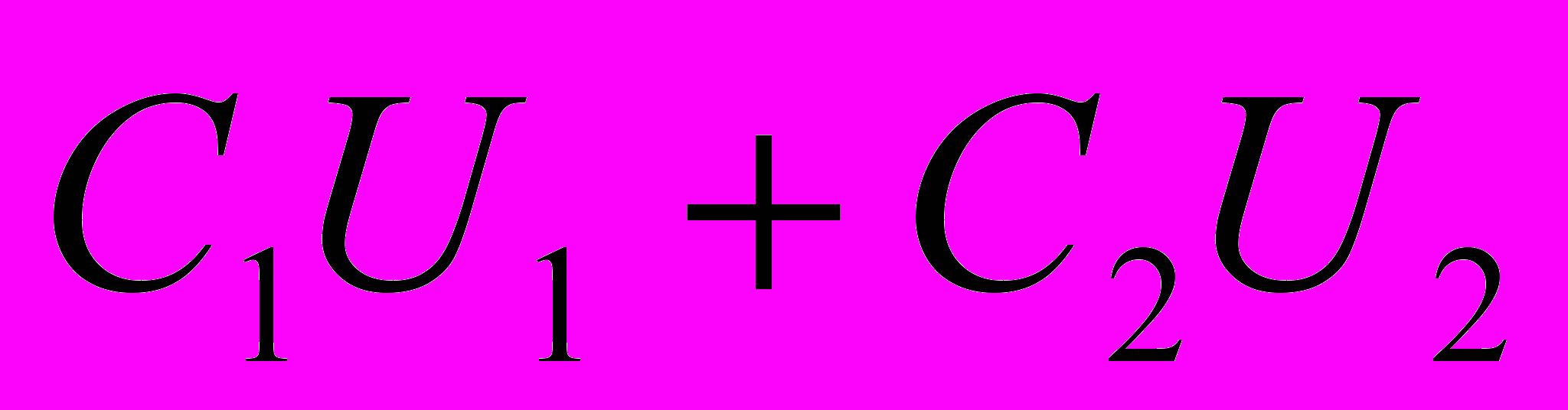. При соединении конденсаторов разноименно заряженными обкладками 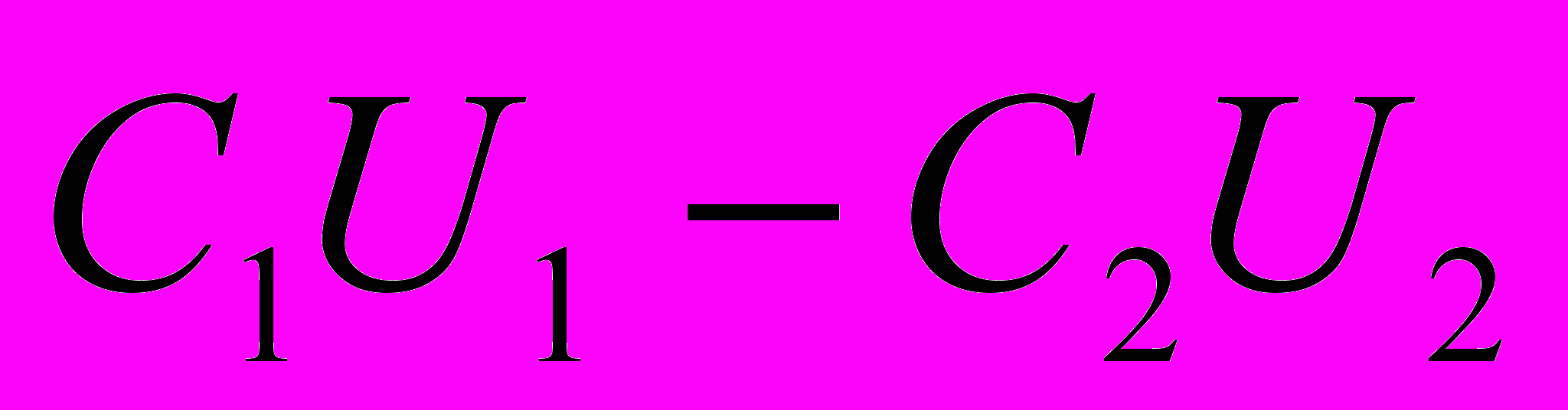. Этим зарядом после замыкания ключа К оказывается заряжен конденсатор емкостью 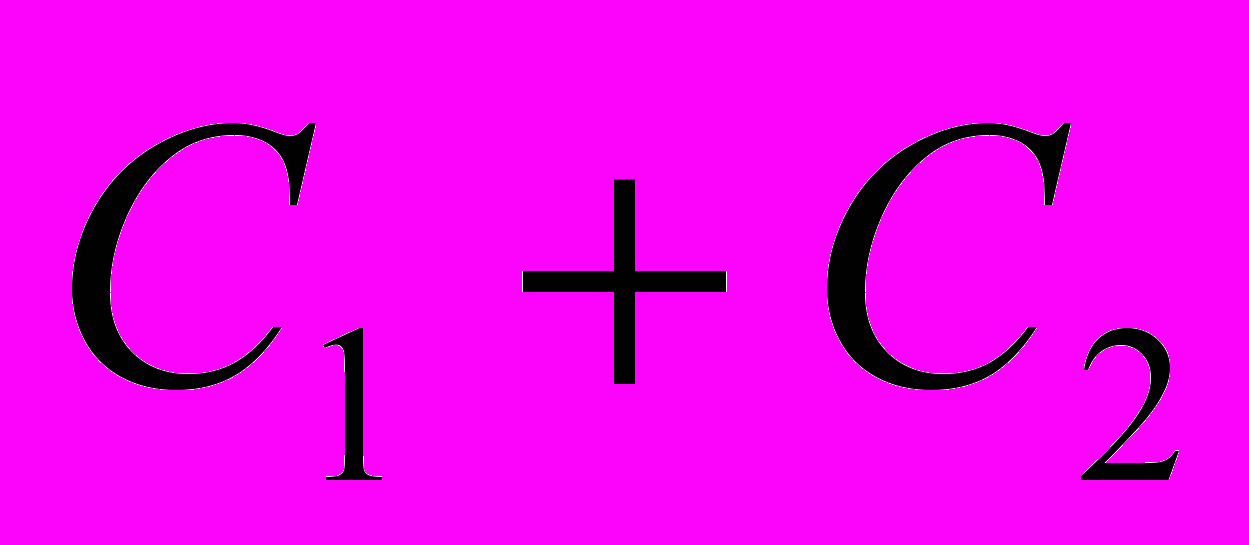так как конденсаторы соединены параллельно. Таким образом

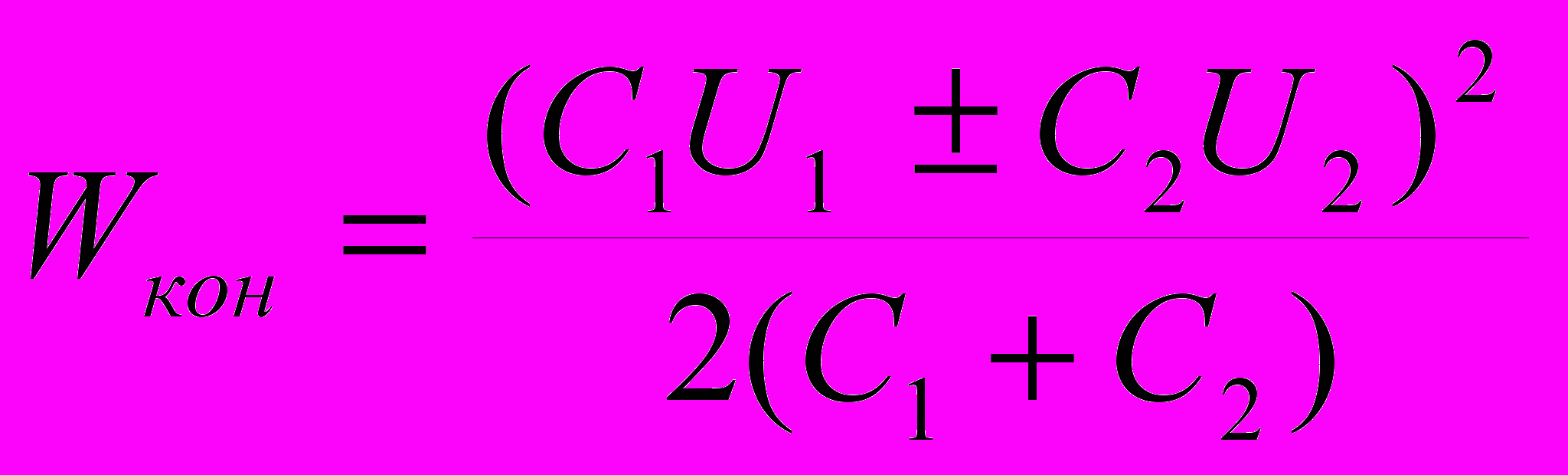и Q = Wнач - Wкон = 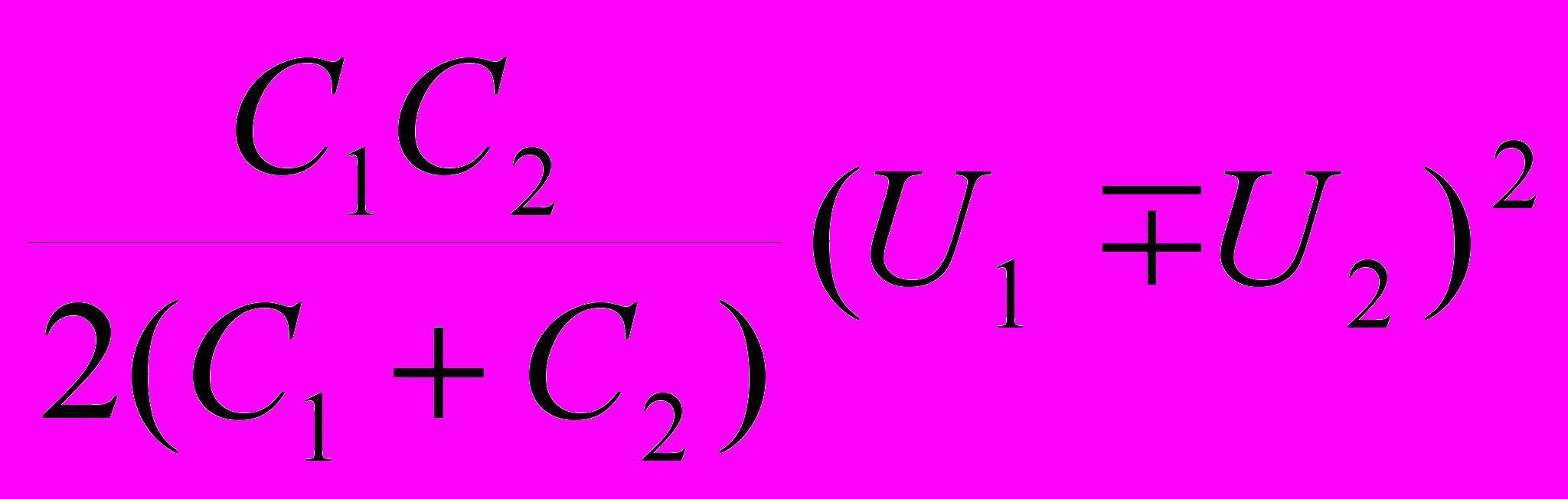. Выделившееся количество теплоты, как видно, не зависит от сопротивления резисторов.

Так как резисторы соединены последовательно, то в любой момент времени через них текут одинаковые токи. Из закона Джоуля- Ленца 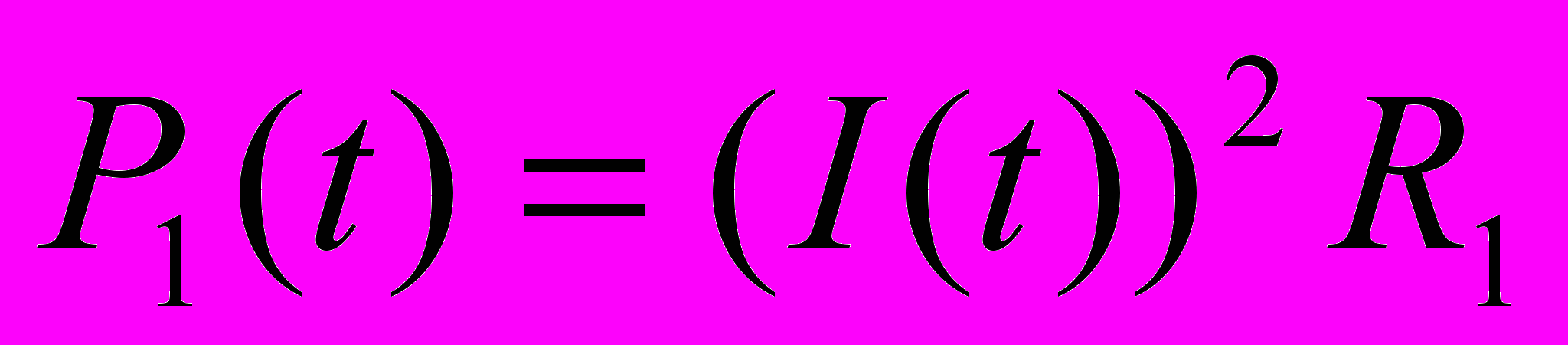и 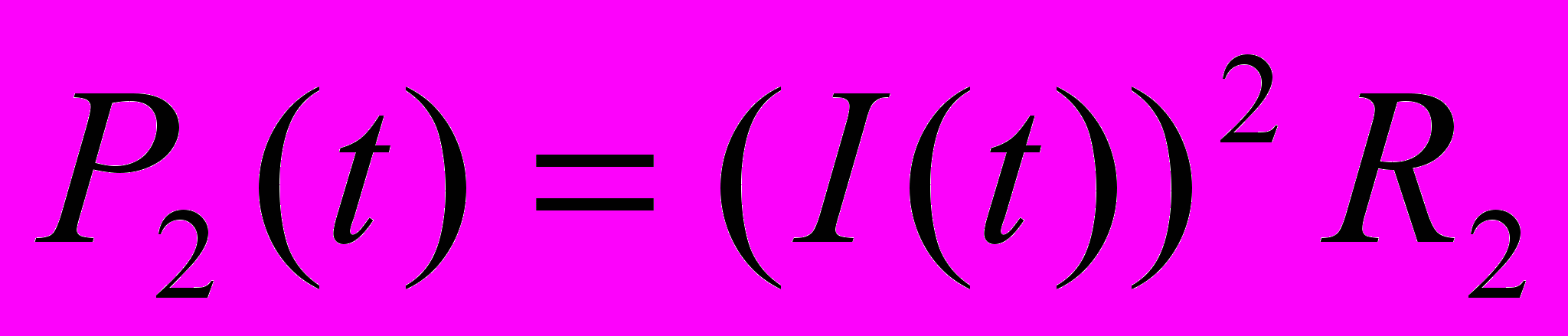. Следовательно 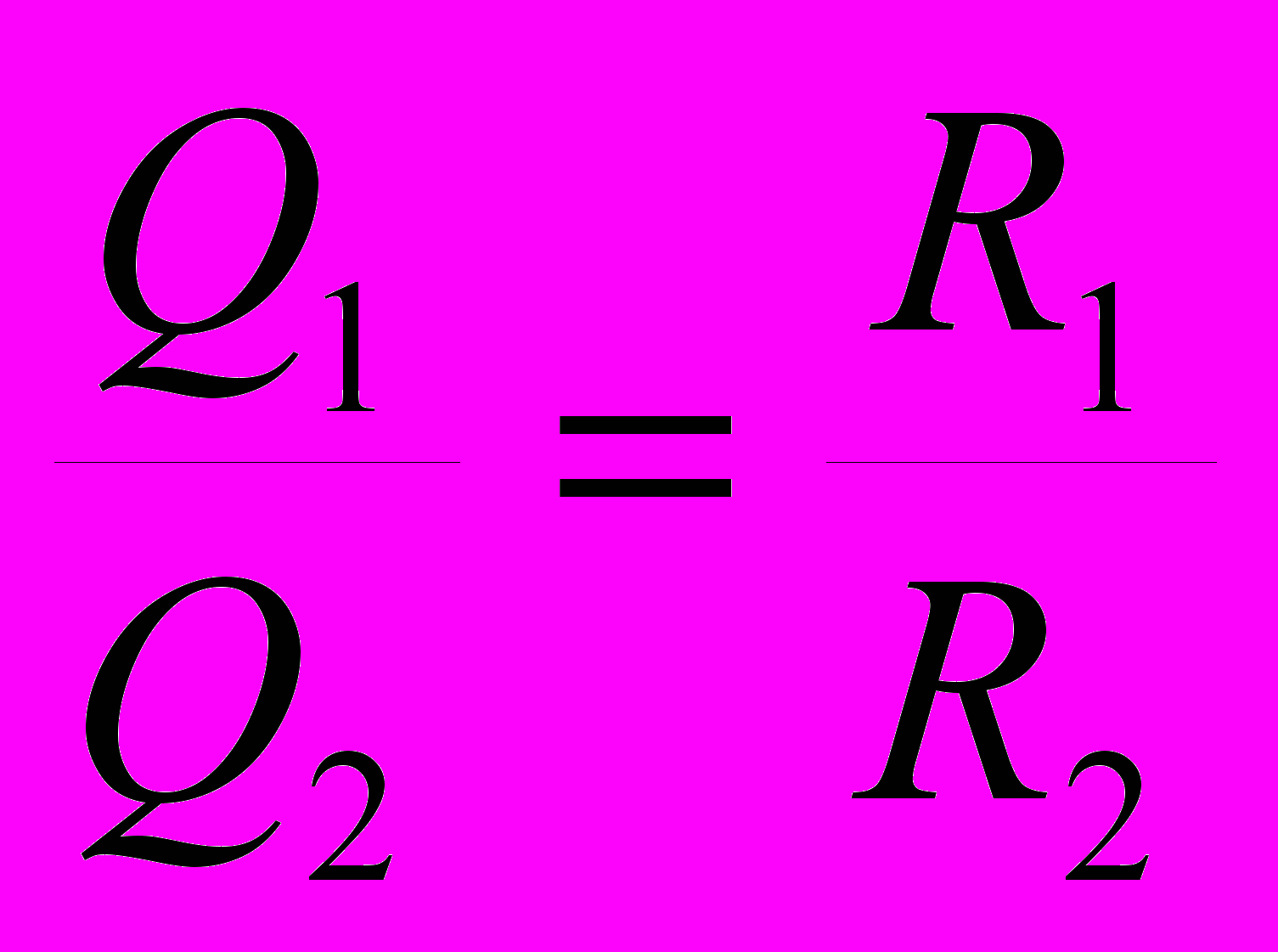и 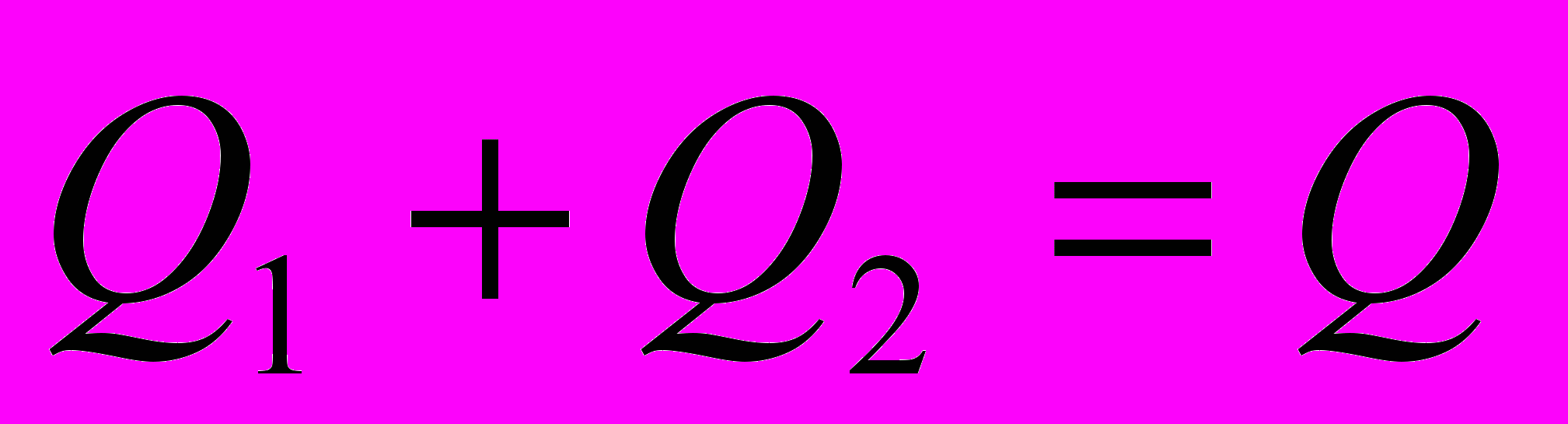. В итоге получаем

,

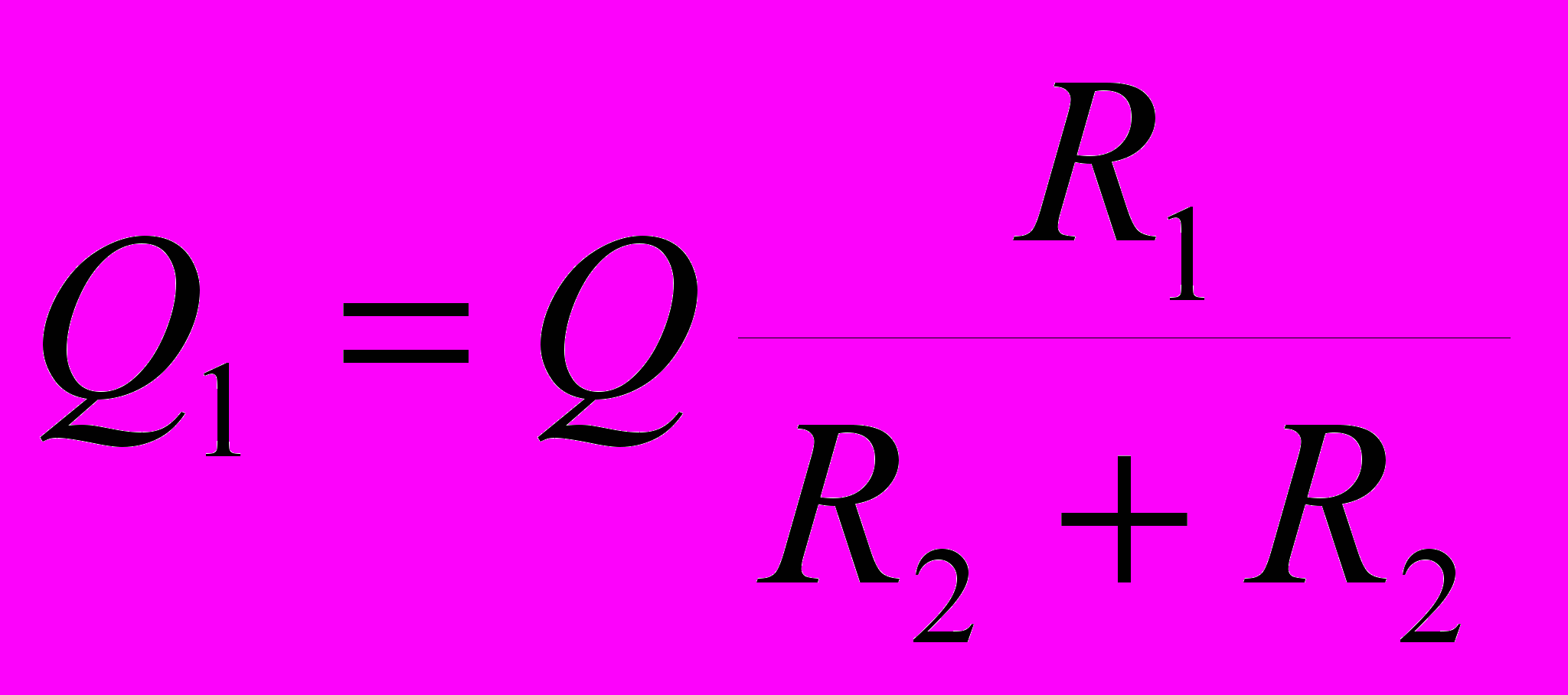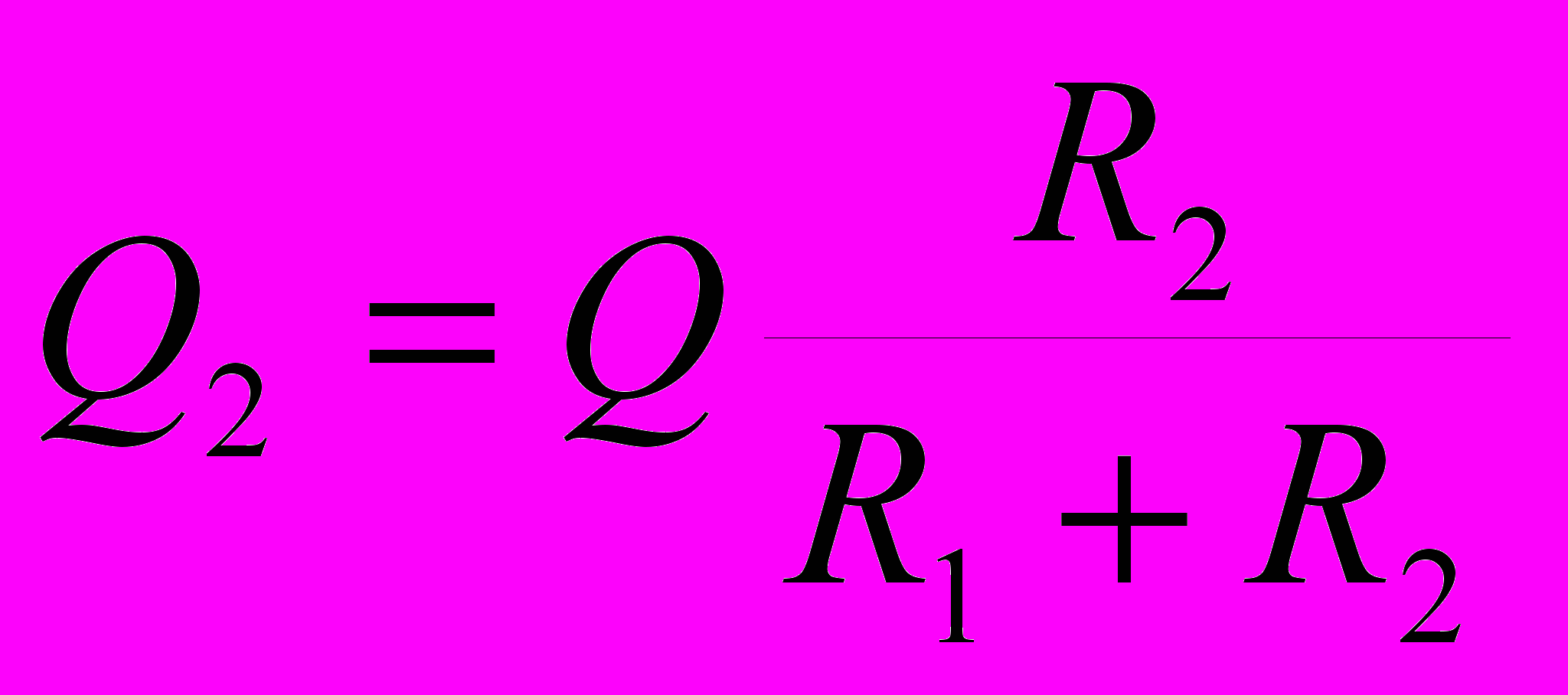
З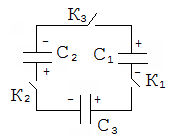адача №4. Трем одинаковым конденсаторам емкостью С каждый сообщили заряды q1, q2 и q3. Затем конденсаторы соединили так, как показано на рисунке. Найдите заряд каждого конденсатора после замыкания ключей.

Решение. Обкладки соединяемых конденсаторов являются замкнутой системой и для них выполняется закон сохранения электрического заряда.

.

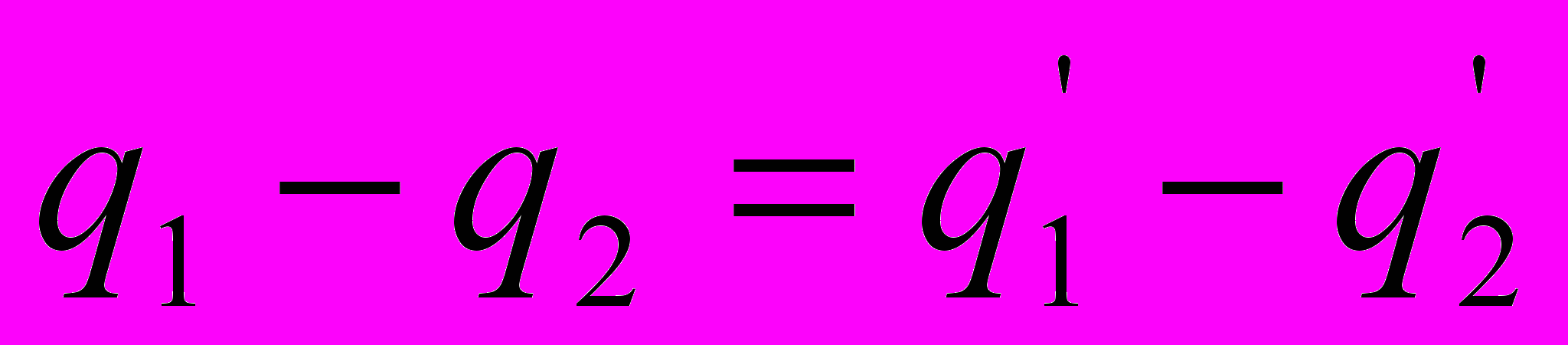
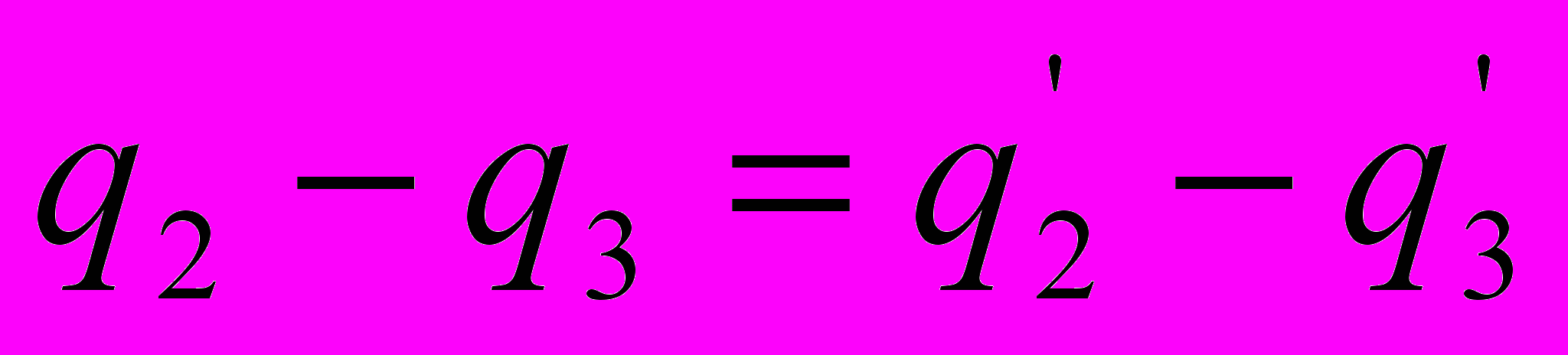Мысленно проведем вдоль цепочки конденсаторов единичный положительный заряд, вернув его в начальную точку. Работа сил электростатического поля по перемещению заряда по замкнутой траектории равна нулю. Значит

.

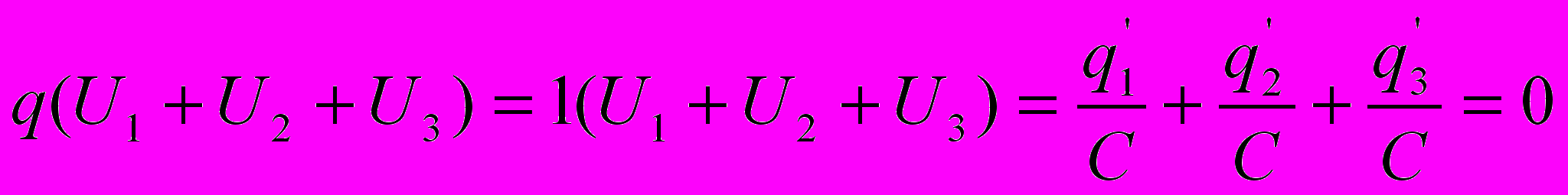Решая уравнения, получаем выражения для зарядов

.
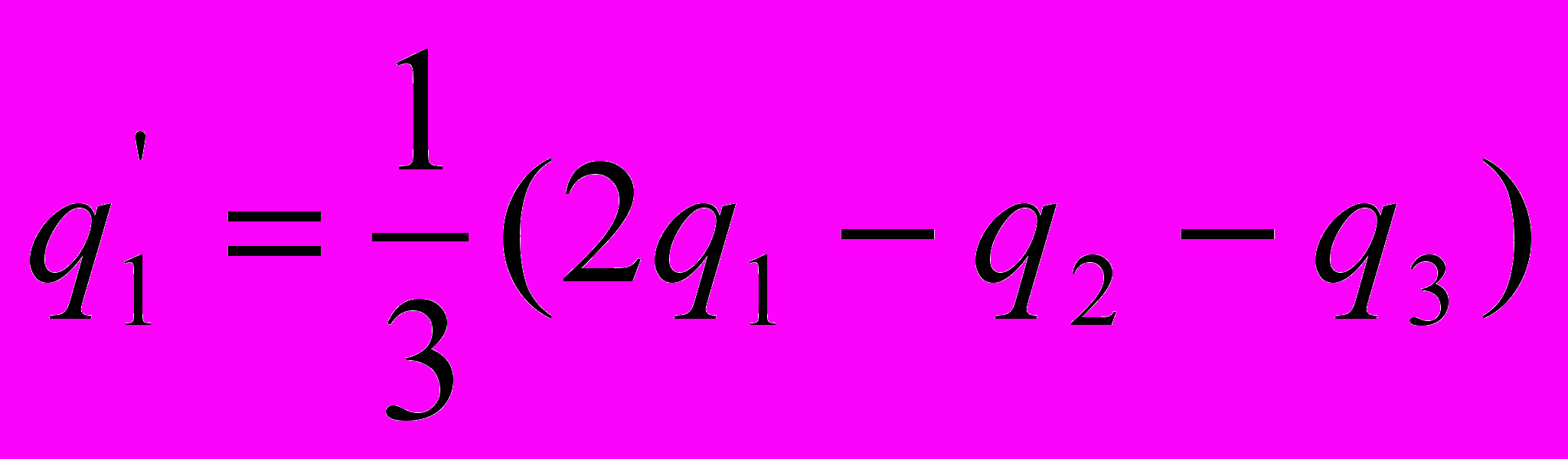
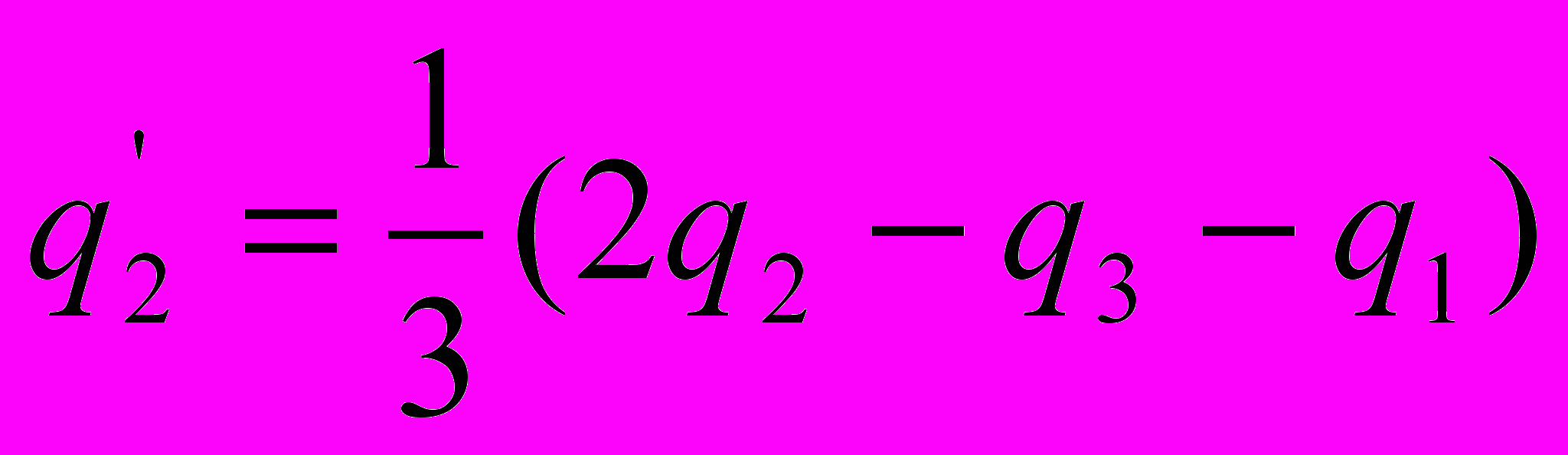
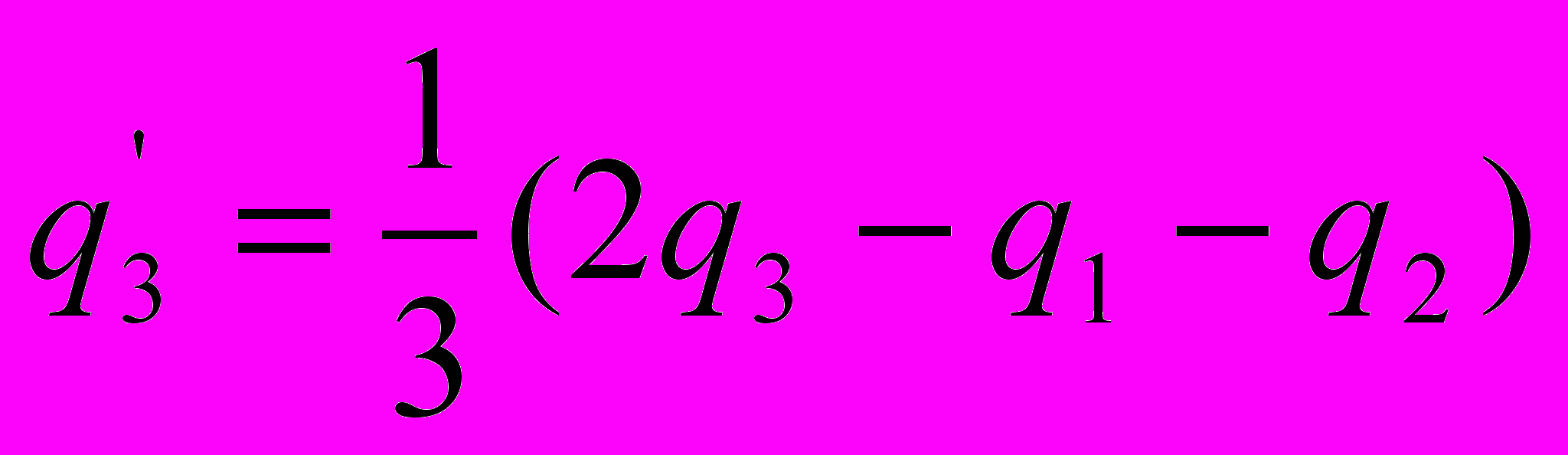