Гаврилов Андрей Владимирович, доцент нгавт 4 закон

Вид материала

Закон

Содержание Задачи для самостоятельного решения Задача №2. Задача №5. Задача №6. Задача №7. Задача №8. Задача №10. Задача №12. Задача №14. Задача №15. Задача №16. Задача №17. Задача №18. Задача №19. Задача №20. Задача №21. Задача №27. Задача №28. Задача №29. Задача №30. ... Полное содержание

Подобный материал:

• Андрей Владимирович Курпатов Средство от депрессии, 2074.53kb.
• Ученого Совета Уральского государственного университета имени А. М. Горького программа, 481.82kb.
• Корляков Андрей Владимирович, к ф. м н, доцент область применения категории слушателей, 256.81kb.
• Фрагменты истории земской статистики, 182.52kb.
• Самостоятельная работа : 60 час. Преподаватели: доцент Наследов Андрей Дмитриевич,, 1089.06kb.
• Федеральный Закон «Об основах туристской деятельности в рф», 221.17kb.
• Методические указания по выполнению контрольной работы 6 Рекомендации по выполнению, 223.73kb.
• Программа курса система государственных закупок Преподаватель: Иванов Андрей Евгеньевич,, 179.08kb.
• Программа курса разработка управленческих решений Преподаватель: Иванов Андрей Евгеньевич,, 143.23kb.
• Родькина Елена Федоровна и председатель профсоюзного комитета Сисейкин Андрей Владимирович., 162.91kb.

Задачи для самостоятельного решения

Задача №1. Определите суммарную энергию взаимодействия электрических зарядов расположенных в вершинах квадрата со стороной а в системах показанных на рисунке.



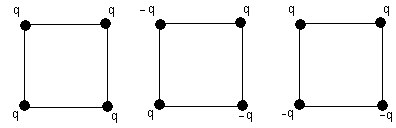
Задача №2. Точечный заряд q находится на расстоянии L от безграничной проводящей плоскости. Найдите энергию взаимодействия этого заряда с зарядами, индуцированными на плоскости.

З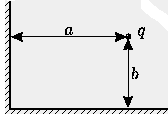адача №3. Две проводящие полуплоскости образуют прямой двугранный угол. Точечный заряд q находится на расстояниях 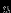и 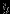от граней этого угла (см. рис.). Найдите полную энергию взаимодействия зарядов в этой системе.  

Задача №4. Два диэлектрических шарика, на поверхности которых находятся заряды q₁ = 5 нКл и q₂ = 10 нКл, находятся на расстоянии 50 см в вакууме. Какую работу надо совершить, чтобы сблизить их до расстояния 10 см?

Задача №5. Два маленьких абсолютно упругих шарика имеют равные массы m, радиусы r и заряды q₁ и q₂ разных знаков, находящиеся строго в их центрах. В начальный момент шарики покоятся в вакууме далеко от других тел так, что их центры расположены друг от друга на расстоянии L> 2r. Какими будут конечные скорости шариков после удара, если в момент соударения за счёт пробоя их заряды выровнялись? Гравитационным взаимодействием пренебречь.  

Задача №6. Точечный заряд q = 10 мкКл находится на расстоянии L = 1 см от проводящей плоскости. Какую работу надо совершить, чтобы удалить его на очень большое расстояние от плоскости?

Задача №7. Маленький заряженный шарик массой m шарнирно подвешен на невесомом непроводящем стержне длиной L. На расстоянии 1,5L слева от шарнира находится вертикальная заземлённая металлическая пластина больших размеров. Стержень отклоняют от вертикали вправо на угол 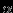и отпускают без начальной скорости. В ходе начавшихся колебаний стержень достигает горизонтального положения, после чего движется обратно, и процесс повторяется. Найдите заряд шарика. Ускорение свободного падения равно g.  

Задача №8. Найдите объемную плотность энергии электрического поля вблизи бесконечной заряженной плоскости с поверхностной плотностью зарядов 10 нКл/м². Объемная плотность энергии – энергия, приходящаяся на единицу объема.

Задача №9. Большая тонкая проводящая пластина площадью S и толщиной d помещена в однородное электрическое поле напряженностью Е. Какое количество теплоты выделиться, если поле мгновенно выключить? Какую минимальную работу надо совершить, чтобы вынуть пластину из поля?

Задача №10. На обкладках плоского конденсатора находятся заряды + q и – q. Площадь обкладки S, расстояние между ними d₀. Какую работу надо совершить, чтобы сблизить обкладки до расстояния d?

Задача №11. Внутри плоского конденсатора, площадь обкладки которого 200 см² и расстояние между ними 1 см находится пластинка из стекла (ε = 5), целиком заполняющая промежуток между обкладками. Как изменится энергия конденсатора, если удалить эту пластинку? Решить задачу для случая 1) конденсатор все время подключен к источнику тока с напряжением 200 В. 2) конденсатор первоначально был присоединен к тому же источнику, затем его отключили, и только после этого удалили пластинку.

Задача №12. Плоский конденсатор заполнили диэлектриком и на пластины подали некоторую разность потенциалов. Энергия конденсатора при этом равна W = 2*10^-5 Дж. После того, как конденсатор отключили от источника, диэлектрик вынули из конденсатора. Работа, которую надо было совершить для этого, равна А = 7*10^-5 Дж. Найдите диэлектрическую проницаемость диэлектрика.

Задача №13. Стеклянная пластинка полностью заполняет пространство между обкладками плоского конденсатора, емкость которого в отсутствии пластинки 20 нФ. Конденсатор подключили к источнику тока с напряжением 100 В. Пластинку медленно без трения вынули из конденсатора. Найдите приращение энергии конденсатора и механическую работу против электрических сил при извлечении пластинки.

Задача №14. Конденсатор емкостью С несет на обкладках заряд q. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью ε?

Задача №15. Плоский конденсатор находится во внешнем электрическом поле напряженностью Е, перпендикулярной пластинам. На пластинах площадью S находятся заряды +q и –q. Расстояние между пластинами d. Какую минимальную работу надо совершить, чтобы поменять пластины местами? Расположить параллельно полю? Вынуть из поля?

Задача №16. Конденсатор емкостью С заряжен до напряжения U. К нему подключают точно такой же конденсатор. Сопротивление подводящих проводов равно R. Какое количество теплоты выделиться в проводах?

Задача №17. Два одинаковых плоских конденсатора емкостью С каждый соединяют параллельно и заряжают до напряжения U. Пластины одного из них медленно разводят на большое расстояние. Какая при этом совершается работа?

Задача №18. Два конденсатора емкостью С каждый, заряжены до напряжения U и соединены через резистор. Пластины одного конденсатора быстро раздвигают, так, что расстояние между ними увеличивается вдвое, а заряд на пластинах за время их перемещения не изменяется. Какое количество теплоты выделится в резисторе?

Задача №19. Конденсатор емкостью С1=1 мкФ зарядили до напряжения 300 В и подключили к незаряженному конденсатору С2 емкостью 2 мкФ. Как изменилась при этом энергия системы?

Задача №20. Два одинаковых плоских конденсатора емкостью С каждый присоединяют к двум одинаковым батареям с ЭДС Е. В какой-то момент времени один конденсатор отключают от батареи, а второй оставляют присоединенным. Затем медленно разводят обкладки обеих конденсаторов, уменьшая емкость каждого в n раз. Какая механическая работа совершается в каждом случае? Объясните полученный результат.

З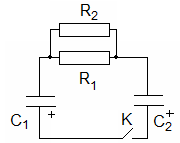адача №21. В схеме, изображенной на рис., найдите количество теплоты, выделившееся в каждом резисторе при замыкании ключа. Конденсатор, емкостью С₁ заряжен до напряжения U₁, а конденсатор емкостью С₂ – до напряжения U₂. Сопротивления резисторов R₁ и R₂.

Задача №22. Два конденсатора емкостями С1 и С2 соединили последовательно и подключили к источнику тока с напряжением U. Затем конденсаторы отключили и включили параллельно так, что + одного конденсатора оказался подключенным к + другого. Какая при этом выделилась энергия?


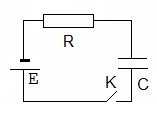
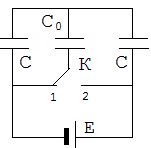
Задача №23. В схеме приведенной на рис. , конденсатор емкостью С, зарядили до напряжения U. Какое количество энергии будет запасено в аккумуляторе с ЭДС ε после замыкания ключа? Какое количество теплоты выделится в резисторе?

Задача №24. Какое количество тепла выделится в цепи при переключении ключа К из положения 1 в положение 2?

З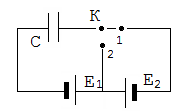адача №25. Какое количество тепла выделится в цепи при переключении ключа К из положения 1 в положение 2?

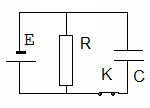
Задача №26. В электрической цепи, схема которой показана на рис., ключ К замкнут. Заряд конденсатора q = 2 мкКл, внутреннее сопротивление батареи r = 5 Ом, сопротивление резистора 25 Ом. Найдите ЭДС батареи, если при размыкании ключа К на резисторе выделяется количество теплоты Q = 20 мкДж.

Задача №27. В электрической цепи, схема которой показана на рис., ключ К замкнут. ЭДС батареи Е=24 В, ее внутреннее сопротивление r = 5 Ом, заряд конденсатора 2 мкКл. При размыкании ключа К на резисторе выделяется количество теплоты 20 мкДж. Найдите сопротивление резистора.

Задача №28. Свинцовая проволочка диаметром 0,3 мм плавится при пропускании через нее тока 1,8 А, а проволочка диаметром 0,6 мм – при токе 5 А. При каком токе разорвет цепь предохранитель, составленный из двух этих проволочек, соединенных параллельно?

Задача №29. В гирлянде для новогодней елки последовательно соединены двенадцать одинаковых лампочек. Как изменится мощность, потребляемая гирляндой, если в ней оставить только шесть лампочек?

Задача №30. Какой ток пойдет по подводящим проводам при коротком замыкании в цепи, если при поочередном включении двух электроплиток с сопротивлением R₁ = 200 Ом и R₂ = 500 Ом на них выделяется одинаковая мощность 200 Вт.

З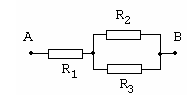адача №31. При прохождении постоянного электрического тока по участку АВ на резисторе сопротивлением R₂ выделяется тепловая мощность P₂. Какая тепловая мощность выделяется на каждом из резисторов сопротивлениями R₁ и R₃?

Задача №32. К 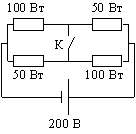источнику постоянного напряжения 200 В подключена схема из четырех резисторов, как показано на рисунке. На двух резисторах выделяется мощность 50 Вт, на других двух - 100 Вт. Как изменятся эти мощности, если замкнуть ключ К?

Задача №33. К выводам сложной цепи, состоящей из резисторов и источников тока, подключили вольтметр – он показал напряжение 6 В. Затем к этим же выводам подключили амперметр – он показал ток 1 А. Какую максимальную мощность можно получить, подключив к этим выводам нагревательный элемент? Приборы считать идеальными.

Задача №34. Нагреватель электрического чайника имеет две секции. При включении одной из них вода закипает за время 15 мин, при включении другой - за время 30 мин. Через какое время закипит вода если а) секции включить последовательно б) секции включить параллельно?

Задача №35. Электродвигатель, сопротивление обмотки якоря которого равно R подключают к источнику постоянного напряжения U, при этом через него протекает ток I. Вычислите потребляемую двигателем мощность, мощность, теряемую на нагрев обмотки, и КПД двигателя.

Задача №36. Электромотор питается от источника тока с постоянным по величине напряжением 24 В. Чему равна мощность, развиваемая мотором, при протекании по обмотке тока 8 А, если известно, что при полностью заторможенном якоре течет ток 16 А?