Міністерство освіти І науки України Національний університет “Львівська політехніка”

Вид материала

Автореферат

Содержание а) б) в) Рис.16. Усталений періодичний режим в неавтономному ФАПЧ з шумом. а) б) в) Рис.18. Залежності довірчого інтервалу фазової похибки від рівня шуму (а), індексу модуляції (б) та параметру m ПІФ (в) Рис.19. Залежності ШСУ (а) та ШСС (б) від рівня шуму за різних індексів модуляції. Шостий розділ Таблиця 1. Синтезовані значення параметрів та показники завадостійкості СФД Основні результати І Висновки

Подобный материал:

• Міністерство Освіти І Науки України Національний університет “Львівська політехніка”, 2021.84kb.
• Міністерство освіти І науки україни національний університет «львівська політехніка», 1080.17kb.
• Міністерство освіти І науки україни національний університет «львівська політехніка», 1068.44kb.
• Міністерство освіти І науки україни національний університет «львівська політехніка», 1259.1kb.
• Національний університет «львівська політехніка» алзаб аєд хамдан, 385.08kb.
• Міністерство освіти І науки україни національний університет «львівська політехніка», 1563.62kb.
• Міністерство освіти І науки україни національний університет «львівська політехніка», 208.38kb.
• Міністерство освіти І науки україни національний університет «львівська політехніка», 723.06kb.
• Міністерство освіти І науки України Національний університет "Львівська політехніка", 526.12kb.
• Міністерство освіти І науки України Національний університет "Львівська політехніка", 305.54kb.

а) б) в)

Рис.16. Усталений періодичний режим в неавтономному ФАПЧ з шумом.

За малих рівнів шуму та індексів модуляції на розмах орбіти усталеного руху ха­рактерного перетину (рис. 16 а) впливає тільки індекс модуляції, а на його розмір – тіль­ки інтенсивність шуму. Торкання еліпсом вхідної сепаратриси через зростання роз­міру або розмаху орбіти свідчить про зрив синхронізму. За більших рівнів збурень ха­рак­терною особливістю періодичних розв’язків є те, що впродовж періоду модулю­валь­ного збурення змінюється і середнє значення (потовщена лінія на рис. 16 б) і СКВ похибки. Порівняння СКВ фазової похибки за наявності кутової модуляції (крива 1 на рис. 16 в) та за її відсутності (пряма 2) показує, що збільшення індексу модуляції за не­змінного рівня шуму суттєво (до 7 разів) збільшує пікові значення СКВ похибки. От­же, отримана математична модель (9) дає можливість аналізувати од­но­час­ну дію шумової завади та кутової модуляції і виявляти ефекти, недоступні іншим методам.

Аналогічні особливості усталених періодичних рухів виявив також аналіз статис­тич­ної динаміки ФАПЧ за наявності фазової маніпуляції (рис. 17).

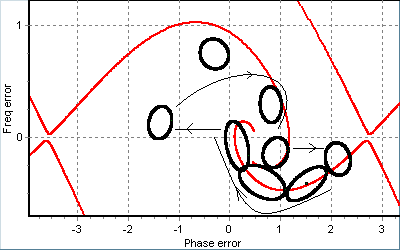
Рис.17. Усталений періодичний режим за наявності фазової маніпуляції.

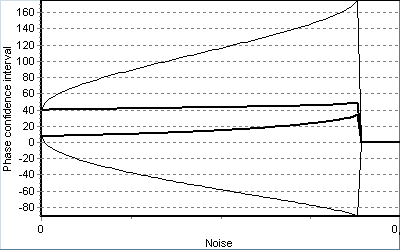
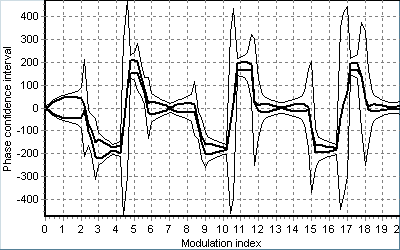
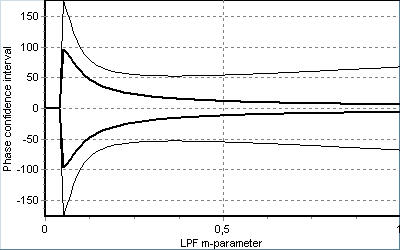
Зміни характеристик усталених періодичних розв’язків системи (9), викликані змі­нами параметрів збурень та пристрою, зображено на рис. 18, де потовщеними лініями відмічений розкид середнього значення за період модуляції, а тонкими – довірчий ін­тер­вал фазо­вої похибки (абсциси граничних точок еліпса). Наближення до межі іс­ну­вання син­хрон­ного режиму викликає різке зростання СКВ фази незалежно від того, яким пара­метром це наближення викликано. Залежність від рівня шуму 1/ (рис. 18 а) по­казує, крім числових значень статис­тич­них характеристик фазової по­хибки, граничну завадостійкість, що дає можливість опти­мізувати параметри при­ст­рою за критерієм макси­муму допустимого рівня шуму. Залежність від індексу моду­ляції μ (рис. 18 б) показує зміни фази основної гармоніки модульованого коливання на ±180° та по­мітні викиди СКВ фазової похибки, коли гармоніка носій­ної частоти має близьку до нуля амплі­туду. Залежність від параметру m ПІФ (рис. 18 в) має мінімум, що умож­ливлює оптимізацію за відомим критерієм мінімуму СКВ, крім того, ця за­леж­ність показує немож­ли­вість синхронізму за деяких значень параметрів (m<0,05).

а) б) в)

Рис.18. Залежності довірчого інтервалу фазової похибки від рівня шуму (а),
індексу модуляції (б) та параметру m ПІФ (в).

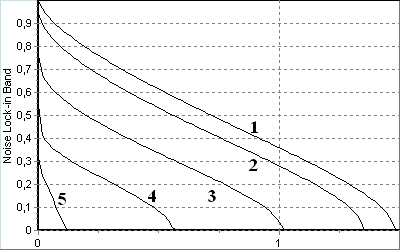
На рис. 19 наведено залежності шумових смуг утримання (рис. 19 а) і схоп­лення (рис. 19 б) від параметру 1/ (відношення шум/сигнал в смузі ФНЧ) при зна­ченнях ін­дексу модуляції = 0; 0,5; 1,0; 1,5; 2,0 (криві 1..5 від­по­відно). Ха­рактерною особ­ли­вістю ШСУ та ШСС є монотонне звуження як з рос­том шу­му, так і з ростом індексу модуляції. Це обмежує можливість збіль­шення вихідного відношення сигнал/шум шля­хом збіль­шення індексу модуляції. Різке звуження смуг (осо­б­ливо ШСС) в області малих шумів показує неможливість за наявності шуму використовувати резуль­тати, відомі для детер­мінованих ФАПЧ.

а) б)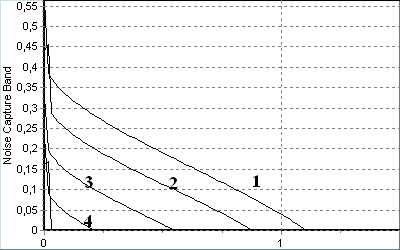

Рис.19. Залежності ШСУ (а) та ШСС (б) від рівня шуму за різних індексів модуляції.

Залежності, наведені на рис. 18 і 19, отримані за допомогою спеціально розробле­ної програми, яка здійснює інтегрування системи рівнянь (9) та автоматичну зміну од­ного (рис.18) або двох (рис. 19) параметрів. Ця програма була використана для оптимі­за­ції параметрів ФАПЧ за критерієм максимальної завадостійкості. Вихідними даними для оптимізації за цим критерієм є тільки параметри модуляції (прийнято γ_М=0,02 та μ=10). Отримані оптимальні значення параметрів (m=0,230; β=0,013) забезпечують мак­си­маль­но допустимий рівень шуму 1/βρ=2,8. Для порівняння були також розра­ховані значення параметрів, оптимальні за критерієм мінімуму СКВ, який вимагає до­датково задавати апріорне значення рівня шуму. Отримані значення (m=0,242; β=0,101 для 1/βρ=0,1 та m=0,115; β=0,016 для 1/βρ=4,0) суттєво відрізняються від рекомендацій роз­робленої програми. На рис. 20 наведені графіки ШСУ для всіх трьох наборів пара­метрів, порівняння яких пока­зує, що нелінійний синтез програє малошумо­вому лі­ній­ному біля 20% допустимої розстройки за малих рівнів шуму, але виграє 25% по зава­до­стійкості. Виграш не­лінійного синтезу порівняно з сильно шу­мо­вим ліній­ним по завадостійкості лише 5%, але по граничній розстройці сягає 25..50%. Крім того, відсут­ність необхідності апріорно задавати рівень шуму значно полегшує задачу проекту­ван­ня порівняно з лінійним методом, нечутливим до порогу завадостійкості.

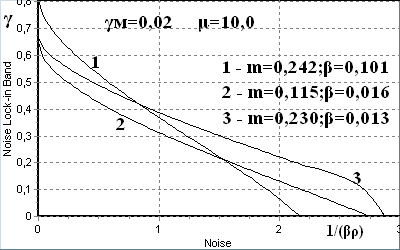
Рис. 20. Залежність ШСУ від рівню шуму за умови лінійної (1, 2) та нелінійної (3) оптимізації параметрів.

Рис. 21. Вибір смуги утримання за критерієм максимального діапазону стеження.

Розроблена програма дає можливість оптимізувати параметри пристрою ще за од­ним кри­терієм, недоступним для лінійного методу, – за максимумом діапазону сте­жен­ня. На рис. 21 на­ве­де­ні залежності час­тотного діапазону стеження від смуги утримання F_УА незбуреної ФАПЧ. За відсутності ФМ (μ=0) малі смуги утримання (до 500 Гц) ви­ко­ристовуються прак­тич­но повністю. Але при знач­ному роз­ши­ренні F_УА (більше 12 кГц) діапазон стеження спадає до нуля через вплив шуму. Реко­мендо­ваним значенням ко­е­фіцієнта підсилення пет­лі ФАПЧ є F_УА =8 кГц (досягну­тий діапазон 1,7..2,2 кГц в за­леж­ності від значення μ). Для порівняння на рис. 21, крім точок максимуму діапа­зо­ну стеження, від­міче­ні точки мінімальної фазової похибки та значення СКВ фази для γ=0, які показують, що кри­терій макси­мального діапазону про­грає 10°..15° по якості син­хронізації, але виграє в 2..3 рази по діапазону стеження.

Отже, з використанням кумулянтної математичної моделі (9) виявлені нові особли­вості ста­тистичної динаміки ФАПЧ під дією комбінованих збурень, зокрема змінність в часі СКВ фазової похибки та його залежність від індексу модуляції. Розроблена про­грама аналізу математичної моделі (9) дає можливість проектувальнику опти­мі­зувати параметри пристрою як за відомим критерієм мінімуму СКВ фазової похибки, так і за критеріями максимуму допустимого рівня шуму і максимуму діапазону сте­жен­ня.

У п’ятому розділі роботи обґрунтована та досліджена структурна модифікація при­строю ФАПЧ, спрямована на усунення основного джерела порогового обмеження завадостійкості, а саме – обмеженості робочої ділянки детекторної характеристики ФД. Зрив син­хронізму відбувається, коли сумарна похибка син­хро­нізації (статична, дина­міч­на і шумова) виходить за межі цієї робочої ділянки (±π/2). На етапі про­ек­ту­вання це викликає необхідність пошуку компромісу між завадостійкістю (статистична складова похибки) та динамічними властивостями пристрою (динамічна складова).

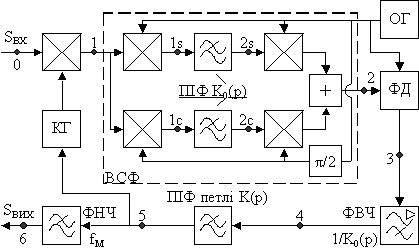Рис. 22. Структурна схема модифікованого пристрою ФАПЧ.

Ідея підвищення завадостій­ко­сті зі збереженням динамічних властивостей полягає у зменшен­ні викидів різниці фаз перед ФД (щоби фазова похибка не вихо­ди­ла за межі робочої ді­лян­ки) і наступному підсиленні вихідно­го сигналу ФД (щоби відновити ди­намічні властивості демоду­ля­тора). Струк­турна схема при­строю¹, який реалізує цю ідею, на­ведена на рис. 22 і відріз­ня­єть­ся від схеми класичного ФАПЧ наявністю вузь­ко­смугового філь­тра (ВСФ) перед ФД та активного фільтра верхніх частот (ФВЧ) піс­ля нього. ВСФ ре­алізовано як синхронно-фазовий фільтр, у квадра­турних каналах якого ви­ко­ристані однакові пропорційно-інтегруючі фільтри (ПІФ) з комп­лекс­ним кое­фіці­єн­том передавання

. (10)

Покладемо, що ФД має трикутну характеристику і максимальний рівень ви­хід­ної напруги U_ФД, а крутість характеристики керованого генератора становить S. Тоді мак­симальне відхилення частоти КГ (смуга утри­мання автономного пристрою) становить Ω_УА=S∙U_ФД. Нехай також сигнали на виході опорного генератора (ОГ) S_ОГ, на виході КГ S_КГ, і вхідний сигнал S_ВХ(t) становлять

S_ОГ(t)=sin(ω_ОГt), S_КГ(t)=sin[(ω_0КГ–Su₅)t+φ_КГ],

S_ВХ(t)= S₀(t)=cos(ω₀t+φ₀(t)+φ_n(t)). (11)

В (11) позначено: ω_0КГ, φ_КГ – власна частота і початкова фаза КГ; ω₀– носійна часто­та, φ₀(t)=μ sin(Ωt) – модулювальна складова фази сигналу; μ – індекс, Ω– частота мо­ду­ля­ції; φ_n(t) – перерахована у фазовий шум канальна шумова завада; u₅ – керуюча на­пруга КГ (точка 5 на рис.22). Позначимо також Ω_П=ω₀–(ω_0КГ+ω_ОГ) – відхилення носій­ної час­тоти S_ВХ від очікуваної (ω_0КГ+ω_ОГ), тобто початкова розстройка частот; ω=Ω_П–Su₅ – мит­тє­ва частотна похибка синхронізації з носійним сигналом; φ(t)=(Ω_П+ Su₅)t –φ_КГ – миттєва фазова похибка синхро­ні­зації з носійним сиг­на­лом; φ₁(t)=φ(t)+φ₀(t)+φ_n(t) – фазовий зсув сигналу на вході ВСФ відносно опор­но­го генератора; φ₂(t)– різниця фаз сигналів на входах ФД. За таких позначень сигнал на вході ВСФ в усталеному режимі має частоту ω_ОГ, а його фаза становить φ₁(t). За умови Ω_П=0 і відсутності шуму на­пру­ги на входах фільтрів квадратурних каналів (точки 1s та 1с на рис 22) становитимуть

u_1S(t)=sin φ= sin (μ sin Ωt); u_1C(t)=cos φ= cos (μ sin Ωt), (12)

і при індексах модуляції μ<π/2 можна вважати, що спектри цих сигналів містять по­стій­ну складову U_1C0 і по одній гармоніці частоти модуляції з амплітудами U_1SM, U_1CM:

u_1S(t)= U_1SM sin Ωt; u_1C(t)= U_1C0+U_1CM cos (2 Ωt). (13)

Сигнал на виході ВСФ матиме частоту ω_ОГ, а його фаза, з огляду на (10), становитиме

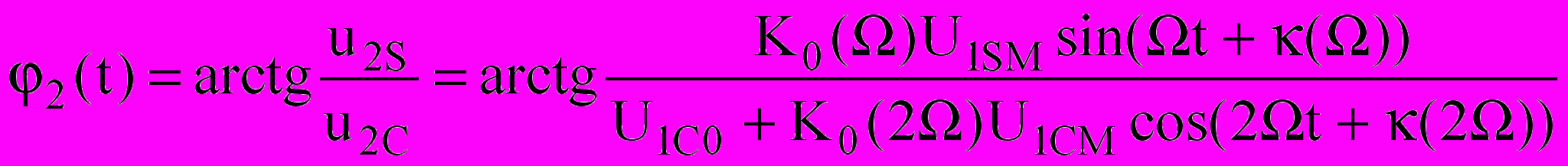, (14)

а для випадку Ω>>1/T₀, тобто при виборі смуги пропускання ПІФ меншою від частоти модуляції, вираз (14) набуває вигляду

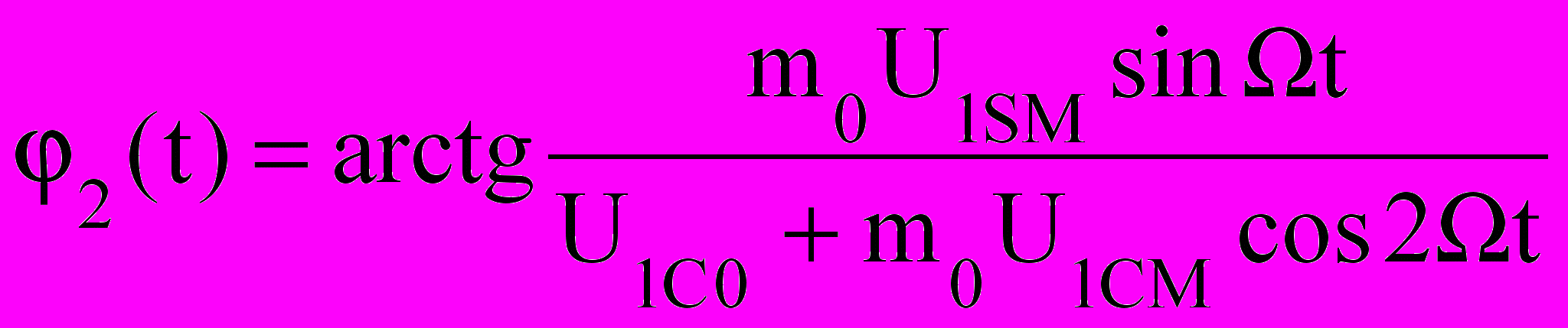. (15)

При дуже малих індексах модуляції (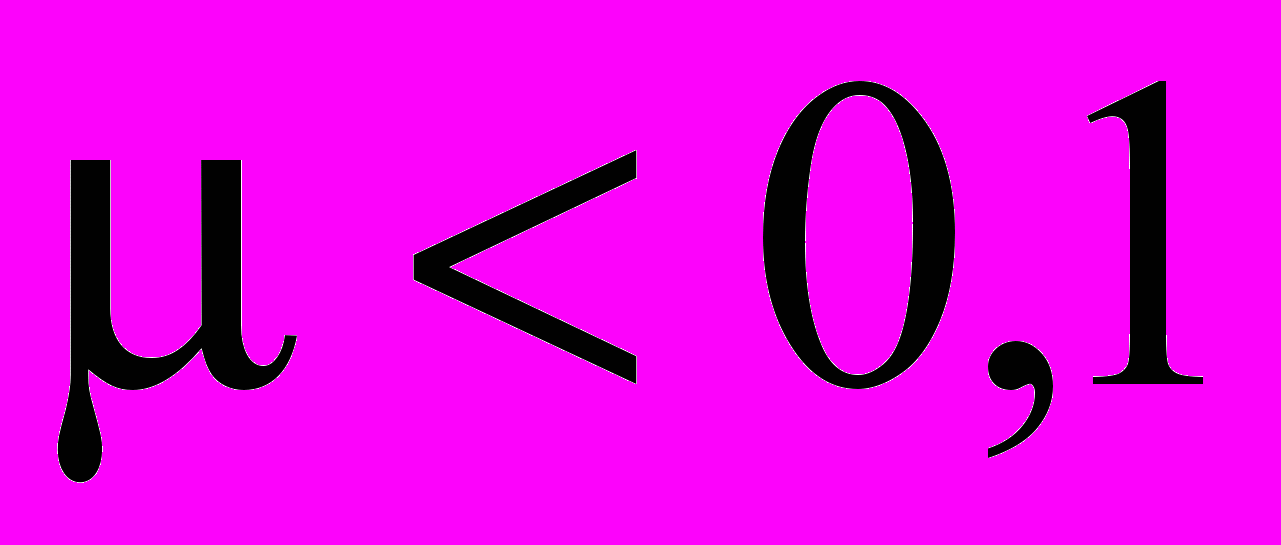) можна вважати u_1S(t)≈μ sin(Ωt), u_1C(t)≈1, tg μ≈sin μ≈μ, і вираз (15) перетворюється на

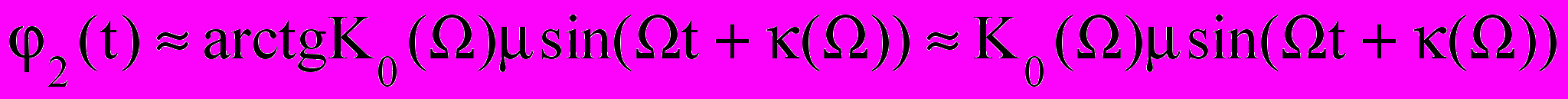, (16)

тобто в лінійному наближенні коефіцієнт передавання фази ВСФ збігається з коефі­ці­єн­том передавання напруги ПІФ квадратурних каналів. Використання пропорці­й­но - диференціюючого фільтра з коефіцієнтом передавання

(17)

в якості коректуючого ФВЧ забезпечує тотожну рівність одиниці коефіцієнта переда­ван­ня „фаза вхідного сигналу – напруга U₄” в лінійному режимі. Це означає, що дина­мічні властивості і фільтруюча здатність модифікованого при­строю будуть такими ж, як і у класичного ФАПЧ, у якому відсутні ВСФ та ФВЧ. Але порогові явища, виклика­ні виходом за межі робочої ділянки характеристики ФД, про­яв­ляться за значно біль­ших викидів різниці фаз φ(t), оскільки, як видно з (15) у моди­фікованому пристрої ці викиди зменшуються приблизно в 1/m₀ разів.

У лінійному наближені отримана аналітична оцінка можли­вого підвищен­ня за­ва­достійкості, яке становить 1/m₀ для високочастотних (порівняно зі смугою ВСФ) завад та (де β₀=1/Ω_УАT₀ – нормована смуга ВСФ) для ши­рокосму­го­вих завад. Це підвищення обмежене лише влас­ними шумами квадратурних каналів ВСФ.

Для аналізу нелінійних явищ у модифікованому ФАПЧ була розроблена його мате­ма­тична модель у вигляді такої системи алгебраїчних та диференціальних рівнянь:

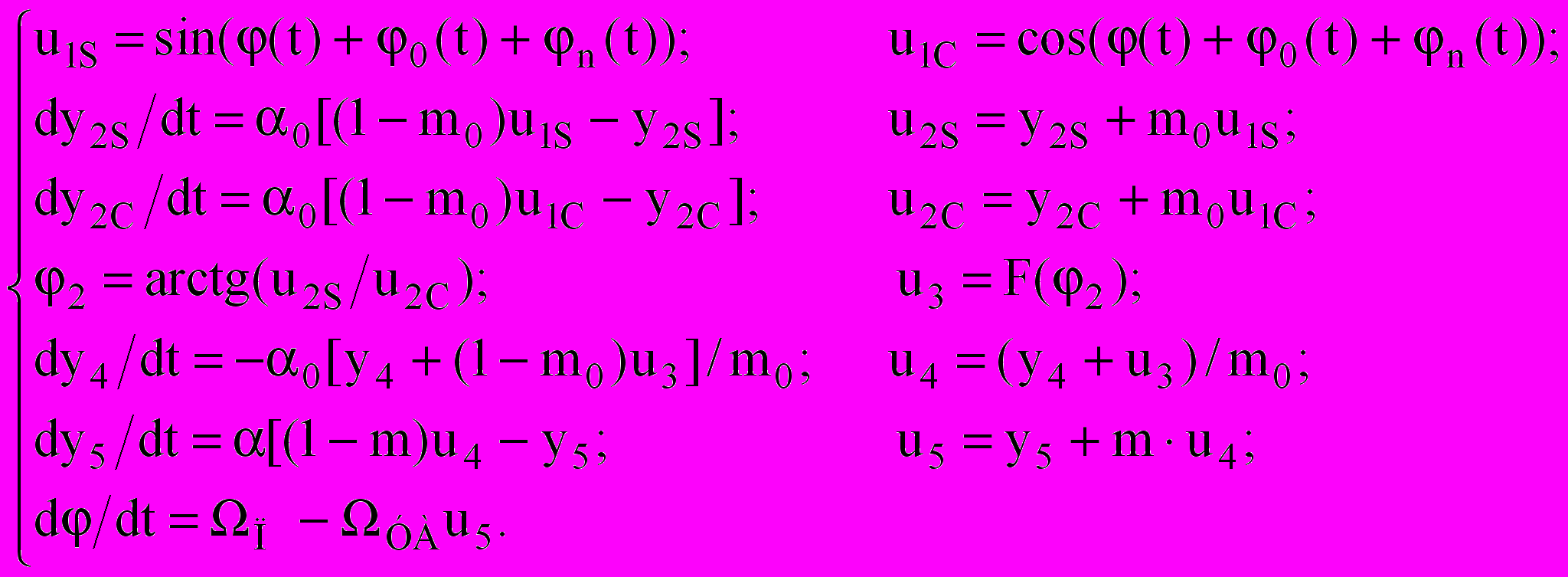(18)

У системі рівнянь (18) індекси змінних відповідають точкам на схе­мі рис. 22, всі напруги нормовані до напруги U_ФД. Впроваджені змінні

y_2S=u_2S–m₀u_1S, y_2C=u_2C–m₀u_1C, y₄=m₀u₄–u₃, y₅=u₅–m₀u₄

є визначальними змінними лінійних фільтрів, які описують стан реактивних еле­мен­тів цих фільтрів. Параметри α=1/T та α₀=1/T₀ – смуги пропускання ПІФ петлі та каналів ВСФ відповідно, F(φ₂) – детекторна характеристика ФД.

Отримані числовим інтегруванням (18) усталені періодичні розв’язки для випадку розімкненої петлі керування та індексу модуляції μ=1,8 рад подані на рис. 23 у вигляді осцилограм напруги u₄(t). У класичному ФАПЧ (крива 1) спо­стерігається обмеження вершини си­гналу при виході за лінійну ділянку ха­рактеристики ФД, а у модифіко­ва­ному (крива 2) фор­ма сигналу прак­тично зберігається, нелінійні спотворення прояв­ляються у неси­мет­рич­ності кривої поблизу екстремумів та постійному фазовому зсуві.

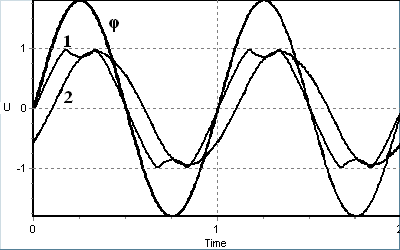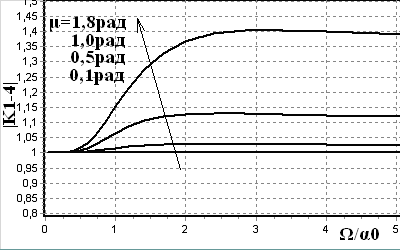Рис. 23. Нелінійні спотворення в класичному (1) і модифікованому (2) ФД.	Рис. 24. АЧХ „фаза сигналу 1 – – напруга U4”.

На рис. 24 наведені АЧХ коефіцієнту передавання „фаза сигналу 1 – напруга U₄”, отри­ма­ні за допомогою нелінійної моделі (18) для випадку розімкненої петлі керуван­ня та різних значень індексу модуляції. Як видно з рисунку, зі зростанням індексу і час­тоти модуляції цей коефіцієнт може значно (до 1,4 рази) відхилятися від постійного значення, розрахованого у лінійному наближенні.

Результати нелінійного аналізу процесів у замкненій петлі ФАПЧ за наявності по­чат­кової розстройки γ=Ω_П/Ω_УА=0,5, фазового шуму φ_n(t) з СКВ σ=0,1 рад та кутової мо­дуляції з індексом μ=1 рад наведено на рис. 25.

а) б) 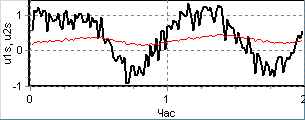в)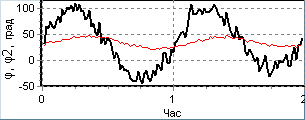

г)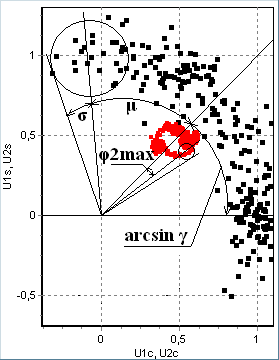

Рис. 25. Осцилограми (а, б) та фазовий портрет (г) квадратурних складових напруг на входах (темні лінії) та виходах (світлі) ВСФ та осцилограма фаз (в) цих напруг.

Осцилограми напруг (рис. 25 а,б) показують зменшення як амплітуди ква­дра­тур­них складових так і СКВ шуму при­близ­но в 1/m₀=10 разів, що є ре­зуль­татом про­ходження через ПІФ з вузькою смугою (α₀=0,1 Ω_УА). Анологічне змен­шення спостері­га­ється і для фаз сигналів на вході і ви­ході ВСФ (рис. 25 в). Більш наочно співвідно­шен­ня напруг і фаз, а також складових фа­зової по­хибки, представлено у вигляді квад­ратурних складових напруг на фазовій пло­щи­ні (рис. 25 г), з якого видно, що повна фазова похибка φ₁(t) на вході ВСФ скла­дається зі ста­тичної (arcsin γ), спричиненої розстройкою частот сиг­на­лу і КГ; дина­мічної (μ), викликаної кутовою модуляцією, та статистичної (σ), ви­кликаної випад­ко­вою зава­дою. Параметри пристрою і завад підібрано в такий спосіб, щоби макси­маль­ний ви­кид пов­ної фазової похибки φ₁(t) був більшим гра­ниці однозначності харак­теристи­ки ФД (π/2). Після проходження ВСФ ста­тична складова фазової похибки φ₂(t) не змінюється по­рівняно з φ₁(t), а динамічна і шумова зменшуються від­по­від­но до виразів (14, 15, 16). Це означає, що окремі скла­дові фазової похибки синхронізації мож­на значно збільшувати, а різниця фаз сиг­на­лів на входах ФД зали­ша­ти­меться у межах робочої ділянки характеристики (±π/2). На­приклад, за відсут­но­с­ті кутової модуляції (μ =0), при фік­сованій інтенсив­ності шуму можна збіль­ши­ти діапазон стеження (статичну похибку), або при фіксо­ваній роз­строй­ці час­тот збільшити граничну інтенсивність шуму (ста­тис­тичну похиб­ку).

Шляхом повного перебору можливих значень параметрів ВСФ та ФВЧ встанов­ле­но, що за відсутності початкової розстройки (γ=0) та модуляції (μ =0) максимальне до­сяжне збільшення завадостійкості ФАПЧ з інтегруючим фільтром (m=0) становить від 1,5 до 3,5 разів (4-10 дБ), а безфільтрового ФАПЧ (m=1) – 5..8 разів (14-18 дБ).




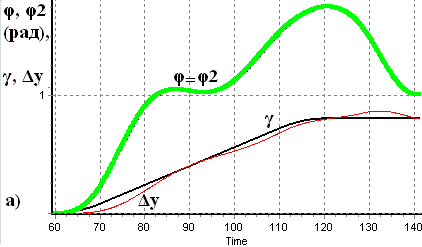
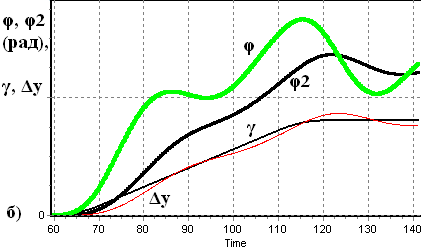
Рис. 26. Стеження за змінною частотою в класичному (а) і модифікованому (б) ФАПЧ.

Дослідження динамічних властивостей модифікованого пристрою за відсутності шу­му та порів­нян­ня їх із властивостями класичного ФАПЧ було здійснено моде­лю­ванням стрибкоподібної та неперервної зміни початкової розстройки за нульових по­чат­кових умов, а також фік­со­ваної розстройки за початкових умов, значно віддалених від стану рівноваги. Результати моделювання наведено на рис. 26.



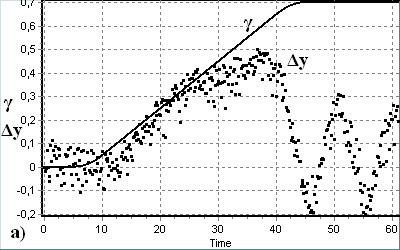
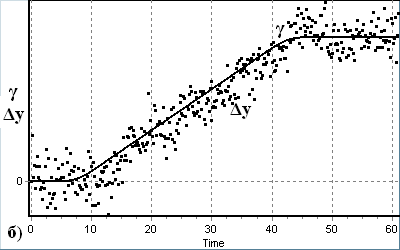
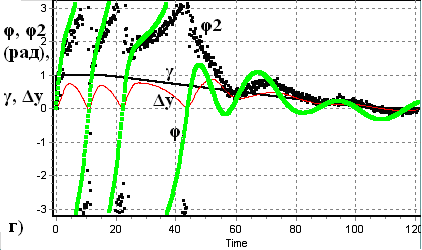
Рис. 27. Процеси утримання (а, б) і схоплення (в, г) змінної носійної частоти
за наявності шуму у класичному (а, в) і модифікованому (б, г) пристроях.

За неперервної зміни початкової розстройки (γ=Ω_П/Ω_УА), як видно з рис. 26, нормо­ва­не відхилення частоти КГ (Δy=Su₅/Ω_УА) збігається з відхиленням но­сій­ної частоти (γ) з практично однаковою похибкою, похибка φ стеження за фазою си­гна­лу у моди­фі­кованому ФАПЧ дещо менша, а різниця фаз φ₂ на входах ФД майже вдвічі менша, ніж у класичному пристрої. Це свідчить про біль­ший запас стійкості син­хро­ні­зації у моди­фіко­ва­ному пристрої. Перебором параметрів ВСФ та ФВЧ виявлена область їх зна­чень, за яких моди­фі­ко­ваний пристрій ФАПЧ є глобально стійким, тобто стаціонарний розв’язок моделі (18) встановлюється за будь-яких по­чат­кових умов, а смуга схоп­лен­ня пристрою до­рів­нює його смузі утримання.

Результати моделювання процесу стеження за змінною носійною частотою з ураху­ванням впливу шумової завади (рис. 27) показали, що статистична і динамічна похиб­ки синхронізації у модифікованому ФАПЧ практично такі ж самі, як і у класичному, але смуги утримання і схоплення є значно ширшими.

Отже, проведені дослідження модифікованого пристрою ФАПЧ (рис.22) показали, що його застосування значно підвищує завадостійкість синхронізації зі збе­реженням динамічних властивостей.

Шостий розділ дисертаційної роботи присвячений застосуванню розроблених ме­тодів підвищення завадостійкості у типових задачах радіолокації, зв’язку та наві­га­ції.

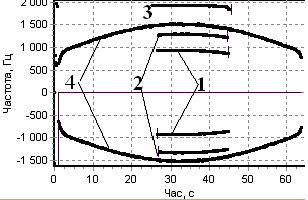Рис. 28. Похибки стеження за частотою відбитого сигналу за різних значень параметрів ФАПЧ.

Системи рівнянь (9) та (18) адаптовано для моделювання пристрою ФАПЧ, призна­чено­го для стеження за носійною частотою відбитого радіолокаційного сигналу на фо­ні шуму. За прийнятих параметрів цілі та високочастотних пристроїв РЛС сигнал на вхо­ді приймача має енергетичний потенціал 7200 Гц і шири­ну спектра частотних флук­туацій 100 Гц. Перевірка працездатності пристроїв стеження проведена за умов лінійної зміни частоти носійного сигналу в діа­па­зоні ±40 кГц від номінального зна­чення, що відповідає рівноприскореному руху цілі. Проведено порівняння власти­вос­тей модифікованого пристрою ФАПЧ (рис. 22) та класичного, в якому відсутні ВСФ та ФВЧ. На рис.28 наведені значення похибок сте­жен­ня за частотою на тестовій тра­єк­торії для наборів параметрів класичного ФАПЧ, опти­маль­них за крите­рія­ми мінімуму СКВ фазової похибки (1), за максимальною за­вадостійкістю (2) та за максимальним діа­па­оном стеження (3). Через прийнятий високий рівень шуму жо­ден з цих наборів параметрів не забезпечує схоплення відби­то­го сигналу та стеження за ним у всьому заданому діапазоні, тобто вико­рис­тання класичного ФАПЧ за прий­нятих умов вимагає збільшення потуж­ності сигналу, коефіцієнтів підсилення антен тощо.

Похибка стеження модифікованого прис­т­рою ФАПЧ також наведена на рис.2 (кри­ва 4). Як видно з результатів моделювання, модифі­кований при­стрій забезпечує сте­жен­ня за носійною частотою відбитого сигналу в усьо­му заданому діапазоні частот. Схоплення сте­ження відбувається при час­то­ті сигналу 38,75 кГц. Отже, використання модифікова­но­го пристрою ФАПЧ забезпечує сте­ження за частотою сигналу у складній зава­до­вій обстановці без збільшення енергетичних параметрів сигналу.

Задача проектування на основі ФАПЧ другого порядку завадостійкого синхрон­но­го фазового детектора (СФД) сигналу з кутовою модуляцією була розв’язана у припу­щенні про застосування фазо­вої модуляції однотональним коливанням з частотою _М=2·5кГц та індексом,  = 3,3, що є наближеним до параметрів сигналу широко­мов­них ЧМ станцій. Вибір значен­ня параметрів ФАПЧ (_УА,  та m) проведено за критерієм узгодження огинаючої дис­кретного спектру модульованого сигналу S(ω) і АЧХ ФАПЧ W₁(ω), яку у лінійному наближенні задає вираз

,

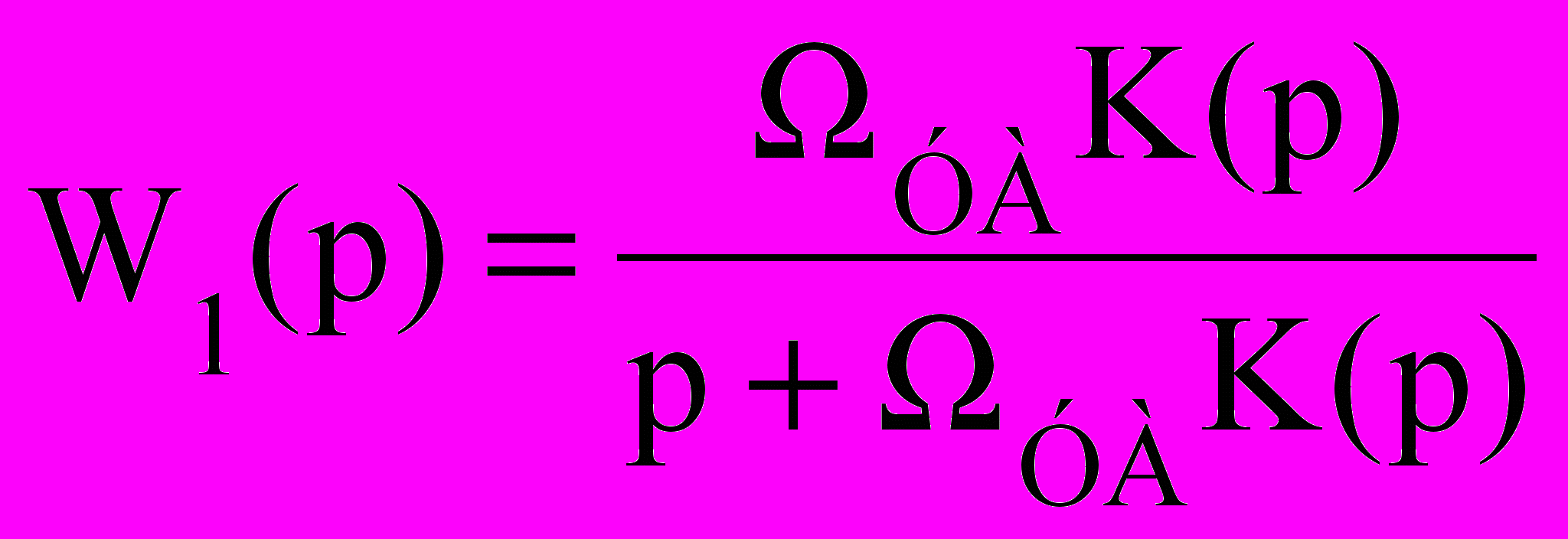де 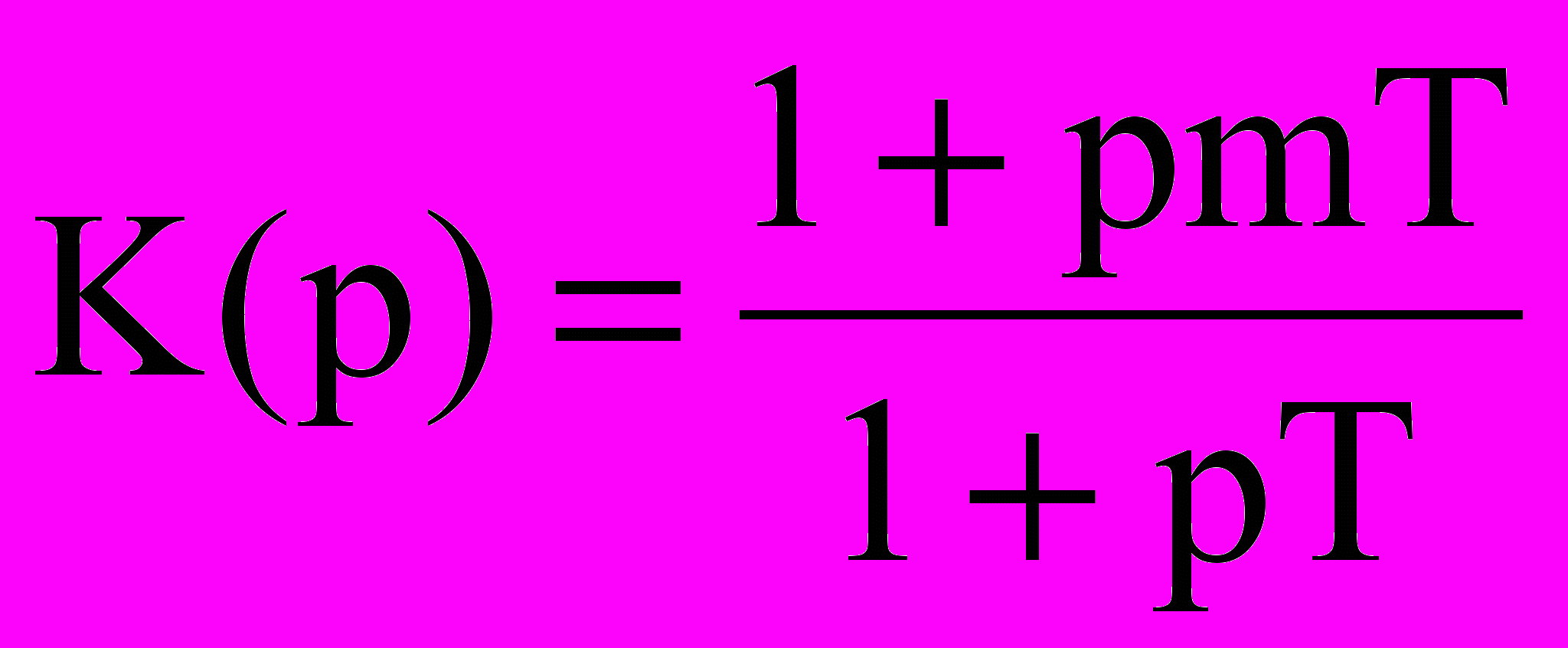– КЧХ ПІФ петлі керування. Смуга утримання автономної ФАПЧ (_УА) має приблизно дорівню­ва­ти девіації частоти модульованого сигналу, тобто _УА ≈ _М. Форма АЧХ 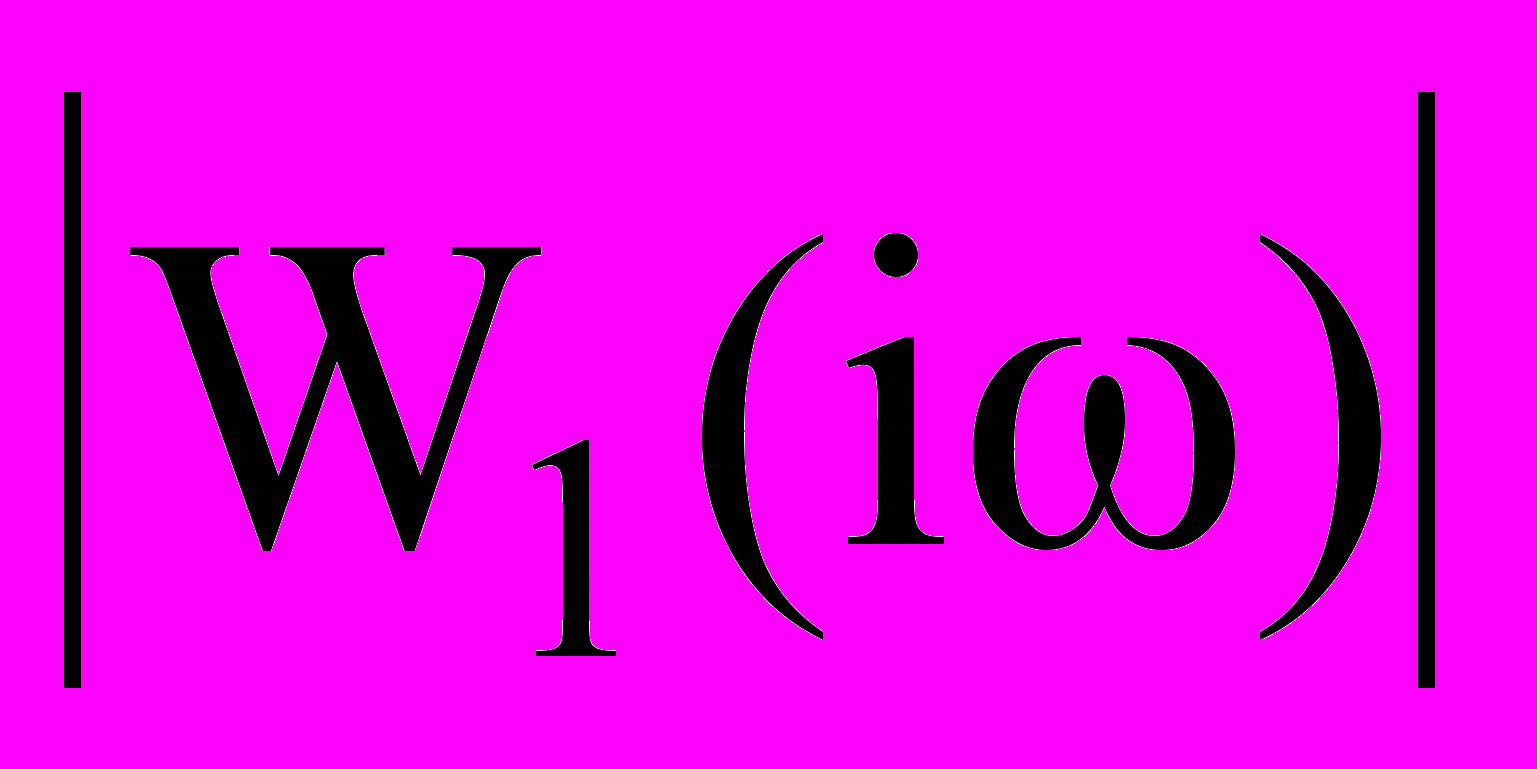залежить від ширини смуги =1/T та коефіцієнта m ПІФ і є неперервною функцією частоти. Результати узгодження АЧХ СФД і спектра ЧМ сигналу зо­бра­жено на рис. 29.

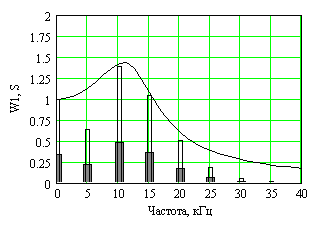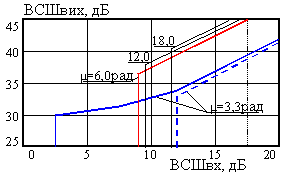Рис. 29. Узгодження АЧХ СФД (W1) зі спектром ЧМ сигналу (S) при індексі модуляції  = 3,3 рад.	Рис. 30 Залежності вихідного відношення сигнал - шум від вхідного у класичному (штрихова) та модифікованому ФАПЧ.

Для зручності порівняння на рис. 29, крім від­нос­них амплітуд гармонік сигналу з кутовою модуляцією (темні стовпчики), нанесені їх мас­штабовані значення (світ­лі стовпчики). Синтезовані значення параметрів _УА,  та m, котрі реалізують квазі­оп­ти­маль­ну АЧХ, наведено в табл. 1. Там же вказані па­раметри ВСФ та ФВЧ модифіко­ва­ного пристрою ФАПЧ (рис. 22), які дозволяють здійснювати приймання сигналу з більш глибокою куто­вою модуляцією.

Крива завадостійкості синтезованого пристрою зображена на рис. 30 штриховою лі­нією і добре узгоджується з відомими з літератури характеристиками оптимального приймача ЧМ сигналу.

Таблиця 1.

Синтезовані значення параметрів та показники завадостійкості СФД

Базовий індекс модуляції, рад	3,3
Смуга утримання FУА, кГц	32,0
Смуга ФНЧ (α/2=1/2T), кГц	5,0
β=1/(2TFУА)	0,156
m	0,16
Смуга ВСФ та ФВЧ (α0/2=1/2T0), Гц	3500
m0	0,06
Мінімальний енерге­тич­ний потенціал сигналу класичного СФД П, кГц	96
Мінімальний енерге­тич­ний потенціал сигналу модифікованого СФД П, кГц	24
Порогове ВСШ у смузі М, відн. од. / дБ	19,05/12,8

Суцільною лінією на рис. 30 показана ана­логічна крива для модифікованого при­строю ФАПЧ та індексу модуляції μ=3,3 рад, яка ілюструє можливість знач­ного зни­ження порогу завадостійкості. Крім того, у модифікованому пристрої ФАПЧ існує мож­ли­вість приймання широкосмугового ЧМ сигналу (μ=6,28 рад; 12 рад; 18 рад) пристроєм з вузькою ефективною смугою. Велика динамічна похибка, яка при цьому ви­никає, буде зменшена ВСФ і не призведе до зриву синхронізму. Проведене моделю­вання модифікованого ФАПЧ показало можливість збільшення завадостій­кос­ті прий­мання сигналів з кутовою модуляцією. Без зміни стандарту модуляції, тобто при вико­рис­танні ЧМ сигналу з індексом модуляції μ=3,3 рад, мо­дифікований СФД дає мож­ливість знизити шумовий по­ріг (тобто збіль­шити чутливість приймача) на 10 дБ. Якість ви­хідного сигналу по­гіршується з ростом інтенсивності шуму, але синхронний режим зберігається. За умови зміни стандарту модуляції ЧМ сигналу зі збільшенням ін­дексу модуляції до μ=6,28 відно­шен­ня сигнал-шум на виході моди­фі­кованого СФД збільшиться на 8 дБ без збільшення енер­гетичних параметрів сигналу на вході прий­ма­ча. Подальше збіль­шення індексу модуляції до 12-18 рад збільшує ВСШ на ви­ході ще на 1-2 дБ і є недо­цільним.

Наступною задачею, розглянутою у дисертаційній роботі, є застосування розроб­ле­них методів підвищення завадостійкості до проектування оптимального приймача ци­ф­рових радіосигналів. Цифрові радіосигнали з фазовою маніпуляцією широко за­сто­со­вують у сучасних системах радіонавігації. Одною з основних проблем приймання цих сиг­налів є наявність шумового порогу детектора, особливо за неможливості збіль­шен­ня по­тужності сигналу. Наприклад, у системах супутникової навігації, внаслідок відда­ле­нос­ті космічного апарату КА (висота геосинхронної орбіти КА системи GPS ста­но­вить 20 240 км) та об­меженої потужності передавача КА, потужність цифрового радіо­сигналу, прийнятого на всеспрямовану антену поблизу поверхні Землі, становить від –165 до –160 дБ Вт, що сут­тє­во обмежує функціональні можливості системи.

Невіддільною складовою приймача цифрового радіосигналу є схема стеження за но­сійною частотою (ССН), яка відслідковує допплерівські відхилення частоти сигналу і забез­пе­чує син­хрон­ний режим роботи інших схем приймача. Змен­шення потуж­ності сигналу внаслідок затінення антени або роботи у закритих при­мі­щеннях у першу чергу порушує синхронізм ССН, що викликає необхідність пов­тор­но­го вход­жен­ня у зв’я­зок, яке триває 5..20 хвилин. Отже, підвищення завадостійкості ССН приймача циф­рових радіосигналів значно підвищить його експлуатаційні ха­рак­теристики.

ССН сучасної АС є фактично синхронним фазовим детектором, побудованим на ос­нові пристрою ФАПЧ. В ро­бо­ті проведено імітаційне моделювання такого де­тек­тора за припущень щодо параметрів пристрою та цифрового ра­діосигналу, характерних для приймачів системи GPS. Зобра­же­ні на рис. 31 результати імітаційного моделювання показали, що за однакових рів­нів завад пристрій рис. 22 має суттєво кращі характерис­тики утримання і схоплення, ніж класичний детектор (світлі лінії).



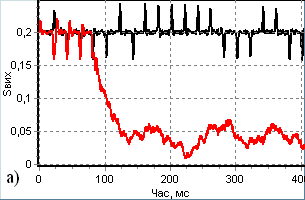
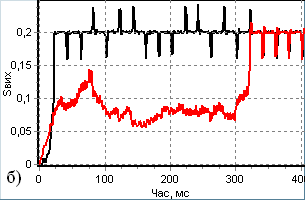
Рис. 31. Процеси утримання (а) і схоплення (б) цифрового радіосигналу у класичній (світлі лінії) та модифікованій (темні) ССН.

Час схоплення для різних реалізацій та за різних значень параметрів модифіко­ва­ного пристрою становить від 3 мс до 20 мс. Час схоплення синхронізму у кла­сич­ному ФАПЧ за тих самих умов становить 300..700 мс, тобто є на 1-2 порядки більшим. За прий­нятих значень параметрів ФАПЧ та енергетичному потенціалі сигналу 20 дБ Гц смуга схоплення модифікованого ССН становить 5 100 Гц, порівняно із 1 170 Гц у класичної ССН із номінальним значенням енергетичного потенціалу 30 дБ Гц.

Досліджений пристрій зберігає здатність утримувати носійну частоту цифрового сиг­налу в режимі фазової синхроні­зації при енергетичному потенціалі на вході 16 дБ Гц, а здатність до де­тектування цифрового сигналу із задовільною імовірністю про­пу­щених бітів – при 20 дБ Гц, що відповідно на 8 дБ Гц та 4 дБ Гц нижче, ніж пороги інформаційного та навігаційного режимів у ві­домих з літератури приймачів сигналів супутникової навігації.

Таким чином, застосування запропонованого пристрою (рис. 22) та розроблених у роботі методів вибору його параметрів дає можливість технічної реа­лі­зації приймання цифрового радіосигналу зі значно меншим енергетичним потенціалом та ско­рочення часу входження в синхронізм ССН цифрового радіоприймача.

У додатках до роботи наведені виведення використаних математичних моделей, за­проваджені у роботі означення та доведена теорема, описи інтерфейсів розробленого програмного забезпечення, акти впровадження результатів дисертаційних досліджень.

Основні результати І Висновки

Основним результатом дисертаційної роботи є теоретичне обґрунтування та нове розв’язання науково-прикладної проблеми розробки методів підви­щен­ня завадо­стій­кості пристроїв синхронізації зі збере­жен­ням їх динамічних властивостей.

До найважливіших теоретичних та практичних результатів можна віднести такі:

1. Виявлено тенденції актуального розвитку методів аналізу та оптимального син­те­зу завадостійких пристроїв фазової синхронізації; сформульовано нові наукові за­дачі, що випливають з теорії оптимальної нелінійної фільтрації, теорії марковських про­цесів та теорії коливань. Для реалізації поставлених задач необхідним є подальший розвиток теорії у напрямку усунення неузгодженості методів аналізу випадкових та детерміно­ваних збу­рень та розробка методів оптимального синтезу, які усувають протиріччя між динамічними властивостями та завадостійкістю пристрою.

2. Розвинуто теорію статистичного представлення випадкових процесів у стохас­тич­них динамічних системах. Вперше запропоновано описувати статистичну динаміку таких систем поведінкою перетину розподілу імовірності на фазовому портреті не­збу­реної сис­те­ми. Обґрунтовано вибір перетину на рівні 1/е², який названо "характерним перетином", як найбільш інформативного.

Для лінійних систем першого і другого порядку виявлені основні закономірності поведінки характерного перетину. Отримані аналітичні вирази для координат та роз­мірів усталеного характерного перетину в околі стійких особливих точок. Доведено теорему, яка дає можливість за значеннями параметрів та початковими умовами без проміж­них розрахунків виявити одностороннє або двостороннє зростання розмірів характер­ного перетину в околі нестійких особливих точок.

Для нелінійних динамічних систем першого і другого порядку виявлені основні особ­ливості поведінки характерного перетину, викликані обмеженістю потенціальної функції та можливістю наявності декількох станів рівноваги. Виявлена біфуркаційна змі­на характеру випадкового процесу – перехід від розривно-стаціонарного до неста­ціонарного. Запроваджені в роботі означення локальної стійкості до шуму, області при­тягання локально стійкої точки рівноваги та граничних (біфуркаційних) значень параметрів у стохастичних системах дали можливість уніфікувати аналіз детер­міно­ва­них та випадкових збурень динамічних систем.

3. Запропоновано і реалізовано застосування розвинутої теорії біфуркацій стохас­тичних динамічних систем до аналізу завадостійкості пристроїв фазової синхронізації. Порівняльним аналізом результатів застосування методу імітаційного моделювання (аналізу ансамблів реалізацій), розв’язків рівняння Фокера-Планка (аналізу розподілів похибки синхронізації) та кумулянтного аналізу у гаусовому наближенні виявлена область застосування кумулянтного методу. Встановлено, що кумулянтний аналіз дає виграш обчислювальної складності на два порядки, похибку визначення СКВ фази – до 10%, похибку визначення граничних параметрів шуму – до 3%.

На основі виявлених якісних відмінностей статистичної динаміки ФАПЧ запро­вад­жено означення шумової смуги схоплення (ШСС), як нової характеристики працездат­ності пристроїв фазової синхронізації. Уточнено раніше запроваджене означення шу­мо­вої смуги утри­мання (ШСУ). На прикладах ФАПЧ другого порядку виявлений статистичний та імовірнісний зміст ШСС та ШСУ.

Порівняння визначених значень ШСС та ШСУ із відомими для детермінованих сис­тем значеннями показало адекватність кумулянтної моделі. Побудована та дослід­жена кумулянтна модель ФАПЧ у ексцесному наближенні показала, що урахування ви­щих кумулянтів збільшує обчислювальну складність на порядок, точність визна­чен­ня СКВ фази – до 0,5%, але майже вдвічі зменшує область застосування методу.

4. Розроблено новий метод аналізу статистичної динаміки нелінійного ФАПЧ, який відрізняється від існуючих можливістю урахування впливу на процес синхронізації де­термінованих і випад­ко­вих збурень з однакових позицій – визначення границь пра­це­здатності пристрою. При проектуванні СФД, призначених для приймання ЧМ сигналу на фоні шуму, метод не вимагає апріорно завдавати параметри завади. Метод і його про­грамна реалізація дають можливість використовувати на етапі про­ек­тування ві­до­мий критерій мінімуму фазової похибки, а крім того, вперше запропо­но­вані для такого викорис­тан­ня критерії максимальної граничної інтенсивності завад та максимального діапазону стеження. Використання цих критеріїв виграш за окре­мими показниками від декількох відсотків до декількох разів порівняно з лінійним пара­мет­рич­ним синтезом.

5. Обґрунтована та розроблена структура модифікованого пристрою ФАПЧ, який забезпечує значне підвищення завадостійкості зі збереженням динамічних власти­вос­тей шляхом локального зменшення рівня сигналу розузгодження фазового детектора.

Імітаційним моделюванням модифікованого пристрою у випадку дії тільки випад­кової завади показана можливість підвищення граничної завадостійкості до 2,5..5 разів та розширення діапазону стеження на 25%..200%, показано, що виграш ВСШ за по­туж­ністю становить 14-18 дБ для безфільтрового ФАПЧ та 4-10 дБ для ФАПЧ з ін­те­груючим фільтром. Шляхом аналізу нелінійної математичної моделі у випадку дії тіль­ки детермінованих збурень визначена область простору параметрів пристрою, в межах якої пристрій є глобально стійким, що дає можливість проектування завадостійких пристроїв синхронізації з широкою смугою схоплення.

6. На прикладах типових задач радіолокації, радіозв’язку та радіонавігації показана можливість підвищення завадостійкості пристроїв фазової синхронізації приймачів ра­діосигналів шляхом застосування розробленої методики вибору параметрів пристроїв синхронізації без збільшення енергетичних параметрів сигналу.

7. Для радіолокаційної задачі показано, що параметричний синтез кумулянтним ме­тодом дає виграш до 5% за завадостійкістю та до 40% за діапазоном стеження. Роз­ра­ховані параметри модифікованого ФАПЧ, які дають можливість збільшити завадо­стій­кість більш ніж у 3 рази, а діапазон стеження і смугу схоплення від 2 до 6 разів.

8. Для задачі проектування синхронного фазового детектора ЧМ сигналу показана можливість технічної реалізації приймання сигналів з глибокою кутовою модуляції (з індексами до 18 рад). Визначені параметри і структура пристрою, які дають можли­вість зни­зити на 10 дБ шумовий поріг (за індексу модуляції 3,3 рад) або збільшити на 8 дБ від­ношення сигнал-шум (ВСШ) вихідного сигналу без збільшення ВСШ на вході (за індексу модуляції 6,28 рад). Показано, що подальше збільшення індексу модуляції (до 12..18 рад) збільшує ВСШ на виході на 1..2 дБ і є недоцільним.

9. Для радіонавігаційної задачі на прикладі вибору параметрів схеми стеження за носійною частотою приймача супутникового навігаційного сигналу системи GPS по­ка­зана можливість збільшення завадостійкості на 2 дБ шляхом нелінійного параметри­ч­ного синтезу та на 8..12 дБ застосуванням модифікованого пристрою ФАПЧ. Моде­лю­вання показало, що смуга схоплення пропонованого пристрою у 4,8 разів більша, а час схоплення у 30..100 разів менший, ніж у існуючих аналогів.

10. Використання розроблених у роботі тео­ретичних положень та математичних моделей дає можливість оптимізувати параметри ФАПЧ з ура­ху­ванням впливу де­тер­мінованих збурень у вигляді полігармонічного моду­лювального сигналу та сигналу із заданою формою спектру, а також враховувати вплив частотних і фазових флуктуацій та адитивних завад.

Список праць автора за темою дисертації

1. Мандзий Б.А., Бондарев А.П. Качественный анализ статистической динамики сис­темы ФАПЧ // Известия ВУЗов МВ и ССО СССР. Радиоэлектроника. –1988. –№ 12. –С.74-76.
   
2. Бондарєв А.П., Мандзій Б.А. Аналіз граничної завадостійкості системи фазо­вої синхронізації // Теоретична електротехніка. –1998. –№ 54. –С.14-17.
   
3. Бондарєв А.П., Капшій О.В. Критерій граничної завадостійкості системи фазо­вої син­хро­нізації // Вісник ДУ "ЛП". Радіо­еле­к­троніка та телекомуні­кації. –1998. –№ 352. –С. 98-100.
   
4. Бондарєв А.П., Харха­ліс О.В. Динаміка систе­ми з періодичною нелінійністю під впливом шумів // Вісник ДУ"ЛП". Радіо­електроніка та телекомунікації. –1999. –№ 367. –С.28-30.
   
5. Бондарєв А.П. Вплив міжканальних і внутрішньоканальних завад на синхроні­за­цію приймача // Моделювання та інформаційні технології. –2002. –Вип. 18. –С. 207-211.
   
6. Бондарєв А.П. Енергетичні умови зриву синхронізації // Моделювання та інфор­ма­ційні технології. –2002. –Вип.19. –С.171-178.
   
7. Бондарєв А.П. Залежність спектру фазових флуктуацій пристрою синхро­нізації від характеристик фазового детектора // Моделювання та інформаційні технології. –2003. –Вип.20.– С. 198-202.
   
8. Бондарєв А.П. Параметричний синтез ФАПЧ з урахуванням подібної завади і шу­му // Вісник НУ"ЛП". Радіо­елек­троніка та телекомунікації. –2003. –№ 477. –С. 83-87.
   
9. Бондарєв А.П. Моделювання пристрою синхронізації з підвищеною завадостій­кіс­тю // Вісник НУ "ЛП". Електро­енер­гетичні та електро­ме­ханічні системи. –2003. –№ 479. –С. 24-29.
   
10. Мандзій Б.А., Бондарєв А.П. Вплив характеристики фазо­вого детектора на якість та завадостійкість синхронізації // Відбір і обробка інформації. –2003. –Вип. 19(95). –С. 63-68.
    
11. Бондарєв А.П. Теоретичні засади аналізу завадостійкості пристроїв синхронізації // Вісник НУ "ЛП". Радіо­електро­ніка та телекому­ні­кації. –2004. –№ 508. –С. 3-18.
    
12. Бондарєв А.П. Статистичний зміст шумової смуги схоплення ФАПЧ // Збірник наукових праць Інституту проблем моделювання в енергетиці ім. Г.Є.Пухова. –2005. –Вип. 29. –С. 128-132.
    
13. Бондарєв А.П., Коханий І.О. Шумові біфуркації безфільтрової ФАПЧ в часовій області // Моделювання та інформаційні технології. –2005. –Вип. 30. –С. 105-109.
    
14. Бондарєв А.П. Шумові смуги утримання і схоплення пристроїв синхронізації // Вісник Вінницького політехнічного інституту. –2005. –№5(62). –С.113-116.
    
15. Бондарєв А.П. Статистичний аналіз ФАПЧ другого порядку в часовій області // Вісник НУ"ЛП". Радіо­електро­ніка та телекому­ні­кації. –2005. –№ 534. –С. 74-77. 
    
16. Бондарєв А.П. Гранична завадостійкість синхронізації з фазомодульо­ва­ним сигналом // Збірник наукових праць Інституту проблем моделювання в енергетиці ім. Г.Є.Пухова. –2005. –Вип. 31. –С. 116-121.
    
17. Бондарєв А.П., Лазько О.В., Недоступ Л.А. Вплив негаусовості розподілу фазової похиб­ки на якість синхронізації та граничну завадостійкість ФАПЧ // Теоретична електротехніка. –2005. –№ 58. –С.8-14.
    
18. Мандзій Б.А., Бондарєв А.П. Статистична динаміка пристрою синхронізації з фа­зо­моду­льо­ваним сигналом // Відбір і обробка інформа­ції. –2005. –Вип. 23(99). –С. 79-82.
    
19. Bondarev A., Lazko O., Nedostup L. Synchronization quality analysis with consideration of high cumulants of phase error distribution // Electronics and electrical engineering. –Kaunas: Technologija. –2006. –No 2(66). –P. 17-20.
    
20. Бондарєв А.П. Розширення робочої ділянки характеристики фазового детектора // Збірник наукових праць Інституту проблем моделювання в енергетиці ім. Г.Є.Пу­хо­ва. –2006. –Вип. 34. –С. 81-90.
    
21. Бондарєв А.П. Нелінійний параметричний синтез слідкуючого фазового детек­то­ра // Радіоелектроніка і інформатика. –2006. –№1(32). –С. 27-30.
    
22. Бондарєв А.П. Зниження шумового порогу фазового автопідстроювання частоти // Вісник НУ"ЛП". Радіо­електро­ніка та телекому­ні­кації. –2006. –№ 557. –С. 25-29 .
    
23. Бондарєв А.П. Шумові та динамічні властивості модифікованого пристрою фазо­во­го автопідстроювання частоти // Радіотехніка. –2006. –Вип.146. –С. 171-177.
    
24. Бондарєв А.П., Мартинів М.С. Порівняльне імітаційне моделювання пристроїв слід­кування за несучою радіолокаційного сигналу // Збірник наукових праць Ін­сти­туту проблем моделювання в енергетиці ім. Г.Є.Пухова. –2006. –Вип. 35. –С. 85-90.
    
25. Мандзій Б.А., Бондарєв А.П. Підвищення завадостійкості демодулятора фазо­мо­ду­льованого сигналу // Відбір і обробка інформа­ції. –2007. –Вип. 26(102). –С. 65-73.
    
26. Бондарєв А.П., Давіденко С.В., Павлов Б.О. Параметричний синтез синхронного детектора багатоканального групового сигналу з частотною модуляцією // Вісник Хмельницького національного університету. –2007. –№2, Т.2(90). –С. 147-150.
    
27. Бондарєв А.П. Параметричне та схемотехнічне підвищення завадостійкості фазово­го демодулятора // Інформаційні технології та комп'ютерна інженерія. –2007. –№2 (9). –С.29-33.
    
28. Mandzij B., Bondarev A. Symulacja komputerowa układu synchronizacji fazowej w obecności sygnału PSK // Zeszyty naukowe Wyższej Szkoły Informatyki w Łodzi. – Łódz: ReadMe, 2006. –Vol.5, Nr 1. –P. 31-36.
    
29. Бондарєв А.П., Давіденко С.В. Підвищення завадостійкості приймача супутни­ко­вих навігаційних сигналів // Сучасні досягнення геодезичної науки та виробни­ц­т­ва. Збірник наукових праць Західного геодезичного товариства. –2007. –С. 109-114.
    
30. Патент України на винахід № 66435. H03L7/00 / Бондарєв А.П., Мартинів М.С. "Пристрій фазової автопідстройки частоти". Заявка № 4869869 від 01.10.90; Опубл.: Бюл. №5, 2004. –4 с.
    
31. Бондарев А.П., Мандзий Б.А. Выбор параметров СФС с учетом шума и узкопо­лос­ной помехи // Тезисы докладов всес. науч.-техн. конференции "Развитие и совер­шен­ство­вание устройств синхрони­зации в системах связи". Горький, 1988. С. 66.
    
32. Бондарев А.П., Мартынив М.С. Помехоустойчивое устройство ФАПЧ // Тезисы докладов науч.-техн. конференции "Разви­тие и совершенствование устройств син­хрони­зации в системах связи". Ярославль, 1993. С. 14.
    
33. Bondarev A. Sync Devices Noise-Immunity Analysis Theoretical Basis // Proceeding of the Internatio­nal Con­ference TCSET'2004. Lviv-Slavsko, 2004. P. 27-34.
    
34. Бондарєв А.П. Шумові смуги утримання і схоплення пристроїв синхронізації // Ма­теріа­ли міжнародної НТК "Сучасні проблеми радіоелек­тро­ніки, телеко­мунікацій та приладобуду­ван­ня”. Вінниця, 2005. С. 57-58.
    
35. Bondarev A. Decreasing of Phase Locked Loop Noise Threshold // Proceeding of the Interna­tio­nal Con­ference TCSET'2006. Lviv-Slavsko, 2004. P. 508-509.
    
36. Bondarev A., Lazko O., Nedostup L. Anallysis of Kurtosis Distribu­tion of Syncro­ni­zation Error // Proceeding of the Internatio­nal Con­ference TCSET'2006. P. 524-526.
    
37. Бондарєв А.П. Програма нелінійного параметричного синтезу синхронного фазо­во­го детектора // Збірник матеріалів міжву­зів­ської науково-технічної кон­ференції науково-педа­гогіч­них працівників. – Львів: Лі­га-прес, 2006. – 248с. / С. 189-190.
    
38. Бондарєв А.П. Нелінійний параметричний синтез синхронного фазового детекто­ра // Материалы 10-го юбилей­но­го международного молодежного форума "Радио­электроника и молодежь в ХХІ веке". –Харків: ХНУРЕ, 2006. С.130.
    
39. Mandzij B., Bondarev A. Nonlinear mathematical model of a sync phase detector sta­tis­tical dynamics // V Sympozjum "Modelowanie i symulacja komputerowa w technice". –Łódź: 2006. P. 87-90.
    
40. Бондарєв А.П. Параметричне та схемотехнічне підвищення завадостійкості фазо­во­го демодулятора // Матеріали другої міжнародної НТК " Сучасні проблеми мікро­елек­троніки, радіоелектроніки, телекомунікацій та приладобудування” СПРТП2-2006”. Вінниця, 2006. С. 136-137.
    
41. Бондарев А.П. Повышение помехоустойчивости демодулятора беспроводных средств телекоммуникации // Материалы 1-й Международной научной конференции "Глобальные информационные системы. Проблемы и тенденции развития". Харь­ков-Туапсе, 2006. С. 314-315.
    
42. Бондарєв А.П., Мартинів М.С. Порівняльне імітаційне моделювання пристроїв слід­кування за несучою радіолокаційного сигналу // Науково-практична кон­фе­ренція "Сучасні проблеми телекомунікацій – 2006". Матеріали. Львів, 2006. С.16-17.
    
43. Бондарєв А.П., Давіденко С.В., Павлов Б.О. Параметричний синтез синхронного детектора багатоканального групового сигналу з частотною модуляцією // П’ята МНПК "Комп’ютерні системи в автоматизації виробничих процесів". Реферативний збірник наукових праць. Хмельницький, 2007. С. 42.
    
44. Бондарєв А.П., Мандзій Б.А. Підвищення завадостійкості приймання сигналу з гли­бокою кутовою модуляцією // Матеріали ІІІ МНТК "Сучасні проблеми радіо­елек­троніки, телекомунікацій та приладобудування". Вінниця, 2007. С. 122-123.
    
45. Бондарєв А.П., Давіденко С.В. Схемотехнічне підвищення завадостійкості детек­то­ра цифрових радіосигналів // Матеріали ІІІ МНТК "Сучасні проблеми радіоелектро­ніки, телекомунікацій та приладобудування". Вінниця, 2007. С. 121.