Geum.ru

Міністерство освіти І науки України Національний університет “Львівська політехніка”

Вид материалаАвтореферат

Содержание


Рис.5. Поведінка характерного перетину в околі стійкого вузла (а, б, в) і фокуса (г).
Рис.6. Стрижнева модель (а) та еволюція розподілу (б, в) ВП у нелінійній ДС.
Рис.7. Фазовий портрет (а) бістабільної нелінійної ДС та варіанти поведінки характерного перетину (б).
Подобный материал:
1   2   3   4   5   6   7

Рис.5. Поведінка характерного перетину в околі стійкого вузла (а, б, в) і фокуса (г).


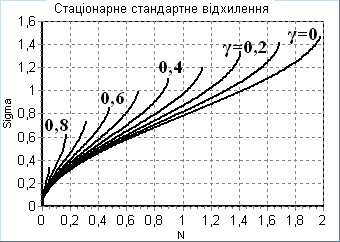
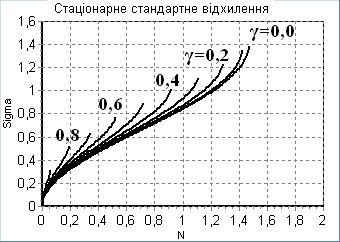
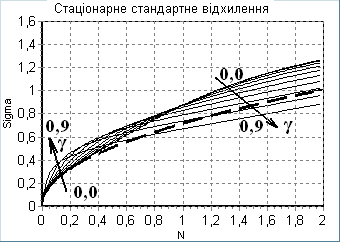
Числовим інтегруванням (5) виявлені основні закономірності поведінки харак­тер­ного перетину в околі особливих точок ДС. Центр перетину завжди рухається вздовж траєкторій фазового портрету незбуреної лінійної ДС. В околі стійких особ­ли­вих точок (рис. 5) характерний перетин має стійке положення і стійкий розмір, який зале­жить від інтенсивності шуму. В околі нестійких особ­ли­вих точок і по­ло­жен­ня і розмір перетину є нестійкими. Залежно від положення і розмірів почат­ко­во­го перетину, згідно з Теоремою 1, перетин може або досягнути або не досягнути осо­б­ливої точки. Торкання перетином нестійкої особливої точки або кривої (вхідної сепаратриси) приз­водить до двостороннього необмеженого зростання розмірів пере­тину, недоторкання – до односторонньо обмеженого зростання.

Як приклад двовимірної стохастичної ДС розглянуто вплив випадкової напруги на послідовне коливальне коло. В результаті аналізу встановлено, що канонічне рівняння уста­леного характерного перетину (еліпсу) на площині "струм котушки – напруга кон­ден­сатора" точно збігається з рівнянням енергетичного балансу в колі.

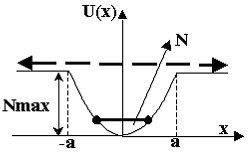
Особливостями нелінійних ДС є негаусовість стаціонарного розподілу, обме­же­ність потенціальної функції та наявність більше одного стану рівноваги. Застосуван­ня стрижневої моделі до ДС з обмеженою потенціальною функцією (рис. 6 а) пока­зує наявність біфуркації за умов перевищення енергією збурення (N) глибини потен­ціальної западини. ВП у такій ДС є нестаціонарним, а його дисперсія необмежено зро­стає незалежно від значення N, але інтегрування рівняння (2) проказало, що для докритичних значень N розподіли в межах западини і поза нею (рис. 6 б) форму­ють­ся незалежно і мають принципово різний характер, а за рівнів шуму більших від кри­тичного (рис. 6 в) межа потенціальної западини впливає тільки на кількісні по­казники розподілу. Це підтвердило якісну правильність стрижневої моделі і дало підстави для формулю­вання таких означень.

Означення. Точка стійкої рівноваги є локально стійкою до шуму, якщо існують початкові розподіли, за яких час встановлення форми розподілу менший, ніж час виникнення моди в околі іншої точки рівноваги.

Означення. Граничним рівнем завад є рівень, за якого зникають локально стій­кі до шуму точки.

а) б) в)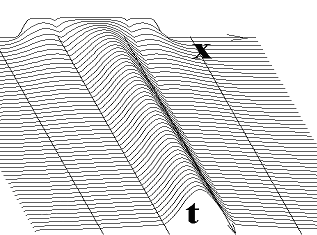

Рис.6. Стрижнева модель (а) та еволюція розподілу (б, в) ВП у нелінійній ДС.


В якості бістабільної ДС проаналізовано колове каскадне з’єднання двох інерцій­них інверторів, фазовий портрет якого (рис. 7 а) має два стійких вузли і сідло. За малих рівнів шуму характерний перетин розподілу прямує до стаціонарного, який, за­лежно від початкових значень, охоплює одну (серії 1, 2 і 3 на рис. 7 б) або обидві (се­рія 4) точ­ки стійкої рівноваги. Зі збільшенням рівня шуму вище деякого гра­нич­ного зна­чен­ня розмір характерного перетину необмежено зростає незалежно від початкових умов.


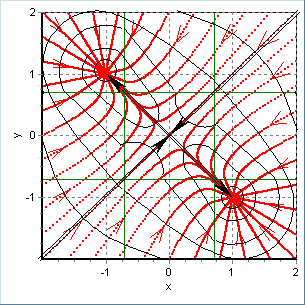
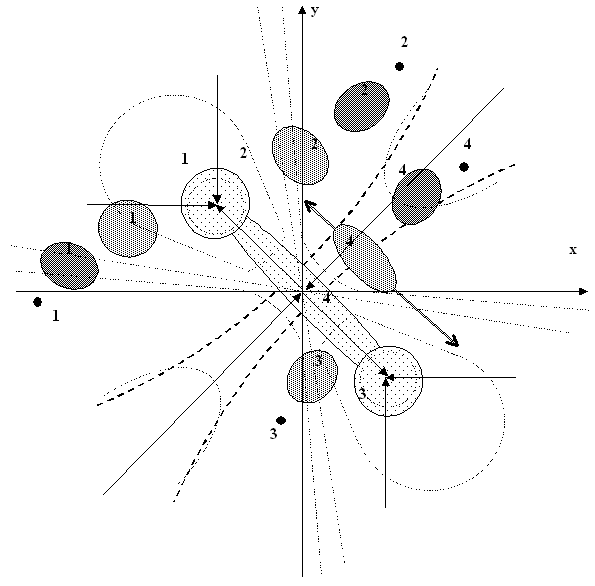
Рис.7. Фазовий портрет (а) бістабільної нелінійної ДС та варіанти поведінки характерного перетину (б).


Безпосереднім інтегруванням стохастичного рівняння (1) вияв­лені якісні особ­ли­вості реалізацій ВП, які відпові­да­ють описаній бі­фуркації. За малих зна­чень шуму (лінія на рис. 8) ВП є ро­зрив­но-ста­ціонарним, тобто релізація пе­ре­буває в околі одного зі станів рів­но­ваги із рідкими перескоками в окіл іншого, а за великих (точки на рис. 8) – тривалий час перебуває в око­лі не­стій­кої точки, а інтервали стаціонар­ності в реалізації від­сут­ні. Дослід­ження бістабільної ДС дало можли­вість озна­чити такі поняття як об­ласть притяган­ня локаль­но стійкої до шуму точки та обмеженість або необмеженість цієї області, а також вста­новити статис­тич­ний зміст цих понять.

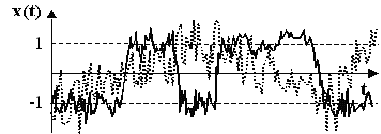Рис. 8. Реалізації випадкового процесу в бістабільній системі.
Виявлені якісні особливості статистичної динаміки ДС, які означені вище, утво­рю­ють понятійний апарат теорії стохас­тич­них біфуркацій. Разом з детер­мі­нованим опи­сом ВП кумулянтними моделями цей апарат уможливлює уніфікований підхід до ана­лізу дії на ДС детермінованих і випадкових збу­рень, а саме – знаходження гранично допустимих (біфуркаційних) значень параметрів ДС і завад.

Третій розділ дисертаційної роботи присвячений адаптації запроваджених по­нять теорії стохастичних біфуркацій до особливостей пристроїв фазової синхроніза­ції і роз­роблення на цій основі методу аналізу граничної завадостійкості пристроїв. Коефіцієн­ти зносу стохастичних рівнянь, які описують пристрої синхронізації і за­ле­жать від різниці фаз, є періодичними і обмеженими функціями, а потенціальна функція від­по­від­них динамічних систем має нескінченну кількість екстремумів і також може бути обмеженою. Стохастичне рівняння (1) для ФАПЧ 1-го порядку має вигляд

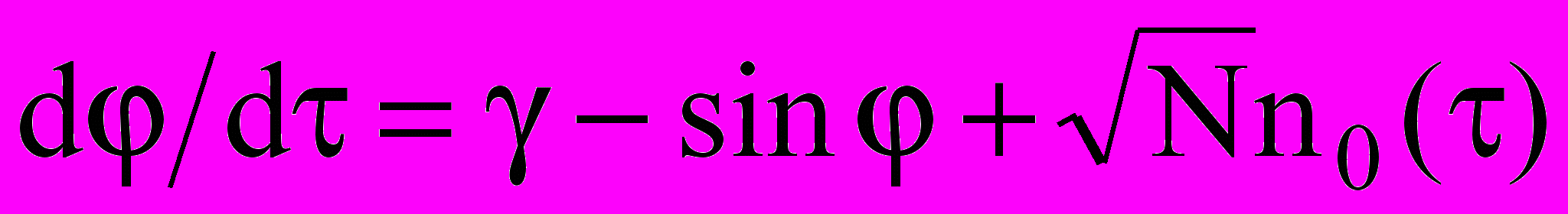, (6)

де  – добуток часу і смуги утримання, φ – повна різниця фаз КГ і сигналу, γ – нормована по­чат­кова розстройка частот КГ і сигналу. У рівняння Фокера-Планка (2) підставлено F(x)=sin x – γ, а рівняння еволюції кумулянтів (4) набуває вигляду

(7)

де mφ, Dφ – середнє значення та дисперсія фазової похибки.