Geum.ru

Міністерство освіти І науки України Національний університет “Львівська політехніка”

Вид материалаАвтореферат

Содержание


Рис.13. Типові реалізації ВП в межах ШСУ (а), поза межами ШСУ (б) та імовірність перебування у квазісинхронному режимі (в).
Рис.14. Типові реалізації ВП в межах ШСС (а), поза межами ШСС (б) та імовірність попадання до найближчої стійкої точки (в).
Рис.15. Перехідні процеси у ФАПЧ з шумом за наявності кутової модуляції, подані еволюцією характерного перетину (а) та часовою з
Подобный материал:
1   2   3   4   5   6   7

Рис.13. Типові реалізації ВП в межах ШСУ (а), поза межами ШСУ (б)
та імовірність перебування у квазісинхронному режимі (в).


Розв’язки рівнянь (8) за віддалених початкових умов показують, що в межах ШСС перехідний процес закінчується в околі одного стану рівноваги (рис. 14 а), а поза ме­жа­ми ШСС – в околах різних (рис. 14 б). Імовірність Pm попадання ВП в окіл тої самої стійкої точки, що і траєкторії детермінованої системи, зображена на рис. 14 в. З грани­цею ШСС збігається крива Pm=0,9. В межах ШСС тривалості перехідних про­цесів в детермінованій та сто­хас­тичній ФАПЧ однакові. Середня три­ва­лість перехідного процесу поблизу границі ШСС збільшується через більшу імовірність проковзу­ван­ня до віддалених станів рів­но­ваги. Виявлений статистичний зміст ШСС дає змогу визна­чити граничну інтенсивність шу­мо­вої завади, за якої трива­лість вход­жен­ня в син­хронізм лишається незмінною, що важливо для проектування зава­достійких ФАПЧ.

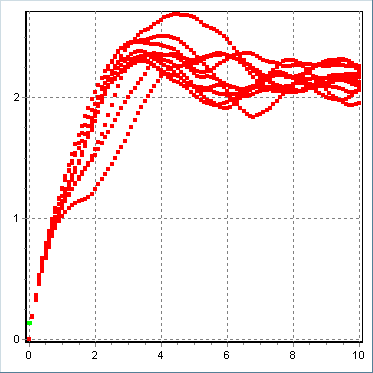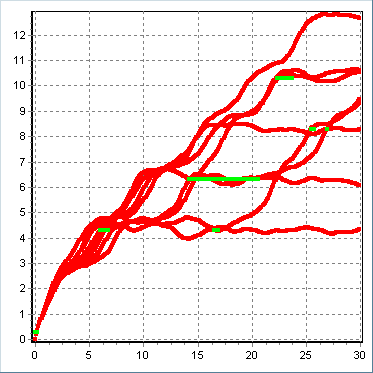а) б) в)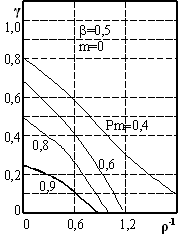

Рис.14. Типові реалізації ВП в межах ШСС (а), поза межами ШСС (б) та імовірність попадання до найближчої стійкої точки (в).


Наступним завданням, яке вирішено у третьому розділі, був аналіз впливу вищих ку­мулянтів густини розподілу фазової похибки на точність отриманих результатів. Для цього були виведені рівняння еволюції перших чотирьох кумулянтів у ексцесному набли­женні, на відміну від нормального наближення в системі (7). Обчислювальна склад­ність інтегрування отриманих рівнянь приблизно в 8 ра­зів більша, ніж ін­те­гру­вання рівнянь (7), але майже на порядок менша, ніж у випадку аналізу ансамблю реалі­зацій стохастичного рівняння (6) або інтегрування у часткових похідних відпо­від­ного рівняння Фокера-Планка. Виявлено, що область стійкості системи рівнянь у екс­цес­ному наближенні значно вужча, ніж рівнянь (7), але похибка визначення СКВ різниці фа­з становить десяті і соті час­тки відсотка, порів­ня­но з одиницями та де­сят­ками відсотків у гаусовому набли­женні.

Крім ФАПЧ з синусоїдною характеристикою ФД, якому відповідає рівняння (6), роз­глянуто також застосування ФД з трикутною, трапецевидною, прямокутною харак­теристиками, а також характеристикою із зонами нечутливості. Для всіх типів характе­ристик ФД кумулянтним методом виявлені границі завадостійкості ФАПЧ та визна­че­но СКВ фазової похибки за різних значень параметрів. Виявлено, що най­біль­шу за­ва­достійкість забезпечує ФД з прямокутною характеристикою (фазовий дискримінатор), а найменшу – з трикутною. Крім того, кумулянтним методом про­аналізований вплив характеристики ФД на спектр фазових флуктуацій, отримані аналітичні вирази для фор­ми спектру. Одним з результатів аналізу спектрів стало виявлення впливу інтен­сив­ності шуму не тільки на значення спектральних скла­до­вих, а і на ширину спектру, що типово для нелінійних систем.

Основним результатом третього розділу є роз­роб­ка і обґрунтування методу ана­лізу завадостійкості ФАПЧ, який полягає у виявленні умов існування стаціо­нар­ного роз­в’язку кумулянтної математичної моделі (9). Параметри стаціонарного розв’язку ха­рак­теризують якість синхроні­за­ції, а його відсутність означає зрив син­хронізму, тобто втрату працездатності пристрою. Мала обчислювальна склад­ність методу уможливлює перебір параметрів пристрою і завад у ши­ро­кому діапазоні.

В четвертому розділі проведено аналіз та параметричний синтез ФАПЧ 2-го по­ряд­ку за умов одночасної дії шуму та детермінованих збурень у вигляді фазової моду­ляції або маніпуляції. У математичній моделі (9) покладено Ф=μ sin(γMτ/β) у випадку фа­зової модуляції або Ф=μ sign sin(γMτ/β) у випадку маніпуляції (μ – індекс, γM – нор­мована частота модуляції). За умови μ > 0 система (9) є неавтономною і не має ста­ці­о­нар­ного розв’язку, тому при аналізі системи здійснюється пошук умов існування і ха­рактеристик усталених періодичних розв’язків, які відповідають режиму квазі­синхро­ніз­му у ФАПЧ.

а) б)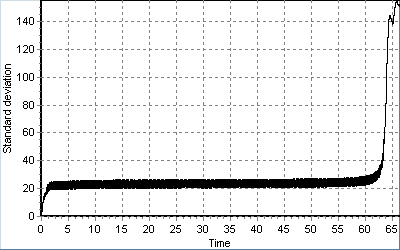

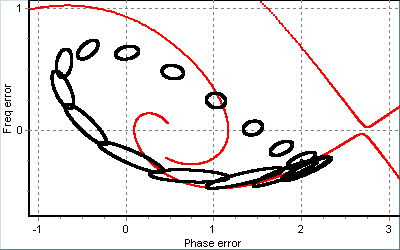
Рис.15. Перехідні процеси у ФАПЧ з шумом за наявності кутової модуляції, подані еволюцією характерного перетину (а) та часовою залежністю СКВ фази (б).


На рис. 15 зображений перехідний режим у неавтономній системі (9) за віддалених початкових умов. Зі збільшенням рівня шуму характерний перетин (рис. 15 а) може то­р­кнутися вхідної сепаратриси, що призведе до необмеженого зростання його роз­мі­ру. На відміну від автономної системи (рис. 11) між першим торканням сепа­ратри­си та різким зростанням СКВ фазової похибки може пройти значний проміжок часу, осо­б­ливо за значень параметрів, близьких до граничних. У наведеному на рис.15 б випад­ку торкання сепа­ра­триси відбулося за значення часу τ≈3..5, а характерні оз­на­ки зриву синхроніз­му, вияв­лені інтегруванням через перехідний процес, проя­ви­лися лише за значення часу τ≈62..63, тобто описаний критерій на порядок скорочує час аналізу.

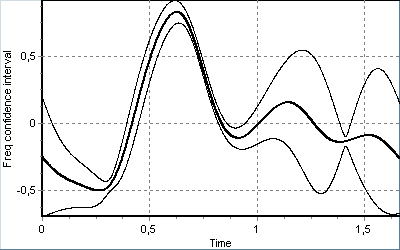
Приклади усталених періодичних розв’язків неавтономної системи (9) наведені на рис. 16 у вигляді періодичних рухів характерного перетину (а) та часових залежностей довірчого інтервалу частотної похибки (б) і СКВ фазової похибки (в).