Міністерство освіти І науки України Національний університет “Львівська політехніка”
| Вид материала | Автореферат |
СодержаниеРис. 1. Представлення випадкових процесів перетинами. Рис.2. "Стрижнева" модель (а) та еволюція розподілу (б) ВП в околі точки стійкої рівноваги. |
- Міністерство Освіти І Науки України Національний університет “Львівська політехніка”, 2021.84kb.
- Міністерство освіти І науки україни національний університет «львівська політехніка», 1080.17kb.
- Міністерство освіти І науки україни національний університет «львівська політехніка», 1068.44kb.
- Міністерство освіти І науки україни національний університет «львівська політехніка», 1259.1kb.
- Національний університет «львівська політехніка» алзаб аєд хамдан, 385.08kb.
- Міністерство освіти І науки україни національний університет «львівська політехніка», 1563.62kb.
- Міністерство освіти І науки україни національний університет «львівська політехніка», 208.38kb.
- Міністерство освіти І науки україни національний університет «львівська політехніка», 723.06kb.
- Міністерство освіти І науки України Національний університет "Львівська політехніка", 526.12kb.
- Міністерство освіти І науки України Національний університет "Львівська політехніка", 305.54kb.
Рис. 1. Представлення випадкових процесів перетинами.
Абстрагуючись від форми розподілу, можна описати густину імовірності одним перетином (точки x1 та x2 на рис. 1 б), який відображає основні характерні риси розподілу – його положення і розмір. В роботі показано, що найпростіше сформулювати умови стаціонарності для перетину, який задовольняє наступному означенню.
Означення. Характерний перетин розподілу імовірності – перетин на рівні 1/е2 від максимального значення.
Для нормального розподілу P(x) точки характерного перетину x1 та x2 є квантілями p*0,023 та p*0,977 відповідно, тобто їх координати становлять m±2σ, де m і σ – середнє значення та СКВ розподілу.
Характерному перетину стаціонарного розподілу притаманна наступна властивість.
Властивість 1. Значення потенціальної функції в усіх точках усталеного характерного перетину дорівнює енергії збудження.
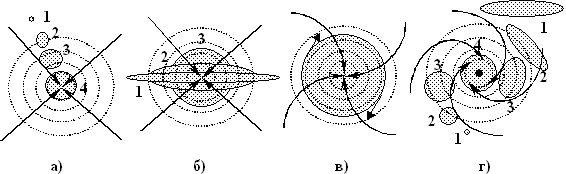
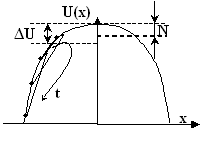
Поняття характерного перетину дає можливість моделювати випадковий процес, описаний рівняннями (1) і (2), не поведінкою усього об’єму важкого газу на потенціальному рельєфі, а поведінкою одного масивного пружного стрижня, кінці якого відповідають точкам характерного перетину. Кінці стрижня невідривно ковзають без тертя по потенціальному рельєфу (рис. 2 а) і відштовхуються один від одного тим сильніше, чим менша відстань між ними і чим більша енергія збурення N. Завдяки масивності стрижень намагається зайняти якомога нижче положення на потенціальному рельєфі. Рівновага, у відповідності до Властивості 1, наступає за виконання умови U(x1,2) = N. Приклад застосування стрижневої моделі для опису стохастичної поведінки лінійної ДС зі стійким станом рівноваги і коефіцієнтом зносу F(x) = a·x при a>0 наведено на рис. 2 для трьох різних початкових положень стрижня.
 б)
б)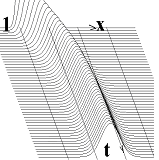
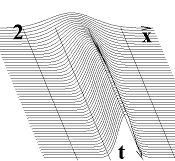
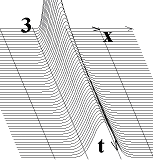
Рис.2. "Стрижнева" модель (а) та еволюція розподілу (б) ВП
в околі точки стійкої рівноваги.
Порівняння з розв’язками рівняння Фокера-Планка (рис. 2 б), отриманими числовим інтегруванням (2) у часткових похідних для різних початкових розподілів, показує, що стрижнева модель якісно вірно описує еволюцію розподілу. Для кількісного опису використано кумулянтний аналіз, який дає можливість перейти від рівняння (1) до детермінованих рівнянь еволюції кумулянтів:
 , (4)
, (4)де m – середнє значення, D – дисперсія процесу x(t). І графічна побудова на рис. 2 а і розв’язок (4) приводять до відомого виразу для СКВ
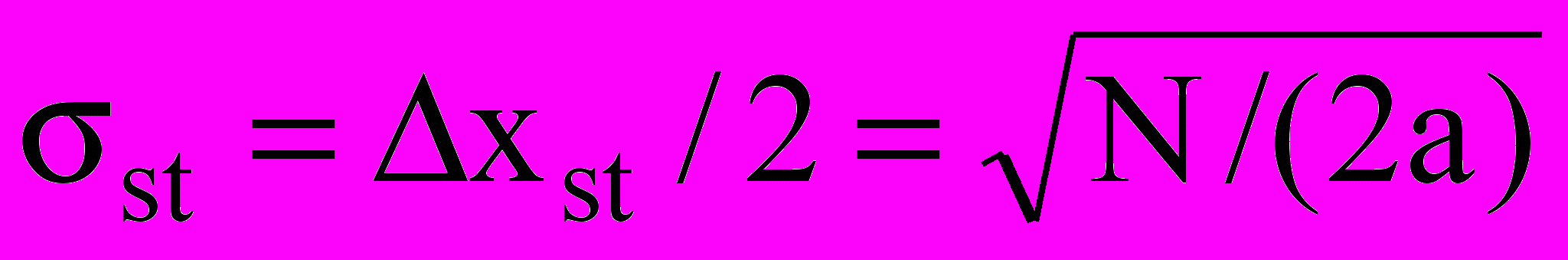 , що підтверджує адекватність моделі.
, що підтверджує адекватність моделі.У випадку лінійної ДС з нестійким станом рівноваги, тобто коефіцієнтом зносу F(x) = a·x при a<0, стрижнева модель та її аналітичний опис (4) показують наявність біфуркації, що сформульовано у вигляді наступної теореми.
Теорема 1. Характерний перетин з початковим нульовим розміром може досягти точки нестійкої рівноваги тоді і тільки тоді, якщо різниця значень потенціальної функції у нестійкій точці і центрі початкового розподілу менша від енергії збурення.
Якісно справедливість Теореми 1, доведеної у дисертації, підтверджують як реалізації, отримані розв’язуванням (1), так і нестаціонарні розподіли імовірності (рис. 3). Але за умови N>0 завжди існує скінчена (хоч і мала) імовірність перетину як завгодно великого потенціального бар’єру, а Теорема 1, яка є основою розвитку теорії стохастичних біфуркацій, описує умови, за яких характерний перетин ніколи не перетне потенціального бар’єру.
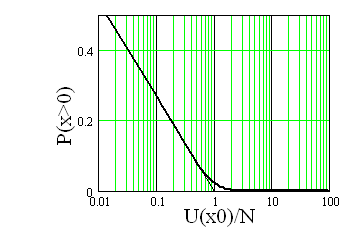
Для з’ясування питання, чи є описана біфуркація наслідком спрощень стрижневої моделі, чи відображує якісні особливості ВП, була розрахована залежність усталеного значення ймовірності перетину потенціального бар'єру від його висоти (рис. 4 а), яка має різний характер за умов U(x0)
а)
 б)
б) в)
в)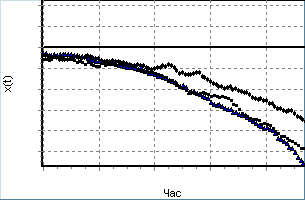
г)
 ґ)
ґ)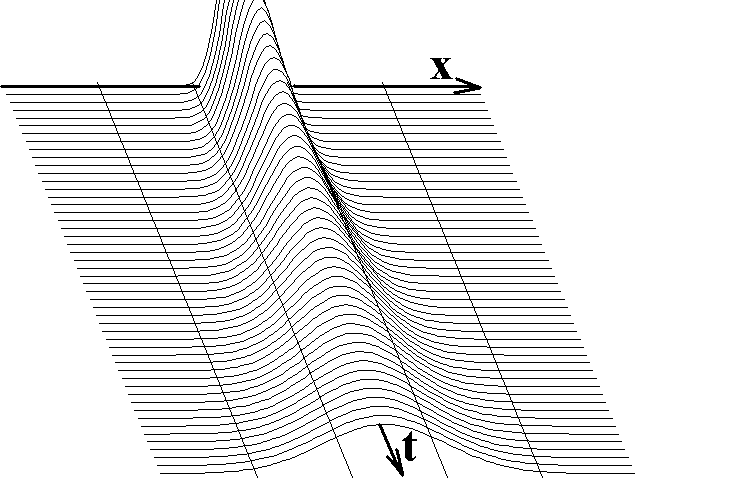 д)
д)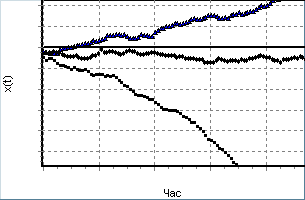
Рис.3. "Стрижнева" модель (а, г), еволюції розподілу (б, ґ) та реалізації (в, д) ВП
з малою (а–в) та великою (г–д) енергією збурення в околі точки нестійкої рівноваги.
Це означає, що характерний перетин не тільки є зручним для опису випадкових процесів, оскільки для нього виконуються досить прості енергетичні співвідношення, описані Властивістю 1, – зміна поведінки характерного перетину означає суттєві зміни у імовірнісних залежностях, зокрема є індикатором подолання випадковим процесом енергетичного бар’єру, що описує Теорема 1.
а)
 б)
б)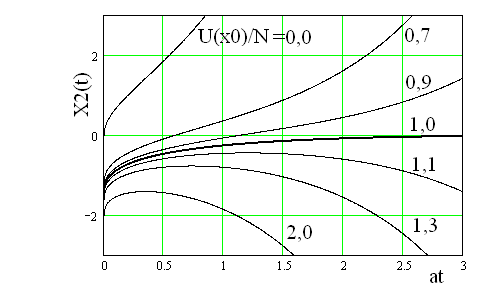
Рис. 4. Імовірність перетину бар'єру (а) і часові залежності квантіля p*0,977(б).
Отже, опис ВП за допомогою кумулянтного метода підтвердив висновки стрижневої моделі про основні якісні особливості поведінки характерного перетину розподілу ВП в околі точок стійкої і нестійкої рівноваги лінійної ДС, дав можливість отримати аналітичні вирази для кількісного аналізу характеристик ВП та визначення біфуркаційних значень інтенсивності випадкового збурення.
ВП у двовимірних лінійних ДС запропоновано описувати характерним перетином двовимірного розподілу густини імовірності, який, згідно з означенням, є замкненою кривою (для нормального розподілу – еліпсом). Всі точки усталеного характерного перетину мають однаковий потенціал, який згідно із Властивістю 1, дорівнює енергії збудження.
Знаходження потенціальної функції ДС другого порядку вимагає афінних перетворень, які маскують фізичну сутність фазових змінних. Тому в теорії коливань стан ДС другого порядку зображують траєкторіями точки на фазовій площині. Стан стохастичної ДС на фазовому портреті відображає поведінка характерного перетину, яка є складнішою, ніж поведінка точки. Для опису перетину необхідні координати центру (положення), характерні відхилення вздовж осей (розміри), нахил головних осей еліпса. Ці параметри однозначно пов’язані зі статистичними характеристиками двовимірного розподілу, поведінку яких кількісно описують рівняння дрейфу кумулянтів, які для ДС другого порядку мають вигляд:
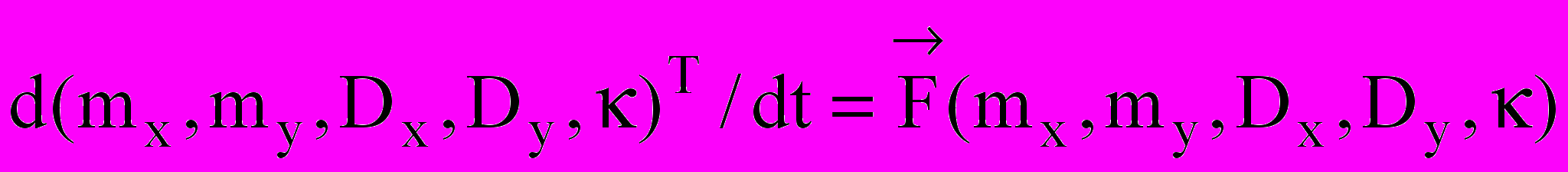 , (5)
, (5)де mx , my – середні значення,
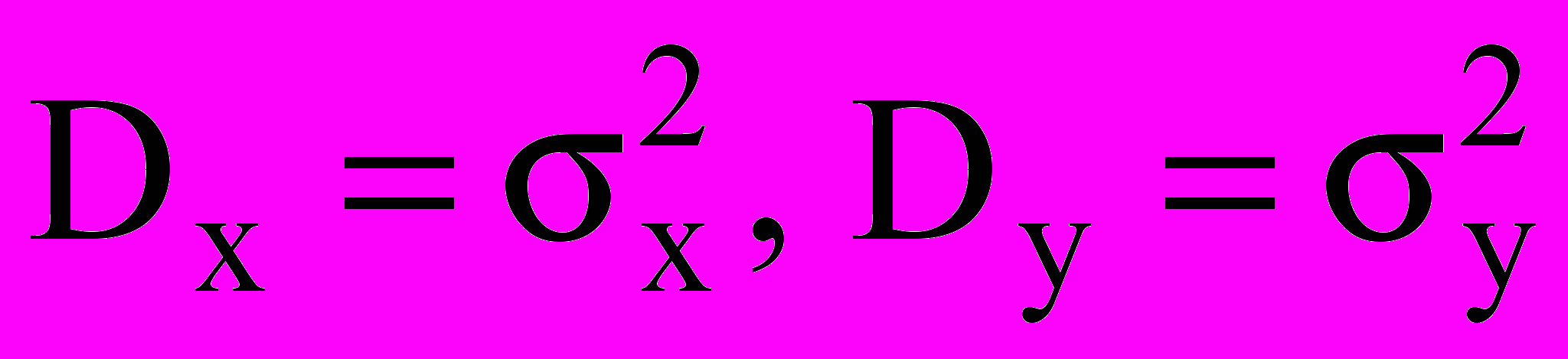 – дисперсії складових ВП, κ=rσxσy, r – коефіцієнт кореляції.
– дисперсії складових ВП, κ=rσxσy, r – коефіцієнт кореляції.