Структура програми навчальної дисципліни «класична механіка» Опис предмета навчальної дисципліни
| Вид материала | Документы |
- Структура програми навчальної дисципліни (курсу) „ криміналістика (за вимогами ects), 2307.09kb.
- Структура програми навчальної дисципліни «електронна І іонна оптика» І. Опис предмета, 90.46kb.
- Робоча програма навчальної дисципліни німецька класична філософія (шифр І назва навчальної, 608.55kb.
- Програма навчальної дисципліни робоча програма навчальної дисципліни кваліфкаційні, 680.22kb.
- Опис навчальної дисципліни, 1681.16kb.
- Вступ мета І завдання навчальної дисципліни, 1615.18kb.
- І. В. Кущенко опис навчальної дисципліни (спецкурсу), 281.83kb.
- Робоча програма навчальної дисципліни інженерна психологія І ергономіка (шифр І назва, 248kb.
- Робоча програма навчальної дисципліни експериментальна психологія (шифр І назва навчальної, 393.52kb.
- Робоча програма навчальної дисципліни організаційна динаміка (шифр І назва навчальної, 370.85kb.
Міністерство освіти і науки України
Cумський державний педагогічний університет
імені А. С. Макаренка
Методичні матеріали щодо
кредитно-модульної системи організації навчального процессу
з курсу “Класична механіка”
для студентів ІII курсу спеціальності
Спеціальність: 6.040203 – Фізика
Суми − 2009 р.
УДК 531:378.14(076)
Методичні матеріали щодо кредитно-модульної системи організації навчального процесу з курсу “Класична механіка” для студентів ІII курсу спеціальності 6.040203-Фізика. / Уклад.: Ворошило О.І. – Вид. центр СумДПУ імені А.С. Макаренка, 2009. – __ с.
Укладачі: Ворошило О.І. – с.н.с., канд. фіз.-мат. наук, доцент кафедри теоретичної і експериментальної фізики СумДПУ імені А.С. Макаренка;
Затверджено вченою радою фізико-математичного факультету СумДПУ
імені А.С. Макаренка
Протокол №_______ від ________________2009 р.
СТРУКТУРА ПРОГРАМИ
НАВЧАЛЬНОЇ ДИСЦИПЛІНИ «КЛАСИЧНА МЕХАНІКА»
- Опис предмета навчальної дисципліни
Предмет: класична механіка
| Курс ІІІ Підготовка бакалаврів | Напрям, спеціальність, освітньо-кваліфікаційний рівень | Характеристика навчальної дисципліни |
| Кількість кредитів, відповідних ECTS: 6 Змістовних модулів : 4 Загальна кількість годин: 216 Тижневих годин: | Галузь знань: 0402 – Фізико-математичні науки Шифр та назва напряму підготовки: 6.040203 – Фізика; Освітньо-кваліфікаційний рівень: бакалавр | Обов‘язкова Рік підготовки : 3 Семестр :1 Лекції (теоретична підготовка): 56 годин Практичні: 42 годин Індивідуальні: 4 години Самостійна робота: 114 годин Вид підсумкового контролю: екзамен. |
Метою навчального курсу є вивчення фізичних основ і математичного апарату класичної механіки та основ механіки суцільних середовищ та її застосувань у різних задачах теоретичної фізики, формування у студентів наукового світогляду в області фізики і математики, створення бази теоретичної підготовки в різних областях фізики і математики.
В результаті вивчення дисципліни студенти повинні:
знати:
- основні поняття класичної механіки;
- функцію Лагранжа, дію, принцип найменшої дії;
- рівняння Лагранжа, поняття узагальнених координат, швидкостей, сил та імпульсів;
- закони збереження, як наслідки однорідності ізотропності простору і однорідності часу;
- функцію Гамільтона, поняття фазового простору; теорему Ліувілля;
- канонічні змінні і канонічні перетворення, дужки Пуассона;
- поняття потоку енергії та імпульсу.
Вміти:
- інтегрувати рівняння руху частинки, яка знаходиться під дією заданих сил;
- знаходити інтеграли руху для частинки, що рухається у заданому полі;
- знаходити формули перетворення для радіус-вектора швидкості, прискорення матеріальної точки при переході з однієї системи відліку в іншу;
- виводити рівняння Лагранжа з принципу найменшої дії;
- записувати функції Лагранжа і Гамільтона для заданої системи матеріальних точок в декартових, сферичних та циліндричних координатах;
- інтегрувати рівняння Лагранжа і рівняння Гамільтона у деяких простих випадках;
- обчислювати момент інерції тіла певної форми відносно заданої осі.
- записувати рівняння руху пружного середовища, рідини.
ВСТУП
Дана програма визначає об’єм знань студента з курсу класичної механіки, необхідний для подальшого вивчення дисциплін фізичного профілю. Курс класичної механіки дає наукове обґрунтування таких важливих понять як: функція Лагранжа, дія, принцип мінімальної дії, рівняння Лагранжа, отримання законів збереження із основних властивостей простору і часу, система центру інерції, задача двох тіл, задача Кеплера, переріз розсіювання, рух в неінерційних системах відліку, малі коливання, рух твердого тіла, функція Гамільтона, канонічні рівняння, канонічні перетворення, теорема Ліувілля, рівняння Гамільтона-Якобі, адіабатичні інваріанти, метод Лагранжа для суцільних середовищ. Ці поняття є базовими для вивчення дисциплін фізичного профілю.
Програма курсу розрахована на I семестр другого року навчання студентів спеціальності «Фізика» та забезпечуються такою кількістю годин:
| Аудиторних занять | Індивідуальних занять | Самостійна робота | Всього | Форма семестрового контролю | |
| Лекцій | Практичних занять | ||||
| 56 | 42 | 4 | 114 | 216 | екзамен |
Змістовий модуль І
Механіка Лагранжа. Закони збереження. Інтегрування рівнянь руху.
Тема 1.1. Механіка Лагранжа.
Зміст. Зв’язки. Принцип Гамільтона. Знаходження рівняння Лагранжа за допомогою принципу Гамільтона. узагальнений імпульс, узагальнена сила. Функція Лагранжа матеріальної точки. Функція Лагранжа системи матеріальних точок. Приклади складання рівнянь Лагранжа. Рівняння Лагранжа для неконсервативних систем і систем із неголономними зв’язками.
Тема 1.2. Закони збереження.
Зміст. Інтеграли руху. Закон збереження енергії. Закон збереження імпульсу. Закон збереження моменту імпульсу. Механічна подібність.
Тема 1.3. Інтегрування рівнянь руху.
Зміст. Одномірний рух. Рух у центральному полі. Задача Кеплера.
Змістовий модуль ІІ
Вибрані задачі механіки.
Тема 2.1. Розсіювання частинок.
Зміст. Розпад частинок. Розсіювання часток в полі центральної сили. Формула Резерфорда.
Тема 2.2. Рух в неінерційній системах відліку.
Зміст. Прискорений поступальний і обертальний рухи системи відліку. Прискорений поступальний рух системи відліку. Рівномірний обертальний рух системи відліку.
Тема 2.3. Механіка твердого тіла.
Зміст. Кутова швидкість. Тензор інерції. Рівняння руху твердого тіла. Кути Ейлера. Рівняння Ейлера.
Тема 2.4. Гармонічні коливання.
Зміст. Вільні одномірні коливання. Коливання систем з багатьма ступенями вільності. Нормальні координати. Загасаючі коливання. Вимушені коливання при наявності тертя. Резонанс.
Тема 2.5. Ангармонічні коливання.
Зміст. Функція Лагранжа системи, що виконує коливання поблизу точки рівноваги. Метод послідовних наближень. Вищі гармоніки. Резонанс.
Змістовий модуль ІIІ
Механіка Гамільтона
Тема 3.1. Рівняння Гамільтона.
Зміст. Перетворення Лежандра. Зв'язок рівняння Лагранжа з рівняннями Гамільтона. Функція Рауса. Дужки Пуассона. Тотожність Якобі
Тема 3.2. Дія як функція координат.
Зміст. Дія як функція координат. Принцип Мопертюи.
Тема 3.3. Канонічні перетворення.
Зміст. Твірна функція. Точкові перетворення. Канонічно спряжені величини.
Тема 3.4. Теорема Ліувілля
Зміст. Фазовий простір. Теорема Ліувілля
Тема 3.5. Рівняння Гамільтона-Якобі
Зміст. Рівняння Гамільтона-Якобі, як основа загального методу інтегрування рівнянь руху. Окремі прийоми знаходження повного інтеграла. Розділення змінних.
Тема 3.6. Адіабатичні інваріанти
Зміст. Адіабатичні інваріанти. Канонічні перемінні дія – кут
Змістовний модуль ІV
Основи механіки суцільних середовищ
Тема 4.1. Перехід від дискретної системи до суцільної. Рівняння Лагранжа для суцільного середовища.
Зміст. Перехід від дискретної системи до суцільної на прикладі повздовжніх коливань нескінченно довгого пружного стрижня. Питомий Лагранжиан. Принцип Гамільтона для суцільного середовища. Функціональна похідна. Рівняння Лагранжа для суцільного середовища. Звукові коливання в газах.
Тема 4.2. Основні рівняння теорії пружності.
Зміст. Тензори напруги і деформацій. Узагальнений закон Гуку. Однорідні деформації. Малі пружні хвилі. Подовжня і поперечна швидкості звуку.
Тема 4.3. Основи механіки рідин.
Зміст. Способи опису руху рідини. Ідеальна рідина: рівняння Ейлера; рівняння неперервності; рівняння Бернуллі; збереження циркуляції швидкості. В’язка рідина:
тензор в’язких деформацій; Рівняння Нав’є-Стокса.
Тема 4.4. Загальна теорія розмірності для різних величин.
Зміст. Розмірні і безрозмірні величини. Формула розмірності. Структура функціональних зв'язків між фізичними величинами.
СТРУКТУРА ЗАЛІКОВОГО КРЕДИТУ КУРСУ
| № | Тема | Кількість годин, відведених на | ||||
| Лекції | Практичні | Індивід. Заняття | Сам ост. роботу | Вид Контролю | ||
| І | Змістовний модуль І Механіка Лагранжа. Закони збереження. Інтегрування рівнянь руху. | 18 | 12 | | 22 | к\р |
| 1.1 | Механіка Лагранжа | 8 | 4 | | 10 | |
| 1.2 | Закони збереження. | 4 | 2 | | 12 | |
| 1.3 | Інтегрування рівнянь руху. | 6 | 6 | | | |
| ІІ | Змістовний модуль ІІ Вибрані задачі механіки. | 14 | 12 | 2 | 36 | к\р |
| 2.1 | Розсіювання частинок. | 4 | 4 | | 18 | |
| 2.2 | Рух в неінерційній системах відліку. | 1 | | 2 | 18 | |
| 2.3 | Механіка твердого тіла. | 5 | 4 | | | |
| 2.4 | Коливання. | 4 | 4 | | | |
| ІІІ | Змістовний модуль ІІІ Механіка Гамільтона. Канонічні рівняння. | 8 | 10 | | 22 | к\р |
| 3.1 | Механіка Гамільтона. Дужки Пуассона. Теорема Ліувілля. Дія як функція координат. | 2 | 4 | | 8 | |
| 3.2 | Канонічні перетворення. | 2 | 4 | 2 | 8 | |
| 3.3 | Рівняння Гамільтона-Якобі. | 2 | 2 | | 6 | |
| 3.4 | Змінні кут-дія. Адіабатичні інваріанти | 2 | | | | |
| IV | Змістовний модуль ІV Основи | 16 | 8 | 2 | 34 | к\р |
| 4.1 | Методи Лагранжа для суцільних середовищ. | 3 | | | 16 | |
| 4.2 | Основні рівняння теорії пружності. | 4 | 2 | | 18 | |
| 4.3 | Основи механіки рідин. | 7 | 4 | 2 | | |
| 4.4. | Загальна теорія розмірності. | 2 | 2 | | | |
| Усього | 56 | 42 | 4 | 114 | 216 | |
Даною програмою передбачається виконання 2-х індивідуальних н.-д. завдань, 4-х контрольних робіт та складання 4-х колоквіумів.
РОЗПОДІЛ БАЛІВ,
ЩО ПРИСВОЮЮТЬСЯ СТУДЕНТАМ ПІД ЧАС
ПОТОЧНОГО КОНТРОЛЮ:
| | Відв. Занять | Відповіді на практ. Заняттях | К\р | Колоквіум | ІНДЗ | Всього |
| ЗМ І | 5 | 5 | 5 | 5 | 5 | 25 |
| ЗМ ІІ | 5 | 5 | 5 | 5 | 5 | 25 |
| ЗМ ІІІ | 5 | 5 | 5 | 5 | 5 | 25 |
| ЗМ ІV | 5 | 5 | 5 | 5 | 5 | 25 |
| Усього | 20 | 20 | 20 | 20 | 20 | 100 |
Примітка: У випадку відсутності на занятті від загальної кількості отриманих балів віднімається 1 бал за кожний пропуск.
ТЕМИ ПРАКТИЧНИХ ЗАНЯТЬ
| Модуль | № | Тема | Год. | Прим. |
| Змістовий модуль І. | 1 | Знаходження функції Лагранжа. | 2 | |
| 2 | Знаходження рівнянь Лагранжа за відомою функцією Лагранжа. Знаходження узагальнених сил і імпульсів. | 2 | | |
| 3 | Закони збереження. | 2 | | |
| 4 | Інтегрування рівнянь руху. | 4 | | |
| 5 | Контрольна робота №1. | 2 | | |
| Змістовий модуль ІІ. | 6 | Розсіювання частинок. Знаходження перерізів розсіювання. | 4 | |
| 7 | Рух твердого тіла. | 4 | | |
| 8 | Малі коливання | 4 | | |
| 9 | Контрольна робота №2 | 2 | | |
| Змістовий модуль ІІІ. | 10 | Механіка Гамільтона. | 3 | |
| 11 | Канонічні перетворення. | 2 | | |
| 12 | Рівняння Гамільтона-Якобі. Змінні кут-дія | 3 | | |
| 13 | Контрольна робота №3. | 2 | | |
| Змістовний модуль IV. | 14 | Теорія пружності | 2 | |
| 15 | Механіка рідин | 2 | | |
| 16 | Теорія розмірності | 2 | | |
| 17 | Контрольна робота №4 | 2 | |
ТЕМИ ІНДИВІДУАЛЬНИХ ЗАНЯТЬ
| Модуль | № | Тема | Год. |
| ЗМ І. | 1 | Знаходження функції Лагранжа. Знаходження рівняння Лагранжа. Знаходження узагальнених імпульсів і сил. Знаходження законів збереження. | 2 |
| ЗМ ІIІ. | 2 | Знаходження функції Гамільтона. Знаходження рівнянь Гамільтона. | 2 |
| Усього | 4 | ||
ЗМІСТ ПРАКТИЧНИХ ТА ІНДИВІДУАЛЬНИХ ЗАНЯТЬ
(46 годин)
Модуль I
Практичне заняття №1
Тема: Знаходження функції Лагранжа. (2 год)
Теоретичні питання:
1 Функція Лагранжа вільної частинки в циліндричних і сферичних системах координат.
2 Знаходження функції Лагранжа для систем з голономними стаціонарними і нестаціонарними зв’язками.
Практичне завдання: 1.1–1.5.
Домашнє завдання: 1.6-1.10
Література: [1], [2], [3].
.
Практичне заняття №2
Тема: Знаходження рівнянь Лагранжа за відомою функцією Лагранжа. Знаходження узагальнених сил і імпульсів. (2 год)
Теоретичні питання:
1 Рівняння Лагранжа.
2 Узагальнені імпульси і сили.
Практичне завдання: 2.1–2.5.
Домашнє завдання: 2.6-2.10.
Література: [1], [2], [3].
Практичне заняття №3
Тема: Закони збереження. (2 год)
Теоретичні питання:
1 Інтеграли руху. Циклічні координати. Теорема про збереження узагальненого імпульсу.
2 Закон збереження енергії, імпульсу, моменту імпульсу.
Практичне завдання: 3.1-3.5.
Домашнє завдання: 3.6-3.10
Література: [1], [2], [3].
Практичне заняття №5
Тема: Інтегрування одномірних рівнянь руху (2 год)
Теоретичні питання:
1 Одномірний рух. Інфінітний і неінфінітний рухи.
2. Період одномірного фінітного руху.
Практичне завдання: 4.1–4.5.
Домашнє завдання: 4.6-4.10
Література: [1], [2], [3].
Практичне заняття №6
Тема: Рух у центральному полі. (2 год).
Теоретичні питання: 1 Задача двох тіл.
2. Загальні властивості руху у центральному полі. Відцентрова енергія. Траєкторія руху. Точки повороту.
3 Задача Кеплера.
Практичне завдання: 5.1–5.5.
Домашнє завдання: 5.6-5.10
Література: [1], [2], [3].
Практичне заняття №7
Тема: Контрольна робота. (2 год)
Зразок контрольної роботи:
Теорія.
1. Рівняння Лагранжа (2.5 бала).
2. Період коливань при інфінітному одномірному русі. (2.5 бала).
Задачі.
1. Знайти узагальнену силу для координати
 механічної системи функція Лагранжа, якої має вигляд:
механічної системи функція Лагранжа, якої має вигляд: 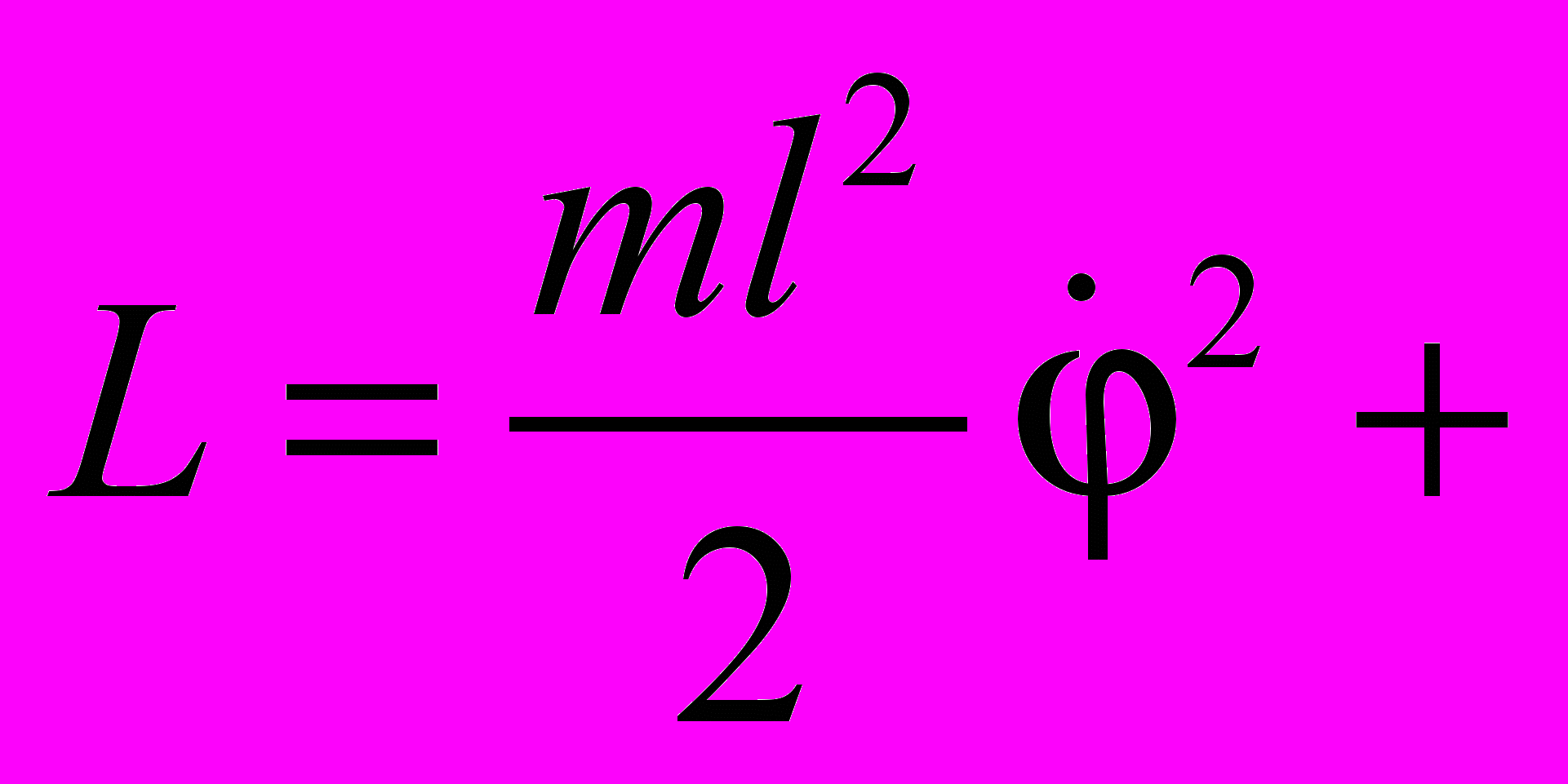
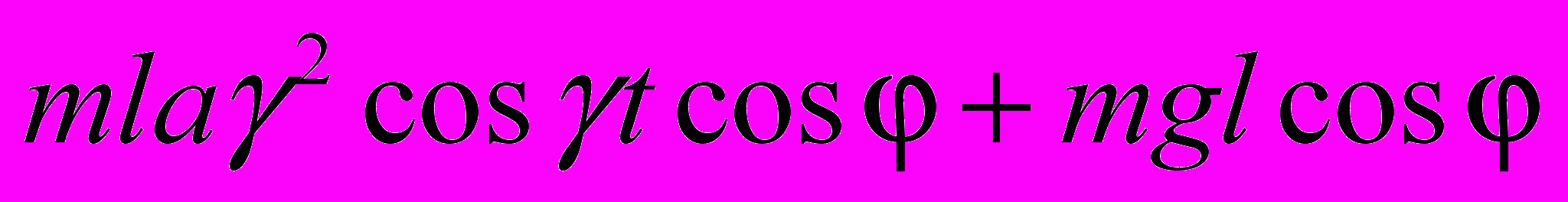 (1 бал).
(1 бал).2. Ідеально пружна кулька рухається вверх і вниз в однорідному полі тяжіння, відбиваючись від пола по законам пружного удару. Знайти зв'язок між середніми по часу значеннями його кінетичної
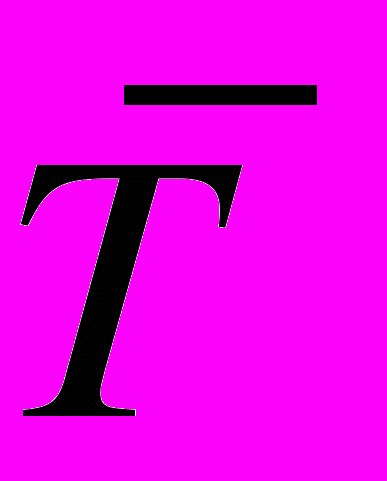 і потенціальної енергії
і потенціальної енергії 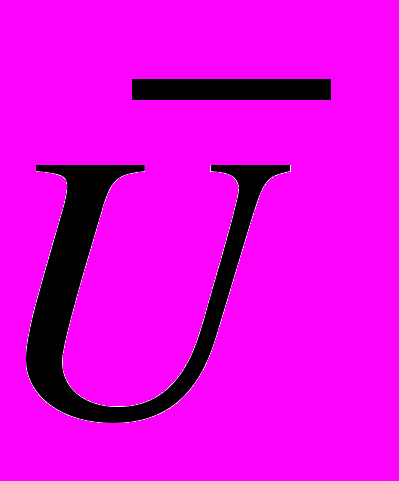 (1бал).
(1бал).3 Які компоненти імпульсу
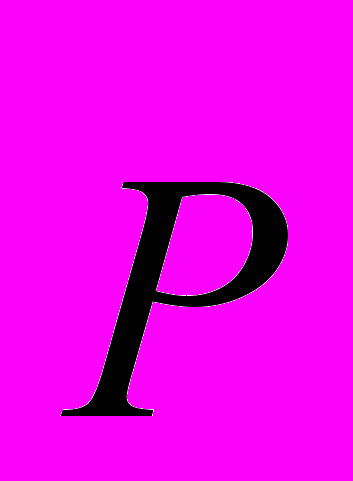 і моменту
і моменту 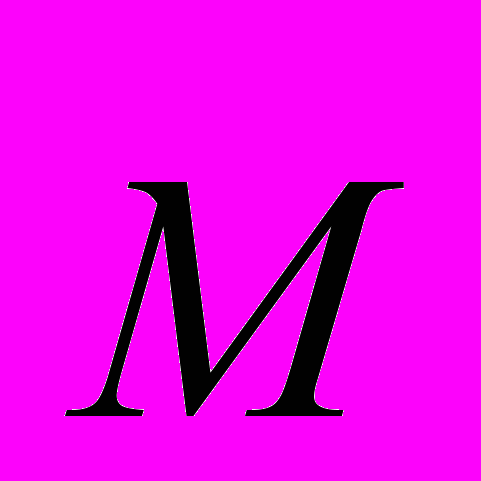 зберігаються в полі нескінченної площини?
зберігаються в полі нескінченної площини? 4. Визначити закон руху частинки в полі
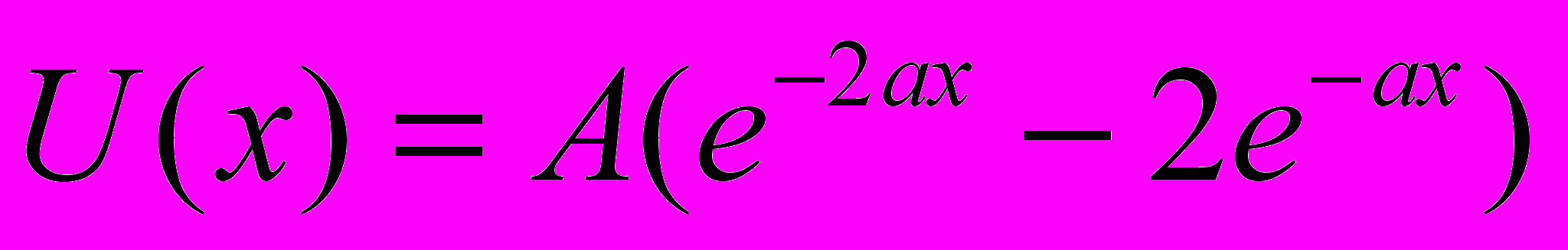 при
при 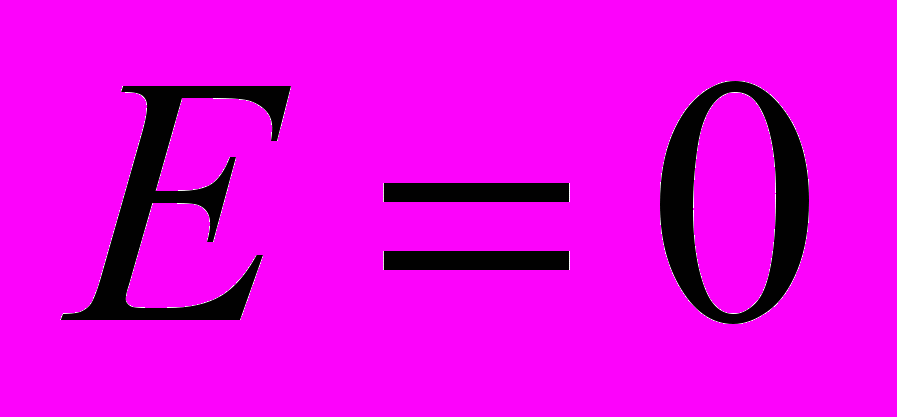 (2 бала).
(2 бала).Модуль II
Практичне заняття №7
Тема: Розсіювання частинок. Знаходження перерізів розсіювання. (4 год)
Теоретичні питання:
1 Лабораторна система відліку. Система центру інерції. Діаграма швидкостей. Зв'язок кутів вильоту.
2 Ефективний переріз розсіювання. Прицільна відстань. Розсіювання на кулонівському центрі.
3 Перетворення диференціального перерізу розсіювання при переході із системи центра інерції в лабораторну систему відліку.
Практичне завдання: 6.1–6.5.
Домашнє завдання: 6.6-6.10
Література: [1], [2], [3].
Практичне заняття №9
Тема: Рух твердого тіла. (4 год)
Теоретичні питання:
1 Тензор інерції.
2 Рівняння руху твердого тіла.
3 Кути Ейлера. Рівняння Ейлера для твердого тіла.
Практичне завдання: 7.1–7.5.
Домашнє завдання: 7.6-7.10
Література: [1], [2], [3].
Практичне заняття №10
Тема: Одномірні малі коливання. Коливання систем з багатьма ступенями вільності..(2 год).
Теоретичні питання:
1 Метод фазової площини.
2 Вільні одномірні коливання. Коливання систем з багатьма степенями вільності.
3 Загасаючі і вимушені коливання.
Практичне завдання:8.1–8.5.
Домашнє завдання: 8.6-8.10
Література: [1], [2], [3].
Практичне заняття №11
Тема: Контрольна робота. (2 год)
Зразок контрольної роботи:
Теорія.
1. Тензор інерції тіла. (2.5 бала).
2. Загасаючі коливання. Коливальний і аперіодичний процеси. Дисипативна функція. Дисипація енергії. (2.5 бала).
Задачі.
1. Визначити головні моменти інерції суцільної однорідної кулі радіусом
 . (2.5 бала).
. (2.5 бала).2. Визначити нормальні частоти і нормальні координати системи з двома степенями вільності, якщо її функція Лагранжа має вигляд:
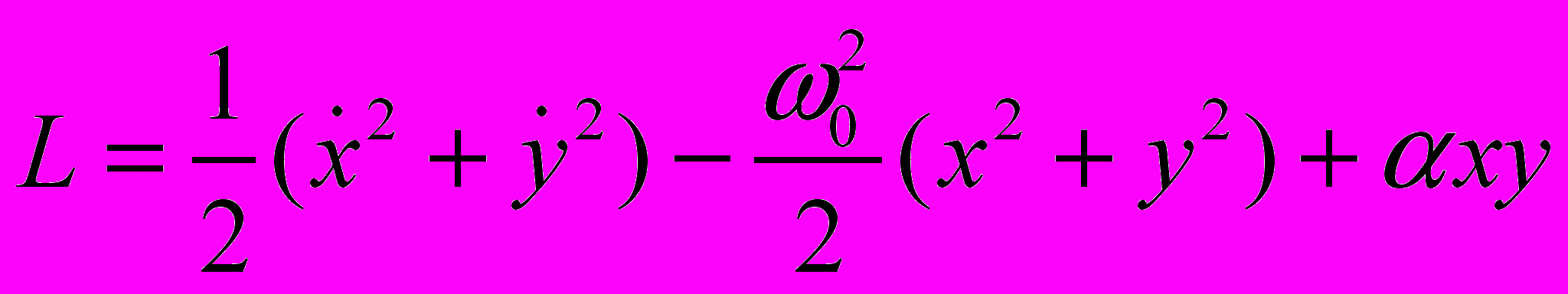 (два одномірних коливання з власною частотою
(два одномірних коливання з власною частотою 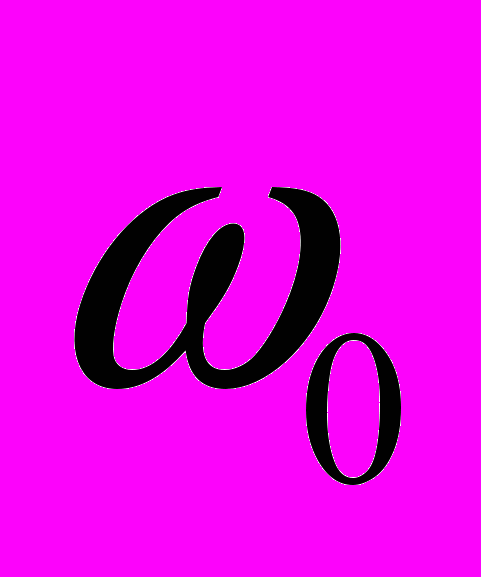 , зв’язаних взаємодією –
, зв’язаних взаємодією – 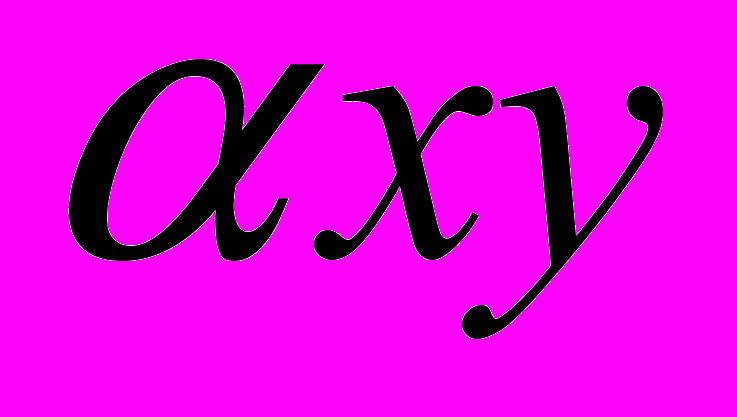 )
)(2.5 бала).
Модуль III
Практичне заняття №10
Тема: Знаходження функції Гамільтона. Зв'язок між функціями Гамільтона і Лагранжа. Рівняння Гамільтона. (4 год).
Теоретичні питання:
1 Функція Гамільтона.
2 Рівняння Гамільтона.
Практичне завдання:9.1–9.5.
Література: [1], [2], [3].
Практичне заняття №11
Тема: Канонічні перетворення. Канонічні рівняння. (2 год).
Теоретичні питання:
1 Канонічні рівняння. Канонічні перетворення і їх властивості.
2 Умова канонічної спряженності.
Практичне завдання: 10.1–10.5.
Домашнє завдання: 10.6-10.10
Література: [1], [2], [3].
Практичне заняття №12
Тема: Дія, як функція координат. Рівняння Гамільтона-Якобі. Змінна кут-дія. Адіабатичні інваріанти (2 год).
Теоретичні питання:
1 Дія, як функція координат.
2 Рівняння Гамільтона-Якобі.
3 Змінні кут-дія. Адіабатичні інваріанти.
Практичне завдання:11.1–11.5.
Домашнє завдання: 12.6-12.10
Література: [1], [2], [3].
Практичне заняття №13
Тема: Контрольна робота. (2 год)
Зразок контрольної роботи:
Теорія.
1. Функція Гамільтона. (2.5 бала).
2. Рівняння Гамільтона-Якобі. (2.5 бала).
Задачі.
1. Записати дужки Пуассона, складені із компонент моменту імпульсу
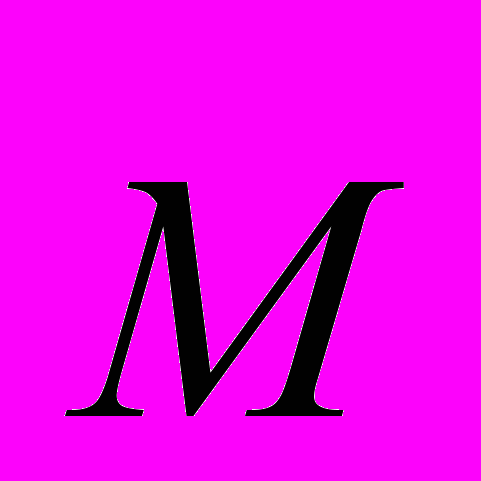 :
: 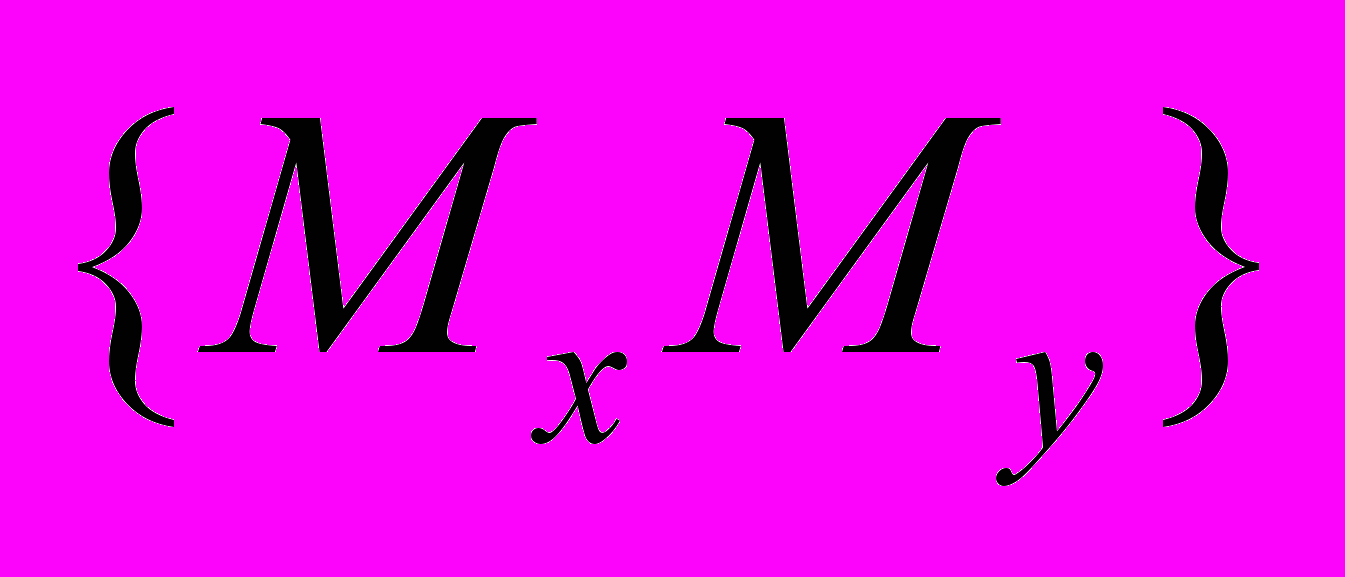 (1.5 бала).
(1.5 бала). 2. Записати функцію Гамільтона ангармонічного осцилятора, функція Лагранжа якого має вигляд:
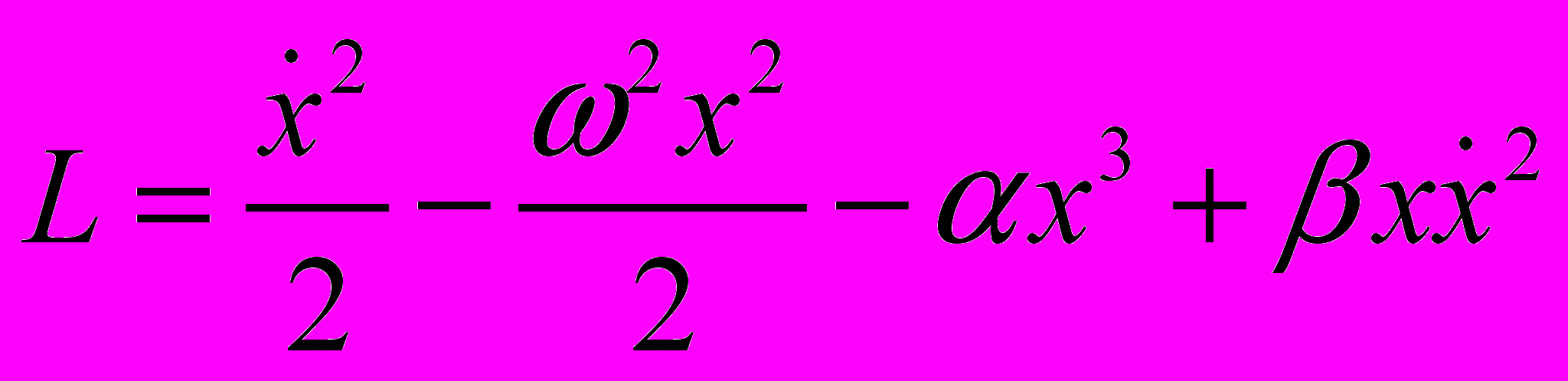 (1.5 бала).
(1.5 бала). 3. Знайти траєкторію руху частинки в полі
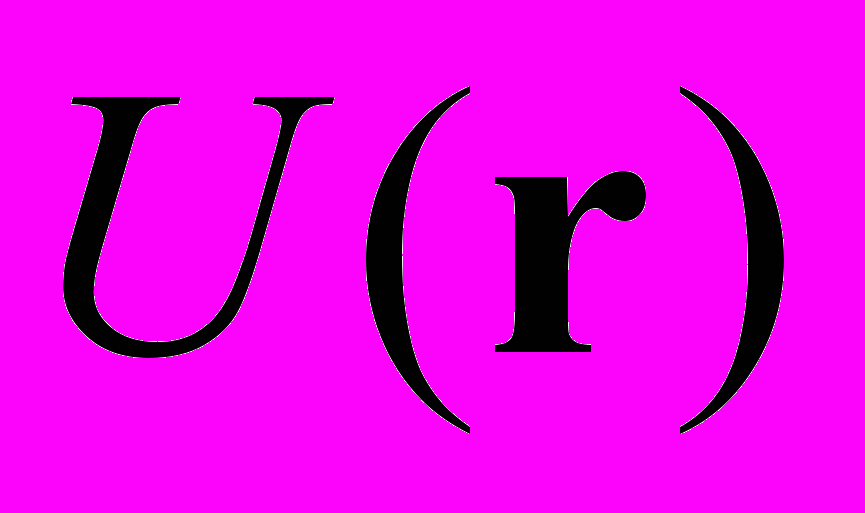 з допомогою рівняння Гамільтона-Якобі:
з допомогою рівняння Гамільтона-Якобі: 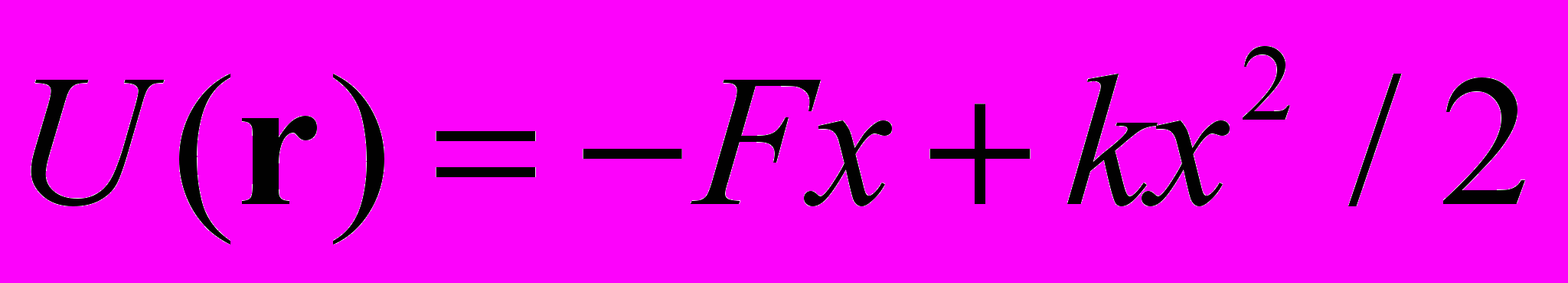 (2 бала).
(2 бала). Модуль IV
Практичне заняття №14
Тема: Рівняння теорії пружності і гідродинаміки в криволінійних координатах (2 год).
Теоретичні питання:
1 Криволінійні координати.
2 Градієнт, дивергенція, ротор в криволінійних координатах.
Практичне завдання:12.1–13.5.
Домашнє завдання: 12.6-12.10
Література: [2], [7], [9].
Практичне заняття №15
Тема: Тензор деформацій в криволінійних координатах (2 год).
Теоретичні питання:
1 Тензор деформацій.
Практичне завдання:13.1-13.5.
Домашнє завдання: 14.6-14.10
Література: [7], [8].
Завдання індивідуальних робіт (на 10 варіантів кожна) знаходяться на кафедрі теоретичної і експериментальної фізики.
ЗМІСТ САМОСТІЙНОЇ РОБОТИ
Питання колоквіуму №1
- Основні величини, що визначають кінематику і динаміку руху матеріальної точки. Закони динаміки матеріальної точки. Закони збереження
- Зовнішні і внутрішні сили. Центр мас системи. Рівняння руху центру мас системи. Імпульс, момент імпульсу, кінетична і потенціальна енергія системи. Закони збереження для системи матеріальних точок.
- Приклади систем зі зв’язками. Класифікація систем зі зв’язками. Ступені вільності. Узагальнені координати.
- Функція Лагранжа. Дія. Принцип Гамільтона. Рівняння Лагранжа, як наслідок принципу найменшої дії.
- Принцип відносності Галілея. Функція Лагранжа вільної частки, як наслідок однорідності і ізотропності простору. Вигляд функції Лагранжа вільної частки в декартових, циліндричних і сферичних координатах. Функція Лагранжа системи матеріальних точок. Рівняння Ньютона, як наслідок рівнянь Лагранжа. Узагальнений імпульс. Узагальнена сила.
- Математичний маятник. Маятник, з точкою підвісу яка рівномірно рухається. Маятник з точкою підвісу яка рухається з сталим прискоренням. Частка, що рухається прямій яка обертається з прискоренням.
- Узагальнено-потенціальна сила. Узагальнений потенціал. Рівняння Лагранжа для неконсервативних систем. Похідна від повної енергії для неконсервативних систем. Дисипативні сили. Функція Релея.
- Інтеграли руху механічної системи як наслідок однорідності часу й однорідності і ізотропності простору.
- Закон збереження енергії механічної системи як наслідок однорідності часу.
- Закон збереження імпульсу як наслідок однорідності простору. Центр інерції. Задача двох тіл
- Закон збереження моменту імпульсу як наслідок ізотропності простору. Перетворення моменту імпульсу при переході з однієї інерційної системи відліку в іншу.
- Теорема про механічну подібність. Приклади застосування. Теорема віріалу.
- Інфінітний та інфінітний рух.
- Період коливань при інфінітному одномірномірному русі. Визначення потенційної енергії по періоду коливань.
- Загальні властивості руху в центральному полі. Відцентрова енергія. Траєкторія руху. Падіння частинки на силовий центр.
- Задача Кеплера. Випадки фінітного та інфінітного руху.
Питання колоквіуму №2
- Лабораторна система відліку. Діаграма швидкостей. Зв'язок кутів вильоту.
- Ефективний переріз розсіювання. Прицільна відстань.
- Розсіювання на кулонівському центрі. Переріз Резерфорда.
- Перетворення диференціального перерізу розсіювання при переході із системи центра інерції в лабораторну систему відліку.
- Функція Лагранжа в неінерційній системі відліку. Сили інерції: відцентрова сила і сила Коріоліса. Закон перетворення енергії.
- Кутова швидкість. Миттєва вісь обертання.
- Тензор інерції тіла. Симетрична, асиметрична і кульова дзиґи. Ротатор.
- Момент імпульсу твердого тіла. Момент сили.
- Рівняння руху твердого тіла.
- Кути Ейлера.
- Рівняння Ейлера для твердого тіла.
- Функція Лагранжа системи, що виконує одномірні малі коливання. Диференціальне рівняння гармонійного осцилятора. Амплітуда, фаза, частота, енергія вільних коливань.
- Коливання систем з багатьма ступенями вільності. Функція Лагранжа системи з багатьма ступенями вільності. Характеристичне рівняння. Нормальні моди коливань. Функція Лагранжа, виражена через нормальні координати. Коливання молекул.
- Загасаючі коливання. Коливальний і аперіодичний процеси. Дисипативна функція. Дисипація енергії.
- Вимушені коливання при наявності тертя. Резонанс. Вимушені коливання. Резонанс зсуву і швидкості. Дисперсійне співвідношення.
- Функція Лагранжа системи, що виконує малі нелінійні коливання. Метод послідовних наближень. Вищі гармоніки. Резонанс.
Питання колоквіуму №3
- Функція Гамільтона.
- Рівняння Гамільтона.
- Дужки Пуассона.
- Дія як функція координат.
- Канонічні перетворення. Канонічно-спряжені координати. Властивості канонічних перетворень.
- Фазовий простір. Теорема Ліувілля.
- Рівняння Гамільтона-Якобі. Порядок розв’язку методом Гамільтона-Якобі.
- Змінні дія-кут.
- Усереднення збурень.
- Адіабатичні інваріанти.
Питання колоквіуму №4
- Методи Лагранжа і Гамільтона для суцільних середовищ.
- Тензор деформацій у декартових, циліндричних і сферичних координатах.
- Внутрішні напруження. Тензор напруги.
- Узагальнений закон Гуку.
- Коефіцієнти Ламе. Модуль усебічного стиску, модуль зсуву. Коефіцієнт стиску.
- Однорідні деформації. Модуль Юнга. Коефіцієнт Пуассона.
- Звукові коливання в газах. Подовжня і поперечна швидкості звуку.
- Ідеальна рідина. Рівняння неперервності.
- Рівняння Ейлера.
- Рівняння Бернуллі.
- Теорема Томсона.
- Потенціальний рух рідини.
- Рівняння руху в’язкої рідини. Тензор в’язких напружень. Рівняння Нав’є-Стокса.
- Теорія розмірності. Безрозмірні комбінації фізичних величин. Правило розмірності.
Завдання до індивідуальної роботи №1
а) Записати функцію Лагранж заданої механічної системи.
б) Знайти узагальнені сили і імпульси.
в) Записати рівняння Лагранжа.
г) За відомою функцією Лагранжа знайти енергію заданої системи.
Завдання до індивідуальної роботи №2
а) Записати функцію Гамільтона заданої механічної системи.
б) Записати рівняння Гамільтона.
г) Записати рівняння Гамільтона-Якобі.
Варіанти.
- Подвійний математичний маятник, який знаходиться в однорідному полі тяжіння (прискорення вільного падіння –
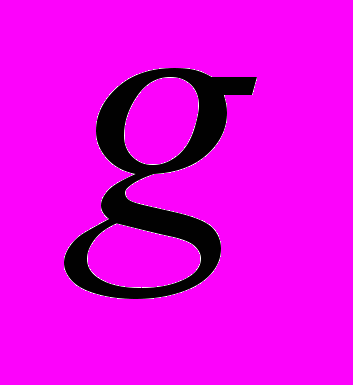 ), точка підвісу якого рівномірно рухається по вертикальному колу з сталою частотою
), точка підвісу якого рівномірно рухається по вертикальному колу з сталою частотою 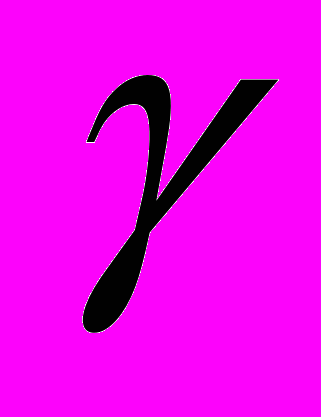 .
.
- Подвійний математичний маятник, який знаходиться в однорідному полі тяжіння (прискорення вільного падіння –
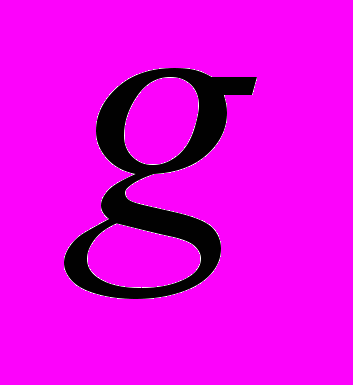 ), точка підвісу якого виконує горизонтальні коливання по закону
), точка підвісу якого виконує горизонтальні коливання по закону 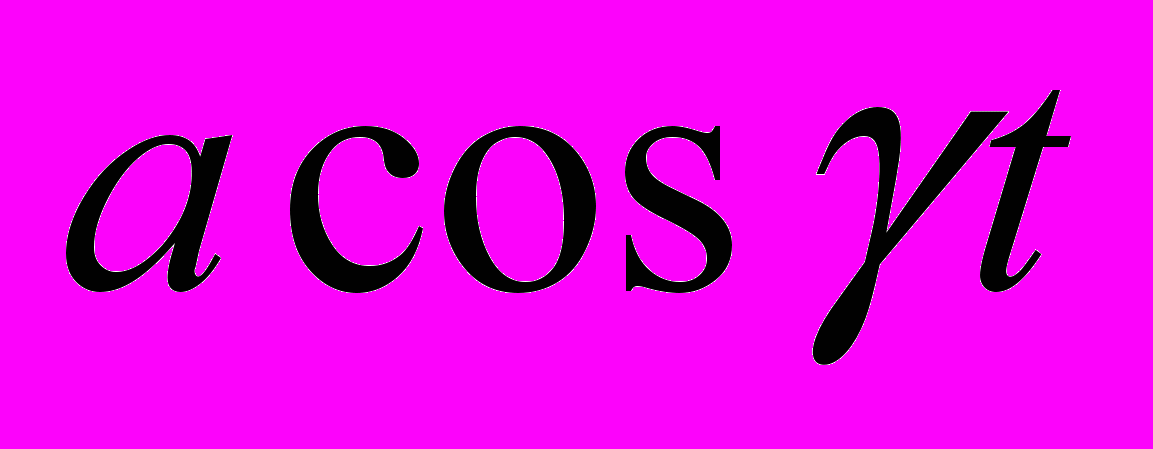 .
.
- Подвійний математичний маятник,, який знаходиться в однорідному полі тяжіння (прискорення вільного падіння –
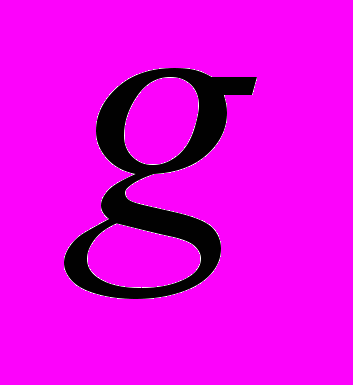 ), точка підвісу якого виконує вертикальні коливання по закону
), точка підвісу якого виконує вертикальні коливання по закону 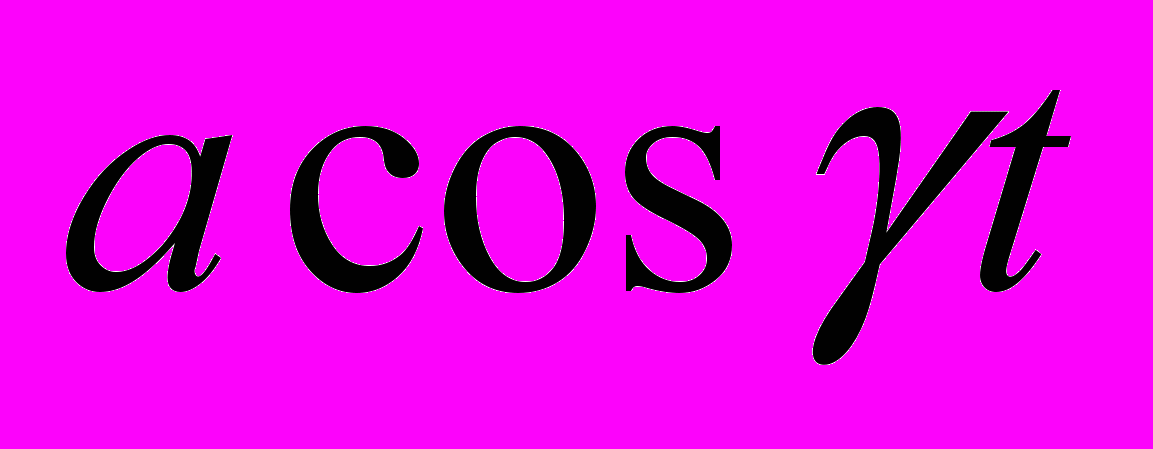 .
.
- Подвійний математичний маятник, який знаходиться в однорідному полі тяжіння (прискорення вільного падіння –
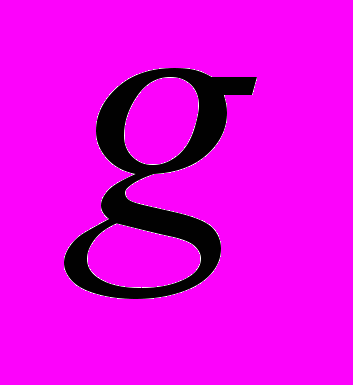 ), точка підвісу якого рухається зі сталим прискоренням
), точка підвісу якого рухається зі сталим прискоренням  вздовж прямої, що складає з горизонтом кут
вздовж прямої, що складає з горизонтом кут  .
.
- Дві частинки однакової маси
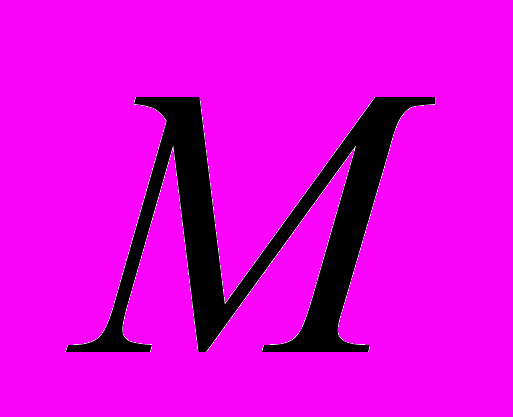 зв’язані між собою, а також з нерухомими опорами однаковими паралельними пружинами з коефіцієнтом пружності
зв’язані між собою, а також з нерухомими опорами однаковими паралельними пружинами з коефіцієнтом пружності 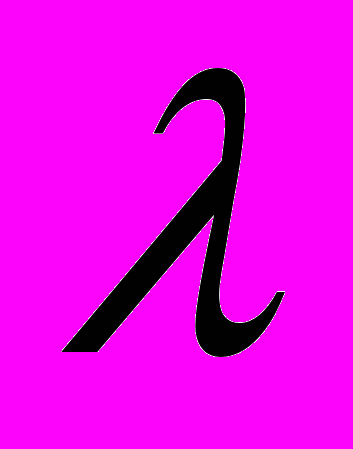 . Нехай довжина ненавантаженої пружини дорівнює
. Нехай довжина ненавантаженої пружини дорівнює  і опори розташовані на відстані
і опори розташовані на відстані 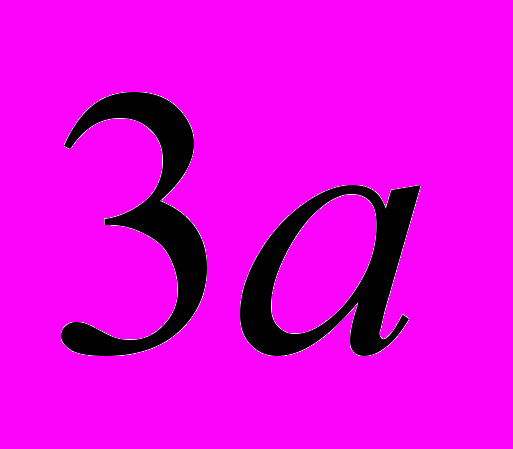 одна від одної. Позначити зміщення двох частинок від положення рівноваги як
одна від одної. Позначити зміщення двох частинок від положення рівноваги як 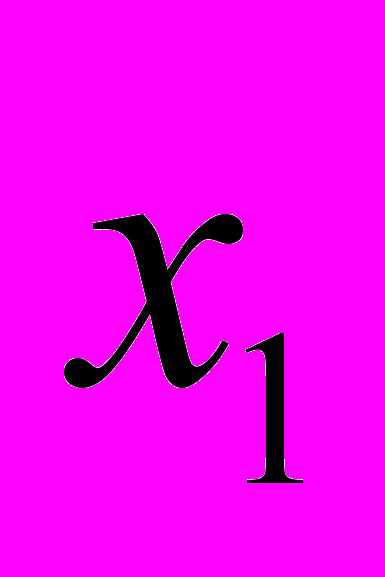 ,
, 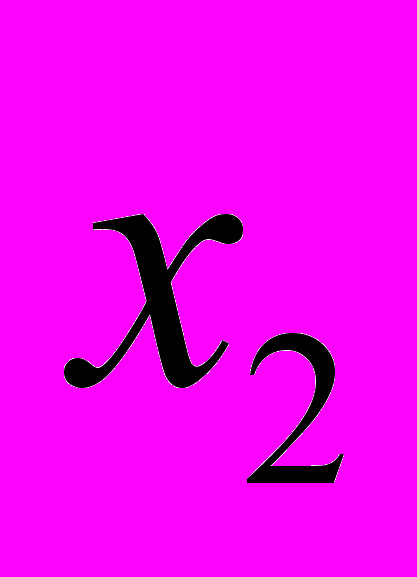 . Записати функцію Лагранжа і рівняння Лагранжа цієї системи через узагальнені координати:
. Записати функцію Лагранжа і рівняння Лагранжа цієї системи через узагальнені координати: 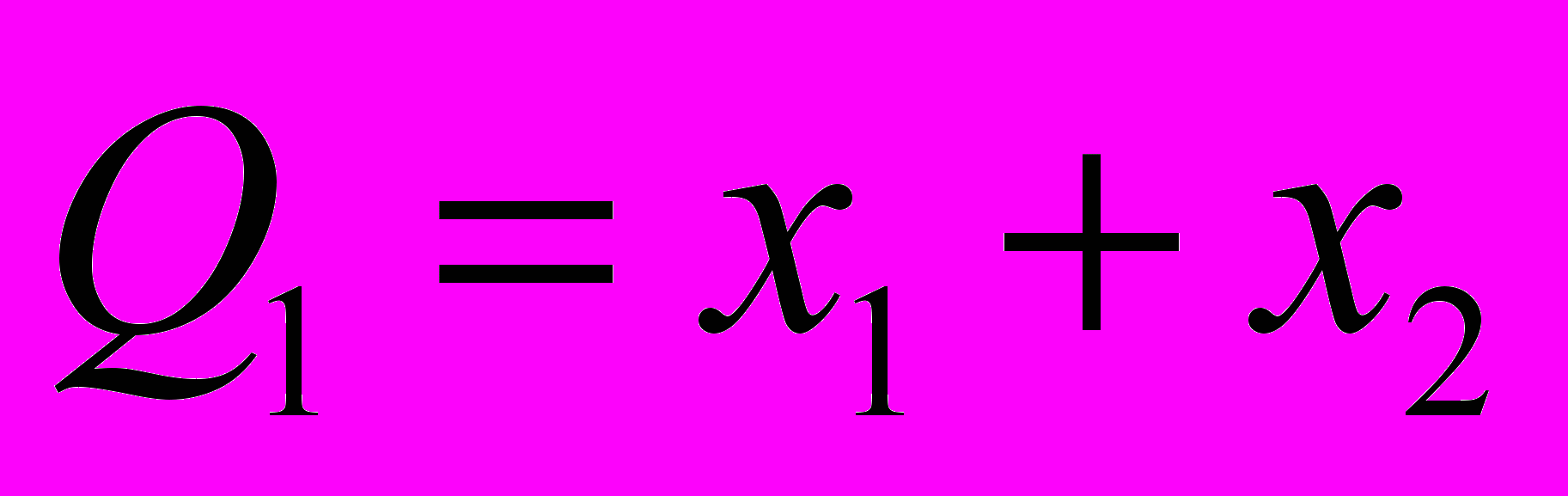 ,
, 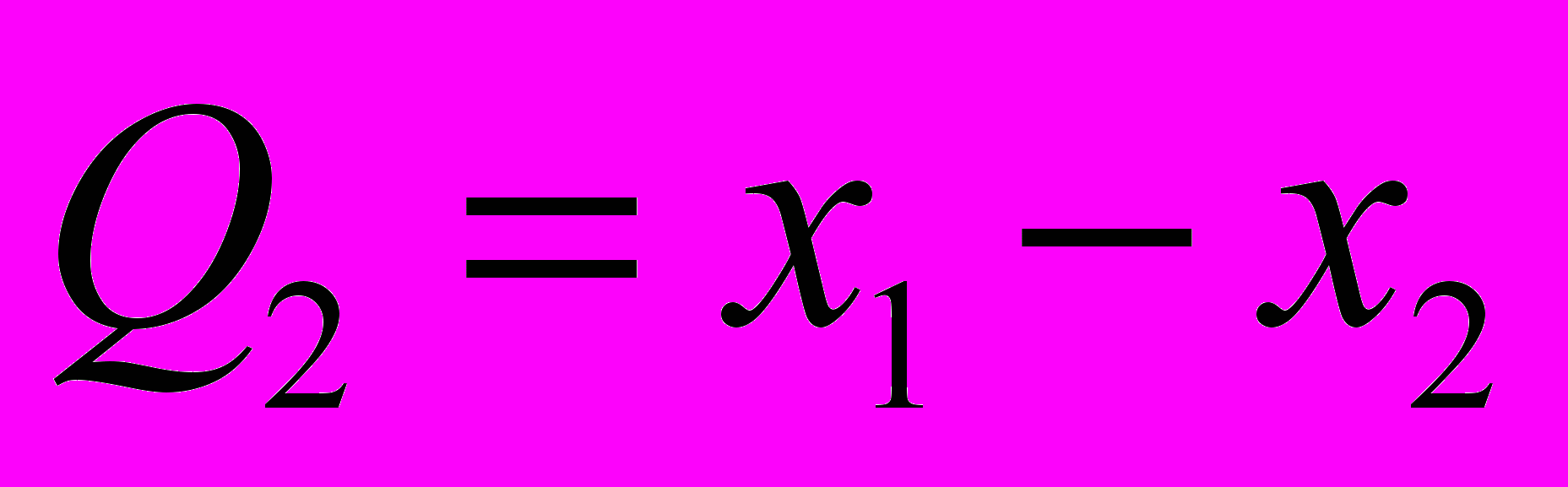 .
.
- Подвійного пружинний маятник, точка підвісу якого рухається у вертикальному напрямку по закону:
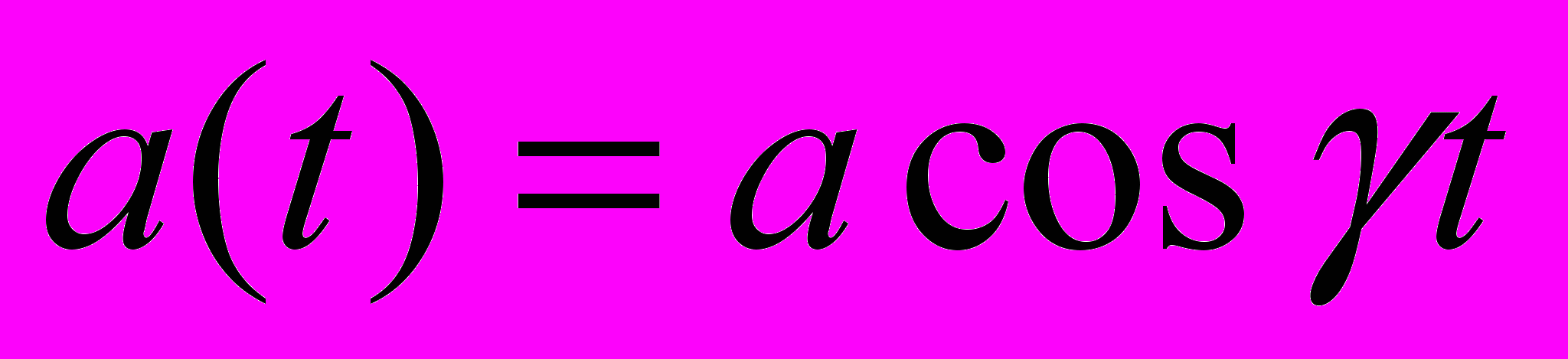 .
.
- Подвійний пружинний маятник, точка підвісу якого рухається у вертикальному напрямку по закону:
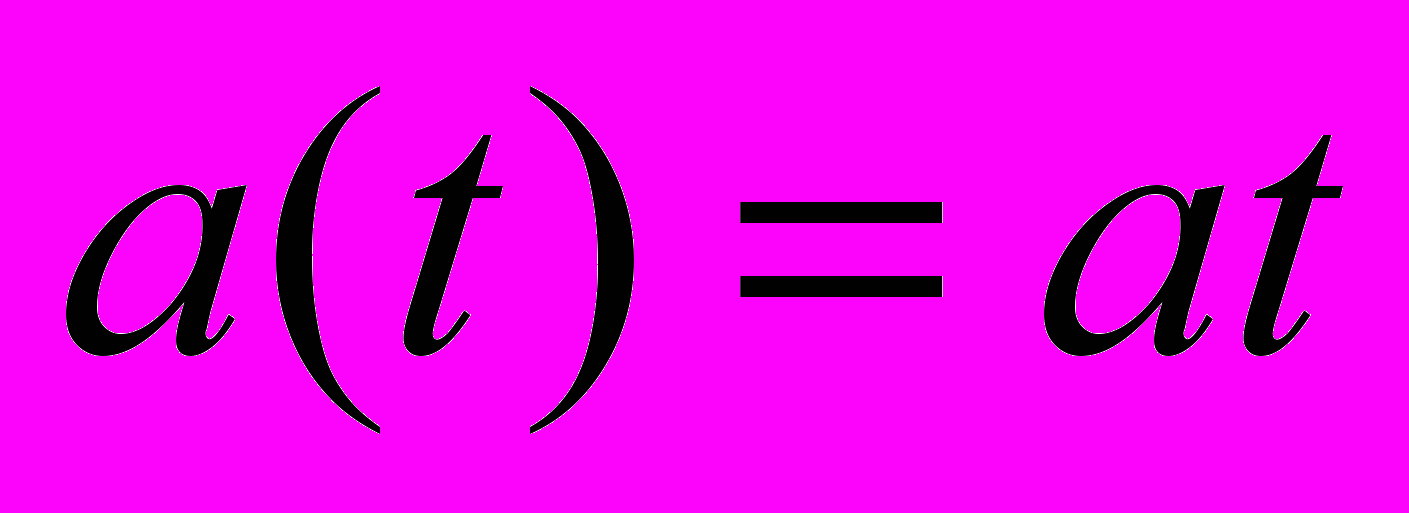 .
.
- Частинка рухається в полі тяжіння вздовж прямої, яка рівномірно обертається навколо вертикалі з частотою
 .
.
Основна література
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, том 1. Механика. - М.: Наука, 1973.
- Савельєв И.В.Основы теоретической физики, том 1. Механика и электродинамика.
- Г.Голдстейн, Классическая механика. М.: Наука, 1975.
- Хаар Д. Тер. Основы Гамильтоновой механики. – М.: Наука, 1974.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, том 1. Механика. - М.: Наука, 1973.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, том 1. Механика. - М.: Наука, 1973.
- Сивухин Д.В. Общий курс физики, том 1. Механика. – М.: Наука, 1989.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, том 7. Теория упругости. - М.: Наука, 1987.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, том 6. Гидродинамика. - М.: Наука, 1986.
Додаткова література
- Матвеев А.Н. Механика и теория относительности. – М.: Высшая школа, 1986.
- Андрєєв В.О., Дущенко В.П., Федорченко А.М. Теоретична фізика. Класична механіка. – К.: «Вища школа», 1984
- Федорченко А.М. Теоретична фізика. Класична механіка і електродинаміка. – К.: «Вища школа», 1992.
- Мултановський В.В. Курс теоретической физики: классическая механіка. – М.: Просвещение, 1988.
