Робоча програма навчальної дисципліни для студентів (назва навчальної дисципліни)

Вид материала

Содержание

Доцент кафедри математичного аналізу
Завідувач кафедрою математичного аналізу
Опис навчальної дисципліни
0403 - “системні науки і кібернетика”
4 самостійної роботи студента 2,3
Мета та завдання навчальної дисципліни
У результаті вивчення даного курсу студент повинен
Структура навчальної дисципліни
Модуль 1. Границя числової послідовності.
Модуль 2. Числові ряди.
Модуль 3. Границя функції.
Модуль 4. Диференціальне числення функцій однієї змінної.
Усього годин
Модуль 5. Невизначений інтеграл.
Модуль 6. Визначений інтеграл та його застосування.
Модуль 7. Функціональні ряди. Степеневі ряди.
Модуль 8. Диференціальне числення функцій кількох змінних.
Усього годин
Модуль 9. Кратні інтеграли Рімана.
Модуль 10. Криволінійні та поверхневі інтеграли першого роду.
...
Полное содержание

Подобный материал:

Міністерство освіти і науки України

Харківський національний університет імені В.Н. Каразіна

Кафедра математичного аналізу

“ЗАТВЕРДЖУЮ”

Перший проректор Харківського національного університету імені В.Н.Каразіна

Александров В.В.

___________________________

“______”_______________20___ р.

РОБОЧА ПРОГРАМА НАВЧАЛЬНОЇ ДИСЦИПЛІНИ

______________________-“математичний аналіз”_____________________

(шифр і назва навчальної дисципліни)

напряму підготовки___________6.040302 - “інформатика”___________________________

(шифр і назва напряму підготовки)

для спеціальності__________________________________________________________

(шифр і назва спеціальності)

спеціалізації______________________________________________________________

(назва спеціалізації)

факультету_________________механіко-математичний________________________

(назва факультету)

Кредитно-модульна система

організації навчального процесу

Харків – 2009

Математичний аналіз Робоча програма навчальної дисципліни для студентів

(назва навчальної дисципліни)

за напрямом підготовки 6.040302 - “інформатика” , за спеціальністю___________

„___” ________, 2009_. - 14 с.

Розробники: (вказати авторів, їхні наукові ступені, вчені звання та посади).

Доцент кафедри математичного аналізу

кандидат фізико-математичних наук

Гефтер Сергій Леонідович

Робоча програма затверджена на засіданні кафедри математичного аналізу

Протокол № 1 від “28” серпня 2009 р.

Завідувач кафедрою математичного аналізу

доктор фізико-математичних наук

професор Гордевський В’ячеслав Дмитрович

_______________________ (Гордевський В.Д.)

(підпис) (прізвище та ініціали)

“ 28 ” серпня 2009 р.

Схвалено методичною комісією механіко-математичного факультету

Протокол № ___ від. “____”________________20___ р.

“_____”________________20__ р. Голова _______________( Тарапова О.І.)

(підпис) (прізвище та ініціали)

Опис навчальної дисципліни

Найменування показників	Галузь знань, напрям підготовки, освітньо-кваліфікаційний рівень	Характеристика навчальної дисципліни
		денна форма навчання	заочна форма навчання
Кількість кредитів –	Галузь знань 0403 - “системні науки і кібернетика” (шифр і назва)	Нормативна
	Напрям підготовки 6.040302 - “інформатика” (шифр і назва)
Модулів – 12	Спеціальність (професійне спрямування):	Рік підготовки:
		1-2-й	1-2-й
Індивідуальне науково-дослідне завдання (назва)		Семестр
Загальна кількість годин – 324		1-3-й	1-3-й
		Лекції
Тижневих годин для денної форми навчання: аудиторних 4 самостійної роботи студента 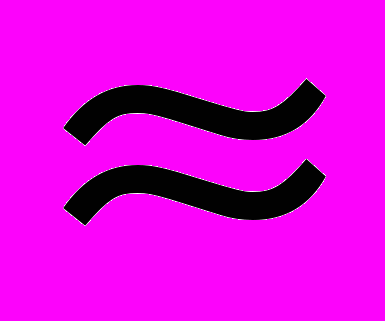2,3	Освітньо-кваліфікаційний рівень: “бакалавр”	106 год.	21
		Практичні, семінарські
		106 год.	21
		Лабораторні

		Самостійна робота
		112 год.	282
		ІНДЗ: 24 год.
		Вид контролю: залік, екзамен

Примітка.

Співвідношення кількості годин аудиторних занять до самостійної і індивідуальної роботи становить:

для денної форми навчання

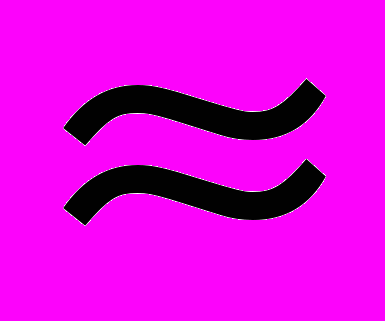7:4

Мета та завдання навчальної дисципліни

Мета курсу полягає у наданні майбутнім спеціалістам знань у галузі сучасного математичного аналізу.

Завданням курсу є навчання студентів теоретичним основам і методам математичного аналізу та застосуванню цих методів для розв’язання різноманітних задач теоретичного та практичного характеру.

У результаті вивчення даного курсу студент повинен

знати:

– властивості границь числових послідовностей та числових функцій;

– властивості неперервних функцій ;

– диференціальне числення функцій однієї та багатьох змінних;

– теорію інтеграла Рімана на відрізку та теорію кратних інтегралів Рімана;

– теорію збіжності невласних інтегралів;

– теорію збіжності числових рядів;

– теорію рівномірної збіжності функціональних послідовностей та рядів;

– теорію степеневих рядів;

– елементи теорії метричних, нормованих та евклідових просторів;

– елементи теорії інтегралів, що залежать від параметру;

– елементи теорії інтеграла Стілтьєса;

– теорію криволінійних та поверхневих інтегралів першого роду;

– теорію криволінійних та поверхневих інтегралів другого роду;

– класичні формули Гріна, Гаусса-Остроградського та Стокса;

– основи теорії векторних полів;

– елементи теорії рядів Фур’є;

– властивості перетворення Фур’є та інтегралу Фур’є.

вміти:

– знаходити границі послідовностей і функцій;

– оцінювати швидкість зростання нескінченно великих послідовностей;

– досліджувати функції на неперервність;

– диференціювати функції однієї та багатьох змінних;

– користуватися розвиненням функції за формулою Тейлора;

– досліджувати функції на монотонність, екстремум та опуклість;

– будувати графік функції за допомогою диференціального числення;

– знаходити невизначені інтеграли;

– обчислювати визначені інтеграли за Ріманом, подвійні та потрійні інтеграли, криволінійні та поверхневі інтеграли;

– застосовувати інтеграл Рімана в геометрії, механіці, фізиці;

– досліджувати на абсолютну та умовну збіжності невласні інтеграли Рімана;

– досліджувати на абсолютну та умовну збіжності числові ряди;

– досліджувати на рівномірну збіжність функціональні послідовності та ряди;

– отримувати розвинення функцій у ряд Тейлора;

– досліджувати на внутрішній та умовній екстремум функції багатьох змінних;

– обчислювати інтеграли за допомогою Г-функцій та В-функцій;

– застосовувати кратні інтеграли в геометрії, механіці, фізиці;

– застосовувати формули Гріна, Гауса-Остроградського, Стокса для обчислення криволінійних та поверхневих інтегралів;

– застосовувати методи та термінологію векторної теорії полів;

– розкладати функцію у ряд Фур’є та досліджувати його на збіжність;

– здійснювати перетворення Фур’є функції та подавати її у вигляді інтегралу Фур’є.

Програма навчальної дисципліни

І семестр

Модуль 1. Границя числової послідовності.

Логічна символіка, множини, функції, послідовності. Аксіоми дійсних чисел. Обмеженість,

точні межі числової множини.

2. Границя числової послідовності і загальні властивості таких границь. Нескінченно малі та

нескінченно великі послідовності.

3. Теорема Вейерштрасса про збіжність монотонних послідовностей. Число e.

4. Порівняння швидкості зростання послідовностей, асимптотика послідовностей. Символи

О і

.

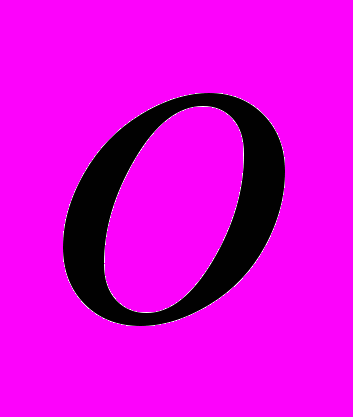5. Часткові границі числової послідовності, верхня та нижня границя послідовності. Принцип

Больцано-Вейєрштрасса для послідовностей.

6. Означення фундаментальної послідовності. Критерій Коші збіжності послідовності.

Модуль 2. Числові ряди.

Означення числового ряду, його часткових сум і збіжності ряду. Найпростіші властивості числових рядів. Критерій Коші та необхідна умова збіжності числового ряду.
Ознаки збіжності рядів з невід’ємними членами.
Абсолютна та умовна збіжність рядів. Ознака Лейбніца.

Модуль 3. Границя функції.

Границя функції за Коші та за Гейне. Загальні властивості границь функцій.
Порівняння функцій, асимптотика функцій, асимптоти графіка функції.
Важливі границі, що пов’язані з елементарними функціями.
Неперервність функції за Коші і за Гейне. Локальні властивості неперервних функцій. Неперервність елементарних функцій.
Властивості функцій, неперервних на відрізку.
Точки розриву та їх класифікація.

Модуль 4. Диференціальне числення функцій однієї змінної.

Означення диференційовної функції в точці. Диференціал та похідна функції в точці.

Механічне та геометричне тлумачення понять похідної та диференціалу функції. Рівняння дотичної до графіка диференційовної функції.

Правила диференціювання функцій. Похідні елементарних функцій.
Теореми Ферма, Ролля, Лагранжа, Коші та їх застосування. Правило Лопіталя.
Похідні вищих порядків. Локальна і глобальна формули Тейлора.
Опуклість і точки перегину. Достатня умова опуклості у термінах другої похідної.
Нерівність Йенсена та її наслідки.

ІІ семестр

Модуль 5. Невизначений інтеграл.

Означення первісної функції на проміжку. Невизначений інтеграл і його властивості. Таблиця первісних деяких елементарних функцій. Формула заміни змінної та формула інтегрування частинами для невизначеного інтегралу.
Інтегрування раціональних функцій. Інтегрування деяких ірраціональностей та деяких трансцендентних функцій.

Модуль 6. Визначений інтеграл та його застосування.

Означення інтегральних сум Рімана та інтеграла Рімана. Необхідна умова інтегрованості функції за Ріманом.
Нижні (верхні) суми Дарбу та їх властивості. Означення нижнього (верхнього) інтеграла Дарбу.

Критерії Дарбу і Рімана інтегрованості функції за Ріманом.

Класи функцій, інтегрованих за Ріманом
Властивості визначеного інтеграла.
Неперервність та диференційовність функції, заданої інтегралом Рімана із змінною верхньою межею інтегрування. Існування первісної у неперервної функції.
Формула Ньютона-Лейбніца. Відновлення функції за її похідною. Формула інтегрування частинами для інтеграла Рімана. Теорема про заміну змінної в інтегралі Рімана.
Застосування визначеного інтеграла до геометрії: площа криволінійної трапеції, довжина кривої, об’єм тіла обертання. Механічні застосування інтеграла.
Невласний інтеграл по необмеженому проміжку та від необмеженої функції. Обчислення невласних інтегралів.
Ознака порівняння збіжності невласних інтегралів і її наслідки. Еталонні інтеграли. Зв'язок з числовими рядами.
Абсолютна та умовна збіжності невласних інтегралів. Головне значення невласного інтеграла в розумінні Коші.
В- і Г- функції Ейлера та їх застосування. Формула Стірлінга для Г-функції та факторіала.

Модуль 7. Функціональні ряди. Степеневі ряди.

Поточкова та рівномірна збіжність. Критерій Коші і ознака Вейерштрасса рівномірної збіжності функціональних рядів.
Теорема про неперервність граничної функції. Почленне інтегрування і диференціювання функціонального ряду.
Означення степеневого ряду. Радіус та інтервал збіжності степеневого ряду. Властивості суми степеневого ряду, почленне диференціювання та інтегрування степеневих рядів. Ряд Тейлора. Ряд Маклорена основних елементарних функцій. Формула Ейлера.
Арифметичні дії над степеневими рядами. Твірна функція числової послідовності.

Модуль 8. Диференціальне числення функцій кількох змінних.

Простір 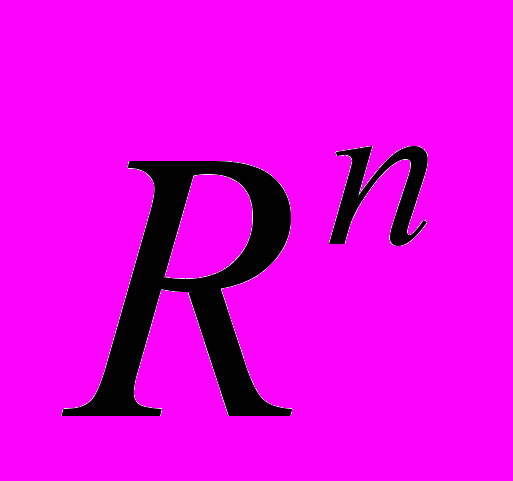. Збіжність і компактність в 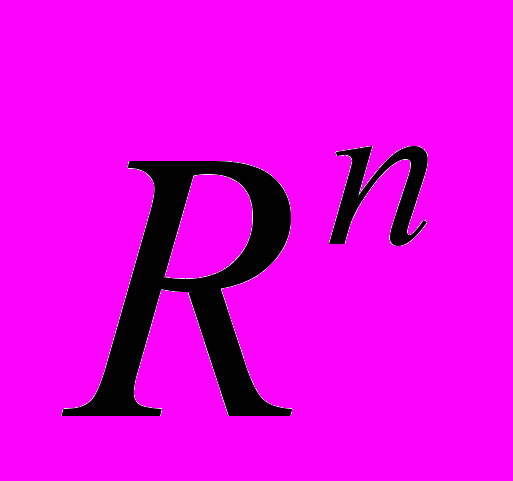. Локальні та глобальні властивості неперервних функцій кількох змінних.
Диференційовність функції кількох змінних в точці, умови диференційовності. Дотична і нормаль до поверхні. Похідна функції за напрямком і градієнт.
Похідна композиції функцій інваріантність форми першого диференціала. Теорема Лагранжа та її наслідки.
Похідні та диференціали вищих порядків. Теорема про рівність змішаних похідних. Формула Тейлора.
Локальний екстремум функції кількох змінних. Метод найменших квадратів.
Теореми про неявну функцію та неявне відображення. ^{Функціональна залежність і незалежність гладких функцій. Умовний екстремум.}

ІІІ семестр

Модуль 9. Кратні інтеграли Рімана.

Означення інтегральних сум Рімана, інтеграла Рімана по брусу та інтегровної за Ріманом функції на брусі. Необхідна умова інтегровності за Ріманом. Верхні та нижні суми Дарбу та їх властивості.
Множини об’єму нуль і міри нуль. Інтегровність неперервної на брусі функції. Інтеграл по обмеженій множині в 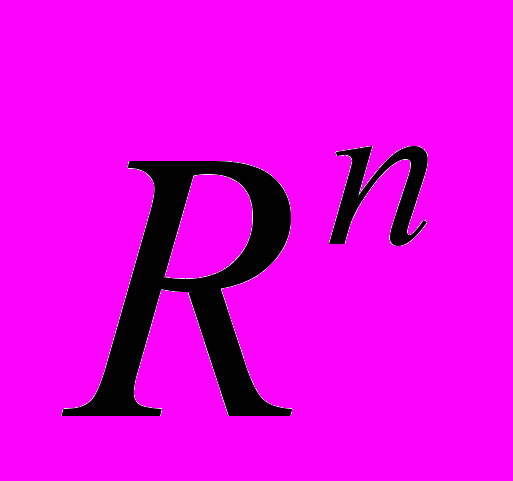. Множини, вимірні за Жорданом. Зведення кратного інтеграла по брусу і циліндроїду до повторних.
Заміна змінних в кратних інтегралах.

Модуль 10. Криволінійні та поверхневі інтеграли першого роду.

^{Означення криволінійного інтеграла 1-го роду по простій гладкій кривій, незалежність від вибору п}^{араметризації та зведення його до інтеграла Рімана.}
^{Означення поверхневого інтеграла 1-го роду по елементарній гладкій поверхні.}^{Площа гладкої поверхні. Формули для обчислення поверхневих інтегралів 1-го роду.}

Модуль 11. Криволінійні та поверхневі інтеграли другого роду.

^{Означення і обчислення}^{криволінійного та}^{поверхневого інтеграла 2-го роду. Приклади (інтеграли роботи та потоку).}
Властивості поверхневих інтегралів 2-го роду. Зв’язок між поверхневими інтегралами 1-го и 2-го родів^.
^{Формули Гріна, Стокса та Гаусса-Остроградського. Дивергенція і ротор. Поняття про диференціальні форми і загальну формулу Стокса.}
Означення потенціального векторного поля и його потенціалу. Необхідна умова потенціальності поля. Робота сил у потенціальному полі. Критерії потенціальності векторного поля.

Модуль 12. Ряди Фур’є та інтеграл Фур’є.

Ортогональні та ортонормовані системи векторів у лінійних просторах зі скалярним добутком. Система тригонометричних функцій на [-,].
Коефіцієнти Фур’є і ряд Фур’є вектора у просторі зі скалярним добутком відносно ортонормованої або ортогональної послідовності. Тригонометричний ряд Фур’є на [-,].
Нерівність Бесселя і рівність Парсеваля. Теорема Ляпунова про повноту тригонометричної системи функцій.
Інтегральні зображення для часткових сум тригонометричних рядів Фур’є. Поточкова та рівномірна збіжність тригонометричних рядів Фур’є. Зв’язок між степенем гладкості функції та швидкістю прямування до нуля коефіцієнтів її тригонометричного ряду Фур’є.
Теорема Фейєра. Теореми Вейєрштрасса про рівномірну апроксимацію неперервних функцій тригонометричними та алгебраїчними поліномами.
Означення перетворення Фур’є та інтеграла Фур’є. Властивості перетворення Фур’є . Формула обернення. Приклади.

Структура навчальної дисципліни

І семестр

Назви модулів	Кількість годин
	Денна форма						Заочна форма
	Усього	у тому числі					Усього	у тому числі
	Усього	л	п	лаб	інд	ср	Усього	л	п	лаб	інд	ср
1	2	3	4	5	6	7	8	9	10	11	12	13
Модуль 1. Границя числової послідовності.	30	12	8			10	25	2	5			18
Модуль 2. Числові ряди.	12	4	4			4	23	1	2			20
Модуль 3. Границя функції.	22	8	8			6	24	1	3			20
Модуль 4. Диференціальне числення функцій однієї змінної.	34	12	16			6	26	2	4			20
Екзамен	10					10	10					10
Усього годин	108	36	36			36	108	6	14			88

ІІ семестр

Назви модулів	Кількість годин
	Денна форма						Заочна форма
	Усього	у тому числі					Усього	у тому числі
	Усього	л	п	лаб	інд	ср	Усього	л	п	лаб	інд	ср
1	2	3	4	5	6	7	8	9	10	11	12	13
Модуль 5. Невизначений інтеграл.	15	4	6			5	23	1	2			20
Модуль 6. Визначений інтеграл та його застосування.	28	10	8			10	26	2	4			20
Модуль 7. Функціональні ряди. Степеневі ряди.	28	10	8			10	25	1	4			20
Модуль 8. Диференціальне числення функцій кількох змінних.	32	10	12			10	29	2	4			23
Залік	5					5	5					5
Усього годин	108	34	34			40	108	6	14			88

ІІІ семестр

Назви модулів	Кількість годин
	Денна форма						Заочна форма
	Усього	у тому числі					Усього	у тому числі
	Усього	л	п	лаб	інд	ср	Усього	л	п	лаб	інд	ср
1	2	3	4	5	6	7	8	9	10	11	12	13
Модуль 9. Кратні інтеграли Рімана.	25	8	9			8	24	1	3			20
Модуль 10. Криволінійні та поверхневі інтеграли першого роду.	24	9	9			6	23	1	2			20
Модуль 11. Криволінійні та поверхневі інтеграли другого роду.	24	9	9			6	27	2	5			20
Модуль 12. Ряди Фур’є та інтеграл Фур’є.	25	10	9			6	24	2	4			18
Екзамен	10					10	10					10
Усього годин	108	36	36			36	108	6	14			88

Теми семінарських занять

№ з/п	Назва теми	Кількість годин
1	Не передбачені навчальним планом

Теми практичних занять

I семестр

№ з/п	Назва теми	Кількість годин
1	Границя числової послідовності. Послідовність. Обмеженість та монотонність послідовності. Границя послідовності, обчислення границь. Асимптотичне порівняння послідовностей.	8
2	Числові ряди. Дослідження на збіжність числових рядів з невід’ємними членами та знакозмінних рядів.	4
3	Границя функції. Границя функції, обчислення границь, Асимптотичне порівняння функцій. Дослідження функцій на неперервність	8
4	Диференціальне числення функцій однієї змінної. Обчислення похідних і диференціалів першого порядку. Геометричні застосування похідних. Наближені обчислення із застосуванням диференціалів. Правило Лопіталя. Обчислення похідних вищих порядків. Формула Тейлора. Дослідження функцій за допомогою похідних. Побудова графіків функцій та кривих.	16
	Разом за І семестр	36

ІI семестр

№ з/п	Назва теми	Кількість годин
5	Невизначений інтеграл. Первісна та невизначений інтеграл. Інтегрування заміною змінної та інтегрування частинами. Інтегрування раціональних функцій. Методи інтегрування ірраціональностей. Інтегрування тригонометричних функцій.	6
6	Визначений інтеграл та його застосування. Обчислення визначених інтегралів. Геометричні застосування визначеного інтеграла та застосування інтеграла Рімана в механіці та фізиці. Обчислення та дослідження на збіжність невласних інтегралів. Застосування функцій Ейлера Г(p) і B(p,q) для обчислення невласних інтегралів.	8
7	Функціональні ряди. Степеневі ряди. Дослідження на поточкову та рівномірну збіжність функціональних послідовностей та рядів. Неперервність суми ряда. Диференціювання та інтегрування функціональних рядів. Дослідження степеневих рядів та розвинення функцій у ряд Тейлора.	8
8	Диференціальне числення функцій кількох змінних. Частинні похідні, диференціал, похідна за напрямком, градієнт. Дотична площина та нормаль до явно заданої поверхні. Похідні та диференціали вищих порядків. Формула Тейлора. Диференціювання неявно заданих функцій. Дослідження функцій на внутрішній та умовний екстремум.	12
	Разом за ІІ семестр	34

ІІI семестр

№ з/п	Назва теми	Кількість годин
9	Кратні інтеграли Рімана. Обчислення подвійних і потрійних інтегралів зведенням їх до повторних у декартових координатах та переходом до полярних, сферичних, циліндричних та інших систем координат. Обчислення площ та об’ємів за допомогою подвійних і потрійних інтегралів. Застосування подвійних і потрійних інтегралів у механіці та фізиці.	9
10	Криволінійні та поверхневі інтеграли першого роду. Обчислення криволінійних та поверхневих інтегралів першого роду та їх застосування у механіці та фізиці.	9
11	Криволінійні та поверхневі інтеграли другого роду. Обчислення криволінійних та поверхневих інтегралів другого роду та їх застосування у геометрії та фізиці. Диференціальні форми, операції над ними та їх властивості. Формули Гріна, Гаусса-Остроградського та Стокса. Елементи теорії поля.	9
12	Ряди Фур’є та інтеграл Фур’є. Розвинення функцій у тригонометричний ряд Фур’є та інтеграл Фур’є	9
	Разом за ІІІ семестр	36

7. Теми лабораторних занять

№ з/п	Назва теми	Кількість годин
1	Не передбачені навчальним планом

8. Самостійна робота

I семестр

№ з/п	Назва теми	Кількість годин
1	Границя числової послідовності.	10
2	Числові ряди.	4
3	Границя функції.	6
4	Диференціальне числення функцій однієї змінної.	6
	Екзамен	10
	Разом за І семестр	36

ІI семестр

5	Невизначений інтеграл	5
6	Визначений інтеграл та його застосування	10
7	Функціональні ряди. Степеневі ряди	10
8	Диференціальне числення функцій кількох змінних	10
	Залік	5
	Разом за ІІ семестр	40

ІІI семестр

9	Кратні інтеграли Рімана	9
10	Криволінійні та поверхневі інтеграли першого роду	9
11	Криволінійні та поверхневі інтеграли другого роду	9
12	Ряди Фур’є та інтеграл Фур’є	9
	Екзамен	9
	Разом за ІІІ семестр	36

9. Індивідуальні навчальні завдання

I семестр

Не передбачені навчальним планом

ІI семест

Побудова графіків функцій та кривих.
Невизначений інтеграл.

IІІ семестр

Кратні інтеграли
Криволінійні та поверхневі інтеграли другого роду.

10. Методи навчання

Навчання математичному аналізу здійснюється у формі навчальних занять (лекції, практичні заняття, консультації), а також у формі самостійної роботи (опрацювання навчального матеріалу, виконання та захист кількох індивідуальних навчальних завдань у кожному семестрі та курсової роботи у заключному семестрі).

11. Методи контролю

Протягом вивчення курсу математичного аналізу використовуються наступні види контролю:

1) вхідний (контрольна робота на початку І семестру);

2) поточний семестровий (контрольні роботи, індивідуальні навчальні завдання та колоквіум протягом кожного семестру, ректорська контрольна робота в третьому семестрі);

3) підсумковий семестровий (екзамен у кожному семестрі та залік з курсової роботи у заключному семестрі).

12. Розподіл балів, які отримують студенти

І семестр

Шкала оцінювання в балах засвоєння складових частин навчального матеріалу

при поточному та підсумковому семестровому контролі знань у І семестрі

Модуль 1. Границя числової послідовності - 15 балів

Модуль 2. Числові ряди - 15 балів

Модуль 3. Границя функції - 15 балів

Модуль 4. Диференціальне числення функцій однієї змінної - 15 балів

ІІ семестр

Шкала оцінювання в балах засвоєння складових частин навчального матеріалу

при поточному та підсумковому семестровому контролі знань у ІІ семестрі

Модуль 1. Невизначений інтеграл - 25 балів

Модуль 2. Визначений інтеграл та його застосування - 25 балів

Модуль 3. Функціональні ряди. Степеневі ряди - 25 балів

Модуль 4. Диференціальне числення функцій кількох змінних - 25 балів

ІІІ семестр

Шкала оцінювання в балах засвоєння складових частин навчального матеріалу

при поточному та підсумковому семестровому контролі знань у ІІІ семестрі

Модуль 1. Кратні інтеграли Рімана - 15 балів

Модуль 2. Криволінійні та поверхневі інтеграли першого роду - 15 балів

Модуль 3. Криволінійні та поверхневі інтеграли другого роду - 15 балів

Модуль 4. Ряди Фур’є та інтеграл Фур’є - 15 балів

Сумарна оцінка за вивчення дисципліни у поточному семестрі розраховується як сума модульних оцінок та балів отриманих за результатами підсумкового семестрового контролю, а також додаткових заохочувальних балів, отриманих у разі успішного складання колоквіуму.

Приклад для екзамену (І семестр)

Поточне тестування та самостійна робота				Заохочу вальні бали	Підсумковий семестровий контроль (екзамен)	Сума
Модуль 1	Модуль 2	Модуль 3	Модуль 4
12	8	9	9	5	30	73

Шкала оцінювання

Сума балів за всі види навчальної діяльності протягом семестру	Оцінка ECTS	Оцінка за національною шкалою
	Оцінка ECTS	для екзамену, курсової роботи (проекту), практики	для заліку
90 – 100	А	відмінно	зараховано
80-89	В	добре
70-79	С	добре
60-69	D	задовільно
50-59	Е	задовільно
1-49	FX	незадовільно	не зараховано

13. Методичне забезпечення

1. Бойко С.С. Понятие функции (начальные сведения).

Методические указания и зачетные задания по математическому анализу, 1999.

2. Сердюк Г.П., Рыжий В.С., Николенко И.Г. Построение плоских кривых.

Учебно-методическое пособие по математическому анализу, 2008.

3. Гордевский В.Д. Методы вычисления неопределенных интегралов.

Методические указания и зачетные задания по математическому анализу, 1990.

4. Бойко С.С. Несобственные интегралы (исследование на сходимость).

Методические указания и зачетные задания по математическому анализу, 2002.

5. Бабец В.А. Замена переменных.

Методические указания и зачетные задания по математическому анализу, 1992.

6. Гордевский В.Д. Интегралы, зависящие от параметра.

Методические указания и индивидуальные зачетные задания, 1990.

7. Кудинцева И.Г. Кратные и криволинейные интегралы.

Методические указания и контрольные задания, 1988.

8. Гордевський В.Д. Криволінійні інтеграли. Формула Гріна.

Методичні вказівки та індивідуальні залікові завдання, 2008.

9. Гордевський В.Д. Поверхневі інтеграли. Формули Стокса та Гауса-Остроградського.

Методичні вказівки та індивідуальні залікові завдання, 2006.

10. Агранович П.З., Папуш Е.Д. Ряды Фурье.

Методические указания и индивидуальные зачетные задания, 1992.

14. Рекомендована література

Базова

Тер-Крикоров А.М., Шабунин М.И., Курс математического анализа. – М.: Физматлит, 2003.
Дороговцев А.Я. Математичний аналіз, ч. I, II. –К.; Либідь, 1994.
Кудрявцев Л.Д. Курс математического анализа, т. I,II. – М.; Высшая школа, 1988.
Никольский С.М. Курс математического анализа, т. I, II. – М.: Наука, 1973.
Кудрявцев Л.Д., Кутасов А.Д. и др. Сборник задач по математическому анализу. Предел. Непрерывность. Дифференцируемость. – М.: Наука, 1984.
Кудрявцев Л.Д., Кутасов А.Д. и др. Сборник задач по математическому анализу. Интегралы. Ряды. – М.: Наука, 1986.
Кудрявцев Л.Д., Кутасов А.Д. и др. Сборник задач по математическому анализу. Функции нескольких переменных. – М.: Наука, 1994.
Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1977.

Допоміжна

Шилов Г.Е. Математический анализ, функции одного переменного. – М.: Наука, 1969.
Шилов Г.Е. Математический анализ, функции нескольких вещественных переменных. – М.: Наука, 1972.
Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. – М.: Высш. шк., 1999.
Рудин У. Основы математического анализа. – М.: Мир, 1976.
Грэхем Р., Кнут Д., Паташник О. Конкретная математика: Основания информатики. – М. : Мир, 1998.

Blog

Робоча програма навчальної дисципліни для студентів (назва навчальної дисципліни)

Содержание

РОБОЧА ПРОГРАМА НАВЧАЛЬНОЇ ДИСЦИПЛІНИ

Опис навчальної дисципліни

Усього годин

Усього годин

Усього годин