Секованов В. С., к ф-м н., профессор кафедры прикладной математики и информационных технологий кгу им. Н. А
| Вид материала | Документы |
- Обоснования в математике (от Евклида до компьютера), 49.75kb.
- Программа проведения всероссийской молодёжной школы «Прикладные методы статистического, 81.95kb.
- Программа проведения всероссийской молодёжной школы «Прикладные методы статистического, 78.37kb.
- Задачи на графах программа, 81.89kb.
- А. В. Бернштейн, заведующий лабораторией, 122.14kb.
- И. И. Мечникова Институт математики, экономики и механики Кафедра математического обеспечения, 900.66kb.
- Нечаев Дмитрий Юрьевич, кандидат технических наук, доцент, профессор кафедры информационных, 419.94kb.
- Токсубаева Лидия Сергеевна доцент кгу трофимов Анатолий Михайлович профессор кгу конференция, 336.82kb.
- Программа дисциплины "Прикладной экономический анализ на основе пакетов: spss и Stata", 105.49kb.
- Владимира Игоревича Соловьева, к э. н., проф кафедры прикладной математики и директора, 31.64kb.
Ответ II группы: при 0 < а <9/16 множеством решений данного неравенства является отрезок [х1;х2], где
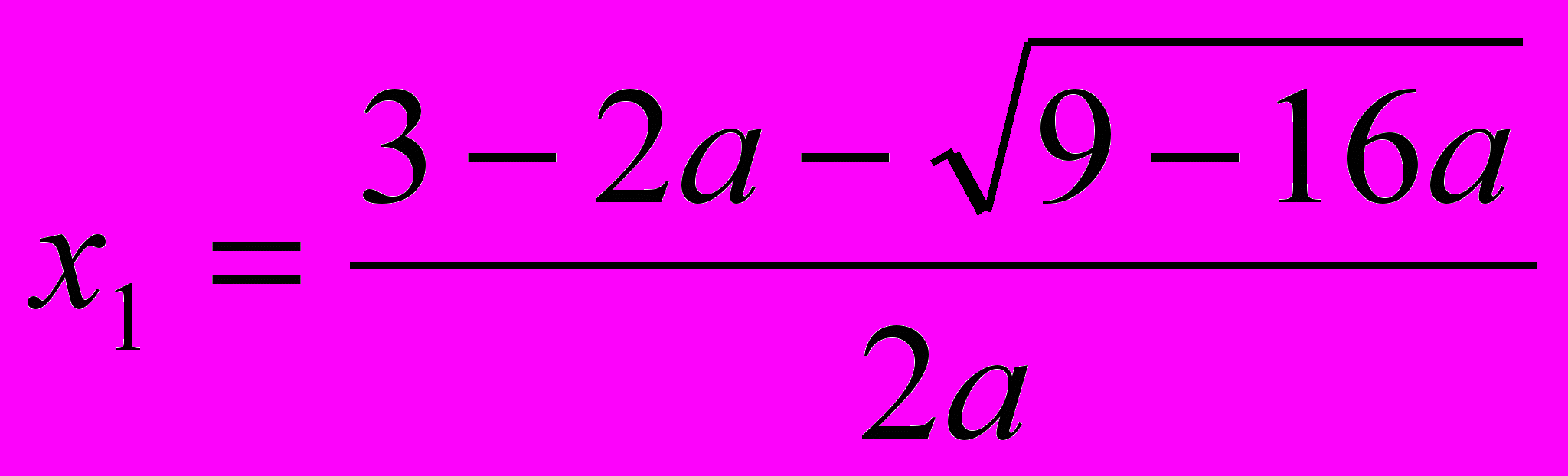 ,
, 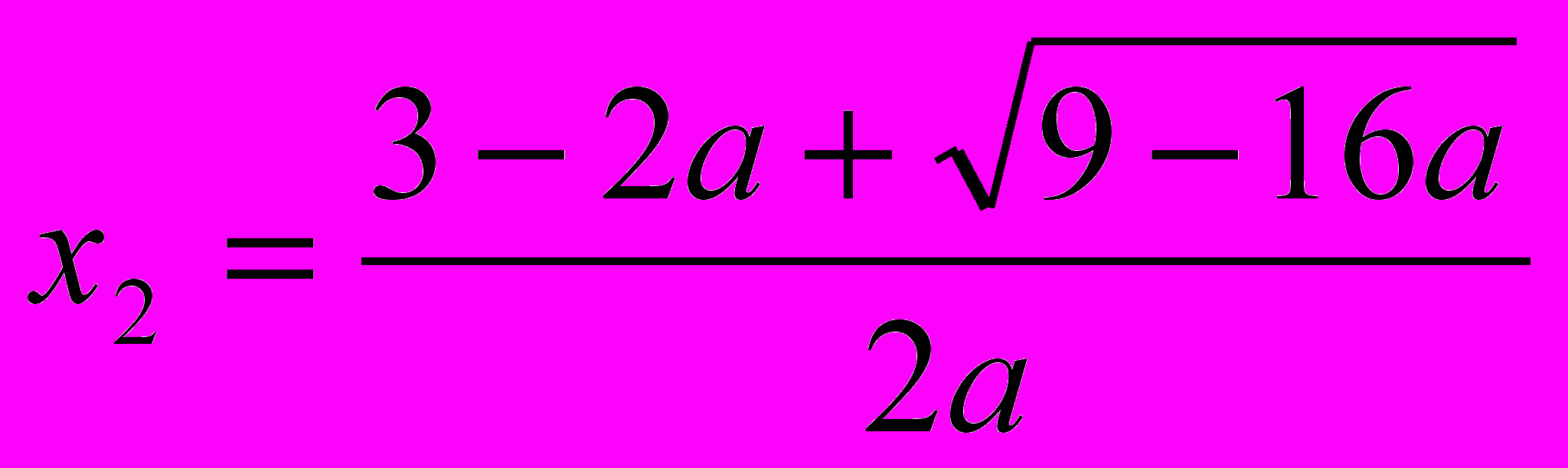 .
.Решение III группы
Множеством решений данного неравенства является точка, если выполняются условия
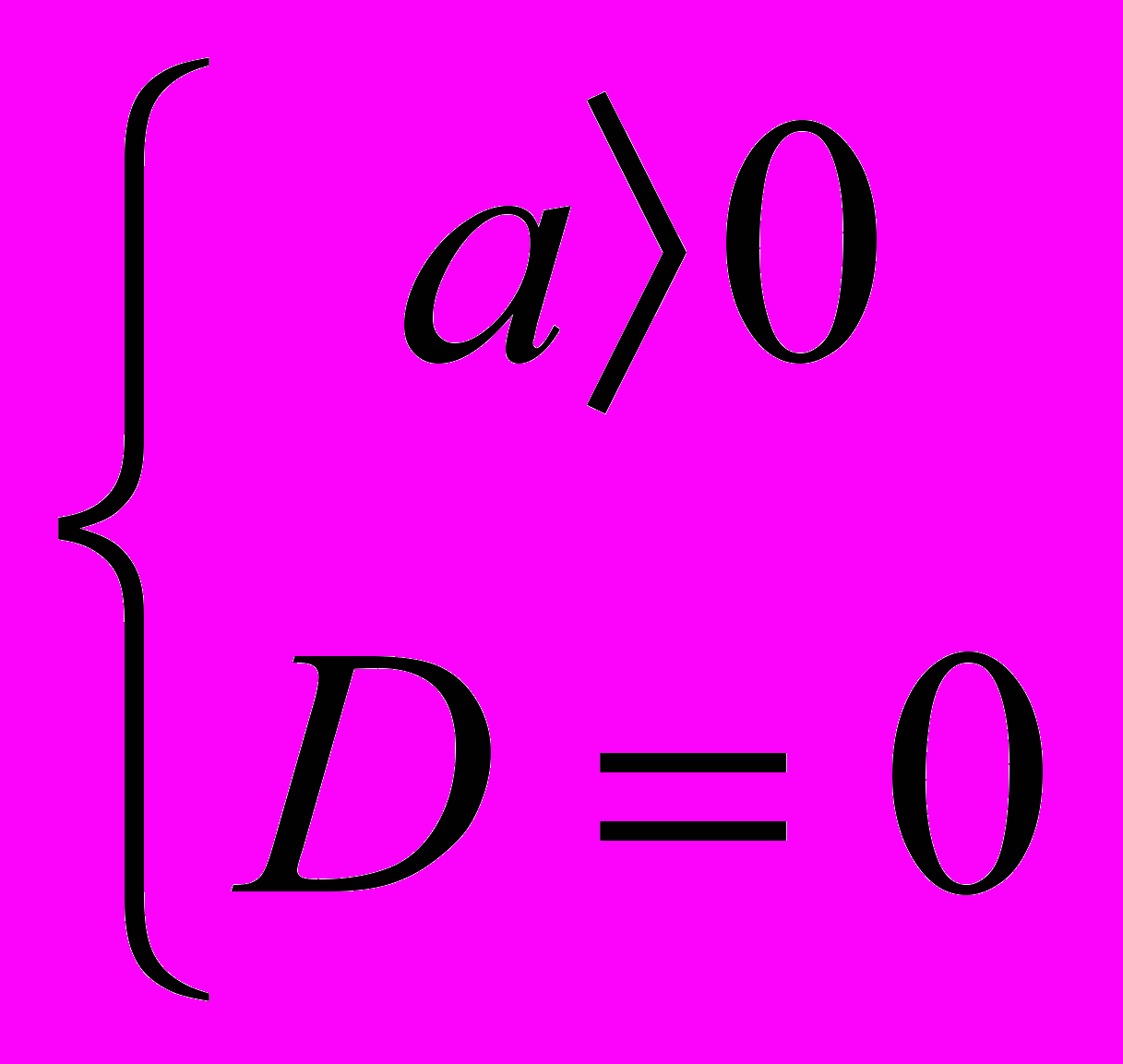 . Подставим значение дискриминанта D= 9-16а в систему и получим
. Подставим значение дискриминанта D= 9-16а в систему и получим 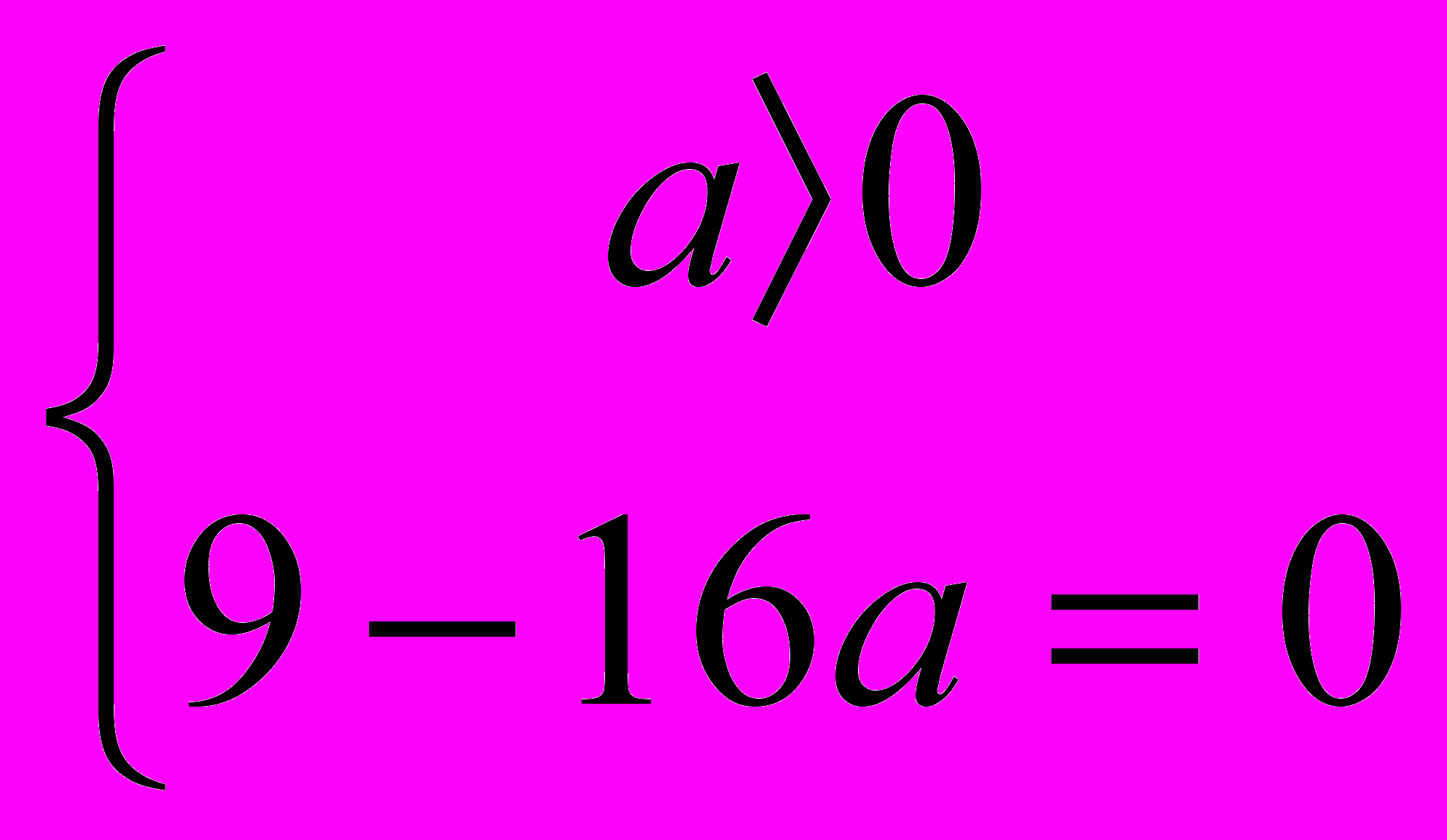 . Решением системы является значение а = 9/16. Найдём значение х.
. Решением системы является значение а = 9/16. Найдём значение х. При D= 0,
 . При а = 9/16,
. При а = 9/16, 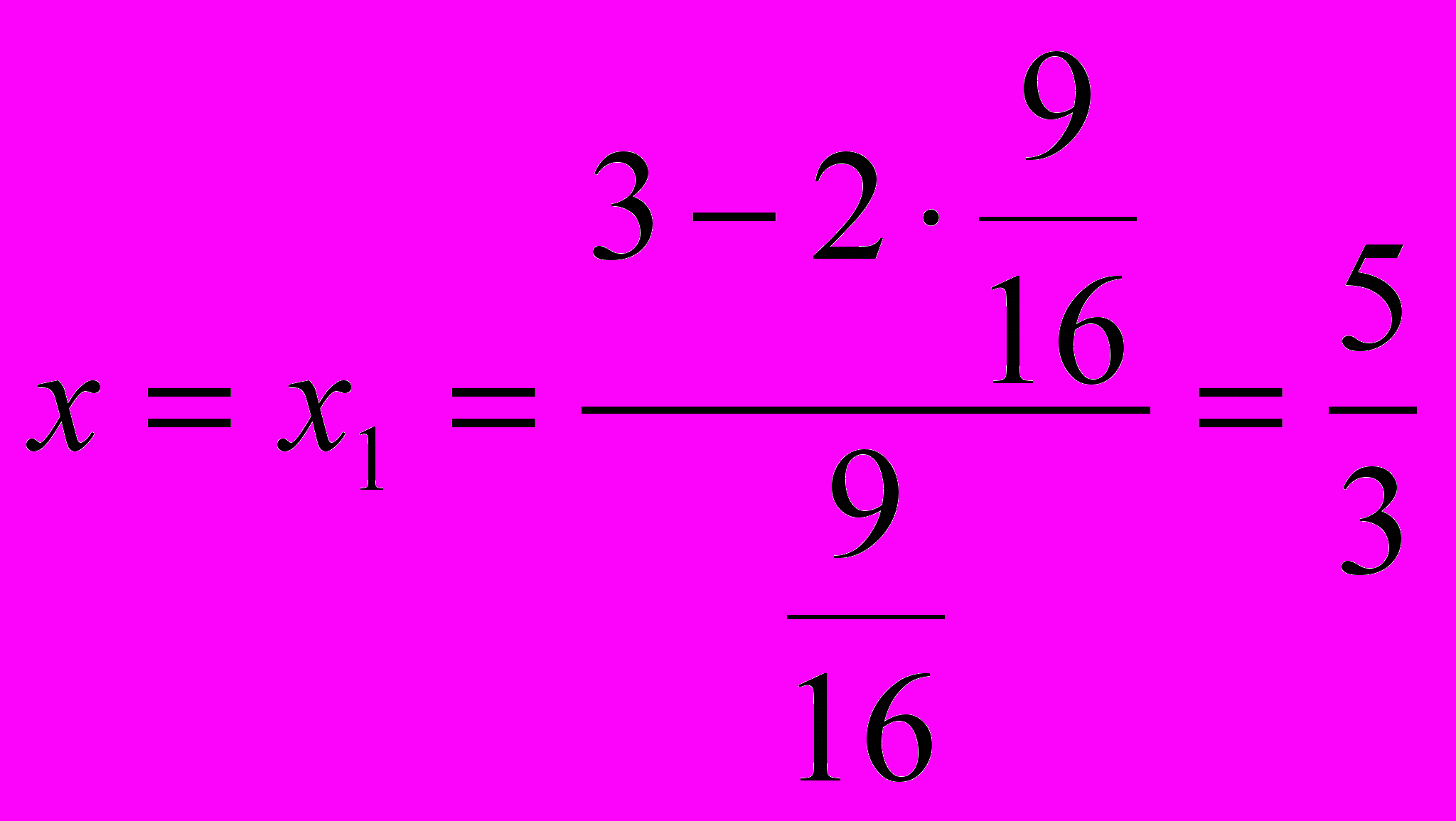 .
.Ответ III группы: при а = 9/16 множеством решений данного неравенства является точка
х=5/3
Решение IV группы
а). Множеством решений данного неравенства является вся прямая, если выполняются условия
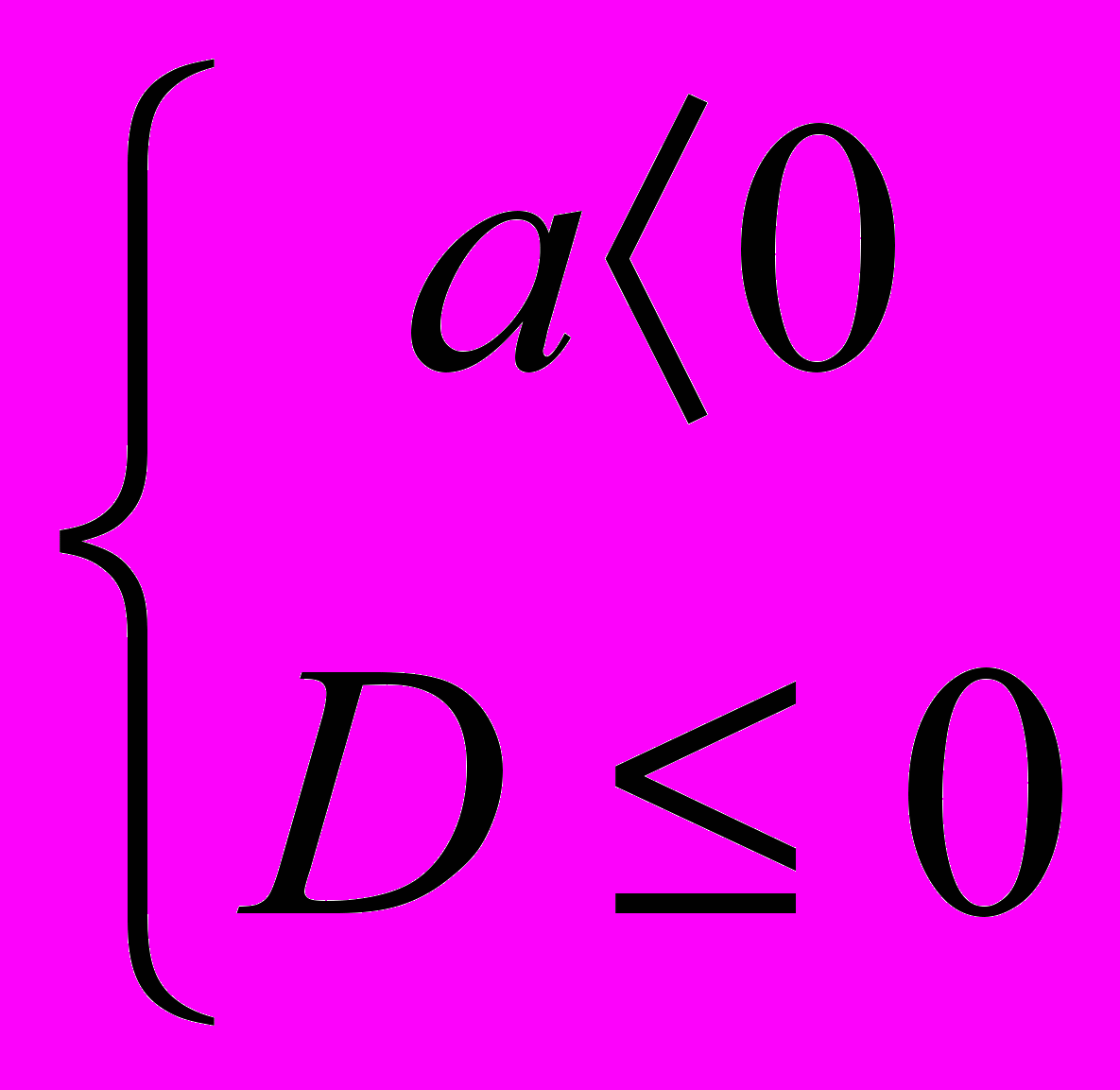 . Подставим значение дискриминанта D= 9-16а в систему и получим
. Подставим значение дискриминанта D= 9-16а в систему и получим 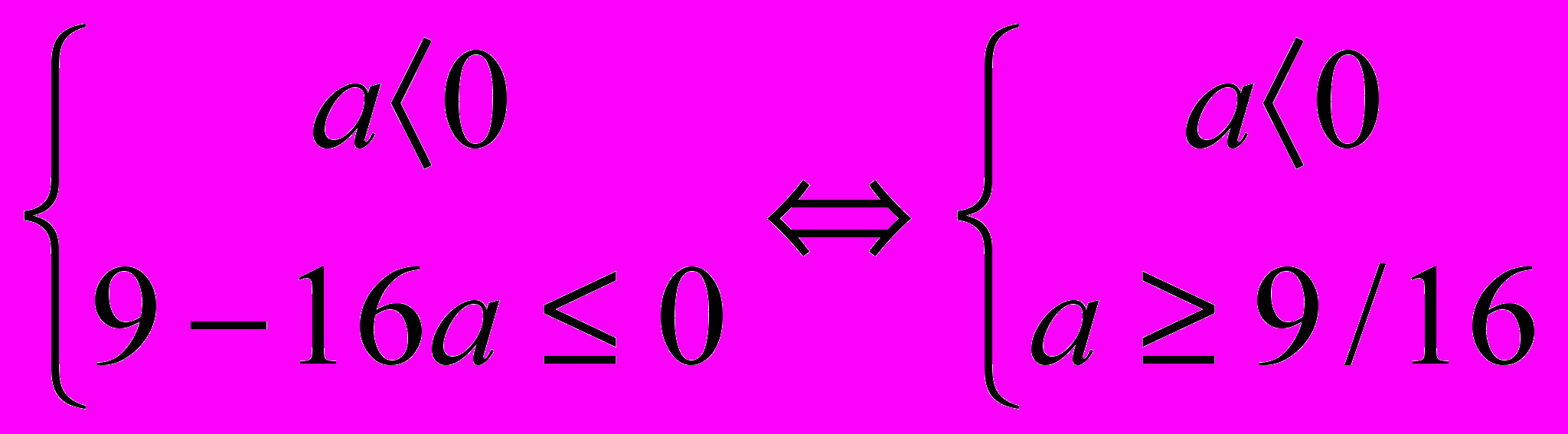 . Данная система решений не имеет, а это значит, что прямая не может являться множеством решений данного неравенства.
. Данная система решений не имеет, а это значит, что прямая не может являться множеством решений данного неравенства.б). Неравенство ах2 + (2a-3)x + а +1≤0 не имеет решений, если выполняются условия
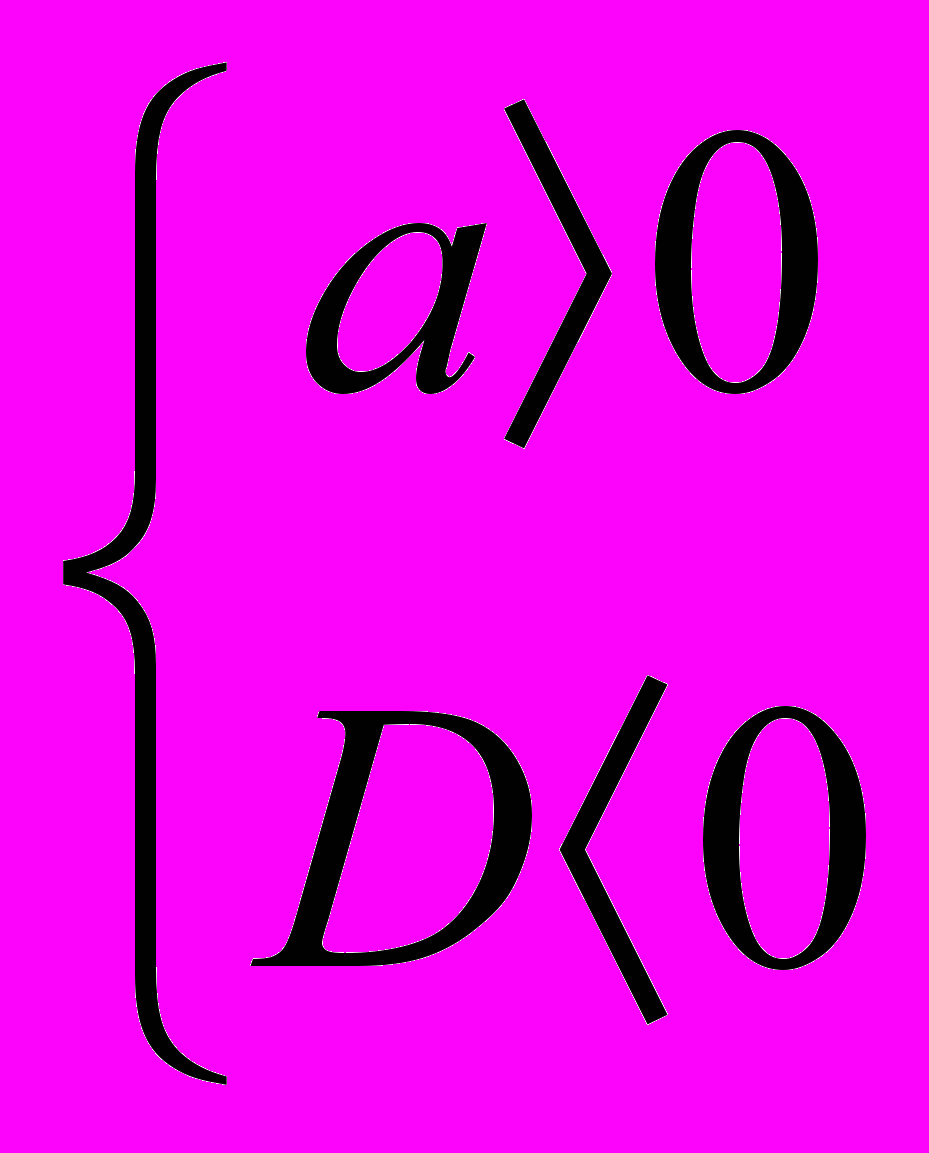 . Подставим значение дискриминанта D= 9-16а в систему и получим
. Подставим значение дискриминанта D= 9-16а в систему и получим 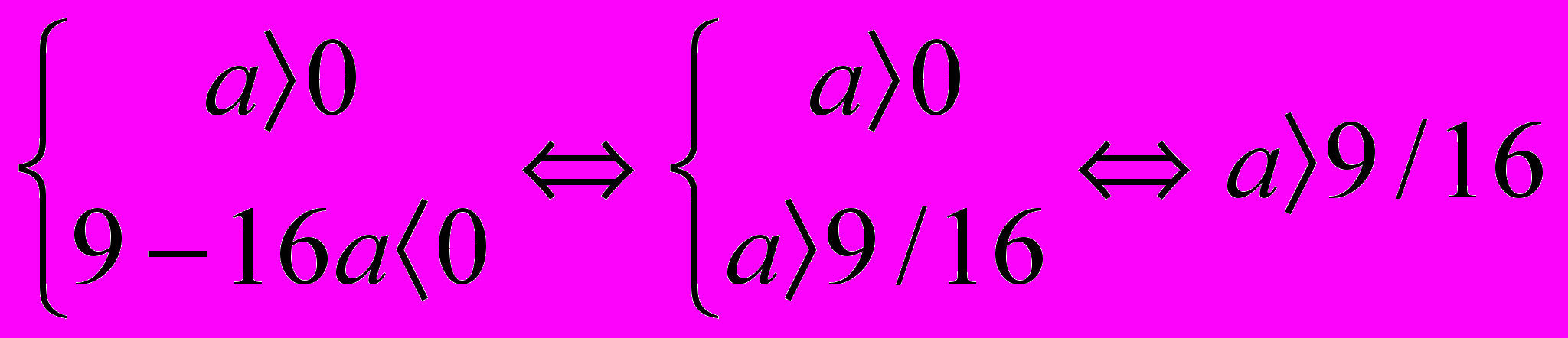 .
.Получили, что неравенство не имеет решений при а (9/16; +∞).
Ответ IV группы: при а (9/16; +∞) неравенство ах2 + (2a-3)x + а +1≤0 не имеет решений
Фиксируем ответы на доске.
при а <0 (- ∞; х2]
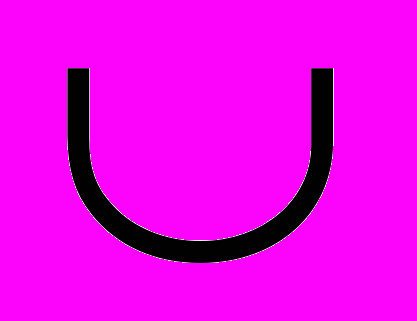 [х1;+∞)
[х1;+∞) при 0 < а <9/16 [x1;х2]
при a=9/16; x = 5/3
при a > 9/16 , где:
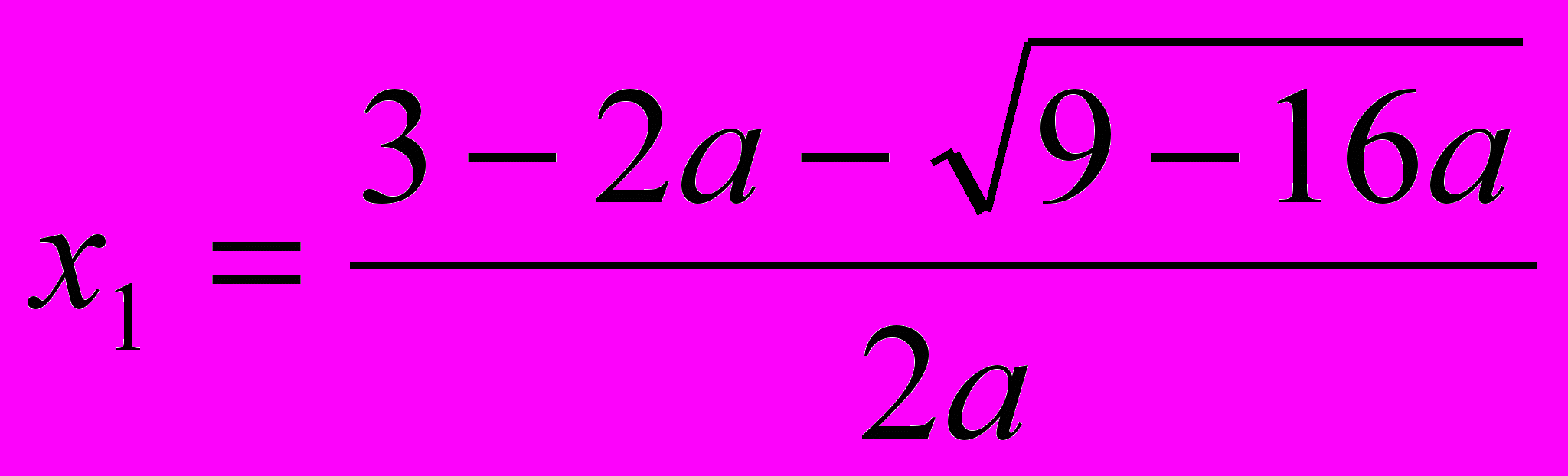 ,
, 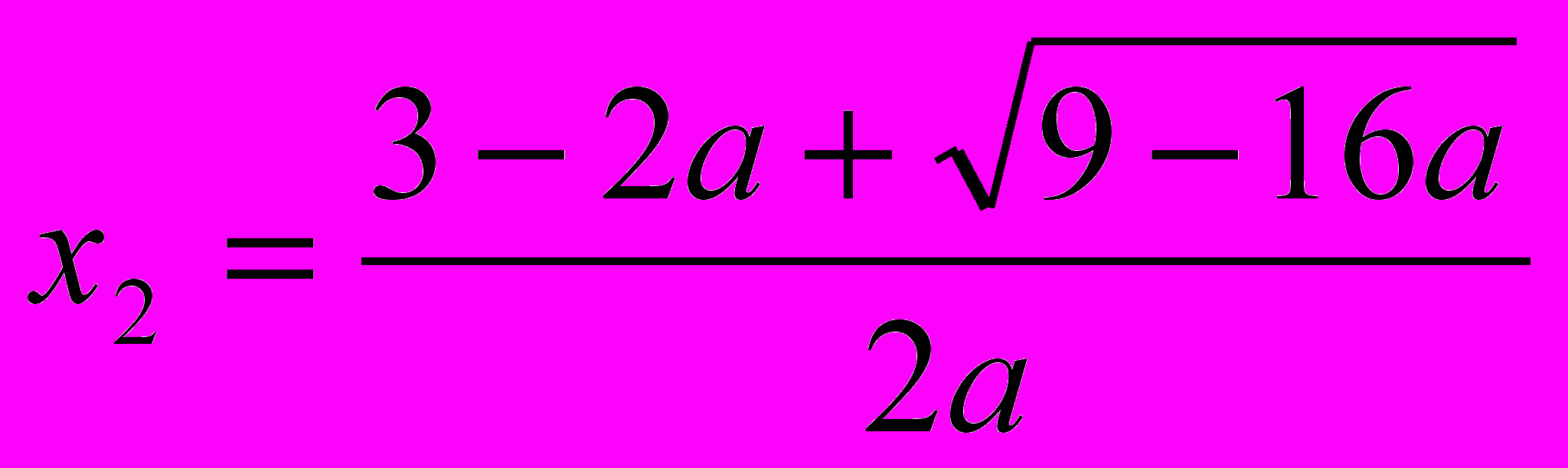 .
.-Какой случай не рассмотрен?
-Не рассмотрен случай а=0.
Решение
При а = 0 неравенство ах2 + (2a-3)x + а +1≤0 примет вид 0·х2 + (2·0-3)·х + 0 +1≤0, отсюда х≥1/3
Ответ: при a=0 [1/3; +∞)
Вынесем все виды ответов на ось параметра а.
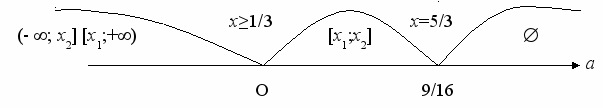


Обратите внимание, для случаев а<0 и 0 < а < 9/16 необходимо сравнить х1 и х2, что вы и сделали.
Запишем ответ к задаче, который наглядно виден на схеме.
Ответ:
при а <0 (- ∞; х2]
 [х1;+∞)
[х1;+∞) при a=0 [1/3; +∞)
при 0 < а <9/16 [x1;х2]
при a=9/16; x = 5/3
при a > 9/16 , где:
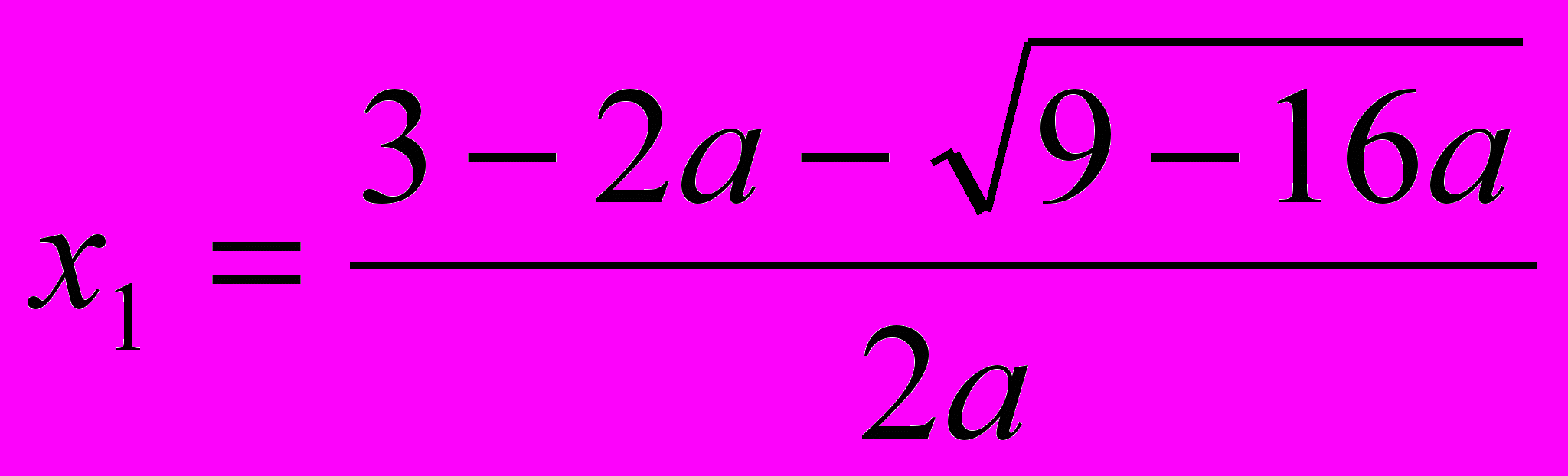 ,
, 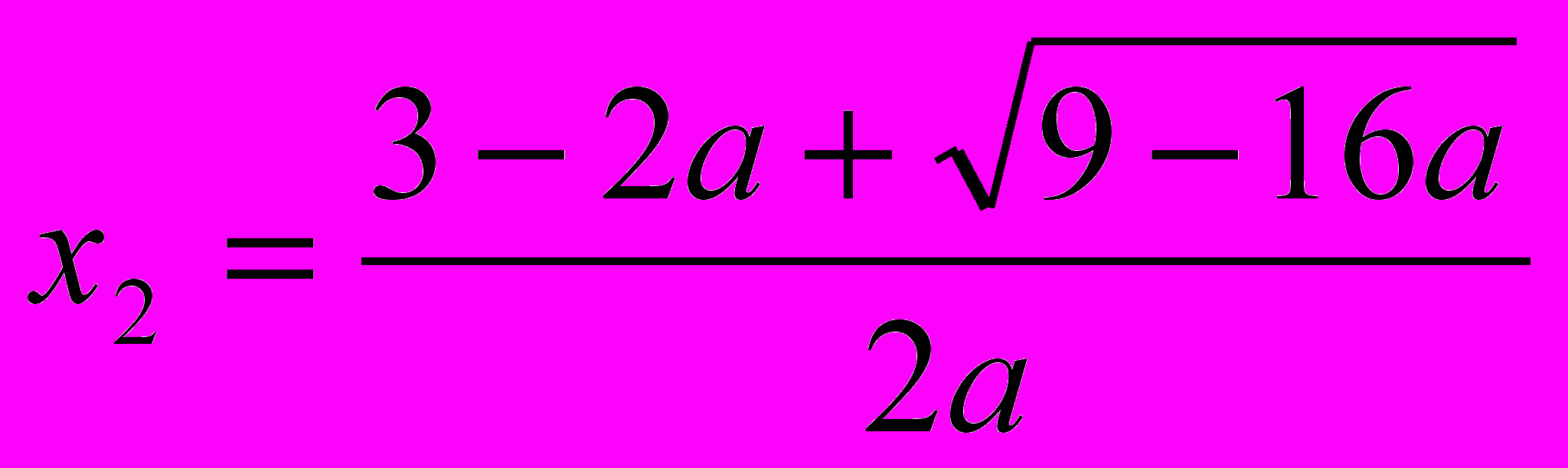 .
.Итак, мы с вами рассмотрели один из подходов к решению неравенств с параметрами.
Надеюсь, что сегодняшнее занятие поможет вам в работе с учащимися на уроках и факультативах.
Спасибо.
Опросный лист
по результатам работы обучающего семинара руководителей методических объединений учителей математики общеобразовательных учреждений города Костромы «Развитие творческих способностей учащихся средствами математического образования»
Уважаемые коллеги, организаторы убедительно просят вас ответить на следующие вопросы:
I. 1. Является ли для Вас предложенная тема актуальной?
- Да
- Да, частично
- Нет, не является
- Другое (уточнить)
2. Ваша дети под Вашим руководством принимали участие (да, нет)
- В турнире математических боёв
- В городских олимпиадах
- В турнирах юных математиков
- В выездных математических мероприятиях
- «Кенгуру»
- «Кенгуру – выпускнику»
3. Ваши дети посещают
- Школьные математические кружки
- Городские математические кружки
- Ездили в ЛМШ
- Другое
4. Какие затруднения испытываете Вы при решении проблемы совершенствования работы по развитию творческих способностей учащихся средствами математического образования?
- В вопросе реализации преемственности развития творческих способностей учащихся средствами математического образования
- В недостатке необходимой методической литературы
- В вопросе формирования единого подхода к организации педагогической поддержки процесса совершенствования работы учителя по перспективным направлениям развития математического творчества учащихся
- В вопросе демонстрации собственных достижений в работе с одарёнными детьми
- В описании работы профессионального сообщества учителей математики образовательного учреждения в рамках программы «Одарённые дети»
- Недостаток времени для решения проблемы совершенствования работы по развитию творческих способностей учащихся
- Слабое представление о технологиях работы с одарёнными учащимися
- Недостаточно знаний содержания программы «Одарённые дети»
- Другое (уточнить)
5. Планируете ли Вы
- Продолжить работу по вопросу развития творческих способностей учащихся средствами математического образования
- Начать впервые работу по вопросу развития творческих способностей учащихся средствами математического образования
- Другое (уточнить)
II. Оцените по 10-ти бальной шкале
- Актуальность семинара
- Полноту содержания семинара
- Степень реализации цели семинара: презентация деятельности образовательного учреждения по развитию творческих способностей учащихся средствами математического образования
- Практическую значимость семинара
- Организацию семинара
- Необходимость дальнейшей работы ГМЦ Управления образования администрации города Костромы в этом направлении
- Атмосферу семинара
III. Какие формы деятельности по сопровождению вопроса развития творческих способностей учащихся средствами математического образования Вы считаете наиболее приемлемыми в дальнейшем (отметить 3 наиболее значимых предложения)?
- Организация и проведение семинаров – практикумов
- Организация сетевого сообщества педагогов города (области), работающих по вопросу развития творческих способностей учащихся средствами математического образования
- Организация и проведение мастер – классов
- Организация и проведение открытых уроков
- Организация и проведение педагогических мастерских, демонстрирующих передовой опыт работы по развитию творческих способностей учащихся средствами математического образования
- Обобщение передового опыта работы педагогов по рассматриваемому вопросу
- Другие (уточнить)
IV. Ваши пожелания
Городской методический центр Управления образования администрации города Костромы
СПРАВКА
По результатам работы семинара учителей математики общеобразовательных учреждений города Костромы
«Развитие творческих способностей учащихся средствами математического образования»
26 октября 2007 года в МОУ лицее №17 г. Костромы проводился обучающий семинар «Развитие творческих способностей учащихся средствами математического образования».
Ответственные за проведение семинара: Борткевич Л.К., методист ГМЦ, и Смирнова Т.Б., заместитель директора МОУ лицея №17 по учебно – воспитательной работе.
Цель семинара: презентация деятельности общеобразовательного учреждения по развитию творческих способностей учащихся средствами математического образования.
В рамках семинара были
- проведены открытые мероприятия
- урок математики в 3 «В» классе, математика, «Объем параллелепипеда. Преобразование объемных фигур», Смирнова С.М., учитель начальных классов высшей квалификационной категории
- урок математики в 5 «А» классе, наглядная геометрия, «Задачи на складывание фигур», Григорьева И.В., учитель математики высшей квалификационной категории
- занятие математического кружка «Математический бой», 6 класс, Коваль Л.Н., учитель математики высшей квалификационной категории
- мастер-класс «Квадратные неравенства. Задачи с параметрами», Шорохова С.А., учитель математики высшей квалификационной категории
- рассмотрены вопросы
- «Анализ состояния работы с одарёнными школьниками в общеобразовательных учреждениях города Костромы», Борткевич Л.К., методист ГМЦ Управления
- «Развитие творческих способностей как составная часть работы с одаренными детьми», Кузнецова Е.Н., зав.отделом научно-методической работы в МОУ лицее №17
- «Опыт работы педагогов начальной школы по развитию творческих способностей учащихся», Лобова Н.П., зам. директора по УВР
- «Основные направления конструирования обучающей среды в процессе развития творческих способностей учащихся», Смирнова Т.Б., зам. директора по УВР
На семинаре присутствовали 45 педагогов из 34 общеобразовательных учреждений города Костромы. Из них 2 преподавателя КГУ им Н.А. Некрасова, методист по математике КОИПКРО, 16 руководителей МО математики и 1 руководитель МО начальных классов МОУ гимназии №1.
Все участники семинара получили анкеты, 26 педагогов сдали их для анализа. Было отмечено, что рассмотренные на семинаре вопросы актуальны (22 человека), все педагоги работают по проблеме одарённые дети:
1. Является ли для Вас предложенная тема актуальной?
- Да - 22
- Да, частично - 4
- Нет, не является - 0
- Другое (уточнить) - 0
2. Ваша ученики под Вашим руководством принимали участие (да, нет)
- В турнире математических боёв - 14
- В городских олимпиадах - 23
- В турнирах юных математиков - 23
- В выездных математических мероприятиях - 4
- «Кенгуру» - 23
- «Кенгуру – выпускнику» - 9
3. Ваши ученики посещают
- Школьные математические кружки - 22
- Городские математические кружки - 13
- Ездили в ЛМШ – 6
- Нет – 1
- Лицей №17 – 2
Педагогами был отмечен недостаток времени для решения проблемы совершенствования работы по развитию творческих способностей учащихся (24 педагога)
При решении проблемы совершенствования работы по развитию творческих способностей учащихся средствами математического образования, учителя испытывают затруднения:
- В вопросе реализации преемственности развития творческих способностей учащихся средствами математического образования - 5
- В недостатке необходимой методической литературы - 7
- В вопросе формирования единого подхода к организации педагогической поддержки процесса совершенствования работы учителя по перспективным направлениям развития математического творчества учащихся - 6
- В вопросе демонстрации собственных достижений в работе с одарёнными детьми - 0
- В описании работы профессионального сообщества учителей математики образовательного учреждения в рамках программы «Одарённые дети» - 4
- Недостаток времени для решения проблемы совершенствования работы по развитию творческих способностей учащихся - 24
- Слабое представление о технологиях работы с одарёнными учащимися - 2
- Недостаточно знаний содержания программы «Одарённые дети» - 6
- Другое (уточнить) - 0
В качестве прикладного значения проведённого семинара можно отметить то, что большинство участников предполагает использование полученных материалов в своей дальнейшей работе:
- Продолжить работу по вопросу развития творческих способностей учащихся средствами математического образования - 23
- Начать впервые работу по вопросу развития творческих способностей учащихся средствами математического образования – 2
- Нет - 1
По 10-ти бальной шкале семинар был оценен присутствующими на самом высоком уровне:
- Актуальность семинара – 9,88
- Полнота содержания семинара – 9,5
- Степень реализации цели семинара: презентация деятельности образовательного учреждения по развитию творческих способностей учащихся средствами математического образования – 9,65
- Практическая значимость семинара – 9,65
- Организация семинара – 9,85
- Необходимость дальнейшей работы ГМЦ Управления образования администрации города Костромы в этом направлении – 9,92
- Атмосфера семинара – 9,92
В ходе обмена мнениями по итогам семинара педагоги отмечали, что для реализации и освоения рассмотренной на семинаре темы они хотели бы получить следующие виды помощи:
- Организация и проведение семинаров – практикумов - 16
- Организация сетевого сообщества педагогов города (области), работающих по вопросу развития творческих способностей учащихся средствами математического образования - 11
- Организация и проведение мастер – классов - 18
- Организация и проведение открытых уроков - 18
- Организация и проведение педагогических мастерских по демонстрации передового опыта работы по развитию творческих способностей учащихся средствами математического образования - 15
- Обобщение передового опыта работы педагогов по рассматриваемому вопросу - 15
- Другие (уточнить) - 0
Пожелания, высказанные педагогами организаторам семинара:
- Спасибо огромное.
- Огромное спасибо! Дальнейшего творчества и демонстрации опыта!
- Спасибо!
- Успехов в этом трудном деле и достойной оценки этой деятельности!
- Творческих вам успехов, чаще проводите такие семинары.
- Дальнейших творческих успехов!
- Спасибо за огромный труд.
- Материально поощрить учителей, принявших участие в проведении семинара.
- Провести семинар или мастер – класс по изучению новых содержательных линий по математике в профильных классах.
Заведующий ГМЦ Управления Т.Н. Скачкова
Методист ГМЦ Управления Л.К. Борткевич
27.11.2007г.

Приложение 1
БЫЛА БЫ ОХОТА,
А ВПЕРЕДИ ЕЩЁ МНОГО РАБОТЫ
МАТЕМАТИЧЕСКАЯ РАЗМИНКА
- Укажи рисунки с изображением плоских фигур









Рис 1 Рис 2 Рис 3 Рис 4 Рис 5 Рис 6
- Укажи рисунки с изображением объёмных фигур
Рис 1 Рис 2 Рис 3 Рис 4 Рис 5


Профессиональный тест на знания
1. Я считаю, что у плоских фигур есть 2 измерения: длина и ширина
| ДА | НЕТ | НЕ ЗНАЮ |
2. Я считаю, что у плоских фигур можно найти площадь (S)
| ДА | НЕТ | НЕ ЗНАЮ |
3. Я считаю, что у объёмных фигур есть три измерения: длина, ширина, высота
| ДА | НЕТ | НЕ ЗНАЮ |
4. Я считаю, что объём прямоугольного параллелепипеда можно найти по формуле
V=(a·b)·c S= a·b
5. Я считаю, что единицей измерения объёма прямоугольного параллелепипеда является
| дм2 | см3 | м |
- Я считаю, что площадь (S) данной фигуры равна
| 10 см2 | 11 см2 | 9 см2 |

2 см
3 см

4 см
1 см
- Я считаю, что объём (V) данной фигуры равен
| 20 см3 | 80 см3 | НЕ ЗНАЮ |
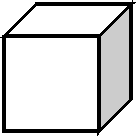
4 СМ
2 СМ

4 СМ
2 СМ
4 СМ
4 СМ
Приложение 2
Т

ЕХНОЛОГИЧЕСКАЯ КАРТА
ИЗГОТОВЛЕНИЯ
ФАНТАСТИЧЕСКОГО ЗАМКА
