Секованов В. С., к ф-м н., профессор кафедры прикладной математики и информационных технологий кгу им. Н. А
| Вид материала | Документы |
- Обоснования в математике (от Евклида до компьютера), 49.75kb.
- Программа проведения всероссийской молодёжной школы «Прикладные методы статистического, 81.95kb.
- Программа проведения всероссийской молодёжной школы «Прикладные методы статистического, 78.37kb.
- Задачи на графах программа, 81.89kb.
- А. В. Бернштейн, заведующий лабораторией, 122.14kb.
- И. И. Мечникова Институт математики, экономики и механики Кафедра математического обеспечения, 900.66kb.
- Нечаев Дмитрий Юрьевич, кандидат технических наук, доцент, профессор кафедры информационных, 419.94kb.
- Токсубаева Лидия Сергеевна доцент кгу трофимов Анатолий Михайлович профессор кгу конференция, 336.82kb.
- Программа дисциплины "Прикладной экономический анализ на основе пакетов: spss и Stata", 105.49kb.
- Владимира Игоревича Соловьева, к э. н., проф кафедры прикладной математики и директора, 31.64kb.
Мы вспомним решение квадратных неравенств, проведем исследовательскую работу, подводящую нас к решению задач с параметрами в этой теме и рассмотрим один из подходов к решению неравенств с параметрами.
II. Итак, вспомним решение квадратных неравенств. У каждого из вас есть лист с задачами. Ваша задача – решить восемь неравенств и ответить на вопрос девятого задания. Справа от предложенных заданий запишите ответы.
| Решите неравенства | Ответ | Для записей |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| 9. f(x) = ax2+bx+c, a≠0 Определить знак a и D ( 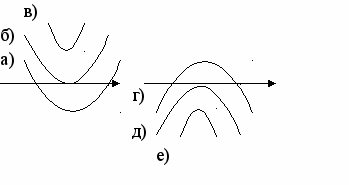 D=в2-4ас) D=в2-4ас) | | |
Контрольная карточка
| Решите неравенства | Ответ | Для записей |
| 1. х2 -6х + 8 <0 | (2; 4) | |
| 2. х2 + 5х + 4 ≥ 0 | (-∞; -4] 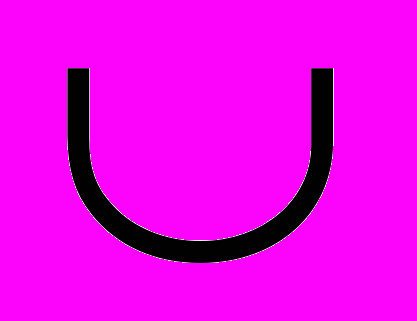 [-1;+∞) [-1;+∞) | |
| 3. (х – 2)2 > 0 | (-∞; 2) 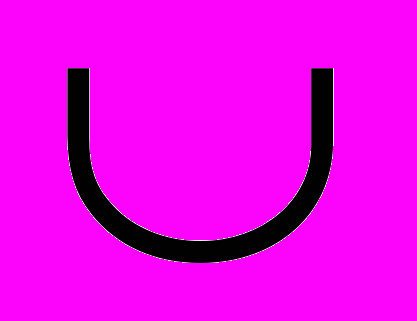 (2;+∞) (2;+∞) | |
| 4. (х + 7)2 ≤ 0 | x=-7 | |
| 5. х2 ≤ 7 | 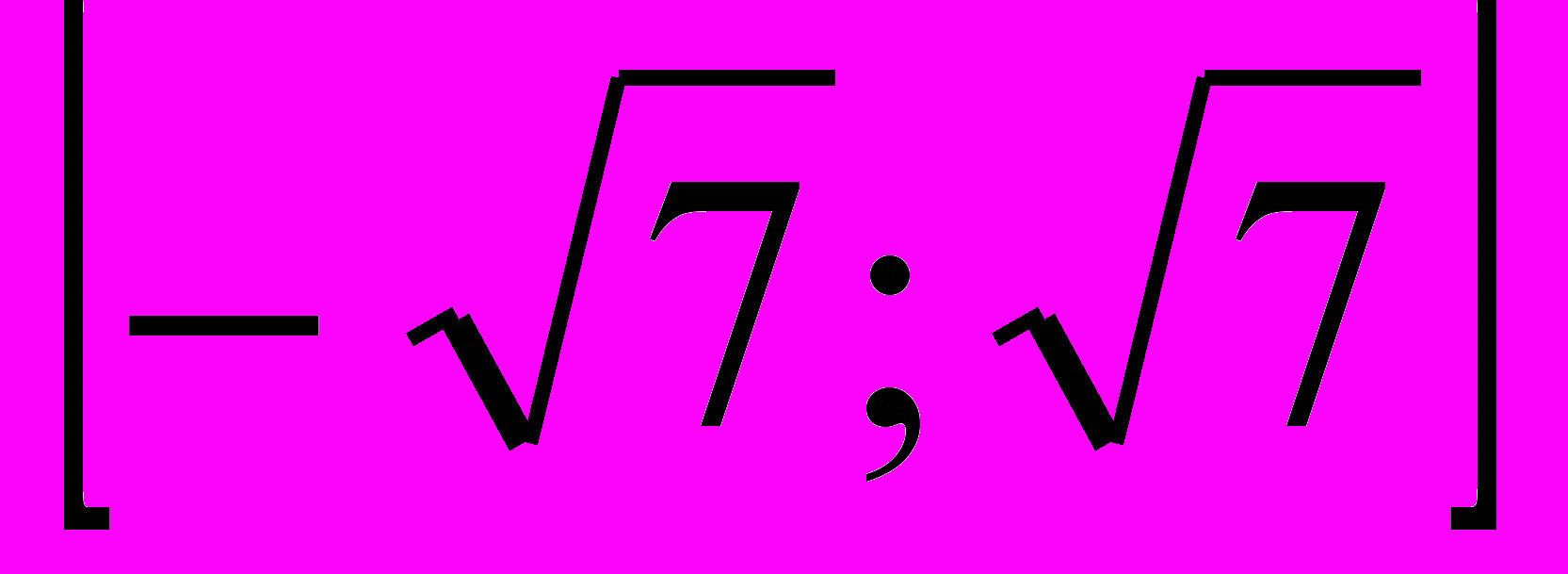 | |
| 6. х2 > 5 | (-∞; 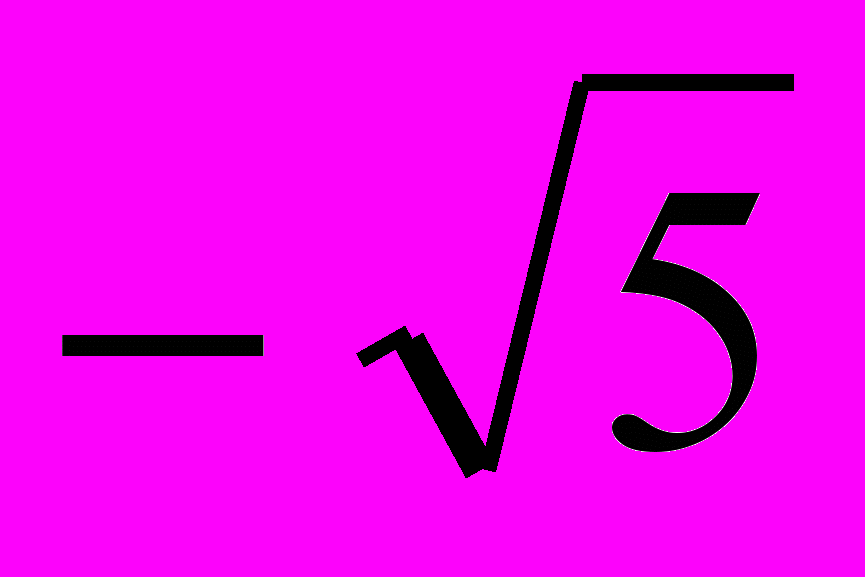 ) ) ( (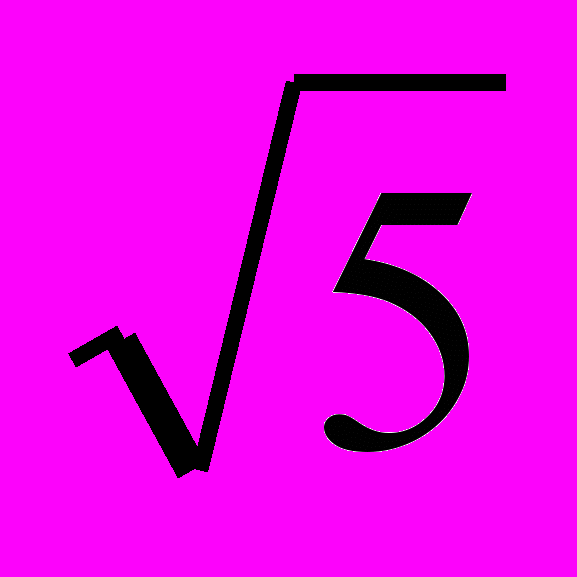 ;+∞) ;+∞) | |
| 7. 2x2 + x + 19 <0 | | |
| 8. 2x2 + x + 19 >0 | (-∞;+∞) | |
| 9 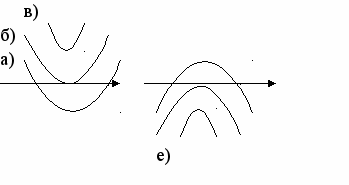 . f(x) = ax2+bx+c, a≠0 . f(x) = ax2+bx+c, a≠0Определить знак a и D ( 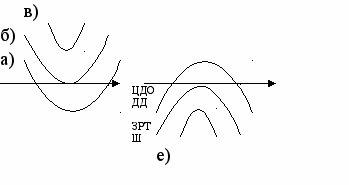 D=в2-4ас) D=в2-4ас)г) д) | а) а>0; D>0 б) а>0; D=0 в) а>0; D<0 г) а<0; D>0 д) а<0; D=0 е) а<0; D<0 | |
Сверим ответы. Проанализируем работу.
Итак, неравенства вида ax2+bx+c v 0, а≠0 – квадратные неравенства.
Если Вы решаете неравенство графически, то используете эскиз графика квадратичной функции и в задании № 9 вспомнили, что возможны шесть положений параболы (служащей графиком квадратичной функции) относительно оси ОХ. Эти положения зависят от старшего коэффициента а и дискриминанта квадратного трехчлена D.
III. Начнем исследовательскую работу.
- Сколько видов квадратных неравенств по знаку существует?
Ответ: четыре
-Какие это неравенства?
Ответ: ax2+bx+c≥0 (1)
ax2+bx+c≤0 (2)
ax2+bx+c>0 (3)
ax2+bx+c<0 (4)
- Какие виды ответов (как числовые множества) могут быть в квадратных неравенствах? Назовите их, используя подготовительную работу. Посовещайтесь в группах. При ответе используйте графическую модель и символическую запись.
Ответ:
| 1 | Отрезок 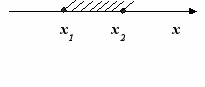 | 5 | Точка 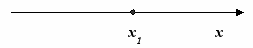 х=х1 |
| 2 | Интервал  | 6 | Вся прямая без одной точки 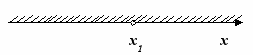 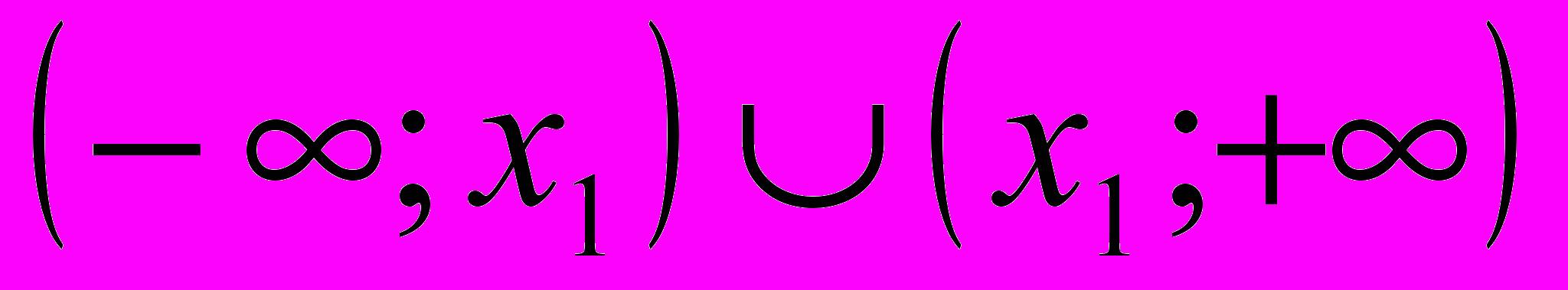 |
| 3 | Объединение двух непересекающихся лучей 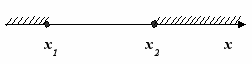  | 7 | Вся прямая  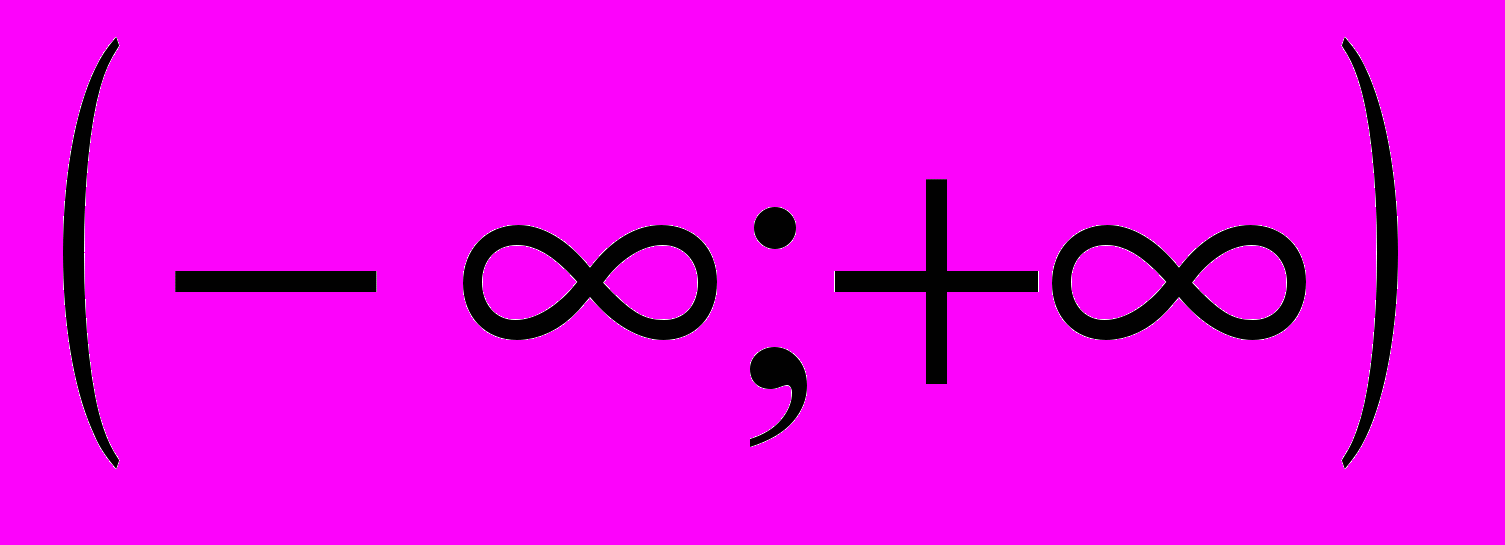 |
| 4 | Объединение двух непересекающихся открытых лучей 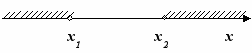 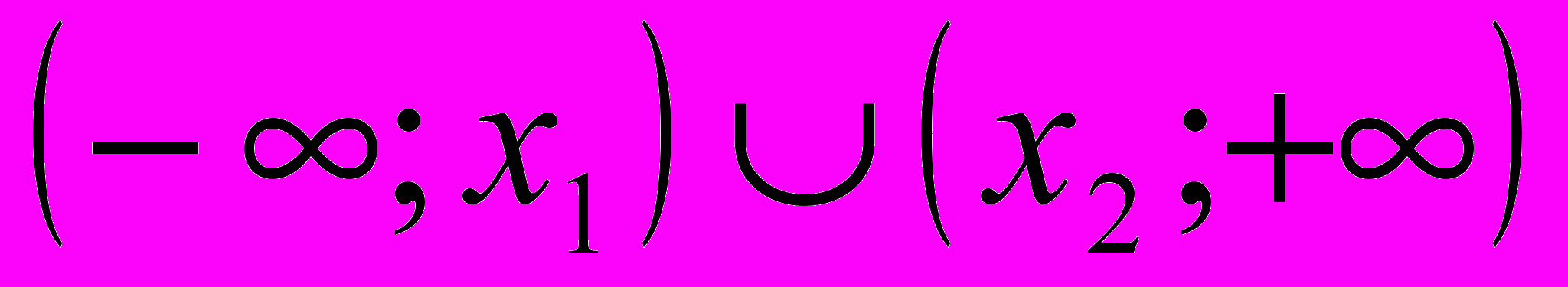 | 8 | Решений нет |
где х1 и х2 – корни уравнения ax2+bx+c=0 , а≠0, х1 < х2
-Четыре вида неравенств и восемь видов ответов связаны между собой старшим коэффициентом квадратного трехчлена а и дискриминантом D. Попробуем найти эту взаимосвязь.
Составим и заполним таблицу. На Ваших столах лежат листы с заготовкой для таблицы.
В верхней строке запишем четыре вида квадратных неравенств по знаку, в левом столбце – восемь видов ответов.
| | | ax2+bx+c≥0 | ax2+bx+c≤0 | ax2+bx+c>0 | ax2+bx+c<0 |
| 1 | Отрезок 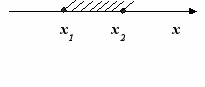 | | | | |
| 2 | Интервал  | | | | |
| 3 | Объединение двух непересекающихся лучей 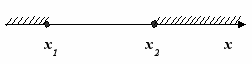  | | | | |
| 4 | Объединение двух непересекающихся открытых лучей 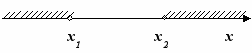 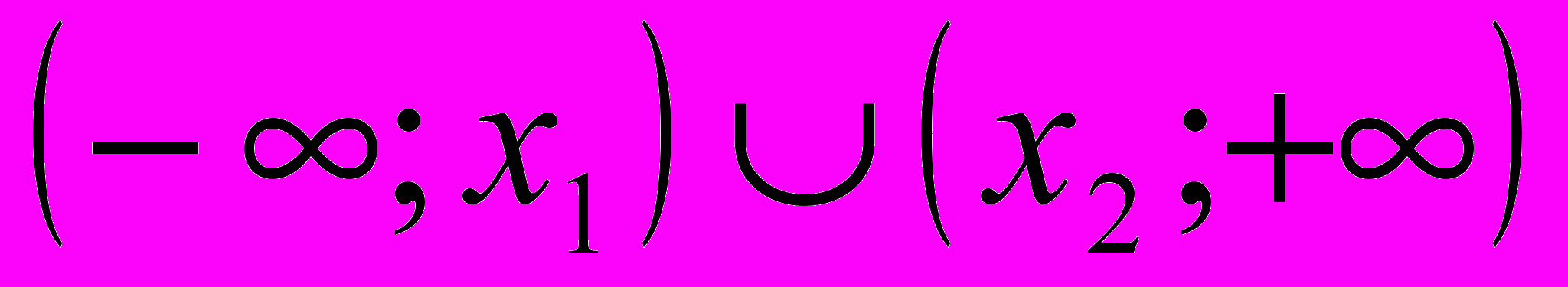 | | | | |
| 5 | Точка 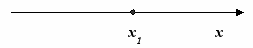 х=х1 | | | | |
| 6 | Вся прямая без одной точки 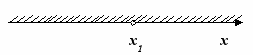 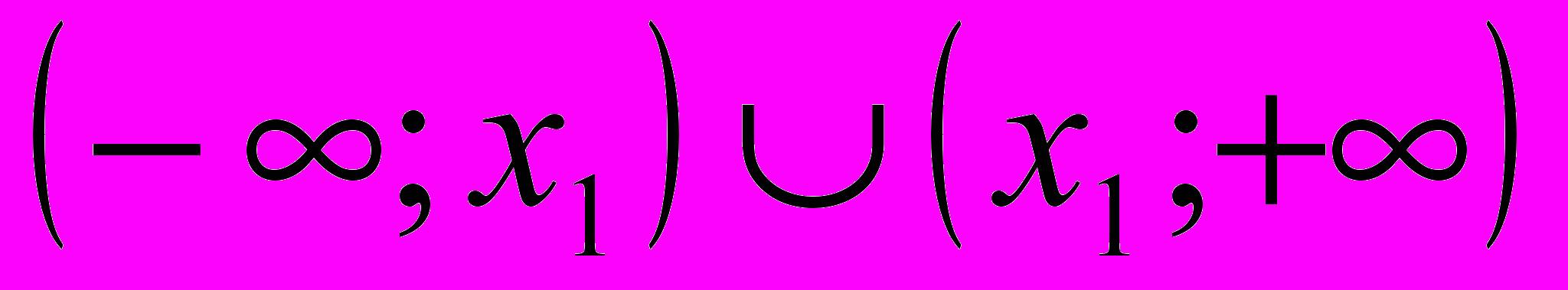 | | | | |
| 7 | В  ся прямая ся прямая  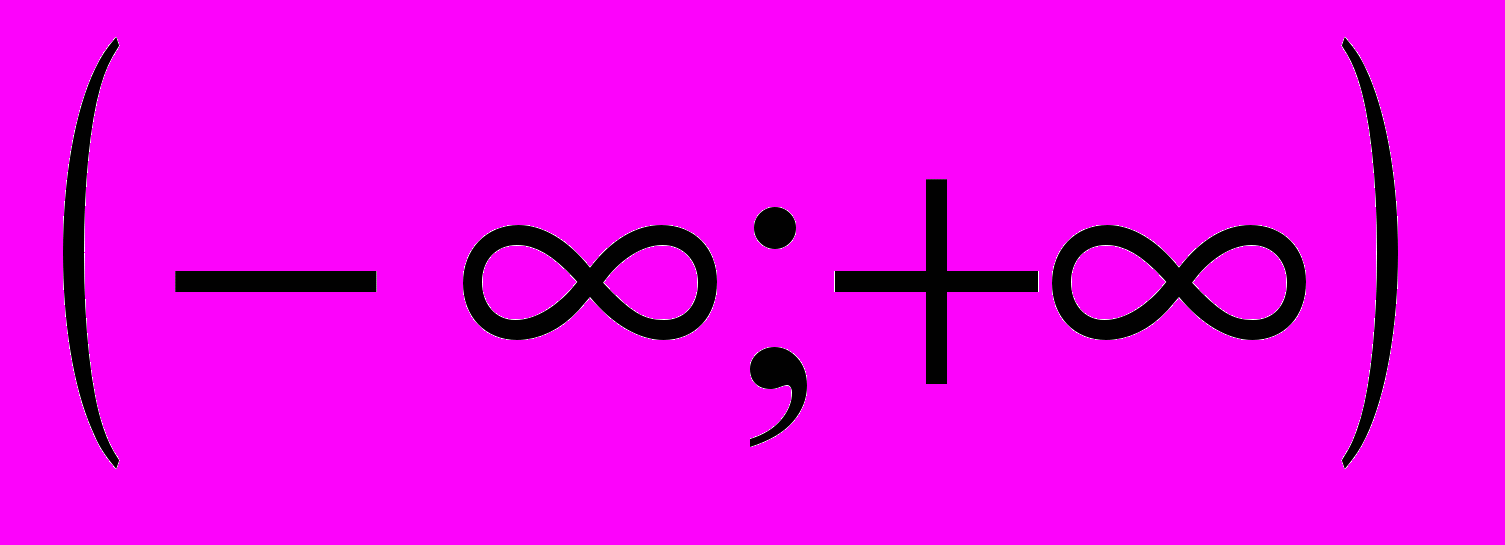 | | | | |
| 8 | Решений нет | | | | |
Задание:
I группа заполняет столбец для (1) неравенства,
II группа заполняет столбец для (2) неравенства,
III группа заполняет столбец для (3) неравенства,
IV группа заполняет столбец для (4) неравенства,
Работаете в группах, совещаетесь, чтобы прийти к верному решению.
Если группа готова – представитель от группы заполняет свой столбец на доске (на доске подготовлена таблица).
Контрольная карточка
| | | ax2+bx+c≥0 | ax2+bx+c≤0 | ax2+bx+c>0 | ax2+bx+c<0 |
| 1 | Отрезок 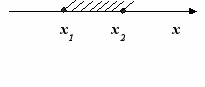 | 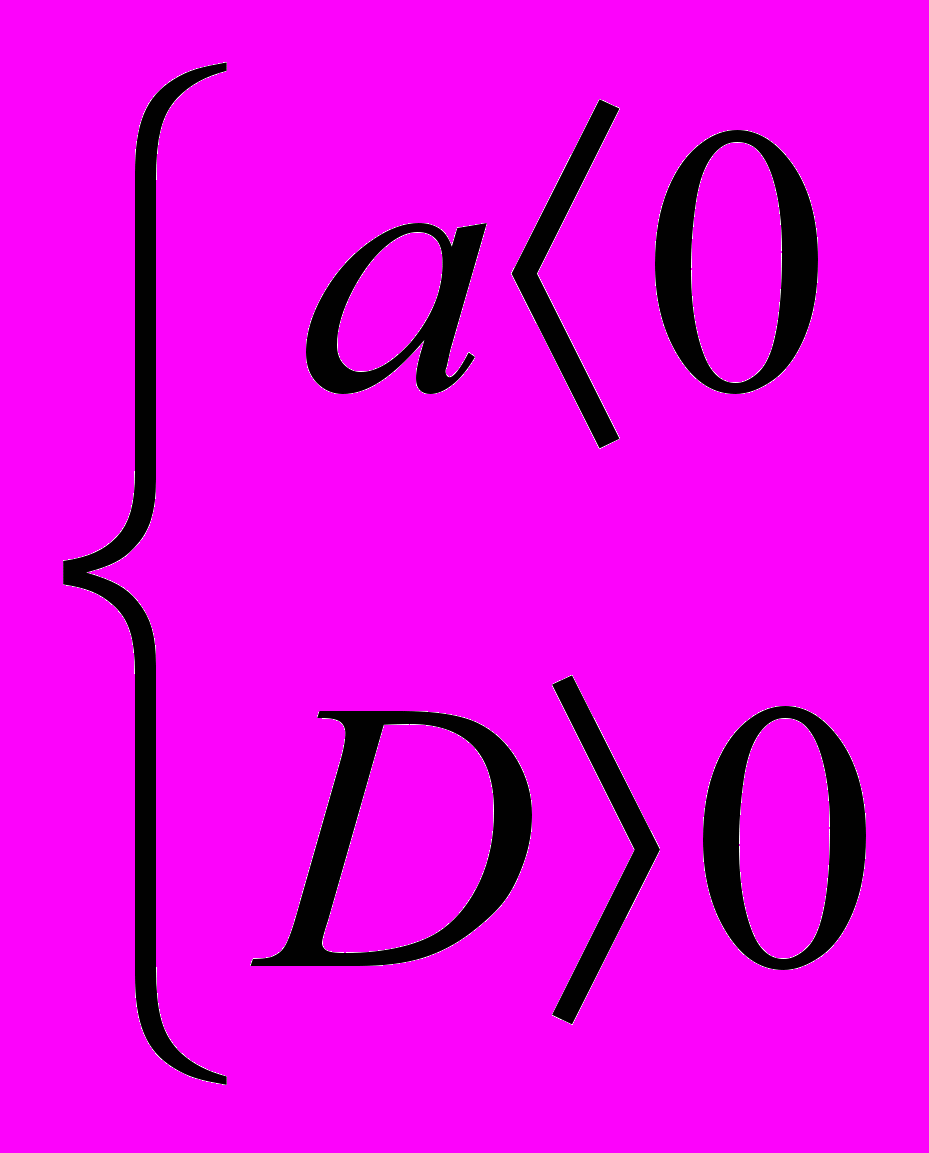 | 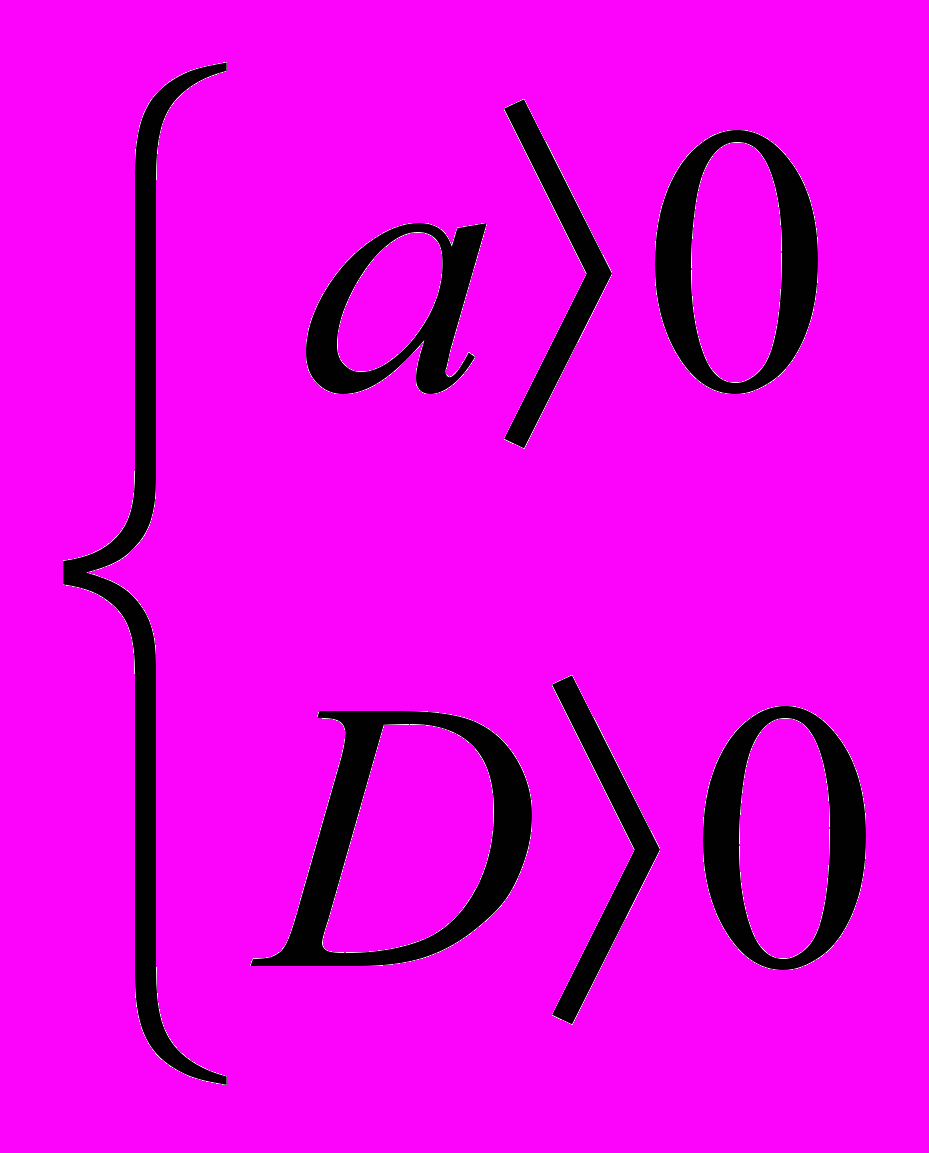 | - | - |
| 2 | Интервал  | - | - | 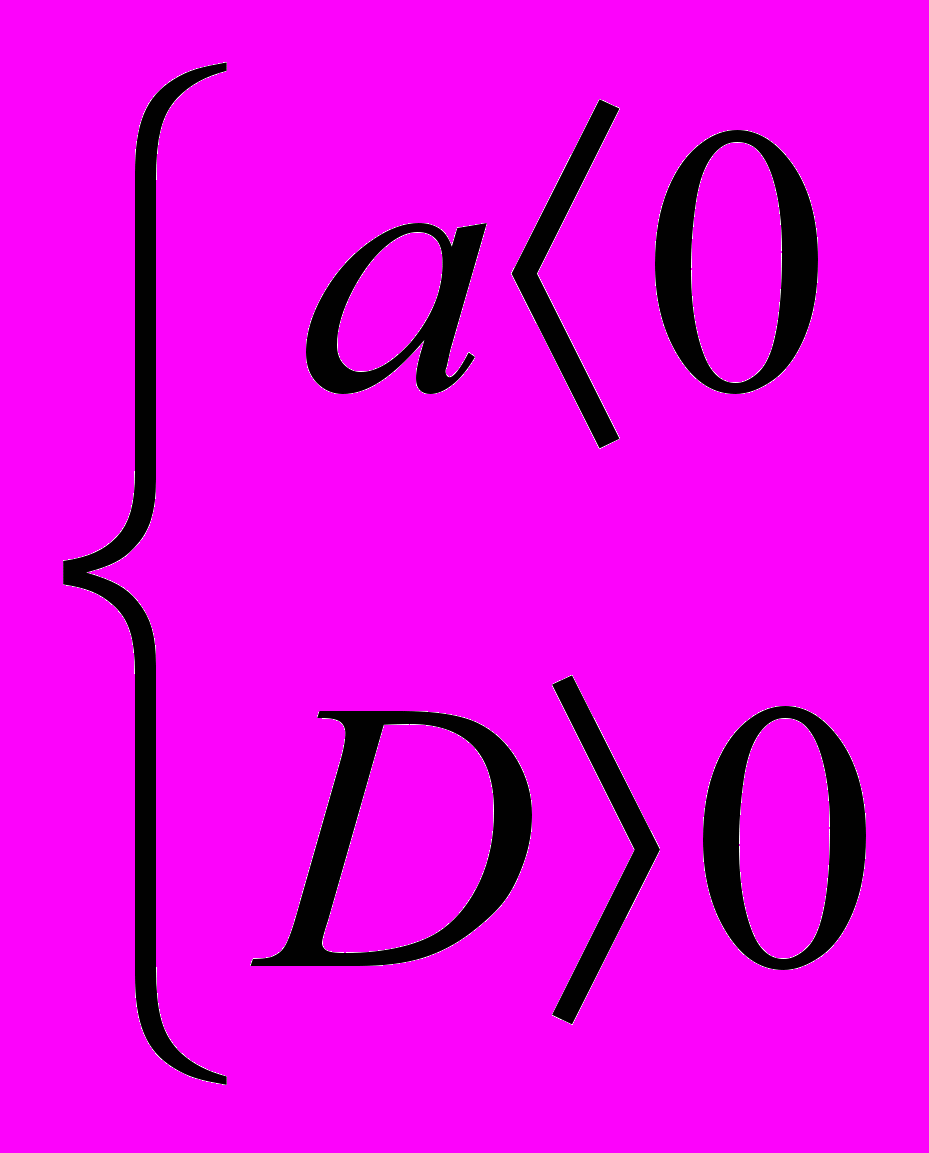 | 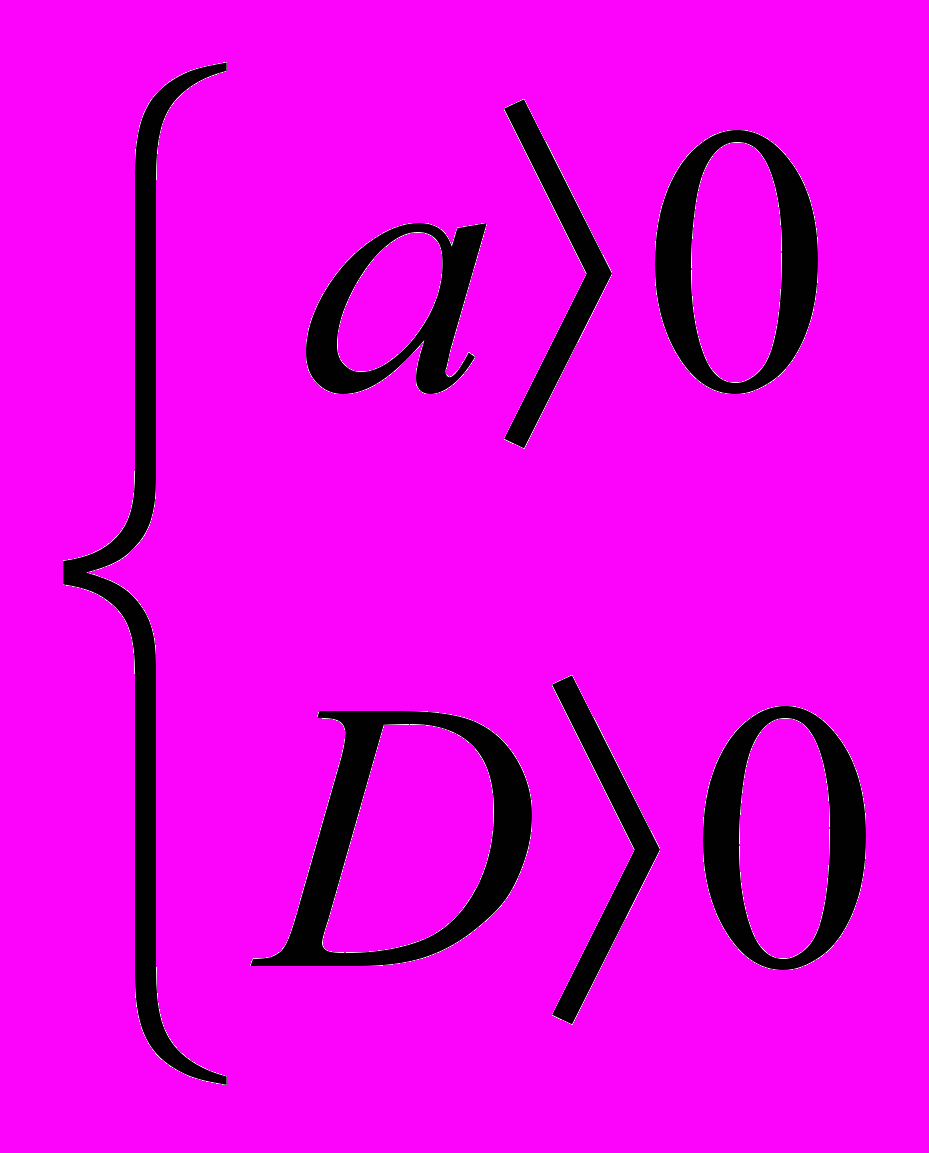 |
| 3 | Объединение двух непересекающихся лучей 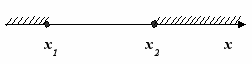  | 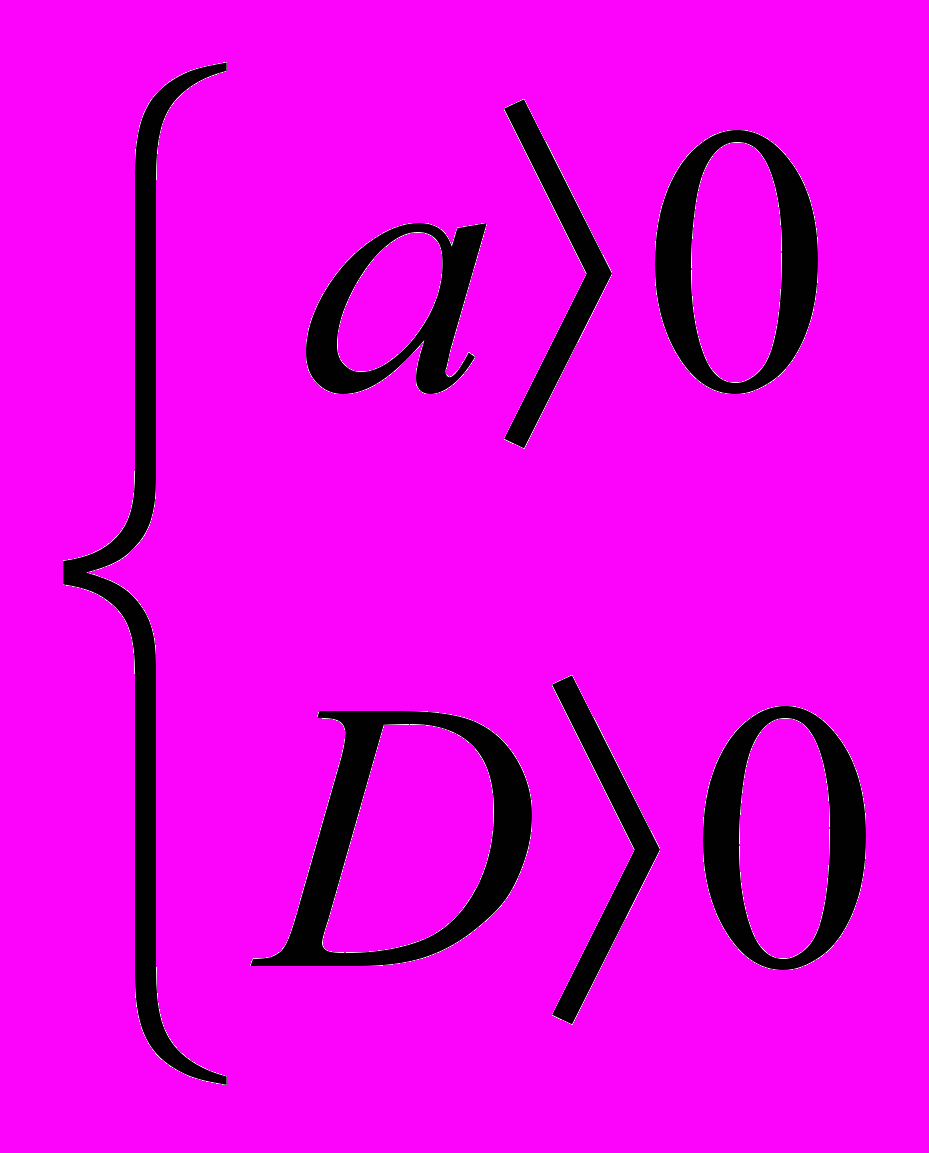 | 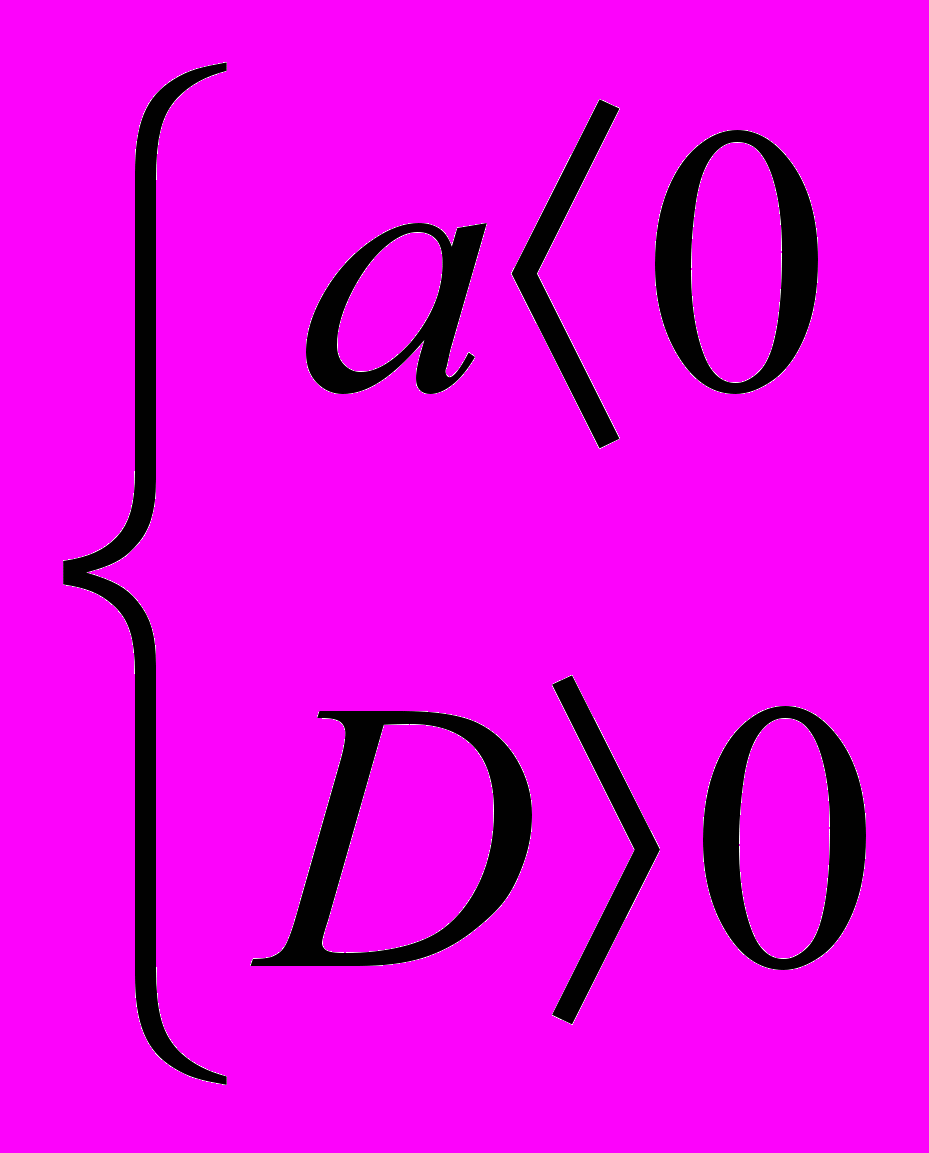 | - | - |
| 4 | Объединение двух непересекающихся открытых лучей 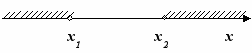 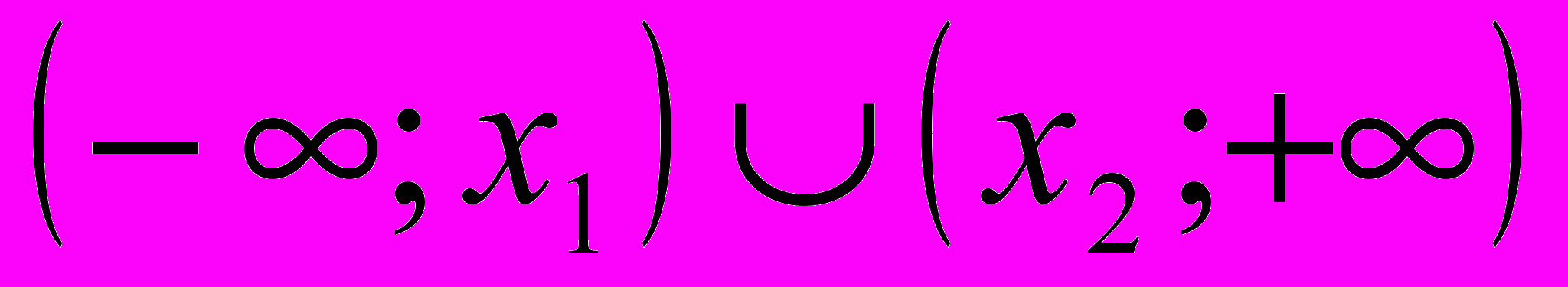 | - | - | 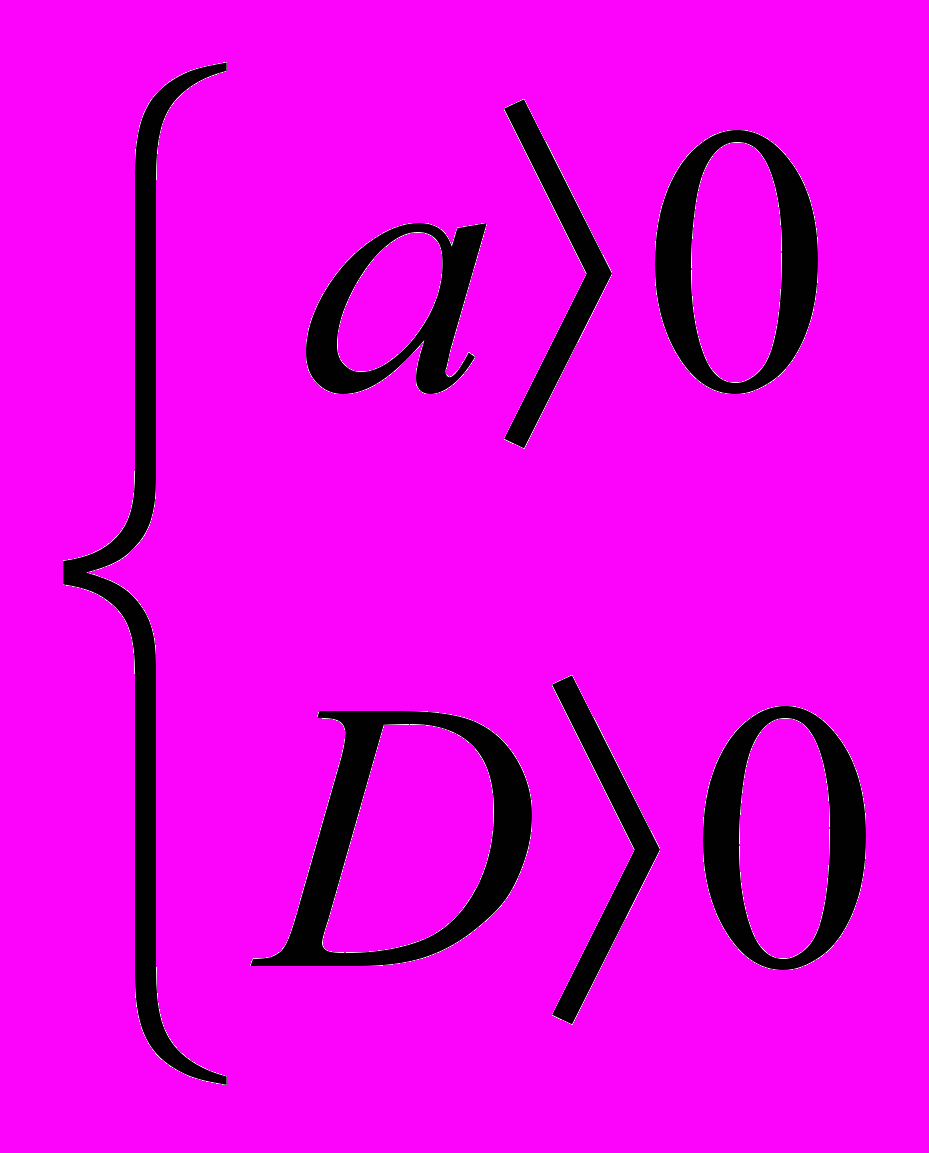 | 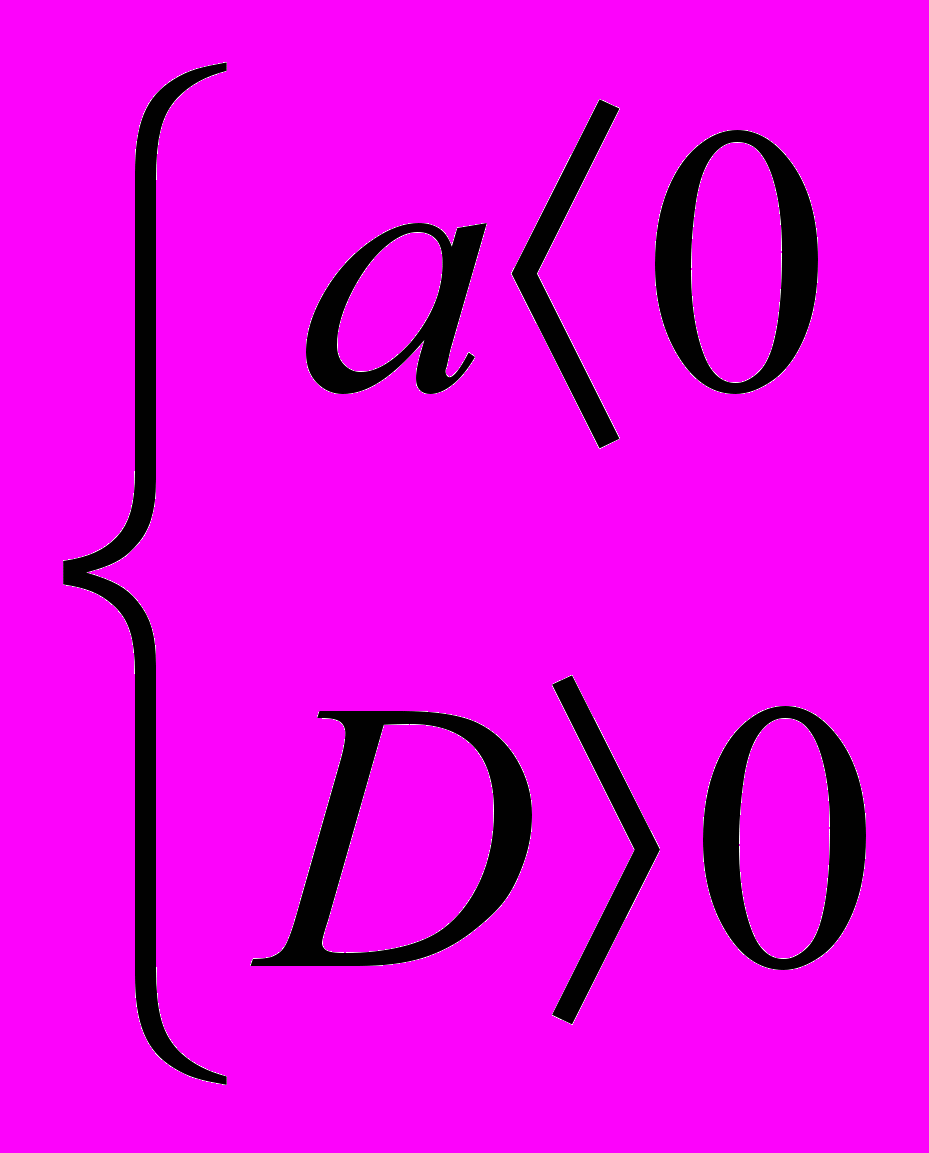 |
| 5 | Точка 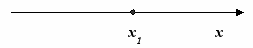 х=х1 | 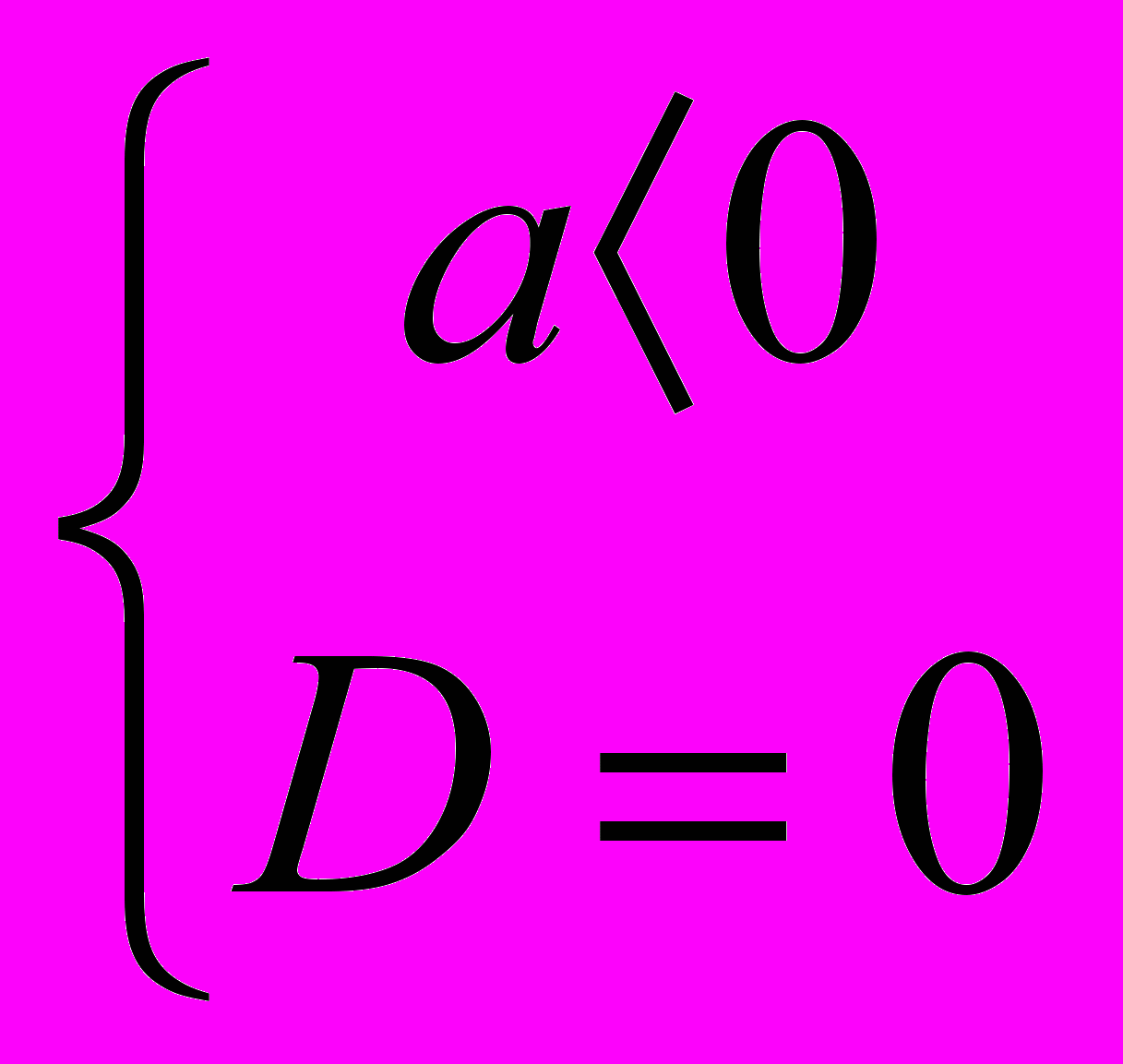 | 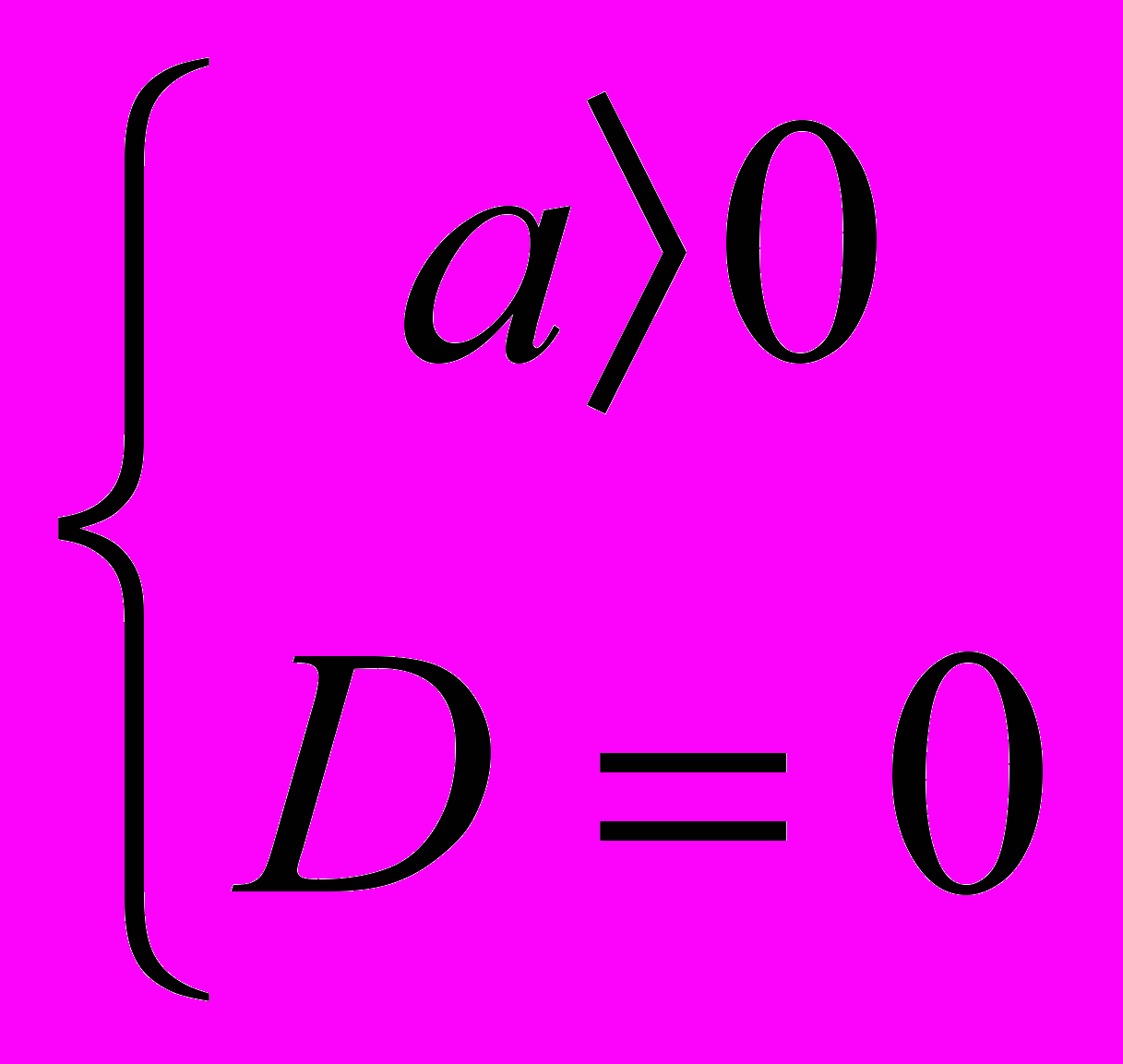 | - | - |
| 6 | Вся прямая без одной точки 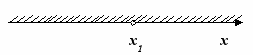 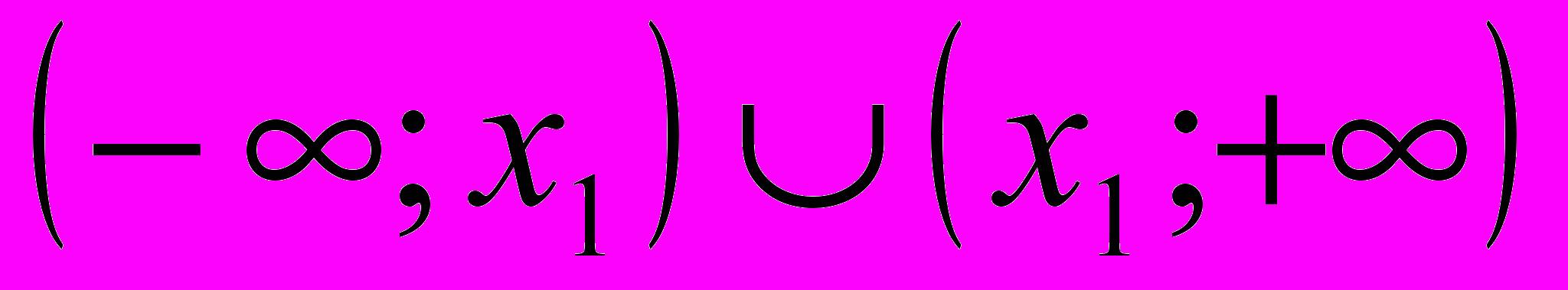 | - | - | 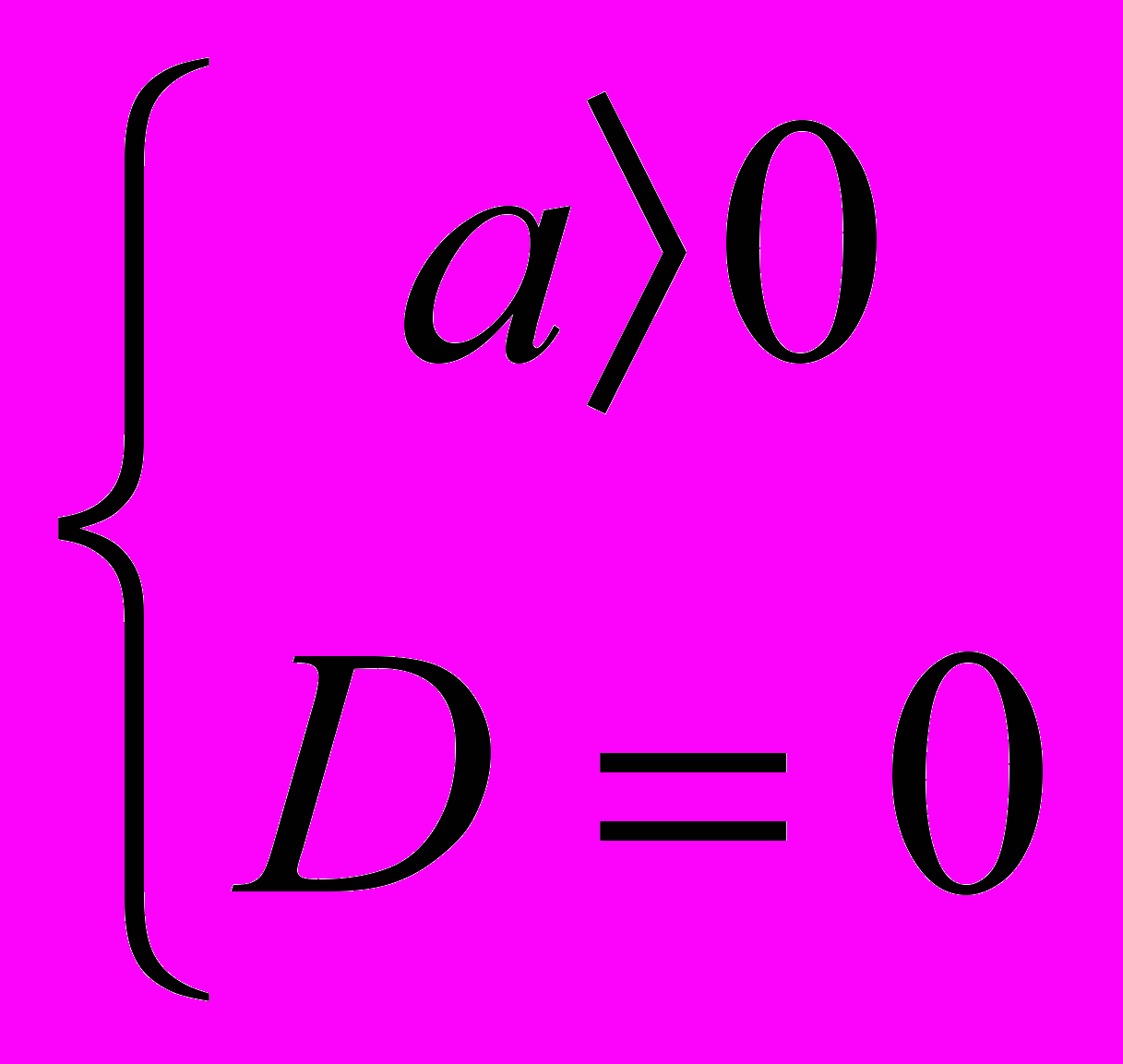 | 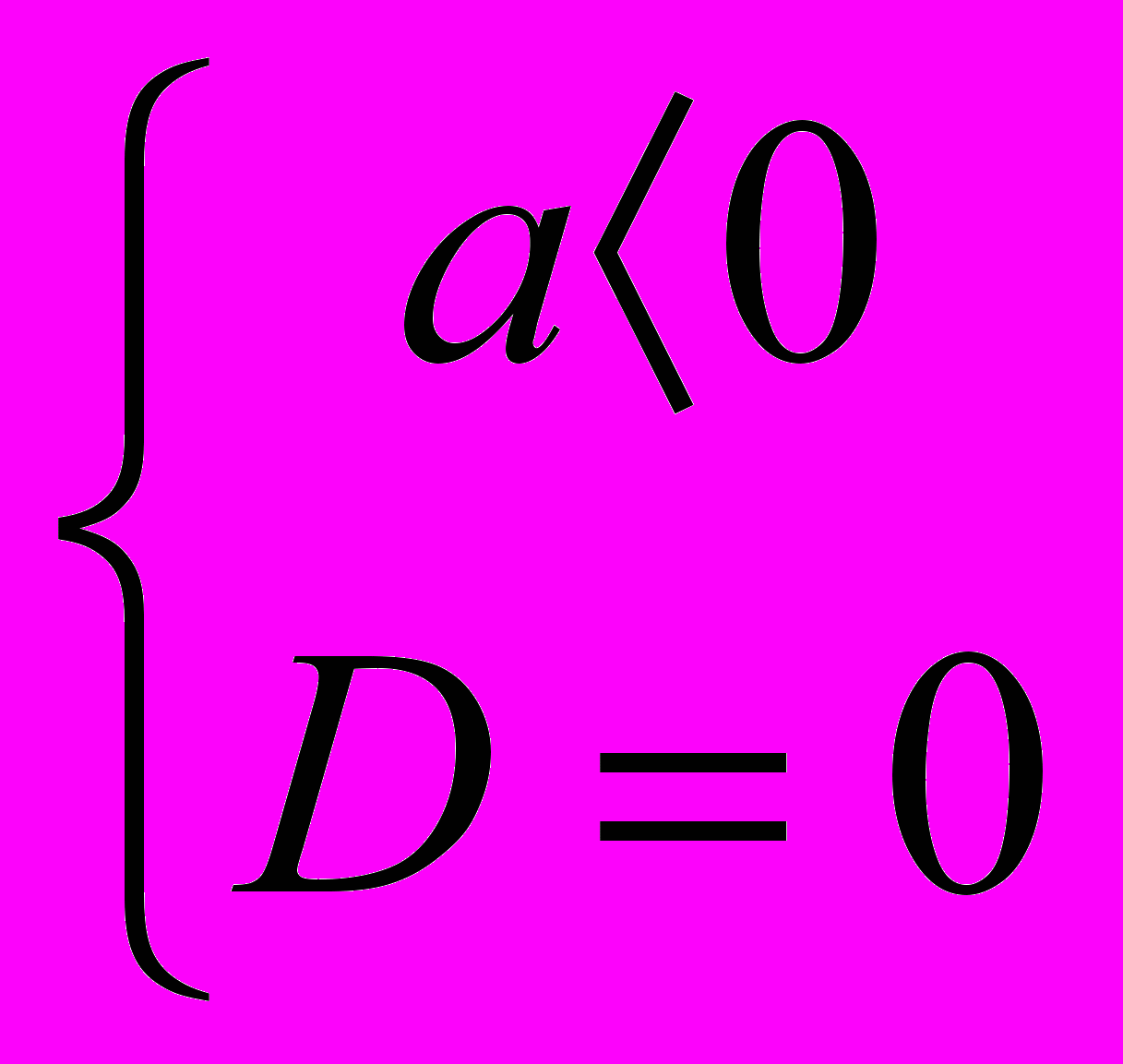 |
| 7 | Вся прямая      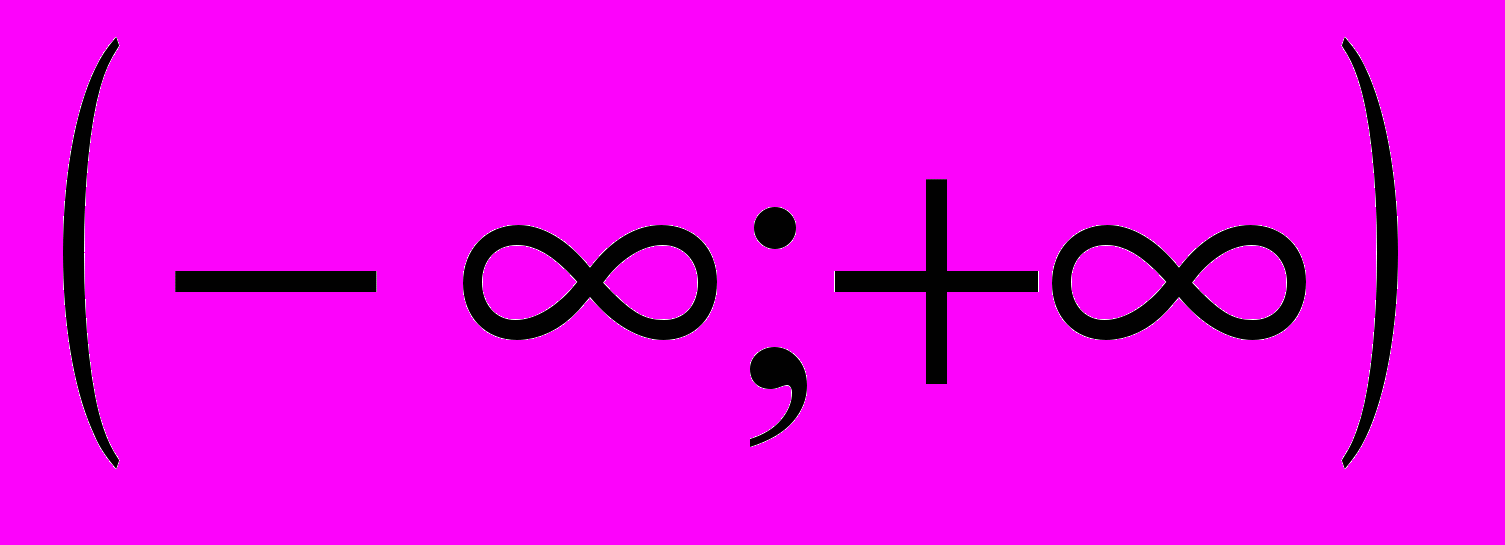 | 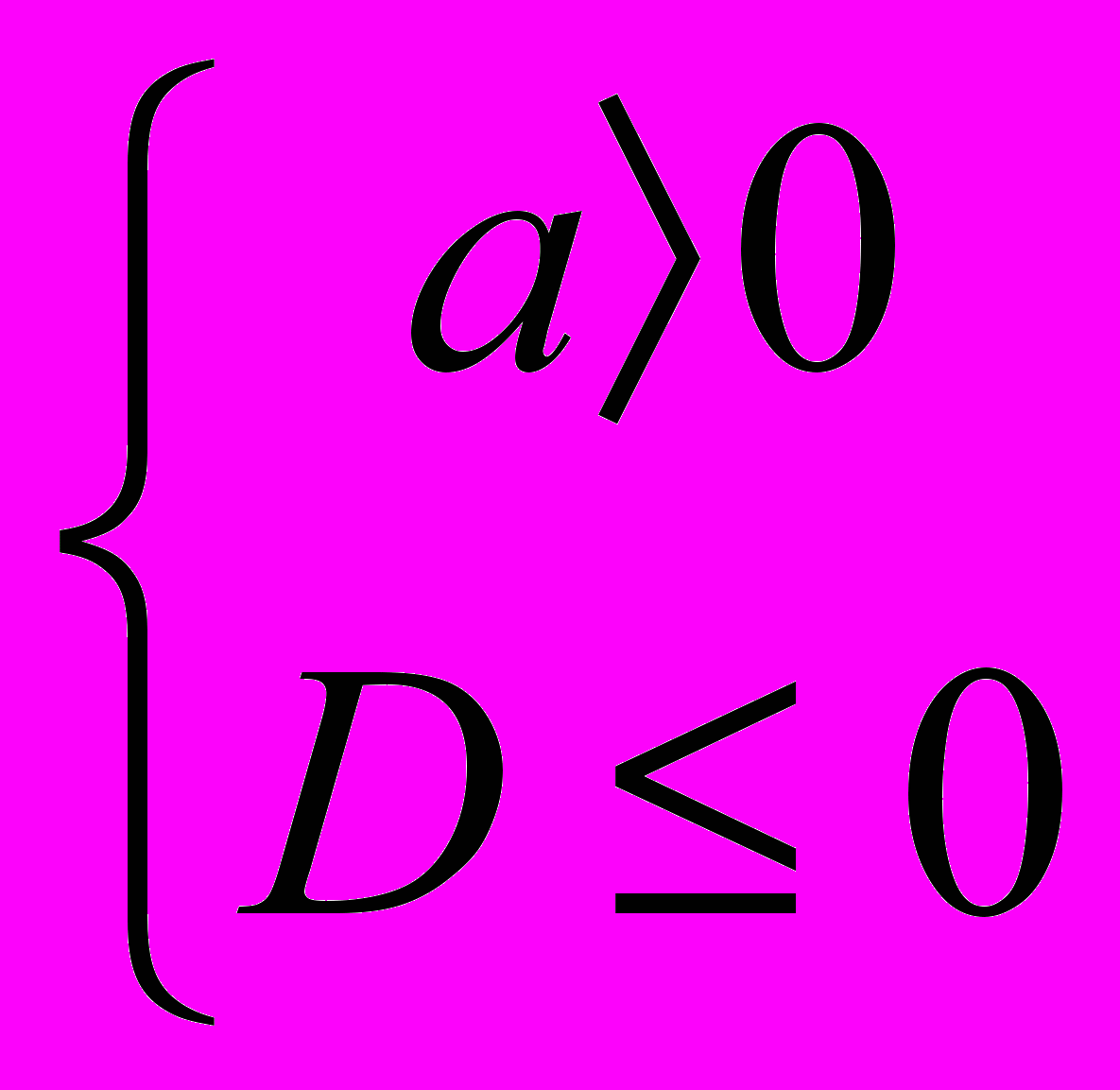 | 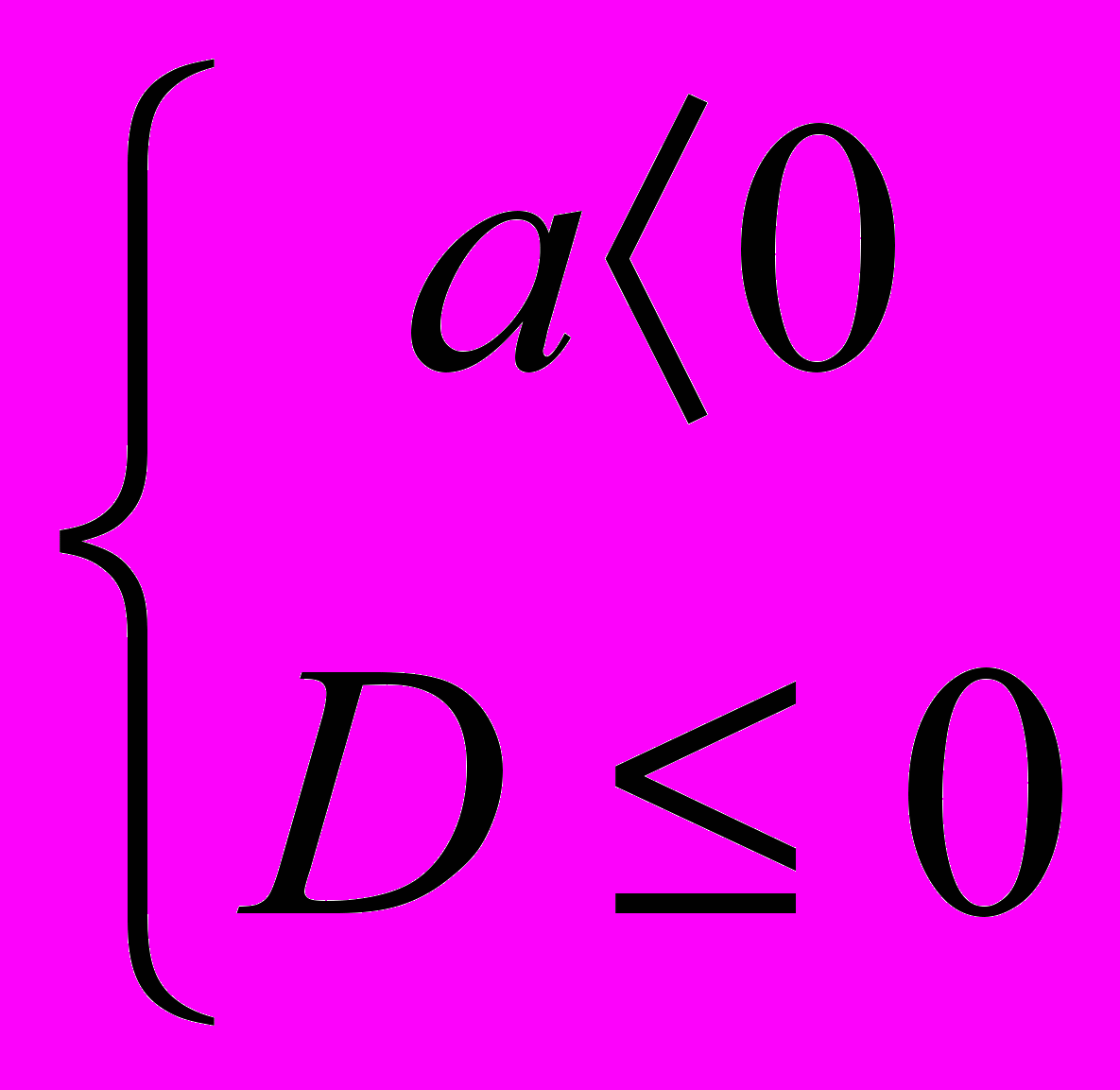 | 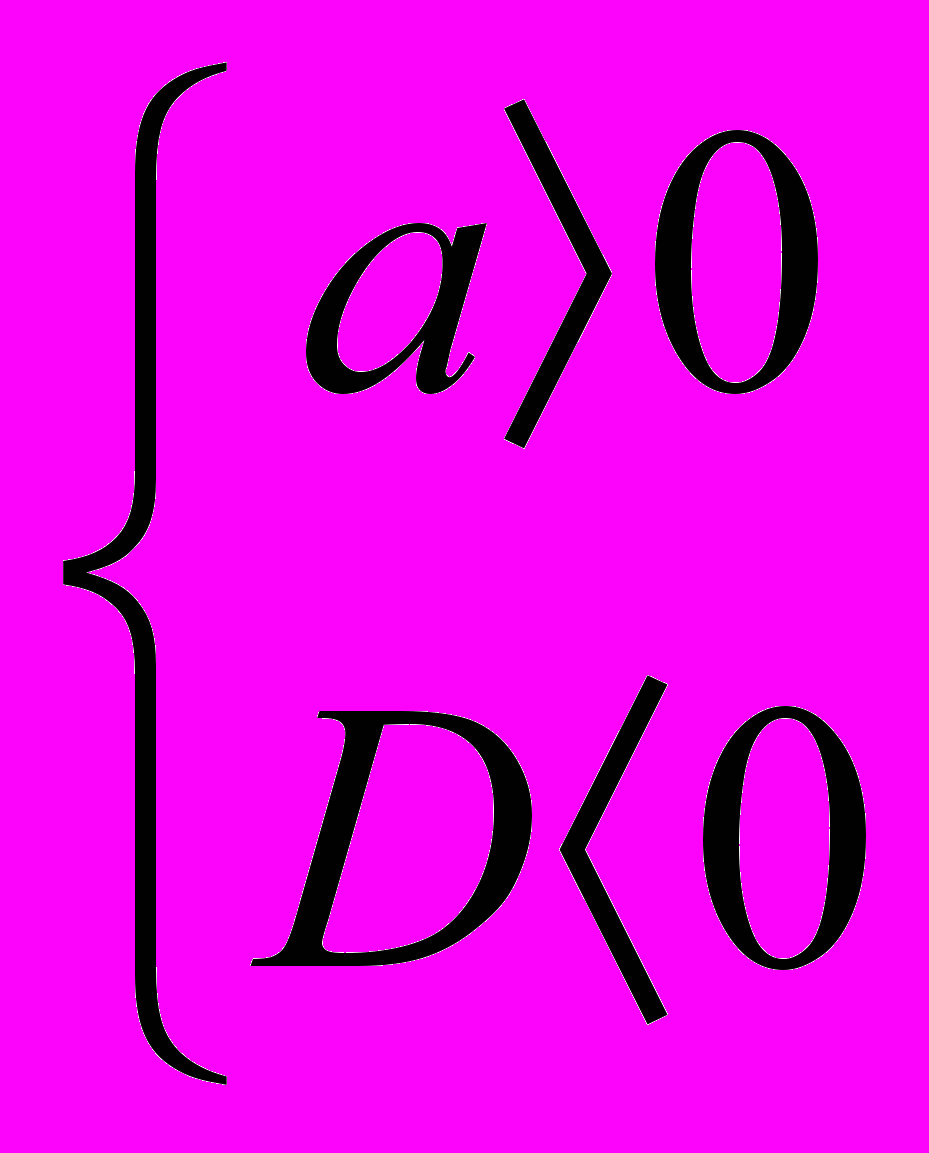 |  |
| 8 | Решений нет |  | 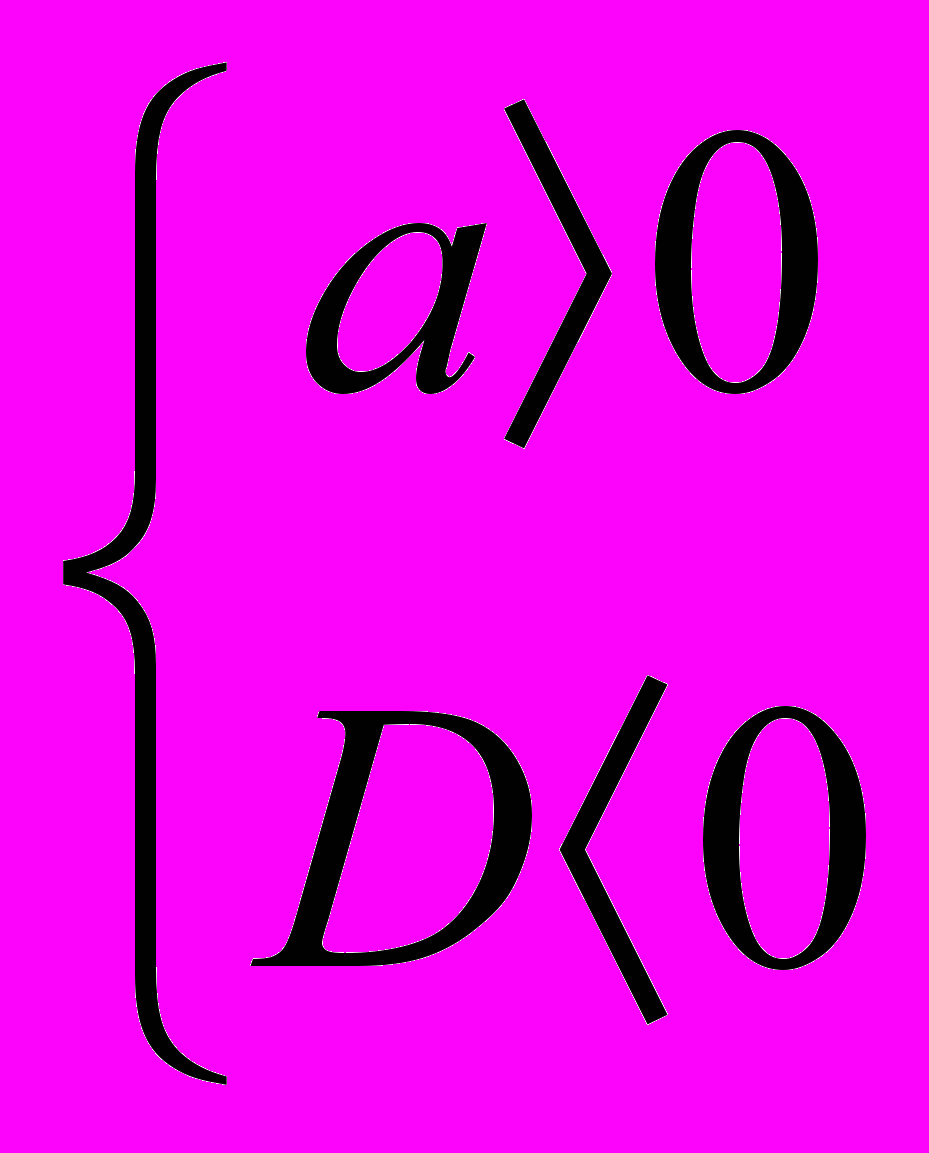 |  | 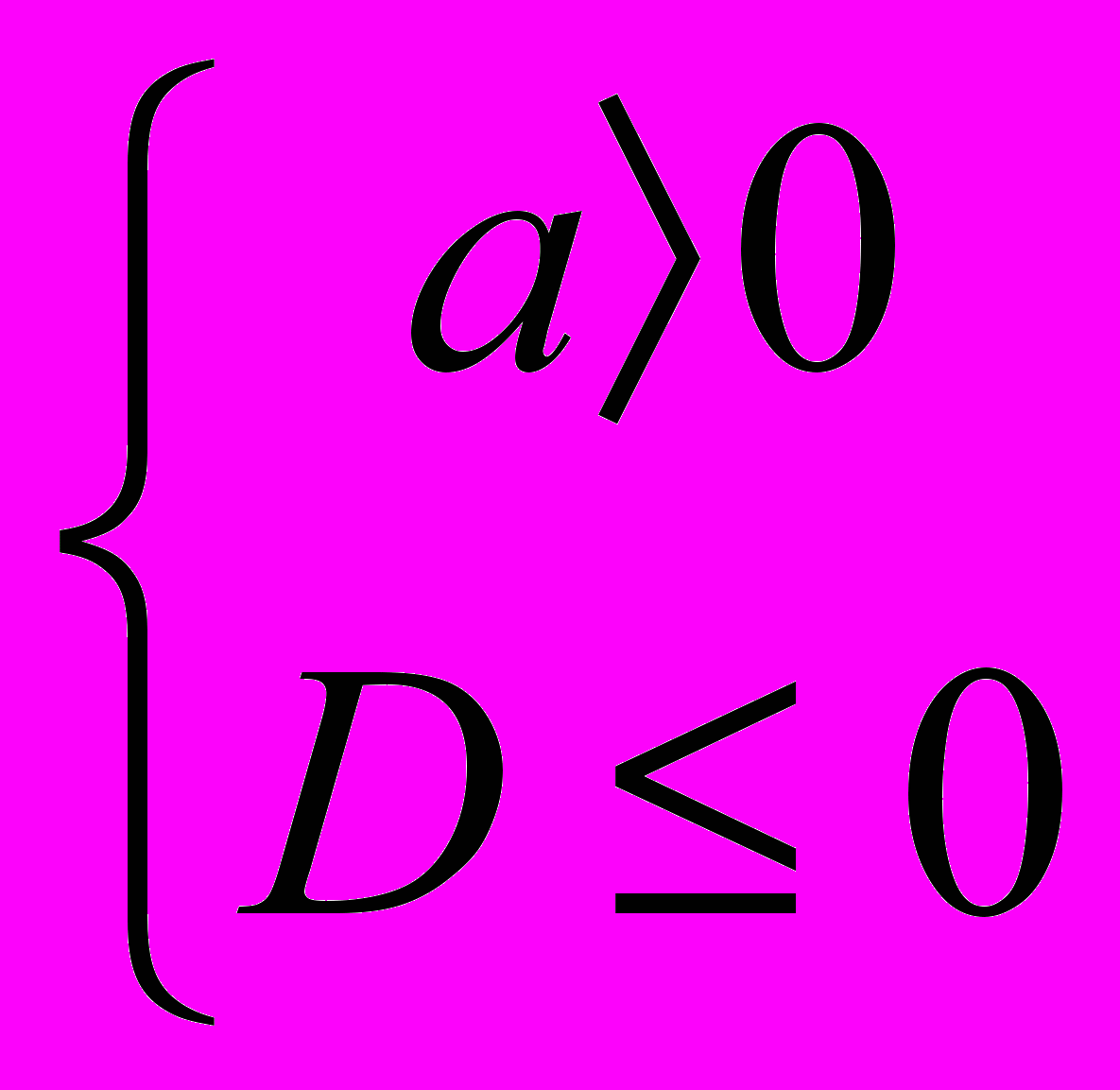 |
После групповой работы каждый поработает самостоятельно – заполнит остальные столбцы таблицы, сверит свои записи с записями на доске.
Таблица заполнена верно.
IV. Используем результаты исследовательской работы.
Предлагается задача с параметром.
Решите неравенство: ах2 + (2a-3)x + а +1≤0 для каждого действительного значения параметра а.
Разобьем решение задачи на случаи.
I группа определит, при каких значениях а множеством решений неравенства является объединение двух непересекающихся лучей.
II группа – отрезок
III группа – точка (и найти значение х)
IV группа рассмотрит два случая: множеством решений является вся прямая и неравенство не имеет решений.
Группы совещаются, находят ответ на вопрос.
Решение I группы
Множеством решений данного неравенства является объединение двух непересекающихся лучей, если выполняются условия
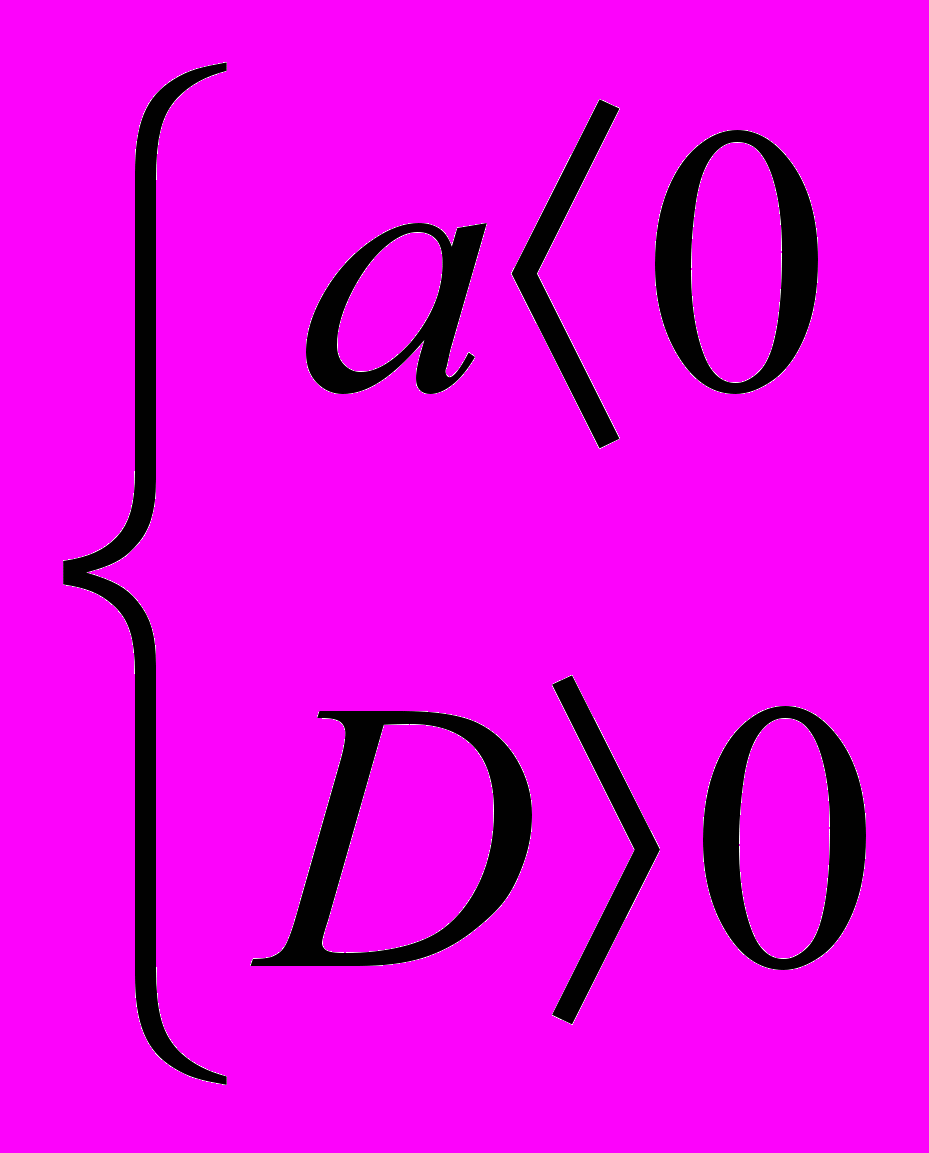 . Найдём дискриминант
. Найдём дискриминант 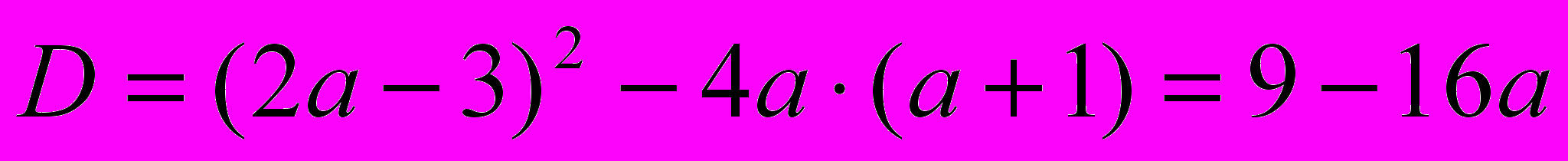 . Подставим значение дискриминанта в систему и получим
. Подставим значение дискриминанта в систему и получим 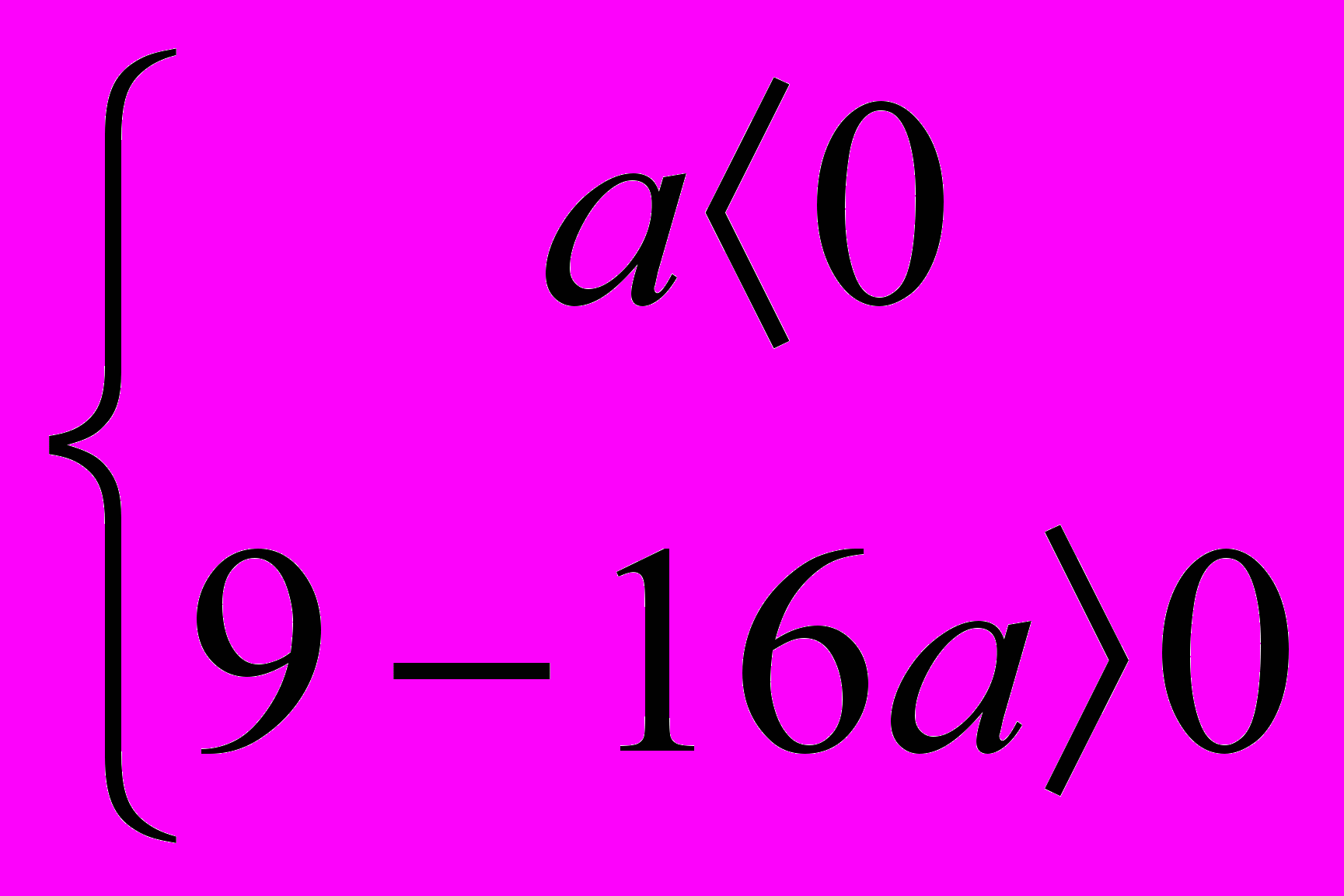 . Решением системы является множество значений
. Решением системы является множество значений 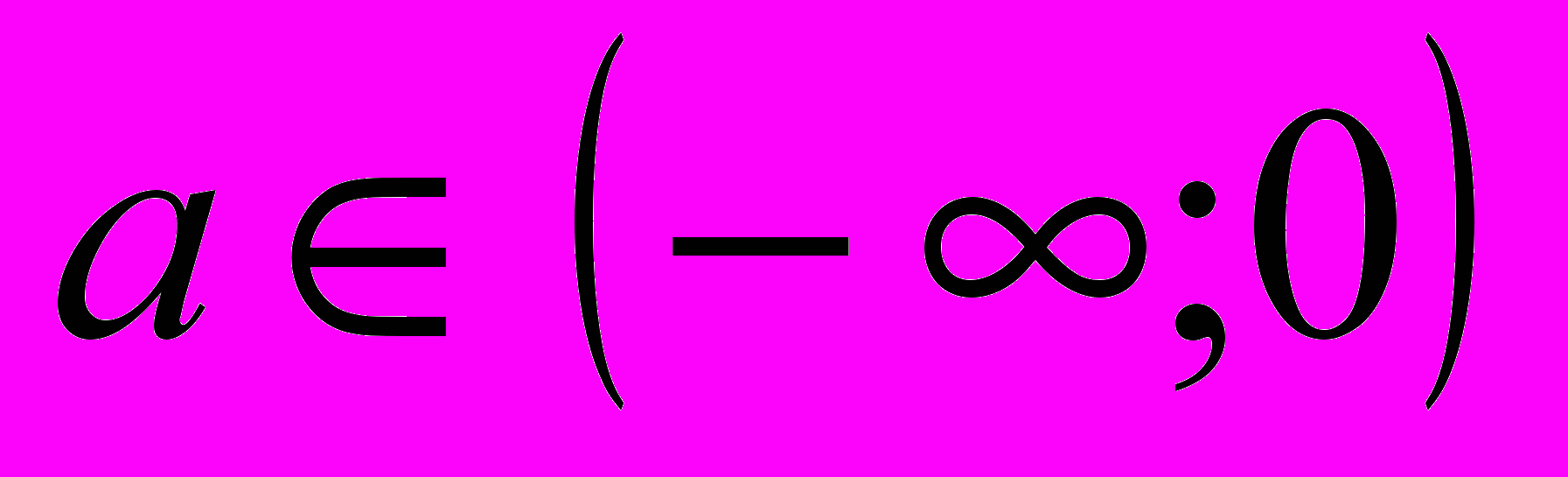 .
.Найдём корни уравнения ах2 + (2a-3)x + а +1=0.
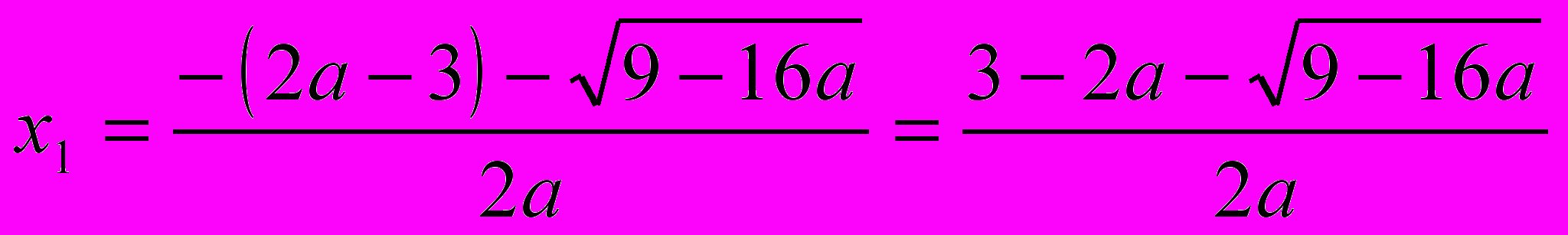 ,
, 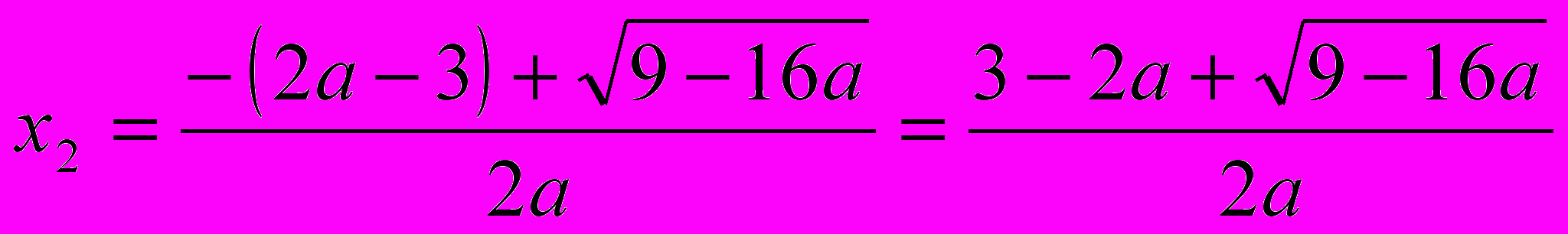 .
.Найдём разность
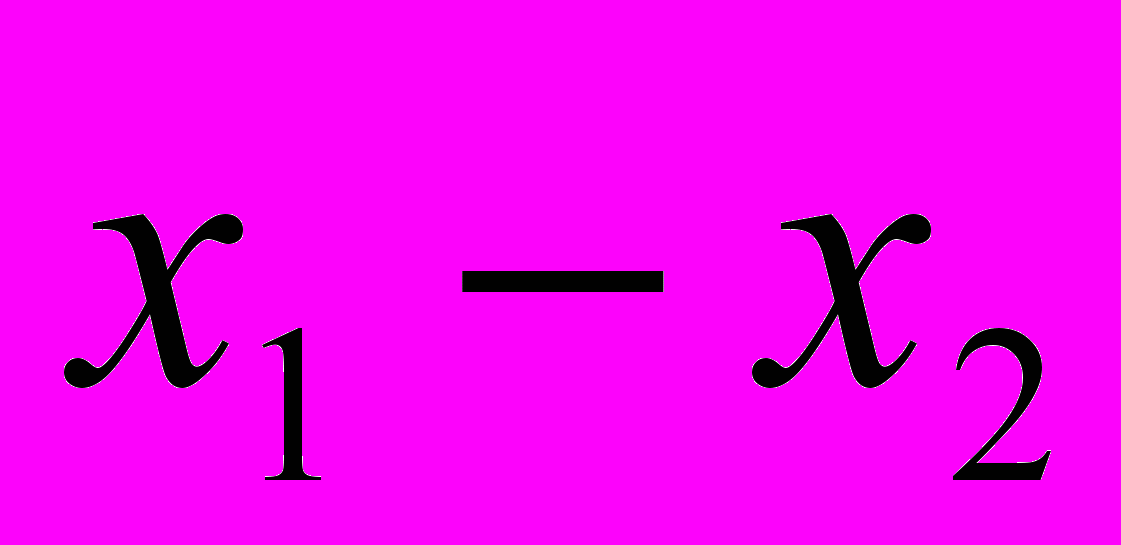 и сравним её с нулём в данном случае.
и сравним её с нулём в данном случае.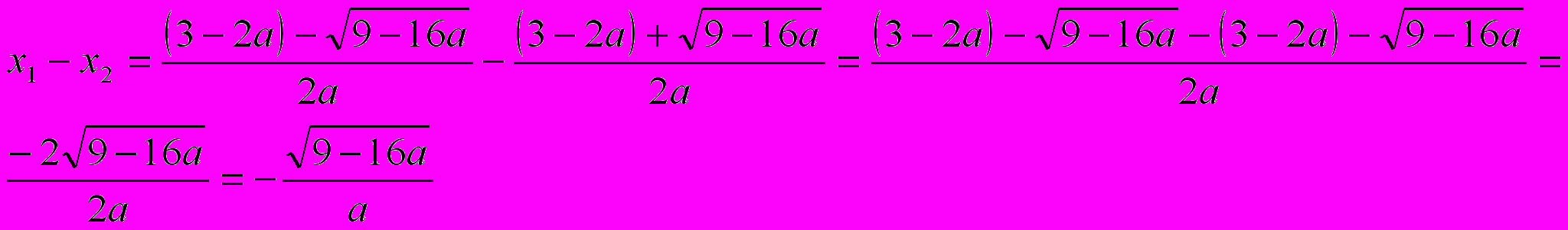
Если
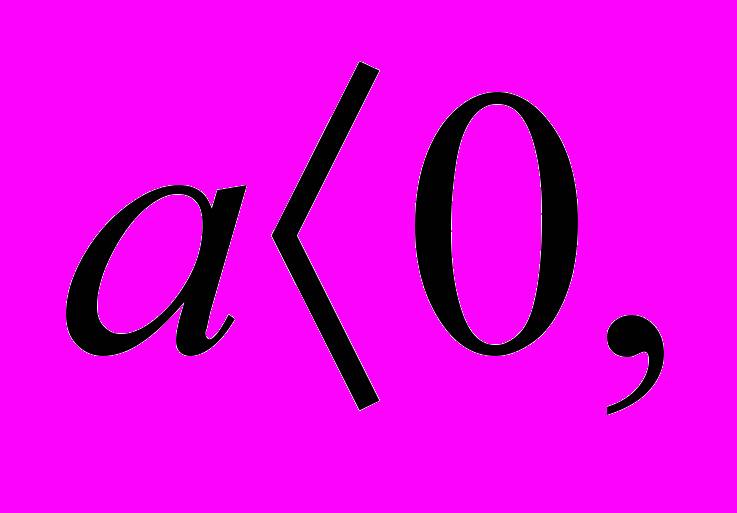 то
то 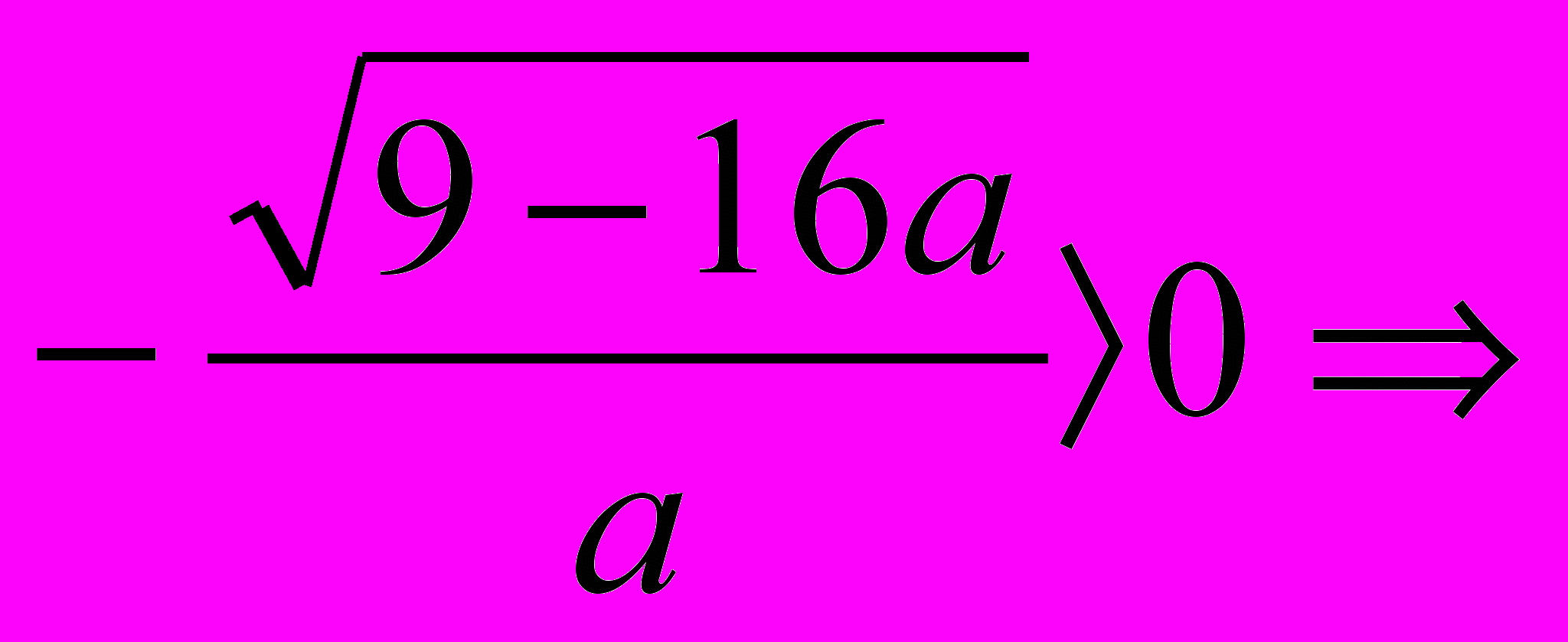
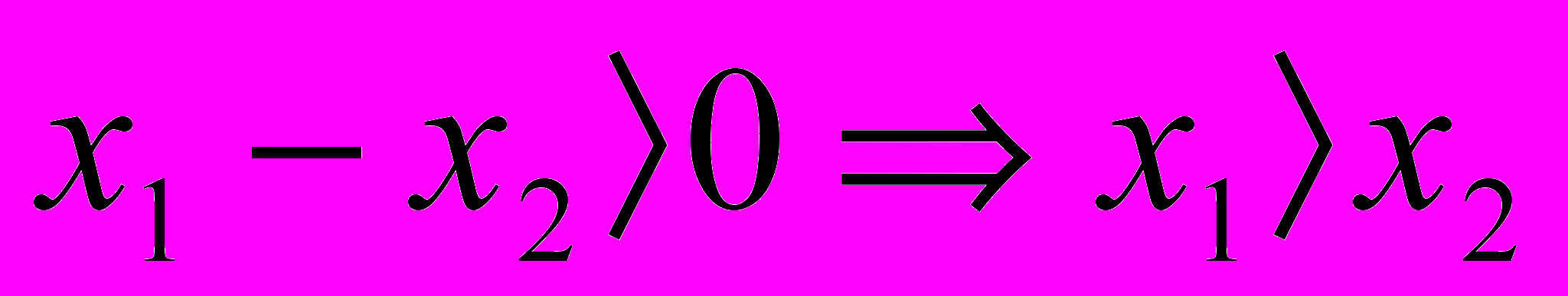
Ответ I группы: при а <0 множеством решений данного неравенства является объединение двух непересекающихся лучей, то есть (- ∞; х2]
 [х1;+∞), где
[х1;+∞), где 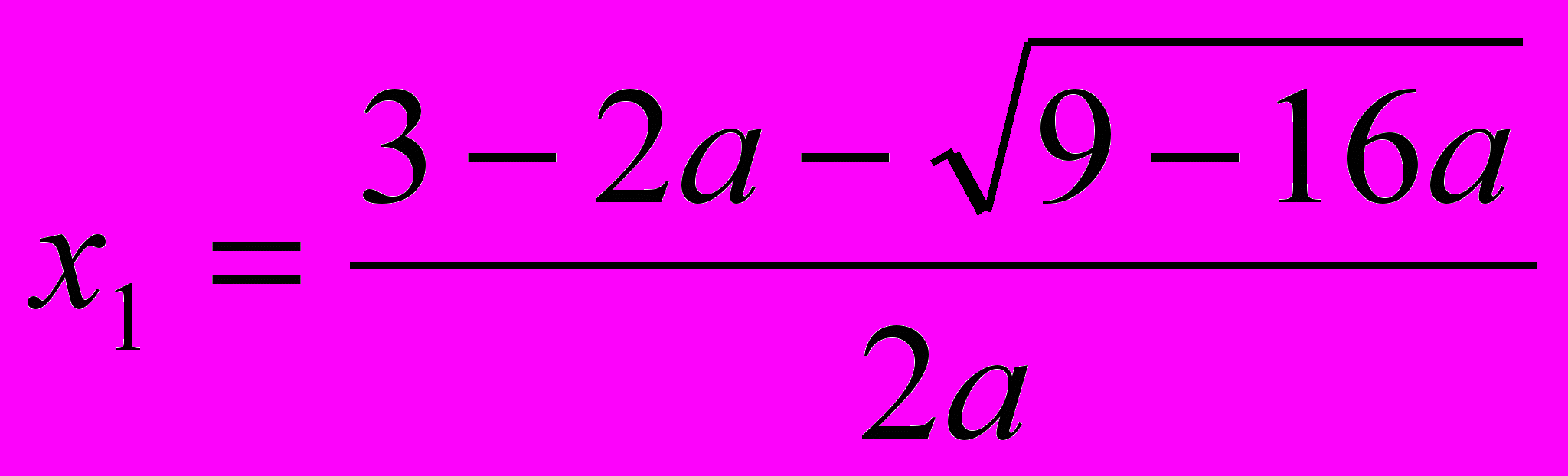 ,
, 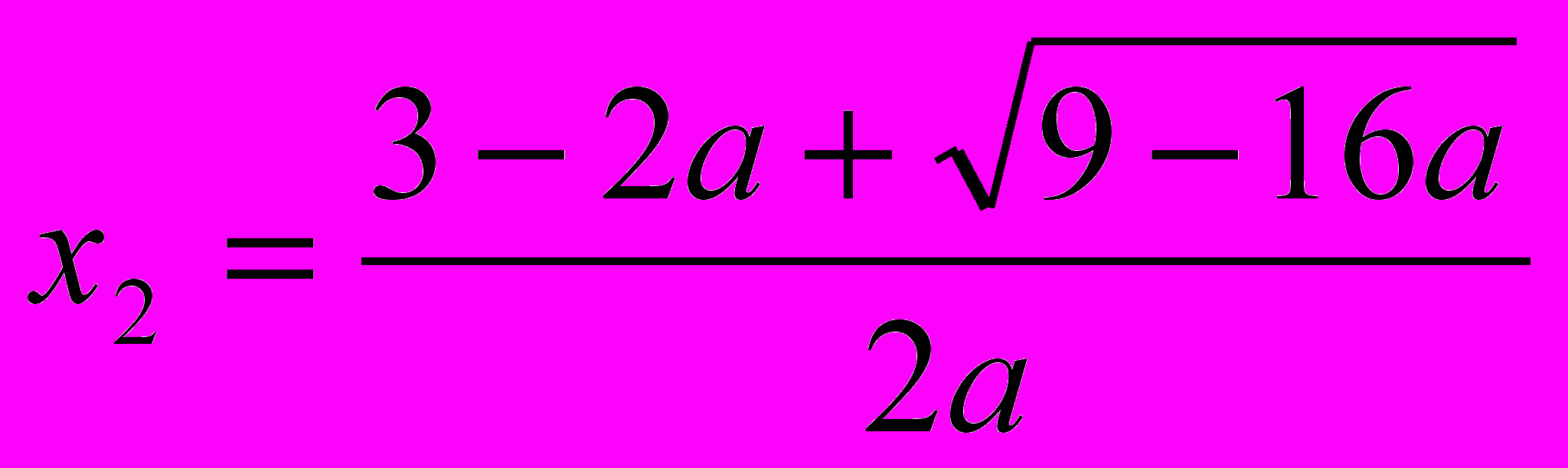 .
.Решение II группы
Множеством решений данного неравенства является отрезок, если выполняются условия
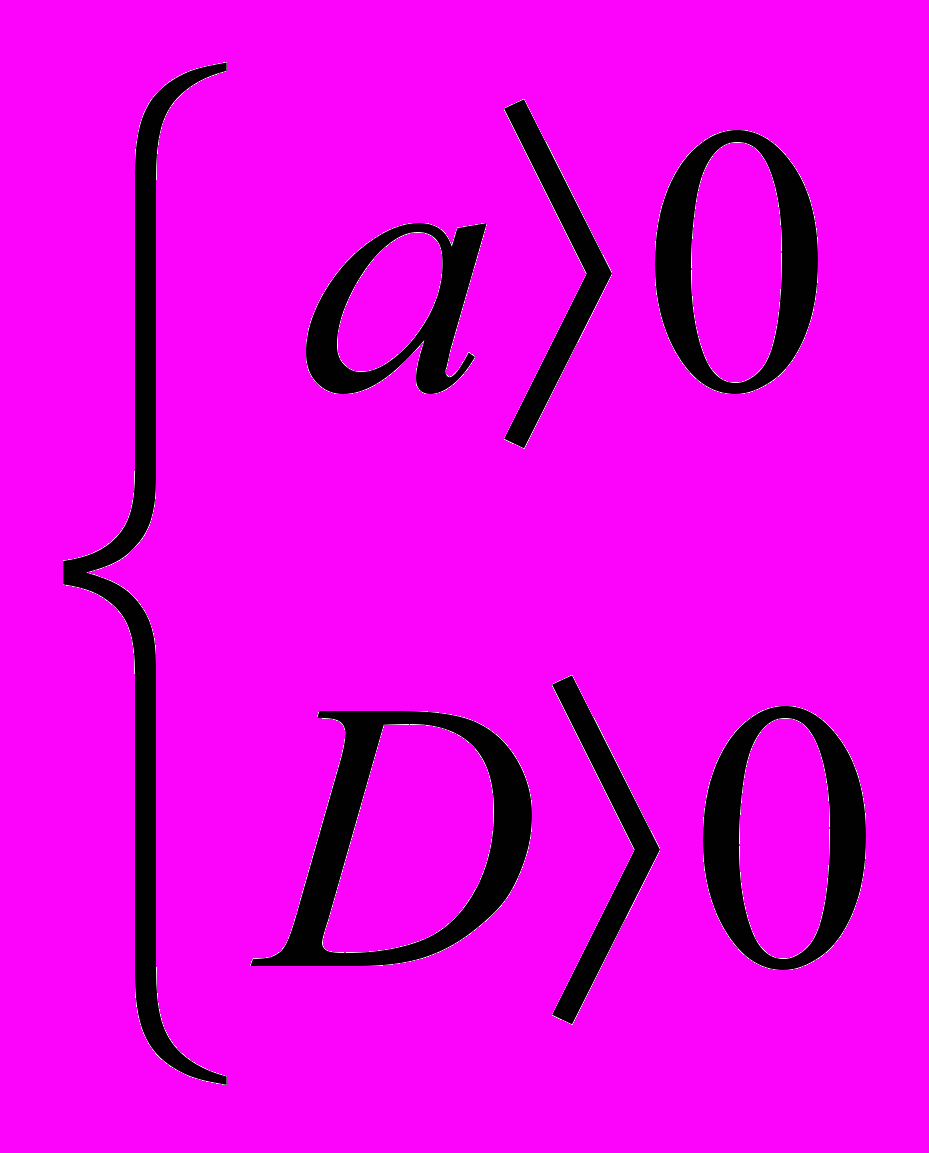 . Подставим значение дискриминанта D= 9-16а в систему и получим
. Подставим значение дискриминанта D= 9-16а в систему и получим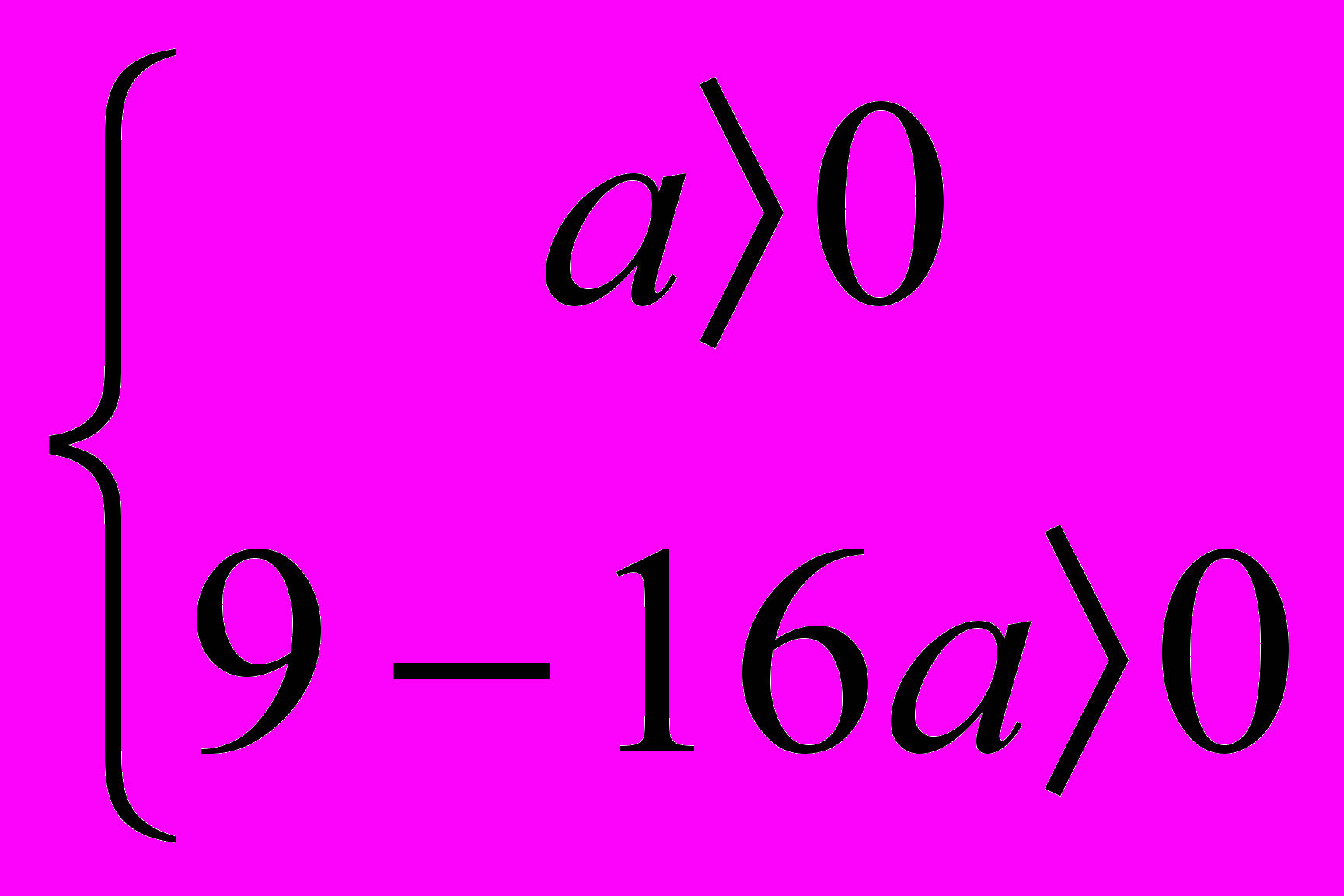 . Решением системы является множество значений а (0; 9/16). Из предыдущего решения (решения I группы) следует, что
. Решением системы является множество значений а (0; 9/16). Из предыдущего решения (решения I группы) следует, что 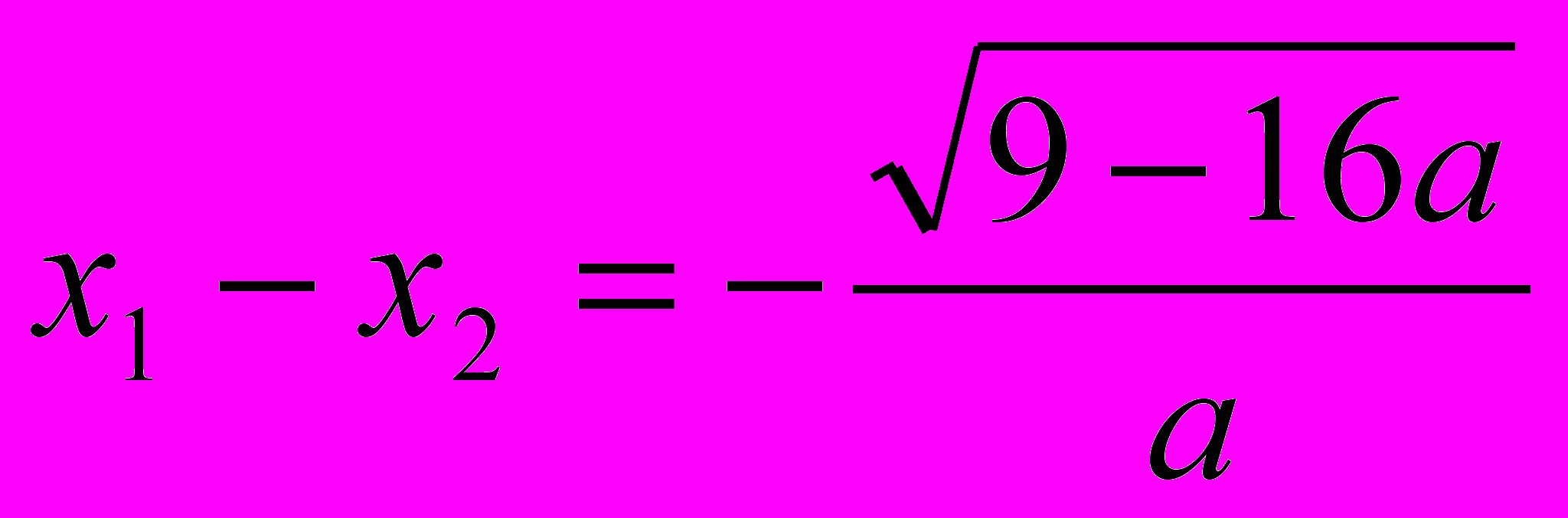 .
.Если а (0; 9/16), то