Секованов В. С., к ф-м н., профессор кафедры прикладной математики и информационных технологий кгу им. Н. А

Вид материала

Документы

Содержание Григорьева Ирина Владиславовна 2 Этот квадрат основа полимино

Подобный материал:

• Обоснования в математике (от Евклида до компьютера), 49.75kb.
• Программа проведения всероссийской молодёжной школы «Прикладные методы статистического, 81.95kb.
• Программа проведения всероссийской молодёжной школы «Прикладные методы статистического, 78.37kb.
• Задачи на графах программа, 81.89kb.
• А. В. Бернштейн, заведующий лабораторией, 122.14kb.
• И. И. Мечникова Институт математики, экономики и механики Кафедра математического обеспечения, 900.66kb.
• Нечаев Дмитрий Юрьевич, кандидат технических наук, доцент, профессор кафедры информационных, 419.94kb.
• Токсубаева Лидия Сергеевна доцент кгу трофимов Анатолий Михайлович профессор кгу конференция, 336.82kb.
• Программа дисциплины "Прикладной экономический анализ на основе пакетов: spss и Stata", 105.49kb.
• Владимира Игоревича Соловьева, к э. н., проф кафедры прикладной математики и директора, 31.64kb.

Тема урока:

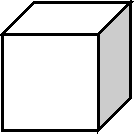
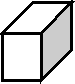
«Объем прямоугольного параллелепипеда. Преобразование объемных фигур».


Цели урока:

а) образовательная: формировать понятие прямоугольного параллелепипеда, учиться вычислять объем сложных объемных фигур;

б) развивающая: развитие логического мышления, пространственного представления, воображения учащихся, выведение целей урока;

в) воспитательная: развитие самоконтроля, сотрудничества при работе в паре.

Оборудование:

а) для учащихся: клей, заготовка макетов прямоугольного параллелепипеда, лист с математической разминкой и профессиональным тестом на знания, техническая карта изготовления фантастического замка;

б) для учителя: колокольчик, карточки с пословицами, таблицы с формулами S=S₁+S₂; V=V₁+V₂.


Ход урока:

I. Организационный момент

- Итак, ребята мы начинаем наш урок. Сядьте поудобнее, закройте глазки и повторяйте за мной.

Сейчас я начну учиться.

Я радуюсь этому.

Внимание мое растет.

Память моя крепка.

Голова мыслит ясно.

Я хочу учиться.

Я готов к работе.

Работаю.

- Откройте глазки. В народе говорят: «Была бы охота, а впереди еще много работы», а у нас впереди работа с геометрическими фигурами.

В наше время геометрия превратилась в серьезную академическую науку. Но если вы считаете, что она доступна только ученым-математикам, то ошибаетесь. И сегодня на уроке мы с вами постараемся в этом убедиться.

II. Математическая разминка.

а) Начнем с математической разминки (Приложение 1 «Математическая разминка»)

- На листах прошу выполнить в математической разминке два задания.

- Прочитайте первое и второе задания (вслух читает 1 ученик)

- Подчеркните карандашом нужные номера рисунков в соответствии с заданием

+ дети выполняют самостоятельно (учитель обозначает конец работы колокольчиком)

б) проверка (фронтально)

- Зачитайте ответы 1 задания

2 задания.

+ дети показывают согласие или несогласие с ответом знаками + или -

в) На какие 2 большие группы можно разделить все геометрические фигуры?

+ Плоские и объемные

- А к какой группе мы отнесем лист газеты? Пенал?

- Оцените свою работу мордашкой и нарисуйте значок в квадратике справа.

+ дети рисуют значок , или 

- Покажите мимикой своего лица, какую мордашку вы нарисовали.

III. Сообщение темы и целей урока.

Игра «Да – нетка»

- С помощью вопросов «да» или «нет» (вспомните алгоритмы по информатике) определите фигуру, с которой мы будем работать на уроке.

+ дети задают вопросы:

-Это фигура плоская?

+ Нет и т.д.

- Итак, тема нашего урока «Прямоугольный параллелепипед».

+ Учитель открывает тему урока, заранее написанную на доске.

- Опираясь на данные слова, предположите, каковы цели нашего урока?

• повторять
  
• учиться
  
• познакомиться с новой формулой V=V₁+V₂
  

+ третья цель закрыта

IV. Актуализация знаний.

- Если вы сейчас выйдете на улицу, то сможете рассмотреть множество геометрических фигур, созданных человеком и природой.

- Ребята, а из каких объемных геометрических фигур состоит здание нашей школы?

- Подумайте, а почему здания имеют форму прямоугольного параллелепипеда, а не шара?

-Зная геометрические фигуры и их свойства, понимаем, что с геометрическими фигурами можно производить различные действия. Сегодня вы побываете в роли архитектора-фантаста, а ваша цель - построить фантастический замок.

VI. Создание «проблемной» ситуации

а) профессиональный тест на знания (Приложение 1 «Профессиональный тест на знания»)

-Но прежде, чем приступить к работе проведем тест на профессиональные знания. На листе в каждом задании подчеркнуть правильный ответ или слово «не знаю» или свой ответ в 7 задании.

+ Учитель читает задания вслух, а дети самостоятельно выполняют тест. По окончании работы звучит колокольчик.

б) проверка

+За доской даны правильные ответы, записанные заранее. Дети проверяют и ставят рядом с ответами на листочках карандашом + или -

1. Да
   
2. Да
   
3. Да
   
4. V=(a·b)·c
   
5. см³
   

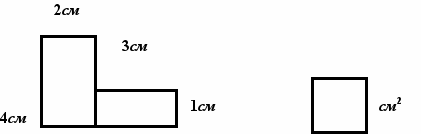6.


- Назовите площадь данной фигуры.

+ 11см² (учитель вписывает ответ на доску)

- А как вы нашли площадь данной фигуры?

+ Учитель вывешивает формулу S= S₁+S₂

7. Каков объем данной фигуры?


4 см


2 см


4 см

2 см


4 см


4 см

+ Учитель записывает на доске разные ответы детей.

- Кто подчеркнул слово «не знаю»? Вернемся к этой проблеме после создания замка.

- Оцените свою работу над тестом мордашкой в квадратике справа на листочках.

- Покажите мимикой лица, какую мордашку вы нарисовали.

VII. Физкультминутка.

- Отдохнем перед работой. Встанем тихо.

- Сколько вершин у прямоугольного параллелепипеда?

+ 8 (дети делают 8 приседаний)

- Сколько ребер?

+ дети делают 12 поворотов туловищем влево, вправо.

- Сколько граней?

+ дети выполняют 6 наклонов туловищем в стороны.

- Потянулись к прямоугольному потолку.

- И нарисовали руками большой плоский круг.

VIII. Практическая работа. (Приложение 2 «Технологическая карта изготовления фантастического замка»)

- Как говорят в народе «Нужно учиться не рассказом, а работой и показом»

а) – Используя профессиональные знания архитектора-фантаста всем необходимо построить фантастический замок. Для этого используйте технологическую карту, в которой описан ход работы. Работайте в паре, приходите к общему решению, старайтесь внимательно выслушивать мнение своего коллеги, выполните необходимые расчеты

+ Дети работают в парах. Макеты заготовок даются по рядам, на каждый ряд – своего размера.

б) проверка

+ По 1 паре от ряда выходят к доске и записывают вычисления.

V1=(3·3) ·3=27 (cм3) V1=(5·3) ·4=60 (cм3) V=27+60= 87 (cм3)

V1=(4·4)4=64 (cм3) V1=(4·4)·2=32 (cм3) V=64+32= 96 (cм3)

V1=(2·2) ·2=8 (cм3) V1=(6·4) ·3=72 (cм3) V=8+72= 80 (cм3)

- Ребята, покажите свои замки.

- Почему, у 1,2,3 рядов замки получились разные, а объёмы одинаковые у 1 ряда -

87 см³, у 2 ряда - 96см³, у 3 ряда - 80 см³?

+ Так как строили из параллелепипедов одинаковых объемов.

- Подумайте в паре, как записать в виде формулы нахождение объема фигуры, состоящей из нескольких параллелепипедов, зная, что S =S₁+S₂. Запишите форму карандашом на листе.

+ После окончания работы учитель дает звоночек. 1 пара записывает выведенную формулу на доске.

V=V₁+V₂.

-Покажите знаком + или –, согласны ли вы с формулой. Оцените себя на листочке мордашкой. Покажите это мимикой лица.

Вывод: Итак, как найти объем фигуры, состоящей из нескольких прямоугольных параллелепипедов?

+ Учитель вывешивает формулу V=V₁+V₂.

IX. Первичное закрепление.

а) – Вернемся к заданию 7 в профессиональном тесте. Как же найти V этой сложной фигуры?

+ ответы детей.

Вывод: Чтобы найти объём сложной фигуры, надо сложить объёмы тех параллелепипедов, из которых она состоит.

Итак цель нашего урока была познакомиться с новой формулой V=V₁+V₂.

+ Учитель показывает цель урока.

- Теперь, используя новую формулу, сосчитайте, чему же равен V фигуры в задании 7 и запишите вычисления на листе

V₁= (4·4) ·4=64 (cм³)

V₁= (4·2) ·2=16 (cм³)

V= 64+16= 80 (cм³)

+ 1 ученик работает за доской

б) проверка.

Х. Итог.

- Народная пословица гласит «Не говори, чему учился, а говори, что узнал».

- Что нового узнали на уроке?

+ Научились находить объём сложной фигуры, состоящей из нескольких параллелепипедов.

XI. Домашнее задание.

- В задании 6 профессионального теста решите задачу с усложнением.

Такой след оставила коробка. Чему равен ее объем, если высота этой коробки 5 см.


- Спасибо за работу. Молодцы! Урок окончен.


Григорьева Ирина Владиславовна,

учитель высшей квалификационной категории


Урок по наглядной геометрии





Тема урока:

«Складывание фигур из квадратов «край в край»»


Вдохновение нужно в геометрии, как и в поэзии.

А.С.Пушкин

Цели урока:

-развитие пространственного воображения, геометрической интуиции, творческих способностей учащихся

-оперирование образами геометрических фигур в простейшем исследовании, развитие комбинаторных способностей детей

-развитие самоконтроля, сотрудничества при работе в парах


Оборудование:

-магнитная доска

-квадраты на магнитах

-цветная бумага, ножницы

-12 магнитов


Ход урока:

Проверим домашнее задание олимпиадного характера: Разрезать квадрат 77 на 5 частей и сложить их так, чтобы получились 3 квадрата: 22, 33, 66.

Рассмотрим одно из решений:


Рис.1

			4					2							3
	1											1
															4			5
2				5
3

Итак, в домашней работе 2 задачи нашего сегодняшнего урока. Как вы думаете, какие? (разрезать и складывать.)

1. Выполним самостоятельную работу и проверим, как вы научились решать задачи на разрезание (см. далее в пункте 1)
   
2. Рассмотрим новые задачи на складывание фигур из квадратов (см. далее в пункте 2)
   

1

На прошлых занятиях мы с вами разрезали фигуры на части. Наибольшее количество упражнений связано с разрезанием на равные фигуры. Вспомним, какие фигуры называются равными (равные фигуры - это фигуры, совпадающие при наложении)


Самостоятельная работа на разрезание: Разрезать фигуры на две равные части по сторонам и диагоналям клеток. На задание отводится не более 10 минут.


Рис.2

Разрезая фигуры по сторонам клеток, мы сначала считали, сколько клеток (квадратов) будет в одной части, а потом придумывали конфигурацию фигуры.

Рассмотрим это на примере одного задания из самостоятельной работы. Здесь большая фигура разрезана на части, состоящие из 6 квадратов.

Рис.3




2

Этот квадрат основа полимино – конструкций из квадратов, имеющих попарно общие стороны. Значит, мы уже решали задачи на складывание фигур из квадратов.

Составляя их, проведем математическое исследование: Сколько фигур и какой формы можно получить, соединяя квадраты «край в край»?


Классная работа. Складывание фигур из квадратов «край в край».