Досвіду
| Вид материала | Документы |
- Тема досвіду: Використання проектної технології на сучасному уроці англійської мови, 183.96kb.
- Тема досвіду, 94.44kb.
- Картка обліку об’єктів ефективного педагогічного досвіду, 33.11kb.
- Картка обліку об’єктів ефективного педагогічного досвіду, 29.8kb.
- Проблема досвіду, 82.17kb.
- Передовий досвід розвитку кластерів for the Programme, 1089.05kb.
- Впровадження передового педагогічного досвіду, 115.73kb.
- Тема досвіду: «Особистісно розвиваючий підхід при використанні групового ( кооперативного, 73.43kb.
- Тема досвіду, 114.12kb.
- Тема (проблема) досвіду, 304.12kb.




Тема досвіду. Метод «згущення знань» як ефективний засіб формування математичної культури учнів математичного класу
Ідея. Вирішення проблеми інтенсифікації навчання математиці учнів класу математичного профілю за рахунок методу згущення знань.
Автор досвіду. Бабак Наталія Анатоліївна, учитель математики Горлівського НВК «ЗОШ І-ІІІ ступенів № 14 – багатопрофільний ліцей «Лідер», спеціаліст вищої категорії, учитель-методист, Заслужений вчитель України
Мета студії. Познайомити учасників студії та практично опанувати методом «згущення знань» як ефективним засобом формування математичної культури учнів математичного класу.
Очікувані результати:
- Систематизація знань учасників секції щодо використання методів інтенсифікації навчання математиці: методу «згущення знань», методу «укрупнення дидактичних одиниць».
- Набуття навичок:
- використання методу «згущення знань» на уроках математики у профільних математичних класах та класах допрофільної підготовки учнів;
- аналізу уроку математики з позицій реалізації принципів інтенсифікації навчання.
- використання методу «згущення знань» на уроках математики у профільних математичних класах та класах допрофільної підготовки учнів;
- Розвиток в учасників секції установки щодо необхідності реалізації нових підходів до викладання математики на шляху підвищення рівня навчальної компетентності учнів математичного класу.
Форма проведення. Майстер-клас
Розподіл навчального часу
| Етап | Зміст роботи | Час |
| 1. | Мотиваційний модуль | 5 хв |
| 2. | Змістовний модуль | 30 хв |
| |
| 4 хв |
| |
| 15 хв |
| |
| 3 хв |
| |
| 8 хв |
| 3. |
| 5 хв |
| |
| 40 хв |
І. Мотиваційний модуль
Школа не завжди справляється зі своєю соціальною функцією – забезпечити підростаюче покоління засобами самовизначення в трудовому, соціальному, політичному й економічному житті. Як показують соціологічні дослідження, сьогодні далеко не кожний учень відповідає вимогам життя, уміє перебудовуватися, організувати свою освіту, компетентність. Тим часом суспільство потребує високоосвічених, ініціативних молодих людей, здатних творчо реформувати наше суспільство. Тому випускники середньої школи повинні бути готові до саморозвитку, до безперервного самовдосконалення.
З цією метою весь навчальний процес, усю його методику і структуру необхідно зорієнтувати так, щоб найбільш ефективно розвивати особливості учня до самостійної діяльності.
Можна скільки завгодно говорити про нові методи навчання, але визначальною їх характеристикою є ставлення до дитини, як до об'єкта педагогічного впливу, або як до особистості, що розвивається, суб'єкта власної учбової діяльності.
Усі згодні з тим, що немає «царського шляху в математику».
Багато праці і терпіння, наполегливості й уваги потрібно від учителя і школяра, щоб останній зміг освоїти програмний мінімум знань з цього предмету.
Якщо проаналізувати кількість годин, передбачених на вивчення, наприклад, теми «Тригонометрія» за різними програмами, то отримаємо наступну картину:
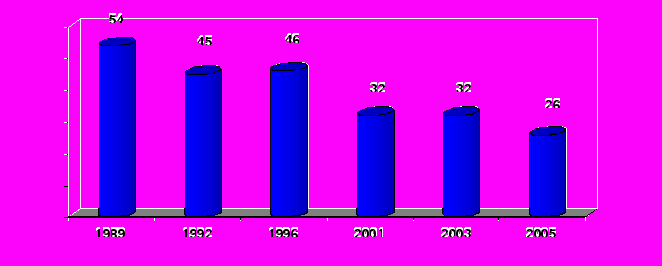
Програми з математики
За діючою програмою фізико-математичного профілю 2003 р. на вивчення цієї теми відводиться 35-40 год.
Автори нині діючої програми В.Г.Бевз, А.Г.Мерзляк, З.І.Слєпкань у 2001 році пояснюють скорочення кількості годин на вивчення математики наступним чином: «Опрацьовуючи розділ «Тригонометричні функції», не слід намагатися доводити і примушувати учнів запам’ятовувати всі формули, які традиційно розглядалися раніше. Важлива і потрібна наука в минулому, сьогодні тригонометрія втратила свою колишню роль. І логарифми у зв’язку з поширенням мікрокалькуляторів відійшли в історію. Також розв’язування сотень тригонометричних, логарифмічних, показникових рівнянь, не пов’язаних з будь-якими прикладними задачами, – традиція, від якої бажано поступово звільнятися».
У пояснювальній записці до програми 2003 року визначено, що перенесення з 9-го до 10-го класу тригонометричного матеріалу, що стосується тригонометричних тотожностей, призвело до перевантаження програми курсу алгебри і початків аналізу. З метою його усунення не слід вимагати від усіх учнів доведення властивостей тригонометричних і обернених до них функцій, захоплюватися розв’язуванням складних тригонометричних, ірраціональних, показникових, логарифмічних рівнянь, нерівностей та їх систем.
Але для використання запропонованих в підручниках вправ учням необхідна попередня підготовка (рішення великої кількості тренувальних вправ).
Випускник школи для успішної здачі державної підсумкової атестації з математики та ЗНО повинний мати міцні знання, зокрема з тригонометрії. І в перспективі у вищих навчальних закладах при вивченні вищої математики студенти зазнають труднощів, якщо мають проблеми у визначенні властивостей тригонометричних функцій та їх застосуванні.
З усього випливає необхідність оволодіння учнем за менший час більшим об'ємом ґрунтовних і дійсних знань. Цього можна домогтися, якщо цілеспрямовано керувати розумовою діяльністю учнів, їхньою увагою, процесами запам'ятовування учбового матеріалу.
ІІ. Змістовний модуль
Знайомство з ідеєю. Теоретичний аспект.
У книзі П.М.Ерднієва, Б.П.Ерднієва «Укрупнення дидактичних одиниць у навчанні математиці» відзначається, що досить часто структуру підручника математики визначають лише формально-логічними зв'язками самої науки математики поза обліком закономірностей засвоєння математичних знань.
Тим часом засоби формальної логіки обмежені, вони впорядковують абстраговані результати мислення, але ніяк не сам процес мислення, який приводить до цих результатів. Формально-логічні міркування не тільки не єдині, але і не головні при вирішенні питань методики: справа в тому, що категорії формальної логіки не враховують фактора часу, облік якого є найважливішим елементом для удосконалювання процесу навчання.
Укрупнення дидактичних одиниць – один з методів сприятливих цьому удосконалюванню.
Укрупнена дидактична одиниця – це клітинка навчального процесу, що складається з логічно розрізнених елементів, які володіють у той же час інформаційною спільністю. Укрупнена дидактична одиниця володіє якістю системності і цілісності, стійкістю до збереження в часі і швидкому виявленню в пам'яті.
Поняття укрупнення одиниці засвоєння досить загальне, воно вбирає наступні взаємозалежні конкретні підходи до навчання:
- Спільне й одночасне вивчення взаємозалежних дій, операцій, функцій, теорем.
- Забезпечення єдності процесів складання і рішення задач (рівнянь, нерівностей і т.п.).
- Розгляд у взаємопереходах певних і непевних завдань (зокрема, деформованих вправ).
- Звернення структури вправи, що створює умови для протиставлення початкової і зміненої вправи.
- Виявлення складної природи математичного знання, досягнення системності знань.
- Реалізація принципу додатковості в системі вправ (розуміння досягається в результаті міжкодових переходів між образним і логічним у мисленні, між його свідомим і підсвідомим компонентами).
Сукупне застосування зазначених методів створює умови для прояву фундаментальних закономірностей мислення.
При навчанні треба якнайбільше складати взаємопов'язаних вправ з невеликого числа носіїв інформації, змінюючи лише комбінацію, іноді вводячи мінімум нових елементів. Спільне рішення взаємопов'язаних завдань приведе до виникнення узагальненої інформації, великої одиниці засвоєння.
Однією з характерних рис системи укрупнення знань виступає застосування «методу обернених задач». Такі завдання природним образом розвивають навички самоконтролю, що діє мимоволі і навіть підсвідомо.
Наприклад, під час засвоєння учнями навичків добутку двох чисел (5 · 8 = 40), можна запропонувати їм відповісти на запитання: «На яке число треба помножити 5, щоб отримати 40?» (5 · = 40).
Уміння вирішувати пряму і обернену задачі є важливим критерієм досягнутої учнем глибини розуміння розділу математиці, що вивчається.
Тригонометрія в 10 класі розділена на три теми:
«Тригонометричні функції і їхні властивості».
«Тригонометричні тотожності».
«Тригонометричні рівняння і нерівності».
Ці теми можна вивчати одночасно, при цьому розглядати вправи так чи інакше пов'язані між собою. Протягом всього етапу навчання чітко простежуються три змістовні лінії, що відповідають даним темам.
Прийоми, які можна запропонувати для використання методу укрупнення одиниць, виглядають наступним образом:
- розв’язання «готової» задачі;
- складання оберненої задачі і її розв’язання;
- складання аналогічної задачі і розв’язання її;
- складання задачі за деякими елементами, спільними з даною задачею;
- розв’язання або складання задачі, яка узагальнена за деякими параметрами.
2. Цілеспрямоване керування розумовою діяльністю учнів.
Можливості удосконалювання методики роботи вчителя істотно залежать від його уміння цілеспрямовано керувати розумовою діяльністю учнів, активізуючи її. Здійснювати таке керування вчитель може, спираючись на знання системи закономірностей, що концентрує в собі знання з психології і дидактики, і відповідну методику застосування цієї системи при навчанні математиці.
У своїй книзі «Вдосконалення методики роботи вчителя математики» (М., «Просвещение», 1990г.) Я.І.Грудьонов описує цю систему психолого-дидактичних закономірностей, методику її застосування, способи її реалізації в практичній роботі вчителя. В цих закономірностях розкриваються залежності між зовнішніми умовами навчального процесу (характером вправ, їх послідовністю, організаційними прийомами) і внутрішніми процесами, що протікають у свідомості учнів (їх увагою, активністю розумової діяльності, самоконтролем і т.д.). Спираючись на ці закономірності, вчитель може шляхом видозміни зовнішніх умов координувати внутрішні процеси, що протікають у свідомості учнів. Тим самим вчитель має можливість вибирати методи навчання, найбільш придатні до умов його роботи, передбачати, прогнозувати можливі наслідки їх застосування, знаходити виходи з численних труднощів, що зустрічаються на практиці, а потім практично перевіряти свої висновки.
Розглянемо, наприклад, деякі прийоми, які забезпечують керування розумовою діяльністю учнів.
- Метод доцільних задач. Суть цього методу полягає в тому, що для кращого розуміння матеріалу, який вивчається (нового визначення, нової теореми, самостійного розв’язування задач), учням пропонують підготовчі задачі.
- «Відкриття» теореми. Підвести учнів до самостійного «відкриття» теореми, ствердження завдяки запропонованим прикладам.
Діяльність учня – основа всього навчально-виховного процесу, основа всіх процесів, що протікають у свідомості учня при виконанні навчальних задач. Розумова діяльність учня розглядається як одна з основних умов у кожній закономірності. Мова йде про розумову діяльність, тому що будь-які дії учня (виготовлення моделей, виконання малюнків, розв’язування задач) спрямовуються його розумовою діяльністю.
Необхідні знання з математики, уміння і навички учні здобувають тільки шляхом самостійних зусиль, а вчитель, спираючись на різні методи і засоби, тільки направляє учнів, організує навчальний процес.
Якщо навчальна діяльність виконується шляхом активних розумових зусиль і при цьому досягається чітке розуміння матеріалу, що вивчається, то така діяльність стає для учня усе більш цікавою і привабливою.
Звідси випливає найважливіший практичний висновок:
Щоб підвищити інтерес учнів до уроку, необов'язково підбирати який-небудь особливо цікавий матеріал. При вивченні будь-якої теми досить домогтися активної розумової діяльності учнів над досліджуваним матеріалом.
Практичний аспект
Демонстрація використання методу «Згущення знань» при вивченні теми «Поняття логарифма числа» (10 кл.).
Завдання до перегляду фрагменту уроку. Приймаючи участь у роботі над засвоєнням поняття «логарифм числа», заповніть «Лист спостереження за уроком», відмітивши використані вчителем прийоми.
Лист спостереження за уроком
Метод «згущення знань»
Суть. Оволодіння учнем за менший час більшим об’ємом ґрунтовних і дійсних знань завдяки цілеспрямованому керуванню його розумовою діяльністю, його увагою, процесами запам’ятовування учбового матеріалу.
Науково-методична основа методу:
- «Укрупнення дидактичних одиниць у навчання математиці». П.М.Ерднієв, Б.П.Ерднієв.
- Цілеспрямоване курування розумовою діяльністю учнів на уроках математики. Я.І.Грудьонов.
- Психолого-педагогічні та методичні основи розвивального навчання математики. З.Слєпкань.
| Прийоми | Опис прийому | Відмітка |
| Розв’язання «готової» задачі | Розв’язати запропоновану задачу, аналогічну прикладу. | |
| Складання оберненої задачі і її розв’язання | Скласти і розв’язати в порівнянні з даною (прямою) задачею нову, обернену задачу, здобуваючи тим самим додаткову інформацію, яка полягає у зв’язках між величинами вирішеної даної задач. | |
| Складання аналогічної задачі і її розв’язання. | Скласти нову задачу за умовою аналогічною вирішеної задачі. | |
| Складання задачі за деякими елементами, спільними з даною задачею. | Скласти нову задачу, змінюючи деякі параметри, які використовувалися у вирішеній задачі. | |
| Метод доцільних задач | Для кращого розуміння матеріалу, який вивчається (нового визначення, нової теореми, самостійного розв’язування задач), учням пропонують підготовчі задачі | |
| «Відкриття» теореми | Підвести учнів до самостійного «відкриття» теореми, ствердження завдяки запропонованим прикладам. | |
Паспорт фрагменту
Тема. Поняття логарифма числа.
Мета. Формування у школярів системи математичних знань на первинному етапі засвоєння теми «Логарифмічна функція»;
Метод. «Згущення знань».
Форма роботи. Усне фронтальне опитування.
Хід уроку
І. Мотивація.
ІІ. Засвоєння нового матеріалу.
| 1. Поняття логарифма числа.
  = 2 = 5 = 2 = 53) Визначення логарифма числа: логарифмом числа N за основою а 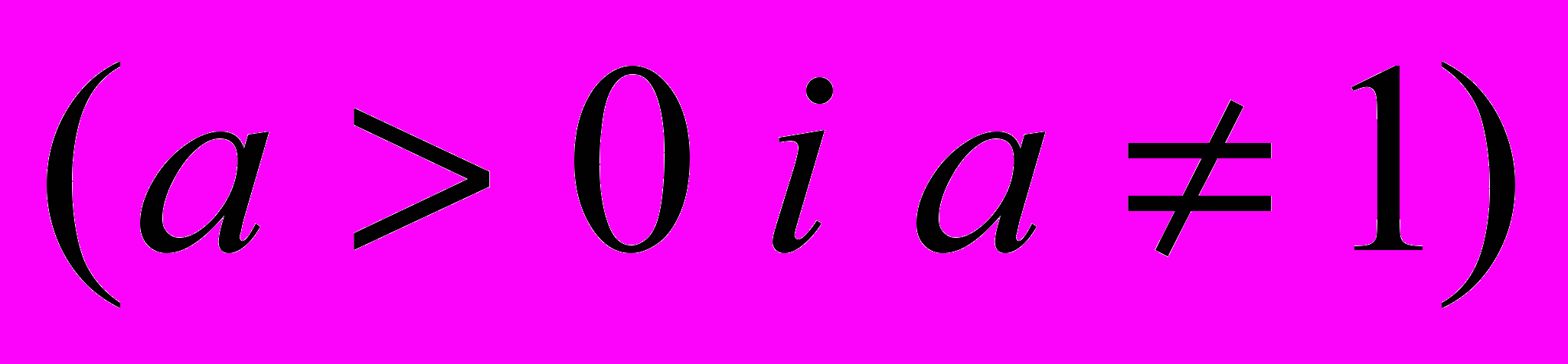 називається показник ступеня х, до якого треба піднести а, щоб дістати число N. називається показник ступеня х, до якого треба піднести а, щоб дістати число N. , , 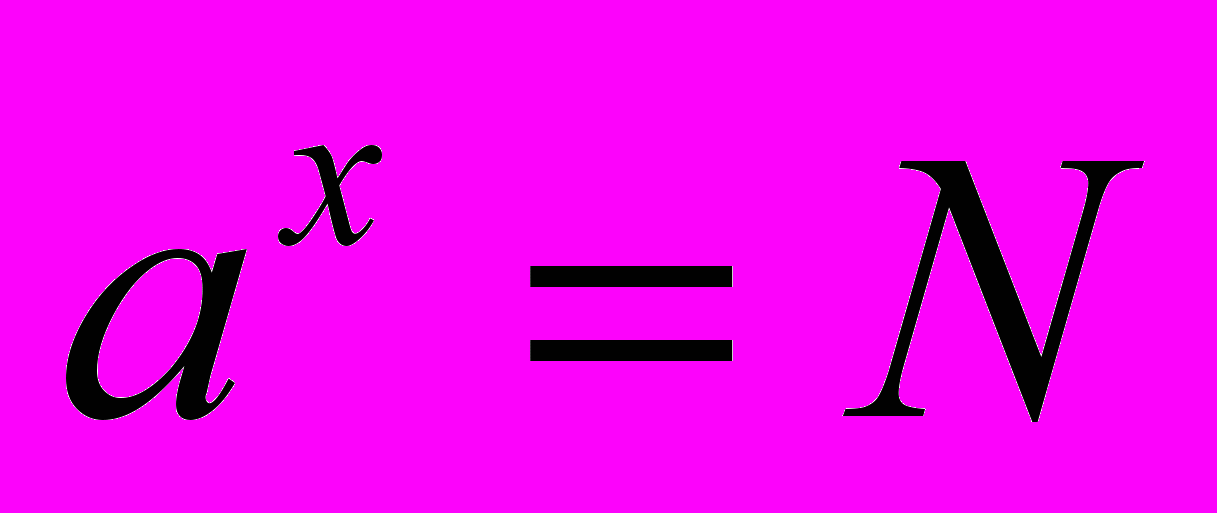 . .4) Обчислити (розв’язання «готової» задачі): а)  , , 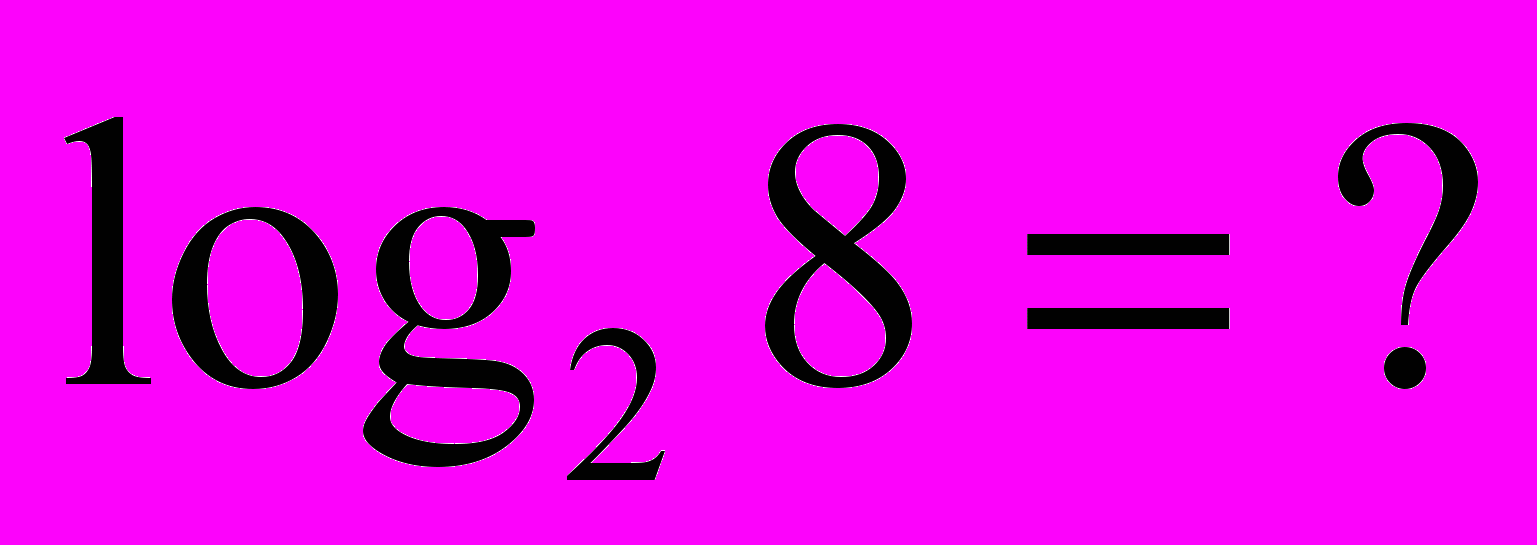 б) 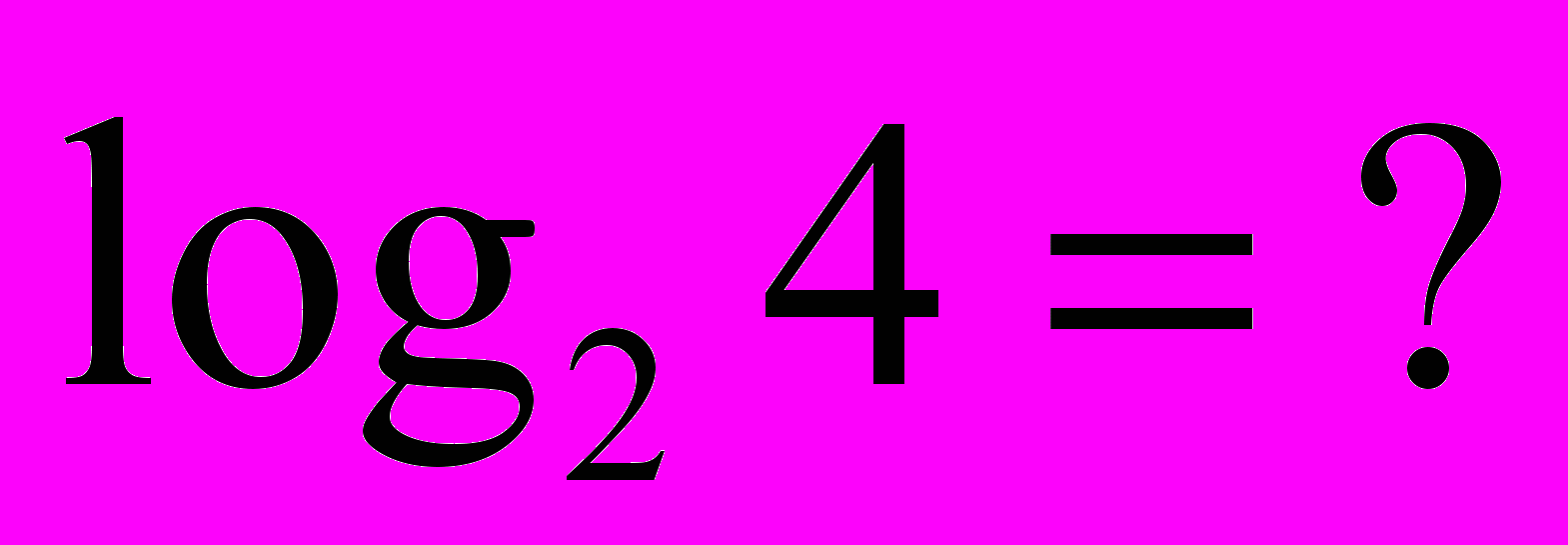 , , 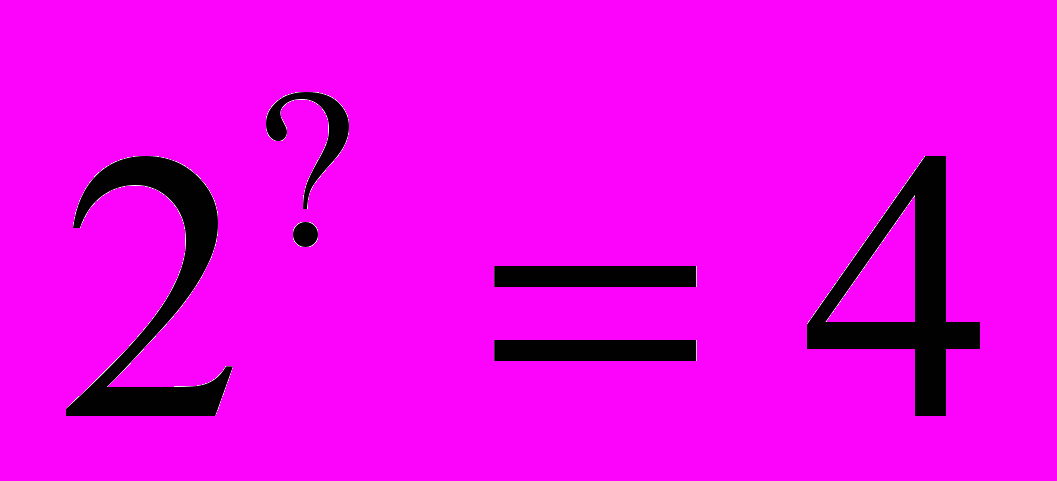 в) 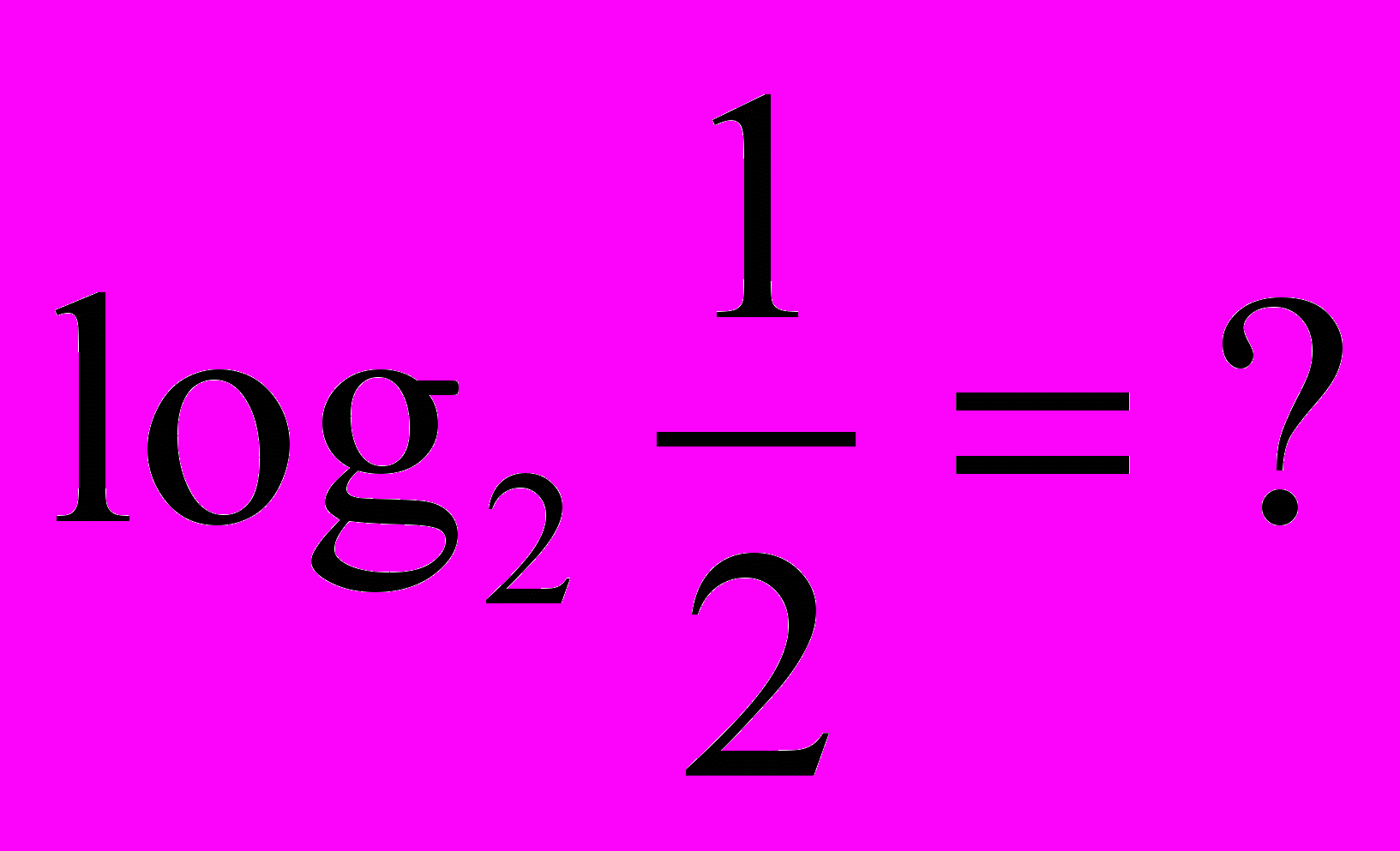 , , 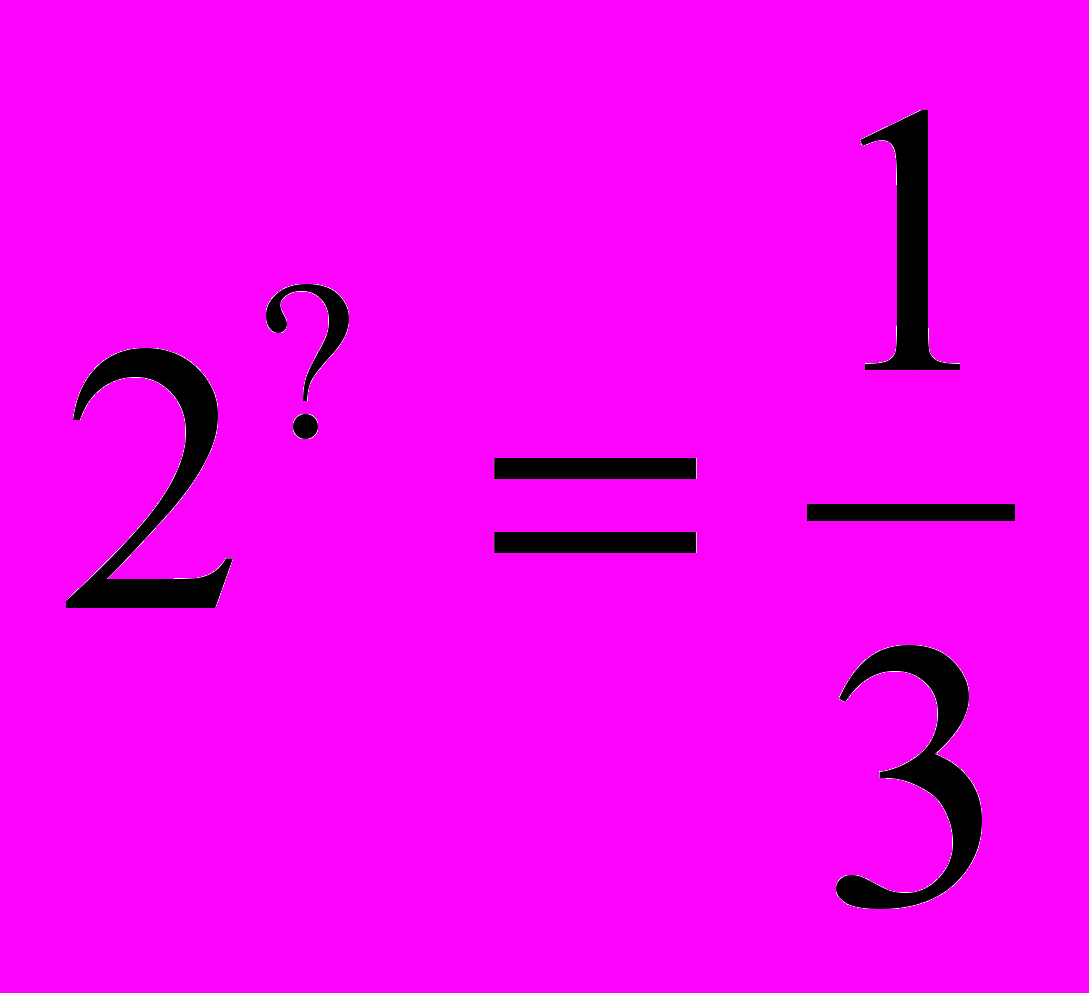 г) 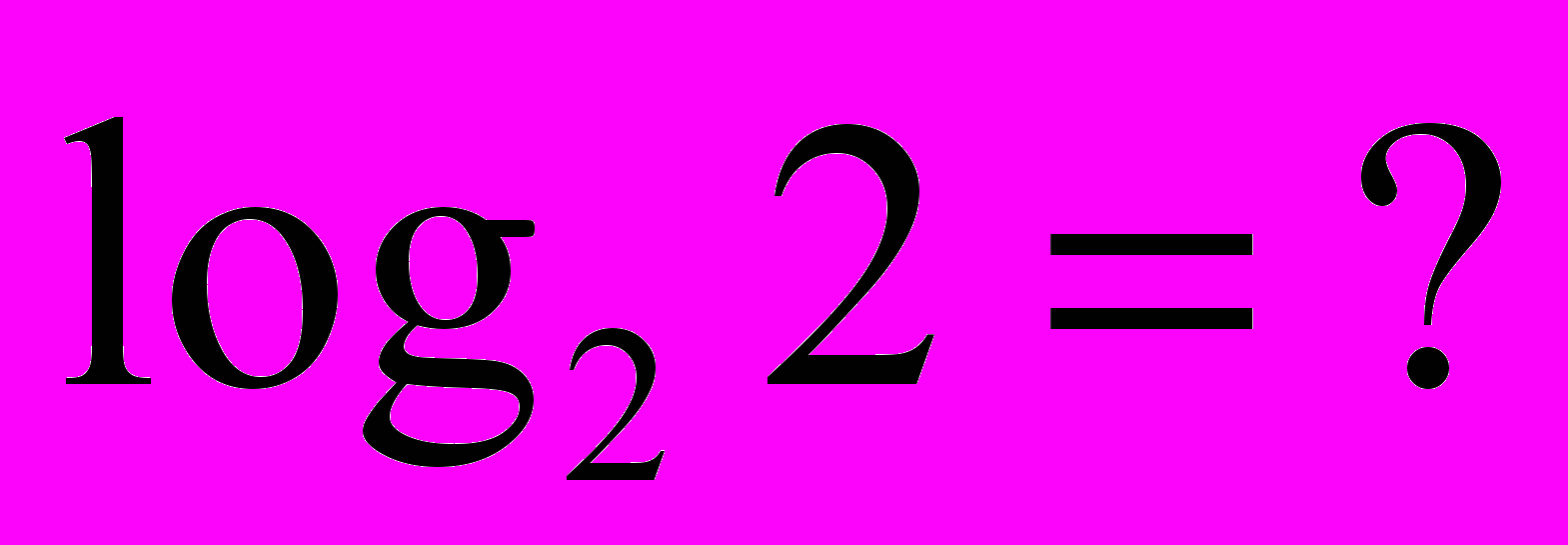 , ,  д) 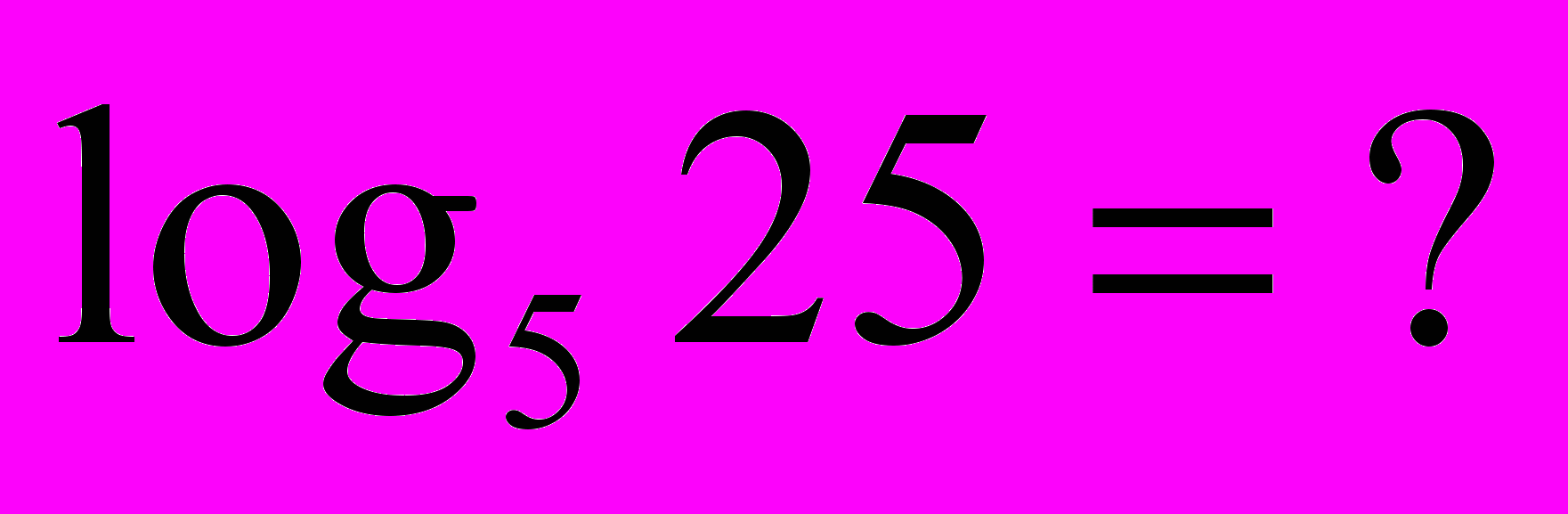 , ,  е) 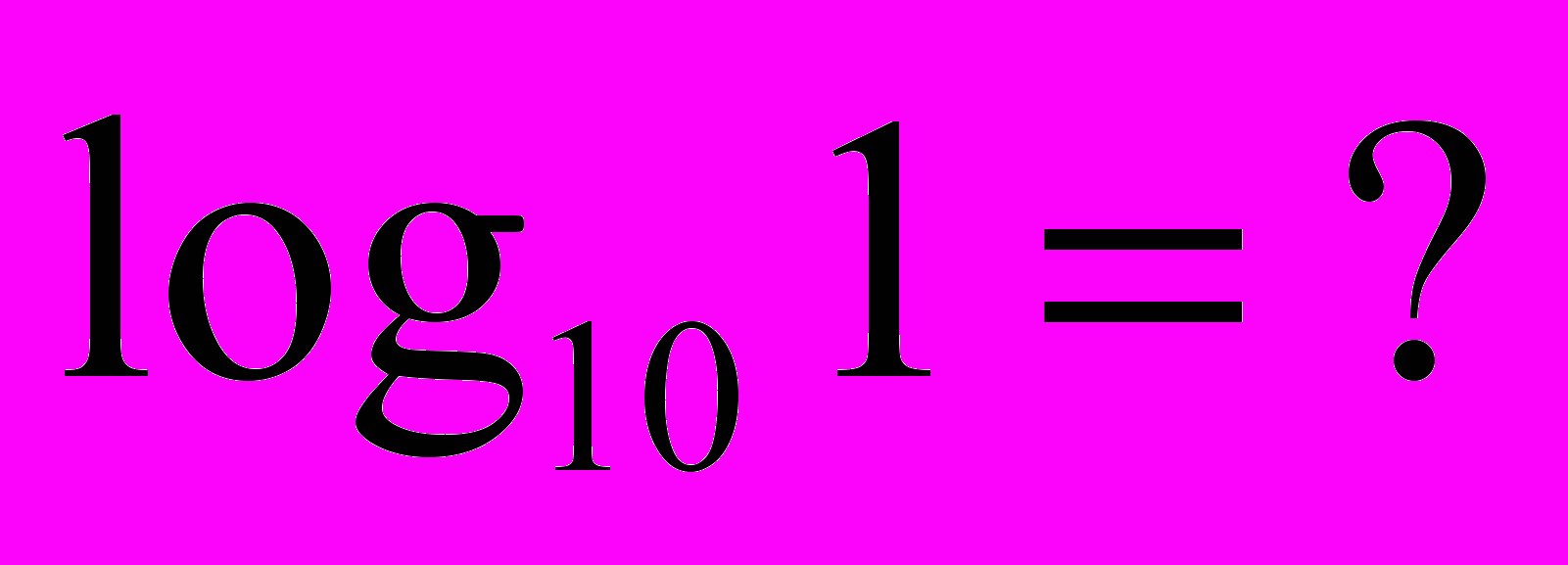 , , 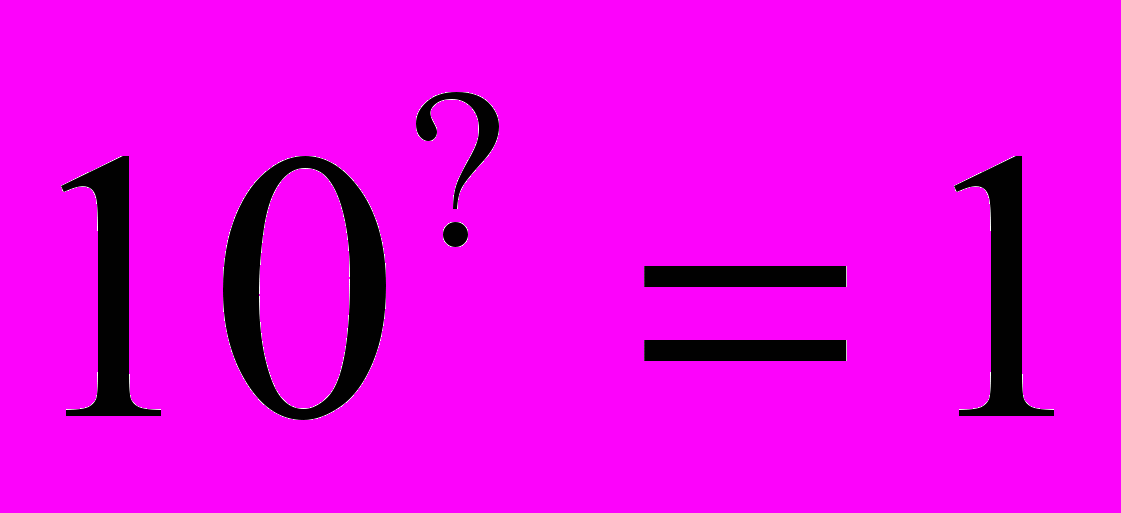 5) Навести приклади (скласти задачі по аналогії): 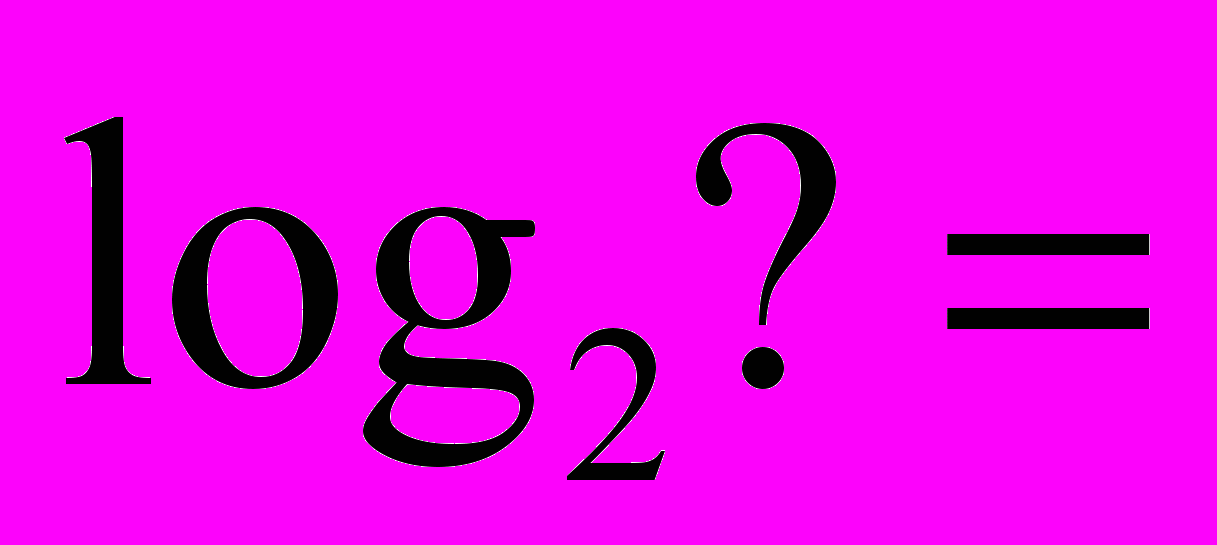 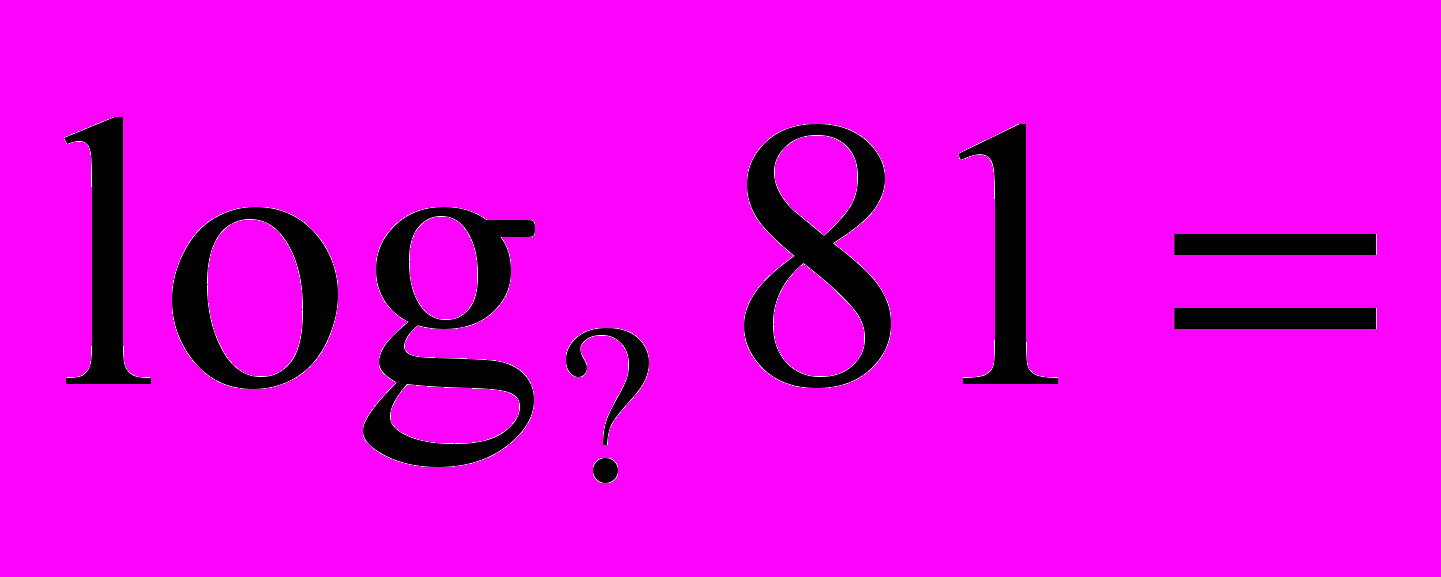  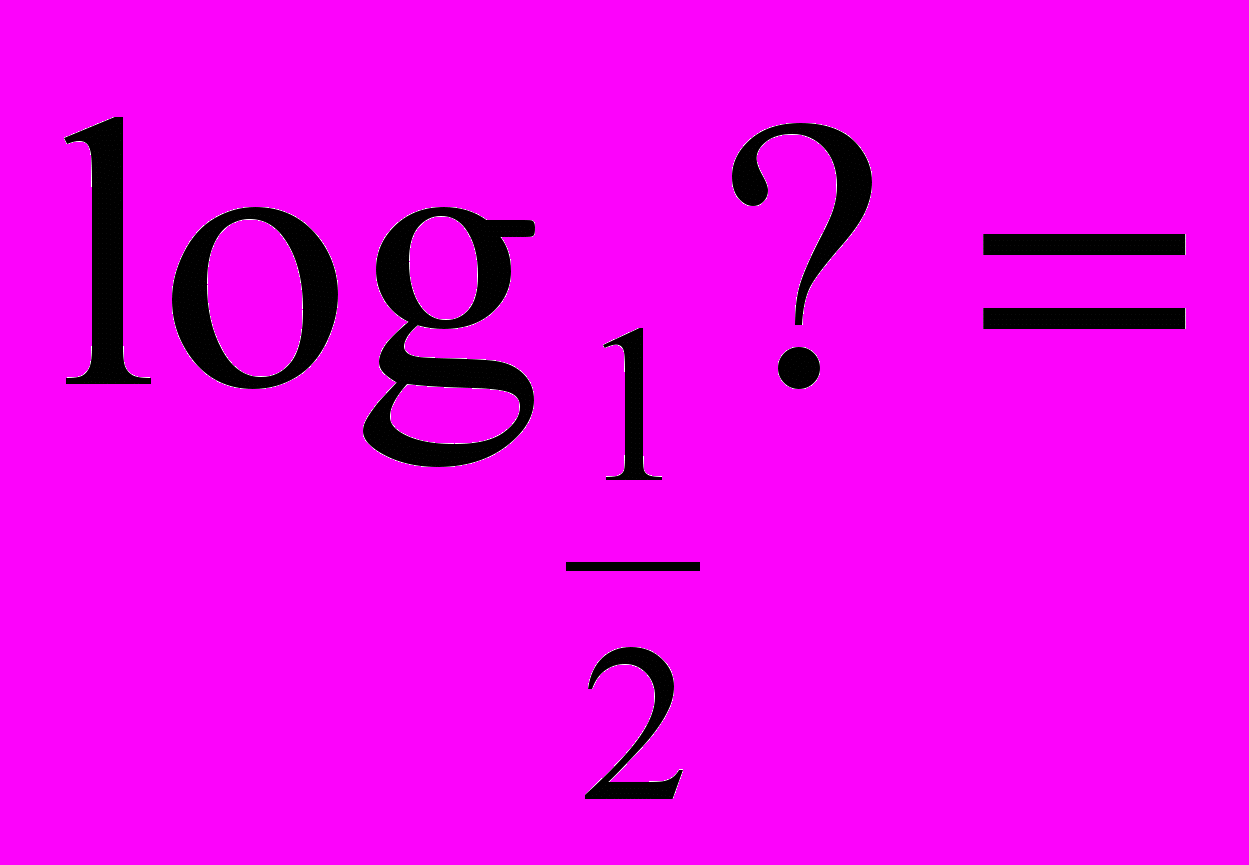 | 2. Основна властивість логарифма числа. («відкриття» теореми). Обчислити і знайти закономірність. 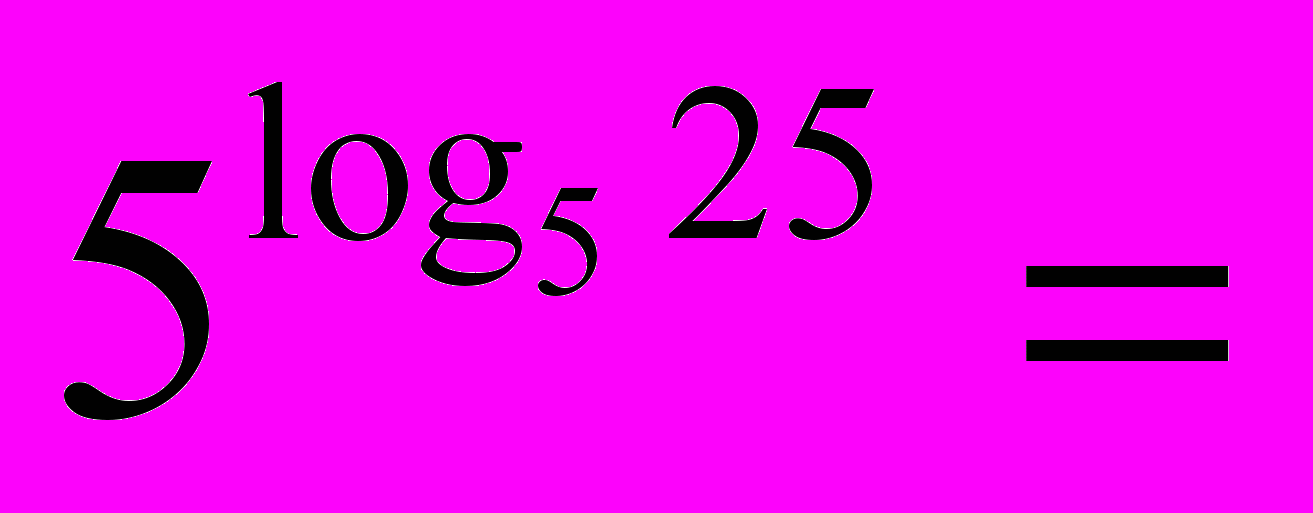 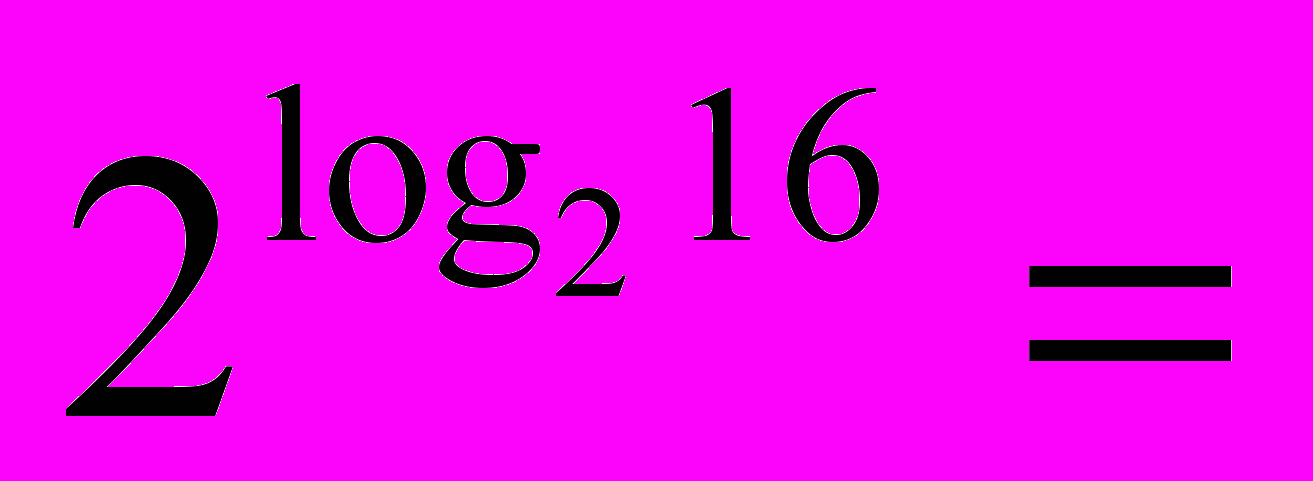 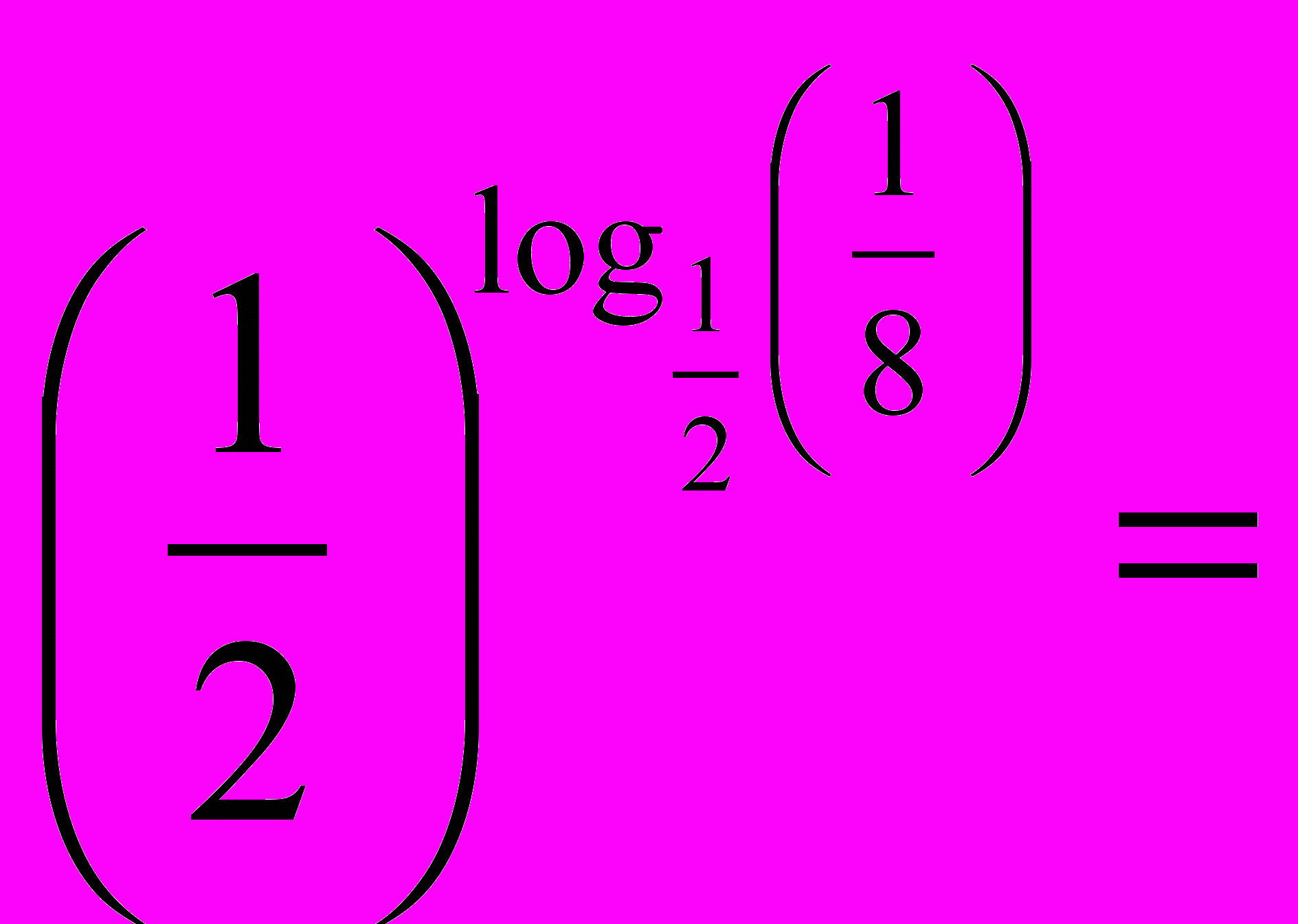 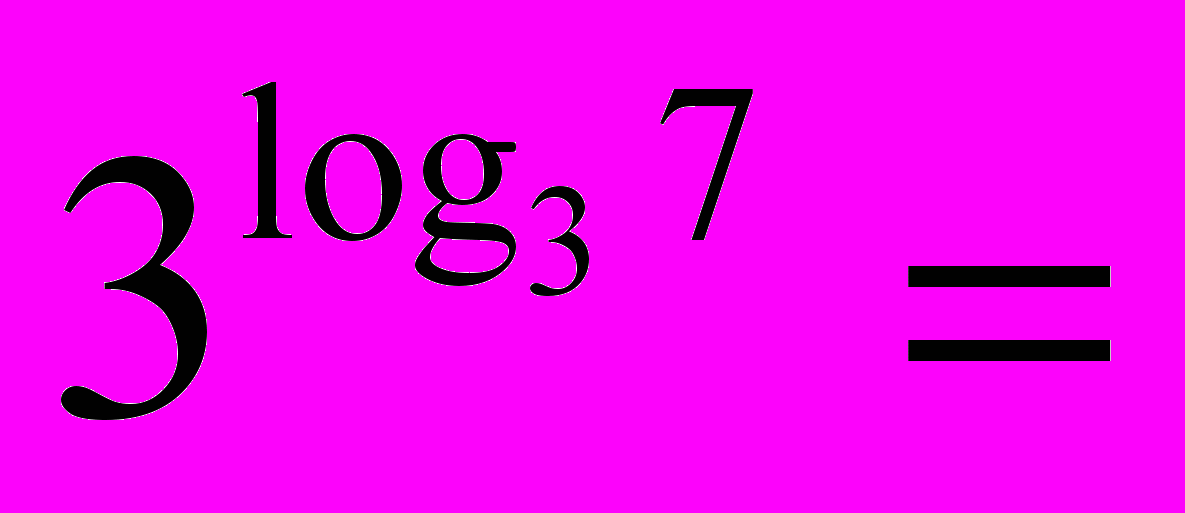 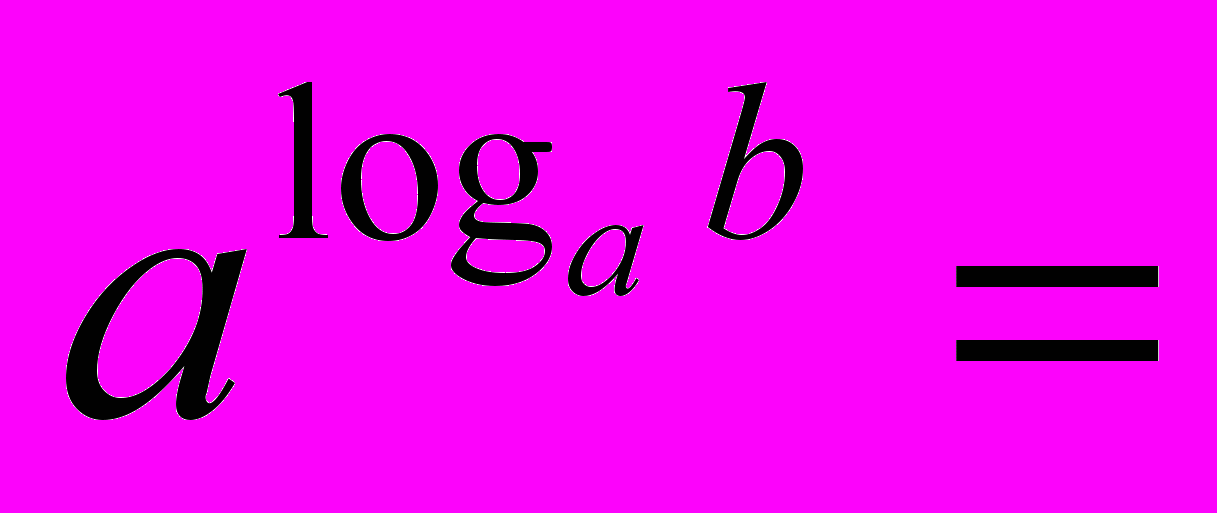 Зробити висновок. Навести приклади (скласти задачі по аналогії). |
| 3. Логарифмічні рівняння. 1) Використовуючи рівність 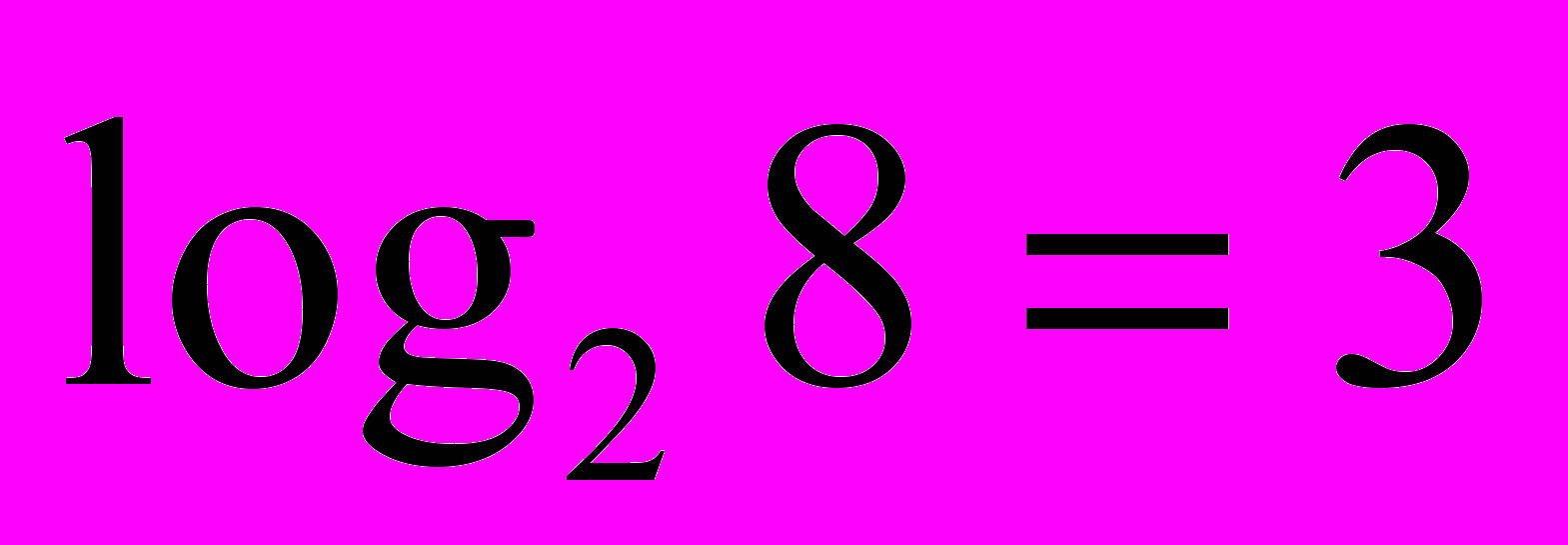 скласти можливі рівняння (складання задачі за деякими елементами, спільними з даною задачею). скласти можливі рівняння (складання задачі за деякими елементами, спільними з даною задачею).  2) Розв’язати запропоновані рівняння (розв’язання «готової» задачі): а) 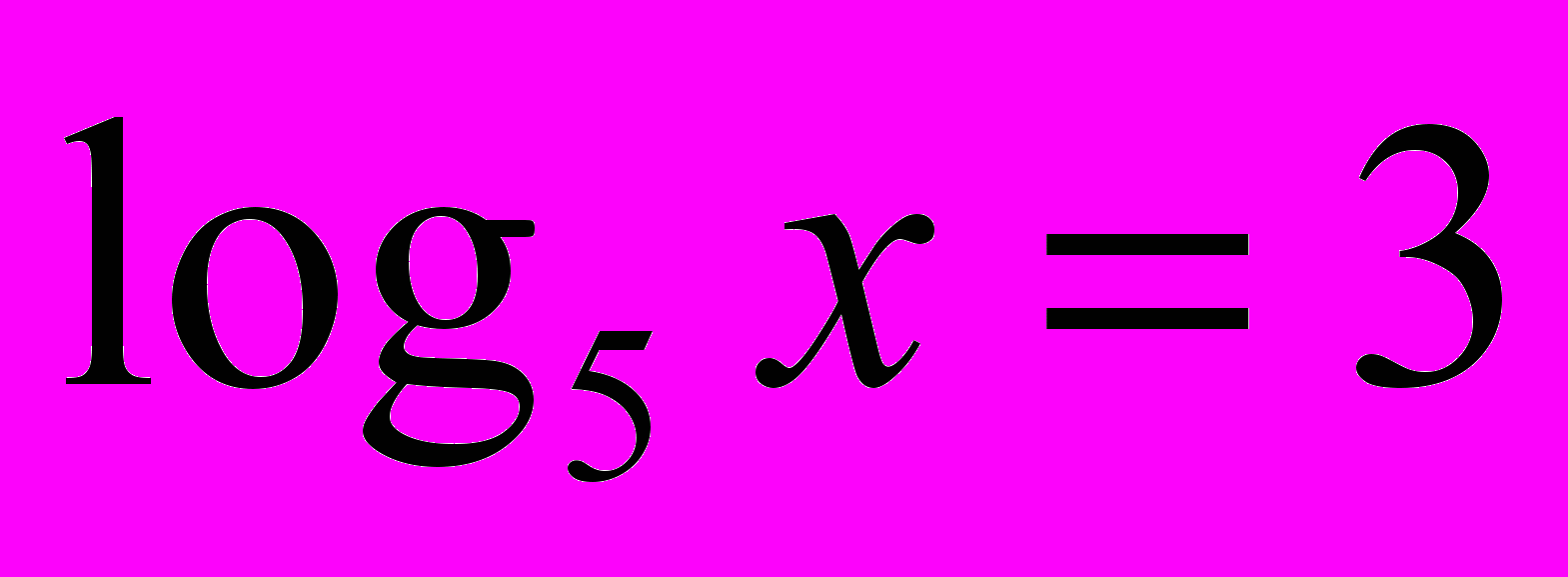 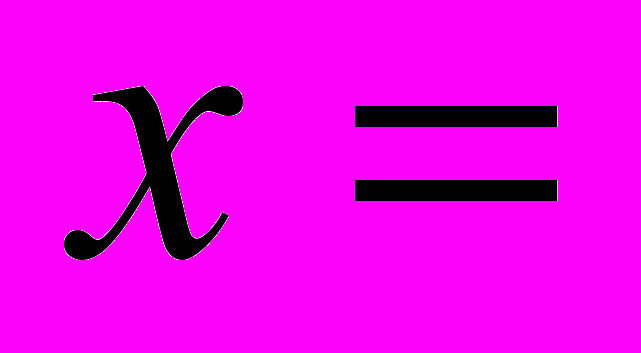 б)  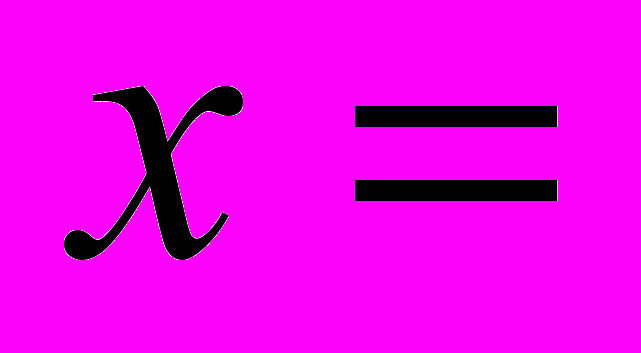 | 4. Логарифмічні нерівності. 1) Порівняти числа і зробити висновок (метод доцільних задач) а) 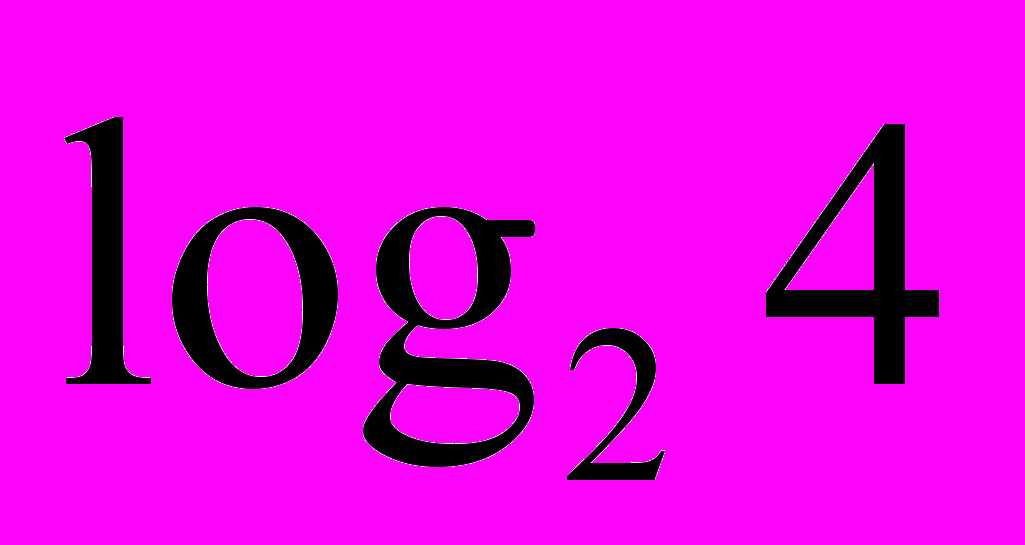 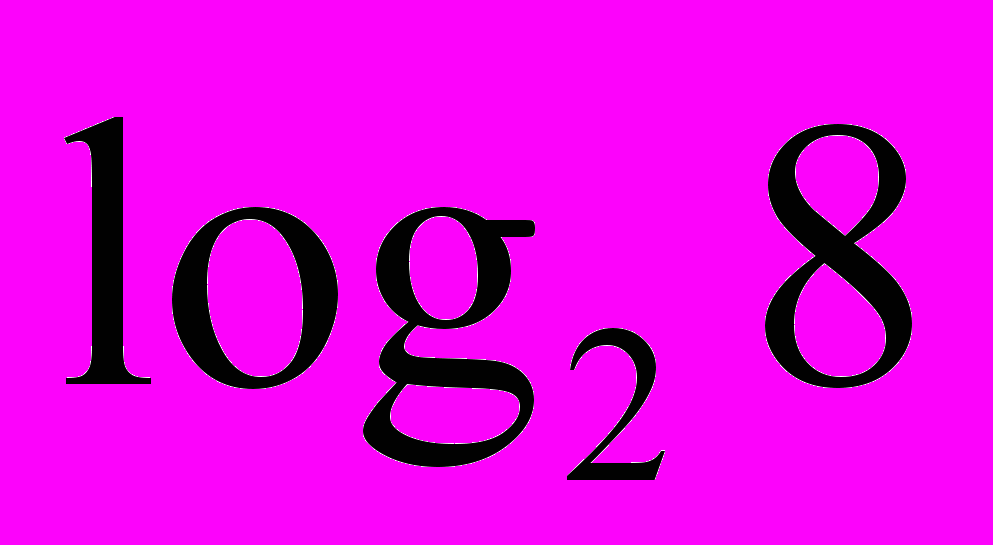 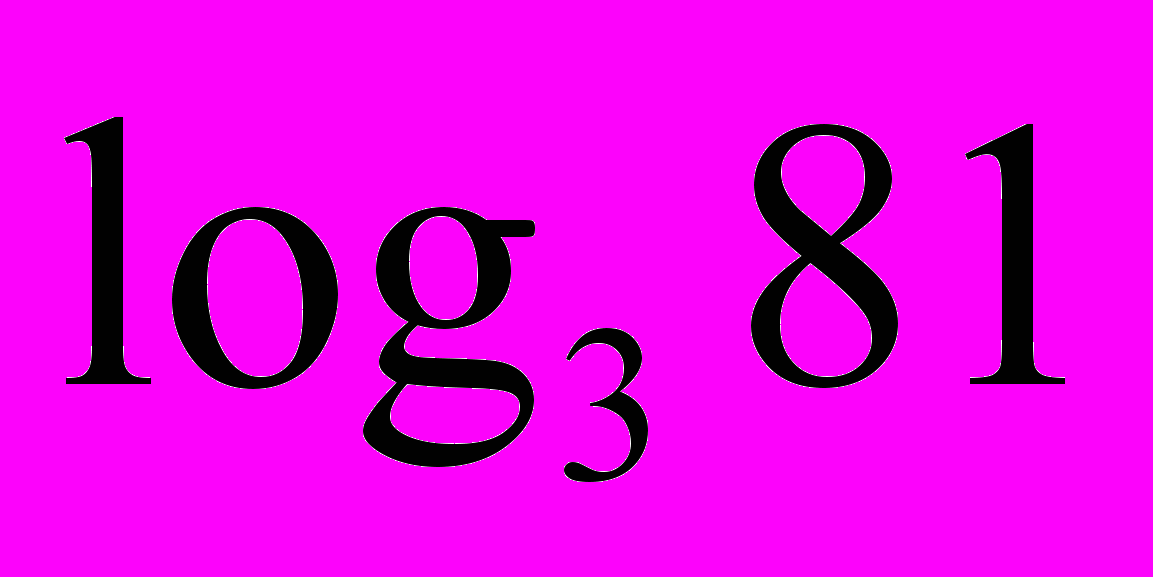 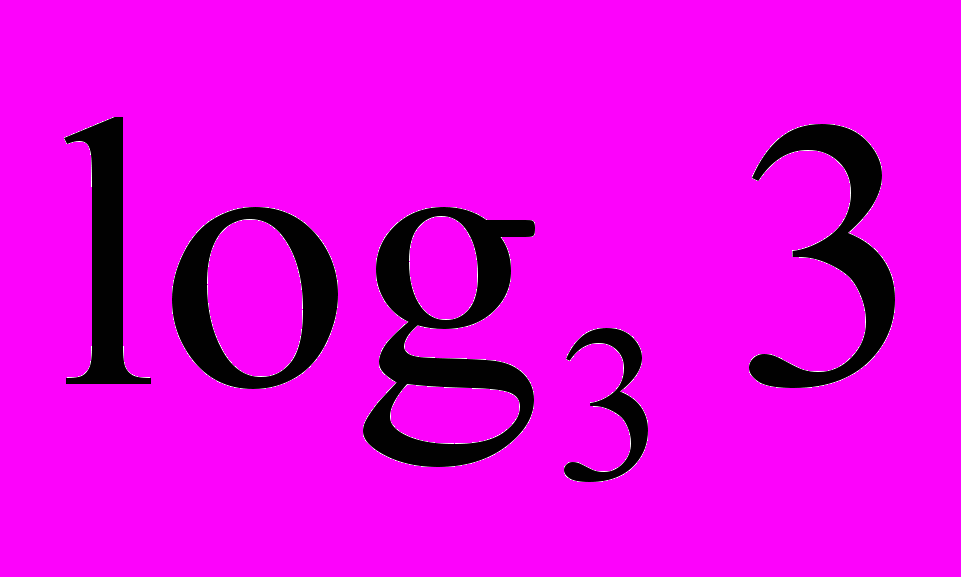 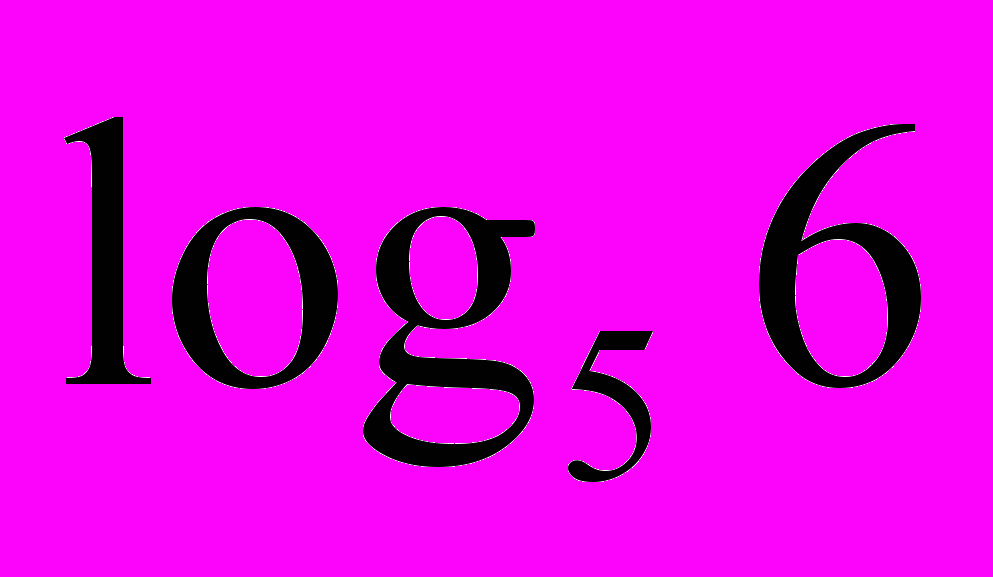 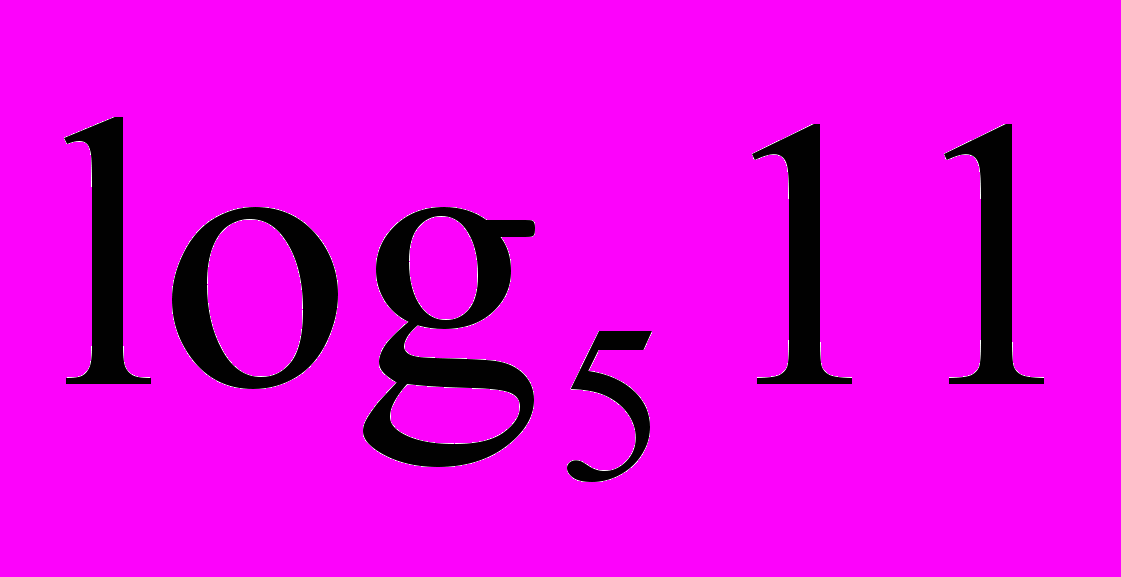 б) 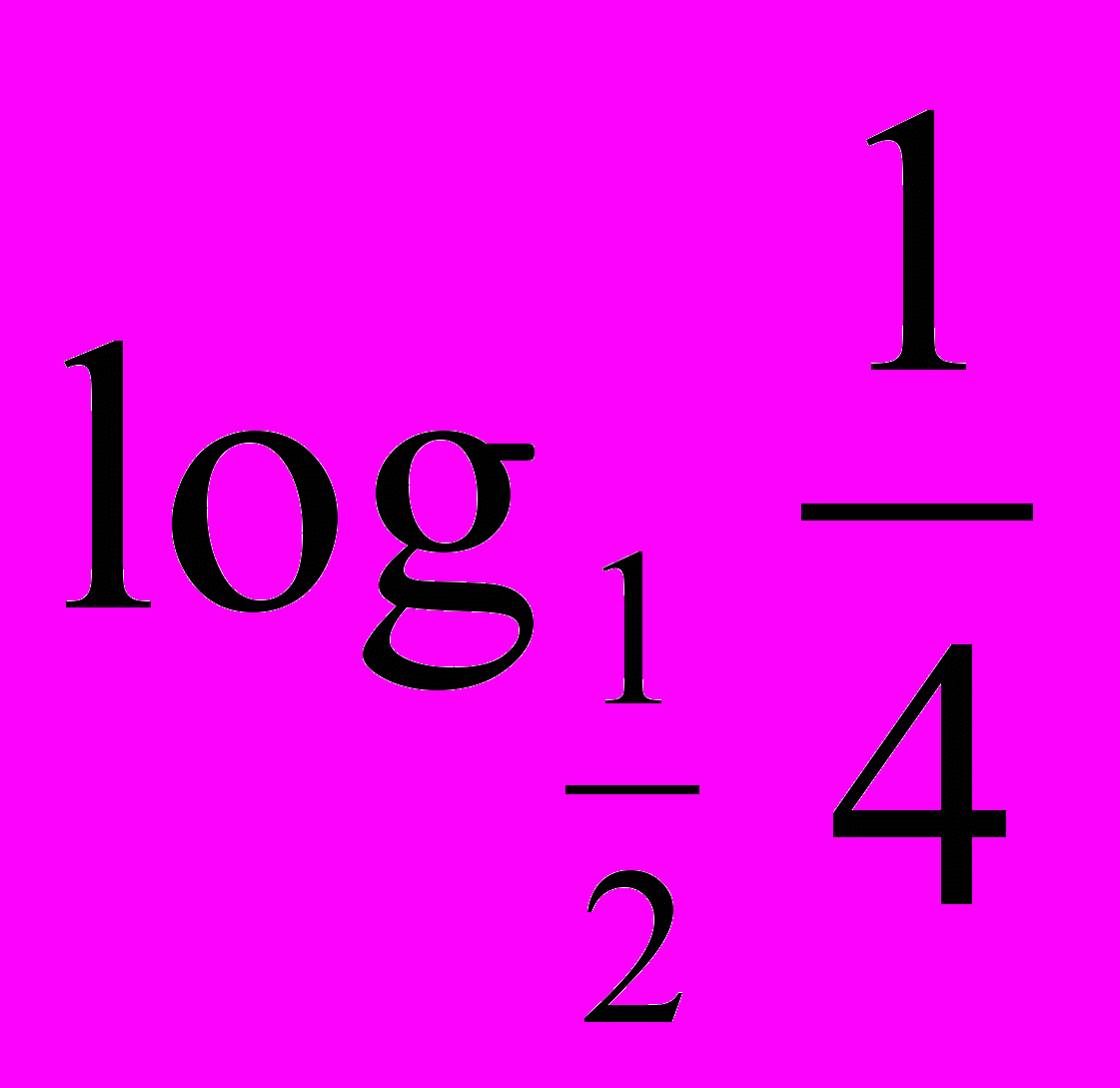 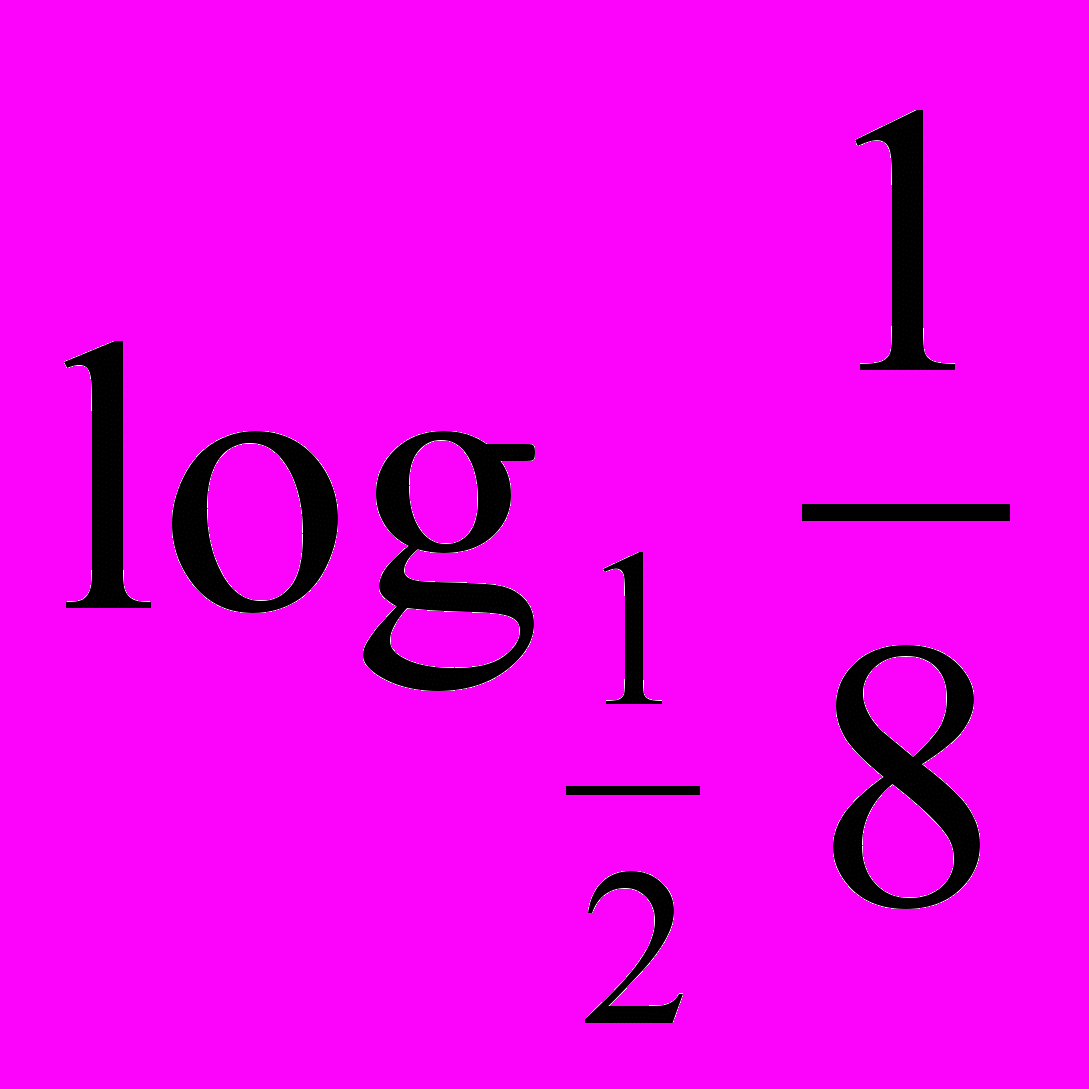 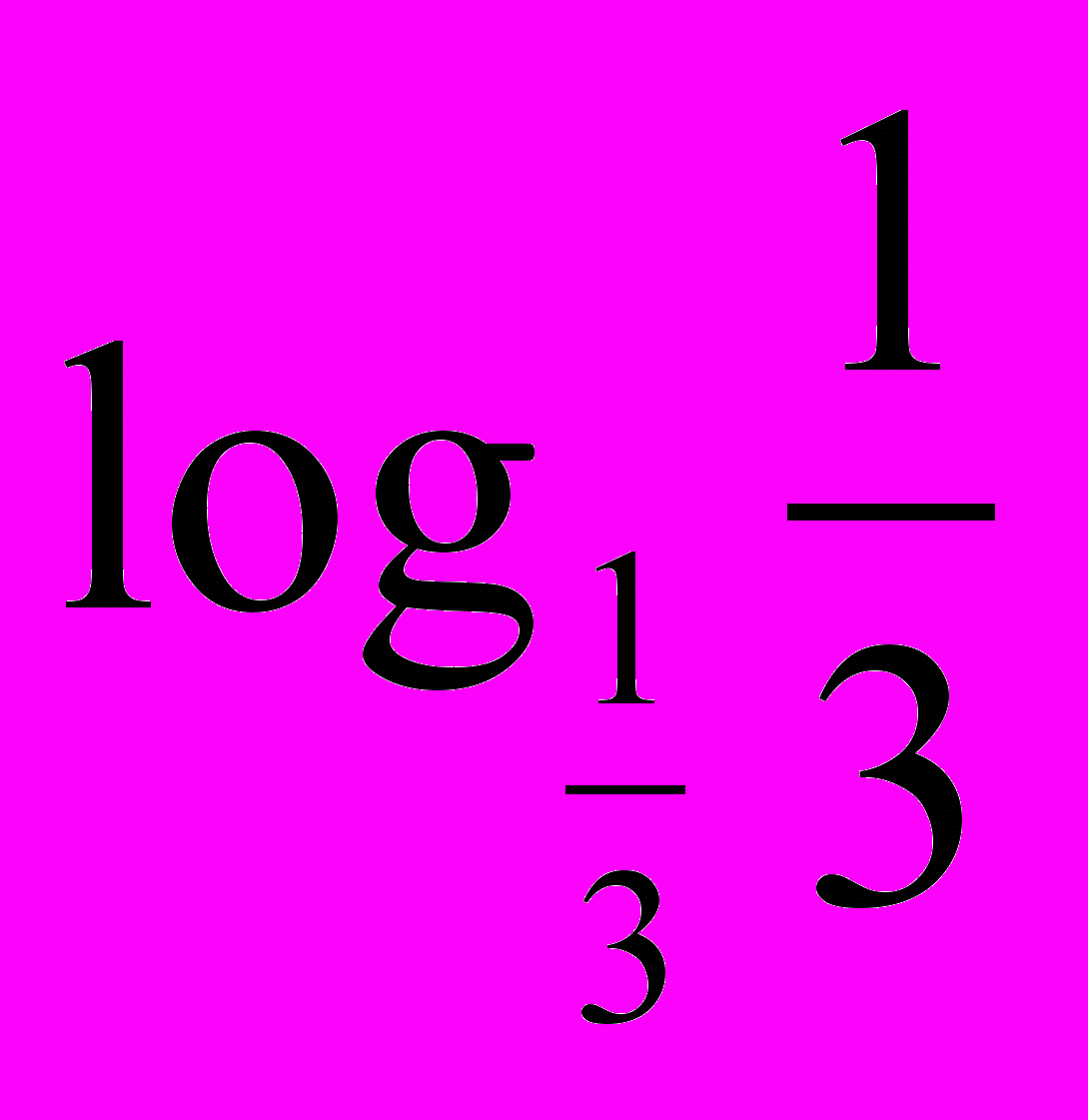 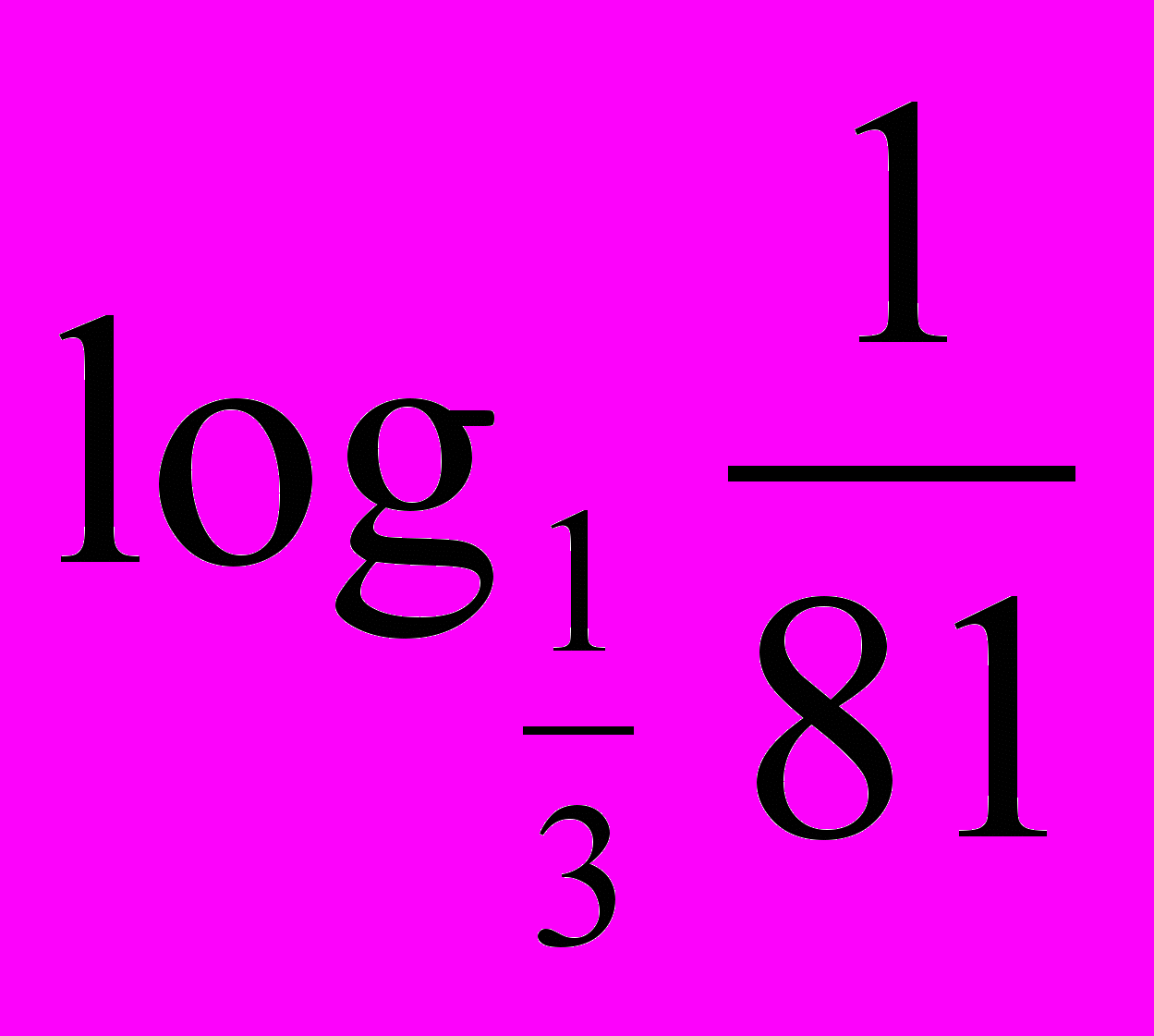  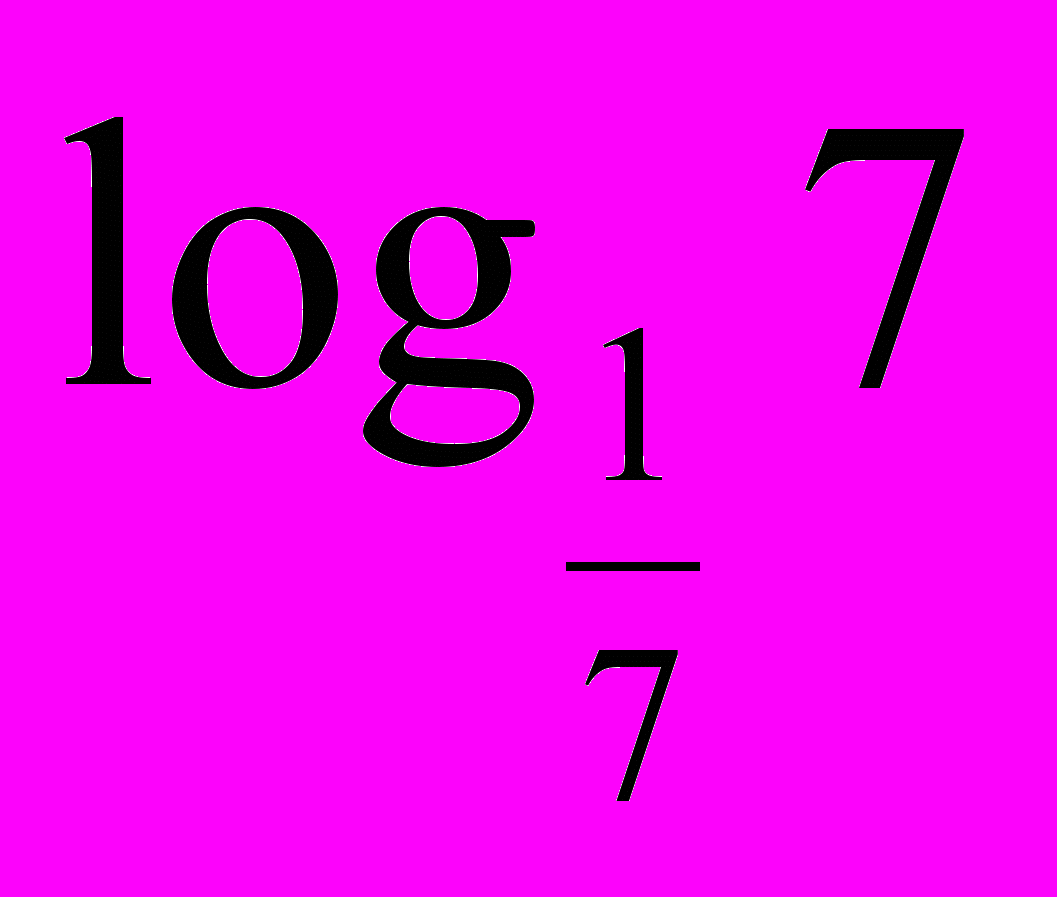 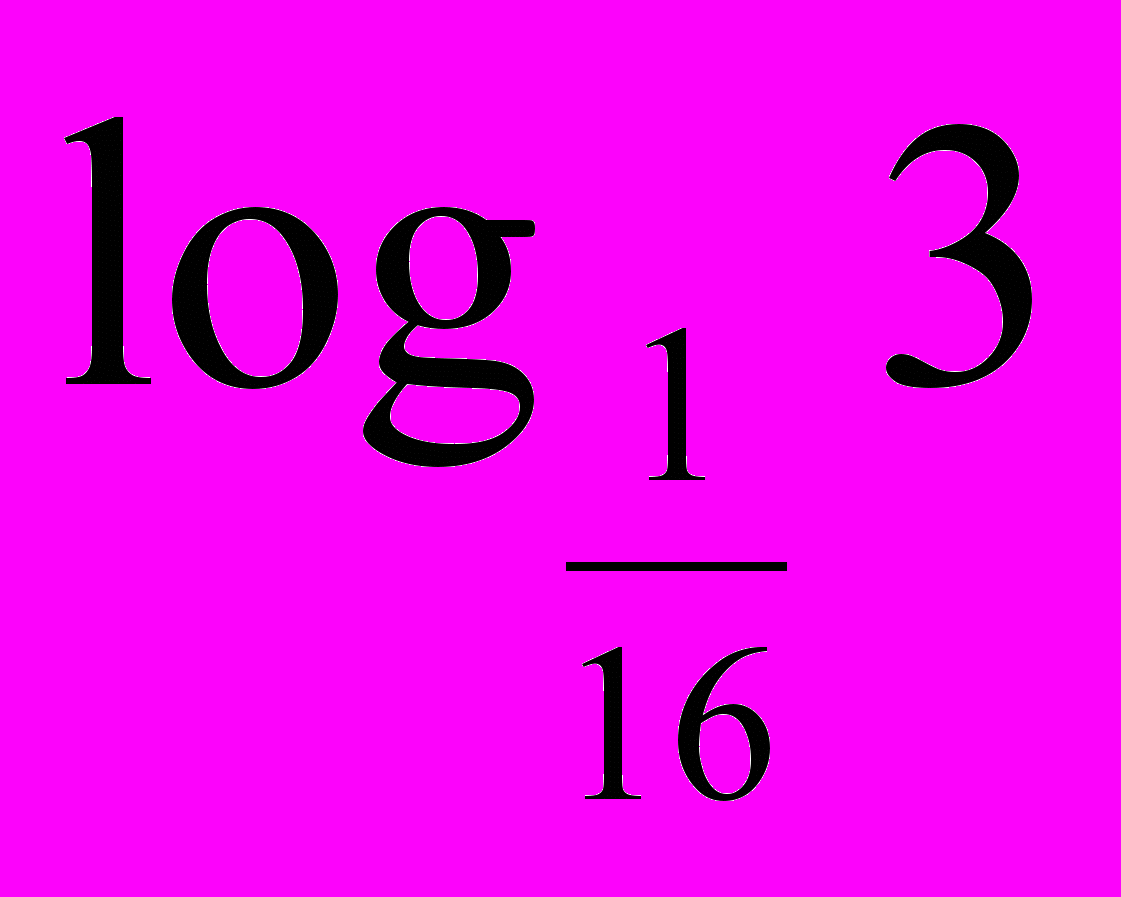 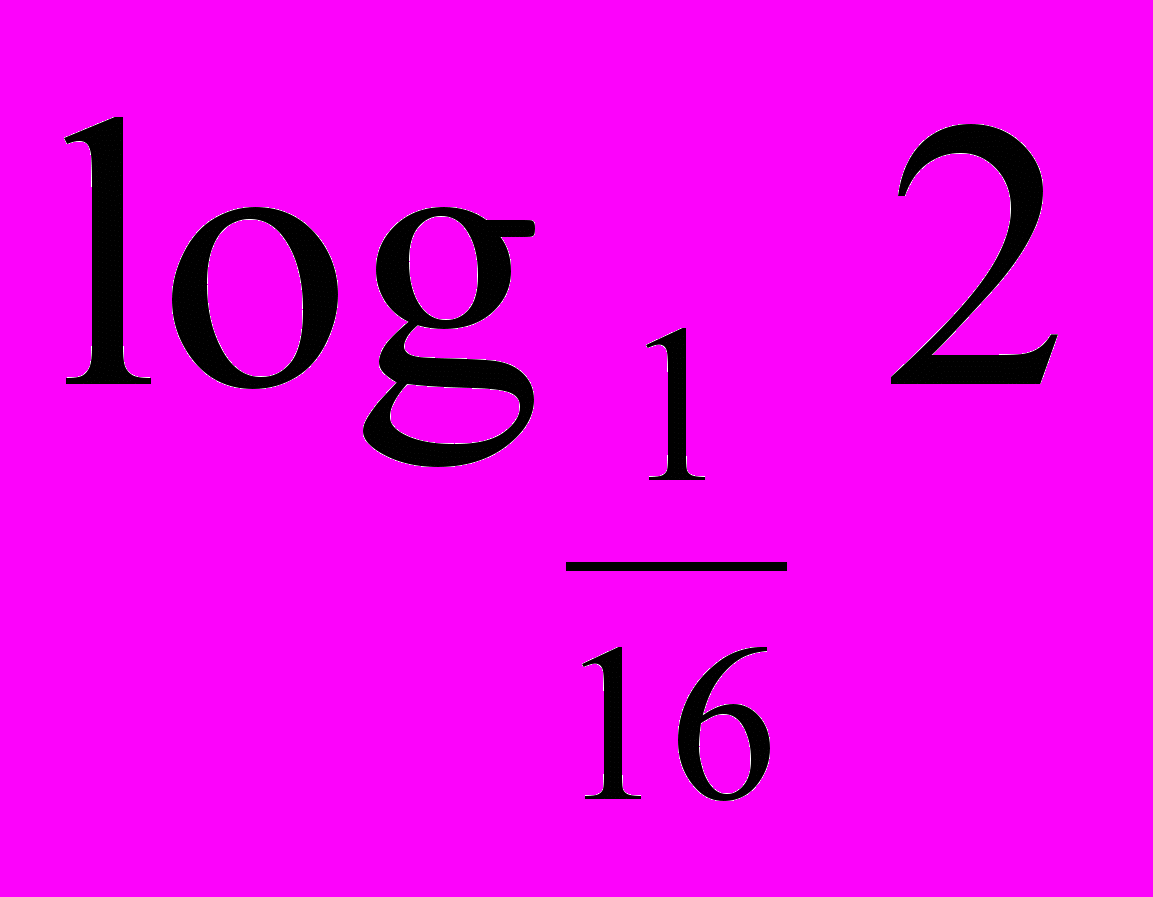 Зробити висновки. Порівняти числа a i b (розв’язання «готової» задачі). 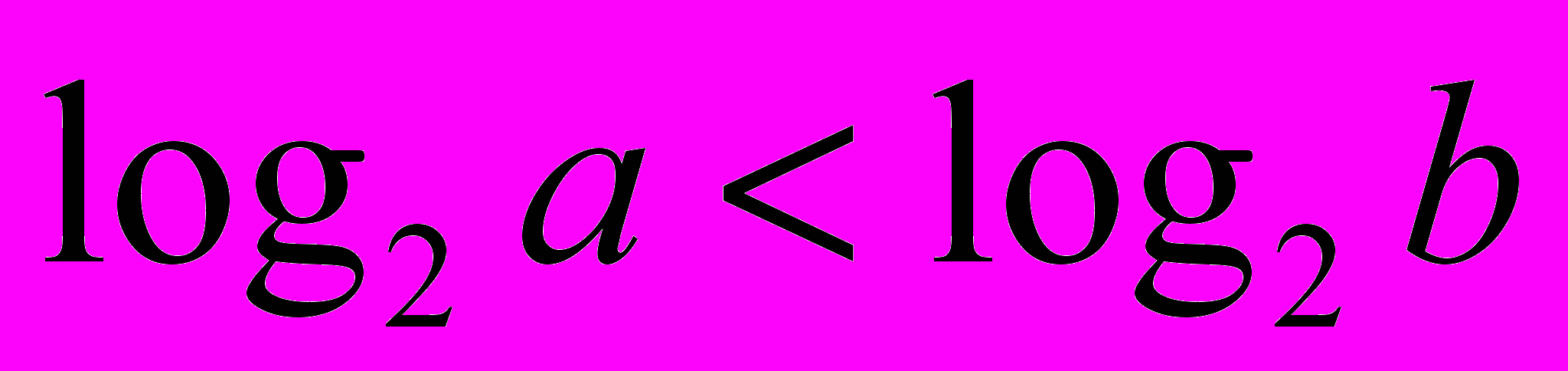 ; ; 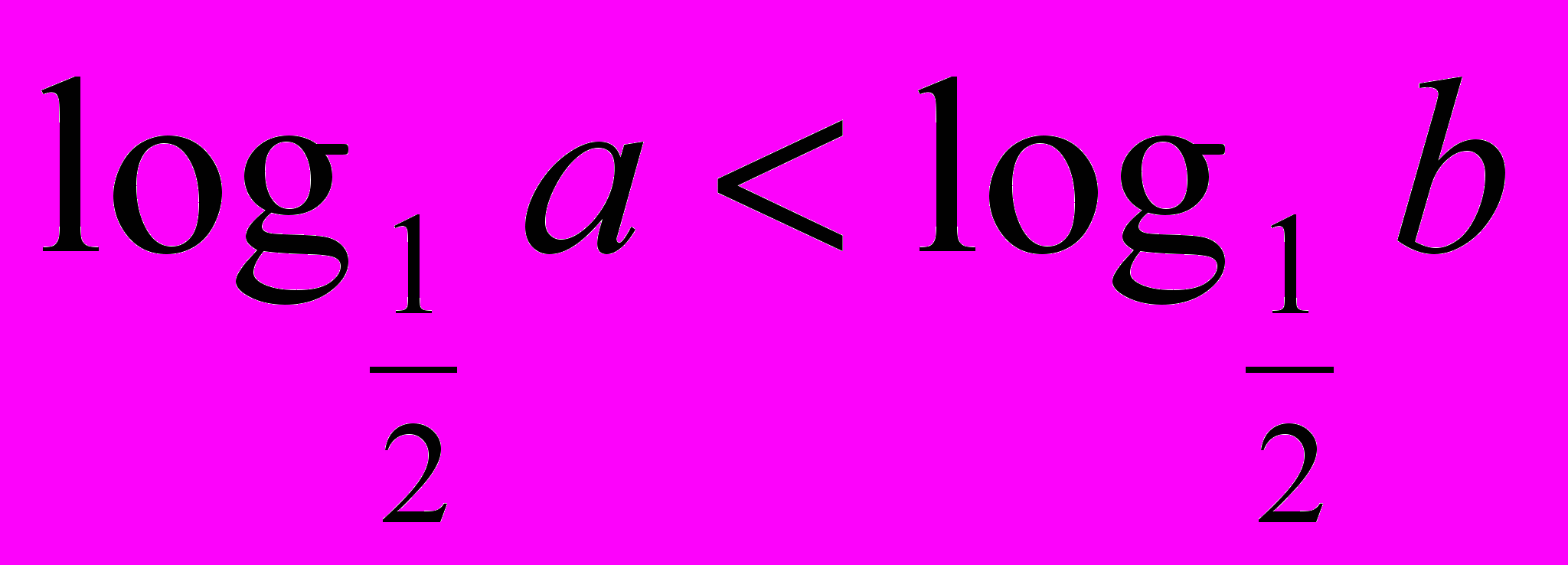 a i b a i b |
ІІІ. Підсумок уроку. Інтерактивне спілкування.
Питання для обговорення:
- З чим познайомилися на сьогоднішньому уроці?
- Що запам’ятали?
- Які прийоми методу «згущення знань» ви спостерігали?
Моделювання навчальної діяльності на основі методу «згущення знань».
Практичні завдання:
- Підготувати вправи для засвоєння учнями переставного закону додавання «Якщо переставити доданки місцями, сума не зміниться» (прийом «відкриття» теореми).
- Завдяки прийому оберненої задачі підготувати учнів до розуміння ділення чисел (дія ділення – це обернена дія множення).
ІІІ. Рефлексивний модуль. Інтерактивне спілкування.
Питання для обговорення:
- Яка практична значимість методу «Згущення знань»?
- Які прийоми методу «Згущення знань» можна запропонувати на інших предметах?
- Прорекламуйте (або подайте антирекламу) метода «згущення знань».
Словник
Доцільні задачі – підготовчі задачі для кращого розуміння нового учбового матеріалу.
Ефективність навчання – міра досягнення навчальної мети, визначається на основі зіставлення мети і здобутих результатів, внаслідок чого робиться
висновок про ефективність навчання.
Знання – перевірені суспільно-історичною практикою результати процесу
пізнання, відображені в свідомості людини у вигляді уявлень, фактів, суджень.
Інновація педагогічна – процес створення, поширення й використання
нових засобів (нововведень) для розв’язання тих педагогічних проблем, які
досі розв’язувались по-іншому.
Мета педагогічної діяльності – свідоме бачення кінцевого результату діяльності, що планується як позитивний перетворювальний вплив на особистість.
Метод навчання – спосіб упорядкованої взаємної діяльності вчителя й учнів, спрямований на розв’язання навчально-виховних завдань.
Навичка – усталений спосіб виконання дій, сформований у результаті багаторазових повторень; характеризується високим рівнем засвоєння і відсутністю свідомої регуляції і контролю (навички рухові, інтелектуальні, перцептивні).
Обернена задача – задача, умовою якої слугує відповідь даної задачі, а відповідь – умовою.
Освіта – процес і результат взаємодії між учителем і учнями, за яким останні оволодівають всіма компонентами змісту навчання, розвиваються і виховуються.
Оцінка – оцінні судження в усній та писемній формі щодо якості певної діяльності; бали – кількісні вимірники, які визначаються нормами оцінок; поєднання балів і оцінних суджень вчителя.
Поєднання методів навчання – вибір та застосування методів навчання з урахуванням їх доповню вальних можливостей для ефективного досягнення конкретної навчальної мети.
Укрупнена дидактична одиниця – це клітинка навчального процесу, що складається з логічно розрізнених елементів, які володіють у той же час інформаційною спільністю. Укрупнена дидактична одиниця володіє якістю системності і цілісності, стійкістю до збереження в часі і швидкому виявленню в пам'яті.
Література
- Бевз Г.П. Методи навчання математики. – Харків: Основа, 2003.
- Бухлова Н.В. Організація самоосвітньої діяльності учнів. – Харків: Основа, 2003.
- Груденов Я.И. Совершенствование методики работы учителя математики. – М: Просвещение, 1990.
- Подмазин С.И. Личностно ориентированное образование. – Запорожье: Просвіта, 2000.
- Програма для загальноосвітніх навчальних закладів. Математика 5-11 класи (від 22.08.2001).
- Програма для загальноосвітніх навчальних закладів. Математика 5-12 класи. – К.: Ірпінь, 2005.
- Програми для загальноосвітніх навчальних закладів. Математика. – К.: Навчальна книга, 2003.
- Программы по математике для 5-11 классов средней общеобразовательной школы. – К.: Освіта, 1992.
- Программы по математике для 5-11 классов средней общеобразовательной школы. – К.: Радянська школа, 1989.
- Слєпкань З.І. Методика математики: Підруч. для студ. мат. спеціальностей пед. навч. закладів. – К.: Зодіак-Эко, 2000.
- Слєпкань З.І. Психолого-педагогічні та методичні основи розвивального навчання математики. – Тернопіль: Підручники і посібники, 2006.
- Хуторской А.В. Развитие одаренности школьников. – М.: Владос, 2000.
- Шаталов В.Ф. Куда и как исчезли тройки. – М.: Педагогика, 1979.
- Эрдниев П.М., Эрдниев Б.П. Укрупнение дидактических единиц в обучении математике. – М: Просвещение, 1986.