Geum.ru

Випадкові процеси

Вид материалаДокументы
1 Вхідні дані
5 Моделювання випадкової величини методом неймана-пирсона
3 Чисельне рішення задач теорії ймовірностей методом монте-карло
1 Умова задачі
4 Моделювання систем масового обслуговування
Подобный материал:
1   2   3   4



2.4.4 Побудова програми для моделювання

а) Описання алгоритму наведено у підрозділі 4.4 лекційного курсу.

б) Студент має право побудувати програму на всякій мові програмування, за його вибором. Але підсумкові результати повинні бути перенесені на робочий аркуш Excel для подальших розрахунків. Нижче наведено варіант листингу програми генерації на мові VBA для Excel.


Sub Генератор_Гистограмма()

''

Randomize

'**** Початок циклу розрахунків *****

For k = 1 To 2000

'****Генерація випадкового числа

a_rand = Rnd

'**** Вибір інтервалу за допомогою селектору***

Select Case a_rand

Case 0 To 0.3065

in_l = 1

Case 0.3065 To 0.6565

in_l = 2

Case 0.6565 To 0.8515

in_l = 3

Case 0.852 To 0.9325

in_l = 4

Case 0.9325 To 0.9695

in_l = 5

Case 0.9695 To 0.9885

in_l = 6

Case 0.9885 To 0.9955

in_l = 7

Case 0.9955 To 0.997

in_l = 8

Case 0.997 To 0.9995

in_l = 9

Case 0.9995 To 1

in_l = 10

End Select

'MsgBox a_rand & " " & in_l ' Відладочний оператор

'**Генерація випадкового числа всередині інтервалу**

aa = 11 * (in_l - 1) + 11 * Rnd

'*** Округлення до дісятих

aa = Int(10 * aa) / 10

'*** Розміщення результату на робочому аркуші***

Cells(3 + k, 2) = aa

Next k

End Sub


2.4.5 Розрахунок частот по генерованої вибірці.

а) Пускаємо програму на виконання розрахунків

б) Копіюємо одержані дані

в) Влучаємо їх на робочий аркуш з проектом обробки вибірки (див.2.4.3), замість заданої вибірки. Рекомендується попереднє скопіювати проект на новий робочий аркуш

г) Після влучення автоматично одержуємо нові абсолютні частоти для даної вибірки.

2.4.6 Перевірка гіпотези про однаковий розподіл. Дані для абсолютних частот влучення у інтервали наведено у таблиці 2.2 . Розрахунки проводимо за формулою (2.1) при n1=n2=2000, у середовищі Excel. Пропонується студентам самостійно скласти таблицю розрахунків за формулою (2.1).

Як випливає з результатів таблиці 2.2, критичне значення критерію Пирсона значно перевищує те, що спостерігається. Тому немає підстав відкинути гіпотезу про однорідність розподілу. Можна вважати, що програма-генератор генерує випадкові числа за тім ж самим законом, що наявний у заданої вибірці.

Таблиця 2.2



Интер-
вал
m1i
m2i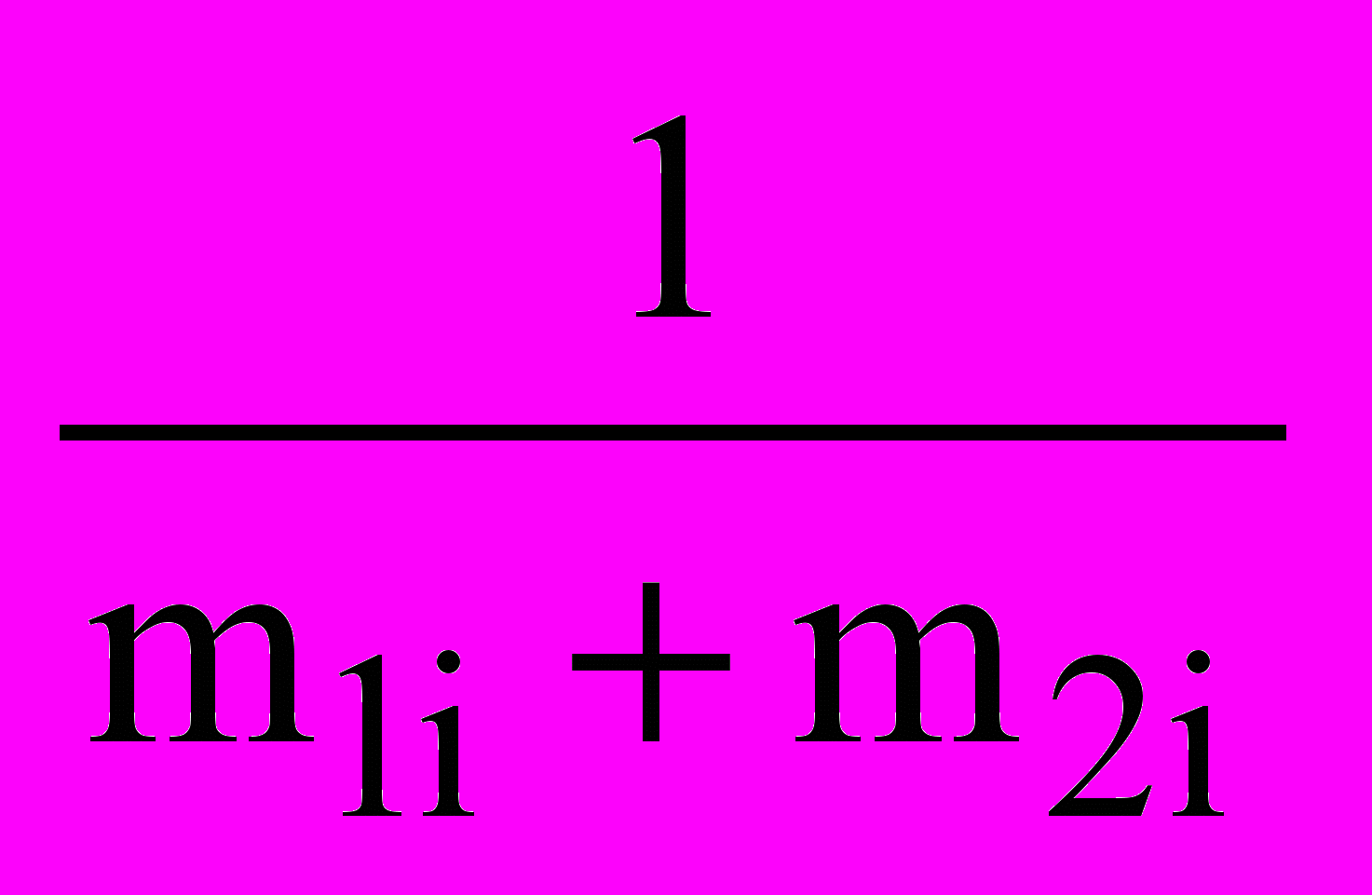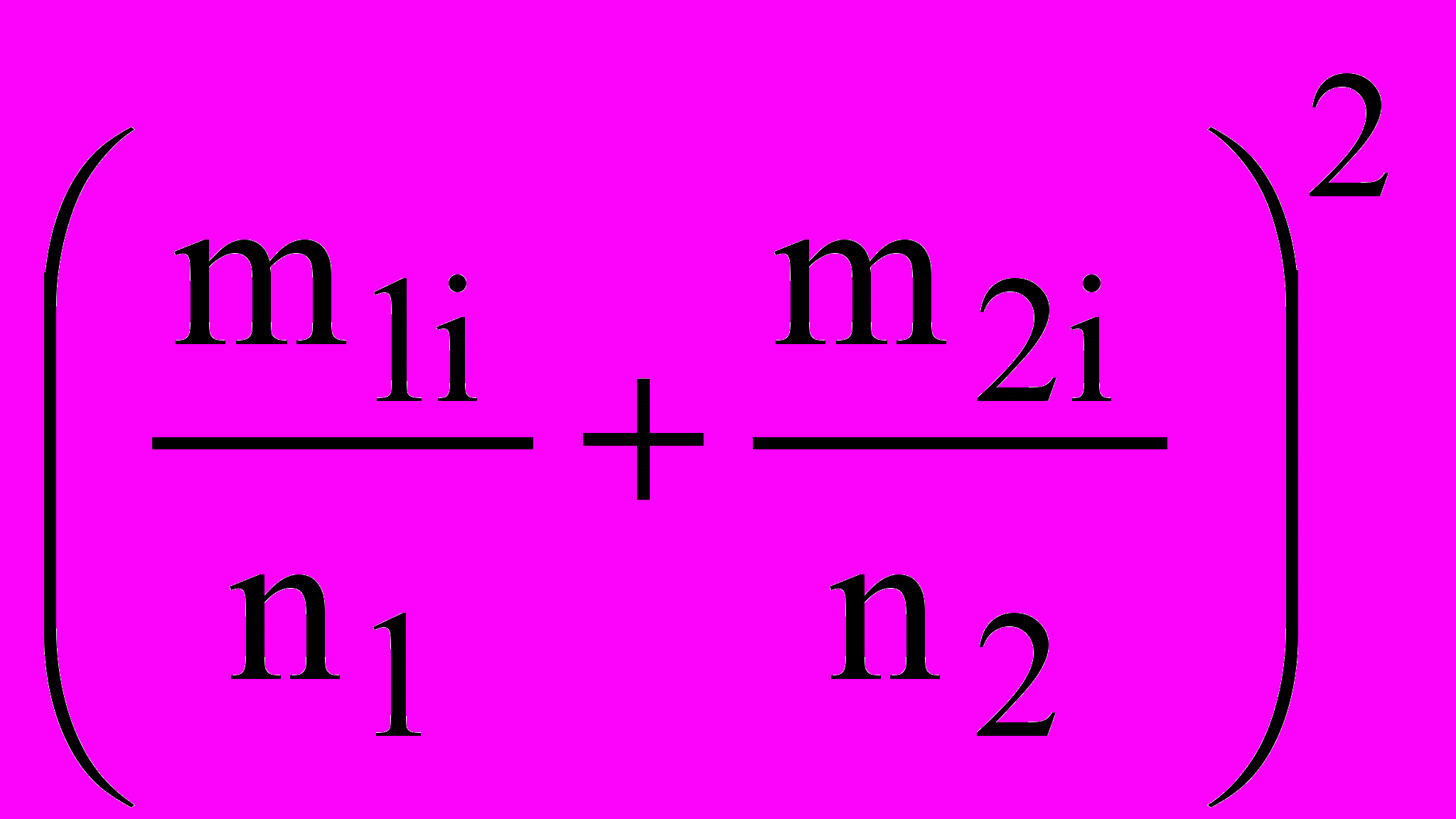




Добуток

1
613
597
0,000826
0,000064
5,2893E-08

2
700
699
0,000715
2,5E-07
1,787E-10

3
390
385
0,00129
6,25E-06
8,0645E-09

4
162
178
0,002941
0,000064
1,8824E-07

5
74
72
0,006849
0,000001
6,8493E-09

6
38
46
0,011905
0,000016
1,9048E-07

7
14
8
0,045455
0,000009
4,0909E-07

8
3
3
0,166667
0
0

9
5
4
0,111111
2,5E-07
2,7778E-08

10
1
1
0,5
0
0

 
 
 
 
Сума
8,8357E-07

Ст волі
розр
кр


Висновок

9
3,5343
16,9
0,05
Різниця не значима



2.4.7 Друга частина завдання – генерація випадкової величин, що мають задану аналітичну функцію розподілу. Задана густина розподілу на відрізку [0;2]:


(2.2)


2.4.7.1 Спочатку найдемо А:


а) Розрахуємо інтегральну функцію розподілу для інтервалу [0;2]:


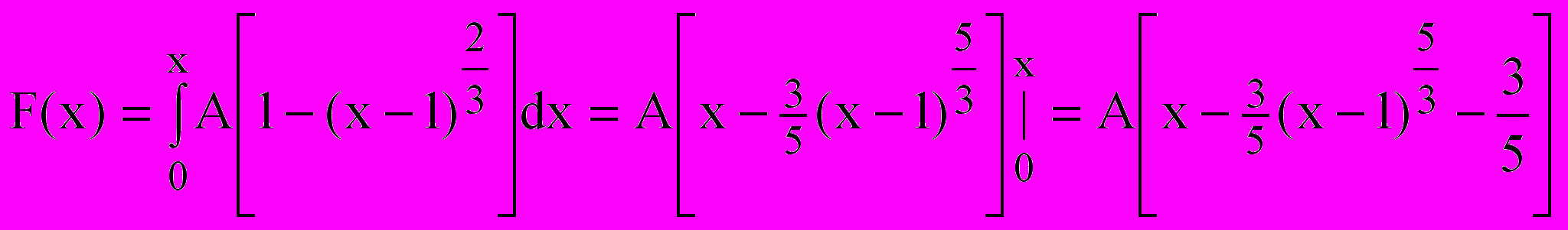. (2.3)


б) Підставимо х=2, знайдемо множник А з умови F(2)=1:





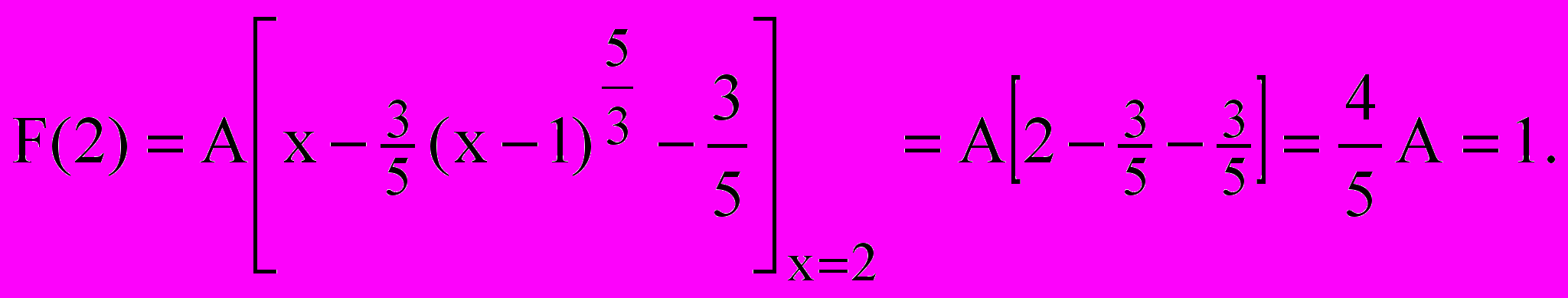
Звідси А=5/4, кінцевій вигляд диференціальної та інтегральної функцій розподілу:


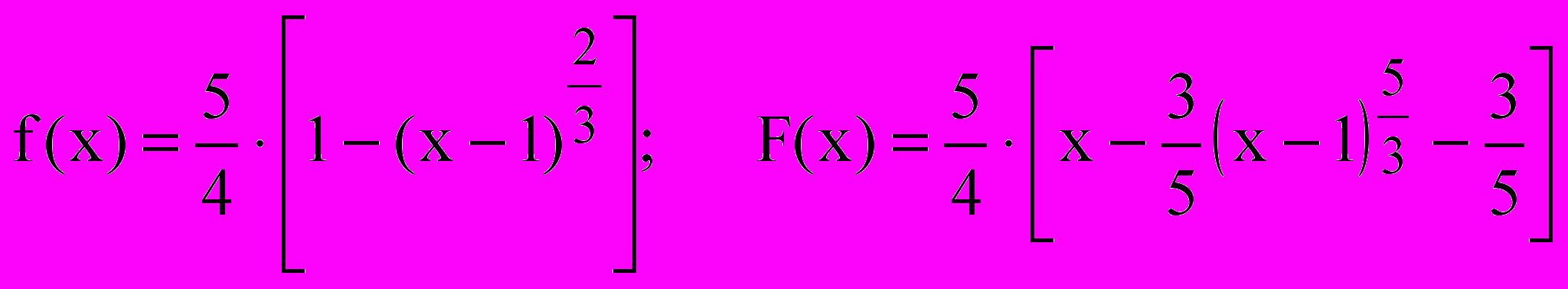. (2.4)


в) Будуємо в Excel графіки обох функцій (рис. 2.2 ).

2.4.7.2 Загальний алгоритм генерації випадкових чисел методом зворотних функцій:

а) Генеруємо рівномірно розподілене випадкове число R (0,1).

б) Знаходимо необхідне випадкове число Х, як рішення рівняння:

F(X) = R, (2.5)


де F(X) – задана інтегральна функція розподілу.

У прикладі, що розглядається, слід знайти рішення рівняння:


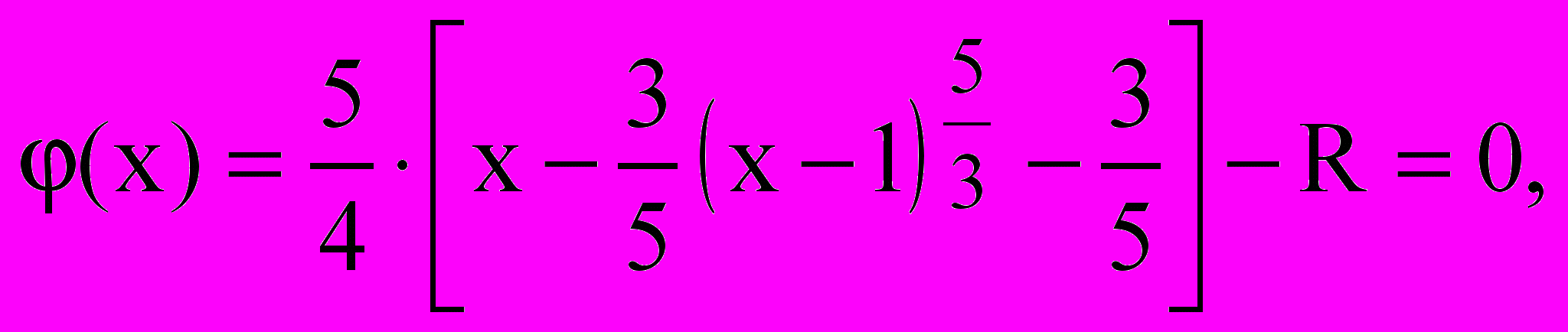(2.6)


причому, з області визначення перемінної, х[0;2].

2.4.7.3 Вважаючи, що функція (2.6) є складною і може мати корені, що не належать ОДЗ, для запобігання знаходження “фіктивного” кореню доцільно використовувати метод дихотомії (половинного ділення), який не виводить за межі ОДЗ х[0;2]. Нагадаємо алгоритм цього методу:

а) Задаємо ліву (a) та праву (b) границі ОДЗ , потрібну точність eps.

б) Перевіряємо, чи виконується нерівності f(a)<0, f(b)>0. Якщо виконуються протилежні нерівності – міняємо місцями а та b.





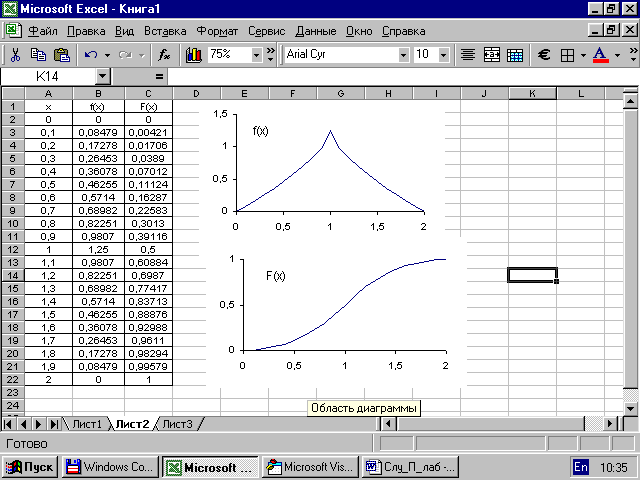
Рисунок 2.2 – Графіки диференціальної та інтегральної функцій розподілу


в) Розраховуємо :


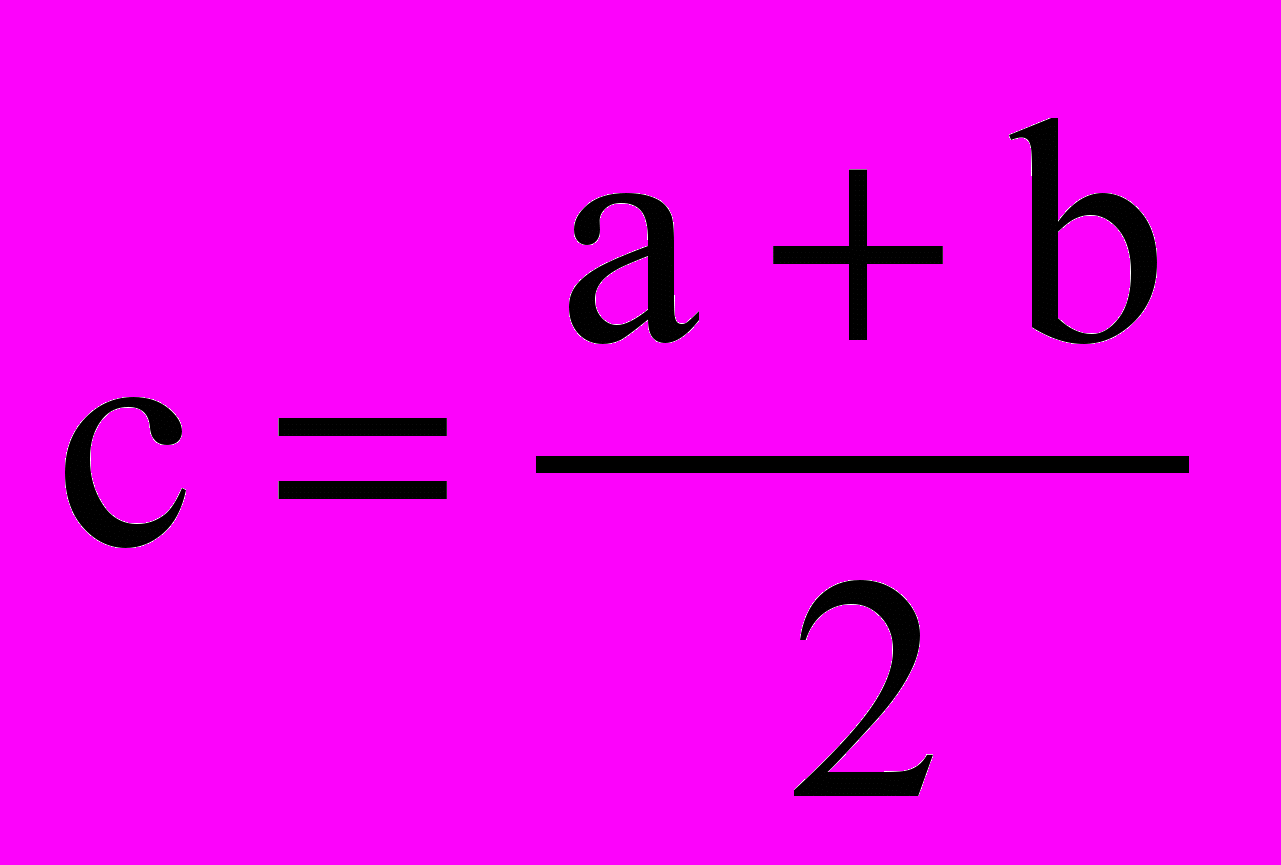(2.7)


г) Перевіряємо виконання умови:


|b-a|

Якщо (2.8) виконується – вважаємо с за рішення, кінець задачі.

д) Якщо умова (2.8) не виконується – перевіряємо умову :

f(c) > 0. (2.9)

1) Якщо (2.9) виконується – позначаємо b = c і переходимо на в).

2) Якщо (2.9) не виконується – позначаємо а = с і переходимо на крок в).

2.4.7.4 Листинг програми генерації випадкових чисел на мові VBA, пов’язаної з робочим аркушем Excel наведено нижче:


Option Explicit

Dim r, a, b, c As Double

Dim i As Integer

Sub Equiatio_2()


Randomize

For i = 1 To 2000

r = Rnd


a = 0

b = 2

If FR(a, r) > 0 And FR(b, r) < 0 Then

c = a

a = b

b = c

End If

While Abs(b - a) > 0.00000001

c = (a + b) / 2

If FR(c, r) > 0 Then

b = c

Else

a = c

End If

Wend

'MsgBox c & " " & FR(c, r)

Cells(3 + i, 2) = c

Next i

'

End Sub

Function FR(x, r)

FR = 5/4*(x-0.6*Sgn(x-1)*Abs(x-1)(5/3)-0.6)-r

End Function

2.4.7.5 За допомогою цей програми була генерована вибірка з 2000 чисел, що розподілені за законом (2.4). З даної вибірки одержали гістограму аналогічно описаному у 2.4.5. Розмах вибірки – від 0 до 2, розподіл – на 10 частин довжиною 0,2. Результати наведено у таблиці 2.3.

2.4.8 Одержання випадкових чисел методом Неймана-Пирсона. Теорію методу викладено у підрозділі 4.6 лекційного курсу. Алгоритм:

а) Генерують 2 рівномірно розподілених випадкових числа R1 i R2.

б) Розраховуємо на їх основі 2 випадкових числа:


y1 = a + (b – a)R1; (2.10)

y2=fmaxR2, (2.11)

де fmax – максимум диференціальної функції розподілу (густини розподилу)

в) Перевіряємо, чи виконується нерівність:


y2  f(y1). (2.12)


Якщо ця нерівність виконується – запам’ятаємо число y1, яке розподілено по заданому закону.

Якщо нерівність (2.12) не виконується – повторюємо розрахунки, починаючи з кроку а).

2.4.8.1 Необхідно створити та відладити на будь-якої мові програмування програму, за допомогою якої розрахувати значення 2000 чисел і скопіювати їх на робочий аркуш Excel.

2.4.8.2 Нижче наведено варіант листингу програми на мові VBA, звязаної з робочим аркушем Excel.


Sub Neumann()

Randomize

fmax = ff(1)

For i = 1 To 2000

y2 = 1000

While y2 > ff(y1)

r1 = Rnd

r2 = Rnd

y1 = 2 * r1

y2 = r2 * fmax

Wend

Cells(3 + i, 2) = y1

Next i


'


End Sub

Function ff(z)

ff = 1.25 * (1 - Abs(z - 1) (2 / 3))

End Function


2.4.8.3 За допомогою цей програми була генерована вибірка з 2000 чисел, що розподілені за законом (2.4). З даної вибірки одержали гістограму аналогічно описаному у 2.4.5. Розмах вибірки – від 0 до 2, розподіл – на 10 частин довжиною 0,2. Результати наведено у таблиці 2.3.

2.4.8.4 Проведемо порівняння двох вибірок за критерієм Пирсона, як це було зроблено у 2.4.6. дані розрахунків наведено у таблиці 2.3.


Таблиця 2.3


Інтервал
Вибірки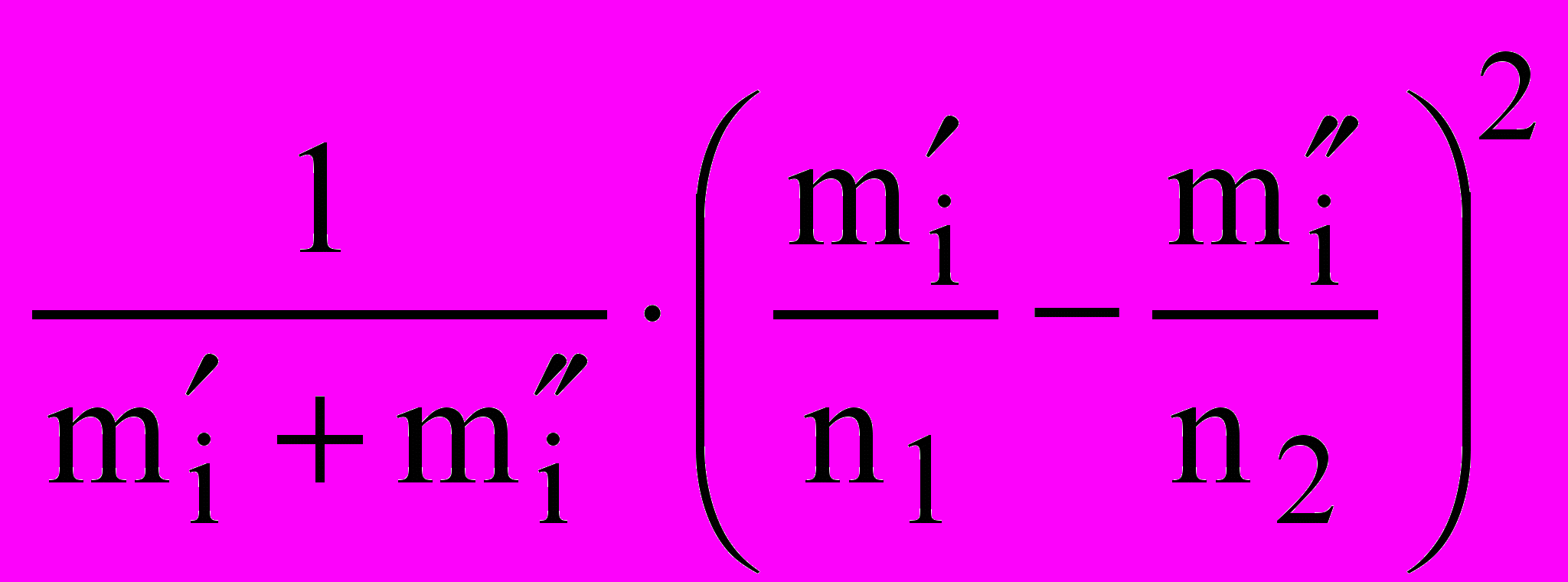


Лівий

кінець
Правий кінець
Обернена функція
метод Неймана

0
0,2
41
29
5,14286E-07

0,2
0,4
97
116
4,23709E-07

0,4
0,6
200
187
1,09173E-07

0,6
0,8
308
247
1,67613E-06

0,8
1
372
370
1,34771E-09

1
1,2
416
422
1,07399E-08

1,2
1,4
266
290
2,58993E-07

1,4
1,6
178
198
2,65957E-07

1,6
1,8
82
97
3,14246E-07

1,8
2
40
44
4,7619E-08










сума
3,6222E-06

2сп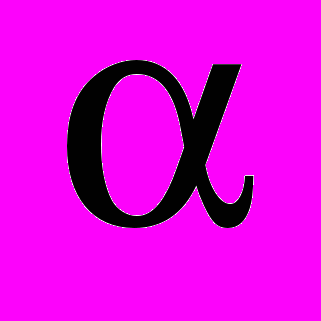


k
2кр
Висновок

14,48879
0,05
9
16,91896
Вибірки однорідні


Як випливає з результатів таблиці 2.3, обидві вибірки є однорідними, тобто, обидва методи дають статистично не відмінні вибірки.


2.5 Вимоги до звіту про роботу.


2.5.1 Звіт виконується у відповідності до загальних вимог, викладених у частині 1. Перший аркуш звіту – титульний аркуш, оформлюється за взірцем (додаток Б).

2.5.2 Основна частина звіту складається з таких розділів:

ВСТУП

1 ВХІДНІ ДАНІ

2 ПОБУДОВА ГІСТОГРАМИ РОЗПОДІЛУ

3 МОДЕЛЮВАННЯ ГІСТОГРАМИ РОЗПОДІЛУ

4 МОДЕЛЮВАННЯ ВИПАДКОВОЇ ВЕЛИЧИНИ МЕТОДОМ ОБЕРНЕНОЇ ФУНКЦІЇ

5 МОДЕЛЮВАННЯ ВИПАДКОВОЇ ВЕЛИЧИНИ МЕТОДОМ НЕЙМАНА-ПИРСОНА

ВИСНОВКИ

До звіту додаються :

а) Робоча книга Excel з проектами розрахунків і вибірками.

б) ехе-Файли програм, що створені студентом під час виконання роботи (якщо студент не користувався мовою VBA).

2.5.3 У розділі ВСТУП:

а) Надається постановка задачі (умова роботи).

б) Надається принциповий шлях рішення.

Розділ пишеться свавільно, у дусі твору.

Приклад:


ВСТУП


У рамках роботи по договору на тему “Розробка системи управління рухом для навчання диспетчерів залізниці” групі імітаційного моделювання фірми “Авант” доручено розробити імітаційну модель системи управління рухом.

У відповідності до технічного завдання, до основи моделі слід покласти реальний набір статистичних даних, який додається замовником.

У даній роботі для імітації необхідно використати ще один генератор, який дозволяє генерувати випадкові числа із заданим аналітичним законом розподілу.

Метою роботи є створення програм-генераторів випадкових чисел, що дозволяють імітувати реальні статистичні дані і задану аналітичну функцію розподілу, доказ того, що значення, які модельовані, є статистично невідмінними від заданих залежностей і даних.

Для досягнення мети роботи необхідно:

а) Одержати гістограму розподілу, виходячи з даних спостережень.

б) Розробити і відладити програму моделювання гістограми.

в) За допомогою програми генерувати вибірку і порівняти її з заданою, встановити, значимо чи ні вони відрізняються статистично, користуючись непараметричним критерієм Пирсона.

г) Розробити програми генерації вибірок, що розподілені за відомим законом, методами зворотної функції і Неймана-Пирсона.

д) За допомогою програми генерувати вибірки і дослідити, значимо чи ні вони відрізняються статистично

2.5.4 У розділі 1 ВХІДНІ ДАНІ наводяться такі дані:

а) Наводиться посилання на робочий аркуш, де міститься вхідна вибірка.

б) Наводиться функція розподілу.

Вхідні дані обираються у відповідності до 2.6

2.5.5. У розділі 2 ПОБУДОВА ГІСТОГРАМИ РОЗПОДІЛУ описати технологію побудови гістограм (з посиланням на робочий аркуш книги Excel з проектом). Навести у виді таблиці результати розрахунків.

При оформленні керуватися, як прикладом, підрозділами 2.4.1 – 2.4.3.

2.5.6 У розділі 3 МОДЕЛЮВАННЯ ГІСТОГРАМИ РОЗПОДІЛУ навести:

а) Алгоритм методу моделювання;

б) Листинг налагодженої програми з коментарями;

в) Посилання на робочий аркуш проекту Excel, де міститься генерована вибірка;

г) Таблиця з результатами розрахунків і аналізу за допомогою критерія Пирсона.

За взірець можна обрати підрозділи 2.4.4 – 2.4.6

2.5.7 У розділі 4 МОДЕЛЮВАННЯ ВИПАДКОВОЇ ВЕЛИЧИНИ МЕТОДОМ ОБЕРНЕНОЇ ФУНКЦІЇ слід:

а) Визначити невідомий параметр функції розподілу, одержати інтегральну функцію розподілу. Це можна зробити вручну або за допомогою пакету МathCAD.

б) Навести графіки диференціальної та інтегральної функцій розподілу.

в) Описати алгоритм методу обернених функцій.

г) Надати листинг налагодженої програми.

д) Надати посилання на робочий аркуш Excel, що містить генеровану за програмою вибірку.

е) Надати посилання на таблицю результатів у звіті з характеристиками вибірки (спільну з методом Неймана).

2.5.8 У розділі 5 МОДЕЛЮВАННЯ ВИПАДКОВОЇ ВЕЛИЧИНИ МЕТОДОМ НЕЙМАНА-ПИРСОНА :

а) Надати алгоритм методу

б) Навести листинг налагодженої програми

в) Надати посилання на робочий аркуш Excel, що містить генеровану за програмою вибірку.

г) Навести таблицю результатів і аналіз однорідності вибірок по методам обернених функцій і Неймана-Пирсона, зробити висновок відносно однорідності.

2.5.9 У розділі ВИСНОВКИ помістити висновки з роботи у формі стислого опису результатів згідно з переліком питань, що наведені у взірці вступу.


2.6 Вибір варіантів


2.6.1 Вхідна вибірка генерується програмою, що знаходиться на робочому аркуші “Лаб_2” книзі Віпад_Проц.xls. Книга знаходиться на кафедрі ВМКТ і в локальної мережі РФ СНУ.

2.6.2 Для генерації Вам необхідно:

а) Відкрити робочу книгу Віпад_Проц.xls .

б) Відкрити робочий аркуш “Лаб_1”

в) Натиснути на кнопку “Пуск” на аркуші

г) Скопіювати у власну робочу книгу дані.

2.6.3 Для запобігання пошкоджень програми копіювання відбувається під керівництвом викладача.

2.6.4 Густина розподілу задається рівнянням:





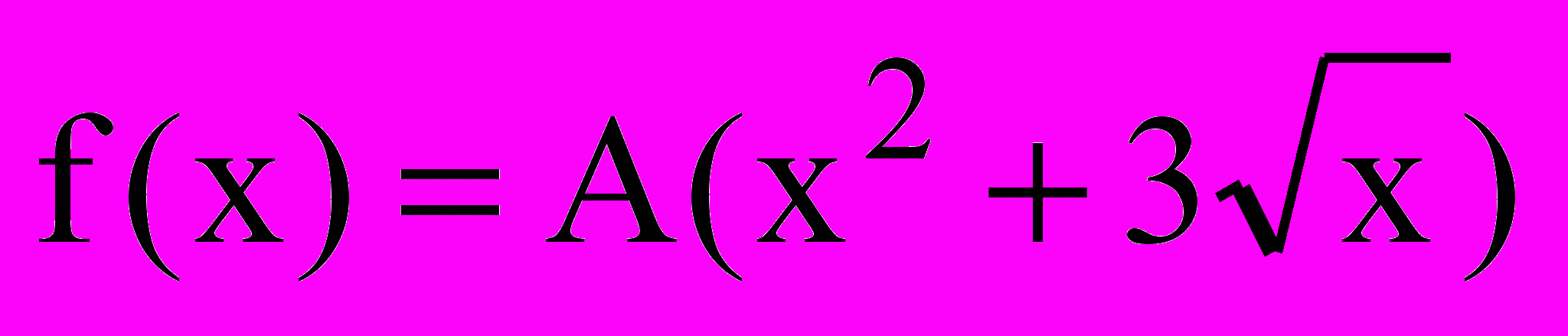
на відрізку [0,B], де В – Ваш порядковий номер у журналі академічної групи.


2.7 Контрольні запитання


1 Чим характеризуються випадкові числа? Яки числа є стандартними для генерації інших

2 Яким чином можна генерувати випадкові числа для моделюваня даних, що задані гістограмою?

3 Як можна перевірити, чи є розподіл у гістограмі і генерованої вибірці однаковим?

4 Як можна побудувати гістограму з великої сукупності даних?

5 Як можна моделювати випадкові числа, що задані відомою функцією розподілу методом обернених функцій?

6 Якими методами можна розв’язувати рівняння у методі зворотних функцій?

7 Суть методу Неймана-Пирсона

8 Пояснити роботу Ваших програм (призначення блоків, організація і зміст підпрограм, особливості виводу результатів).


3 ЧИСЕЛЬНЕ РІШЕННЯ ЗАДАЧ ТЕОРІЇ ЙМОВІРНОСТЕЙ МЕТОДОМ МОНТЕ-КАРЛО


3.1 Мета роботи


3.1.1 Засвоїти основи методу статистичного моделювання (Монте-Карло).

3.1.2 Скласти алгоритм і програму для розв’язання заданої задачі методом статистичного моделювання.

3.1.3 Провести статистичне моделювання і аналіз рішення

3.1.4 Скласти звіт з роботи


3.2 Легенда і вхідні дані


3.2.1 Необхідно розв’язати методом статистичного моделювання задачу, обрану з підрозділу 3.6 згідно таблиці варіантів, провести дослідження рішення.


3.3 Теоретична частина


3.3.1 Теоретичний матеріал викладено у розділі 4, зокрема, у підрозділі 4.7 лекційного курсу.


3.4 Приклад виконання


3.4.1 Приклад виконання задач теорії імовірності наведено і розібрано в розділі 4.7 лекційного курсу.

3.4.2 Загальна послідовність вирішення задач, якой рекомендується дотримуватись:

а) Розробка алгоритму одиничного жеребу (випробування)

б) Розробка загального алгоритму задачі

в) Розробка та налагодження програми розрахунків. Програму можна укладати на будь якої мові програмування. Кінцеві результати слід переносити на робочий аркуш Excel для подальшого статистичного дослідження.

г) Статистичне дослідження рішення:

1) Результати паралельних розрахунків при різній кількості випробувань (від 100 до 10000).

2) Розрахунок середніх і середньоквадратичних відхилень ришень при різної кількості випробувань.

3) Кількісне дослідження впливу кількості випробувань на середньоквадратичне відхилення (у відповідності до п. 4.7.5 лекційного курсу.


3.5 Вимоги до звіту про роботу.


3.5.1 Звіт виконується у відповідності до загальних вимог, викладених у частині 1. Перший аркуш звіту – титульний аркуш, оформлюється за взірцем (додаток Б).

3.5.2 Основна частина звіту складається з таких розділів:

ВСТУП

1 УМОВА ЗАДАЧІ

2 ОРГАНИЗАЦІЯ ОДИНИЧНОГО ЖЕРЕБУ

3 АЛГОРИТМ І ПРОГРАМА МОДЕЛЮВАННЯ

4 РЕЗУЛЬТАТИ МОДЕЛЮВАННЯ

ВИСНОВКИ

До звіту додаються :

а) Робоча книга Excel з проектом розрахунків

б) ехе-Файли програм, що створені студентом під час виконання роботи (якщо студент не користувався мовою VBA).

3.5.3 У розділі ВСТУП:

а) Надається постановка задачі (умова роботи).

б) Надається принциповий шлях рішення.

Розділ пишеться свавільно, у дусі твору.

3.5.4 У розділі 1 УМОВА ЗАДАЧІ надається повністю умова задачі

3.5.5 У розділі 2 ОРГАНИЗАЦІЯ ОДИНИЧНОГО ЖЕРЕБУ надаються результати розробки алгоритму проведення одиничного випробування. Приклад опису у п. 4.7.3 лекційного курсу.

3.5.6 У розділі 3 АЛГОРИТМ І ПРОГРАМА МОДЕЛЮВАННЯ наводяться опис алгоритму (або його блок-схема) та листинг налагодженої програми. Приклад опису наведено у пп..4.7.3.2 лекційного курсу.

3.5.7 У розділі 4 РЕЗУЛЬТАТИ МОДЕЛЮВАННЯ наводяться результати дослідження впливу на рішення кількості випробувань, розрахунки середніх величин, середньоквадратичних відхилень (з повним описом роботи проектів Excel). Приклад оформлення наведено у п.4.7.4 лекційного курсу.

У розділі результати представляють у виді таблиць, графіків. При представленні залежності середньоквадратичного відхилення від зворотного кореню квадратного від кількості випробувань слід на графіку надати коефіцієнт детермінації і рівняння. Кількість точок (кількостей випробувань) – не менше, ніж 10 у діапазоні від 100 до 10000. Кількість паралельних випробувань – не менше, ніж 10.

3.5.8 В розділі ВИСНОВКИ стисло описати основні результати роботи. Висновки нумерують. Перший висновок – узагальнюючий.

Приклад


ВИСНОВКИ


1 Проведено рішення задачі теорії імовірностей методом статистичного моделювання.

2 Розроблено алгоритм одиничного жереба, що полягає (надати стислий опис)

3 Розроблено алгоритм рішення задачі, на основі якої розроблено програму моделювання на мові (вказати мову програмування).

4 За допомогою створеної програми проведено моделювання і одержано рішення задачі (навести його).

5 Проведено вивчення вплив на рішення кількості випадкових випробувань. Встановлено, що ... (стисло навести результати).


3.6 Вибір варіантів


3.6.1 Нижче наведено 25 варіантів завдань (5 типів задач по 5 варіантів). Вибір завдань відбувається згідно таблиці 3.1, в залежності від порядкового номеру в журналі академічної групи. Наприклад , Ваш номер по журналу 12. З таблиці 3.1 находимо для № 12 варіант 4.5. Перша цифра – номер задачі (4), друга – номер варіанту цей задачі (5).


Таблиця 3.1


№
Вар
№
Вар
№
Вар
№
Вар
№
Вар

1
3.1
6
2.2
11
2.3
16
1.1
21
2.5

2
4.3
7
4.2
12
4.5
17
2.1
22
5.5

3
1.5
8
1.2
13
1.3
18
5.3
23
1.4

4
3.5
9
4.1
14
3.4
19
3.2
24
4.4

5
5.4
10
3.3
15
2.4
20
5.1
25
5.2



3.6.2 Задачі


Задача 1 Гральну кість кидають k разів Знайти імовірність того, що сума очок кратна числу Р (=P) або перевищує Р (>P)

Варианти:


№ варіанту
1
2
3
4
5

k
4
4
5
4
5

P
4
5
6
>17
>23


Задача 4 Учасники жеребкування тягнуть зі скрині жетони з номерами від 1 до 99. Знайти імовірність того, що номер першого, випадково витягнутого жетону :

Варіант 1 - не містить цифри 5.

Варіант 2 – містить цифру, кратну 7

Варіант 3 – містить двозначну цифру, у якої сума чисел розрядів кратна 3

Варіант 4 – містить двозначну цифру, у якої сума чисел розрядів є повним квадратом,

Варіант 5 – містить двозначну цифру, добуток чисел розрядів міститься у інтервалі від 40 до 70


Задача 3

В ВНЗ 20% студентів за фахом – технологи, 35 % - механіки, 30 % - економісти, 15 % - інформатики. В буфеті у черзі стоять 10 студентів. Знайти імовірність того, що серед них:

Варіант 1 – наявний хоча б один студент-інформатик

Варіант 2 – наявно 3 або 4 студенти-механіки

Варіант 3 – немає жодного студента-інформатика

Варіант 4 – наявно більше 2 студентів-економістів

Варіант 5 – наявно менше 3 студентів-технологів


Задача 4

Імовірність попадання стрільцем у мішень складає Р. Стрілець робіть k пострілів Знайти ймовірність того, що він влучив у мішень не менше, ніж m разів.

Варіанти


№ варіанту
1
2
3
4
5

P
0,5
0,5
0,6
0,6
0,65

k
4
5
5
7
5

m
2
3
3
4
3



\ Задача 5 Імовірність поразки цілі при одному пострілі першим стрільцем складає Р1, другим – Р2, третім – Р3. Усі 3 стрільці стріляють водночас. Знайти імовірність того, що ціль буде поражена одним із стрільцев.


Варіанти


№ варіанту
1
2
3
4
5

P1
0,8
0,85
0,9
0,85
0,8

Р2
0,9
0,8
0,75
0,75
0,8

Р3
0,9
0,9
0,8
0,8
0,9

3.7 Контрольні запитання


1 Загальні принципи методу Монте-Карло.

2 Як випадково розіграти цілі числа з рівномірним розподілом?

3 Як випадково розіграти інтервал попадання із заданою імовірністю?

4 Яким чином проводится дослідження результатів статистичного моделювання?

5 У яких випадках метод статистичних випробувань не слід використовувати?

6 Як можна моделювати подію, що відбувається з імовірністю Р?

7 Поясніть деталі алгоритму рішення Вашої задачі.

8 Поясніть деталі Вашої програми розрахунків.

9 Як залежить точність моделювання від кількості випадкових випробувань.? У скільки разів треба збільшити кількість випробувань, щоб зменшити похибку визначення у 3 рази?


4 МОДЕЛЮВАННЯ СИСТЕМ МАСОВОГО ОБСЛУГОВУВАННЯ


4.1 Мета роботи


4.1.1 Засвоєння методів моделювання СМО

4.1.2 Розробка алгоритму і програми моделювання СМО заданого виду

4.1.3 Виконання розрахунків і інтерпретація результатів.

4.1.4 Оформлення звіту про роботу


4.2 Легенда і завдання


До Вас звернувся підприємець – володар перукарні. Він володіє помешканням, що дозволяє працювати N1 перукарям і кімнату очікування, що містить N2 посадкових місць. Середній час обслуговування клієнта перукарем складає t1 хвилин. Середній інтервал часу між приходом клієнтів складає t2 хв. Середній прибуток від 1 обслуженого клієнта складає 2 грн. Коли у перукарню приходить клієнт і бачить, що вільних місць немає, він уходить.

Тривалість робочого дня у перукарні: 10 годин (600 хв.). Порядок обслуговування клієнтів наприкінці робочого дня такий: після 600 хв. доступ нових клієнтів припиняється, а ті клієнти, що очікують у черзі у перукарні, обслуговуються усі.

У підприємця є можливість організувати ще одне робоче місце, але для цього прийдеться зменшити кількість посадкових місць у кімнаті очікування на 3. Його цікавить питання, чи зможе він за рахунок реорганізації одержати додатковий прибуток.

Слід розглянути такі варіанти:

а) Час між приходом окремих клієнтів і час обслуговування окремого клієнту розподілений за показовим законом.

б) Час між приходом окремих клієнтів і час обслуговування окремого клієнту розподілений за рівномірним законом.

Розрахунки провести в середньому за 1 робочий день.

4.3 Теоретична частина


4.3.1 Теоретичні основи розрахунків СМО і їх статистичного моделювання викладені у розділі 5 лекційного курсу.

4.3.2 Систему у задачі слід розглядати, як 2- та 3-х канальну, з обмеженою чергою. На відмінність від задачі, що була розглянута у лекційному курсі, слід задатися часовим інтервалом 600 хв і дослідити, скільки у середньому буде клієнтів протягом цього часу і скільки з них буде обслугованою а скільки – ні.


4.4. Порядок і приклад виконання завдання


4.4.1 Розглянемо моделювання на прикладі показового розподілу часу, тільки для двох перукарів и 5 місць у черзі.

Вхідні дані:

середній час обслуговування клієнта: 30 хв;

середній проміжок часу між приходом клієнтів: 10 хв

Для підвищення точності розіб’ємо 1 хв на 10 тактів. Тобто, тривалість робочого дня складає 6000, середній час обслуговування 200, а проміжок часу між клієнтами – 100 тактів.

4.4.2 Основна ідея рішення – знайти середню кількість клієнтів, що обслуговуються у обох випадках ( з 2 та 3 перукарями) протягом робочого дня. Якщо ці величини помножити на прибуток від обслуговування клієнта – одержимо добовий прибуток, по зміні величини якого можна судити про вигідність або невигідність впровадження нової системи обслуговування.

4.4.3 Алгоритм:

4.4.3.1 Задаємо значення перемінної NW - кількість випробувань (“кількість днів спостереження”)

4.4.3.2 Визначаємо масив PER(1 to 7) У цьому масиві у PER(1), PER(2) буде міститись час обслуговування клієнтів (0-якщо їх немає) . У PER(3) PER(7) – вказуеться поточний стан місць у черзі на обслуговування: 0 – місце вільне, 1 – місце зайнято.

4.3.3.3 Визначаємо перемінні:

NW – кількість “діб” спостережень – циклів випадкових подій.

N_C –кількість часу до приходу наступного клієнту;

N_Yes - кількість клієнтів, що обслуговано;

N_No – кількість клієнтів, що не обслуговано;

N-Per – загальна кількість місць у системі “перукарі-кімната очікування” (7)

N_Barb – кількість робочих місць перукарів.

tcl – середній проміжок часу між приходом клієнтів;

tser – середній проміжок часу обслуговування одного клієнту.

Ці величини доцільно уводити з робочого аркуша.

Перемінні

4.4.3.4 Для кожного “робочого дня” від і=1 до і=NW на “нульовому” кроці перед початком розрахунків:

а) Oбнульовуємо перемінні N_Yes, N_No.

б) Генеруємо час до приходу другого клієнту і поміщуємо у N_C (тобто, імітуємо появу першого клієнту).

в) Генеруємо час обслуговування першого клієнту і поміщуємо у PER(1).

4.4.3.5 У циклі щодобових випробувань для кожного такту з 1 до 6000 виконуються таки дії:

а) Перевіряється, чи дорівнює N_C нулю?

б) Імітується поведінка системи у наступний такт часу.

4.4.3.6 Якщо перемінна N_C дорівнює нулю:

а) Генеруємо нове значення N_C.

б) Знаходимо, чи є у перукарні вільні місця. Для цього визначаємо перемінну NS=0, відбуваємо перебір змісту масиву PER(i). Якщо поточний елемент більше 0 – зміст NS збільшуємо на 1

в) Якщо NS=N_PER – вільних місць немає, поточний клієнт не обслуговується. Зміст N_No збільшуємо на 1

г) Якщо NS < N_PER – збільшуємо на 1 зміст N_Yes, знаходимо, які елементи є вільними.

- Якщо вільним є хоча б один з елементів від 1 до N_Barb, це означає, що черзі немає і хоча б один перукар є вільний. Тоді у елементі масиву PER, що відповідає вільному перукареві, генеруємо час його обслуговування.

- Якщо елементи, які відповідають перукарям, відьінні від 0 (зайняті) – знаходимо першій вільний елемент, що відповідає черзі і присвоюємо йоту значення 1.

4.4.3.7 Для імітацій поведінки системи у наступний момент часу:

а) Зменшуємо на 1 зміст N_C

б) У комірках PER(1)  PER(N_BARB), що відмінні від нуля, зменшуємо на 1.

Якщо внаслідок цього зміст поточної комірці дорівнює 0 і наявні комірки черзі, зміст яких дорівнює 1, то обираємо першу з таких комірок і обнульовуємо.

Водночас у вільній комірці перукаря генеруємо час обслуговування клієнту. Тим самим моделюється обслуговування поточного клієнту з черзі.

4.4.3.8 По закінченні добового циклу тактів (6000) на робочий аркуш виводять поточне значення змінної доби, N_Yes, N_No.

4.4.4 Після закінчення розрахунків одержані вибірки обробляють засобами Еxcel:

а) Розраховують середні значення і середньоквадратичне відхилення.

б) розраховують розмах вибірки

в) Будують гістограму, користуючись проектом роботи 2.

г) Розраховують прибуток, як добуток середньодобової кількості обслугованих клієнтів на прибуток від одного клієнту.

4.4.5 Проводять розрахунки з іншими значеннями вхідних параметрів.

При використанні рівномірного розподілу необхідно внести зміни у підпрограми-функції програми. При цьому нижня границя часу (a) буде дорівнювати нуля, а верхня границя (b) буде дорівнювати подвоєному значенню середнього часу.

Підпрограму слід скласти самостійно, користуючись тим, що проміжок часу повинен бути цілим. (див. п. 4.3.5, 4.3.6 лекційного курсу).

4.4.6 Нижче наведено листинг програми.


Option Explicit

Global N_c, PER(1 To 7), N_Yes, N_No As Integer

Global N_Barb, N_Per, tcl, tser As Integer


Dim i, j, k, m, N_s, NW As Integer


Sub Barber()

Randomize

NW = Cells(7, 2)

N_Per = Cells(3, 2)

N_Barb = Cells(4, 2)

tcl = Cells(6, 2)

tser = Cells(5, 2)

'***Початок випробувань

For i = 1 To NW

N_No = 0

N_Yes = 1

N_c = Time_Cli()

PER(1) = Time_Ser()

For j = 2 To N_Per

PER(j) = 0

Next j

'MsgBox n_c & " " & PER(1)

For j = 1 To 6000

'**Випадок n_c=0

If N_c = 0 Then

N_c = Time_Cli

N_s = 0

For k = 1 To N_Per

If PER(k) > 0 Then N_s = N_s + 1

Next k

If N_s = N_Per Then

N_No = N_No + 1

End If

If N_s < N_Per Then

N_Yes = N_Yes + 1

'*** чи є пустi місця у перукарів

If N_s < N_Barb Then

For k = 1 To N_Barb

If PER(k) = 0 Then

PER(k) = Time_Ser()

Exit For

End If

Next k

End If ' Кінець N_s < N_Barb

If N_s >= N_Barb Then

For k = N_Barb + 1 To N_Per

If PER(k) = 0 Then

PER(k) = 1

Exit For

End If

Next k

End If '**кінець N_s > N_Barb

End If ' ***Кінець N_s < N_Per

End If ' ***Кінець n_с=0

'**** Положення у тактi i

N_c = N_c - 1

For k = 1 To N_Barb

If PER(k) > 0 Then PER(k) = PER(k) - 1

Next k

'm = PER(1)

For k = 1 To N_Barb

If PER(k) = 0 Then

For m = N_Barb + 1 To N_Per

If PER(m) = 1 Then

PER(m) = 0

PER(k) = Time_Ser

Exit For

End If

Next m

End If

Next k

Next j

Cells(i + 3, 4) = i

Cells(i + 3, 5) = N_Yes

Cells(i + 3, 6) = N_No

'For k = 1 To N_Per

' Cells(1, 3 + k) = PER(k)

' Next k

Next i

'

End Sub

Function Time_Cli()

Time_Cli = Int(-tcl * Log(Rnd) + 1)

End Function

Function Time_Ser()

Time_Ser = Int(-tser * Log(Rnd) + 1)

End Function


4.4.7 На рис. 4.1 наведено приклад оформлення робочого аркушу з проектом. Результати обробки не наведено.