Випадкові процеси

Вид материала

Подобный материал:

1 2 3 4

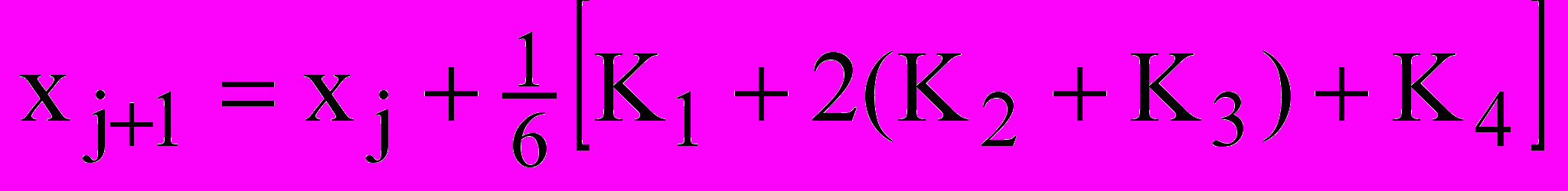, (1.2)

де j=0,1,2,…,m, причому,

;

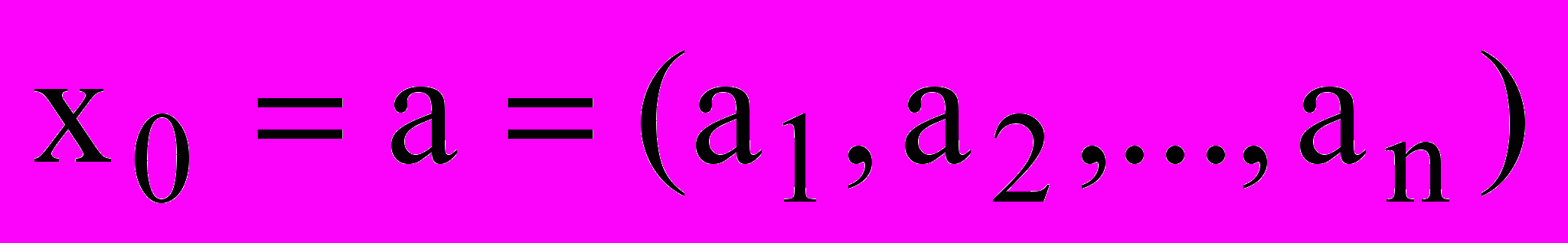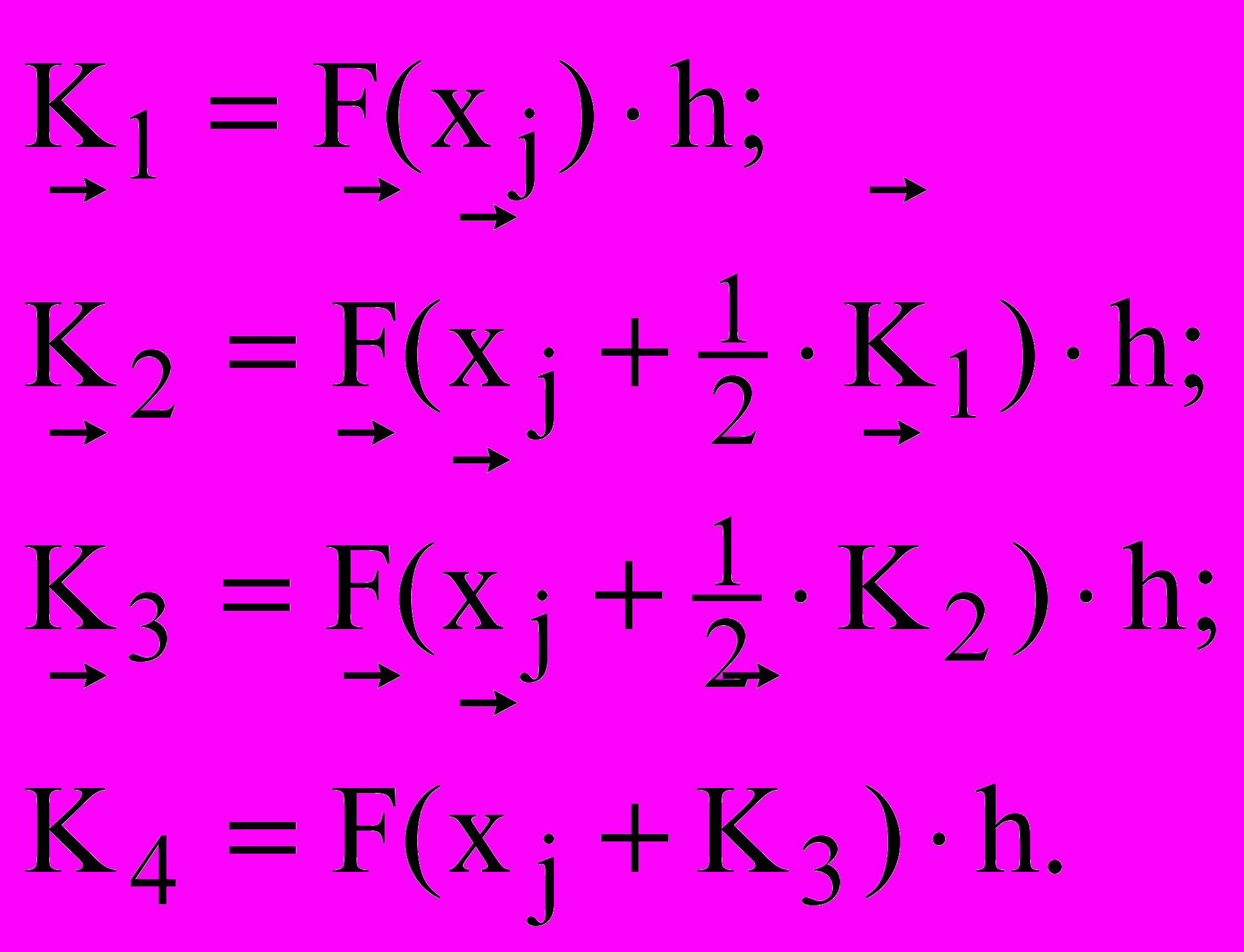
Розмірність кожного з наведених векторів дорівнює n.

1.3.3.3 Приклад програми буде наведено нижче. Метод Рунне-Кути відрізняється невеликою погрішністю, що є пропорційною від h⁵. Для підвищення точності і контролю досягнення потрібної точності необхідно виконувати розрахунки при двох значеннях h (друге значення обирають, як правило, у 2 рази менше за перше). Якщо результати розрахунків не відрізняються у межах потрібної точності – рішення вважають досягнутим.

1.4 Приклад виконання завдання

1.4.1 Задана матриця інтенсивностей:

0	2	0	0
1	0	0	2
0	4	0	1
0	0	3	0

1.4.2 На основі матриці інтенсивностей будуємо граф переходів (рис. 1.1)

Рисунок 1.1

1.4.3 Граф станів системи є ергодичним Марківським ланцюгом, бо з кожного стану можна попасти до всякого іншого.

1.4.4 Будуємо систему рівнянь Колмогорова для імовірностей, користуючись правилами, що викладені у підрозділі 3.2 лекційного курсу:

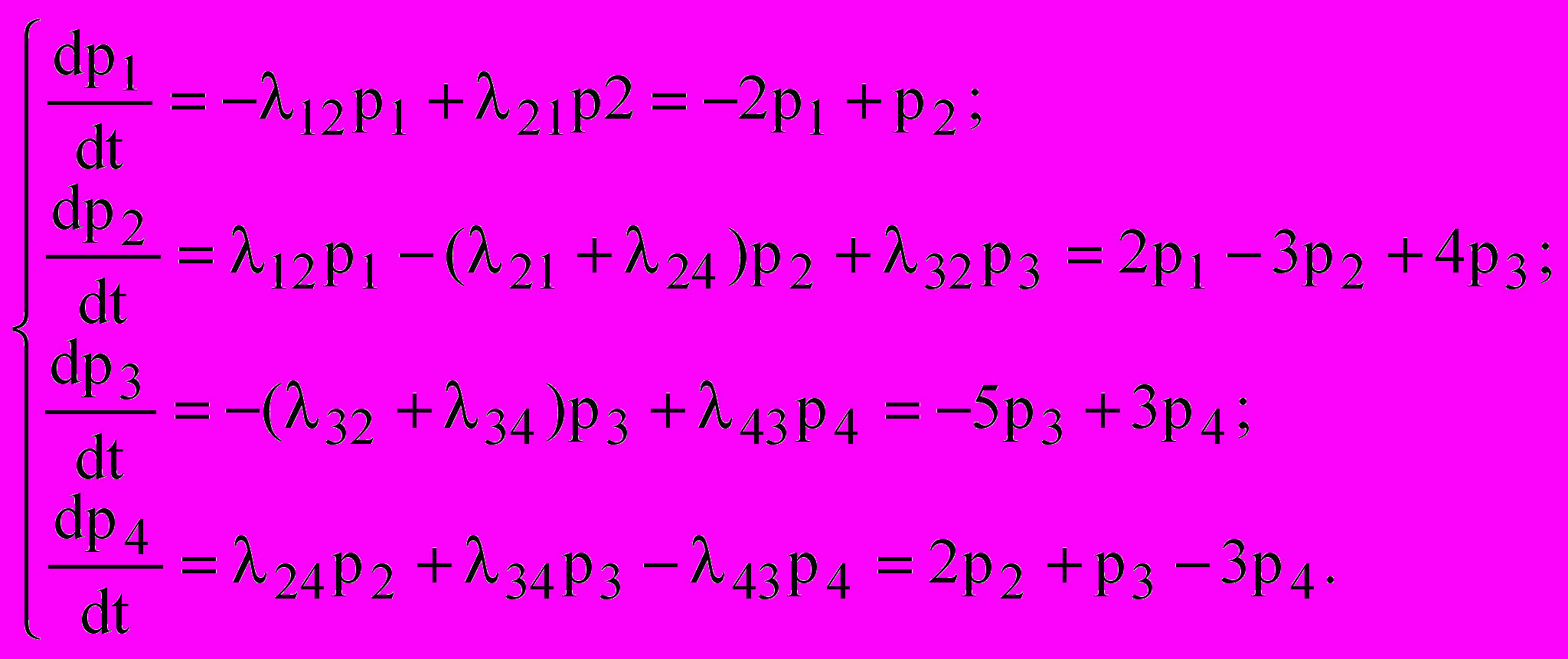(1.3)

1.4.5 Укладаємо систему рівнянь у стаціонарному стані для знаходження фінальних ймовірностей. Для цього:

а) Усі похідні дорівнюємо до 0;

б) Замість четвертого рівняння записуємо умову того, що усі стани створюють повну групу:

р₁ + р₂ + р₃ + р₄ = 1 (1.4)

1.4.6 Записуємо систему рівнянь для стаціонарного стану у матричному виді:

-2	1	0	0		р₁	=	0	(1.5)
2	-3	4	0		р₂		0
0	0	-5	3		р₃		0
1	1	1	1		р₄		1

1.4.7 Розв’язуємо систему (1.5) у середовищі Excel. Робочий аркуш наведено на рис. 1.2.

а) У комірках (В2:F5) наведено розширену матрицю: матрицю коефіцієнтів з доданням стовпця вільних членів.

б) У комірках (В7:Е10) будуємо зворотну матрицю. Формула масиву (В7:Е10): =МОБР(B2:E5)

в) У комірках (Н7:Н10) будуємо масив фінальних імовірностей шляхом матричного множення. Формула масиву (Н7:Н10):

=МУМНОЖ(B7:E10;F2:F5)

г) Для уводу натиснути комбінацію клавіш: + + .

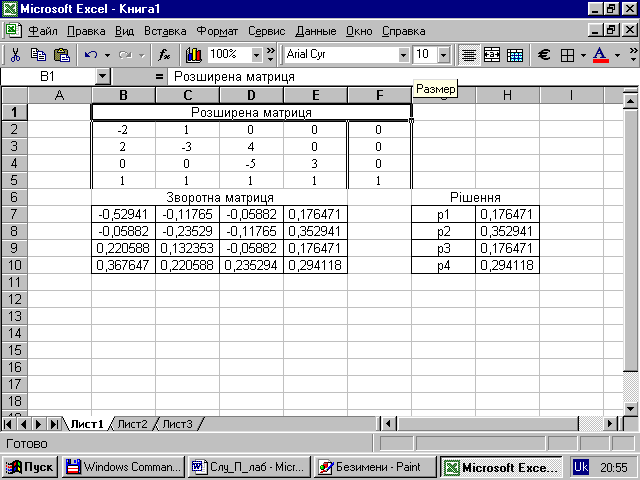
Рисунок 1.2

1.4.8 Для виконання подальших завдань необхідно скласти і відладити програму чисельного рішення диференціальних рівнянь методом Рунге-Кути.

Програма може бути складена на будь-якої мові програмування, якою краще володіє студент. Варіант листинга програми на мові VBA з прив’язкою до Excel наведено на рис. 1.3. Листинг підпрограми розрахунків функцій наведено на рис. 1.4. Робочий лист Excel, що зв’язаний з програмою, наведено на скріншоті (рис. 1.5).

1.4.8.1 У комірках В11:Е11 містяться початковіі наближення імовірностей. Вважаємо, що у початковий момент часу система находиться у стані 1 з імовірністю 1, а імовірності інших станів дорівнюють 1.

1.4.8.2 У комірках В12:Е12 містяться рішення – значення імовірностей у момент часу t, що міститься у комірці А12. Для його одержання слід пустити програму (у нашому випадку – шляхом натиснення на кнопку).

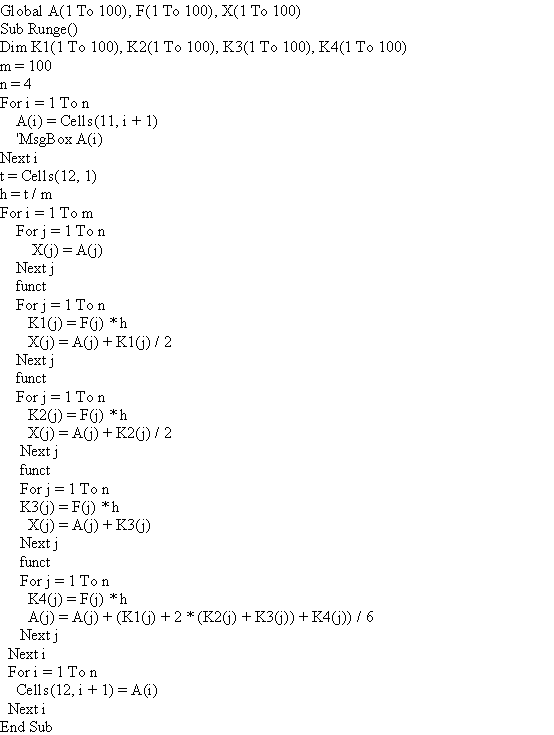
Рисунок 1.3

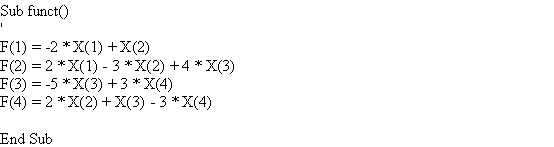
Рисунок 1.4

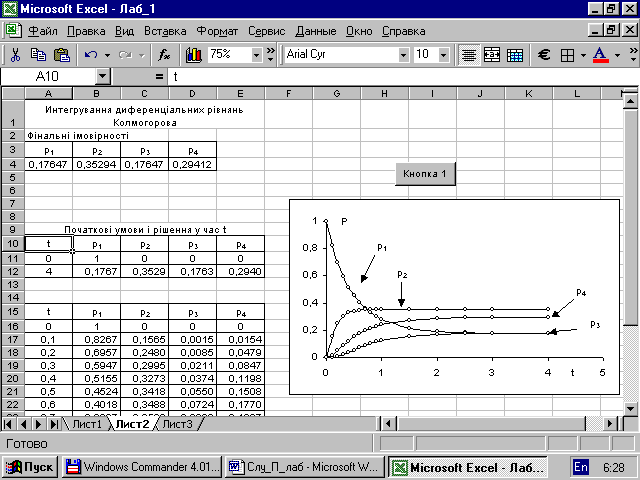
Рисунок 1.5

1.4.8.3 У комірках А4:D4 наведені довідкові значення фінальних ймовірностей для контролю розрахунків.

1.4.8.4 Розрахунки проводять таким чином:

а) У комірку А12 уводять значення часу.

б) У програмі встановлюють відносно велике значення кількості кроків m (100)

в) Натискують кнопку, одержують рішення

г) Збільшують кількість кроків m=200, одержують нове рішення.

д) Якщо “на око” різниця між двома рішеннями менше, ніж 0,001 – вважають, що рішення знайдено. У протилежному випадку збільшують кількість кроків і повторюють

е) Порівнюють, суттєво чи ні, відрізняється одержане рішення від довідкового значення фінальних імовірностей. Якщо різниця – менше за 0,01 – вважаємо, що стаціонарний стан досягнуто. Як випливає з рис. 1.5, через 4 години можна вважати, що досягнуто стаціонарний розподіл імовірностей.

ж) Виконуємо розрахунки у проміжних точках, копіюємо результати у таблицю, будуємо графіки (рис. 1.5). При цьому, час - підбираємо вручну. Виходячи з графіку, уточнюємо період наступу стаціонарного стану (у нашому випадку це – практично 2,5 год). При цьому, можна встановити кількість кроків при великому часі і далі його не змінювати.

1.4.9 За допомогою програми виконуємо такі дослідження:

1.4.9.1 Вивчаємо, яким чином впливає на фінальні імовірності початковий розподіл імовірностей. Для цього:

а) По черзі, встановити при t=0 спочатку р₂=1, інші – нульові, потім р₃=1, інші – нульові, потім p₄=1, інші – нульові.

б) Порівняти результати розрахунків фінальних імовірностей, зробити висновок.

в) Вивчити, як впливає початковий розподіл імовірностей на час встановлення стаціонарного стану, зробити висновок.

1.5 Вимоги до звіту про роботу.

1.5.1 Звіт виконується у відповідності до загальних вимог, викладених у частині 1. Перший аркуш звіту – титульний аркуш, оформлюється за взірцем (додаток Б).

1.5.2 Основна частина звіту складається з таких розділів:

ВСТУП

1 ВХІДНІ ДАНІ

2 ПОБУДОВА РІВНЯНЬ КОЛМОГОРОВА

3 РОЗРАХУНОК ФІНАЛЬНИХ ІМОВІРНОСТЕЙ

4 МОДЕЛЮВАННЯ ВСТАНОВЛЕННЯ СТАЦІОНАРНОГО СТАНУ

ВИСНОВКИ

1.5.3 У розділі ВСТУП:

а) Надається постановка задачі (умова роботи).

б) Надається принциповий шлях рішення.

Розділ пишеться свавільно, у дусі твору.

Приклад:

ВСТУП

За умовами завдання слід для технічної системи, що може знаходитись випадково у декількох станів, за її матрицею інтенсивностей переходів:

а) побудувати граф переходів,

б) одержати систему рівнянь Колмогорова,

в) розрахувати фінальні імовірності з рівнянь для стаціонарного стану

г) промоделювати час наступу стаціонарного стану, побудувати графіки часових залежностей,

д) вивчити, як впливає на величини фінальних ймовірностей і час наступу стаціонарного стану.

1.5.4 У розділі 1 ВХІДНІ ДАНІ наводяться у вигляді таблиці вхідні дані до роботи – матриця інтенсивностей.

1.5.5 У розділі 2 ПОБУДОВА РІВНЯНЬ КОЛМОГОРОВА:

а) Навести граф переходів (у виді рисунка у формати Word, Paint Brush або інших графічних редакторах, влучений, як об’єкт, у текст)

б) Описати принцип побудови рівнянь Колмогорова.

в) Навести систему рівнянь.

За взірець обрати опис у підрозділі 1.4.

1.5.6 У розділі 3 РОЗРАХУНОК ФІНАЛЬНИХ ІМОВІРНОСТЕЙ навести систему рівнянь для стаціонарного стану, навести опис послідовності розрахунків в Excel (можна влучили таблицю Excel у текст звіту), навести результати розрахунків. Взірець – підрозділ 1.4.

1.5.7 Розділ 4 МОДЕЛЮВАННЯ ВСТАНОВЛЕННЯ СТАЦІОНАРНОГО СТАНУ є найбільшім у звіті за обсягом і змістом. Його доцільно розбити на такі підрозділи:

4.1 Принципи моделювання. Метод Рунге-Кути.

У цьому підрозділі у свавільній формі висвітити суть методу, навести листинг складеної та налагодженої Вами програми (шляхом копіювання тексту з редактору програми у документ Word).

4.2 Результати моделювання

у цьому підрозділі навести:

а) Описання послідовності дій.

б) Таблиці результатів для побудови графіків для різних початкових розподілів імовірностей.

в) Надати інформацію відносно величини та часу наступу стаціонарного стану у залежності від початкового розподілу імовірностей, що випливає з результатів.

г) Навести графіки змін імовірностей станів у залежності від початкового розподілу.

1.5.8 У розділі ВИСНОВКИ послідовно навести:

а) Загальний висновок про роботу (що було зроблено).

б) Висновки і результати з кожного етапу роботи.

Приклад

ВИСНОВКИ

1 За заданою матрицею інтенсивностей переходів проведено розрахунки і моделювання встановлення розподілу ймовірностей, вивчено вплив початкового розподілу ймовірностей на величини фінальних імовірностей і час встановлення стаціонарного стану.

2 Розроблено граф станів, систему рівнянь Колмогорова, знайдено їх рішення у стаціонарному стані. Фінальні ймовірності складають:

(навести значення)

3 Розроблено і відлажено програму рішень системи диференціальних рівнянь методом Рунге-Кути. За допомогою цей програми проведено моделювання встановлення фінальних імовірностей у часі.

4 Встановлено, що фінальні імовірності...(описати, як залежать від початкового розподілу ймовірностей,)

5 Встановлено, що час досягнення стаціонарного стану .... (описати, як час залежить від початкового розподілу імовірностей)

1.6 Вхідні дані

1.6.1 Вхідна матриця інтенсивностй генерується програмою, що знаходиться на робочому аркуші “Лаб_1” книзі Віпад_Проц.xls. Книга знаходиться на кафедрі ВМКТ і в локальної мережі РФ СНУ.

1.6.2 Для генерації Вам необхідно:

а) Відкрити робочу книгу Віпад_Проц.xls .

б) Відкрити робочий аркуш “Лаб_1”

в) Натиснути на кнопку “Пуск” на аркуші

г) Скопіювати у власну робочу книгу дані.

1.6.3 Для запобігання пошкоджень програми копіювання відбувається під керівництвом викладача.

1.7 Контрольні запитання

1 Зміст понять “імовірність станів”, “інтенсивність переходів”, “Марковський випадковий процес”.

2 Що відображають рівняння Колмогорова?

3 Принцип побудови рівнянь Колмогорова (показати на прикладі роботи)

4 Зміст поняття “стаціонарний стан”.Властивості стаціонарного стану. Вигляд рівнянь Колмогорова у стаціонарному стані (показати на прикладі роботи)

5 Зміст поняття “фінальна імовірність”. Як їх можна розрахувати?

6 Як можна розв’язати рівняння Колмогорова у часі? Суть методу Рунне-Кути

7 Алгоритм методу Рунге-Кути (пояснити на прикладі власно створеної програми)

8 Як впливає початковий розподіл імовірностей на фінальні ймовірності? Чому? Для яких типів ланцюгів Маркова спостерігається протилежний вплив?

2 ОДЕРЖАННЯ І АНАЛІЗ ВИПАДКОВИХ ЧИСЕЛ

ІЗ ЗАДАНИМ ЗАКОНОМ РОЗПОДІЛУ

2.1 Мета роботи

2.1.1 Засвоїти методи генерації випадкових чисел із заданим законом розподілу методом зворотних функцій і Неймана-Пирсона.

2.1.2 Засвоїти методи аналізу розподілу випадкових чисел.

2.1.2 Скласти звіт про роботу

2.2 Легенда і завдання

2.2.1 Ви – працівник фірми “Авант”, яка розробляє програмне забезпечення для систем управління. Вашої групі доручено розробити імітаційну модель системи управління рухом для навчання диспетчерів залізниці. До основи моделі слід покласти реальний набір статистичних даних, який Вам додається. Необхідно створити генератор, який дозволяє одержувати випадкові числа, що розподілені за тім ж самим законом, що експериментальні.

2.2.2 Друга частина Вашого завдання – створити послідовність випадкових чисел, що розподілені за відомим законом, за допомогою метода Неймана-Пирсона і методом обернених функцій і порівняти результати. Обсяг чисел: 2000.

2.3 Теоретична частина

2.3.1 Для виконання роботи необхідно ознайомитися з методами, що викладені у розділах 4.5 – 4.6 лекційного курсу.

2.3.2 Методика порівняння двох послідовностей випадкових чисел

а) розподіляємо обидві вибірки на 10 однакових частин з однаковими верхніми та ніжними границями;

б) підраховуємо частоти попадання випадкових величин у кожний з інтервалів;

в) для встановлення однорідності вибірок використовуємо непараметричний критерій Пирсона:

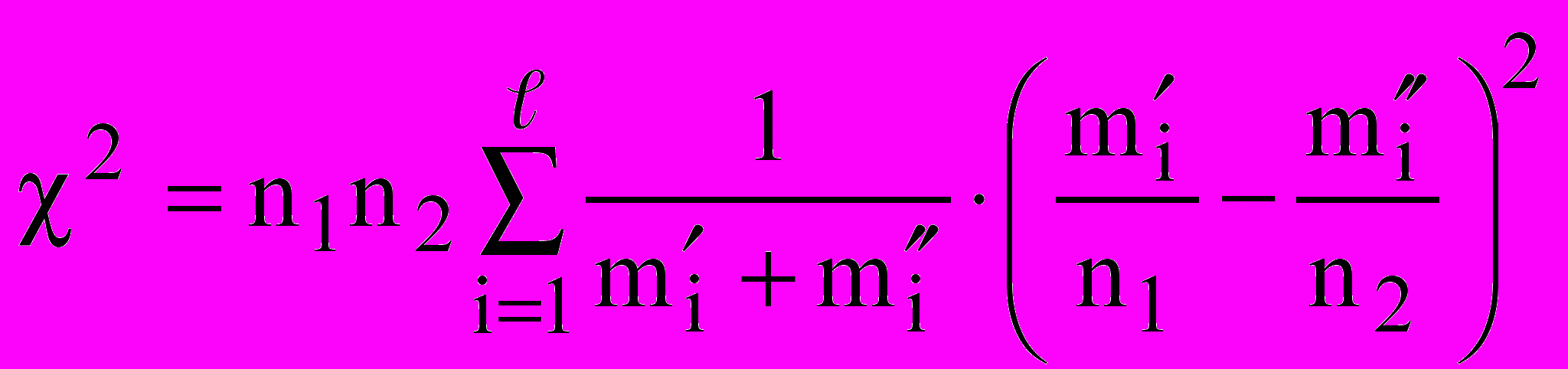, (2.1)

де n₁,n₂ – кількість елементів першої та другої вибірок;

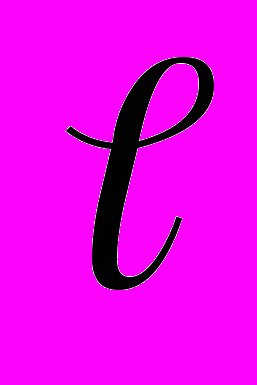- кількість груп, на яке розподілена кожна з вибірок;

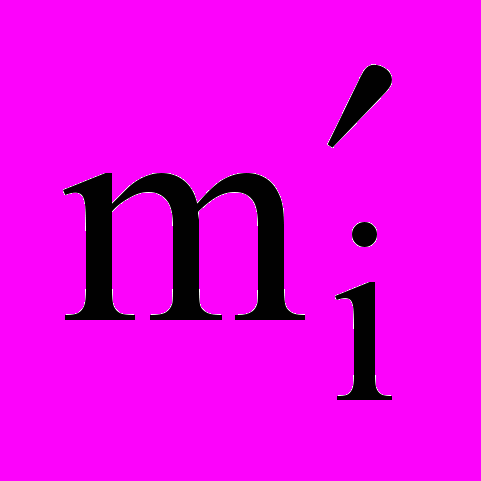- кількість елементів першої вибірки, що попали у і-й інтервал;

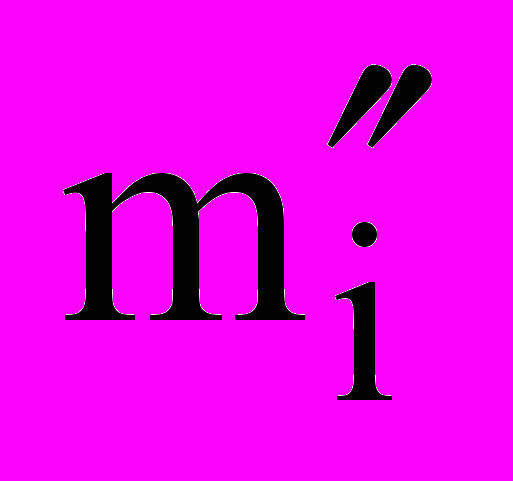- кількість елементів другої вибірки, що попали у і-й варіант.

Цей критерій при достатньо великих n₁та n₂ розподіляється по закону Пірсона “xі квадрат” з

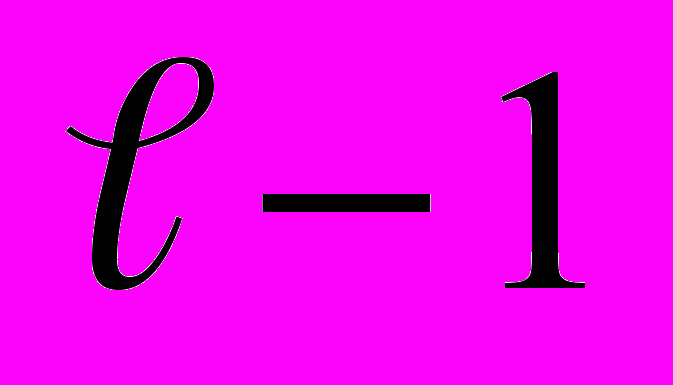ступенем волі . Тому процедура перевірки полягає у :

1) розрахунку по (2.1) сподіваного значення критерію;

2) знаходженню критичного значення Хі квадрат при заданому рівні значимості по таблицям або за допомогою комп’ютерних програм;

Якщо сподіване значення менше за критичне – немає підстав відкинути гіпотезу про однорідність розподілу. Якщо навпаки – розподіл у обох вибірках слід вважати різним.

2.4 Приклад виконання завдання

2.4.1 Перша частина завдання – розробка програми-генератора випадкових чисел за даними спостережень, містить такі етапи:

а) обробку даних спостережень, побудова гістограми розподілу,

б) створення та відладку програми-генератора,

в) генерацію послідовності чисел та перевірку її відповідності розподілу

2.4.2 При роботі з великими вибірками використання “перетаскування” становиться незручним. Тому рекомендується такий прийом:

а) Поділити екран пополам, перетягнув на середину розподілювач, що міститься у верхньому правому куту, вище смуги вертикальної прокрутки.

б) У верхній частині розмістити початок вибірки, у ніжній частині - останні рядки вибірки.

в) Для виділення вибірки:

1) Встановити курсор на першу комірку вибірки.

2) Натиснути клавішу і, не відпускаючи її, встановити курсор на останню комірку.

3) Після відпускання клавіш діапазон буде виділеним, з ним можна проводити операції копіювання, форматування, т.д.

г) Для копіювання формули комірок по діапазону:

1) Створюємо формулу у перший комірці діапазону.

2) Копіюємо її у буфер за допомогою клавіші копіювання на панелі інструментів.

3) Виділяємо діапазон, де повинна міститись формула (як у пп. в))

Натискуємо на клавішу “Вставить” на панелі інструментів.

д) Аналогічно можна вставити декілька формул у суміжні комірки:

2.4.3 Обробка даних спостережень, побудова гістограми розподілу:

а) Дані завдання у кількості 2000 елементів переносяться у стовпець на робочому аркуші Excel. З метою економії місця повна вибірка у друкованому виді не наводиться. Робочий аркуш ділиться на 2 частини згідно пп. 2.4.2а).

б) За допомогою функції МАКС() визначається величина максимального елемента вибірки. Округляємо його у більшу сторону до найближчого кратного 10.

в) За найменший елемент приймаємо 0.

г) Поміщаємо значення верхніх границь діапазонів у рядку над першим рядком вибірки. При цьому, безпосередньо над першим елементом вибірки поміщаємо значення “0” (рис.2.1, рядок 3).

д) У комірці С4 створюємо формулу, яка поміщає у комірку 1 або 0, в залежності від того, міститься лі елемент вибірки між двома границями:

=ЕСЛИ(И($B4>B$3;$B4<=C$3);1;0)

е) Копіюємо формулу в буфер, виділяємо весь діапазон і вставляємо формулу.

ж) У рядку 2004 розраховуємо суми елементів рядків – абсолютні частоти. Формула комірки С2004:

=СУММ(C4:C2003)

Протягуємо формулу до кінця рядку.

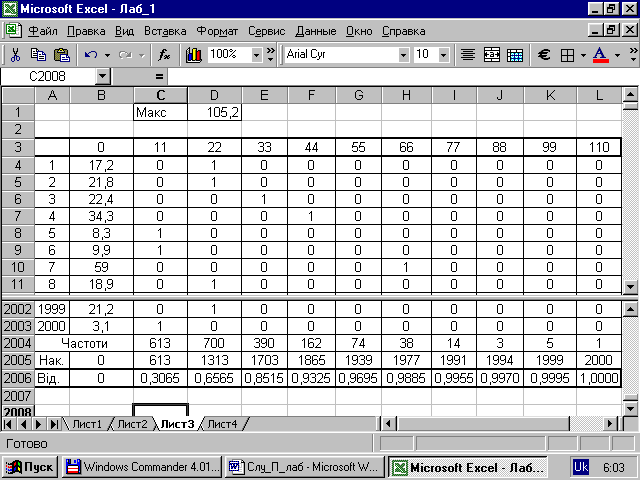
Рисунок 2.1

з) У рядку 2005 розраховуємо накопичені частоти – суму абсолютних частот усіх комірок, що попереджають даної. У комірці В2006 поміщуємо значення “нуль”. У комірці C2005 будуємо формулу:

=B2005+C2004

Протягуємо формулу до кінця рядку таблиці.

и) Підраховуємо відносні накопичені частоти шляхом ділення вмісту комірок рядку 2005 на суму елементів вибірки (2000).

з) Одержуємо дані - таблицю накопичених відносних частот, прообраз інтегральної функції розподілу (табл. 2.1)

Таблиця 2.1

№	Інтервал		Р	№	Інтервал		Р
	лів.	пр			лів.	пр
1	0	11	0,3065	6	55	66	0,9885
2	11	22	0,6565	7	66	77	0,9955
3	22	33	0,8515	8	77	88	0,997
4	33	44	0,9325	9	88	99	0,9995
5	44	55	0,9695	10	99	110	1

Blog

Випадкові процеси