Geum.ru

Краевые задачи механики сплошной среды, численные и численно-аналитические методы решения

Вид материалаЗадача

Содержание


Список литературы
Подобный материал:

Секция “Краевые задачи механики сплошной среды, численные и численно-аналитические методы решения”

УДК 519

Цветков А.Б., Цветков Б.Г.

Новокузнецкий филиал-институт Кемеровского государственного университета, г. Новокузнецк

Сибирский государственный индустриальный университет, г. Новокузнецк

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ УПРУГОГО ПРЯМОУГОЛЬНОГО ТЕЛА ПОД ВОЗДЕЙСТВИЕМ ПОВЕРХНОСТНЫХ СИЛ ПРИ СМЕШАННЫХ ГРАНИЧНЫХ УСЛОВИЯХ

Распространен метод конечных элементов на решение краевых задач теории упругости без их вариационной постановки. Разработана компьютерная программа для расчета напряженно-деформированного состояния упругого прямоугольного тела при заданных смешанных граничных условиях на его любой части геометрической границы.


Авторами составлена компьютерная программа для решения численными методами смешанных краевых задач теории упругости в прямоугольнике G: axb, dyc, где a, b, c ,d – заданные постоянные (рисунок 1). Пусть в области G заданы кусочно–непрерывные функции:

p=p(x,y), q=q(x,y), = (x,y), = (x,y). Значения параметров в задачах 1,2: a=0, b=100, c=10, d=0, h=30, H=30, =1, =1, p=0, q=0.

Задача 1. Найти вектор перемещений U=(u,v), u=u(x,y), v=v(x,y), удовлетворяющий в области G системе дифференциальных уравнений теории упругости:

(uxx+ uyy)+(+)(uxx+ vxy)=p,

(vxx+ vyy)+(+)(uxy+ vyy)=q.

На сторонах x=a и x=b, y(d,c) области G выполняются условия: u(a,y)=0; u(b,y)=0; v(a,y)=0; v(b,y)=0. На отрезках y=d, x(a,h), и y=d, x(H,b), где h и H, ah, заданные постоянные, выполняются условия: v(x,d)=0, axh, и v(x,d)=0, Hxb.

На границе y=c, axb, напряжение y =y(x,y) удовлетворяет условию: y(x,c)=0.1, а на границе y=d, axb, выполняется условие y(x,d)=0, x(h,H). При вычислении по программе не требуется вариационной постановки задачи [1,2,3,4,5].



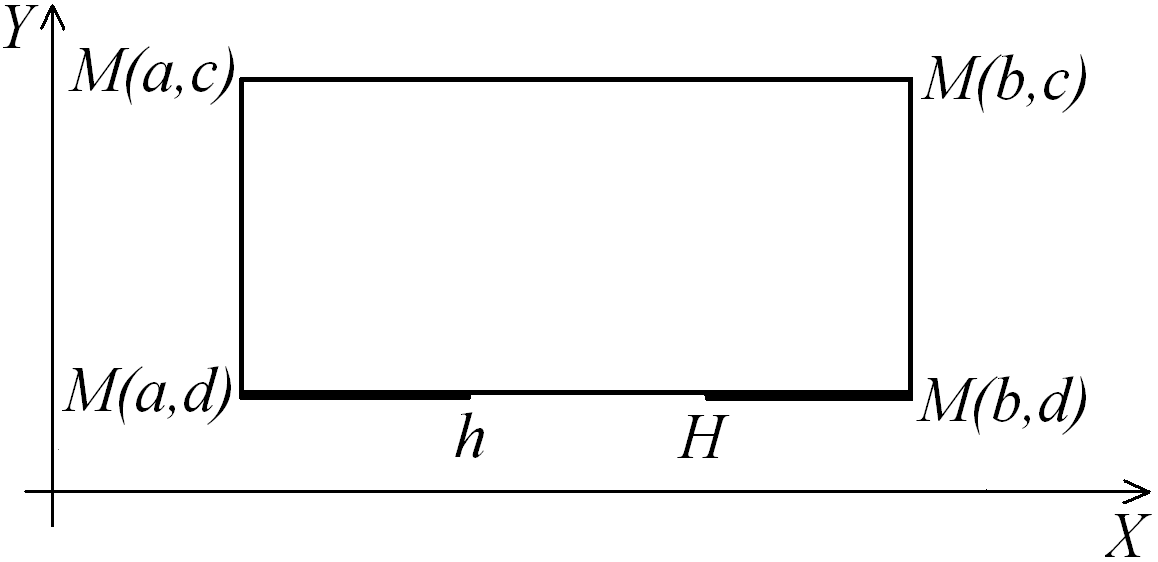
Рисунок 1 - Расчетная область



а б

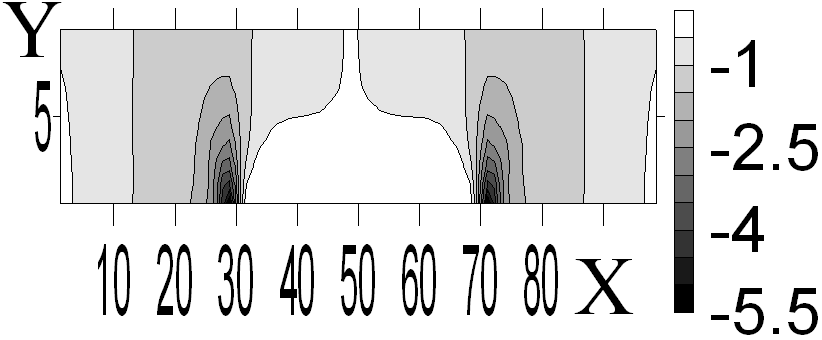
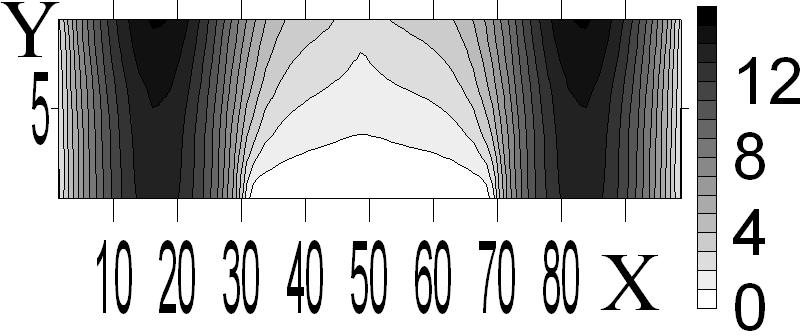
Рисунок 2 - Результаты математического моделирования: а – перемещения v; б - компонента y

Для получения численного решения по программе расчетная область G разбивалась на 800 конечных элементов – прямоугольников. Значения напряжений и перемещений вычислялись в центрах конечных элементов. Ниже приведены картины линий уровня перемещений v и напряжений y (рисунок 2).

На рисунках 2а приведены картины распределения перемещений v, 2б распределение напряжений y, полученных в результате проведения вычислительного эксперимента. Тонкие линии - это линии уровня, построенные по численным значениям перемещений (рисунок 2а) и напряжений (рисунок 2б). Из рисунка 2а видно, что у нижней границе расчетной области унок=10, на участках с заданными нулевыми перемещениями x(a,h) и x(H,b) соответствующая компонента перемещений равна нулю. Перемещения на участке x(h, H) отличны от нулевых. Из рисунка 2б видно, у нижней границы расчетной области y=10, на участке x(h, H) с напряжения y равны нулю. Модуль напряжения y на участках x(a,h) и x(H,b) отличен от нуля. У нижней границы на рисунке 2б наблюдаются две области концентрации напряжений y.

Задача 2. На отрезках y=d, x(a,h), и y=d, x(H,b), выполняются условие: y(x,d)=0, а на отрезке y=d , x(h,H), выполняется условие: v(x,d)=0. Остальные условия сохраняются.

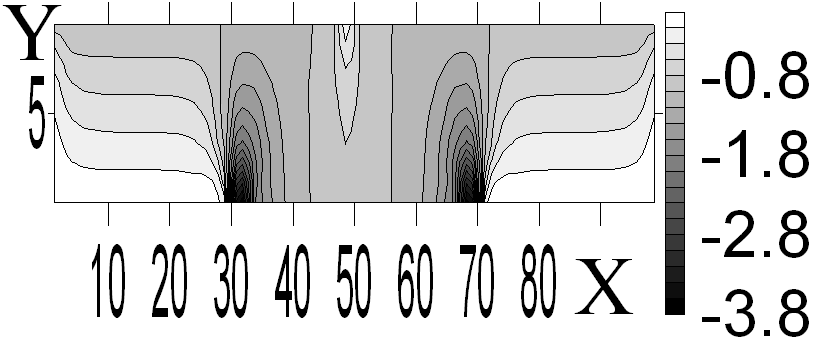
Ниже приведены картины распределения линий уровня перемещений v и напряжений y (рисунок 3).




а б

Рисунок 3 - Результаты математического моделирования после изменения граничных условий: а – перемещения v; б - компонента y

Из рисунка 3а видно, что у нижней границы расчетной области y=10, на участке с заданными нулевыми перемещениями x(h, H) соответствующая компонента перемещений равна нулю. Перемещения на участках x(a,h) и x(H,b) отличны от нулевых. Из рисунка 3б видно, что на нижней границе расчетной области y=10, на участках x(a,h) и x(H,b) напряжения y равны нулю. Напряжение y на участке x(h, H) отлично от нуля.


Примеры 1 и 2 иллюстрируют применение разработанной программы для моделирования напряженно-деформированного состояния упругой расчетной области при смешанных граничных условиях, заданных на одной геометрической границе.

СПИСОК ЛИТЕРАТУРЫ

1. Цветков А.Б. О методе глобальной аппроксимации / А.Б.Цветков // Материалы четырнадцатой международной конференции по вычислительной механике и современным прикладным программным системам (ВМСППС-2005) – Алушта: - М.: Вузовская книга, 2005. - С. 439-440.

2. Цветков А.Б. Восстановление значений функций внутри пространственной области по заданным значениям на границе численным методом / А.Б.Цветков, Б.Г.Цветков // VI Всероссийская конференция молодых ученых по математическому моделированию и информационным технологиям - Кемерово: Изд-во Кемеровского государственного унивеситета, 2005. – С. 26.

3. Цветков Б.Г. Восстановление значений функции внутри пространственной области по заданным ее значениям на границе / Б.Г.Цветков, А.Б.Цветков // IV Всероссийская научно-практическая конференция “Информационные технологии и математическое моделирование (ИТММ-2005) – Анжеро-Судженск: Изд-во Томского университета, 2005. – С. 81-83.

4. Цветков А.Б. Восстановление значений функции по ее заданным значениям на границе / А.Б.Цветков, Б.Г.Цветков // IV Всероссийская конференция “Математика, информатика, управление” (МИУ-2005) – Иркутск. 2005. – CD-ROM

5. Цветков А.Б. Восстановление вектора перемещений краевой задачи теории упругости по заданным его значениям на границе прямоугольной двусвязной области / А.Б.Цветков, Б.Г.Цветков // XI Международная научная конференция, посвященная памяти генерального конструктора ракетно-космических систем академика М.Ф. Решетнева – Красноярск: Изд-во Сиб.гос. аэрокосмич. ун-та, 2007. – С. 265-267.