Geum.ru

Секция “Численные и численно-аналитические методы решения краевых задач

Вид материалаДокументы
Подобный материал:

Секция “Численные и численно-аналитические методы решения краевых задач

тепло- и массообмена”

УДК 541.124/128

Евсеева С.И.

Омский государственный технический университет, г. Омск

Вычисление концентрационной зависимости коэффициента диффузии при помощи имитационного моделирования простейших поверхностей методом Монте-Карло без использования формул Кубо

Моделирование процессов на поверхности методом Монте-Карло имеет ряд преимуществ, в частности, метод Монте-Карло позволяет вводить в модель по существу любые представления о реальном процессе. В данной работе рассматривается случай поверхностной диффузии мономеров в рамках модели решеточного газа (МРГ). Для этой модели традиционно используются два подхода: детерминистский и имитационный.
Т=500; е=10
Здесь предлагается новый подход, сочетающий достоинства обоих методов. Показана высокая эффективность предложенного подхода.


Термодинамическое описание неравновесных процессов возможно лишь при достаточно медленном изменении параметров состояния в пространстве и во времени для состояний, близких к равновесным.

Проблема диффузии — это одна из ключевых проблем физики. Важнейшим показателем диффузионной подвижности атомов является коэффициент диффузии.

Вычисление коэффициента диффузии для системы сильно взаимодействующих частиц является непростой задачей. Мы рассматриваем случай поверхностной диффузии мономеров в рамках модели решеточного газа (МРГ).

Для этой модели традиционно используются два подхода: детерминистский [1], основанный на следующем соотношении:

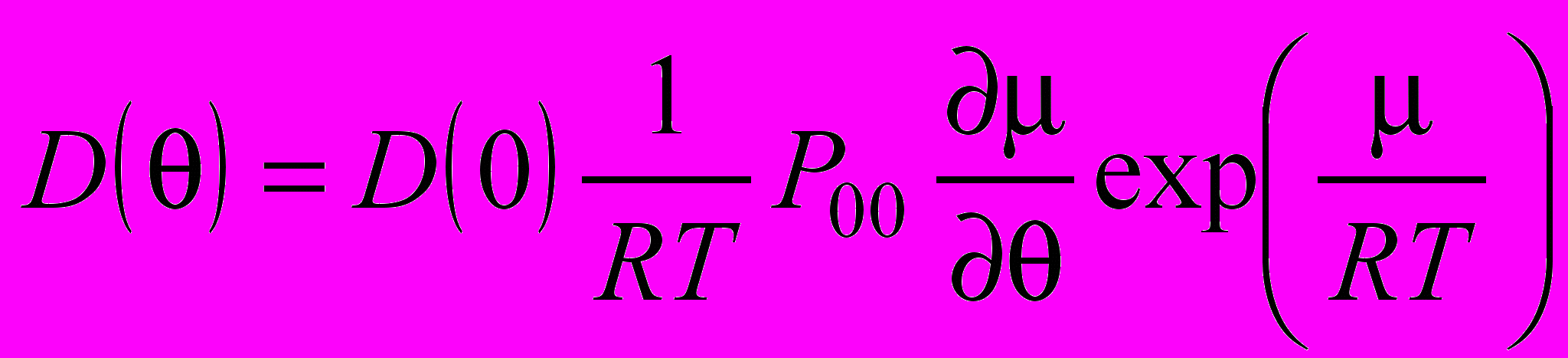, (1)

где 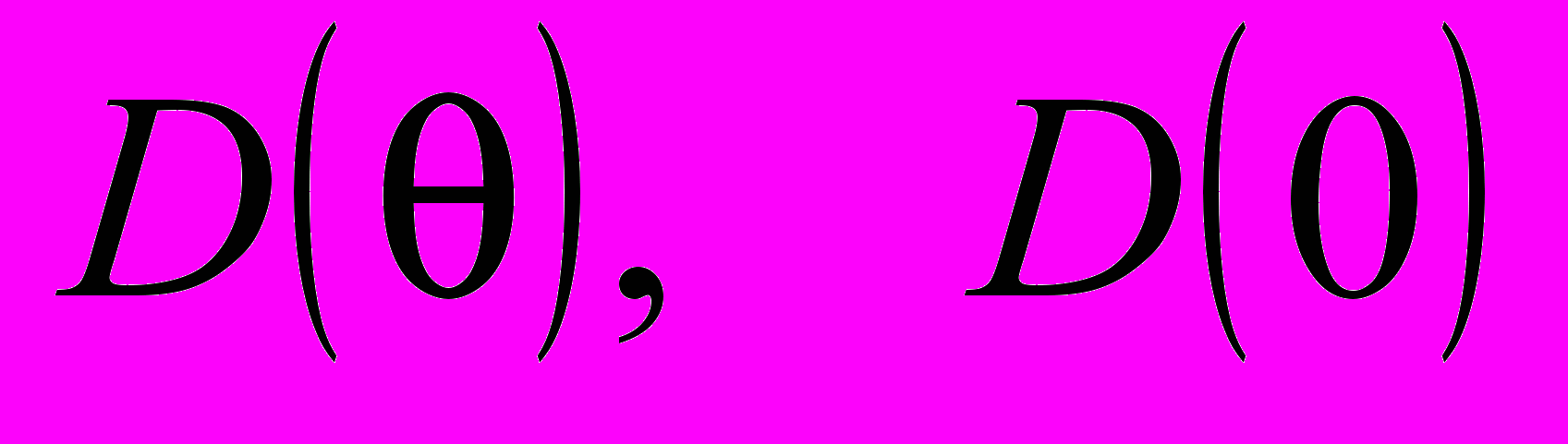- коэффициент диффузии как функция степени покрытия и для чистой поверхности соответственно;

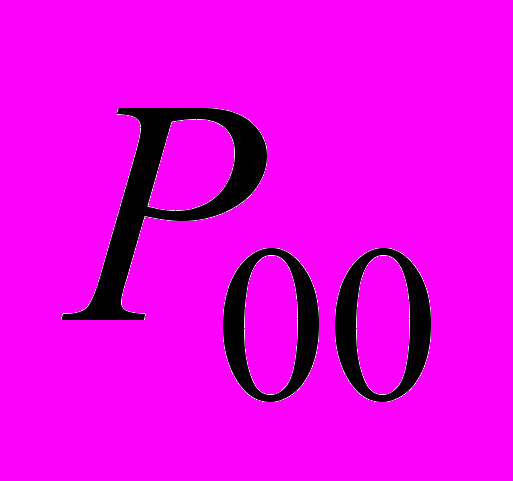- вероятность найти пару пустых соседних ячеек;

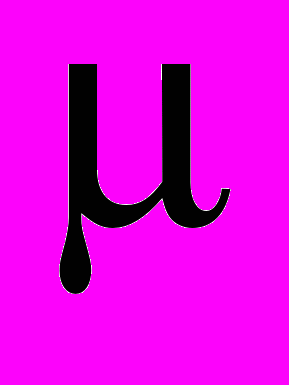- химический потенциал;

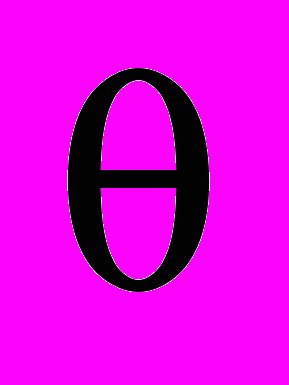- степень покрытия;

R, T - универсальная газовая постоянная и абсолютная температура.

Второй подход – имитационный, использует формулы Кубо [1]. Формула (1) является точной в рамках МРГ, теории переходного состояния и предположении о локальной термодинамической равновесности адсорбционного слоя. При вычислении параметров формулы (1) используется один из кластерных методов или реже метод трансфер-матрицы и ренорм-группы. Основным недостатком первого подхода является то, что с его помощью не удаётся рассмотреть более сложные модели, а недостаток второго метода состоит в трудоёмкости вычислений.

Мы предлагаем новый подход, сочетающий достоинства обоих методов, т.е. будем пользоваться формулой (1), но вычислять параметры методом Монте-Карло.

Была разработана модель поверхности на квадратной решётке, основанная на стандартной модели решётчатого газа. В модели учитываются как биографическая, так и индуцированная неоднородность.

Термодинамический гамильтониан для построенной модели может быть записан следующим образом:

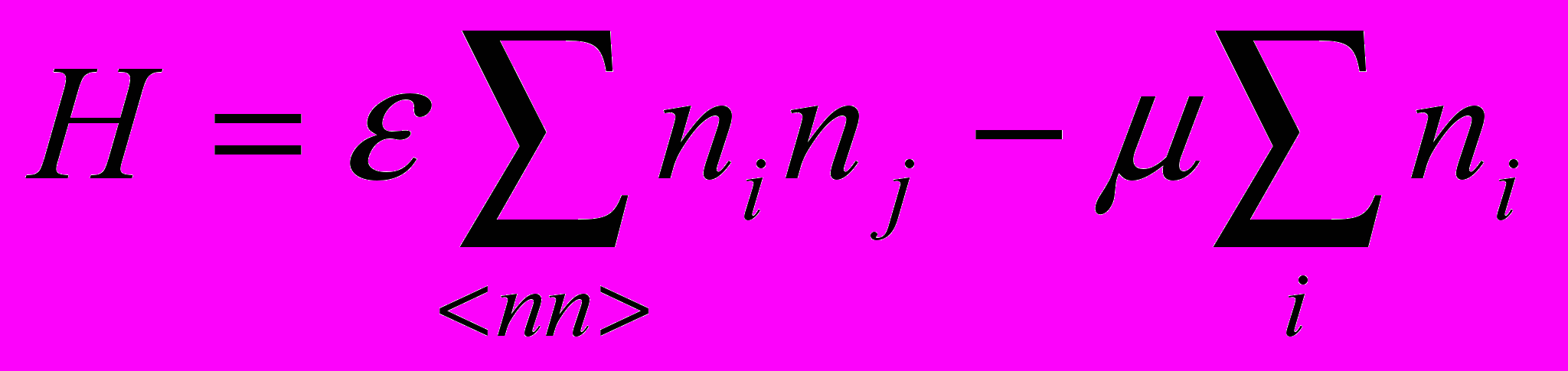, (2)

где ε - латеральная энергия взаимодействий ближайших соседей;

µ - химический потенциал частиц;

обозначает суммирование по всем ближайшим соседним парам ячеек;

ni - числа заполнения, принимающие значение 1, если ячейка занята и 0, если свободна.

Метод Монте-Карло основан на использовании случайных чисел. Его сущность состоит в следующем: производят n испытаний, в результате которых получают n возможных значений и вычисляют их среднее арифметическое. Поскольку метод Монте Карло требует проведения большого числа испытаний, при его использовании уменьшается дисперсия случайных величин, в результате чего уменьшается ошибка.

Моделирование процессов на поверхности методом Монте-Карло имеет ряд преимуществ, в частности, метод Монте-Карло позволяет вводить в модель по существу любые представления о реальном процессе. Основой метода является так называемое основное уравнение (уравнение Колмогорова, master equation):

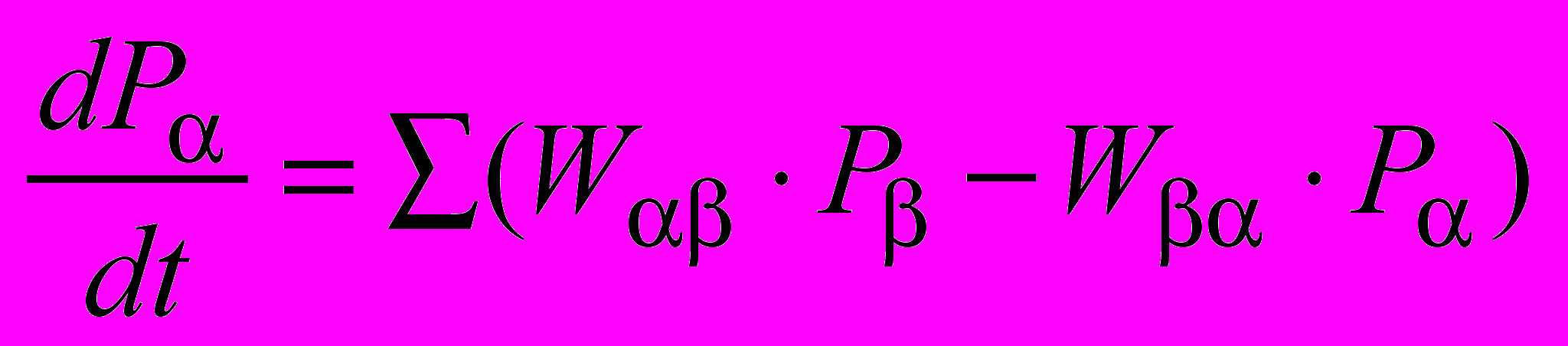, (3)

где t - время,

α, и β – конфигурации состояния поверхности,

Pα, и Pβ - их вероятности,

Wαβ и Wβα - так называемые вероятности перехода в единицу времени, которые определяют скорость, с которой изменяется состояние поверхности при реакции.

Основное уравнение наиболее общее уравнение изменения вероятности состояния системы (в данном случае поверхности). Из уравнения (3) видно, что полная вероятность сохраняется

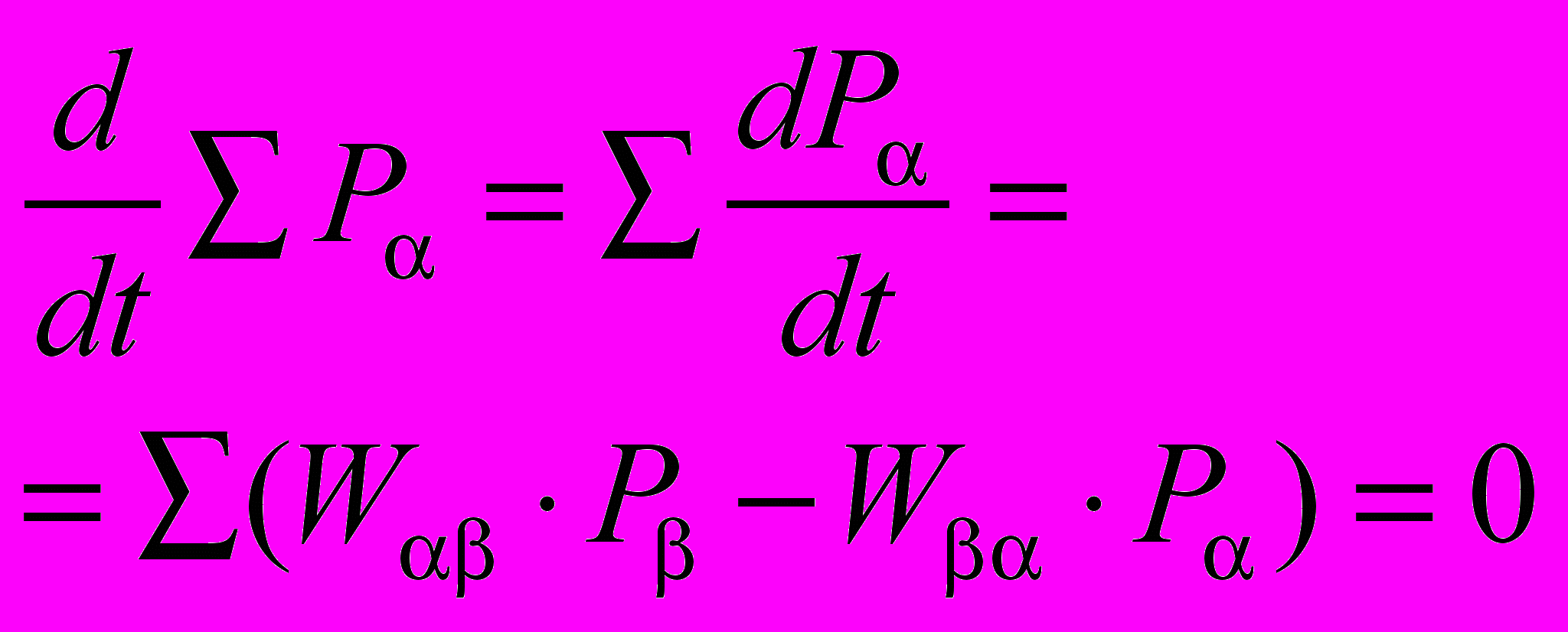(4)

Значения вероятностей перехода могут быть вычислены при помощи квантово-химических методов или из экспериментальных данных. Существует много различных алгоритмов, реализующих метод Монте-Карло: одни выводятся из основного уравнения и приводят к результатам, которые являются статистически идентичными, другие не могут быть получены из основного уравнения, и от них нужно отказаться.

При моделировании нами использовался упрощённый вариант кинетического метода Монте-Карло. Проблема реального времени в алгоритмической формулировке метода Монте-Карло была решена Fichthorn и Weinberg. Их метод называют Кинетическим методом Монте-Карло (KMC). Основное предположение, лежащее в основе метода – интервалы времени между последовательными событиями распределены в соответствии с распределением Пуассона, а переходные вероятности определяются из распределения Больцмана.

Блок алгоритма кинетического метода Монте-Карло состоит в следующем:

1. Инициализация

Генерируется начальная конфигурация α. Устанавливается начальный момент времени t. Выбирается условие, при котором нужно остановить моделирование.

2. Время реакции

Генерируется интервал времени Δt, в которое не происходит реакция. Время изменяется от t к t + + Δt.

3. Реакция

Изменяется конфигурация, в зависимости от вероятности перехода, то есть происходит реакция.

4. Проверка условий

Если условия остановки выполнены, тогда происходит остановка. Если нет, то повторение со второго шага.

Так как нас интересует только равновесное состояние поверхности, мы упрощаем алгоритм, по существу, исключая время, но сохраняем выбор вероятностей перехода. Такой упрощённый алгоритм оказывается, за исключением выбора вероятностей перехода, тождественным алгоритму Метрополиса [2].

Подсчёт вероятности изменения состояния для пустой ячейки производится по формуле:

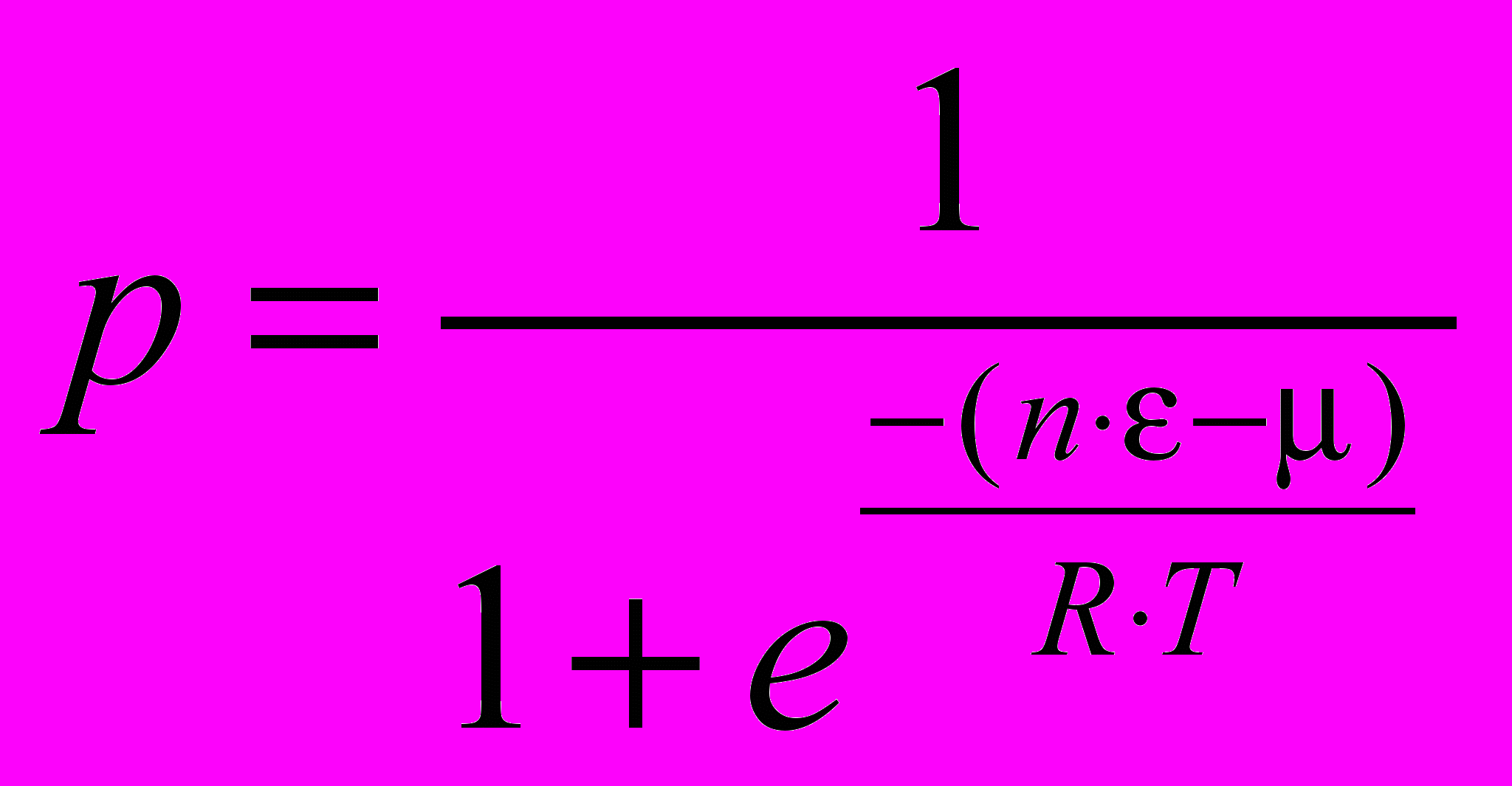, (5)

где n*ε - энергия взаимодействия ближайших соседей.

Подсчёт вероятности изменения состояния для занятой ячейки производится по соответствующей формуле:

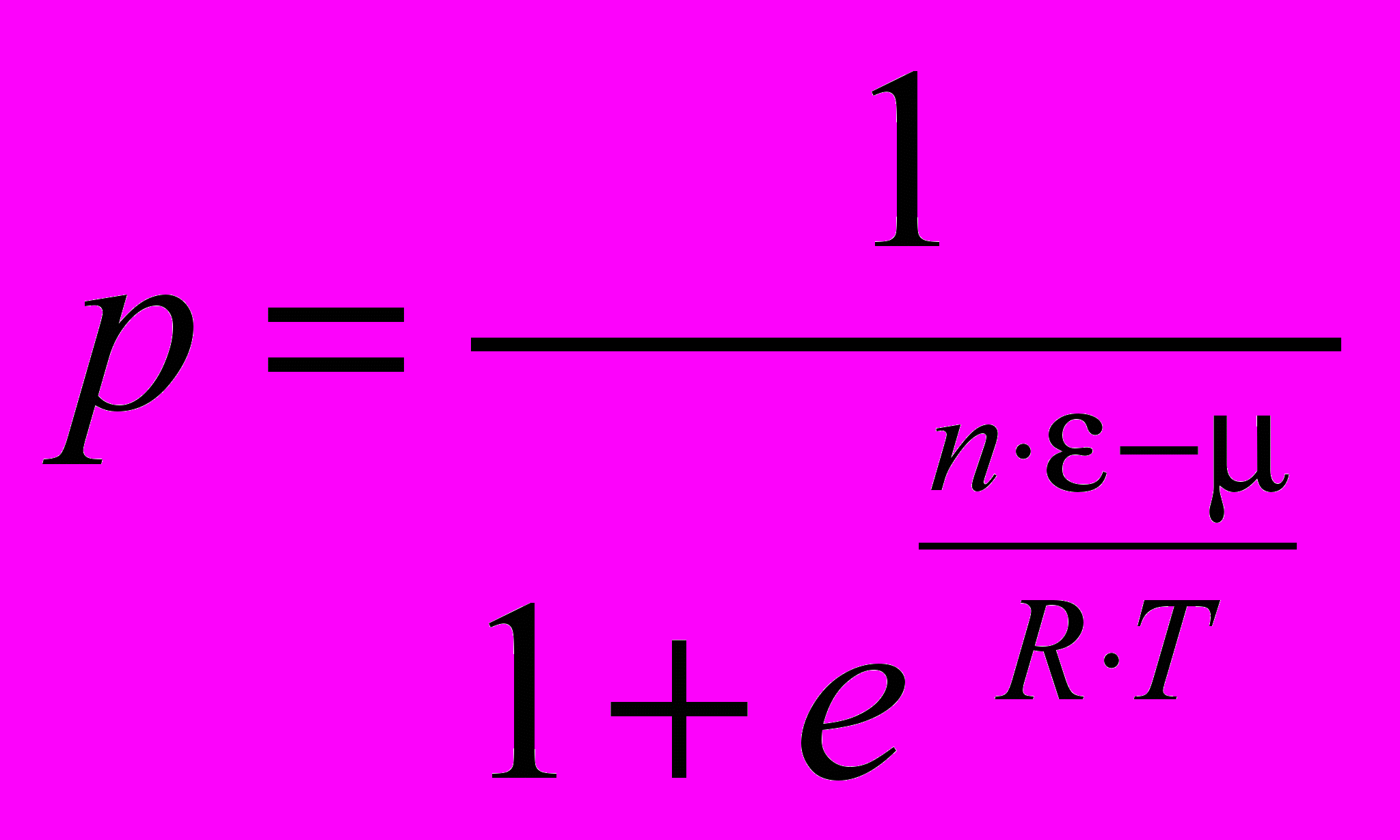, (6)

При построении изотерм при каждом значении химического потенциала производилось от 105 до 106 монтекарловских шагов (мы пользуемся стандартным определением шага как количества попыток, равного количеству ячеек на решётке). Усреднение проводилось по второй половине шагов. Размер решётки варьировался от 100х100 до 100х300.

На рисунках показана зависимость логарифма коэффициента диффузии, производной и вероятности от степени покрытия для модели с отталкиванием ближайших соседей на квадратной решетке, которая воспроизводит зависимость, полученную ранее другими методами.



Рисунок 1 - График зависимости логарифма коэффициента диффузии от степени покрытия


Предложен новый подход к вычислению коэффициента диффузии, позволяющий соединить достоинства двух методов, использовавшихся ранее. Предложенный подход показал свою высокую эффективность. Результаты, полученные нами в ходе исследования, полностью совпадают с результатами, полученными ранее детерминистскими методами. Использование метода Монте-Карло для вычисления параметров формулы (1) позволяет исследовать более сложные решёточные модели поверхности.



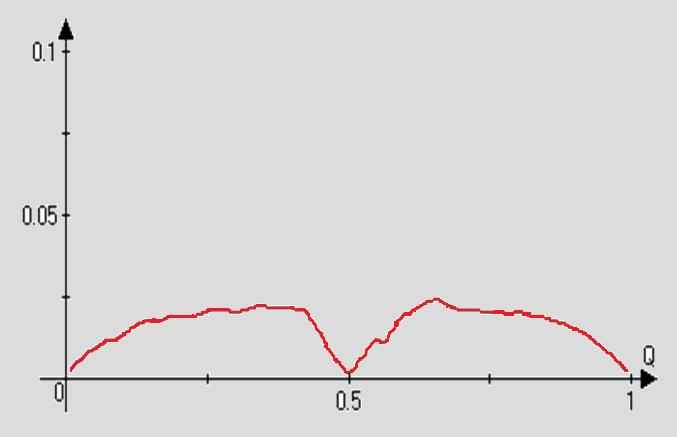
Рисунок 2 - График зависимости производной от степени покрытия



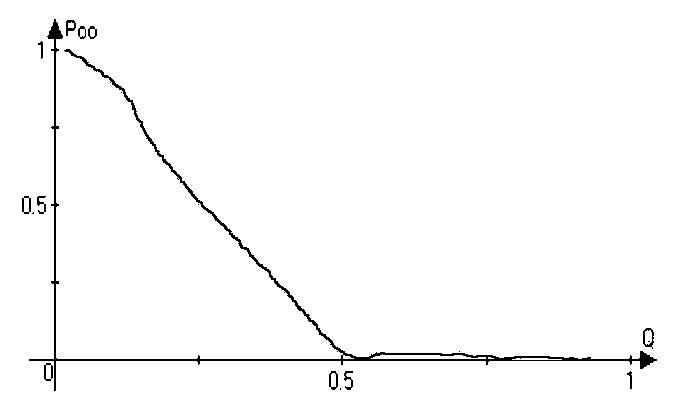
Рисунок 3 - График зависимости вероятности Р00 от степени покрытия


СПИСОК ЛИТЕРАТУРЫ

1. A.V. Myshlyavtsev, A.A. Stepanov, Ch. Uebing, V.P. Zhdanov. Surface diffusion and continuous phase transitions in adsorbed overlayers, Phys. Rev., V 52, № 8, P. 5977 (1995).

2. Metropolis N., Rosenbluth A. W., Rosenbluth M. N., Teller A. W., Teller E. Equation of state calculations by fast computing machines//J. Chem. Phys. – 1953. – V.21. – P.1087.

3. Zhdanov V.P. Elementary Physicochemical Processes on Solid Surfaces. New York: Plenum, 1991.