Н. А. Болячина Руководитель работы

Вид материала

Документы

Содержание 2 Основные понятия экономико-математического моделирования 3 2Основные понятия экономико-математического моделирования Математическое моделирование Экономико-математическое моделирование 3ПОСТРОЕНИЕ МОДЕЛИ ЗАДАЧИ 3.1Постановка задачи Изготовитель → потребитель Таблица 1. Параметры перевозок от изготовителей к оптовым базам Таблица 2. Параметры перевозок от оптовых баз к потребителям Таблица 3. Параметры перевозок от изготовителей к потребителям 3.2Поэтапное построение модели 3.2.2Построение содержательной модели Управляющие (независимые) переменные 3.2.3Построение математической модели Общая сумма затрат на перевозки 3.2.4Математический анализ модели, выбор метода решения Исходные параметры модели транспортной задачи Искомые параметры модели ТЗ 3.2.5Подготовка исходных данных Формулы экранной формы задачи. =суммпроизв(b3:f6; b12:f15) ... Полное содержание

Подобный материал:

• Работы, 13.71kb.
• Задачи центра: анализ работы каждой группы; подготовка решения педагогический совета., 119.94kb.
• Н. С. Герасимов Руководитель работы, 211.79kb.
• Меркулова Галина Петровна Место работы : учитель моу сош №15, руководитель литературно-краеведческого, 65.04kb.
• Тезисы Тема работы, 37.22kb.
• Лиснюк Оксаны Вячеславовны по русскому языку Рассмотрено на заседании педагогического, 2394.08kb.
• Работы, 11kb.
• Руководитель работы: Голованова О. В., педагог дополнительного образования гбоу лицей, 36.63kb.
• Чешенко Елена Константиновна. Матвей Коротаев, дк «Прометей», руководитель Тамеева, 32.3kb.
• Положение о работе классного руководителя классный, 88.53kb.

Министерство образования и науки российской федерации Государственное образовательное учреждение высшего профессионального образования Московский государственный индустриальный университет (ГОУ МГИУ)

Кафедра экономики и управления производством

К У Р С О В А Я Р А Б О Т А
по дисциплине: «Экономико-математическое моделирование»
на тему «Создание модели и решение задачи оптимизации на примере организации системы снабжения»
Группа	6168(в)
Студент	_______________ (подпись)	Н.А. Болячина
Руководитель работы, старший преподаватель	_______________ (подпись)	И. В. Риттер
Оценка работы Дата	_____________	«___» ___________

МОСКВА 2011


СОДЕРЖАНИЕ

1ВВЕДЕНИЕ

Моделирование, как метод научного познания, стало применяться еще в глубокой древности и постепенно захватило все новые области научных познаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки.

Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования XX век. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться важная роль моделирования как универсального метода научного познания.

Применение математических методов, в том числе и методов математического моделирования, в экономике в целом имеет длительную историю.

2ОСНОВНЫЕ ПОНЯТИЯ ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Моделирование – исследование какого-либо явления, процесса или системы объектов путём построения и изучения моделей.

Моделирование используется тогда, когда невозможно исследовать или объект ещё не существует, и для проверки различного рода гипотез. Целью математического моделирования экономических систем является использование методов математики для наиболее эффективного решения задач, возникающих в сфере экономики, с использование, как правило, современной вычислительной техники.

Современная экономическая наука широко использует математические методы как для решения прикладных, практических задач, так и для теоретического моделирования социально-экономических явлений и процессов. Математические методы стали составной частью методов любой экономический науки, включая экономическую теорию. Её использование в единстве с обстоятельным экономическим анализом открывает новые возможности для экономической науки и практики.

Как и всякое моделирование, экономико-математическое моделирование основывается на принципе аналогии, т.е. возможности изучения объекта посредством построения и рассмотрения другого, подобного ему, но более простого и доступного объекта его модели.

Практическими задачами экономико-математического моделирование являются, во-первых, анализ экономических объектов; во-вторых, экономическое прогнозирование, предвидение развитие хозяйственных процессов и поведение отдельных показателей; в-третьих, выработка управленческих решений на всех уровнях управления.

Моделирование – непрерывный процесс совершенствования модели, в котором знания о реальном объекте извлекаются из выявления несоответствий между моделью и объектом, их осмысления и устранения.

Математическое моделирование – метод исследования реальных объектов при помощи постановки экспериментов на их математических моделях. Математическая модель – это представление модели в математической форме, т.е с помощью математических формул, таблиц, графиков и т.п.

Экономико-математическое моделирование (по В.С.Немчинову) – это концентрированное выражение наиболее существенных взаимосвязей и закономерностей поведения управляемой экономической системы в математической форме.

Модели по фактору времени распределяются на статические и динамические. В статических моделях система представляется неизменной во времени. Динамические модели содержат информацию о поведении системы и ее составных частей во времени. По учету фактора неопределенности модели делятся на детерминированные и стохастические. Стохастическая модель — такая экономико-математическая модель, в которой параметры, условия функционирования и характеристики состояния моделируемого объекта представлены случайными величинами и связаны стохастическими (т. е. случайными, нерегулярными) зависимостями, либо исходная информация также представлена случайными величинами. Следовательно, характеристики состояния в модели определяются не однозначно, а через законы распределения их вероятностей. Детерминированная модель — аналитическое представление закономерности, операции и т. п., при которых для данной совокупности входных значений на выходе системы может быть получен единственный результат.

По отношению к принятию решения модели разделяются на дескриптивные и нормативные.

Модели, предназначенные для объяснения наблюдаемых фактов или прогноза поведения объекта, называют дескриптивными. Модель, при построении которых преследуется цель определения состояния объекта, которое является наилучшим с точки зрения определенного критерия, называется нормативным.

Итак, практической задачей нашего экономико-математического моделирования является анализ выбора оптимального способа организации снабжения потребителей продукцией предприятий-изготовителей. Наша модель является статической, детерминированной и нормативной.

3ПОСТРОЕНИЕ МОДЕЛИ ЗАДАЧИ

3.1Постановка задачи

Цель: Приобретение навыков решения задач линейного программирования в табличном редакторе Excel. Формирование транспортной модели задачи линейного программирования и решение задачи средствами табличного редактора Excel. Приобретение навыков адаптации транспортной модели линейного программирования для оптимизации системы снабжения, допускающей транзитные перевозки.

ЗАДАЧА

По заказу пяти потребителей А, Б, В, Г, Д на четырех предприятиях-изготовителях производится продукция. В процессе доставки к потребителям продукция может храниться на трех оптовых базах. Существуют следующие три способа организации снабжения потребителей продукцией:

ИЗГОТОВИТЕЛЬ → ПОТРЕБИТЕЛЬ,

то есть вся продукция, произведенная изготовителями, напрямую доставляется потребителям, минуя оптовые базы.

ИЗГОТОВИТЕЛЬ → ОПТОВАЯ БАЗА → ПОТРЕБИТЕЛЬ,

то есть вся продукция, произведенная изготовителями, сначала складируется на оптовых базах и только потом развозится потребителям. Если мощностей оптовых баз не хватает, остатки продукции развозятся напрямую с предприятий потребителям.

ИЗГОТОВИТЕЛЬ ,

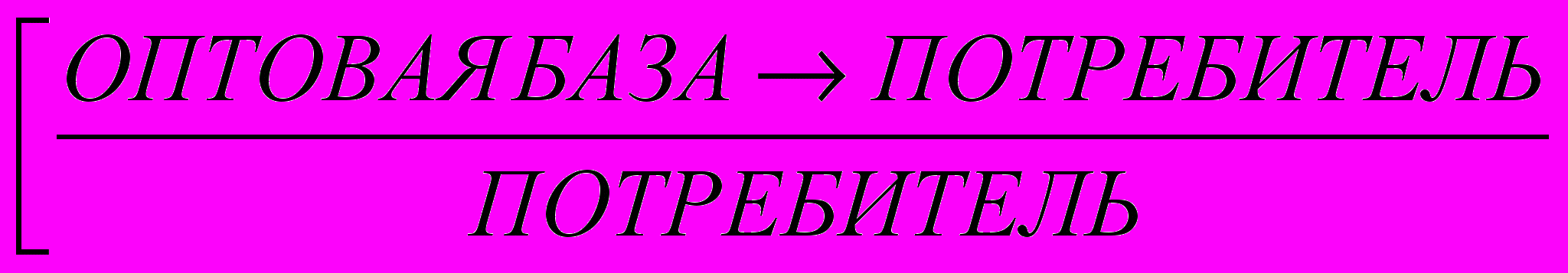то есть продукция, произведенная изготовителями, доставляется потребителям частично напрямую, а частично транзитом через оптовые базы, исходя исключительно из задачи минимизации расходов.

Необходимо выбрать оптимальный способ организации снабжения потребителей продукцией предприятий-изготовителей.

В таблицах 1-3 приведены стоимость перевозки и товарные мощности производителей, оптовых баз и потребителей товара.

Таблица 1. Параметры перевозок от изготовителей к оптовым базам

	Оптовая база 1	Оптовая база 2	Оптовая база 3	Произведено изготовителями
Изготовитель 1	14	15	45	720
Изготовитель 2	18	12	40	770
Изготовитель 3	21	18	25	800
Изготовитель 4	25	16	10	1040
Запасы на базах	800	700	1200

Таблица 2. Параметры перевозок от оптовых баз к потребителям

	Потреби-тель А	Потреби-тель Б	Потреби-тель В	Потреби- тель Г	Потреби- тель Д	Запасы
Оптовая база 1	15	12	21	30	25	800
Оптовая база 2	20	24	25	41	13	700
Оптовая база 3	12	13	26	16	36	1200
Спрос на товар потребителями	730	600	620	880	500

Таблица 3. Параметры перевозок от изготовителей к потребителям

	Потреби-тель А	Потреби-тель Б	Потреби-тель В	Потреби- тель Г	Потреби- тель Д	Произве-дено
Изготовитель 1	10	22	34	50	20	720
Изготовитель 2	24	18	20	14	26	770
Изготовитель 3	32	43	16	28	10	800
Изготовитель 4	16	30	55	45	46	1040
Спрос на товар потребителями	730	600	620	880	500

Математическая модель – это некоторый математический образ исследуемой экономической системы, который адекватно отражает структуру переменных системы, их свойства и взаимосвязи.

3.2Поэтапное построение модели

3.2.1Постановка экономической проблемы (цели).

Экономическая проблема состоит в минимизации транспортных расходов при транспортировке товаров. Разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, неэффективных перевозок. Это сокращает время продвижения товаров, уменьшает затраты предприятий.

3.2.2Построение содержательной модели

На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.

Построим модель задачи на примере варианта ИЗГОТОВИТЕЛЬ – ПОТРЕБИТЕЛЬ.

Определим существенные с точки зрения достижения поставленной цели элементы задачи.

Параметры (фиксированные значения):

• количество потребителей;
  
• количество изготовителей;
  
• количество оптовых баз;
  
• мощности потребителей (заказываемые объемы продукции);
  
• мощности изготовителей (объемы производимой продукции);
  
• мощности оптовых баз (допустимое количество одновременно хранящейся продукции);
  
• цены перевозок от изготовителей на оптовые базы;
  
• цены перевозок от изготовителей потребителям;
  
• цены перевозок из оптовых баз потребителям.
  

Другие данные по организации, осуществляющей перевозку товаров, с точки зрения поставленной задачи, будем считать несущественными.

Мы можем видеть, что в таблице 3 заданы значения всех перечисленных выше параметров.

Управляющие (независимые) переменные: количество перевозимой продукции по каждому из маршрутов. В нашей задаче, единственные переменные на которые мы можем влиять – это количество продукции, доставляемой по заданным маршрутам перевозок. Меняя количество продукции, перевозимой по различным маршрутам, мы можем оптимизировать наши затраты на перевозку товара.

Итак, пусть х_ij – количество продукции, перевозимой от i-го изготовителя j-му потребителю, где i=1,…,4, j=1,…,5.

Управляемые (зависимые, рассчитываемые) переменные: суммарные затраты на перевозку F(x).

3.2.3Построение математической модели

Построение математической модели состоит в переводе сконструированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.

х_ij – количество продукции, перевозимой от i-го изготовителя j-му потребителю, где i=1,…,4, j=1,…,5.

Общая сумма затрат на перевозки:

F(x)=10*x₁₁+22*x₁₂+34x₁₃+50*x₁₄+20*x₁₅+24*x₂₁+18*x₂₂+20*x₂₃+

+14*x₂₄+26*x₂₅+32*x₃₁+43*x₃₂+16*x₃₃+28*x₃₄+10*x₃₅+16*x₄₁+ (1)

+30*x₄₂+55*x₄₃+ 45*x₄₄+46*x₄₅ → min


Ограничения:

По предприятиям-изготовителям:

x₁₁+x₁₂+x₁₃+x₁₄+x₁₅=720

x₂₁+x₂₂+x₂₃+x₂₄+x₂₅=770

x₃₁+x₃₂+x₃₃+x₃₄+x₃₅=800

x₄₁+x₄₂+x₄₃+x₄₄+x₄₅=1040


По потребителям продукции:

x₁₁+x₂₁+x₃₁+x₄₁=730 (2)

x₁₂+x₂₂+x₃₂+x₄₂=600

x₁₃+x₂₃+x₃₃+x₄₃=620

x₁₄+x₂₄+x₃₄+x₄₄=880

x₁₅+x₂₅+x₃₅+x₄₅=500


x_ij ≥ 0 для любого i, j (3)

3.2.4Математический анализ модели, выбор метода решения

Наша модель является задачей математического программирования, так как цель ее решения – оптимизация функции цели при заданных ограничениях.

Построенная нами математическая модель является задачей линейного программирования, так и функция цели является линейной функцией и все ограничения представлены в виде линейных равенств.

Общая задача линейного программирования имеет вид:
Дана система m линейных уравнений и неравенств с n переменными

a₁₁ x₁ + a₁₂ x₂ + ………..a_1n x_n ≤ b ₁

a₃₁ x₁ + a₂₂ x₂ + ………. a_2n x_n ≤ b ₂

a_k1 x₁ + a_{k 2}x₂ + …….….a_kn x_n ≤ b _k (4)

a_{k +1,1} x₁ + a_k1,2x₂ +……+ a_k+1,_n x_n = b_k+1

a_{k +2,1} x₁ + a_k2,2x₂ +…….+ a_k+2,_n x_n = b<sub>k+2

…………………………………………</sub>

a_m1x₁₊a_m2x_{2+………………+.} a_mnx_n x_n=b_n

и линейная функция

F = c₁x₁₊ c₂x₂₊ …..+c_nx_n (5)


Необходимо найти такое решение системы X = (x₁, х₂,…., х_j, ….. x_n),

где х_j >= 0 ( j = 1,2, …, l; l <= n ), (6)


при котором линейная функция F(x) принимает оптимальное (т.е. максимальное или минимальное) значение.

Система (4) называется системой ограничений, (5) – линейной функцией или функцией цели, (6) – прямые ограничения или неотрицательность переменных.

При этом: функция цели F(x) – линейная; система ограничений (4) является линейной; и выполняется условие неотрицательности, т.к. хij>=0 для любого i, j, следовательно наша модель математического программирования является линейной.

Кроме того, данная задача является частным случаем задач линейного программирования – транспортной задачей.

Стандартная транспортная задача определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Исходные параметры модели транспортной задачи

n - количество пунктов отправления, m - количество пунктов назначения.

- запас продукции в пункте отправления A_i (i = 1,n ) [ед. тов.].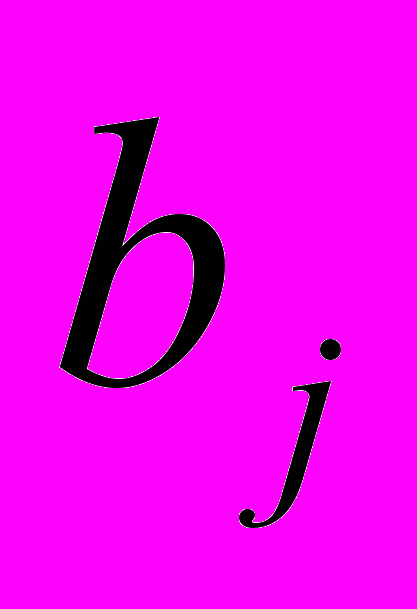

- спрос на продукцию в пункте назначения В_j: (j = l,m) [ед. тов.].

c_ij - тариф (стоимость) перевозки единицы продукции из пункта отправления A_i в пункт назначения В_j, [руб./ед. тов.].


Искомые параметры модели ТЗ

x_ij - количество продукции, перевозимой из пункта отправления A_i в пункт назначения В_j [ед. тов.].

F(X) - транспортные расходы на перевозку всей продукции [руб.].


Транспортная модель


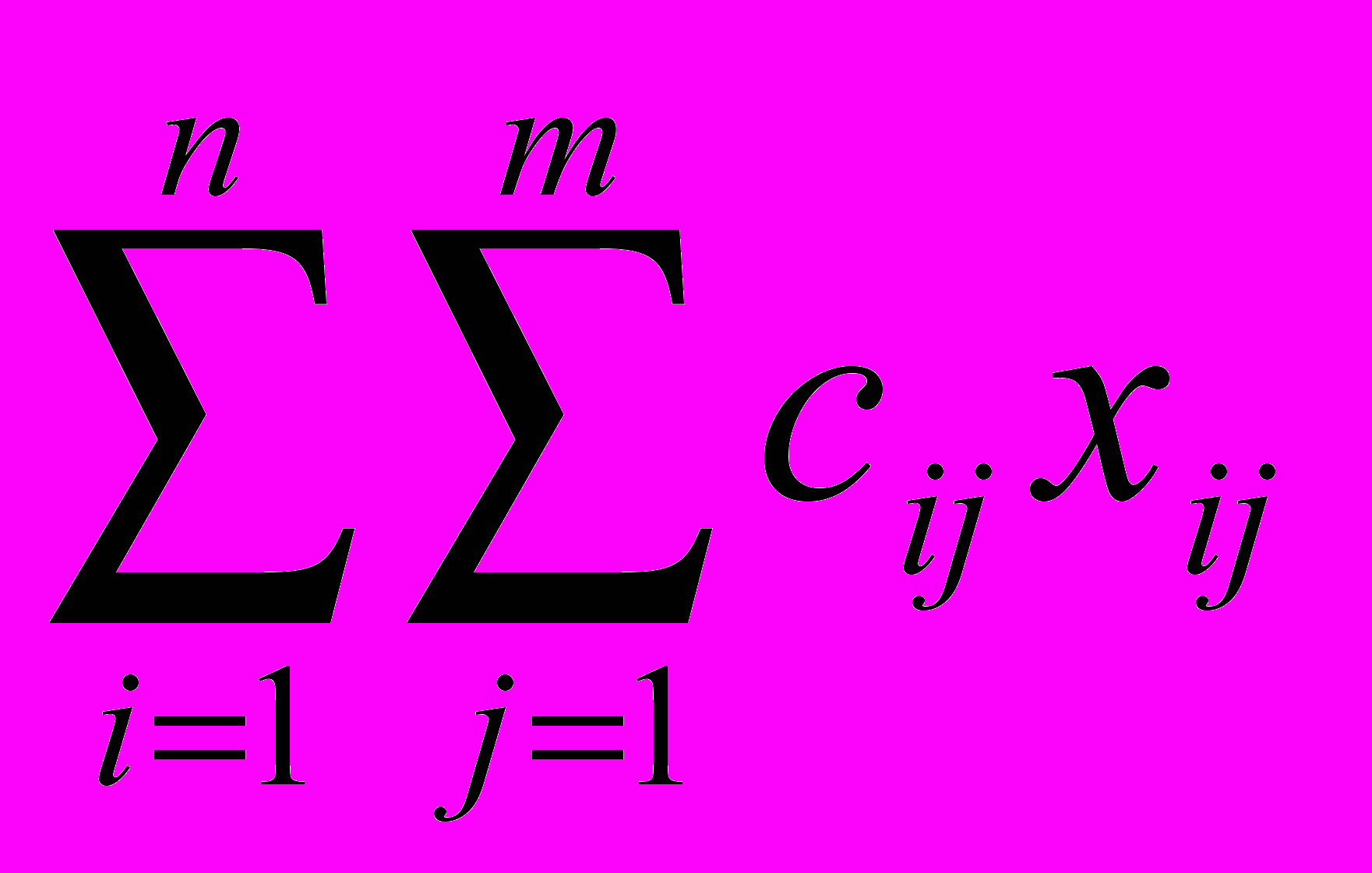
^{F(x)= min}

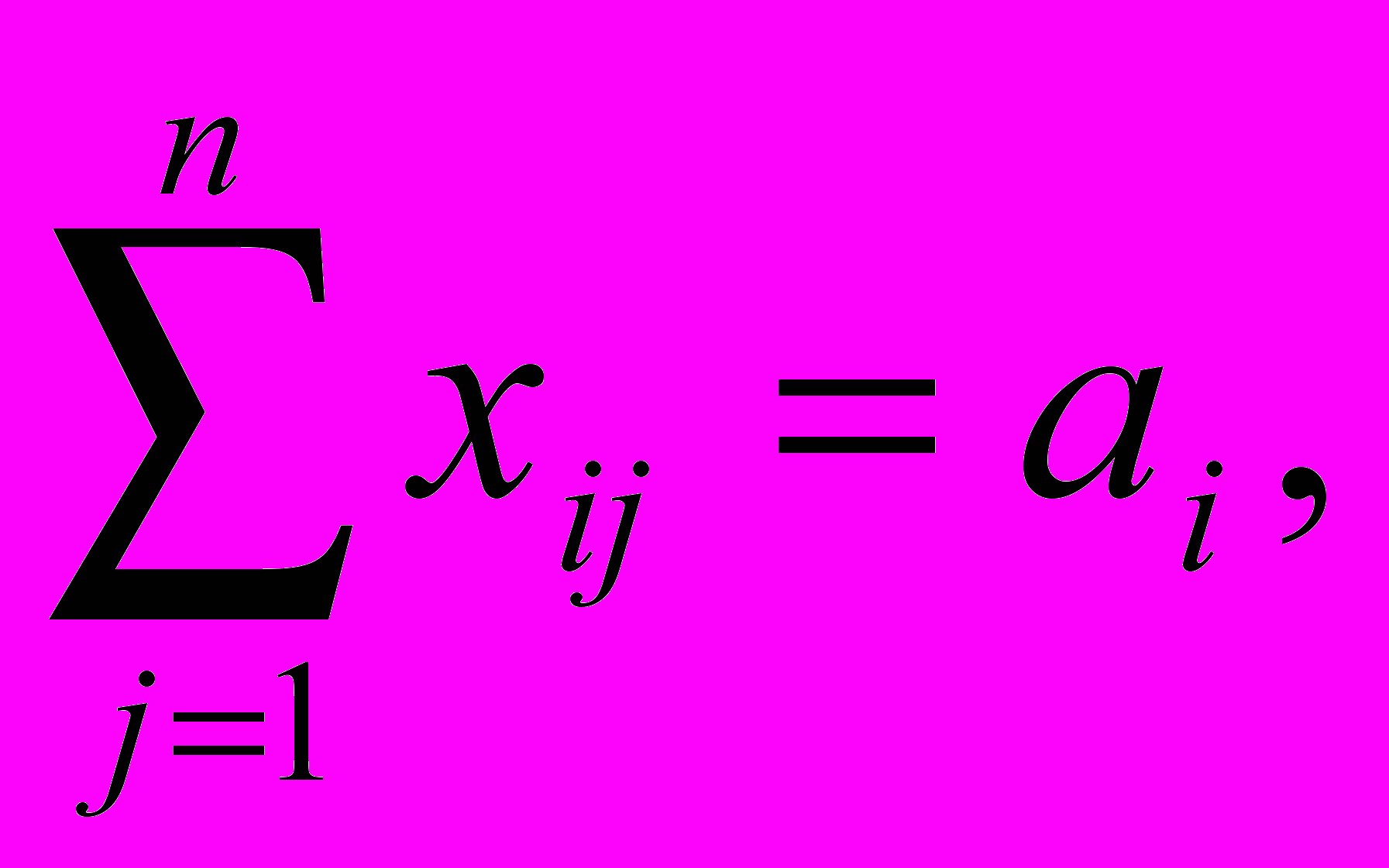i=1,n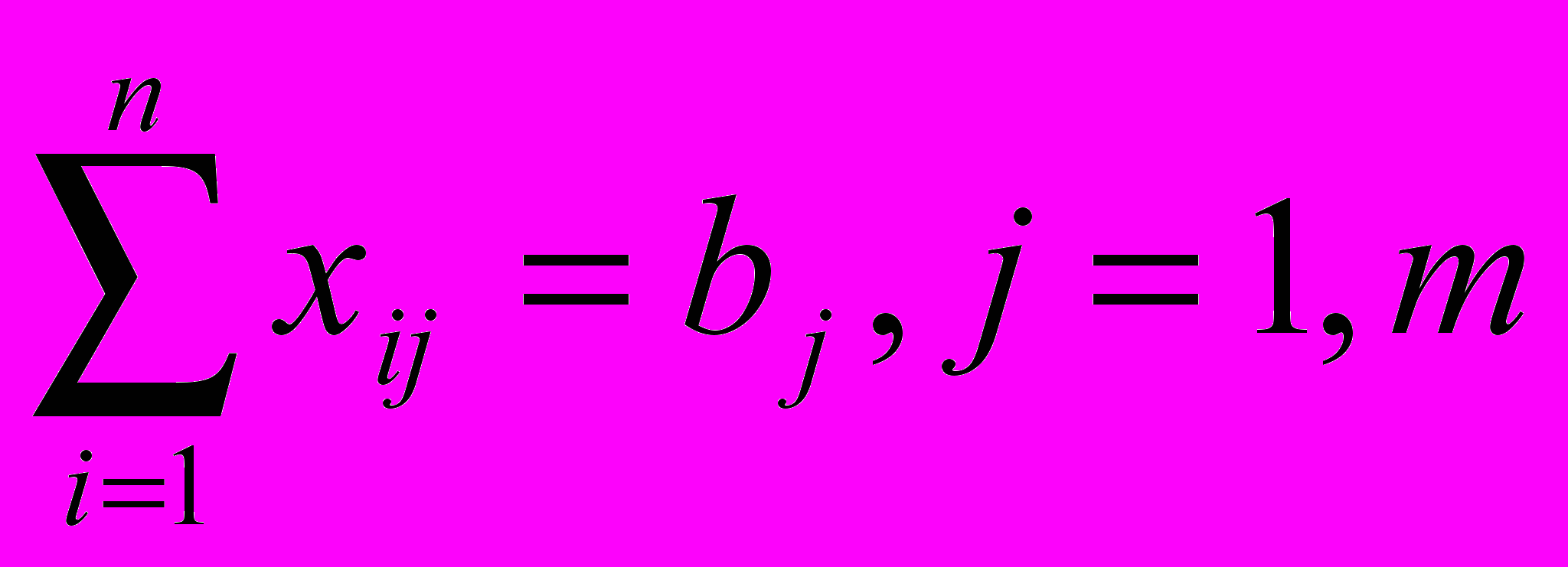





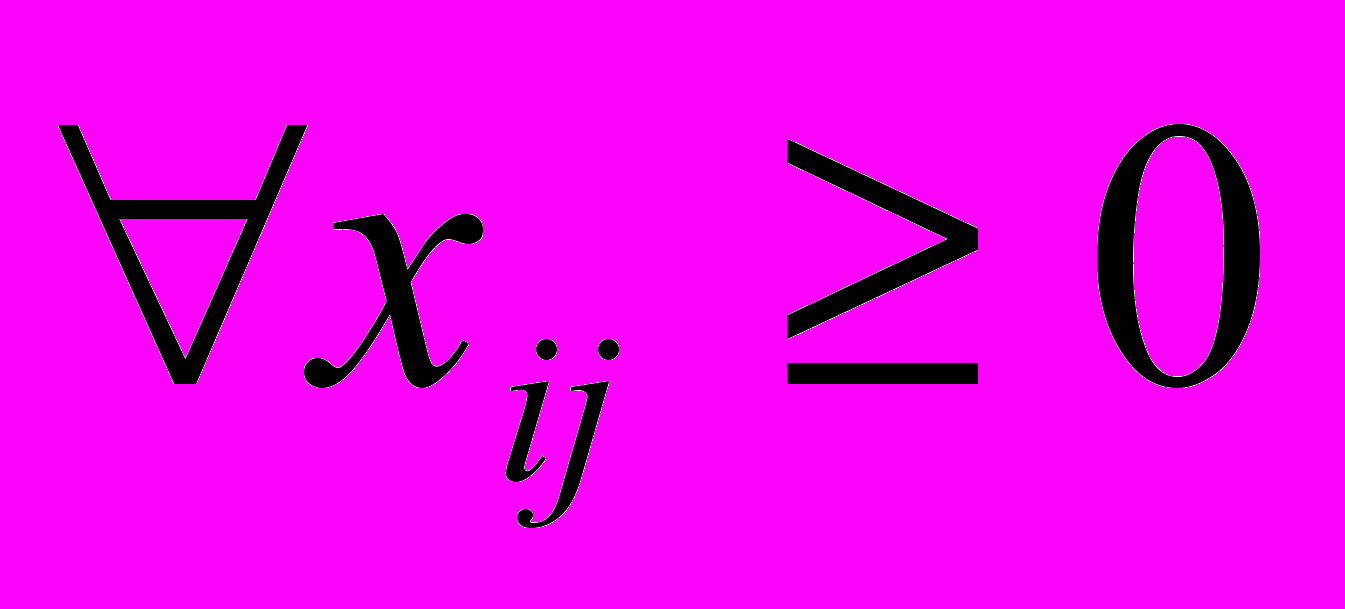
Целевая функция представляет собой транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления.



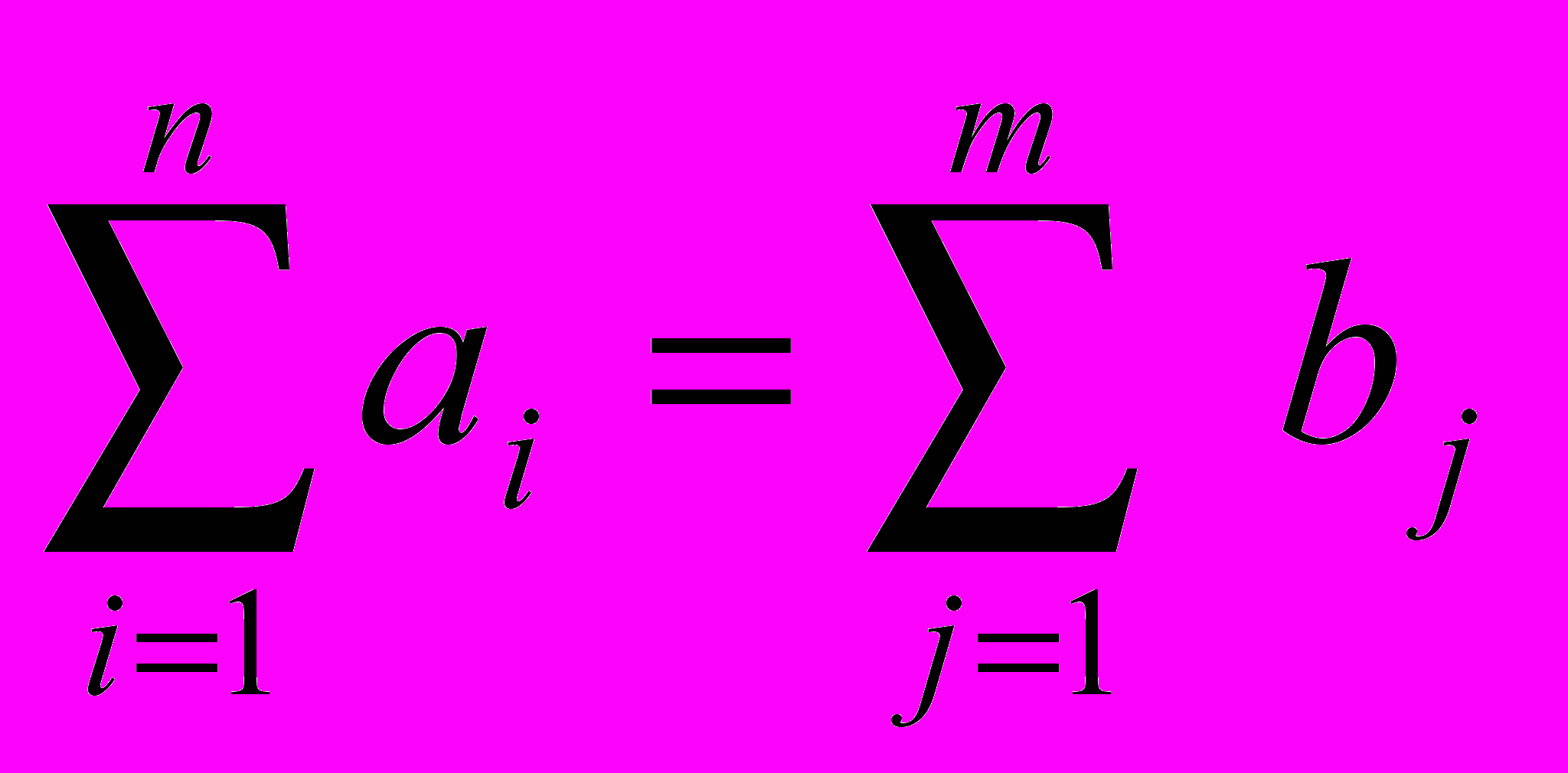
Если это условие выполняется, то транпортная задача называется сбалансированной, в противном случае - несбалансированной. Поскольку ограничения модели приведенные выше могут быть выполнены только при сбалансированной транспортной задаче, то при построении транспортной модели необходимо проверять условие баланса. В случае, когда суммарные запасы превышают суммарные потребности, необходим дополнительный фиктивный пункт потребления, который будет формально потреблять существующий излишек запасов, то есть



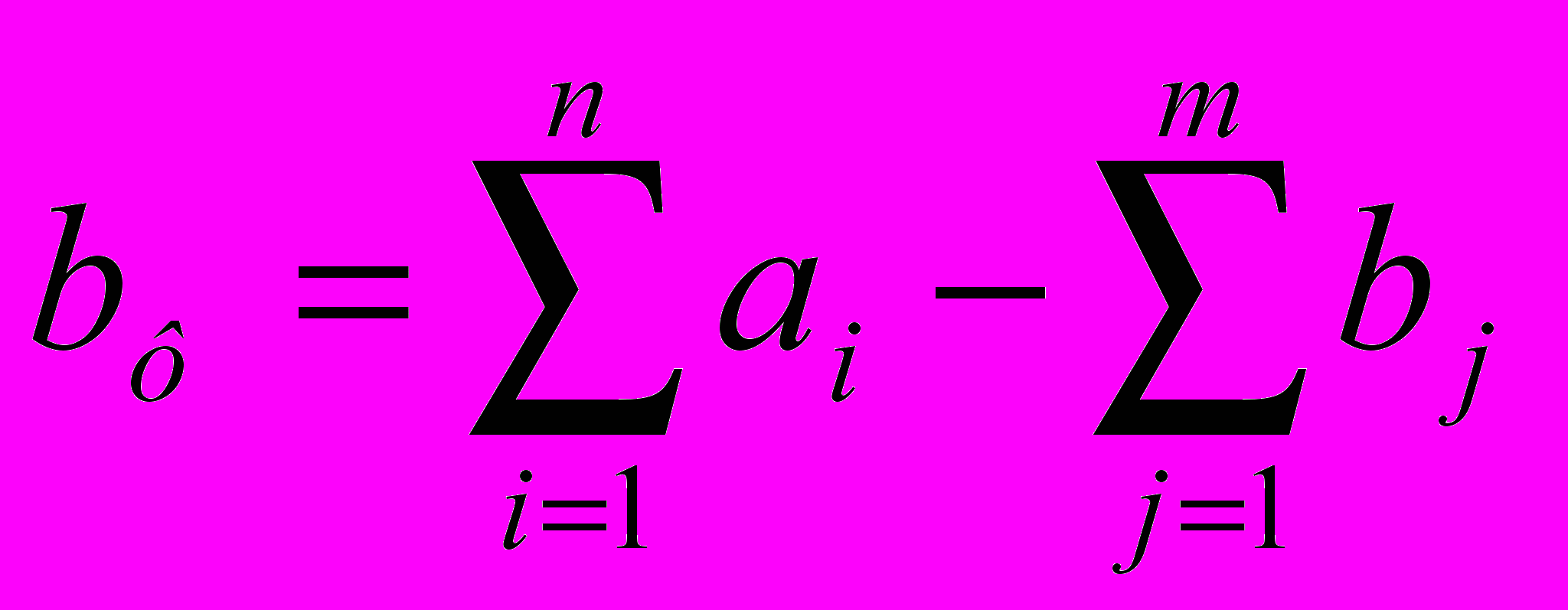
Если суммарные потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:



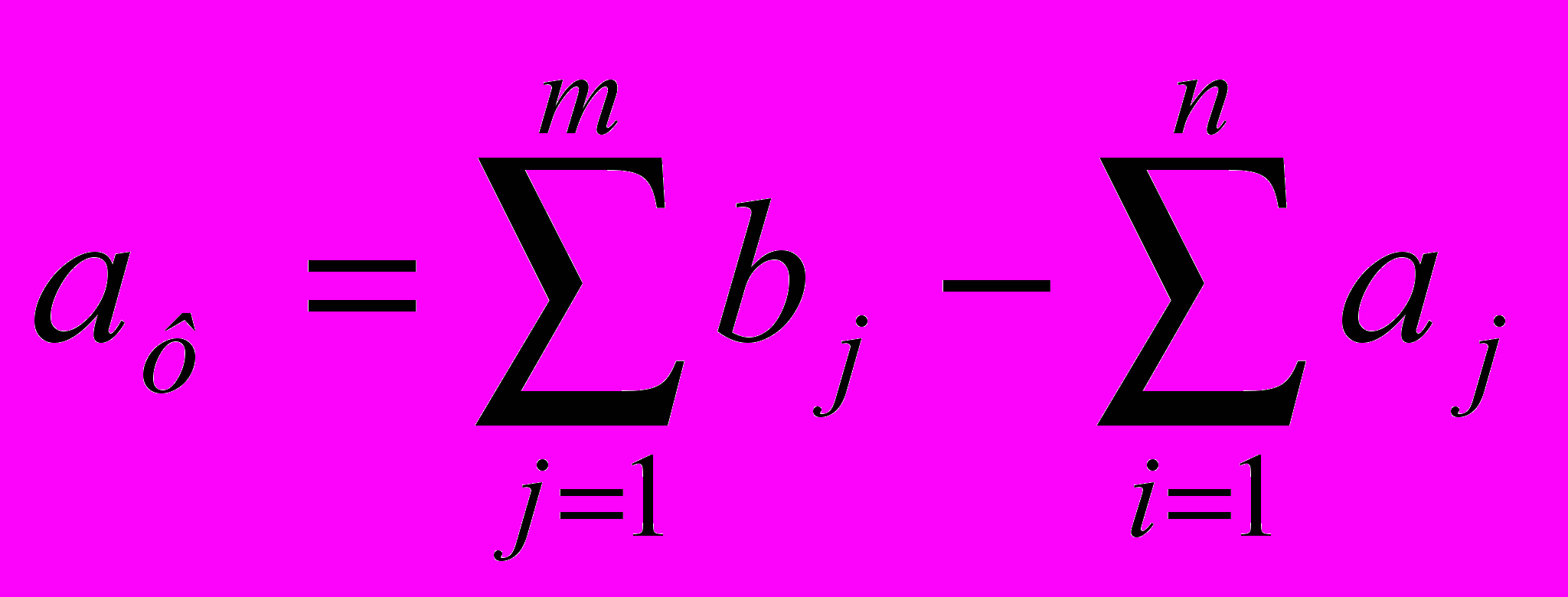
Введение фиктивного потребителя или отправителя повлечет необходимость формального задания фиктивных тарифов 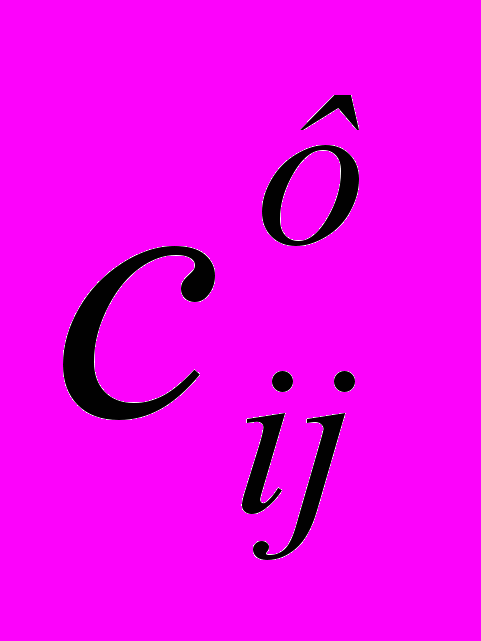(реально не существующих) для фиктивных перевозок. Поскольку нас интересует определение наиболее выгодных реальных перевозок, то необходимо предусмотреть, чтобы при решении задачи (при нахождении опорных планов) фиктивные перевозки не рассматривались до тех пор, пока не будут определены все реальные перевозки. Для этого надо фиктивные перевозки сделать невыгодными, то есть дорогими, чтобы при поиске решения задачи их рассматривали в самую последнюю очередь. Таким образом, величина фиктивных тарифов должна превышать максимальный из реальных тарифов, используемых в модели, то есть

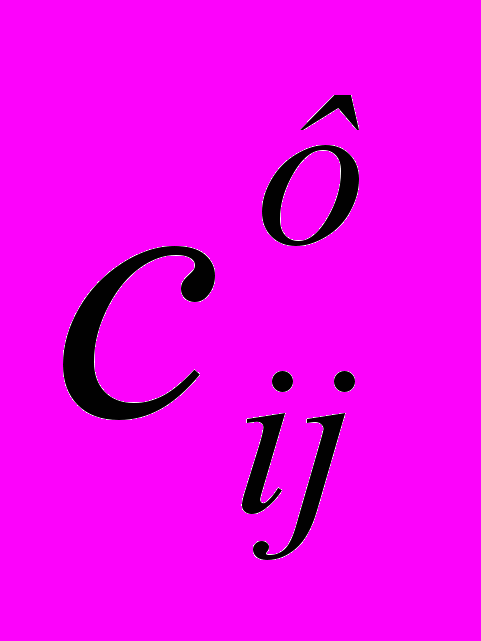>max

На практике возможны ситуации, когда в определенных направлениях перевозки продукции невозможны, например, по причине ремонта транспортных магистралей. Такие ситуации моделируются с помощью введения так называемых запрещающих тарифов . Запрещающие тарифы должны сделать невозможными, то есть совершенно невыгодными, перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна превышать максимальный из реальных тарифов, используемых в модели:

>max

В нашем случае задача является сбалансированной, так как сумма запасов продукции во всех пунктах отправления равняется суммарной потребности во всех пунктах потребления.

720+770+800+1040=730+600+620+880+500

Оптимальным решением такой задачи может стать, решение задач в табличном редакторе Excel методом подбора «Поиска решения», предназначенного для решения задач математического программирования, в частности, задач линейного программирования.

Наша модель является статической, так как заданные на входе параметры, в ходе решения задачи остаются неизменными.

Наша модель является нормативной и целью ее построения является выбор оптимального пути (приведенных выше) перевозок, который потребует наименьших затрат на перевозку.

Наша модель является детерминированной, так как в процессе решения задачи входные параметры – цены перевозок, объем выпускаемого товара, объем склада однозначно определяют затраты на перевозку.

3.2.5Подготовка исходных данных

Параметры перевозок от изготовителей к потребителям

	Потреби-тель А	Потреби-тель Б	Потреби-тель В	Потреби- тель Г	Потреби- тель Д	Произве-дено
Изготовитель 1	10	22	34	50	20	720
Изготовитель 2	24	18	20	14	26	770
Изготовитель 3	32	43	16	28	10	800
Изготовитель 4	16	30	55	45	46	1040
Спрос на товар потребителями	730	600	620	880	500

Формулы экранной формы задачи.

Объект математической модели	Выражение в Excel
Переменные задачи	B3:F6
Формула в целевой ячейке B19	=СУММПРОИЗВ(B3:F6; B12:F15)
Суммарные значения по строкам в ячейках:G3;G4;G5;G6	=СУММ(B3:F3) =СУММ(B4:F4) =СУММ(B5:F5) =СУММ(B6:F6)
Суммарные значения по столбцам в ячейках:B7;C7;D7;E7;F7	=СУММ(B3:B6) =СУММ(C3:C6) =СУММ(D3:D6) =СУММ(E3:E6) =СУММ(F3:F6)
Ограничения по столбцам	G3:G6= H3:H6
Ограничения по строкам	B7:F7=B8:F8
Суммарные запасы и потребности в ячейках H7; G8	=СУММ(H3:H6) =СУММ(B8:F8)

3.2.6Численное решение модели

Вариант 1: Перевозки от изготовителей к потребителям





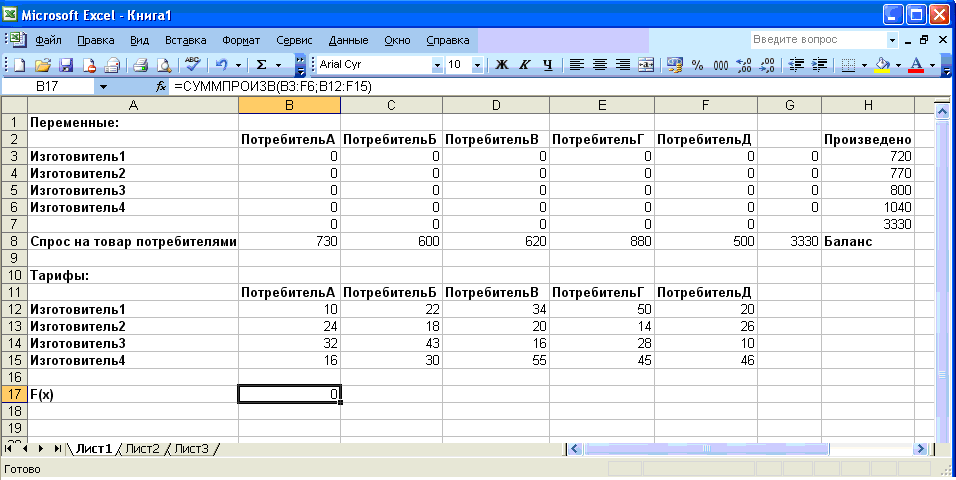
Д
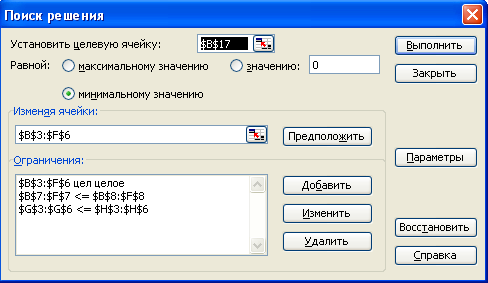
ля решения задачи линейного программирования воспользуемся функцией табличного редактора Excel «Поиск решения».






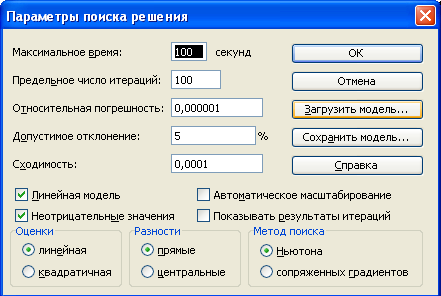
Результаты:





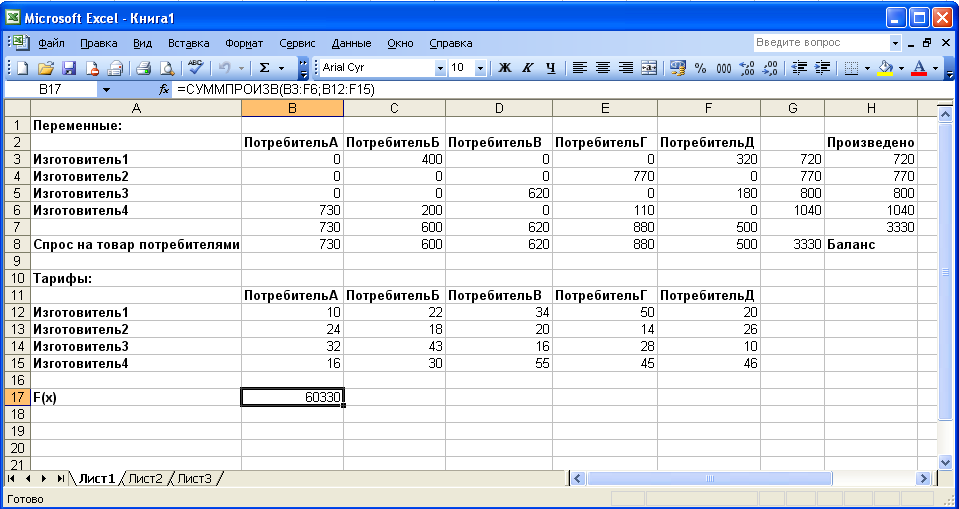
Минимальные суммарные затраты при варианте перевозок от изготовителя непосредственно потребителю составляют 60330 единиц.

Вариант 2: перевозки от изготовителей к оптовым базам, затем к потребителям.

Объем всех имеющихся оптовых баз рассчитан на 2700 единиц продукции, в то же время изготовитель способен удовлетворить спрос на 3330 единиц продукции. Таким образом 630 единиц продукции будут отправлены потребителю напрямую.

В данной задаче есть запрещенные перевозки:

• от оптовой базы к оптовой базе.
  

Для запрещенных перевозок устанавливается стоимость перевозки, превышающая все имеющиеся значения (в этом случае, она окажется самой невыгодной).

Подготовка исходных данных

Параметры перевозок от изготовителей к оптовым базам

	Оптовая база 1	Оптовая база 2	Оптовая база 3	Произведено изготовителями
Изготовитель 1	14	15	45	720
Изготовитель 2	18	12	40	770
Изготовитель 3	21	18	25	800
Изготовитель 4	25	16	10	1040
Запасы на базах	800	700	1200

Параметры перевозок от оптовых баз к потребителям

	Потреби-тель А	Потреби-тель Б	Потреби-тель В	Потреби- тель Г	Потреби- тель Д	Запасы
Оптовая база 1	15	12	21	30	25	800
Оптовая база 2	20	24	25	41	13	700
Оптовая база 3	12	13	26	16	36	1200
Спрос на товар потребителями	730	600	620	880	500

Формулы экранной формы задачи.

Объект математической модели.	Выражение в Excel.
Переменные задачи	B4:I10
Формула в целевой ячейке B29	=СУММПРОИЗВ(B4:I10; B17:I23)
Суммарные значения по строкам в ячейках:J4;J5;J6;J7;J8;J9; J10	=СУММ(B4:I4) =СУММ(B5:I5) =СУММ(B6:I6) =СУММ(B7:I7) =СУММ(B8:I8) =СУММ(B9:I9) =СУММ(B10:I10)
Суммарные значения по столбцам в ячейках:B11;C11;D11;E11;F11;G11;H11;I11	=СУММ(B4:B10) =СУММ(C4:C10) =СУММ(D4:D10) =СУММ(E4:E10) =СУММ(F4:F10) =СУММ(G4:G10) =СУММ(H4:H10) =СУММ(I4:I10)
Ограничения по столбцам	J4:J10=K4:K10
Ограничения по строкам	B11:I11=B12:I12
Суммарные запасы и потребности в ячейках K11; J12	=СУММ(K4:K10) =СУММ(B12:I12)

Численное решение модели




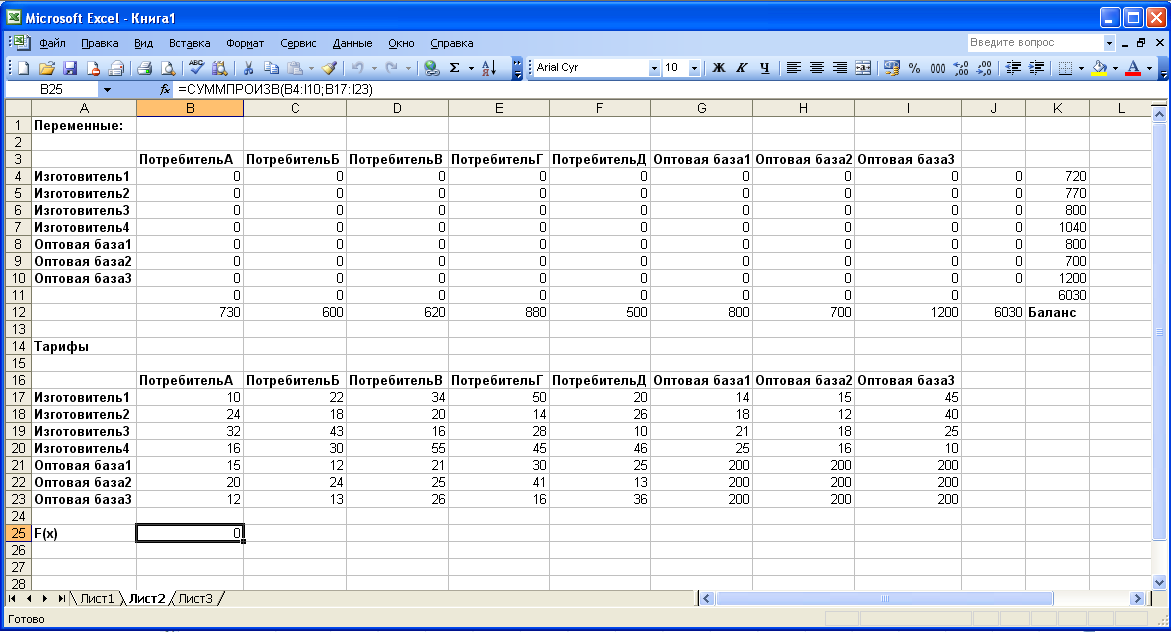
Д
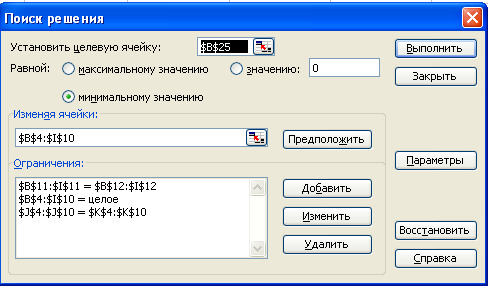
ля решения задачи линейного программирования воспользуемся функцией табличного редактора Excel «Поиск решения».

Р
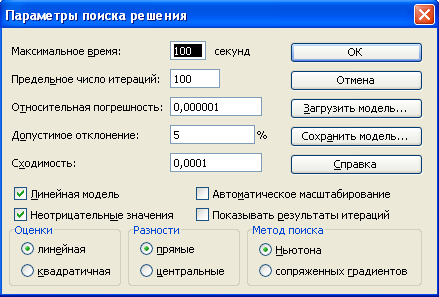
езультаты:

Вставьте сами!!!


Минимальные суммарные затраты при варианте перевозок от изготовителя непосредственно потребителю составляют ____+ единиц.


Вариант 3: Перевозки ИЗГОТОВИТЕЛЬ – ОПТОВАЯ БАЗА – ПОТРЕБИТЕЛЬ; ИЗГОТОВИТЕЛЬ – ПОТРЕБИТЕЛЬ

В третьем варианте «поставщиками» из определения транспортной задачи являются как изготовители продукции, так и оптовые базы. «Потребителями» являются как организации-потребители, так и оптовые базы.

В данной задаче есть запрещенные перевозки: от оптовой базы к оптовой базе.

Для запрещенных перевозок устанавливается стоимость перевозки, превышающая все имеющиеся значения (в этом случае, она окажется самой невыгодной).

Отличием третьего варианта от второго является необязательность использования всех мощностей оптовых баз. Оптовые базы используются только в том случае, если перевозка через них дешевле, чем напрямую. Это изменяет систему ограничений задачи по сравнению со вторым вариантом.

Во-первых, для оптовых баз равенства заменяются на <=, так как превысить мощность нельзя, а не завозить товар на базы (т.е. везти напрямую потребителю) можно.

Во-вторых, количество товара, завезенного на любую из баз, должно быть равно товару, вывезенному с этой базы.

Объект математической модели.	Выражение в Excel.
Переменные задачи	B4:I10
Формула в целевой ячейке B29	=СУММПРОИЗВ(B4:I10; B17:I23)
Суммарные значения по строкам в ячейках:J4;J5;J6;J7;J8;J9; J10	=СУММ(B4:I4) =СУММ(B5:I5) =СУММ(B6:I6) =СУММ(B7:I7) =СУММ(B8:I8) =СУММ(B9:I9) =СУММ(B10:I10)
Суммарные значения по столбцам в ячейках:B11;C11;D11;E11;F11;G11;H11;I11	=СУММ(B4:B10) =СУММ(C4:C10) =СУММ(D4:D10) =СУММ(E4:E10) =СУММ(F4:F10) =СУММ(G4:G10) =СУММ(H4:H10) =СУММ(I4:I10)
Ограничения по столбцам	J4:J7=K4:K7 J8:J10<=K8:K10
Ограничения по строкам	B11:F11=B12:F12 G11:I11<=G12:F12
По мощностям оптовых баз	J8=G11 J9=H11 J10=I11
Суммарные запасы и потребности в ячейках K11; J12	=СУММ(K4:K10) =СУММ(B12:I12)

Численное решение модели




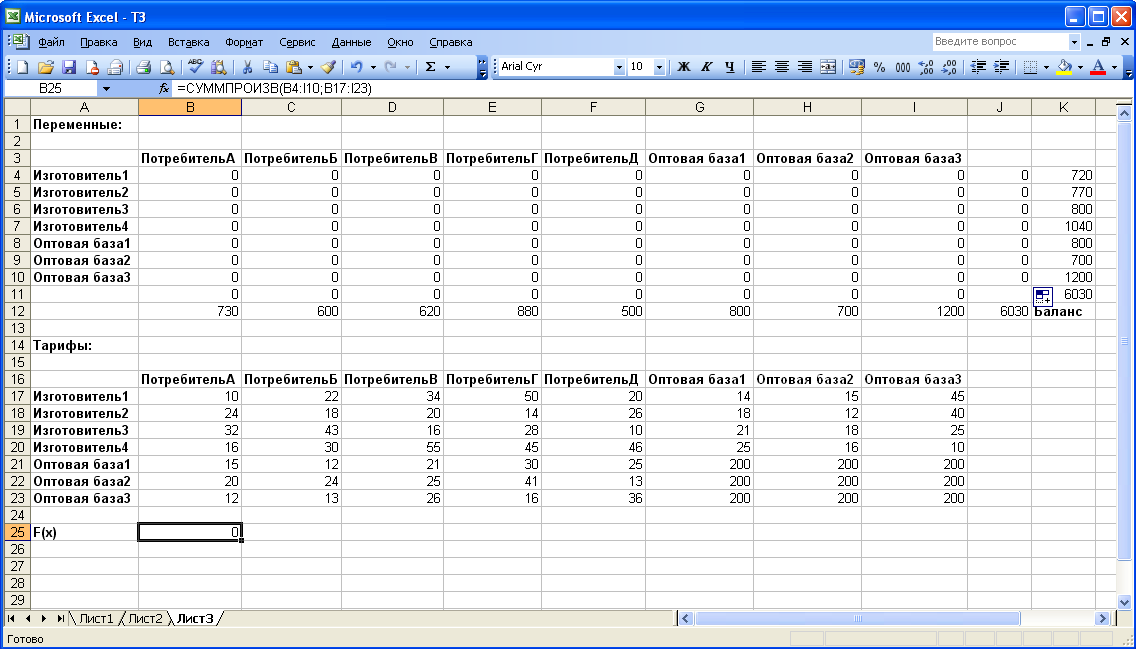
Для решения задачи линейного программирования воспользуемся функцией табличного редактора Excel «Поиск решения».


Сами вставьте!


Результаты:

Сами вставьте


Суммарные затраты в третьем варианте рассчитываются как сумма затрат на перевозку от реальных организаций-изготовителей к оптовым базам и производителям плюс денежных единиц за доставку от оптовых баз производителям.

Суммарные затраты составляют _______ денежных единиц.

4ЗАКЛЮЧЕНИЕ

Проанализировав все варианты перевозок мы видим, что:

1. Вариант перевозок от изготовителей к оптовым базам, а затем к потребителям приведет к затратам на перевозки в размере _____ руб.

2. При варианте перевозок от изготовителей к потребителям затраты составляют _______ руб.

3. При варианте ИЗГОТОВИТЕЛЬ – ОПТОВАЯ БАЗА – ПОТРЕБИТЕЛЬ; ИЗГОТОВИТЕЛЬ – ПОТРЕБИТЕЛЬ затраты составляют _____ руб.

Следовательно самый оптимальный вариант перевозок – ______________.

Данная задача является примером решения оптимизационных задач для реального производства. Она помогает принять правильные управленческие решения на основании проделанных расчетов различных вариантов решений.

Экономико-математические модели помогают в текущей, ежедневной работе предприятий, в частности при решении задач оптимизации транспортных перевозок. Пстроенная модель легко адаптируется к динамически меняющимся условиям реальности – изменяются стоимости перевозок по отдельным маршрутам, спрос на продукцию и объемы производства. Меняя значения параметров, добавляя новые или убирая имеющиеся ограничения, мы всегда можем быстро применить построенную модель для принятия новых плановых решений.

Список используемой литературы:

1. Исследование операций в экономике: Учеб. пособие для вузов /Под ред. проф. Н.Ш.Кремера. – М.:ЮНИТИ, 2006. – 407 с.
   
2. Экономико-математическое моделирование производственных систем: Учебное пособие/С.Н.Миненко – М.: МГИУ, 2006. – 140 с.
   
3. Учебно-методическое пособие по курсу «Экономико-математические методы и модели. Линейное программирование"/Алесинская Т.В., Сербин В.Д., Катаев А.В. - Таганрог: Изд-во ТРТУ, 2001. - 79 с.
   
4. Анализ данных и бизнес-моделирование. /У.Винстон - Пер. с англ. – М: Изд-во «Русская Редакция», 2008. – 608 с.