Н. С. Герасимов Руководитель работы

Вид материала

Документы

Содержание Создание математической модели и решение задачи оптимизации на примере работы фармацевтической компании Построение модели задачи ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Основные понятия экономико-математического моделирования Математическая модель Математическое моделирование Экономико-математическое моделирование 1.2 Стандартная модель транспортной задачи Исходные параметры модели транспортной задачи Искомые параметры модели ТЗ ПОСТРОЕНИЕ МОДЕЛИ ЗАДАЧИ Постановка задачи Таблица 2.1. Цена, налоговая ставка и затраты на производство лекарства Регион продажи Регион продажи Таблица 2.4. Транспортные расходы, тыс. руб. Поэтапное построение модели Построение содержательной модели Построение математической модели Таблица 2.5 Прибыль компании от продажи 1 единицы лекарства Подсчитайте сами!!! Ограничения (с учетом несбалансированности задачи) Математический анализ модели, выбор метода решения ... Полное содержание

Подобный материал:

• Работы, 13.71kb.
• Задачи центра: анализ работы каждой группы; подготовка решения педагогический совета., 119.94kb.
• Меркулова Галина Петровна Место работы : учитель моу сош №15, руководитель литературно-краеведческого, 65.04kb.
• Тезисы Тема работы, 37.22kb.
• Лиснюк Оксаны Вячеславовны по русскому языку Рассмотрено на заседании педагогического, 2394.08kb.
• Герасимов Сергей Павлович диплом, 245.85kb.
• Работы, 11kb.
• Руководитель работы: Голованова О. В., педагог дополнительного образования гбоу лицей, 36.63kb.
• Герасимов А. Ф., Федотов Н. Г. Опотоковом методе анализа движений денежных средств, 28.85kb.
• Полный список книг, 262.28kb.

Министерство образования и науки российской федерации Государственное образовательное учреждение высшего профессионального образования Московский государственный индустриальный университет (ГОУ МГИУ)

Кафедра экономики и управления производством

К У Р С О В А Я Р А Б О Т А
по дисциплине: «Экономико-математическое моделирование»
на тему « СОЗДАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ И РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ НА ПРИМЕРЕ РАБОТЫ ФАРМАЦЕВТИЧЕСКОЙ КОМПАНИИ»
Группа	6167
Студент	_______________ (подпись)	Н.С. Герасимов
Руководитель работы, старший преподаватель	_______________ (подпись)	И. В. Риттер
Оценка работы Дата	_____________	«___» ___________

МОСКВА 2011


СОДЕРЖАНИЕ

ВВЕДЕНИЕ Теоретическая часть Основные понятия экономико- математического моделирования Стандартная модель транспортной задачи ПОСТРОЕНИЕ МОДЕЛИ ЗАДАЧИ Постановка задачи Поэтапное построение модели Постановка экономической проблемы (цели). Построение содержательной модели Построение математической модели Математический анализ модели, выбор метода решения Подготовка исходных данных Численное решение модели ЗАКЛЮЧЕНИЕ Список литературы

3 4 4 5 8 8 9 9 9 10 11 12 14 16 17

ВВЕДЕНИЕ

Моделирование - исследование объектов познания на их моделях; построение и изучение моделей реально существующих предметов и явлений и конструируемых объектов.

Моделирование как познавательный приём неотделимо от развития знания. По существу, моделирование как форма отражения действительности зарождается в античную эпоху одновременно с возникновением научного познания. Однако в отчётливой форме (хотя без употребления самого термина) моделирование начинает широко использоваться в эпоху Возрождения; Брунеллески, Микеланджело и другие итальянские архитекторы и скульпторы пользовались моделями проектируемых ими сооружений; в теоретических же работах Г. Галилея и Леонардо да Винчи не только используются модели, но и выясняются пределы применимости метода моделирования. И.Ньютон пользуется этим методом уже вполне осознанно, а в 19—20 вв. трудно назвать область науки или её приложений, где моделирование не имело бы существенного значения; исключительно большую методологическую роль сыграли в этом отношении работы Кельвина, Дж. Максвелла, Ф. А. Кекуле, А. М. Бутлерова и других физиков и химиков — именно эти науки стали, можно сказать, классическими "полигонами" методов моделирования. Появление же первых электронных вычислительных машин (Дж. Нейман, 1947) и формулирование основных принципов кибернетики(Н. Винер, 1948) привели к поистине универсальной значимости новых методов — как в абстрактных областях знания, так и в их приложениях. Моделирование ныне приобрело общенаучный характер и применяется в исследованиях живой и неживой природы, в науках о человеке и обществе.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

   1. Основные понятия экономико-математического моделирования

Модель – условный образ объекта управления (исследования). Модель конструируется субъектом управления (исследования) так, чтобы отобразить характеристики объекта – свойства, взаимосвязи, структурные и функциональные параметры и т. п., существенные для цели управления (исследования). Содержание метода моделирования составляют конструирование модели на основе предварительного изучения объекта и выделения его существенных характеристик, экспериментальный или теоретический анализ модели, сопоставление результатов с данными об объекте, корректировка модели.

В экономическом анализе используются главным образом математические модели, описывающие изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств. 

Современная экономическая наука широко использует математические методы как для решения прикладных, практических задач, так и для теоретического моделирования социально-экономических явлений и процессов. Математические методы стали составной частью методов любой экономический науки, включая экономическую теорию. Её использование в единстве с обстоятельным экономическим анализом открывает новые возможности для экономической науки и практики.

Как и всякое моделирование, экономико-математическое моделирование основывается на принципе аналогии, т.е. возможности изучения объекта посредством построения и рассмотрения другого, подобного ему, но более простого и доступного объекта его модели.

Практическими задачами экономико-математического моделирование являются, во-первых, анализ экономических объектов; во-вторых, экономическое прогнозирование, предвидение развитие хозяйственных процессов и поведение отдельных показателей; в-третьих, выработка управленческих решений на всех уровнях управления.

Моделирование – непрерывный процесс совершенствования модели, в котором знания о реальном объекте извлекаются из выявления несоответствий между моделью и объектом, их осмысления и устранения.

Математическая модель – это некоторый математический образ исследуемой экономической системы, который адекватно отражает структуру переменных системы, их свойства и взаимосвязи.

Математическое моделирование – метод исследования реальных объектов при помощи постановки экспериментов на их математических моделях. Математическая модель – это представление модели в математической форме, т.е с помощью математических формул, таблиц, графиков и т.п.

Экономико-математическое моделирование (по В.С.Немчинову) – это концентрированное выражение наиболее существенных взаимосвязей и закономерностей поведения управляемой экономической системы в математической форме.

Итак, практической задачей моего экономико-математического моделирования является анализ выбора оптимального способа организации снабжения потребителей продукцией предприятий-изготовителей. Мое задание является транспортной задачей.

1.2 Стандартная модель транспортной задачи

Задача о размещении (транспортная задача) – это распределительная задача, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.

Стандартная транспортная задача определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Исходные параметры модели транспортной задачи

n - количество пунктов отправления, m - количество пунктов назначения.

- запас продукции в пункте отправления A_i (i = 1,n ) [ед. тов.].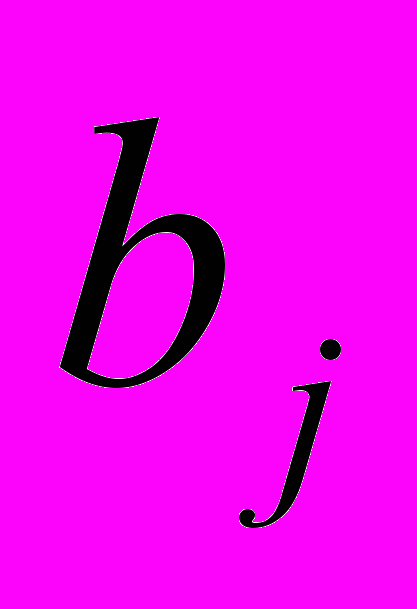

- спрос на продукцию в пункте назначения В_j: (j = l,m) [ед. тов.].

c_ij - тариф (стоимость) перевозки единицы продукции из пункта отправления A_i в пункт назначения В_j, [руб./ед. тов.].


Искомые параметры модели ТЗ

x_ij - количество продукции, перевозимой из пункта отправления A_i в пункт назначения В_j [ед. тов.].

L(X) - транспортные расходы на перевозку всей продукции [руб.].


Транспортная модель



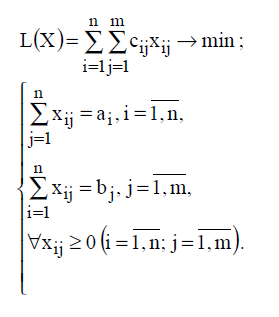
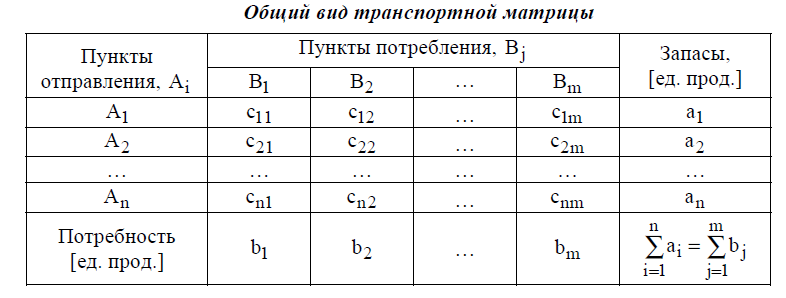
Целевая функция представляет собой транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления модели ТЗ является транспортная матрица (табл. 1.1.) Таблица 1.1.



Из модели (2.1) следует, что сумма запасов продукции во всех пунктах

отправления должна равняться суммарной потребности во всех пунктах

потребления, то есть



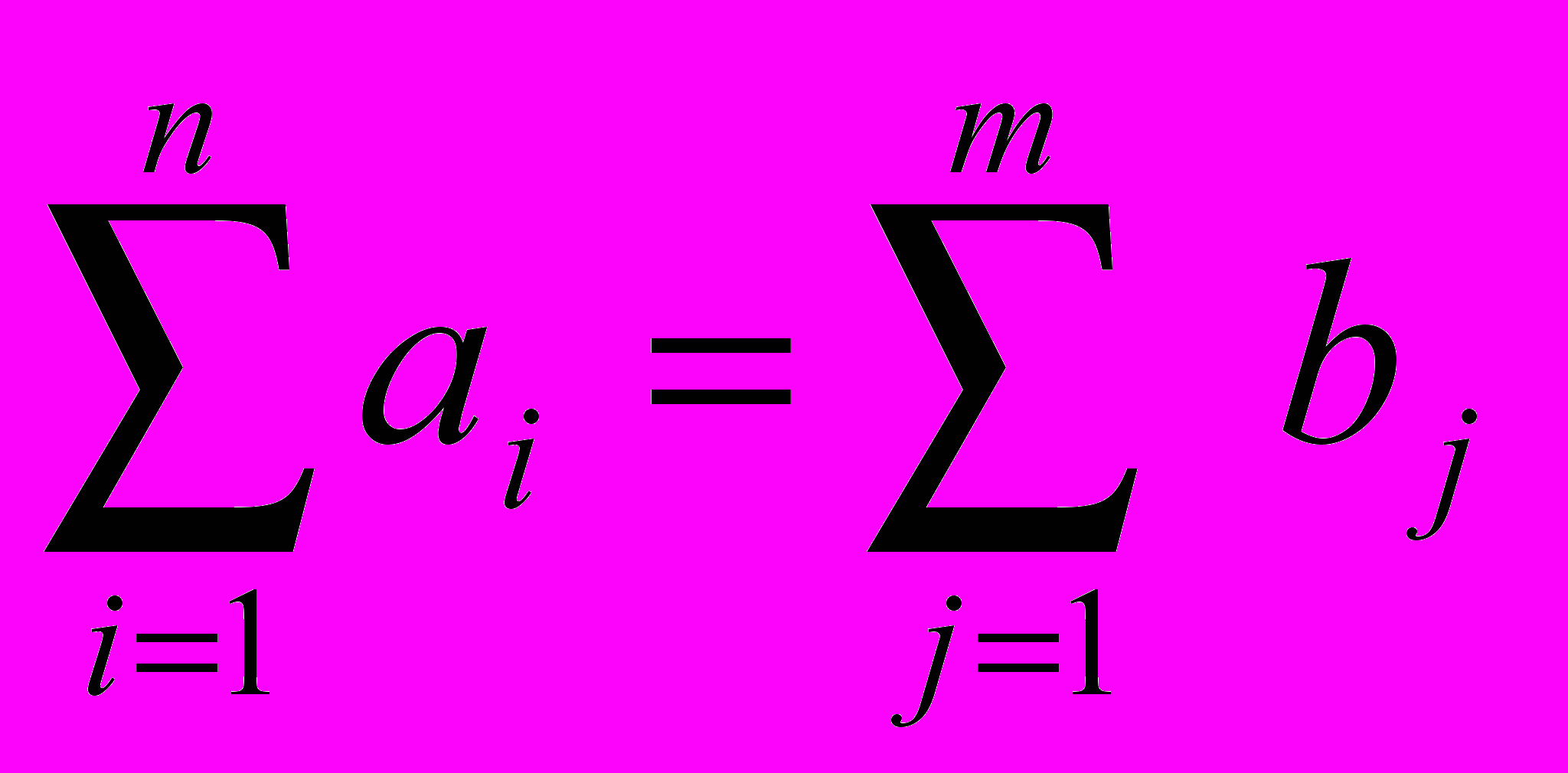
Если это условие выполняется, то транспортная задача называется сбалансированной, в противном случае - несбалансированной. Поскольку ограничения модели, приведенные выше, могут быть выполнены только при сбалансированной транспортной задаче, то при построении транспортной модели необходимо проверять условие баланса. В случае, когда суммарные запасы превышают суммарные потребности, необходим дополнительный фиктивный пункт потребления, который будет формально потреблять существующий излишек запасов, то есть



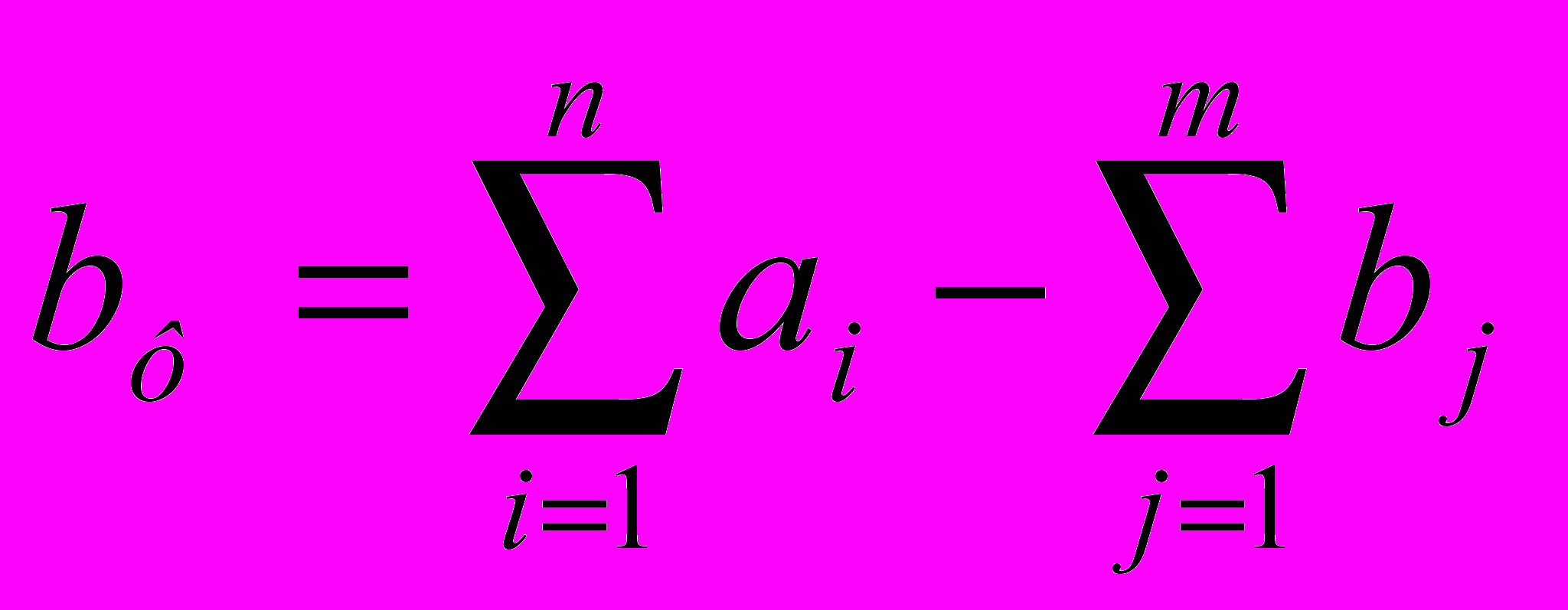
Если суммарные потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:



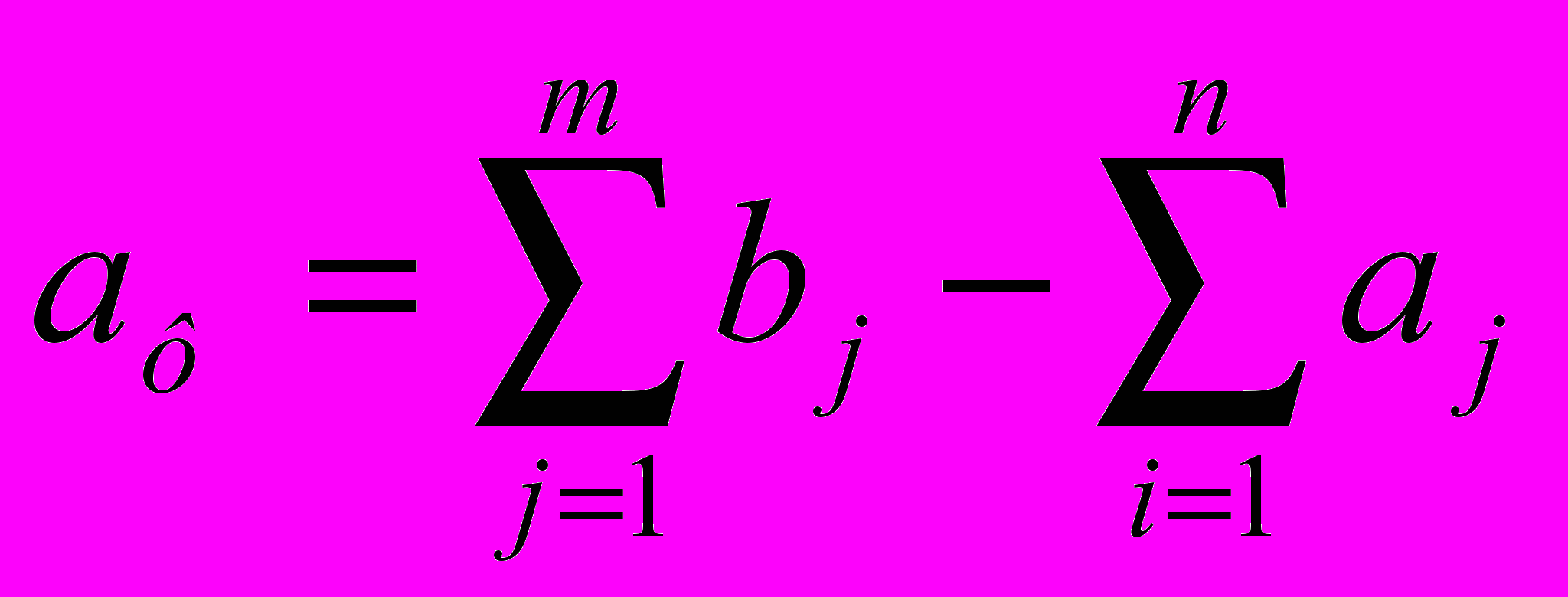
Введение фиктивного потребителя или отправителя повлечет необходимость формального задания фиктивных тарифов 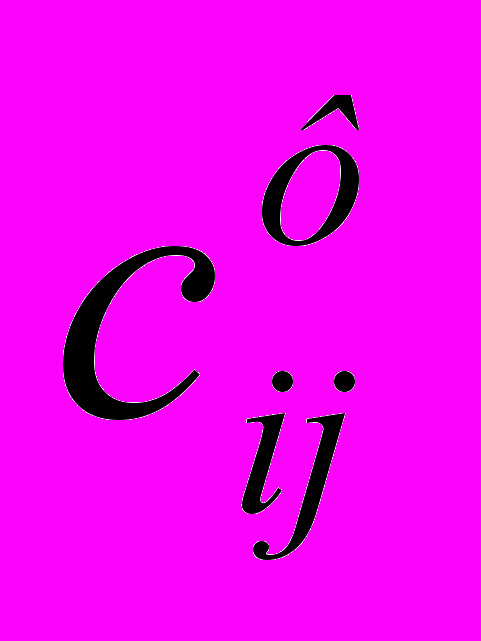(реально не существующих) для фиктивных перевозок. Поскольку нас интересует определение наиболее выгодных реальных перевозок, то необходимо предусмотреть, чтобы при решении задачи (при нахождении опорных планов) фиктивные перевозки не рассматривались до тех пор, пока не будут определены все реальные перевозки. Для этого надо фиктивные перевозки сделать невыгодными, то есть дорогими, чтобы при поиске решения задачи их рассматривали в самую последнюю очередь. Таким образом, величина фиктивных тарифов должна превышать максимальный из реальных тарифов, используемых в модели, то есть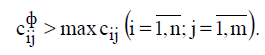



На практике возможны ситуации, когда в определенных направлениях перевозки продукции невозможны, например, по причине ремонта транспортных магистралей. Такие ситуации моделируются с помощью введения так называемых запрещающих тарифов . Запрещающие тарифы должны сделать невозможными, то есть совершенно невыгодными, перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна превышать максимальный из реальных тарифов, используемых в модели:

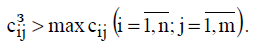
2. ПОСТРОЕНИЕ МОДЕЛИ ЗАДАЧИ

   1. Постановка задачи

Цель: Приобретение навыков решения задач линейного программирования в табличном редакторе Excel. Формирование транспортной модели задачи линейного программирования и решение задачи средствами табличного редактора Excel. Приобретение навыков адаптации транспортной модели линейного программирования для оптимизации практических задач.

ЗАДАЧА

Фармацевтическая компания производит определенное лекарство на своих производственных мощностях в Москве, Нижнем Новгороде, Санкт-Петербурге, Орле, Курске и Перми. Компания поставляет свои лекарства в шесть регионов: Москву, Московскую область, Ленинградскую, Пермскую, Курскую и Нижегородскую область. Затраты на производство 1 единицы лекарства приведены в Таблице 2.1.

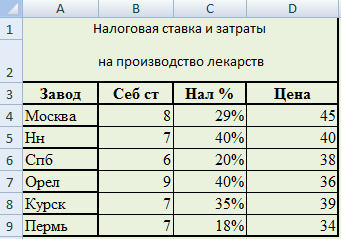
Налоговая ставка и затраты на производство лекарства (себестоимость и цена) зависят от места производства лекарства (табл. 2.1).

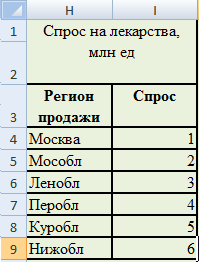
Спрос на лекарства зависит от места продажи (табл. 2.2).

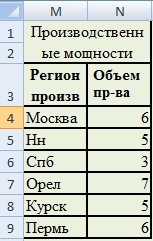
Каждый из шести заводов может производить до 6 млн. единиц продукции в год (табл. 2.3).

Стоимость доставки единицы продукции (в рублях) зависит от завода и региона продажи (табл. 2.4).

Таблица 2.1. Цена, налоговая ставка и затраты на производство лекарства

Завод	Себестоимость, руб.	Налоговая ставка, %	Цена, руб.
Москва	8	29	45
Нижний Новгород	7	40	40
Санкт-Петербург	6	20	38
Орел	9	40	36
Курск	7	35	39
Пермь	7	18	34

Таблица 2.2. Спрос на лекарства, млн. ед.

Регион продажи	Спрос
Москва	1
Московская область	2
Ленинградская область	3
Пермская область	4
Курская область	5
Нижегородская область	6

Таблица 2.3. Производственные мощности изготовителей, млн. ед.

Регион продажи	Мощности
Москва	6
Нижний Новгород	5
Санкт-Петербург	3
Орел	7
Курск	5
Пермь	6

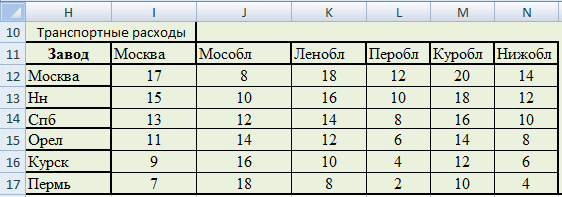
Таблица 2.4. Транспортные расходы, тыс. руб.

Завод	Москва	Московская область	Ленинградская область	Пермская область	Курская область	Нижегородская область
Москва	17	8	18	12	20	14
Нижний Новгород	15	10	16	10	18	12
Санкт-Петербург	13	12	14	8	16	10
Орел	11	14	12	6	14	8
Курск	9	16	10	4	12	6
Пермь	7	18	8	2	10	4

Требуется, выбрать вариант распределения лекарственных средств по потребителям, дающий максимальную прибыль после уплаты налогов при ограниченных производственных мощностях.

2. Поэтапное построение модели

   1. Постановка экономической проблемы (цели).

Цель задачи состоит в поиске варианта распределения произведенных лекарственных средств по регионам, обеспечивающем получение максимальной прибыли фармацевтической компанией. При этом должны быть учтены себестоимость, транспортные и налоговые расходы. Необходимо выбрать наиболее эффективные пути транспортировки товаров и устранить неэффективные маршруты.

2. Построение содержательной модели

На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.

Определим параметры задачи.

Параметры (фиксированные значения):

• количество потребителей;
  
• количество изготовителей;
  
• мощности потребителей (заказываемые объемы продукции);
  
• мощности изготовителей (объемы производимой продукции);
  
• стоимости перевозок от изготовителей потребителям;
  
• налоговые ставки на товары разных заводах;
  
• себестоимость 1 ед. продукции для каждого завода;
  
• цена 1 ед. готовой продукции для каждого завода.
  

Управляющие (независимые) переменные: количество перевозимой продукции по каждому из маршрутов. Меняя количество продукции, перевозимой по различным маршрутам, мы можем выбрать маршруты перевозок, приносящие самую большую суммарную прибыль.

Итак, пусть х_ij – количество продукции, перевозимой от i-го изготовителя j-му потребителю, где i=1,…,6, j=1,…,6.

Управляемые (зависимые, рассчитываемые) переменные: суммарная прибыль F(x).

3. Построение математической модели

Построение математической модели состоит в переводе сконструированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.

х_ij – количество продукции, перевозимой от i-го изготовителя j-му потребителю, где i=1,…,6, j=1,…,6.

Т.к. в задаче указанно несколько факторов, увеличивающих или уменьшающих прибыль, для удобства расчетов посчитаем предварительно прибыль для каждого варианта перевозки с учетом себестоимости, налогового вычета и цены за единицу продукции.

Расчет прибыли производится по следующей формуле:

[Цена]-[цена*налоговая ставка]-[себестоимость]-

-[транспортный расход]=[прибыль]

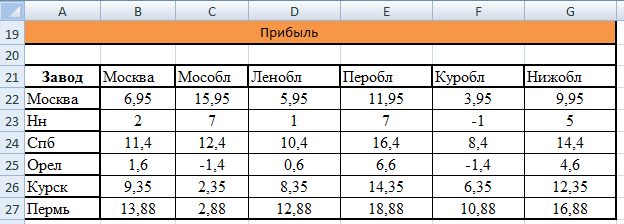
В таблице 2.5 приведена прибыль от продажи лекарственного средства для каждой пары регионов – поставщика и потребителя за единицу продукции.

Таблица 2.5 Прибыль компании от продажи 1 единицы лекарства

Подсчитайте сами!!!


Общая сумма затрат на перевозки:

F(x)=6.95*x₁₁ + 15,95*x₁₂ + 5,95*x₁₃ + 11,95*x₁₄ + 3,95*x₁₅ + 9,95*x₁₆ +2*x₂₁+7*x₂₂ + +1*x₂₃ + 7*x₂₄ + (-1)*x₂₅ + 5*x₂₆ + 11,4*x₃₁ + 12,4*x₃₂ + 10,4*x₃₃ + 16,4*x₃₄ + +8,4*x₃₅ + 14,4*x₃₆ + 1,6*x₄₁ + (-1,4)*x₄₂ + 0,6*x₄₃ + 6,6*x₄₄ + (-1,4)*x₄₅ + 4,6*x₄₆ + +9,35*x₅₁ + 2,35*x₅₂ + 8,35*x₅₃ + 14,35*x₅₄ + 6,35*x₅₅ + 12,35*x₅₆ + 13,88*x₆₁ + +2,88*x₆₂ + 12,88*x₆₃ + 18,88*x₆₄ + 10,88*x₆₅ + 16,88*x₆₆→ max (1)


Ограничения (с учетом несбалансированности задачи):

По предприятиям-изготовителям:

x₁₁+x₁₂+x₁₃+x₁₄+x₁₅+x₁₆=6000000 (2)

x₂₁+x₂₂+x₂₃+x₂₄+x₂₅+x₂₆=5000000

x₃₁+x₃₂+x₃₃+x₃₄+x₃₅+x₃₆=3000000

x₄₁+x₄₂+x₄₃+x₄₄+x₄₅+x₄₆=7000000

x₅₁+x₅₂+x₅₃+x₅₄+x₅₅+x₅₆=5000000

x₆₁+x₆₂+x₆₃+x₆₄+x₆₅+x₆₆=6000000


По потребителям продукции:

x₁₁+x₂₁+x₃₁+x₄₁+x₅₁+x₆₁<=1000000 (3)

x₁₂+x₂₂+x₃₂+x₄₂+x₅₂+x₆₂<=2000000

x₁₃+x₂₃+x₃₃+x₄₃+x₅₃+x₆₃<=3000000

x₁₄+x₂₄+x₃₄+x₄₄+x₅₄+x₆₄<=4000000

x₁₅+x₂₅+x₃₅+x₄₅+x₅₅+x₆₅<=5000000

x₁₆+x₂₆+x₃₆+x₄₆+x₅₆+x₆₆<=6000000


x_ij ≥ 0 для любого i, j (4)

4. Математический анализ модели, выбор метода решения

Наша модель является задачей математического программирования, так как цель ее решения – оптимизация функции цели при заданных ограничениях.

Построенная нами математическая модель является задачей линейного программирования, так и функция цели является линейной функцией и все ограничения представлены в виде линейных равенств.

Системы (2,3) называется системой ограничений, (1) – линейной функцией или функцией цели, (4) – прямые ограничения или неотрицательность переменных.

В нашем случае задача является не сбалансированной, так как суммарное количество производимой продукции на всех заводах-изготовителях не равняется суммарной потребности во всех пунктах потребления.

Оптимальным решением такой задачи может стать решение задач в табличном редакторе Excel методом подбора «Поиска решения», предназначенного для решения задач математического программирования, в частности, задач линейного программирования.

5. Подготовка исходных данных

Доход от продажи продукции с 1-го завода 1-му потребителю определяется с помощью следующей формулы:


=$D4-($D4*$C4)-$B4-I12 - для перевозки из Москвы в Москву.


Значения для других маршрутов получаем переносом формулы в ячейки B22:G27. При переносе зафиксируем положение столбцов первых трех таблиц, значения которых участвуют в расчетах.







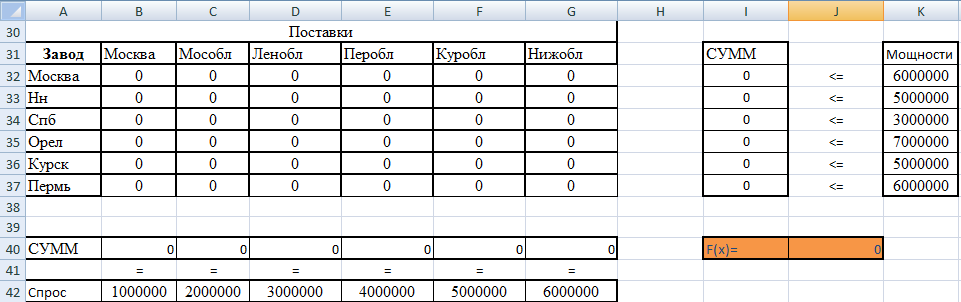
Формулы экранной формы задачи.

Объект математической модели	Выражение в Excel
Переменные задачи	B32:G37
Формула в целевой ячейке J40	=СУММПРОИЗВ(B32:G37; B22:G27)
Суммарные значения по строкам в ячейках: I32:I37	=СУММ(B32:G32) =СУММ(B33:G33) =СУММ(B34:G34) =СУММ(B35:G35) =СУММ(B36:G36) =СУММ(B37:G37)
Суммарные значения по столбцам в ячейках: B40:G40	=СУММ(B32:B37) =СУММ(C32:C37) =СУММ(D32:D37) =СУММ(E32:E37) =СУММ(F32:F37) =СУММ(G32:G37)
Ограничения по строкам	I32:I37<=K32:K37
Ограничения по столбцам	B40:G40= B42:G42
Суммарные запасы и потребности в ячейках H7; G8	=СУММ(K32:K37) =СУММ(B42:G42)

6. Численное решение модели

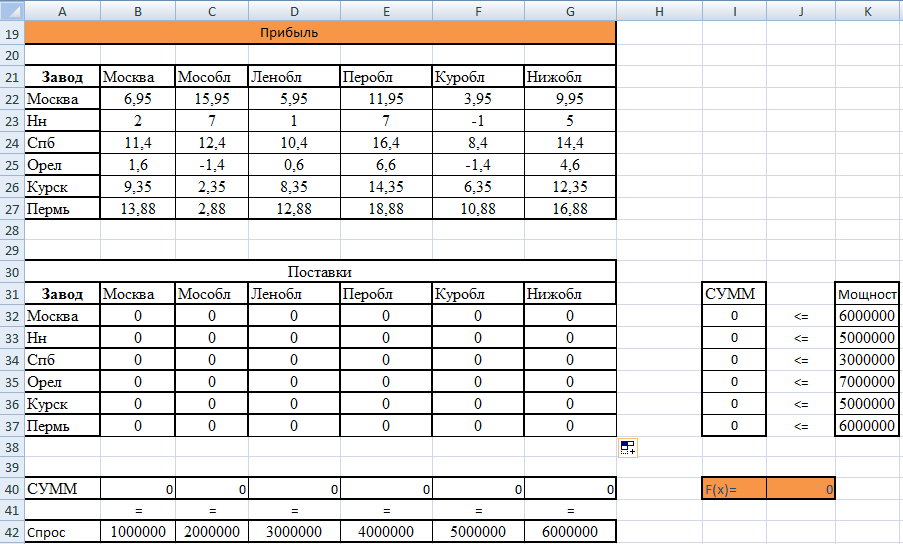
Для решения задачи линейного программирования воспользуемся функцией табличного редактора Excel «Поиск решения».











Результаты:




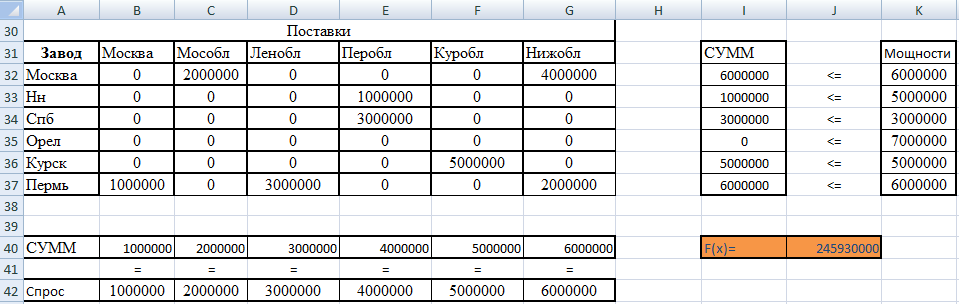
Спрос на продукцию удовлетворен полностью.

Продукция, производимая на заводе в г. Орел, не использована полностью, в Нижнем Новгороде - большая часть. Для этих заводов необходимо искать новые рынки сбыта продукции или закрывать производство. Если обратиться к таблице 2.5, то видно, что прибыль от продажи лекарства, изготовленного на этих заводах с учетом транспортных расходов, значительно ниже, чем на других заводах.

Максимальная суммарная прибыль составляет 245930000ед.

3. ЗАКЛЮЧЕНИЕ

Можно выделить, по крайней мере, четыре аспекта применения математических методов в решении практических проблем.

1. Совершенствование системы экономической информации. Математические методы позволяют упорядочить систему экономической информации, выявлять недостатки в имеющейся информации и вырабатывать требования для подготовки новой информации или ее корректировки. Разработка и применение экономико-математических моделей указывают пути совершенствования экономической информации, ориентированной на решение определенной системы задач планирования и управления. Прогресс в информационном обеспечении планирования и управления опирается на бурно развивающиеся технические и программные средства информатики.

2. Интенсификация и повышение точности экономических расчетов. Формализация экономических задач и применение ЭВМ многократно ускоряют типовые, массовые расчеты, повышают точность и сокращают трудоемкость, позволяют проводить многовариантные экономические обоснования сложных мероприятий, недоступные при господстве "ручной" технологии.

3. Углубление количественного анализа экономических проблем. Благодаря применению метода моделирования значительно усиливаются возможности конкретного количественного анализа; изучение многих факторов, оказывающих влияние на экономические процессы, количественная оценка последствий изменения условий развития экономических объектов и т.п.

4. Решение принципиально новых экономических задач. Посредством математического моделирования удается решать такие экономические задачи, которые иными средствами решить практически невозможно, например: нахождение оптимального варианта народнохозяйственного плана, имитация народнохозяйственных мероприятий, автоматизация контроля за функционированием сложных экономических объектов.

Список используемой литературы:

1. Исследование операций в экономике: Учеб. пособие для вузов /Под ред. проф. Н.Ш.Кремера. – М.:ЮНИТИ, 2006. – 407 с.
   
2. Экономико-математическое моделирование производственных систем: Учебное пособие/С.Н.Миненко – М.: МГИУ, 2006. – 140 с.
   
3. Учебно-методическое пособие по курсу «Экономико-математические методы и модели. Линейное программирование"/Алесинская Т.В., Сербин В.Д., Катаев А.В. - Таганрог: Изд-во ТРТУ, 2001. - 79 с.
   
4. Анализ данных и бизнес-моделирование. /У.Винстон - Пер. с англ. – М: Изд-во «Русская Редакция», 2008. – 608 с.