Аннотация и ключевые слова
| Вид материала | Обзор |
| Анализ сочетания классического и дистанционного обучения в школе Содержательное описание и формализация Дисциплина обслуживания Граф состояний-переходов и конечные вероятности |
- Реферат Отчет содержит 32 с. Ключевые слова, 25.16kb.
- Реферат Ключевые слова, 70kb.
- Отчет представлен на 51 с., состоит из 5 ч., 12 рис., 2 табл. Ключевые слова, 22.72kb.
- Россия в формирующемся миропорядке: ресурсы и внешнеполитический статус Ключевые слова, 2487.84kb.
- Описание психокоррекционной работы по методу символдрамы и в технике игровой психотерапии, 318.93kb.
- Механизм воздействия инфразвука на вариации магнитного поля земли, 48.07kb.
- Содержит 180 страниц, 39 таблиц, 26 рисунков. Ключевые слова, 222.29kb.
- Омус-2012 Ключевые слова: , 13.52kb.
- «Теория и методология взаимодействия финансового и реального секторов экономики в современных, 493.73kb.
- Отчет представлен на 47 с.; состоит из 4 частей; основная часть содержит 26 пунктов, 23.76kb.
Анализ сочетания классического и дистанционного обучения в школе
В данном разделе демонстрируются возможности моделей массового обслуживания для анализа сочетания классического классно-урочного обучения и альтернативного обучения – например дистанционного. Модель позволяет определять средние характеристики.
Содержательное описание и формализация
Под системой массового обслуживания {Артамонов} понимают время-логическую систему, представляющую собой единство трех категорий:
- входящих потоков заявок или требований на обслуживание;
- параметров обслуживающих приборов;
- дисциплин обслуживания.
В простейшем случае система массового обслуживания может состоять из одного обслуживающего прибора, на вход которого поступает единственный поток заявок. Один учитель – один ученик.
Вернемся для примера в обычную общеобразовательную школу с классической классно-урочной формой проведения занятий. Обычный школьный нормированный класс из 25 учеников, пусть для примера изучающих основы информатики по базовой 68 часовой программе, то есть 34 спаренных урока по 45 школьных минут. Среднее время обслуживания учителем одного ученика – около 4 минут.
Но это в среднем. При широком диапазоне времени обслуживания – большой дисперсии – каждый преподаватель знает о сложностях работы с группой, представленной слишком разнородными учениками.
Система трактуется в теории массового обслуживания как многоканальная система.
-
1

Дисциплина обслуживания
Обслуживающий
прибор
(Учитель)
Параметры модели:
- интенсивность входящих потоков заявок 1 - n;
- среднее время обслуживания заявки Учителем - ;
- дисперсия среднего времени обслуживания заявки - d.
 2
2
…

n
Рис. 3. Обучение как многоканальная система
- интенсивность входящих потоков заявок 1 - n;
Дисциплина обслуживания
Наиболее простые и известные дисциплины обслуживания – «первым пришел – первым обслужился» и «первым пришел – последним обслужился» (стек или магазин с патронами). Малое время обслуживания, особенно при разной подготовленности учеников (большой дисперсии времени обслуживания), заставляет учителя прибегать к методам бюрократического обучения – см. Дружинин-Конторов {__} – модель Учителя-Бюрократа.
| | | | ||||||||
| | Ученики | | | | | | Учитель | |||
| | (  1, 2, … N) 1, 2, … N) | | | | | 4  | | | ||
| | | | |  |  |  | 2  | | ||
| | | 9  | | | | | |  | | |
| | | | | |  | | 6  | | | |
| | | 1  0 0 | | | 14 | 8 | | 1 | | |
| | |  | | |   |  |  |  | | |
| | | 1  1 1 | | | | | 7 | | 3 | |
| | |  | | | | | | | | |
| | |   | | | | | | 5 | | |
| | | 12 | | | | | | | | |
| | Задачи | | | | | | | | | |
| | | 13 | | | | | | | | |
| | | | | | 15 | | | | | |
| | | | | | | | | Контроль | | |
| | | | | | 1  6 6 | | 1  9 9 | | | |
| | | | | |  | |  | | | |
| | | | | | 17 | | 20 | | | |
| | | | | |  | |  | | | |
| | | | | | 18 | | 2  1 1 | | | |
| | | | | | | | | | | |
| | Рис. 4. Модель бюрократического обучения | | ||||||||
| 1- система обслуживания; 2- дисциплина обслуживания; 3- отбор элиты; 4- выбор ученика; 5 – выбор задачи; 6 – предъявление; 7 – оценка; 8 – подкрепление; 14 – взаимодействие с учеником (конфликт); 9 – контингент (1-N); 10 – прием задачи; 11 – ответ; 12 – парные ассоциации; 13 – парные сравнения; 15 – ресурс подкреплений; 16 – выбор ученика; 17 – предъявление; 18 – оценка; 19 – определение средней оценки; 20 – контроль расхода подкреплений; 21 – оценка учителя. | ||||||||||
| | ||||||||||
| Y1 y2 | 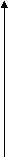 Y1       y2   t | |     Отрицательный Положительный исход исход  -12 -8 -4 0 4 8 12 | |||||||
| | Рис. 5. Характеристики обучения; Y1 – типовая средняя оценка; y2 - средняя оценка для У-Б; - темп обслуживания | | Рис. 6. Распределение исходов бюрократического давления на учащихся, приведшего к строгому конфликту (в условных оценках социальной опасности) | |||||||
Граф состояний-переходов и конечные вероятности
Рассмотрим «прогрессивную» школу, делящую поток обучения на 2 направления и предлагающую кроме классно-урочной формы обучения альтернативные формы и методы на основе информационных технологий, дистанционного метода и проектного подхода к обучению.
Граф состояний и переходов школы как системы массового обслуживания представлен на рис. 7.
| | | ||||
 | | Д  ообучение ообучение | | | Формализация. Предположим, что альтернативное обучение предлагается для % учеников. Среднее время обслуживания для альтернативного обучения - 1, а для классно-урочной формы - 2 . Независимый тестер со средним временем тестирования 3 с вероятностью признает его состоявшимся, а с вероятностью 1 - признает не успешным, и возвращает на дообучение. |
| | |  | | | |
| | | z  1 Альтернативное обучение 1 Альтернативное обучение | | | |
  | 01 | 13 | 30 | ||
| z  0 0 Н  ачальное состояние ачальное состояние | | (1 ) | | z  3 3 Тестирование (3) | |
| | | | |||
| 02 | z   2 2 Классно-урочное обучение (2) | 23 | |||
| | | | | ||
| | | | | ||
| Рис. 7. Граф состояний и переходов. z0 - начальное (необученное) состояние; z1 - альтернативное обучение со средним временем обслуживания 1; z2 - классическое классно-урочное обучение со средним временем 2; z3 - тестирование со средним временем 3 | |||||
| | |||||
Предельные вероятности состояний находятся решением уравнений Колмогорова с учетом нулевой скорости изменения вероятности состояний и условия нормировки p0 + p1 + p2 + p3 = 1.
| dp0/dt = p3 30 - p1 10 - p2 20 = 0 dp1/dt = p0 01 - p1 13 = 0 dp2/dt = p0 02 - p2 23 = 0 dp3/dt = p1 13 + p2 23 - p3 30 = 0 | p0 = 1/(1 + 01/13 +02/23 + (01 + 02)/30) p1 = p0 01 / 13 p2 = p0 02 / 23 p3 = p0 (01 + 02 ) / 30 | 13 = 1 / 1 23 = 1 / 2 30 = 1 / 3 01+02=1/(1 +2) |
При наличии общего решения попробуем свести формулы к известным величинам.
Введем дополнительную переменную = 01 / 02 , дающую нам соотношение 02 = 01.
Тогда 01 = 1/(1 + ) (1 +2), а 02 = /(1 +2)(1 + )
Проведя подстановки значений интенсивностей переходов в формулу для определения p0, окончательно получаем:
p0 = [1+ 1 (1 + ) / (1 +2) + 2 /(1 + ) (1 +2) + 3 / (1 +2)]–1
Соотношение вероятностей пребывания в состоянии альтернативного обучения к классическому:
p1 / p2 = 01 23 / 02 13 = 01 / 02 (1 / 2) = (1 / 2) , где = 01 / 02.
Соотношение вероятностей пребывания в состоянии тестирования к исходному необученному:
p3 / p0 = 3 / 1 + 2
Для аналитиков интересно соотношение 1 - p0 , то есть собственно вероятность успешного обучения предлагаемой 2-х канальной системой.
