Знание в интеллектуальных системах Вагин В. Н. Введение. Характерные особенности знания
| Вид материала | Документы |
- Ложения темпоральной (временной) логики для ветвящегося времени в плане ее использования, 138.35kb.
- Мультиагентные системы в экономике, 104.75kb.
- Статья раскрывает характерные особенности социальной политики «ельцинского», 314.76kb.
- Тема: Класс Двудольные. Семейство Сложноцветные. Место урока, 174.72kb.
- Урок биологии в 7 классе. Интегрированный. Тема: Характерные особенности растений семейства, 188.8kb.
- Курс моделирование процессов переноса в турбулентных течениях программа курса лекций, 16.73kb.
- Цель: Обобщить и систематизировать знания о топографическом плане и географической, 51.45kb.
- Урок по теме "Земноводные", 80.88kb.
- Г. В. Мелихов миф. Идентичность. Знание: введение в теорию социально-антропологических, 741.74kb.
- Лекция №2 Тема: характеристика социологического знания, 195.16kb.
1 2
Знание в интеллектуальных системах
Вагин В.Н.
Введение. Характерные особенности знания
Данные и знания суть основные понятия системы представления знаний, являющейся одной из главных компонент интеллектуальной системы принятия решений. Исторически в теории и практике программирования понятие «данные» видоизменялось и усложнялось. Сначала под данными понимались двоичные слова фиксированной длины. С развитием структуры вычислительных машин происходило развитие информационных структур для представления данных. Появились способы описания данных в виде векторов и матриц, возникли списочные и иерархические структуры. Вознило понятие абстрактных типов данных, структура которых может задаваться. Появление БД знаменовало собой еще один шаг на пути организации работы с данными. Специальные средства, образующие систему управления БД (СУБД), позволяют эффективно манипулировать с данными, при необходимости извлекать их из БД и записывать в нужном порядке в БД.
Таким образом, данные – это факты, характеризующие объекты, процессы и явления предметной области, а также их свойства.
По мере развития исследования в области интеллектуальных систем возникла новая концепция - концепция знаний, которая стала доминирующей в исследованиях по искусственному интеллекту.
Д.А. Поспелов выделяет шесть основных факторов, наличие которых говорит о том, что речь идет о знаниях. [1, 2].
1. Внутренняя интерпретируемость.
На заре развития программирования каждой информационной единице – данному – программист отводил определенную ячейку памяти, которой соответствовал ее адрес в памяти, т.е. приписанное ей уникальное имя. Такое приписывание имени информационной единице приводило к тому, что только сам программист знал содержимое, скрывающееся под тем или иным именем. При необходимости он использовал это содержимое в программе, вызывал его по имени, причем, что скрывается за тем или иным именем машине не было известно.
Переход от физических адресов к относительным, а позднее и к символьным создал большие удобства для программиста. Он освобождался от забот по распределению реальной памяти в машине. Автоматически распределяя физическую память, машина формировала таблицу соответствий, в которой относительным или символьным адресам соответствовали физические адреса, назначаемые машиной. Но и в этом случае машина не получала информации о том, что именно скрывается за введенными программистом именами, соответствующими относительным или символьным адресам.
Имена информационных единиц не подвергались ее анализу, и машина не могла ответить ни на один запрос, который касался бы содержимого ее памяти, если программист не составил для ответа специальной программы.
Если, например, в память машины нужно было записать сведения о студентах университета, представленные в таблице 1, то без внутренней интерпретации в память машины была бы занесена совокупность из четырех машинных слов, соответствующих строкам этой таблицы.
Таблица 1.
| Ф.И.О. | Год рождения | Факультет | Курс | № зачетной книжки | Специализация |
| Железнов В.П. | 1979 | АВТ | 4 | М1273 | прикладная математика |
| Попов П.С. | 1981 | РТ | 3 | Р523 | Радиотехника |
| Иванов А.П. | 1978 | ЭТ | 5 | Э1451 | Электротехника |
| Петухова С.С. | 1983 | ПТ | 2 | Т485 | Теплоэнергетика |
Информационная единица, которой, например, приписано имя «Железнов В.П.», выглядит так: (<Год рождения, 1979> <Факультет, АВТ> <Курс, 4> <№ зачетной книжки, М1273> <Специализация, прикладная математика>). Круглые скобки здесь служат для выделения содержания информационной единицы, а угловые скобки выделяют в ней самостоятельные части, называемые обычно слотами. Полная запись информационной единицы, таким образом, имеет вид: (Имя информационной единицы <Имя 1-го слота, Значение 1-го слота> <Имя 2-ого слота, Значение 2-ого слота> … <Имя n-ого слота, Значение n-ого слота>).
При этом информация о том, какими группами двоичных разрядов в этих машинных словах закодированы сведения о студентах, у системы отсутствуют. Они известны лишь программисту, который использует данные таблицы 1 для решения возникающих у него задач.
При переходе к знаниям в память машины вводится информация о некоторой протоструктуре информационных единиц, «шапка» таблицы в нашем примере. Она представляет собой специальное машинное слово, в котором указано, в каких разрядах хранятся данные о Ф.И.О., годах рождения, факультета, курсах, номерах зачетных книжек и специализациях. При этом должны быть заданы специальные словари, в которых перечислены имеющиеся в памяти системы Ф.И.О., года рождения, факультеты и т.п. Все эти атрибуты могут играть роль имен для тех машинных слов, которые соответствуют строкам таблицы. По ним можно осуществлять поиск нужной информации. Каждая строка таблицы будет экземпляром протоструктуры. В настоящее время СУБД обеспечивает реализацию внутренней интерпретируемости всех информационных единиц, хранимых в реляционной БД.
2. Структурированность.
Сначала данные обладали очень простой внутренней структурой типа «машинное слово – совокупность разрядов». Затем, когда отдельные машинные слова стали объединяться в более сложные структуры (например, в списки), появилась возможность работать с информационными единицами с более богатой внутренней структурой. Для таких информационных единиц должен выполняться «принцип матрешки», т.е. рекурсивная вложимость одних информационных единиц в другие. Каждая информационная единица может быть включена в состав любой другой, и из каждой информационной единицы можно выделить некоторые ее составляющие. Другими словами, должна существовать возможность произвольного установления между отдельными информационными единицами отношений типа «часть-целое», «род-вид» или «элемент-класс».
Таким образом, информационная единица может задаваться в виде структуры, показанной на рис. 1, где
означает имя слота j-ого уровня вложенности с порядковым номером i, Р – имя всей информационной единицы,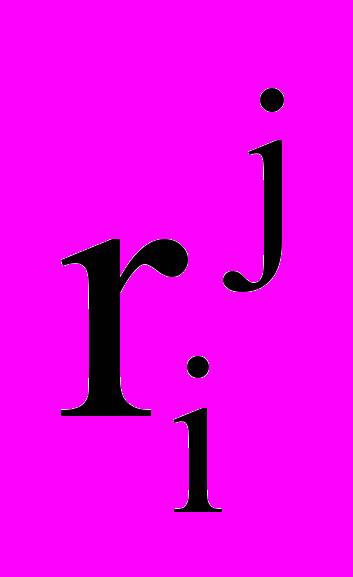 
– значение слота с порядковым номером i в j-ом уровне.| | | | | | | | | | | | |
| P |  |  |  | … |  |  |  |  | … |  |  |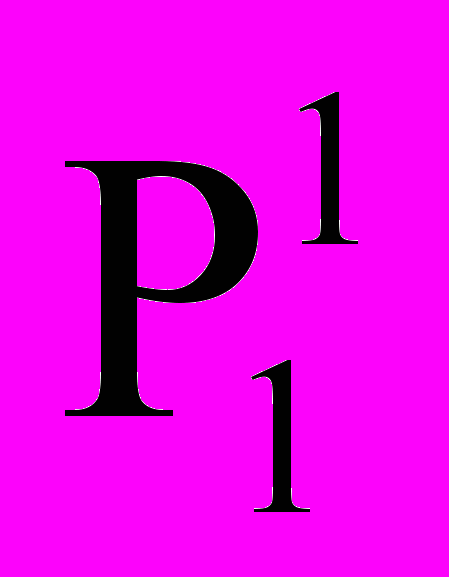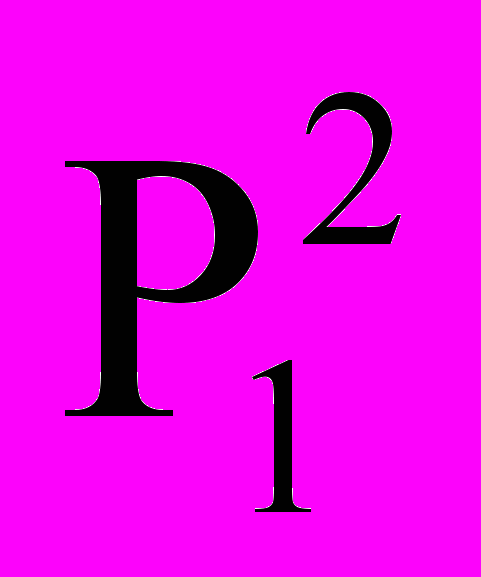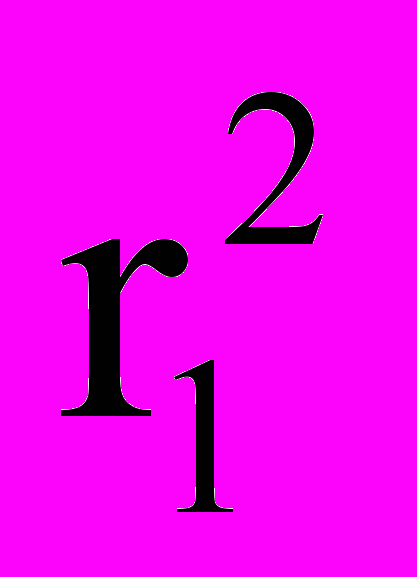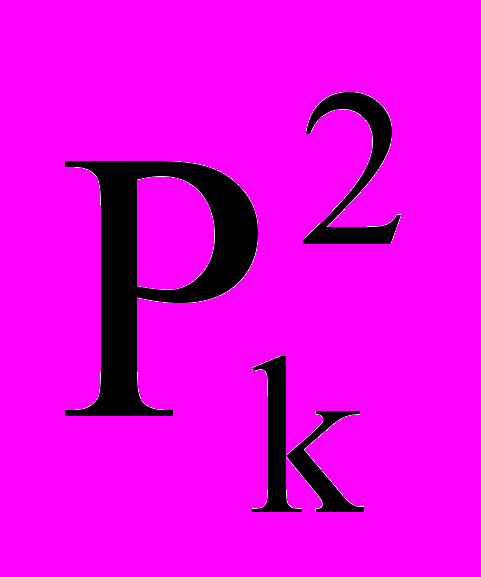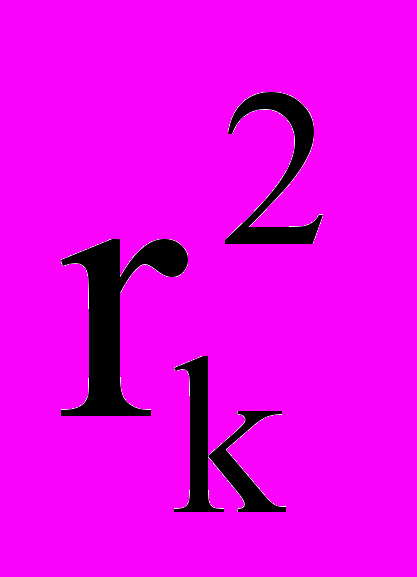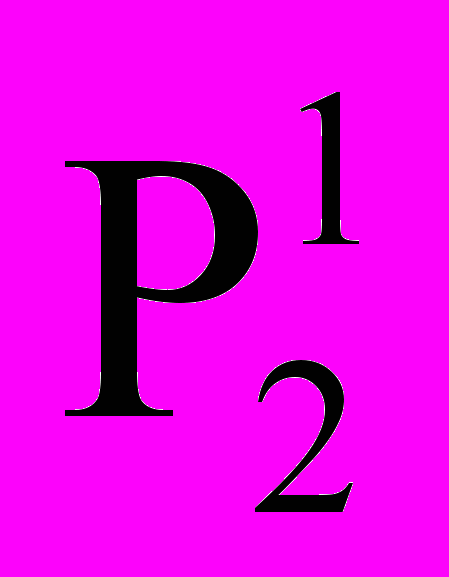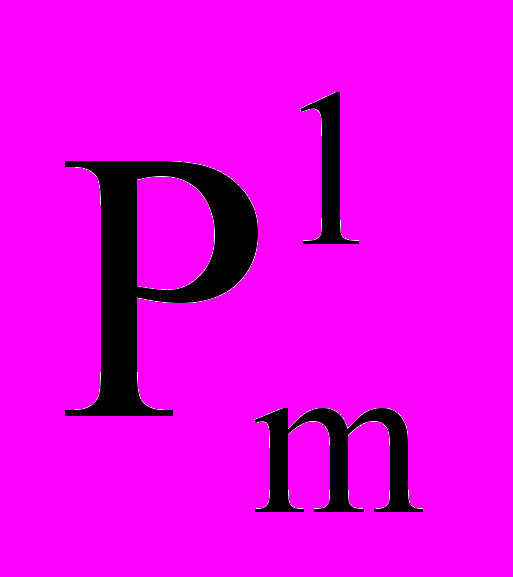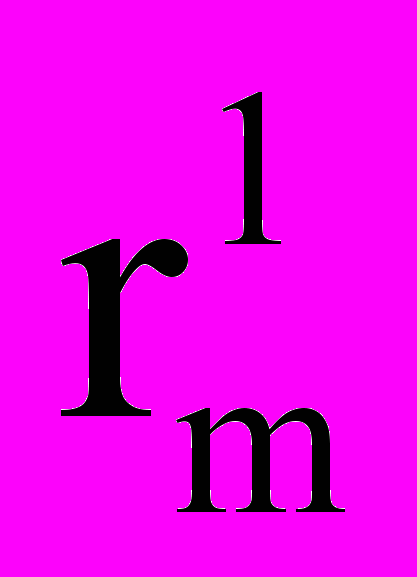
| | | | | | | | | | | | |
Рис. 1.
Видно, что информационная единица задается так, что ее первый слот в качестве своего значения содержит k слотов второго уровня, а все остальные слоты первого уровня не разбиваются на более мелкие единицы. Иногда в представлении знаний вместо термина «слот j-ого уровня» используют специальные названия для частей информационной единицы. Например, части слота 1-ого уровня называют ячейками, а их части – фасетами.
Между слотами разных уровней (точнее, между их именами) могут устанавливаться отношения различного типа. На рис. 2 (см. также таблицу 1) показан пример многоуровневой информационной единицы.
Она имеет глубину вложения слотов, равную четырем. Именем слота первого уровня служит слот «работники университета». На втором уровне два слота: «студенты» и «преподаватели». На третьем уровне имена слотов – это «Железнов В.П.», «Попов П.С.» и т.д. Остальные слоты вместе с их значениями являются слотами четвертого уровня.
Информационные единицы, структурированные таким образом, обычно называются фреймами. Они также обладают внутренней интерпретируемостью и наличием внутренней структуры связей.
3. Связность.
Между информационными единицами может быть также предусмотрена возможность установления внешней структуры связей различного типа.
| Работники университета | Студенты | | | | | | | | | | | |
| Железнов В.П. | Год рожд. | 1979 | Фак-т | АВТ | Курс | 4 | № кн. | М1273 | Спец. | ПМ | ||
| | | | | | | | | | | | ||
| | | | | | | | | | | | ||
| Попов П.С. | Год рожд. | 1981 | Фак-т | РТ | Курс | 3 | № кн. | Р523 | Спец. | Радиотехника | ||
| | | | | | | | | | | | ||
| . . . . . . . . . . . | ||||||||||||
| Преподаватели | | | | | | | | | | | | |
| Жуков В.А. | Год рожд. | 1955 | Фак-т | АВТ | Каф. | ПМ | Долж. | доц. | Какой курс читает | Дискретная математика | ||
| | | | | | | | | | | | ||
| | | | | | | | | | | | ||
| Крюков А.Т. | Год рожд. | 1953 | Фак-т | РТ | Каф. | РПУ | Долж. | проф. | Какой курс читает | Радиоприемники | ||
| | | | | | | | | | | | ||
| . . . . . . . . . . . | ||||||||||||
Рис. 2.
Например, информационные единицы могут быть связаны каузальным отношением, задающим причинно-следственные связи, или отношением «аргумент-функция», связанным с вычислением определенных функций. Можно также говорить об отношении структуризации, задающем иерархию информационных единиц.
Между информационными единицами могут устанавливаться также пространственные и временные отношения, а также отношения, определяющие порядок выбора информационных единиц из памяти машины или указывающие на то, что две информационные единицы несовместимы друг с другом в одном описании.
Наиболее полно различные типы связей воплощены в общей модели представления знаний, называемой семантической сетью, представляющей собой иерархическую сеть, в вершинах которой находятся информационные единицы. Эти единицы снабжены индивидуальными именами. Дуги такой сети соответствуют различным связям между информационными единицами. При этом иерархические связи определяются отношениями структуризации, а неиерархические связи – отношениями иных типов. Так, в качестве иерархических связей выступают отношения ISA (is an instance of) и AKO (a kind of). ISA-отношение связывает элементы (примеры) класса с самим классом, включающим группу объектов (явлений, процессов), обладающих общими свойствами. AKO-отношение используется для связи одного класса с другим. Например, индивидуальный объект «Попов П.С.» связывается ISA-отношением с классом «группа А 13 99», который, в свою очередь, связывается AKO-отношением с более общим классом «факультет АВТ».
4. Шкалирование.
Отдельные информационные единицы могут соотноситься между собой с помощью различных шкал. Простейшие из них – метрические шкалы. С их помощью можно устанавливать количественные соотношения и порядок тех или иных совокупностей информационных единиц.
Метрические шкалы, у которых начало отсчета абсолютно, т.е. не зависит ни от событий, ни от момента или места нахождения, называются абсолютными. Примером такой абсолютной метрической шкалы является начальное событие «Рождество Христово», от которого мы отсчитываем историческое время. С помощью этой шкалы можно упорядочить по возрасту всех людей, известных интеллектуальной системе и ответить на любой вопрос, связанный с их возрастом.
Другой тип метрических шкал – относительные метрические шкалы. Начало отсчета на них меняется, и каждый раз служит предметом специального договора. Очень часто это начало определяется текущим моментом высказывания или местом нахождения. Такое высказывание как «через полчаса я буду на кафедре Прикладной математики» проецируется именно на относительную шкалу. Для относительных шкал используют те же единицы измерений, что и для абсолютных.
Наконец, еще один вид шкал – порядковые шкалы. На них фиксируется лишь порядок информационных единиц. Примером такой шкалы может служить шкала тяжести преступлений, имеющая место в юриспруденции. В этой шкале кража – преступление менее значительное, чем убийство, а мелкое хулиганство менее значительно, нежели кража. Другим примером порядковой шкалы является шкала оценок обучающихся в университете: неудовлетворительно, удовлетворительно, хорошо, отлично. На этой шкале нет никакой метрики, и мы не можем количественно оценить, насколько оценка «хорошо» превосходит оценку «удовлетворительно».
Среди порядковых шкал выделяют нечеткие порядковые шкалы. Их иногда называют лингвистическим шкалами. Пример такой шкалы «никогда-всегда». Метки на ней характеризуют частоту появления событий или процессов. Шкала ограничена с двух сторон маркерами «никогда» и «всегда». В первом случае частота появления события равна нулю, а во втором – единице. Остальным маркерам, которым соответствует упорядоченный список нечетких квантификаторов типа «очень редко», «редко», «не часто – не редко», «часто», «очень часто», соответствуют не точечные деления, а некоторые интервалы, величина и расположение которых зависят от интерпретации словесных оценок, относящихся к шкале. Например, можно считать, что маркеру «редко» соответствует случай, когда частота появления события лежит в интервале от 0.2 до 0.3.
Для нечетких квантификаторов при построении такой шкалы можно равномерно разделить отрезок между концевыми маркерами на столько отрезков, сколько промежуточных маркеров в ней находится или опросить экспертов в целью определения границ отрезков, соответствующих каждому из промежуточных маркеров.
В теории нечетких множеств, как известно, используются функции принадлежности, интерпретируемые как характеристические функции для нечетких множеств. Функция принадлежности для множества А обозначается символом А(х). Ее значение, равное 0, соответствует утверждению, что данный элемент х не принадлежит А, а ее значение, равное 1, свидетельствует о безусловной его принадлежности данному множеству. Промежуточные значения А(х) не следует трактовать в вероятностном смысле, так как степень принадлежности элемента к нечеткому множеству не обязана иметь статистическую природу.
Следует отметить, что нечеткие квантификаторы фиксируют лишь порядок, образующийся на нечетких шкалах. Например, что значит «редко»? Во фразах типа «Я редко бываю в кинотеатре» и «Редко удается поехать в зарубежную командировку» вряд ли говорится об одинаковой частоте случающихся событий. Трудность сравнения между собой информационных единиц, расположенных на различных нечетких шкалах, решается путем введения универсальных нечетких шкал, на которые с помощью специальных процедур проецируются различные нечеткие шкалы, соответствующие одним и тем же спискам нечетких квантификаторов.
Кроме абсолютных и относительных метрических шкал, порядковых шкал и их смешанных типов, следует отметить оппозиционные шкалы. Как считает Д.А. Поспелов, именно оппозиционные шкалы заложили основу восприятия мира человека не как хаотического набора ситуаций и фактов, а как определенным образом упорядоченное их единство. Бинарная оппозиция типа противопоставления двух фактов, явлений или свойств, – левое и правое, мужское и женское, – лежит в основе мировосприятия у всех народов мира. Такая шкала образуется с помощью пар слов-антонимов. Примерами их могут служить красивый – безобразный, хороший – плохой, сильный – слабый и т.п. В середине оппозиционной шкалы находится нейтральное значение типа не красивый – не безобразный, не хороший – не плохой и т.п.
Постигая закономерности физического мира, с помощью оппозиционных шкал можно любое понятие естественного языка как бы спроецировать на второй план. Отсюда и употребляются эпитеты острый ум, недалекий человек и т.п.
5. Семантическая метрика.
На множестве информационных единиц упорядочение сведений в когнитивных структурах человека происходит не только благодаря оппозиционным шкалам, но и также благодаря ассоциативным связям, характеризующим ситуационную близость этих единиц. Эту связь можно было бы назвать отношением релевантности для информационных единиц. Такое отношение дает возможность выделять в информационной базе некоторые типовые ситуации (например, «покупка», «учеба», «отдых»). Отношения релевантности при работе со знанием позволяет сузить пространство поиска нужной информации и находить знания, близкие к уже найденным.
Другая оценка близости информационных единиц опирается на частоту появления тех или иных ситуаций или конкретных представителей в типовых ситуациях. Выбор того или иного конкретного представителя из множества возможных подчиняется закону частоты его появления. Если, например, провести с представителями социума, в котором мы живем, эксперимент, в ходе которого испытуемый должен не задумываясь давать ответы на вопросы экспериментатора о названиях конкретных представителей типовых ситуаций или слов-понятий, то результат в подавляющем числе случаев будет демонстрировать действие закона частоты появления.
Если мы просим назвать поэта, то, как правило, русский человек даст ответ «Пушкин», а не «Байрон». На требование назвать инструмент, мы, как правило, получим ответ «молоток».
Такие эксперименты показывают, что у нас «на языке» готовые ответы на возможные запросы к нашей памяти всегда те, которые соответствуют наиболее часто встречавшемуся верному ответу. Подобный механизм позволяет при дефиците времени на обдумывание и поиск нужной информации в памяти всегда иметь нужные «клише», наиболее часто встречавшиеся в нашей жизни.
6. Наличие активности.
В связи с непрерывным развитием теории и практики программирования программы и данные, с которым эта программа работала, были отделены друг от друга. В программе было сосредоточено процедурное знание. Оно хранило в себе информацию о том, как надо действовать, чтобы получить нужный результат. Машина выступала в роли мощного калькулятора, в котором программа играла роль активатора данных.
Знания другого типа, которые обычно называют декларативными, хранили в себе информацию о том, над чем надо выполнять эти действия. Процедурное знание формировало обращение к декларативному знанию, воплощенному на первом этапе развития программирования в пассивно лежащие в памяти машины данные.
Для интеллектуальных систем складывается противоположная ситуация. Не процедурные знания активизируют декларативные, а наоборот – та или иная структура декларативных знаний оказывается активатором для процедурных знания. Появление в базе фактов или описаний событий, установление связей может стать источником активности системы.
Совокупность средств, обеспечивающих работу со знанием, образует систему управления базой знаний (СУБЗ), разработка которых сейчас усиленно развивается.