Знание в интеллектуальных системах Вагин В. Н. Введение. Характерные особенности знания

Вид материала

Документы

Содержание Знание как обоснованное истинное убеждение Не-факторы знания Вторая группа Знание и нетрадиционные логики Ключевой вопрос Второй тип рассуждений, названный автоэпистемическими

Подобный материал:

• Ложения темпоральной (временной) логики для ветвящегося времени в плане ее использования, 138.35kb.
• Мультиагентные системы в экономике, 104.75kb.
• Статья раскрывает характерные особенности социальной политики «ельцинского», 314.76kb.
• Тема: Класс Двудольные. Семейство Сложноцветные. Место урока, 174.72kb.
• Урок биологии в 7 классе. Интегрированный. Тема: Характерные особенности растений семейства, 188.8kb.
• Курс моделирование процессов переноса в турбулентных течениях программа курса лекций, 16.73kb.
• Цель: Обобщить и систематизировать знания о топографическом плане и географической, 51.45kb.
• Урок по теме "Земноводные", 80.88kb.
• Г. В. Мелихов миф. Идентичность. Знание: введение в теорию социально-антропологических, 741.74kb.
• Лекция №2 Тема: характеристика социологического знания, 195.16kb.

Знание как обоснованное истинное убеждение

По мере развития исследований в области интеллектуальных систем возникла концепция знания, которая объединила в себе многие черты процедурной и декларативной информации.

Хотя строгого понятия знания и не существует, само это понятие волновало лучшие умы человечества, начиная с древних греков. Так, по Платону знание делится на чувственное и интеллектуальное. Чувственное знание – низший вид, интеллектуальное – высший. Каждая из этих сфер в свою очередь делится на «мышление» (noēsis) и «рассудок» (dianoia) [3,4].

Под «мышлением» Платон понимает деятельность одного лишь ума, свободную от примеси чувственности, непосредственно созерцающую интеллектуальные предметы.

Второй вид интеллектуального знания – «рассудок». Под «рассудком» Платон понимает такой вид интеллектуального знания, при котором познающий также пользуется умом, но уже не ради самого ума, а для того, чтобы понимать чувственные вещи. «Рассудок» Платона уже не непосредственный, не интуитивный, а опосредственный, «дискурсивный» вид знания. Рассудок, согласно Платону, ниже ума и выше ощущений.

Чувственное знание Платон также делит на две области: «веру» (pistis) и «подобие» (eicasia). С помощью «веры» мы воспринимаем вещи в качестве существующих и утверждаем их в этом качестве. «Подобие» – вид уже не восприятия, а представления вещей, или интеллектуальное действование с чувственными образами вещей. «Подобие», по Платону, – мыслительное построение, основывающееся на «вере».

Платон различает знание и мнение. Одно истинное мнение еще не дает знания, и что для возникновения знания к истинному мнению должно присоединится еще нечто – «смысл». Но Платон идет еще дальше. Как бы ни понимать «смысл», то ли как выражение в слове, то ли как перечисление элементов, то ли как указание на отличительный признак, прибавка «смысла» к «правильному мнению» не создает и не может создать того, что зовут знанием.

Таким образом, знание не есть ни ощущения, ни правильное мнение, ни соединение правильного мнения со смыслом. Мнение не есть незнание, но оно не есть и знание: оно темнее знания и яснее незнания.

В отличие от мнения знание есть потенция, особый род существующего. Род этот характеризует направленность: знание направляется к своему предмету, и всякая потенция, направляющаяся к одному и тому же и делающая одно и то же, называется той же самой в отличие от всякой, направленной на иное и делающей иное.

Математические предметы и математические отношения Платон выделяет в особый предмет знания. В системе видов знания математическим предметам также принадлежит некое «серединное» место. Это место между областью «идей» и областью чувственно воспринимаемых вещей, а также областью их отображений.

«Идеи» постигаются только посредством знания, и знание возможно только относительно «идей».

В отличие от «идей» математические предметы и математические отношения постигаются посредством рассуждения, или размышления рассудка. Это и есть второй вид знания.

Чувственные вещи постигаются посредством мнения (doxa). О них невозможно достоверное знание, их нельзя постигнуть с помощью рассуждения; если их можно постигнуть, то лишь недостоверно, лишь гипотетически.

Почему же математические предметы занимают середину между подлинным знанием и мнением? Дело в том, что математические предметы родственны и вещам, и «идеям». Предметы эти как «идеи» неизменны; природа их не зависит от отдельных экземпляров, представляющих их в чувственном мире. Математики вынуждены, считает Платон, прибегать для достижения своих предметов к помощи отдельных фигур как в геометрии. Фигуры же эти рисуются или представляются посредством воображения. Именно поэтому математическое знание не есть знание, совпадающее с тем, при помощи которого постигаются «идеи». Оно совмещает в себе черты истинного знания с некоторыми чертами мнения.

Русскому слову «наука» соответствует древнегреческое «епистэмэ», которое в языке эллинов первоначально понималось как «умение», «искусство», «опытность», затем – как «знание» и, наконец, как «научное знание». Для Платона «епистэмэ» – достоверное знание, а не субъективное мнение. Так же понимал этот термин и Аристотель – ученик, последователь и критик Платона.

Научное, или достоверное, знание для Аристотеля – не результат веры, некритически воспринятой традиции, субъективного опыта. Оно – результат логического рассуждения, направленного на открытие начал, причин и элементов того, что дано нам в непосредственном чувственном опыте: «… всякое знание, основанное на рассуждениях … имеет своим предметом, – говорится в «Метафизике», – более или менее точно определенные причины и начала» [5,6].

«Знать же, почему нечто есть, – значит знать через причину» – пишет он во «Второй аналитике». Научное знание должно быть также логически доказательным: нужно не просто выявить причину данного предмета, но и доказать, что для этого предмета именно она, а не нечто иное, является причиной. Поэтому Аристотель подчеркивает: «… наука связана с доказательством…».

Аристотель абсолютизировал научное знание и считал, что не может быть науки ни о привходящем (случайном), ни о преходящем (изменчивом). Случайное как таковое не может быть предметом никакого вида знания.

Нельзя сказать, чтобы Аристотель игнорировал правдоподобное знание, принцип правдоподобия, который в латиноязычной философии получил название пробабилизма (от лат. «пробабилис» – вероятный, правдоподобный, возможный). Он определяет правдоподобное как «то, что кажется правильным всем или большинству людей…». Здесь он говорит об особом типе умозаключения – об умозаключении, которое строится из правдоподобных положений. Гениальный Стагирит называл его «диалектическим». Но такое умозаключение он вовсе не считал научным, доказательным, ведь доказательство имеет место только там и тогда, где и когда мы исходим непосредственно или опосредственно из безусловно истинных положений. Следовательно, в отличие от скептиков Аристотель допускал возможность абсолютно достоверного знания и именно его считал научным.

Как правило, определение знания носит метафорический характер, начиная от знаменитой метафоры «знание – сила» и кончая различными определениями, данными в различных энциклопедических справочниках.

В области искусственного интеллекта этот ключевой термин мы будем употреблять как следующую метафору: знание – это обоснованное истинное убеждение (вера) [7]. Здесь каждое слово нуждается в объяснение: что такое убеждение (belief), истина и обоснование (подтверждение)?

Интересно отметить, что до появления вычислительных машин, задолго до эры искусственного интеллекта в Большой энциклопедии (под ред. С.Н. Южакова, СПБ, т. 9, 1902 г.) было дано следующее определение этого термина.

«Знание в объективном смысле то же, что истинное знание (познание), в субъективном – убеждение в его истине по реальным причинам. В первом отношении оно противополагается заблуждению, как неистинному знанию, во втором – вере, мнению».

Здесь те же самые «три кита», на которых зиждется это метафорическое понятие. Начнем с «убеждения» (веры).

Пусть имеется база знаний для описания реального мира (предметной области), состоящая из пары <БЗ₀, ├_L>, где БЗ₀ – совокупность утверждений на языке некоторой логики L, например, логики предикатов первого порядка, и ├ _L – отношение выводимости (доказуемости) в этом языке L. Тогда утверждение Р  БЗ₀ тогда и только тогда, когда БЗ₀ ├ _L Р.

Пусть дана некоторая интеллектуальная система А, основанная на знании, со своей БЗ. Тогда предполагается, что в этой системе утверждение Р имеет место только тогда, когда Р находится в БЗ этой системы, т.е. убеждение есть нечто, литерально представленное в БЗ.

Конечно, в такой БЗ могут находиться какие угодно утверждения. Однако, потребуем, чтобы такие утверждения были истинными, непротиворечивыми друг другу, хотя это может потребовать обоснования.

Фундаментальным понятием семантики является понятие истины реального мира. Мы будем рассматривать истину в модели, где под моделью и понимается реальный мир. Состояние реального мира позволяет приписать семантические значения «истинно» или «ложно» (истинностные значения) к утверждениям интеллектуальной системы А. Так, для логики предикатов первого порядка имеет место семантика А. Тарского, состоящая из тройки , где D – непустое множество предметов (индивидуумов), называемое областью интерпретации (универсумом), а R и F являются множествами отношений и функций соответственно межу предметами, содержащимися в описываемом реальном мире.

Интерпретация представляет собой распространение исходных положений какой-либо формальной системы на реальный мир. Она придает смысл каждому символу формальной системы и устанавливает взаимно однозначное соответствие между символами формальной системы и реальными предметами. Если в логике высказываний интерпретация формулы понимается как приписывание истинностных значений пропозициональным символам этой формулы, то в логике предикатов первого порядка, как известно, каждому n-местному предикатному символу формулы соответствует n-местное отношение (т.е. Dⁿ  {И, Л}), каждому n-местному функциональному символу – n-местная функция (т.е. Dⁿ  D) и каждой константе – некоторый предмет из D, где D – область интерпретации. Говорят, что интерпретация является моделью БЗ тогда и только тогда, когда все утверждения в БЗ становятся истинными в этой интерпретации.

Как правило, системы, основанные на знании, имеют дело с одним знанием или с одним убеждением (верой). Для таких систем логика предикатов первого порядка пополняется оператором K, где KP читается как «известно (верно), что утверждение Р истинно». Имеем ли мы дело со знанием или убеждением относительно утверждения Р, зависит только от того, представлена ли в БЗ или нет аксиома вида KP  P, которая читается как «если известно, что Р истинно, тогда утверждение Р действительно истинно». Если эта аксиома представлена, то имеет место знание, если нет – убеждение [7].

Конечно, в динамически изменяющемся мире истинность некоторых утверждений может меняться. Тут мы подходим к пояснению слова «обоснованное» в метафорическом определении понятия «знание».

Действительно, чтобы убедиться в истинности или ложности некоторого утверждения, надо обосновать его статус новыми объяснениями, фактами или наблюдениями и в зависимости от подтверждения или опровержения его истинности перевести это утверждение в статус или знания, или ошибочного убеждения. Будем называть убеждение гипотезой, которая по мере ее обоснования превращается или в знание (в случае, если все объяснения, факты или наблюдения говорят о ее истинности), или в ошибочное убеждение, которое надо удалить из БЗ.

В качестве примера рассмотрим следующие три утверждения.

1. Все студены юны или х (Студент(х)  Юн(х)).
   
2. Петров – студент или Студент(Петров).
   
3. Петров юн или Юн(Петров).
   

Если мы убеждены, что первые два утверждения истинны, то истинность третьего утверждения достоверно подтверждена вследствие правила дедуктивного вывода Modus Ponens. Обоснование третьего утверждения здесь не требуется, если нам удалось обосновать истинность первых двух утверждений (такое обоснование легко сделать для второго утверждения, но что касается первого утверждения, возникают трудности с квантором «все»).

Теперь считаем, что истинны первое и третье утверждения. Выдвигаем гипотезу: «Студент ли Петров?» Эта гипотеза перейдет в статус знания, если мы усилим нашу веру в эту гипотезу путем дополнительных объяснений, фактов или наблюдений, одно из которых, например, может быть следующим: «Петров учится на факультете вычислительной техники».

Этот тип рассуждений носит название абдуктивного вывода, к рассмотрению которого мы перейдем позднее.

Наконец, имеется третья возможность, когда истинны второе и третье утверждения. Выдвигается гипотеза в виде общего закона: «Все ли студенты юны?» Этот пример является примером индуктивного умозаключения, обоснование которого является трудной задачей.

Говорят, что классификация утверждений о реальном мире на убеждения, гипотезы и знание выражает эпистемический статус утверждений [7]. Большинство теорий о реальном мире на данном периоде исследований являются знанием, так как они подтверждаются многочисленными объяснениям, фактами и наблюдениями.

Кроме эпистемического статуса утверждений имеется еще и ассерторический статус [7]. Рассмотрим следующее утверждение: «Студенты юны». Его можно трактовать по-разному.

1. «Все студенты юны». Как уже говорилось, это слишком сильное утверждение из-за квантора «все». По-видимому, исключения в реальной жизни все-таки бывают.
   
2. «Обычно (в большинстве случаев, как правило) студенты юны». Это утверждение предполагает некоторую возможность (вероятность) того, что студенты юны.
   
3. «Студенты юны». В этом случае исключения, конечно, предполагаются, но и признается неявно некоторая связь (какая?) между студенчеством как некоторым социумом и его возрастом.
   

Отсюда вытекают три различных подхода при определении смысла (семантики) утверждений.

В первом случае имеет место так называемый аналитический (дефинициальный) тип утверждений, т.е. тот тип, когда истинность утверждений не подвергается сомнению, как не подвергаются сомнению утверждения типа «квадрат – равносторонний прямоугольник» или «Земля вращается вокруг солнца». Конечно, к этому типу нежелательно относить утверждения типа нашего примера, так как имеются студенты не юные, если считать юность до 23 лет.

Во втором случае подчеркивается стереотипный взгляд на утверждения, в котором имеет место типичный случай. Известно, что в искусственном интеллекте теория прототипов широко используется в системах представления знаний, основанных на фреймах, в которых выводится стереотипная ситуация. Но если в классической логике предикатов первого порядка, как правило, используется вывод с аналитическими утверждениями (достоверный вывод), то в выводе с прототипами находят применение вероятностные, нечеткие и т.п. схемы (правдоподобный вывод).

Третий случай страдает отсутствием строгого формализма при описании смысла того или иного утверждения. Здесь можно говорить лишь о выдвижении некоторой гипотезы, которая будет подтверждаться или опровергаться при наличии дополнительных фактов, объяснений или наблюдений.

Таким образом, в семантической теории знания основная трудность заключается в том, что истинностное значение утверждения может быть как известно, так и неизвестно, независимо от того, какое оно в действительности.

Если мы охарактеризуем БЗ как один из возможных миров, то некоторое утверждение будет истинным тогда и только тогда в этом мире, когда оно истинно во всех возможных мирах, совместимых с нашей БЗ.

Пусть, например, мы имеем в БЗ следующие три утверждения.

1. Профессор(Бурлаков).
   
2. Профессор(Фролов)  Профессор(Коптев).
   
3. х (Профессор(х)  Работник_Университета(х)).
   

Здесь утверждается, что Бурлаков и Фролов или Коптев являются профессорами как в этой БЗ, так и во всех возможных мирах, совместимых с ней, чего нельзя сказать о других индивидуумах, не перечисленных в нашей БЗ. Аналогично, в мире нашей БЗ легко вывести, что Бурлаков также является работником университета. Таким образом, наша БЗ может быть охарактеризована как один из возможных миров, в котором некоторое утверждение будет истинным тогда и только тогда, когда оно истинно во всех возможных мирах, совместимых с БЗ.

Недостаток этого подхода заключается в том, что моделирование знаний влечет логическое всеведение, т.е. все логические следствия убеждений должны быть обоснованы.

Альтернативным к подходу возможных миров является так называемый синтаксический подход, который изоморфен только явно заданному множеству утверждений БЗ. Так, возвращаясь к примеру нашей БЗ, мы имеем только три заданных утверждения, считающиеся истинными. Однако никакие выводимые утверждения типа «Бурлаков является работником университета» не должны быть в БЗ, что позволяет избежать логического всеведения. Все, что обосновано, явно присутствует в БЗ. Правда, при таком подходе не обосновывается утверждение Профессор(Коптев)  Профессор(Фролов) в силу его явного отсутствия в БЗ, с чем трудно согласиться.

Упомянем еще об одном подходе, связывающем понятие возможного мира с миром ситуаций. Утверждения, в том числе и выводимые, будут поддерживаться только те, которые релевантны данной ситуации. Так, для нашего примера истинны будут утверждения о том, что Бурлаков является профессором, а также, что Фролов или Коптев – тоже профессора, причем, если обосновано утверждение Профессор(Фролов)  Профессор(Коптев), то обосновано и Профессор(Коптев)  Профессор(Фролов). Выводимое утверждение о Бурлакове как работнике университета также обосновано, если обосновано утверждение, что все профессора являются работниками университета.

Таким образом, ситуационный подход расширяет стандартную структуру возможных миров, и если в «возможных мирах» определяется истинностное значение всех утверждений, то в ситуационном подходе истинностное значение может быть как определено, так и не определено.

Не-факторы знания

В идеале было бы замечательно, если БЗ интеллектуальной системы содержала бы только аналитические утверждения, обоснование которых не требуется. К сожалению, данные и знание, описывающие сущности и связи какой-либо проблемной области, как правило, неполны, противоречивы, немонотонны, неточны, неопределенны и нечетки. Остановимся на этих особенностях знания [7,8].

В классических логических системах свойство полноты обычно формулируется следующим образом: для множества формул с заданными свойствами исходная система аксиом и правил вывода должна обеспечить вывод всех формул, входящих в это множество. Важно также свойство непротиворечивости, суть которого сводится к тому, что исходная система аксиом и правил вывода не должна давать возможность выводить формулы, не принадлежащие заданному множеству формул с выбранными свойствами.

Например, полные системы аксиом и правил вывода в классическом исчислении предикатов первого порядка позволяют получить любую общезначимую формулу из множества общезначимых формул и не дают возможности получить какие-либо формулы, не обладающие этим свойством.

Однако на практике трудность получения полной и непротиворечивой БЗ состоит в том, что знания о некой конкретной проблемной области, как правило, плохо формализованы или не формализованы совсем, а значит трудно сформулировать или даже невозможно сформулировать и те априорные свойства, которым должны удовлетворять формулы, выводимые в данной системе.

От полноты содержащейся в БЗ информации зависит и полнота ответов на запросы, предъявляемые к БЗ. Если в БЗ, содержащую сведения о студентах и преподавателях данного университета, поступил запрос «Бурлаков – профессор?», то ответ будет положительным, если это на самом деле так. В случае неудачи с этим запросом могут быть два варианта: а) Бурлаков – не профессор и б)  статус Бурлакова не известен. Первый вариант имеет место, если мы придерживаемся предположения о замкнутости мира (Рейтер), рассматривающего факты, которые не могут быть найдены (выведены) в БЗ, как их отрицания. О втором варианте трудно что-либо сказать. Таким образом, если в БЗ содержатся сведения только о нескольких преподавателях университета, хотя их на самом деле намного больше, то, естественно, такая неполная БЗ и будет давать ответы только об этих преподавателях, и может быть возможен случай, когда система знает о других, неизвестных ей преподавателях. Можно отметить, что проблеме обработки запросов при неполноте знаний посвящена логика вопросов и ответов (эротетическая логика), в которой наряду с обычными истинностными значениями {И, Л} добавлены еще два: «неизвестно» и «противоречиво» [9].

Что касается противоречивости знания, то ее последствия в силу потери разницы между истиной и ложью (вспомним, что из противоречия выводима любая формула (ex falso quodlibet), т.е. А, А ├ В) поистине катастрофически. При представлении и обработке противоречивых знаний возникают две проблемы. Первая касается ассимиляции (усвоения) противоречивой информации, т.е. способности включать противоречия в БЗ и возможности работать с противоречивой БЗ. Вторая проблема заключается в аккомодации (приспособлении) противоречивого знания, т.е. такой модификации БЗ, при которой она становится непротиворечивой. Эти две проблемы тесно связаны между собой и от их совместного решения зависит общая проблема вывода утверждений в противоречивой БЗ.

На первый взгляд, исходя из здравого смысла, проблема ассимиляции противоречий может быть разрешена путем введения порядка реализации вывода, т.е. сначала пытаются вывести рассуждения, связанные с частными фактами, нежели с общими законами. Рассмотрим следующую БЗ.

1. Студенты изучают биологию или х (Ст(х)  Биол(х)), предполагая, что все студенты изучают биологию.
   
2. Рыбин – студент или Ст(Рыбин). Отсюда следует, что студент Рыбин изучает биологию.
   

Однако, введение в эту БЗ дополнительной информации типа:

3. Студенты радиотехнического факультета не изучают биологию или х  (СтРад(х)  Биол(х));
   
4. Рыбин – студент радиотехнического факультета или СтРад(Рыбин),
   которая носит более частный и уточняющий характер, блокирует предыдущий вывод, отдавая предпочтение этим частным утверждениям. Отсюда выводимо, что студент Рыбин не изучает биологию.
   

Трудность нахождения порядка реализации вывода заключается, конечно, в семантике утверждений, которая в общем случае неочевидна. Можно говорить, что утверждение В выводимо из гипотез А₁, А₂, …, A_n (или А₁, А₂, …, A_n ├ В), если каждая гипотеза релевантна этому утверждению. Но построение такой релевантной логики связано с большими трудностями. Здесь можно найти связь с ситуационной семантикой, где выводы делаются только в пределах той ситуации, которая имеет место в данный момент. Естественно, при переходе к другой ситуации имеет место ревизия БЗ и выведенные ранее утверждения не должны использоваться для вывода новых.

Проблема ассимиляции противоречия имеет место и в уже упоминавшейся эротетической логике. Если, например, из одного источника получено, что Студент(Петров) истинно, а из другого – Студент(Петров) истинно, то в этой логике данному утверждению будет приписано истинностное значение «противоречиво», что дает возможность работать с противоречивой информацией.

Что касается аккомодации противоречия, то проблема заключается в обработке так называемых «подозрительных» формул (т.е. формул, которые могли бы быть противоречивыми) в качестве гипотез. Так как эти формулы находятся среди формул, общезначимость которых не вызывает сомнений, то тут возникают вопросы установления непротиворечивости «подозрительных» формул, нахождения и описания множества формул, выдвигаемых в качестве гипотез, и наконец, каким образом эти гипотезы могут взаимодействовать с другими утверждениями для дедуктивного вывода новых утверждений.

Конечно, поддержка истинности таких утверждений должна проверяться исключениями, которые имеют место в реальной БЗ, что приводит к ее ревизии и усложняет саму процедуру вывода.

В классической логике предикатов первого порядка отношение выводимости удовлетворяет следующим свойствам:

1. рефлексивности: А₁, А₂, …, A_n ├ A_i, i = 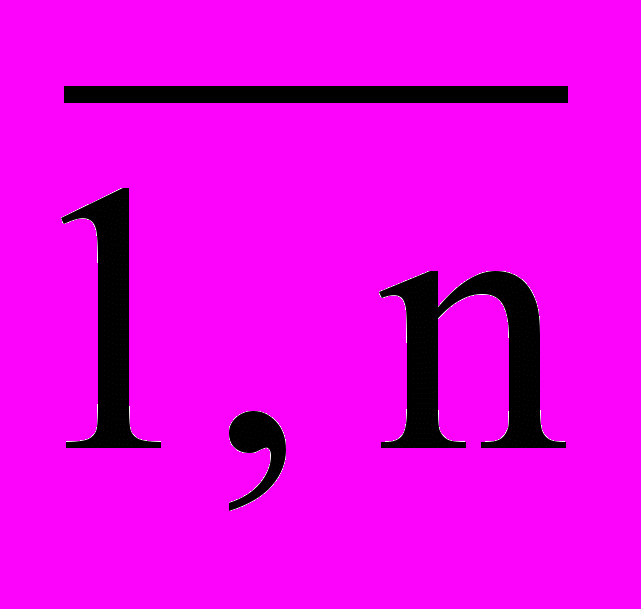, т.е. вывод заключения, идентичного одной из посылок, есть общезначимая операция;
   
2. транзитивности: если А₁, А₂, …, A_n ├ В₁ и А₁, А₂, …, A_n, В₁ ├ В₂, то А₁, А₂, …, A_n ├ В₂, т.е. промежуточные результаты можно использовать для вывода заключения В₂;
   
3. монотонности: если А₁, А₂, …, A_n ├ В₁, то А₁, А₂, …, A_n, {F} ├ В₁, где {F} – множество добавочных утверждений, т.е. добавочно введенные утверждения не отменяют ранее выведенное утверждение В₁.
   

К сожалению, свойство монотонности не выполняется для динамических проблемных областей, БЗ которых содержит неполную, неточную и динамически изменяющуюся информацию. Рассуждения в таких БЗ, говорят, часто предположительны, правдоподобны и должны подвергаться пересмотру. Довольно очевидно, что для таких пересматриваемых рассуждений логическая система должна быть немонотонной [10,11,12]. Это значит, что пересматриваемые рассуждения не являются в классическом смысле общезначимыми, и если заключение В выводимо из посылок А₁, А₂, …, A_n, существует модель для {А₁, А₂, …, A_n}  {F}, не подтверждающая В.

Например, «Петров юн» не является общезначимым следствием из двух посылок: «Большинство студентов юны» и «Петров – студент». Оно просто выполнимо с этими посылками. И, следовательно, это заключение принадлежит к возможно выполнимому на основе этих двух посылок образу мира.

Конечно, если у нас нет дополнительной информации, то мы по умолчанию полагаем: «Если Вы не знаете ничего другого, то предположите, что все студенты действительно юны». Тогда унаследовав это свойство, можно вывести, что и Петров, будучи студентом, также юн.

При поступлении новой информации предположения могут стать невыполни­мы­ми с новым множеством посылок и будут отвергнуты. Узнав, например, что Петров не юн, и получив, таким образом, противоречивую БЗ, мы или отвергнем ранее выведенное заключение, или потребуем дополнительной информации.

Такой тип немонотонных рассуждений был реализован в логике умолчаний.

Отметим только, что проблема немонотонности тесно связана с проблемами неполноты и противоречивости знаний.

При описании динамически изменяющегося реального мира мы часто имеем дело с неточной информацией, которая будучи помещенной в БЗ обрабатывается как истинная информация, хотя это не соответствует действительности. Например, пусть в БЗ хранятся следующие сведения:

Студент(Петров),

Читать_курс(Фролов, Математическая логика).

Однако эти сведения могут не соответствовать действительности, если студент Петров месяц назад был отчислен из университета, а Фролов уже читает другой курс.

Неточность относится к содержанию информации (или значению сущности) и наряду с неполнотой и противоречивостью должна обязательно учитываться при представлении знаний в БЗ. Неточная информация может быть как непротиворечивой, так и противоречивой. Так, например, возраст студента Петрова, записанный в БЗ, равен 32 годам, хотя ему на самом деле 23. Это пример непротиворечивой, хотя и неточной информации. Может быть и другая ситуация, когда по ошибке в БЗ ему записали 123 года, что противоречит действительности, так как возраст людей, как правило, колеблется от 0 до 100 лет.

Для того чтобы неточные данные стали точными, можно воспользоваться ранее упоминавшимся модальным оператором K, который подчеркивает, что если известно, что некоторое утверждение истинно, то оно на самом деле истинно. Например, если известно, что все находящиеся в БЗ личности являются студентами, то это на самом деле так, или х (K Студент(х)  Студент(х)).

К неточности будем относить также величины, значения которых могут быть получены с ограниченной точностью, не превышающей некоторых порог, определенный природой соответствующих параметров. Очевидно, что практически все реальные оценки являются неточными, и сама оценка неточности также является неточной. Примеры неточности данных встречаются при измерении физических величин. В зависимости от степени точности измерительного прибора, от психического состояния и здоровья человека, производящего измерения, получаемое значение величины колеблется в некотором интервале. Поэтому для представления неточности данных мы можем использовать интервал значений вместе с оценкой точности в качестве меры доверия к каждому значению.

Если неточность относится к содержанию информации, то неопределенность – к ее истинности, понимаемой в смысле соответствия реальной действительности (степени уверенности знания). Каждый факт реального мира связан с определенностью информации, которая указывает на степень этой уверенности.

Понятия «определенности» и «уверенности» довольно трудно формализуемы, и для их определения чаще всего используются количественные меры. Основная идея такой меры заключается во введении функции неопределенности unc(p), понимаемой как определенность того, что высказывание p, содержащееся в БЗ, истинно, т.е. говорят, что утверждение p более определенно, чем q, если unc(p)  unc(q).

Традиционным подходом для представления неопределенности является теория вероятностей – хорошо разработанная на сегодняшний день математическая теория с ясными и общепринятыми аксиомами.

Пусть  – конечное множество утверждений, замкнутое относительно отрицания и конъюнкции (т.е. любая суперпозиция функций из множества  снова принадлежит ), а  и  обозначают противоречивое и общезначимое утверждения соответственно в множестве . Тогда вероятностная мера P, определенная на , представляет собой определенность (вероятность, правдоподобность, уверенность) утверждения такую, что

1. P () = 0;
   
2. P () = 1;
   
3. P (p  q) = P (p) + P (q), если p & q = .
   

Однако классическая теория вероятностей страдает рядом недостатков и до сих пор не утихают споры насчет того, какого рода действительность хотят выразить с помощью этой теории. Например, как найти вероятностную меру P для конкретного множества утверждений или на основании чего должно выполняться равенство P(q) + P (q) = 1. Действительно, если БЗ конкретно неизвестно, является ли Петров студентом или нет, то почему P (Студент(Петров)) + P (Студент(Петров)) = 1?

Основной вопрос, возникающий при выборе функции неопределенности для множества утверждений, заключается в нахождении ограничений этой функции теми утверждениями, которые логически или вероятностно связаны между собой. Решение этого вопроса обеспечивается правилом Байеса:

P(H | E1, E2, …, En) =	P(H)  P(E1, E2, …, En | H)
	P(E1, E2, …, En)	,

где P (H | E₁, E₂, …, E_n) – условная вероятность утверждения Н при условии E₁, E₂, …, E_n, т.е. это вероятность того, что утверждение Н истинно, если истинны утверждения (события) E₁, E₂, …, E_n. Однако на практике определить вероятность того, что утверждения E₁, E₂, …, E_n истинны и условную вероятность P (E₁, E₂, …, E_n | H) довольно трудно. Конечно, можно упростить проблему и считать, что утверждения E_i статистически независимы, т.е. P (E₁, E₂, …, E_n) = P (E₁)  P (E₂)  …  P (E_n). Однако, насколько достоверно и обоснованно предположение о статистической независимости E_i – это вопрос, требующий дополнительного анализа для каждого конкретного случая. Другое упрощение касается статистической независимости утверждение E_i при условии Н, т.е. P (E₁, E₂, …, E_n | H) = P (E₁ | H)  P (E₂ | H)  …  P (E_n | H).

В теории Демпстера-Шейфера требование к условию P (q) + P (q) = 1 ослаблено и вместо него имеет место P (q) + P (q)  1. Здесь основным средством для распределения и манипулирования степенями уверенности утверждений является функция вероятностной меры Mr, представляющая собой распределение базовых вероятностей на все возможные утверждения. Исходя из этого распределения, поддержка утверждению p определяется как sup(p) = Mr(q), если {q  p}, т.е. вероятностная мера любого утверждения q, из которого следует р, кладется в общую копилку для р [13,14].

Правдоподобность утверждения р определяется следующим образом: pls(p) = 1 – sup(p). Легко показать, что sup(p)  pls(p). Отсюда степень уверенности утверждения р определяется доверительным интервалом: conf(p) = [sup(p), pls(p)].

Возвращаясь к примеру, являтеся ли Петров студентом или нет, мы получим доверительный интервал [0, 0], если в БЗ нет никаких сведений о студенте Петрове, и conf(p) = [1, 1], если Петров не является студентом.

Однако, и в подходе Демпстера-Шейфера имеются свои трудности. Так, неясно, что делать при выборе утверждений, доверительные интервалы которых перекрываются или значительно отличаются размерами.

Таким образом, и классическая теория вероятностей, и теория Демпстера-Шейфера нуждаются в обосновании в каждом конкретном случае, когда мы имеем дело с неопределенностью. И только тщательный анализ видов неопределенности может дать ответ, какой из подходов более предпочтителен.

Наконец, остановимся на проблеме представления нечетких знаний, являющейся ключевой при разработке интеллектуальных систем различного назначения. Нечеткие знания по своей природе разнообразны и могут быть условно разделены на следующие категории: неточность, недоопределенность, неоднозначность, словом, любые нечеткости, между которыми нельзя провести четкой границы.

Один из способов описания нечеткости основывается на понятии нечеткого множества, введенного Л. Заде [15]. Пусть  – произвольное непустое множество. Нечетким множеством множества  называется множество пар:  = {<_A(x)/x}, где x  , (x)  [0, 1].

Функция :   [0, 1] называется функцией принадлежности нечеткого множества , а  – базовым множеством. Для каждого конкретного значения x   величина (x) принимает значения из замкнутого интервала [0, 1], которые называются степенью принадлежности элемента х нечеткому множеству .

Носителем нечеткого множества называется подмножество А множества , содержащее те из , для которых значения функции принадлежности _А(x) > 0.

Например, пусть  – множество натуральных чисел. Тогда его нечеткое множество «очень малых» чисел может быть таким:  = {<1/1>, <0.8/2>, <0.7/3>, <0.6/4>, <0.5/5>, <0.3/6>, <0.1/7>}.

Носителем нечеткого множества является множество А = {1, 2, 3, 4, 5, 6, 7}. Отметим, что носитель нечеткого множества – это обычное, «четкое» подмножество множества .

В настоящее время существует целый ряд моделей представления нечеткости в интеллектуальных системах, среди которых модель коэффициентов уверенности в MYCIN, вероятностная логика Нильсона, теория свидетельств Шейфера, теория возможностей Заде, модель голосования Бэлдвина, лингвистическая модель в MILORD и другие.

Несмотря на различную природу нечеткости, формализованную в моделях, мы можем условно разбить эти модели на три группы по типу нечетких множеств, используемых для оценок объектов (значений, функций принадлежности) в моделях.

К первой группе относятся модели с числовым значением функции принадлежности: модель коэффициентов уверенности, вероятностная логика.

Вторая группа включает в себя интервально-значные модели: теория свидетельств, теория возможностей, модель голосования и т.д.

Третья группа – нечетко-значные модели, в частности, лингвистическая модель в MILORD.

Если не учитывать внешние проявления знаний в разных моделях, которые могут изменяться с одной модели на другую, то можно представить любое нечеткое знание в формальном виде M: Z, где M – некоторое нечеткое выражение, отражающее понятия, утверждения, отношения, правила и т.п., а Z – мера доверия к тому, что M истинно.

В моделях с числовым значением обычно Z представляет собой действительное число (в большинстве случаев число интервала [0, 1]) и интерпретируется как степень уверенности истинности выражения М.

Формальным аппаратом для выражения меры доверия Z в интервально-значных моделях является интервал. В различных моделях нижняя и верхняя границы интервала объясняются по разному. Они могут быть нижней и верхней вероятностями как в теории свидетельств, степенями необходимости и возможности в теории возможностей, необходимой и возможной поддержками в модели голосования и пр.

Нечетко-значные модели обычно применяются в случаях, в которых лингвистические переменные используются для описания объектов предметной области. Лингвистические переменные могут быть языковой единицей (словом, словосочетанием и т.д.), отражающей свойства объектов, лингвистическим квантором, определенным на множестве объектов и т.п.

При этом Z интерпретируется лингвистическим значением и представляется некоторым нечетким множеством.

Знание и нетрадиционные логики

Как известно, классическая логика типа логики предикатов первого порядка есть формальная система, состоящая из множества термов и операций, множества правил конструирования правильно построенных выражений (синтаксиса), системы аксиом и множества правил вывода. Она дает различные средства формализации и анализа правильности дедуктивных рассуждений. Язык классической логики является основой для выражения декларативных знаний, где рассуждение определяется как операция доказательства общезначимости (противоречивости) логического утверждения.

Так, логика предикатов первого порядка с равенством дает возможность:

• выразить, что нечто обладает определенным свойством, не указывая, что именно (роль -квантификации);
  
• выразить, что каждый элемент некоего класса обладает определенным свойством, без указания, что представляет из себя каждый такой элемент (роль -квантификации);
  
• выразить, что хотя бы одно из двух утверждений истинно, не говоря, какое именно (роль дизъюнкции);
  
• явно сказать, что нечто ложно (роль отрицания);
  
• утверждать или оставлять неустановленным тот факт, что два различных выражения означают один и тот же объект (роль равенства).
  

Эти парадигмы полезны и подчас необходимы при решении многих проблем искусственного интеллекта.

Велика роль формальной логики также в семантическом анализе знаний и обосновании выводов. Представить знание – это значит выразить в некотором формализме имеющийся у нас образ мира. Соответствие между миром и его представлением устанавливается семантическим анализом. Такой анализ имеет целью определить объекты представления и уточнить образ мира, определяемый представлением. Следовательно, оно должно позволить осуществлять анализ истинности высказываний о мире. Иначе говоря, для плодотворности представления нужно, чтобы оно могло быть предметом анализа, использующего информацию из этого представления для выявления того, что свойственно миру, а что нет. С этой точки зрения обоснованный вывод или дедукция «подтверждаются» видением мира, который определяется семантическим анализом представления.

Семантический анализ представленного в некотором формализме знания должен позволять определить, что в этом воображаемом мире влечет истину, а что – ложь. Даже если анализ облечен другими аспектами, подобная операция относится по определению к компетенции формальной логики и делает особенно полезным обращение к теории моделей.

Классическая логика формализует строго корректные рассуждения и, к сожалению, не принимает во внимание некоторые аспекты человеческих рассуждений (здравый смысл, неопределенность, противоречивость, нечеткость информации). Имея дело с неполной, неточной, противоречивой или нечеткой информацией, человеческие рассуждения всего лишь правдоподобны и должны подвергаться пересмотру (ревизии). Для представления такой информации, семантического ее анализа и обоснования выводов и разработаны нетрадиционные, «нестандартные» логики, являющиеся расширением классических логик. Эти расширения касаются языка логики и понятия вывода.

Возвращаясь к примеру о том, что большинство студентов юны, мы видели, что связывание этого утверждения квантором общности приводило к его состоятельности, если не было исключений. Любое исключение типа «Петров – студент, но он не юн» приводило к противоречию БЗ. Перечисление всех исключений становится нереальным при работе с прикладными системами. Таким образом, роль квантора общности при анализе рассуждений здравого смысла может быть подвергнута сомнению.

Однако, не перечисляя все исключения, мы можем выразить исключение неявным образом, например, х Студент(х) & Юн(х) – существуют неюные студенты без указания их имен. Однако, такого типа формулы сложны при их обработке вследствие нечеткости термина «существуют». Можно ли ограничиться одним неюным студентом или их большинство? Отсюда и роль квантора существования также становится недостаточной при анализе и выводе рассуждений здравого смысла.

Далее, если в БЗ имеется факт «Иванов – студент», то вывод «Иванов юн» может быть осуществлен только введением предположения об уникальности имен, т.е. (Иванов = Петров). Отсюда для вывода желаемых заключений в логике предикатов с равенством необходимо сначала доказать, что эти заключения не попадают под случай исключений.

Если закон исключенного третьего (tertium non datur) выполняется в классической формальной логике, то он может не выполняться в нетрадиционных логиках. Действительно, почему Студент(Петров)  Студент(Петров) = И, когда мы можем считать, что статус Петрова не известен.

Роль отрицания также может быть неоднозначной в таких логиках. Будем называть факты, принимающие значение «ложь», негативными фактами. Они явно присутствуют в БЗ. Кроме явного отрицания в БЗ могут находиться факты, которые не доказуемы в данной системе, как их отрицания (negation as failure), если мы придерживаемся предположения (гипотезы) о замкнутом мире. Содержательно это значит, что факт q считается доказуемым, если любое доказательство q терпит неудачу. Придерживаясь этого предположения, считаем, что нет «брешей» в знании предметной области и это знание полно.

К сожалению, предположение о замкнутом мире не всегда бывает продуктивным при рассмотрении случаев пересматриваемых рассуждений. Пусть Т – множество формул, и имеет место предположение о замкнутом мире, т.е. ASS(T) = {q | q – атомарная формула и not T ├ q}. Тогда для случая T = {a  b} в ASS(T) находятся как а, так и b, которые вместе с {a  b} дают противоречие.

Что касается вывода и его свойств, прежде всего, остановимся на правилах вывода Modus Ponens и Modus Tollens. Как мы уже видели на примере о том, что большинство студентов юны и Петров – студент, вывод о юности Петрова получается применением правила Modus Ponens. Считая эти утверждения выполнимыми, мы оставляем возможность для пересмотра (ревизии) заключения при поступлении новой информации. Сложнее обстоит дело с Modus Tollens, который получается применением теоремы дедукции и аксиомы контрапозиции к утверждению p  q, т.е. если p  q ├ q  p и выводимо q, то будет выводимо p или ├ p  q и ├ q, то ├ p. Возвращаясь к нашему примеру, мы имеем:

1. большинство студентов юны;
   
2. Петров не юн.
   

Следовательно, применяя Modus Tollens, получим: «Петров не является студентом». Интуитивно чувствуется, что для таких выполнимых утверждений, идя от следствия к причине, степень уверенности конкретного факта, связанного с причиной, становится недостаточной для такого вывода.

Из всех свойств вывода остановимся на свойстве немонотонности. Как мы уже видели, свойство монотонности препятствует прямой формализации пересматрива­емых рассуждений. Следовательно, с чисто синтаксической точки зрения построение немонотонной системы вывода делает необходимым ослабление свойств дедуктивных систем классической логики.

Логика умолчаний Рейтера является одной из версий немонотонных рассуждений [16]. В ней немонотонность обусловлена необщезначимостью правил вывода, присущих той или иной прикладной области.

Тесно связан с рассуждениями по умолчанию абдуктивный вывод, теория которого была заложена Пирсом. Формально абдукция устанавливает, что из P  Q и Q возможно вывести P. Однако абдукция является несостоятельным правилом вывода, означающим, что заключение необязательно истинно для каждой интерпретации, в которой истинны посылки [17].

Пусть Th, f и h – три множества замкнутых формул языка логики предикатов первого порядка, представляющие знание о рассматриваемой предметной области, наблюдаемое событие этой области и объяснение этого события соответственно. Предположим, что f совместимо с Th (т.е. Th & f выполнимо), но f не является логическим следствием Th, т.е. Th не объясняет f. Следовательно, необходимо вывести дополнительные факты h, объясняющие f в предполагаемой интерпретации, описанной Th.

Формально экзистенционально квантифицированная конъюнкция h литер есть абдуктивное объяснение наблюдаемого события относительно знания Th, если Th, h ╞ f, где, как и раньше, ╞ – знак логического следования.

Рассмотрим пример.

Пример 1.

Th: х (Студент(х)  Юн(х))

f: Юн(Петров)

h: Студент(Петров), Студент(Иванов) & Юн(Иванов),

Студент(Петров) & Смертен(Пет­ров) – три абдуктивных объяснения наблюдаемого события f относительно Th.

Заметим, что представление абдуктивного объяснения в виде конъюнкции фактов является синтаксическим ограничением, отличающим абдукцию от других моделей объяснений, например, от индуктивного обобщения.

Ключевой вопрос в абдуктивных рассуждения заключается в нахождении так называемых «интересных» объяснений. Эти объяснения могут быть формально охарактеризованы двумя семантическим свойствами: непротиворечивостью и минимальностью. Интуитивно минимальные и непротиворечивые абдуктивные объяснения интересны в том смысле, что они являются довольно общими фактами относительно Th и не вступают в противоречие со знанием предметной области.

Считаем, что абдуктивное объяснение h для наблюдаемого события f относительно Th непротиворечиво (с Th), если Th & h – выполнимая формула.

Продолжая пример 1 видим, что Студент(Петров) – непротиворечивое абдуктивное объяснение события Юн(Петров) относительно х (Студент(х)  Юн(х)). Однако, другое объяснение Студент(Иванов) & Юн(Иванов) является противоречивым абдуктивным объяснением наблюдаемого события Юн(Петров) относительно х (Студент(х)  Юн(х)), так как одновременно были бы выводимы Юн(Иванов) и Юн(Иванов).

Аналогично абдуктивное объяснение h для события f относительно Th минимально, если каждое абдуктивное объяснение для наблюдаемого события f относительно Th, являющееся логическим следствием h, эквивалентно h.

Из примера 1 видно, что Студент(Петров) – минимальное абдуктивное объяснение события Юн(Петров) относительно х (Студент(х)  Юн(х)), а Студент(Пет­ров) & Смертен(Петров) таковым не является. Очевидно, что свойство минимальности устраняет объяснения, которые не являются общими. Так, из двух объяснений Студент(Пет­ров) и Студент(Пет­ров) & Смертен(Петров) общим объяснением является Студент(Петров).

Отметим, что процесс абдукции может быть выполнен с помощью процедуры дедуктивного вывода следующим образом: Th, h ╞ f тогда и только тогда, когда Th, f ╞ h. Этот результат получается применением теоремы дедукции и аксиомы контрапозиции.

В другой немонотонной логике, предложенной Мак-Деромоттом и Дойлом, вводится оператор М, интерпретируемый как «непротиворечивый» (как впрочем и в логике умолчания) [18]. Тогда утверждение типа «Как правило (обычно, в большинстве случаев), студенты юны» будет записано в следующем виде: х (Студент(х) & М Юн(х)  Юн(х)), т.е. если кто-то является студентом и это не противоречит тому, что он юн, то этот кто-то действительно юн. Если в БЗ вводится информация типа «Петров – студент» и невозможно вывести Юн(Петров), т.е. М Юн(Петров) истинно, то можно сделать вывод о том, что Петров юн.

Однако система вывода здесь немонотонна, так как введение добавочной информации может блокировать предыдущий вывод. Например, после добавления нового факта, что Петров не юн, первоначальное заключение будет отвергнуто, так как в данном случае М Юн(Петров) не будет истинным.

Трудность вывода в немонотонной системе Мак-Дермотта заключается в том, что понятие «непротиворечивости» здесь довольно «слабое» в том смысле, что истинностные значения утверждений Р и М Р не связаны между собой никаким отношением, т.е. пара {M P, P} необязательно может быть противоречивой.

Мур развивает идею немонотонного вывода дальше, вводя два типа рассуждений по умолчанию [19]. Первый тип рассуждений характеризуется тем, что он имеет дело с фактами, касающимися внешнего мира: вообще объекты типа Х имеют свойство Р. Если А – объект типа Х, то можно сделать вывод, что А (по-видимому) обладает свойством Р. Например, если Петров – студент, то можно сделать вывод, что (по-видимому) Петров юн.

Второй тип рассуждений, названный автоэпистемическими рассуждениями, касается рассуждений, связанных с чьими-то убеждениями (верами). Этот тип рассуждений пересматривается, исходя из текущего состояния знаний агента, из его интроспективной природы. Например, если мне ничего не известно о том, что Петров не юн, то я делаю вывод, что Петров, будучи студентом, юн.

Механизм рассуждений интроспективен и основан на предположении о том, что все знания, касающиеся этого вопроса, таковы: «если бы Петров был не юн, то я бы об этом знал». Иначе говоря, можно потребовать от рассуждений «общезначимости» относительно этого состояния знаний. Пересматриваемый характер рассуждений протекает из зависимости от состояния знаний. Оно присуще рассуждающему агенту и может изменяться.

Появление нетрадиционных логик связано также с прикладными аспектами создания различного рада интеллектуальных систем, в частности, экспертных систем. Эти системы служат для решения диагностических и классификационных проблем, проблем управления и принятия решений. Знания в таких системах представляются продукциями, имеющими вид: «если А₁ и А₂ и … и А_n, то В», где A_i (i = 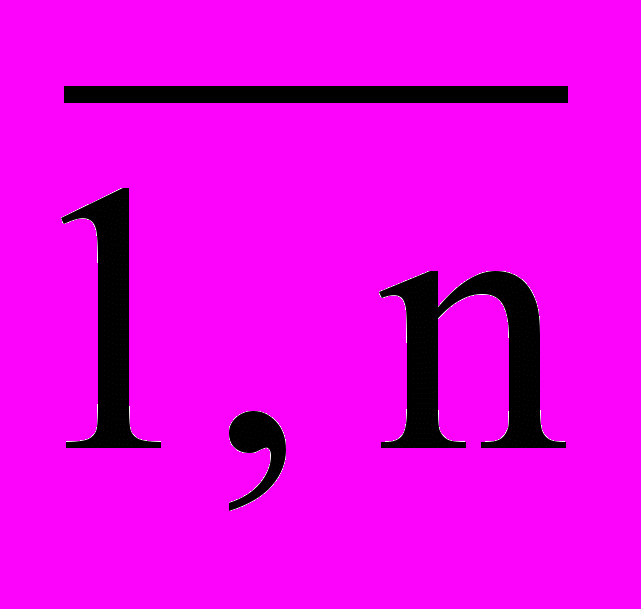) – условия, а В – выполняемое действие. Чтобы подчеркнуть «экспертный» характер таких продукций, в них добавлен так называемый «фактор определенности», подчеркивающий степень неопределенности данного условия и заключения. Неопределенность знания, таким образом, обрабатывается с помощью распространения факторов определенности от условий продукций к их заключениям. Хотя здесь в явной форме исключения не обрабатываются, неопределенность в продукциях предполагает существование исключений. Факторы определенности выражаются численно с привлечением теории вероятностей или аппарата нечеткой логики. Однако такой подход сталкивается с большими трудностями в силу отсутствия строгой семантики при взвешивании продукций факторами определенности. Здесь проявляется проблема обоснования (подтверждения) численного значения фактора определенности, которая усугубляется конфликтными ситуациями в продукциях, проводящих к конфликтным заключениям. Наглядным примером является хорошо известная система MYCIN, в которой факторы определенности, распространяемые дедуктивно по цепочке вывода, определяются в терминах относительной разницы между апостриорной и априорной вероятностями.

Хотя экспертные системы с факторами определенности продолжают развиваться и проявляют завидное упорство к дальнейшему распространению, нетрадиционные логики для обработки неопределенной, противоречивой, неточной и нечеткой информации продолжают вносить свой вклад в модели и методы представления и обработки знаний.

Резюмируя сказанное, отметим, что при представлении и обработке неполных, противоречивых и немонотонных знаний в интеллектуальных системах необходим аппарат таких нетрадиционных логик как логика умолчания, немонотонная модальная логика, автоэпистемическая логика и ряд других [20,21]. Для представления и обработки нечетких знаний, отражающих неточность, неопределенность, неоднозначность знаний, используются такие нестандартные логики как вероятностная логика, логика возможности, нечеткая логика и другие.


Литература

1. Кондрашина Е.Ю., Литвинцева Л.В., Поспелов Д.А. Представление знаний о времени и пространстве в интеллектуальных системах. / Под ред. Д.А. Поспелова. Москва: Наука, 1989, 328 стр.
   
2. Искусственный интеллект. – В 3-х книгах. Книга 2. Модели и методы: Справочник. / Под ред. Д.А. Поспелова. М.: Радио и связь, 1990, 304 стр.
   
3. Асмус В.Ф. Платон. М.: Мысль, 1975, 220 стр.
   
4. Платон. Сочинения в 3-х томах. Под ред. В.Ф. Асмуса и А.Ф. Лосева. T.1. M., 1968.
   
5. Чанышев А.Н. Аристотель. Издание 2, дополненное. М.: Мысль, 1987, 221 стр.
   
6. Аристотель. Соч.: В 4-х томах. М., 1975-1983.
   
7. Delgrande J.P. and Mylopoulos J. Knowledge Representation: Features of Knowledge. // Fundamentals of Artificial Intelligence. An Advanced Course. W. Bibel and Ph. Jorrand (eds.) / Lecture Notes in Computer Science. Springer-Verlag. 1986, vol. 232, pp. 3-36.
   
8. Вагин В.Н. Не-факторы знания и нетрадиционные логики. // Третья международная школа-семинар по искусственному интеллекту для студентов и аспирантов (Браславская школа-1999). Сборник научных трудов. Беларусь, 1999, стр. 10-14.
   
9. Белнап Н., Стил Т. Логика вопросов и ответов. М.: Прогресс, 1981, 288 стр.
   
10. Тей А., Грибомон П., Луи Ж. и др. Логический подход к искусственному интеллекту. От классической логики к логическому программированию. М.: Мир, 1990, 429 стр.
    
11. Journal of Applied Non-Classical Logics. Special Issue. Uncertainty, Conditionals and Non-Monotonicity. Vol. 1, № 2, 1991, 310 p.
    
12. International Journal of Intelligent Systems. Special Issue. Reasoning under Incomplete Information in Artificial Intelligence. Vol. 5, № 4, September 1990, 472 p.
    
13. Dempster A.P. A Generalization of Bayesian Inference. // Journal of the Royal Statistical Society, vol. 30, 1968, pp. 205-247.
    
14. Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике. М.: Радио и связь, 1990, 287 стр.
    
15. Zadeh L.A. Fuzzy Logic and Approximate Reasoning. // Synthese 30, 1975, pp. 407-428.
    
16. Reiter R. A Logic for Default Reasoning. // Artificial intelligence, 13, 1980, pp. 81-132.
    
17. Marquis P. Extending Abduction from Propositional to First-Order Logic. P. 141-155. // Lecture Notes in Artificial Intelligence. Vol. 535. / Ph. Jorrand, J. Kelemen (eds.) Fundamentals of Artificial Intelligence Research. Springer-Verlag, 1991, 255 p.
    
18. McDermott D. and Doyle J. Non-Monotonic Logic I. / Artificial Intelligence, 13, 1980, pp. 41-72.
    
19. Moore R.C. Semantical Considerations on Non-Monotonic Logic. // Proceedings IJCAI 83, Karlsruhe, 1983, pp. 272-279.
    
20. Vagin V.N. Non-Classical Logics in Semiotic Systems. // CAI’98. Sixth National Conference with International Participants. Proceedings Workshop Applied Semiotics and Abstracts of CAI’98. Reports, vol. III, Pushchino, 1998, pp. 34-39.
    
21. Вагин В.Н. Зачем нужны нетрадиционные логики? // Международный форум информатизации 98: Доклады международной конференции «Информационные средства и технологии», том 1, 20 22 октября 1998, М.: Издательство «Станкин», с. 6-14.