Рабочая программа Программа лекционного курса План практических занятий

Вид материала

Рабочая программа

Содержание Числовые функции. линейная функция Величины и их измерение Именованные числа и действия над ними Геометрические фигуры. треугольник Круглые тела Комплексные числа Комплексные числа Алгебраические операции и их свойства Алгебраические системы. группа. Алгебраические системы Математические структуры Программа и список литературы к экзамену

Подобный материал:

• Рабочая программа Программа лекционного курса План практических занятий, 1059.44kb.
• Методика преподавания математики рабочая программа Программа лекционного курса Планы, 266.77kb.
• Методика преподавания математики рабочая программа Программа лекционного курса Планы, 384.99kb.
• Рабочая программа Программа лекционного курса Планы лабораторных занятий, 88.79kb.
• Рабочая программа Программа лекционного курса Планы лабораторных занятий, 97.54kb.
• Рабочая программа Тематика и планы семинарских занятий График текущего и промежуточного, 127.07kb.
• Программа курса психологии продажи товара Тематический план лекций, семинаров, практических, 54.58kb.
• Программа лекционного курса для магистрантов факультета философии гу-вшэ цель курса, 174.59kb.
• М к. Аммосова Педагогический институт Рабочая программа, 114.38kb.
• Программа лекционного курса для студентов 5 курса спец. «история», 413.6kb.

Тема: ТЕКСТОВЫЕ ЗАДАЧИ. РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ ЛОГИЧЕСКИМ И ПРАКТИЧЕСКИМ МЕТОДАМИ

Литература:

(2) гл. V, §§ 1-3; (8) гл. 14.

Контрольные вопросы:

1. Задачи на переливание и на взвешивание.

2. Задачи на переправы, на разъезды, на дележки.

3. Из истории текстовых задач.

Выполните упражнения:

1. Зачетное задание № 6.

2. (8) №№ 14.12-14.23.


Занятия №№ 12-13.

Тема: ЧИСЛОВЫЕ ФУНКЦИИ. ЛИНЕЙНАЯ ФУНКЦИЯ

Литература:

(3) гл. I, § 10 пп. 46,47; (5) гл.II, § 9 пп. 44-46; (8) гл. 18.

Контрольные вопросы:

1. Общее понятие функции (отображения). Основные поня­тия, примеры.

2. Числовая функция. Область определения, множество значений, график числовой функции. Способы задания числовой функции.

3. Линейная функция. Определение. Свойства и график линейной функции.

4. Прямая пропорциональность. Свойства, график

5. Квадратичная функция. Свойства и график квадратичной функции.

6. Обратная пропорциональность, свойства, график.

7. Дробно-линейная функция. Свойства и график дробно-линейной функции. Частные случаи.

8. Построение графиков функций.

9. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 7. (16.1 - 16.23)

2. (3) гл. I, №№ 528-538, №№ 539-557; (8) №№ 18.1-18.17.


Занятие № 14

Тема: ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЕ

Литература:

(3) гл. V, §§ 17,18; (5) гл. IV, § 25, пп. 120-125; (8) гл. 21.

Контрольные вопросы:

1. Понятие величины и ее измерения.

2. Основные свойства скалярных величин.

3. Длина, площадь, масса, стоимость, время, скорость и дру­гие величины.

4. Зависимости между величинами. Решение задач.

5. Из истории развития системы единиц величин. Междуна­род­ная система единиц СИ.

6. Связь с начальным курсом математики.

Выполните упражнения:

1. Зачетное задание № 7. (16.8 - 16.9; 17.9 - 17.13)

2. (3) гл. III, №№ 91-105, №№ 115-129; (8) №№ 21.1-21.19.


САМОСТОЯТЕЛЬНО:


Тема: ИМЕНОВАННЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ

Литература:

(8) гл. 21.

1. Именованное число.

2. Преобразование именованных чисел.

3. Действия над именованными числами.

4. Связь с начальным курсом математики.

Выполните упражнения:

1. (8) 21.20-21.37.


Занятие № 15

 Тема: ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ТРЕУГОЛЬНИК

Литература:

(4) §§ 1, 3, 4, 9, 13; (8) гл. 20.

Контрольные вопросы:

1. Геометрии. Аксиоматическое построение геометрии Евк­лида. Аксиоматика Гиль­берта.

2. Угол. Определение. Виды углов (смежные; вертикальные; прямые; острые; тупые; углы, образованные при пересечении двух параллельных прямых третьей прямой).

3. Треугольник. Определение. Свойство медиан, биссектрис, высот.

4. Признаки равенства и подобия треугольников.

5. Соотношение между сторонами и углами треугольника.

6. Площадь треугольника.

7. Задачи на построение.

8. Связь с начальным курсом математики.

Выполните упражнения:

1. Зачетное задание № 8.

2. (8) №№ 20.1-20.6, 20.11, 20.14, 20.33.


Занятие № 16

Тема: ЧЕТЫРЕХУГОЛЬНИКИ

Литература:

(4) §§ 1, 6, 12, 13; (8) гл. 20.

Контрольные вопросы:

1. Многоугольники. Выпуклые многоугольники. Четырех­угольник.

2. Параллелограмм. Трапеция. Определение. Свойства. Площадь.

3. Прямоугольник. Ромб. Квадрат. Определение. Свойства. Площадь.

4. Задачи на построение.

5. Связь с начальным курсом математики.

Выполните упражнения:

1. Зачетное задание № 8.

2. (8) №№ 20.16-20.20.


САМОСТОЯТЕЛЬНО:


Тема: ОКРУЖНОСТЬ

Литература:

(4) §§ 1, 5, 13; (8) гл. 20.

Контрольные вопросы:

1. Окружность. Круг. Определение. Основные свойства.

2. Длина окружности. Площадь круга.

3. Основные задачи на построение.

4. Связь с начальным курсом математики.

Выполните упражнения:

1. Зачетное задание № 8.

2. (8) №№ 20.8-20.10, 20.12-20.13, 20.21-20.25.


Тема: МНОГОГРАННИКИ

Литература:

(4) §§ 18-21; (8) гл. 20.

Контрольные вопросы:

1. Многогранный угол. Многогранная поверхность. Много­гранники.

2. Призма. Объем. Площадь поверхности.

3. Параллелепипед. Куб. Объем. Площадь поверхности.

4. Пирамида. Усеченная пирамида. Объем. Площадь поверх­ности.

5. Правильные многогранники.

6. Теорема Эйлера.

7. Связь с начальным курсом математики.

Выполните упражнения:

1. Зачетное задание № 8.

2. (8) №№ 20.34-20.41, 20.45-20.49.


Тема: КРУГЛЫЕ ТЕЛА

Литература:

(4) §§ 19-21; (8) гл. 20.

Контрольные вопросы:

1. Цилиндр. Объем. Площадь поверхности.

2. Конус. Усеченный конус. Объем. Площадь поверхности.

3. Сфера. Шар. Объем. Площадь поверхности.

4. Части шара: шаровой слой, шаровой сектор, шаровой сег­мент.

5. Из истории развития геометрии.

Выполните упражнения:

1. Зачетное задание № 8.

2. (8) №№ 20.44, 20.50-20.52, 20.60.


Занятие № 17- 18.

Тема: КОМПЛЕКСНЫЕ ЧИСЛА

Литература:

(8) гл. 13; (10) гл. I, п. 1.1.

Контрольные вопросы:

1. Необходимость расширения множества действительных чисел.

2. Комплексные числа как пары действительных чисел. Оп­ределение, условие равен­ства, сложение и умножение ком­плексных чисел.

3. Множества комплексных чисел как расширение множе­ства действительных чисел.

4. Алгебраическая форма комплексных чисел. Геометриче­ская интерпретация ком­плексных чисел.

5. Операции (сложение, умножение, вычитание, деление) над комплексными числами, заданными в алгебраической форме. Свойства операций, геометрический смысл.

6. Модуль и аргумент комплексного числа. Геометрическая интерпретация. Тригоно­метрическая форма комплексных чисел.

7. Теорема о представлении комплексного числа в тригоно­метрической форме.

8. Умножение, деление, возведение в степень комплексных чисел, представленных в тригонометрической форме. Геометри­ческая интерпретация.

Задание на дом:

1. Зачетное задание № 9.

2. (8) №№ 13.1-13.10.


САМОСТОЯТЕЛЬНО:


Тема: КОМПЛЕКСНЫЕ ЧИСЛА

Литература:

(8) гл. 13. (10) гл. I, п. 1.1., 1.2.

Контрольные вопросы:

1. Свойства модуля комплексных чисел.

2. Показательная форма комплексного числа. Сравнение комплексных чисел.

3. Извлечение корня из комплексного числа.

4. Основная теорема алгебры.

5. Из истории развития теории комплексных чисел.

Задание на дом:

1. Зачетное задание № 9.

2. (8) 13.11-13.17.


Занятие № 19

Тема: АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ И ИХ СВОЙСТВА

Литература:

(8) гл. 19; (10) гл. II, п. 2.1.

Контрольные вопросы:

1. Общее понятие n-арной алгебраической операции. Бинарные и унарные алгебраические операции. Операции в нечисловых множест­вах.

2. Частичные алгебраические операции, область определе­ния. Мультипликативные и аддитивные операции.

3. Коммутативность, дистрибутивность, сократимость би­нарных алгебраических опе­раций.

4. Нейтральный элемент и его существование.

5. Поглощающий элемент и его существование.

6. Симметричные элементы, их существование.

7. Обратные операции. Свойства обратных операций.

8. Тождественные преобразования выражений.

9. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 10.

2. (3) №№ 575 - 582; №№ 623 – 628; № 630-640;(8) 19.1-19.8.


Занятие № 20

Тема: АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ. ГРУППА.

Литература:

(8) гл. 19; (10) гл. II, п 2.2, с. 68-83.

Контрольные вопросы:

1. Общее понятие алгебраической системы (алгебры).

2. Гомоморфные и изоморфные отображения алгебраических систем. При­меры.

3. Алгебраические системы с одной операцией. Группы, по­лугруппы. Основные опре­деления. Примеры. Коммутативные (абелевы) группы.

4. Подгруппы. Примеры.

5. Основные свойства групп.

6. Группы и обратные операции.

7. Вычисления в группе.

8. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 10.

2. (8) № 19.9.-19.11

)

САМОСТОЯТЕЛЬНО:


Тема: АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ

С ДВУМЯ ОПЕРАЦИЯМИ (КОЛЬЦО, ПОЛЕ) (К.С.Р.)

Литература:

(8) гл. 19; (10) гл. II, п 2.2.

Контрольные вопросы:

1. Кольцо. Определение, примеры. Виды колец.

2. Основные свойства колец.

3. Вычисления в кольце.

4. Числовые кольца.

5. Поле. Определение, примеры.

6. Основные свойства полей.

7. Вычисления в поле.

8. Числовые поля. Поле рациональных, действительных, комплексных чисел.

Задание на дом:

1. Зачетное задание № 10.

2. (8) №№ 19.12-19.17.


Тема: МАТЕМАТИЧЕСКИЕ СТРУКТУРЫ

Литература:

(10) гл. II, п 2.3.

Контрольные вопросы:

1. Понятие математической структуры.

2. Алгебраические структуры.

3. Порядковые структуры.

4. Топологические структуры.

5. Булева алгебра.

6. Булева алгебра чисел. Булева алгебра множеств. Булева алгебра высказываний.

7. Принцип двойственности.

8. Числовые системы в начальном курсе математики, их свойства.

9. Из истории развития алгебры.

Задание на дом:

1. Зачетное задание № 10.


Контроль за самостоятельной работой (8 час.)


ПРОГРАММА И СПИСОК ЛИТЕРАТУРЫ К ЭКЗАМЕНУ

за 1-2-й курсы (переаттестация)


1. Понятие множества. Способы задания множеств. Примеры. Конечные и бесконечные множества.

Отношения между множествами (равенства, включения, пересечения). Круги Эйлера.

(3) гл. I, § 1 пп. 1, 2; (5) гл. I, § 1, с. 6-13; (7) гл. I § 1, п. 2; (8) гл. I, с. 31-47; (9) гл. I, п. 1.1.

2. Операции над множествами: объединение, пересечение, разность двух множеств, свойства. Дополнение до универсаль­ного множества.

(3) гл. I, § 1 пп. 3;4; (5) гл. I, § 1, с. 14-25; (7) гл. I, § 1 пп. 2; 3;4; (8) гл. I, с. 31-47; (9) гл. I, п. 1.2.

3. Декартово произведение двух и более множеств, свой­ства. Примеры. Число элементов объединения и декартова произведения множеств.

(3) гл. I, § 1 п. 6; (5) гл. I, § 1, с. 29-33, 38-39; (7) гл. I, § 1, пп. 5,6; (8) гл. I, с. 31-47; (9) гл. I, п. 1.4.

4. Разбиение множества на попарно-непересекающиеся подмножества (классы). Примеры. Разбиение множества на классы с помощью одного, двух и трех свойств.

(3) гл. I, § 1 п. 5; (5) гл. I, § 1, с. 26-27; (7) гл. I, § 1 п. 5; (8) гл. I, с. 45-47; (9) гл. I, п. 1.3.

5. Соответствие между элементами двух множеств. Основные понятия. При­меры. Способы задания соответствий. Виды соответствий (обратное, противопо­ложное данному).

(5) гл. II, § 8, с. 166-170; (7) гл. I, § 2 п. 9; (8) гл. III, с. 103; (9) гл. III, п. 3.1.

6 Взаимно-однозначные соответствия. Равномощные множества. Свойства отношения равномощности мно­жеств на множестве множеств.

Отображения. Виды отображений.

(3) гл. I, § 10 п. 46; (5) гл. II, § 8, с. 172-174; (7) гл. I, § 2 п. 10; (8) гл. III, с. 107; (9) гл. I, п. 1.5., гл. III, п. 3.2.

7. Отношения на множестве. Основные понятия. Спо­собы задания. Свойства отношения на множестве.

(3) гл. I, § 10 пп. 44-45; (5) гл. II, § 10, с. 188-196; (7) гл. I, § 2, п. 11-12; (8) гл. III, с. 108-111; (9) гл. III, п. 3.3.

8. Отношение эквивалентности. Связь отношения экви­валентности с разбие­нием множества на классы.

Отношение порядка. Упорядоченные множества.

(3) гл. I, § 10 п. 45; (5) гл. II, § 10, с. 198-201; (7) гл. I, § 2, п. 13; (8) гл. III, с.112 ; 114; (9) гл. III, п. 3.3.

9. Определяемые и неопределяемые понятия. Объем и содержание понятия. От­ношения между понятиями. Требо­вания к определению понятий.

(3) гл. I, § 5 пп. 23,24; (5) гл. I, § 2, с. 41-44; (7) гл. I, § 3 п. 17; (8) гл. II, с. 66; (9) гл. II, п. 2.3.

10. Способы определения понятий. Структура определе­ния через род и видовое отличие.

(3) гл. I, § 5 п. 25; (5) гл. I, § 2, с. 46-50; (7) гл. I, § 3 пп. 17,24; (8) гл. II, с. 67; (9) гл. II, п. 2.3.

11. Правильные и неправильные рассуждения. Простей­шие формы дедуктивных рассуждений.

(3) гл. I, § 6 пп. 27,28; (5) гл. I, § 4, с. 89-92, 94-97; (7) гл. I, § 3 п. 25; (8) гл. II, с. 75; (9) гл. II, п. 2.4.

12. Способы доказательства математических утвер­ждений.

(5) гл. I, § 4, с. 99-103; (7) гл. I, § 3 пп. 26,27; (8) гл. II, с. 80-82; (9) гл. II, п. 2.5.

13. Высказывания. Отрицание высказываний. Закон двой­ного отрицания. Отри­цание высказываний, содержащих кванторы.

(3) гл. I, § 3 пп. 15-17; (5) гл. I, § 3, с. 73; (7) гл. I, § 3, пп. 20,21; (8) гл. II, с. 58, 63; (9) гл. II, п. 2.1.

14. Высказывания. Операции над высказываниями: конъюнкция, дизъюнкция, импликация и эквиваленция двух высказываний. Свой­ства.

(3) гл. I, § 3 пп. 13,14; (5) гл. I, § 3, с. 53-59, (7) гл. I, § 3, пп. 18,19; (8) гл. II, с. 57-59; (9) гл. II, п. 2.1.

15. Высказывательные формы (предикаты). Область оп­ределения, множества истинности и ложности предиката.

Кванторы. Обращение предиката в вы­сказывание.

(3) гл. I, § 3 пп. 13-17; (5) гл. I, § 3, с. 55-56, 61-62; с. 67-71, 73; (7) гл. I, § 3, пп. 18,21; (8) гл. II, с. 62-63; (9) гл. II, п. 2.2.

16. Операции над предикатами (отрицание, дизъюнкция, конъюнк­ция, импликация, эквивалениция).

(8) гл. II, с. 64; (7) гл. I, § 3 пп. 18-20; (3) гл. I, § 3 п. 14; (9) гл. II, п. 2.2.

17. Отношение логического следования и равносильности на множестве предло­жений. Необходимые и достаточные условия.

(3) гл. I, § 4 пп. 19,20; (5) гл. I, § 3, с. 77-81; (7) гл. I, § 3 п. 22; (8) гл. II, с. 85;.

18. Строение теоремы. Виды теорем. Закон контрапози­ции.

(3) гл. I, § 4 п. 21; (5) гл. I, § 3, с. 83-86; (7) гл. I, § 3 п. 23; (8) гл. II, с. 85; (9) гл. II, п. 2.5.

19. Комбинаторные задачи. Правила суммы и произведе­ния. Перестановки без повторений и с повторениями. Примеры.

(3) гл. I, § 2 п. 8;10; (5) гл. I, § 6, с. 142-147; (7) гл. I, § 1 п. 6;7 (8) гл. V, с. 151, с. 154; (9) гл. IV, п. 4.1 - 4.2.

20. Размещения и сочетания без повторений и с повторениями.

(3) гл. I, § 2 п. 9; 11; (5) гл. I, § 6, с. 145-149; (7) гл. I, § 1 п. 7; 8; (8) гл. V, с. 153, 154; (9) гл. IV, п. 4.2.

21. Свойства чисел 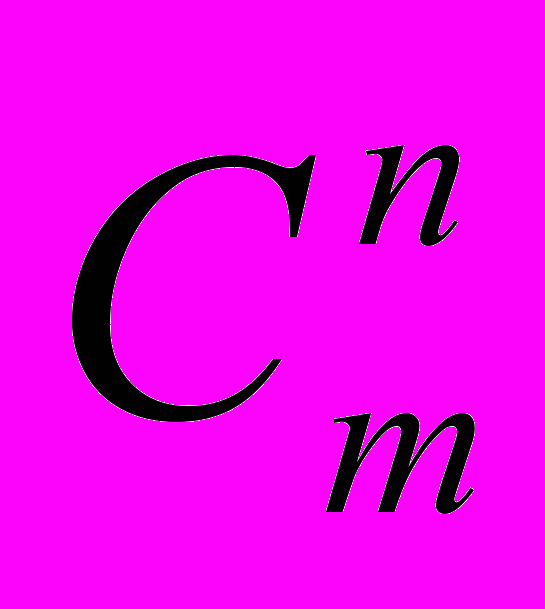. Треугольник Паскаля. Число подмно­жеств конечного мно­жества.

(8) гл. V, с. 155; (9) гл. IV, п. 4.2.

22. Понятие об аксиоматическом методе построения тео­рии. Аксиомы Пеано для множества целых неотрицатель­ных чисел, их применение к доказательству теорем. Метод математической индукции.

(3) гл. II, 11, п 50, 51; (5) гл. III, § 14; (6) гл. I, 1, 2, 7; (7) гл. II, 4, пп 28,29, 36; (8) гл. VIII, с. 225,с. 228-229, с. 240.

23. Аксиоматическое определение сложения целых неотри­ца­тельных чисел. Суще­ствование и единственность суммы. Таб­лица сложения однозначных чисел.

(3) гл. II, 11, п 50; (5) гл. III, § 14, п. 61; (6) гл. I, 3; (7) гл. II, 4, п 30; (8) гл. VIII, с. 229-231.

24. Законы сложения (аксиоматическая теория):

1. 0+x = x; 2. x+1 = x'; 3. x+(y+z) = (x+y)+z;

4. x+y = y+x; 5. x+y = y.

(3) гл. II, 11, п 50; (5) гл. III, § 14, п. 61 (6) гл, I, 3;; (7) гл. II, 4, п 30; (8) гл. VIII, с. 236.

25. Аксиоматическое определение умножения целых неот­ри­цательных чисел. Су­ществование и единственность про­изведе­ния. Таблица умножения однозначных чи­сел.

(3) гл. II, 11, п 50; (5) гл. III, § 14, п. 62; (6) гл. I, 4; (7) гл. II, 4, п 31; (8) гл. VIII, с. 231-233.

26. Законы умножения (аксиоматическая теория):

1. 0·x = 0; 2. x·1 = x; 3а. (x+y)·z = x·z+y·z;

3б. z·(x+y) = z·x+z·y; 4. (x·y)·z = x·(y·z); 5. x·y = y·x.

(3) гл. II, 11, п 50; (5) гл. III, § 14, п. 62 (6) гл. I, 4;; (7) гл. II, 4, п 31; (8) гл. VIII, с. 236-237.

27. Вычитание целых неотрицательных чисел. Существо­вание и единственность разности. Правила вычитания числа из суммы, суммы из числа и др.

(3) гл. II, 11, п 50; (5) гл. III, § 14, п. 64; (6) гл. I, 6; (7) гл. II, 4, пп 33,34; (8) гл. VIII, с. 235, 237-238.

28. Отношение порядка на множестве целых неотрица­тель­ных чисел.

(5) гл. III, § 14, п. 63; (6) гл. I, 5; (7) гл. II, 4, п 32; (8) гл. VIII, с. 233-234.

29. Свойства множества целых неотрицательных чисел (бесконечность, упорядо­ченность, дискретность, наличие наи­меньшего элемента и др.).

(5) гл. III, § 14, п. 66; (6) гл. I, 5; (7) гл. II, 4, п 32; (8) гл. VIII, с. 244.

30. Деление целого неотрицательного числа на натураль­ное. Условия существова­ния частного.

(5) гл. III, § 14, п. 65; (6) гл. I, 6; (8) гл. VIII, с. 235-236.

31. Теоретико-множественный подход к построению мно­жества целых неотри­цательных чисел. Понятие натурального числа и нуля. Счет. Порядковые и количественные натуральные числа. Отношение "равно", "меньше", "больше" на множе­стве целых неотрицатель­ных чисел (количественная тео­рия).

(3) гл. II, 12, п 54; (5) гл. III, § 15, пп. 70, 75; (6) гл. II, 10, 11; (7) гл. II, 4, п 37; гл. II, 5, пп 38-39; (8) гл. VIII, с. 240-243.

32. Определение суммы целых неотрицательных чисел. Суще­ствование и единст­венность суммы (количественная теория).

(3) гл. II, 12, п 55; (5) гл. III, § 15, пп. 71, 75; (6) гл. II, 12; (7) гл. II, 5, п 40; (8) гл. VIII, с. 244-245.

33. Законы сложения (количественная теория).

(5) гл. III, § 15, пп. 71, 75; (6) гл. II, 12; (7) гл. II, 5, п 40; (8) гл. VIII, с. 248.

34. Теоретико-множественный смысл разности целых не­от­рицательных чисел. Существование и единственность разно­сти. Правила вычитания числа из суммы и суммы из числа.

(3) гл. II, 12, п 55; (5) гл. III, § 15, пп. 72, 75; (6) гл. II, 13; (7) гл. II, 5, п 41; (8) гл. VIII, с. 245-246.

35. Теоретико-множественный смысл произведения, его су­ществование и единст­венность. Определение произведения че­рез сумму.

(3) гл. II, 12, п 56; (5) гл. III, § 15, пп. 73, 75; (6) гл. II, 14; (7) гл. II, 5, п 42; (8) гл. VIII, с. 246-247.

36. Законы умножения (количественная теория).

(5) гл. III, § 15, пп. 73, 75; (6) гл. II, 14; (7) гл. II, 5, п 42; (8) гл. VIII, с. 248-249.

37. Теоретико-множественный смысл частного целого не­отрицательного числа на натуральное, его существование и единственность.

(3) гл. II, 12, п 56; (5) гл. III, § 15, пп. 74, 75; (6) гл. II, 15; (7) гл. II, 5, п 43; (8) гл. VIII, с. 247-248.

38. Понятие системы счисления. Позиционные и непози­цион­ные системы счисле­ния. Десятичная система счисления. Запись и название чи­сел в десятичной системе счисления.

(3) гл. II, 14, п 60; (5) гл. III, § 17, пп. 81, 87; (6) гл. IV, 18, 19,22, 25; (7) гл. II, 6, пп 44-45; (8) гл. IX, с. 270-273.

39. Алгоритм сложения, вычитания, умножения и деления многозначных чисел в десятичной системе счисления и его обоснование.

(5) гл. III, § 17, пп.82- 85, 87; (6) гл. IV, 20- 22; (7) гл. II, 6, пп 46-49; (8) гл. IX, с. 277-282.

40. Позиционные системы счисления, отличные от деся­тич­ной: запись чисел, арифметические действия, переход от записи чисел в одной системе к записи в дру­гой.

(3) гл. II, 14, пп 61,62; (5) гл. III, § 17, п. 86; (6) гл. IV, 23; (7) гл. II, 6, п 50; (8) гл. IX, с. 273-277.

41. Отношение делимости и его свойства. Делимость суммы, разности и произведения целых не­от­рицательных чисел.

(3) гл. II, 15, п 64-65; (5) гл. III, § 18, пп. 88, 93; (6) гл. V, 26-28; (8) гл. X, с. 300-302.

42. Признаки делимости на 2,3,4,5,8,9,10,25 в десятичной системе счисления.

(3) гл. II, 15, п 65; (5) гл. III, § 18, п. 89; (6) гл. V, 29; (8) гл. X, с. 303-307.

43. Простые и составные числа. Свойства простых чисел. Существование простого делителя у всякого на­турального числа, большего единицы. Ре­шето Эратосфена.

(3) гл. II, 15, п 66; (5) гл. III, § 18, п. 91; (7) гл. II, 7, п 53; (8) гл. X, с. 310-313.

44. Деление с остатком.

(3) гл. II, 11, п 52; (6) гл. I, 9; (7) гл. II, 4, п 35; (8) гл. X, с. 302-303.

45. Общие кратные, общие делители. НОД и НОК чисел. Теоремы: "Всякое общее крат­ное двух чисел делится на их НОК". и "Если a  b, то НОК (a,b) = a; НОД (a,b)= b.

(3) гл. II, 15, п 67; (5) гл. III, § 18, п. 90; (8) гл. X, с. 308-309, 318.

46. Взаимно простые числа. Примеры. Вычисление НОК(a,b), если a и b - взаимно простые числа. Теорема о делимости натурального числа на произведе­ние двух взаимно про­стых чисел. Признаки делимости на составные числа 6,12,15,30 и дру­гие.

(3) гл. II, 15, п 68; (6) гл. V, 30; (8) гл. X, с. 307-310.

47. Основная теорема арифметики.

(7) гл. II, 7, п 54; (8) гл. X, с. 313-314.

48. Нахождение НОК и НОД чисел, представленных в кано­ническом виде. Алгоритм Евклида. Нахождение НОД двух чисел.

(5) гл. III, § 18, п. 92; (6) гл. II, 30; (7) гл. II, 7, п 54, 55; (8) гл. X, с. 318-321.

49. Задачи, приводящие к понятию рационального числа. По­нятие дроби. Основное свойство дроби. Операции над обыкно­венными дробями. Равносильные дроби. Рацио­нальное число.

(3) гл. III, 16, п 70; (5) гл. III, § 19, пп. 94, 95, 99; (8) гл. XI, с. 333-339.

50. Арифметические действия над рациональными чис­лами.

(3) гл. III, 16, пп 71,72; (5) гл. III, § 19, п. 94; (8) гл. XI, с. 339-343.

51. Законы сложения и умножения положительных рацио­нальных чисел.

(3) гл. III, 16, пп 71, 72; (8) гл. XI, с. 343-344.

52. Свойства множества рациональных чисел (бесконеч­ность, плотность, упоря­доченность, счетность и др.).

(3) гл. III, 16, пп 73; (8) гл. XI, с. 345-346.

53. Десятичные дроби, операции над ними. Проценты. Ос­новные задачи на про­центы.

(5) гл. III, § 19, п. 97; (8) гл. XI, с. 348.

54. Рациональные числа как бесконечные десятичные пе­рио­дические дроби. Преобразование периодических десятичных дробей в обыкновенные.

(3) гл. III, 16, п 74; (5) гл. III, § 19, п. 97; (8) гл. XI, с. 352-356.

55. Натуральное число как результат измерения величин.

(3) гл. II, 13, пп 58,59; (8) гл. VIII, с. 249-250.

56. Приемы рациональных вычислений.

(8) гл. IX, с. 282-290.

57. Понятие "текстовая задача". Структура задачи. Клас­сификация текстовых задач. Методы решения текстовых задач.

(2) гл. I, § 1, 2, 3; (5) § 5, п 29, 30; (8) гл. XIV, с. 416-425.

58. Этапы решения текстовой задачи и приемы их вы­пол­не­ния. Моделирование в процессе решения текстовых задач.

(2) гл. I, § 4, 5; (5) § 5, п 31; (8) гл. XIV, с. 422-448.

59. Текстовые задачи на тройное правило. Текстовые за­дачи на среднее арифмети­ческое.

(2) гл. II, §§ 2, 6; (8) гл. XIV, с. 448, 454.

60. Текстовые задачи на нахождение неизвестных по ре­зультатам действий.

(2) гл. II, § 3; (8) гл. XIV, с. 449-451.

61. Текстовые задачи на пропорциональное деление.

(2) гл. II, § 4; (8) гл. XIV, с. 451-453.

62. Текстовые задачи на исключение одного из неизвест­ных.

(2) гл. II, § 5; (8) гл. XIV, с. 453.

63. Текстовые задачи на проценты и части.

(2) гл. II, § 7; (5) § 5, п 32; (8) гл. XIV, с. 456-458.

64. Текстовые задачи "на движение", "на работу", "на смеси".

(2) гл. II, §§ 9-11; (5) § 5, п 33; (8) гл. XIV, с. 458-462.

65. Текстовые задачи, связанные с измерением величин.

(2) гл. II, §§ 12-13; (8) гл. XIV, с. 463-465.