Α Множество всех подмножеств данного множества называется булеаном данного множества. Каждому подмножеству м сопоставим его характеристическую функцию

Вид материала

Лекция

Содержание Каждому подмножеству М сопоставим его характеристическую функцию Счетность множества целых чисел Счетность множества рациональных чисел Счетность множества алгебраических чисел К вопросу о приведении числовых систем к натуральным числам (добавить в лекцию №7) Метод Вейштрасса Метод Кантора Несчетность множества действительных чисел Несчетность множества комплексных и трансцидентных чисел Счетность множества вычислимых действительных чисел. Существование вычислимых трансцидентных чисел. Невычислимые числа. Вычислимость рациональных чисел. Вычислимость алгебраических чисел.

Подобный материал:

• Вопросы к экзамену «дискретная математика» (пм-91), 26.54kb.
• Для кафедр пм и к вопросы по курсу «Дискретная математика». 19. 05. 2010г, 52.29kb.
• Понятие множества, 186.12kb.
• Лекция №9, 54.68kb.
• Лекция Понятия множества и элементы множества. Способы задания множеств, 353.91kb.
• Линия состоит из множества точек, плоскость из бесконечного множества линий; книга, 55.53kb.
• Программа курса "Основы дискретной математики", 14.41kb.
• Введение в математическую логику, 29.8kb.
• Операции над множествами, 57.55kb.
• Алгоритмы на графах. Обходы графов. Кратчайшие пути. Остовные деревья, 114.51kb.

Лекция 8.

Счетность множества натуральных, целых, рациональных и алгебраических чисел. Несчетность множества трансцидентных, действительных и комплексных чисел.

Вычислимые действительные числа. Вычислимость алгебраических и существование вычислимых трансцидентных чисел. Невычислимые числа.


Теорема Кантора (забыла включить в лекцию№7)

Для любого кардинального числа α справедливо α<2^α


Множество всех подмножеств данного множества называется булеаном данного множества.


Каждому подмножеству М сопоставим его характеристическую функцию:

f M(x)=1 если x принадлежит М

f M(x)=0 если x принадлежит А но не принадлежит М

Всего характеристических функций: 2^|Α|


α =|Α|

2^α=| {0,1}^Α |


Счетность множества натуральных чисел


Множество натуральных чисел является счетно-бесконечным по определению. Это некий эталон, мощность которого определена как число Алеф-нуль (_–первое трансфинитное число. Счетно-бесконечными также будут все множества, для которых удастся доказать равномощность с множеством натуральных чисел. Для доказательства того, что множества равномощны, обычно используется какой либо способ, позволяющий поставить в соответствие каждому элементу рассматриваемого множества какое то натуральное число. Далее рассматривается «расширенное» множество натуральных чисел, включающее в себя стандартный ряд натуральных чисел (1,2,3,…) и число 0.


Будем обозначать множество натуральных чисел буквой N.


Множество натуральных чисел является также эффективно перечислимым (тоже по определению)


Счетность множества целых чисел


Целые числа: -n, …, -3,-2,-1,0,1,2,3,…, n,…

Будем обозначать множество целых чисел буквой Z


Расположим их следующим образом

0, 1, -1, 2, -2, 3, -3, …., n, -n, …

Тогда каждому числу можно поставить в соответствие натуральное число

0, 1, -1, 2, -2, 3, -3, …. , n, -n, …

0, 1, 2, 3, 4, 5, 6,…., 2n-1, 2n, …

Таким образом доказано, что множество Z равномощно множеству N, а значит оно счетно.


Для доказательства эффективной перечислимости множества Z необходимо установить тот факт, что все элементы множества Z могут быть перебраны по алгоритму и должны получить в результате такого перебора порядковые номера, причем без пропусков и повторений. Позже для некоторых случае оговорка «без пропусков и повторений» будет снята, однако важным остается факт перечисления ПО АЛГОРИТМУ, т.е. неким регулярным образом.


Факт эффективной перечислимости множества Z напрямую следует из приведенного способа нумерации элементов натуральными числами.


Счетность множества рациональных чисел


Определим рациональное число как q=n/m, где n и m – целые числа, причем m не равно 0.

Рассмотрим сначала положительные рациональные числа и запишем их в виде бесконечной матрицы, строки и столбцы которой пронумерованы натуральными числами начиная с 1. Элемент стоящий на пересечении i-ой строки и j-ого столбца получит наименование q_ij


1 2 3 4

1 q₁₁ q₁₂ q₁₃ q₁₄ …

2 q₂₁ q₂₂ q₂₃ q₂₄……

3 q₃₁ q₃₂ q₃₃ q₃₄……

4 q₄₁ q₄₂ q₄₃ q₄₄……



…………………………...



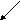
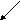
n q_n1 q_n2…………………

……………………………

Используя диагональный метод, перечислим их (пронумеруем натуральными числами):


q₁₁ q₂₁ q₁₂ q₁₃ q₂₂ q₃₁ q₄₁ q₃₂ q₂₃ q₁₄ q₁₅ q₂₄ q₃₃

1 2 3 4 5 6 7 8 9


Т.о. каждое рациональное число получит соответствующий номер, что означает счетность множества рациональных чисел.

Факт эффективной перечислимости множества Z напрямую следует из приведенного способа нумерации элементов натуральными числами.


Счетность множества алгебраических чисел


Алгебраическое число – корень уравнения ненулевой степени с целыми коэффициентами.

Общий вид алгебраического уравнения: a₀+a₁*x¹+a₂*x²+…+a_n*xⁿ=0

где a₀,a₁,…- рациональные коэффициенты.


Нумеруем: a₁₀+a₁₁x¹+a₁₂x² …=0

a₂₀+a₂₁x¹ +a₂₂x² …=0

a₃₀+a₃₁x¹ +a₃₂x² …=0

Получаем упорядоченную n-ку рациональных чисел: (a₁₀,a₁₁,a₁₂…a_1n) для каждого алгебраического уравнения.

Выпишем на первой строке будущей матрицы все упорядоченные пары рациональных чисел (они соответствуют линейным уравнениям и будут иметь по одному корню)

На второй строке выпишем все упорядоченные тройки рациональных чисел (они соответствуют квадратным уравнениям и будут иметь максимум по два корня): т.о. вместо каждой тройки можно указать подряд два числа, являющихся решением соотв. Уравнения.

На третьей строке – по три числа на каждое кубическое уравнение соотв. Упорядоченным четверкам и т.д.


Т.о. получим матрицу, которую можно обойти при помощи диагонального процесса Кантора. Т.о. каждое алгебраическое число получит соответствующий номер, что означает счетность множества алгебраических чисел.


Факт эффективной перечислимости множества Z напрямую следует из приведенного способа нумерации элементов натуральными числами.


К вопросу о приведении числовых систем к натуральным числам (добавить в лекцию №7)


Метод Дедикинда.

Действительное число: сечение множества рациональных чисел, т.е. упорядоченная пара двух множеств рациональных чисел (А, В).

Каждое число множества А меньше каждого числа множества В, а в сумме они составляют все множество рациональных чисел.

Например зададим √2 = (А,В)

А = }


B = }








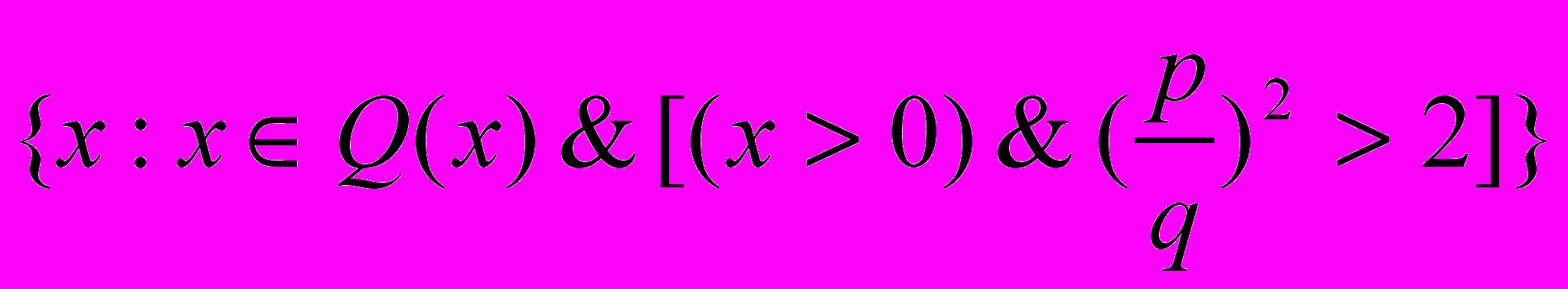A √2 B

Т.о. действительные числа представимы как сечения множеств рациональных чисел.


Метод Вейштрасса

Действительное число – предел сходящейся последовательности рациональныз чисел. Существует признак сходимости – и каждая сходящаяся последовательность дает некоторое действительное число.


Метод Кантора

Действительное число – предел бесконечной систематической дроби.

Систематическая дробь: выражение числа через последовательные степени данного основания. Систематическая дробь всегда есть сходящийся ряд. Ряд может сходиться к пределу, который не является рациональным числом.


Несчетность множества действительных чисел


Множество действительных чисел обозначается латинской буквой R.


Теорема: Множество R действительных чисел несчётно.

Доказательство:

(от противного)

Пусть множество действительных чисел счетно. Любое подмножество счетного множества тоже счетно. Возьмём на множестве действительных чисел интервал(0,1) и выкинем из этого отрезка числа, содержащие хотя бы в одном своём разряде нули или девятки.(Примеры таких чисел: 0.9, 0.0001 etc.) Множество A, составленное из оставшихся чисел является подмножеством множества R. Предположим, что множество A – счётно.

Тогда пронумеруем числа в разрядах:

0.a₁₁a₁₂a₁₃…

0.a₂₁a₂₂a₂₃…

……………

0.a_n1a_n2a_n3…


Теперь построим число b=0.b₁b₂…, причём b_i=a_ij+1(т. е. если a_ij=1, то b_i=2; а_ij=2 – то b_i=3). Таким образом построенное число b будет отличаться от каждого из чисел множества A хотя бы в одном разряде, и, следовательно не попадёт в составленный список. Тогда предположение неверно и множество A - несчётно.

Так как множество A является по условию подмножеством R, то и множество действительных чисел – несчётно. Теорема доказана.


Примечание: можно и не выбрасывать числа, содержащие 0 и 9. Т.о. в наш ряд некоторые числа войдут дважды. Это связано с тем, что конечные дроби могут быть превращены в бесконечные. Например:

½=0,5=0,5(0)=0,4(9)

0.01111…=1/2²+1/2³+1/2⁴…=lim==1/2

В общем случае это могло стать причиной того, что не удалось сосчитать множество действительных чисел. Но множество чисел, представимых двояким образом (конечные дроби) – это подмножество рациональных чисел. Следовательно их счетное количество. Можно показать, что это множество эффективно перечислимо. Т.о. даже двойное представление множества таких чисел образует счетное мн-во, следовательно доказательство верно.


Несчетность множества комплексных и трансцидентных чисел


Комплексное число задается парой (r1, r2), где R – действительное число. Так как множество действительных чисел R(несчётное по доказанной ранее теореме) является подмножеством множества комплексных чисел С, то множество комплексных чисел – также несчётно.


Трансцидентным называется действительное число, не являющееся алгебраическим. Поскольку действительных чисел – несчетное множество, а алгебраических – счетное, то трансцидентных чисел – несчетное множество.


Счетность множества вычислимых действительных чисел.


Действительное число вычислимо, если существует алгоритм его вычисления с любой степенью точности.

Вычислимые числа включают в себя все алгебраические и некоторые трансцендентные числа.

Так как каждому вычислимому действительному числу соответствует хотя бы одна машина Тьюринга, а машин Тьюринга - 0, то значит вычислимых чисел никак не больше чем ₀ . С другой стороны поскольку все алгебраические числа вычислимы, а их тоже ₀, то вычислимых действительных чисел никак не меньше чем ₀. Значит множество вычислимых действительных чисел счетно.


Существование вычислимых трансцидентных чисел. Невычислимые числа.


Пример невычислимого действительного числа:

Пусть имеются Т1,……,Тn,…. Машин Тьюринга и число Х можно представить как: Х=0,А1……Аn….

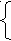1, если Тi останавливается на чистой ленте

Где Аi=

0, в противном случае

Такое число является невычислимым, так как задача об остановки Тi на чистой ленте алгоритмически не разрешима.


Пример вычислимого, но не алгебраического числа: ,


Вычислимость рациональных чисел. Вычислимость алгебраических чисел.


Рациональное число p/q- это частное двух целых чисел.

Все рациональные числа вычислимы, так как существует алгоритм их вычисления до любого знака, то есть с любой степенью точности.


Алгебраическое число это корень алгебраического уравнения с рациональными коэффициентами. Алгебраическим называется уравнение, у которого слева стом многочлен , а справа ноль.

а0+а1*х+ а2*х*х+…+аn*х *… *х = 0

n штук

Алгебраические числа являются вычислимыми, так как существуют численные методы их вычисления (алгоритм Ньютона) , позволяющие их определить с любой степенью точности.