Лекция №9

Вид материала

Лекция

Содержание 6.1.6. Табличное обозначение преобразований 6.1.7. Свойства подстановок

Подобный материал:

• «Социальная стратификация и социальная мобильность», 46.19kb.
• Первая лекция. Введение 6 Вторая лекция, 30.95kb.
• Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
• Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
• Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
• Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
• Тема Лекция, 34.13kb.
• Лекция посвящена определению термина «транскриптом», 219.05kb.
• А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.

Лекция № 9 (26.03.10)


6.1.5. Преобразования и подстановки

Определение. Отображение φ, отображающее множество A в себя, называется преобразо­ванием (множества A).

Во множестве всех преобразований данного множества A определена операция умножения (композиции). Она ассоциативна.

Определение. Биективное (или, равносильно, обратимое) преобразование называется под­становкою.

Произведение двух подстановок есть подстановка. Следовательно, на множестве всех под­становок также корректно определена операция умножения (композиции). Тождественное ото­бражение ε_A является подстановкою. Отображение, обратное к подстановке, всегда существует и также будет подстановкою. Следовательно, множество всех подстановок данного множества обра­зует группу относительно операции композиции отображений. (Группою называется множество объектов произвольной природы, на котором определена ассоциативная операция умножения, су­ществует единица и у каждого элемента есть обратный.)

6.1.6. Табличное обозначение преобразований

Если все элементы данного множества записаны без повторений в виде некоторой последо­вательности (так можно сделать, например, со множеством всех натуральных чисел N, а также с любым конечным множеством), то изобразить данное преобразование можно в виде таблички (матрицы), подобной, например, следующим:

; .

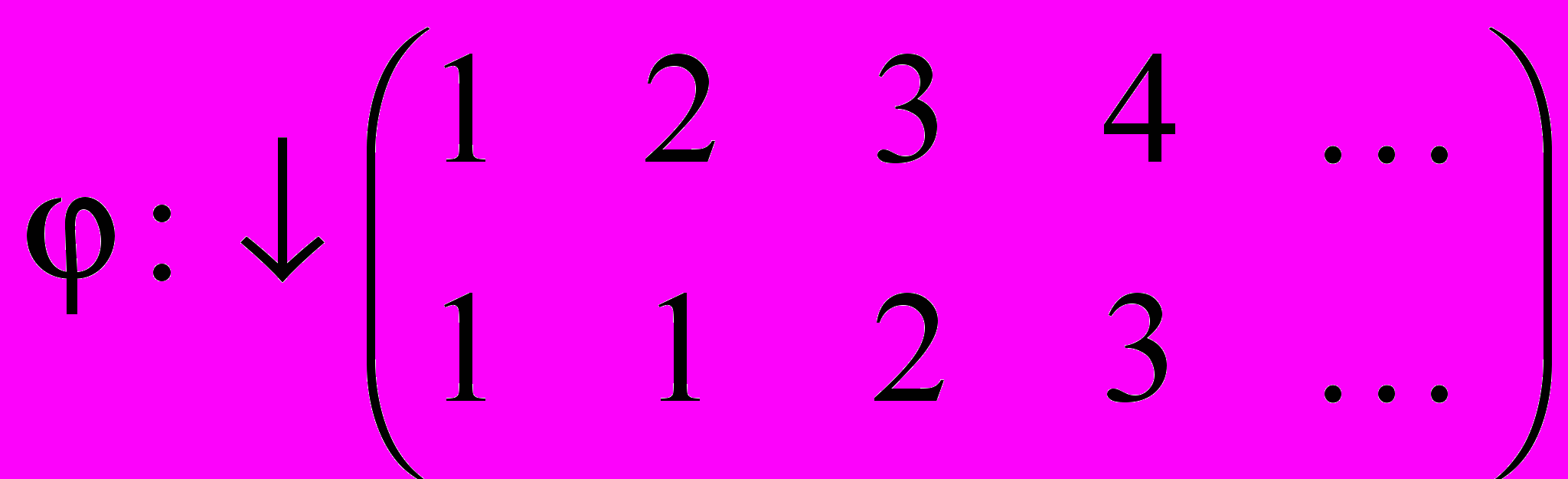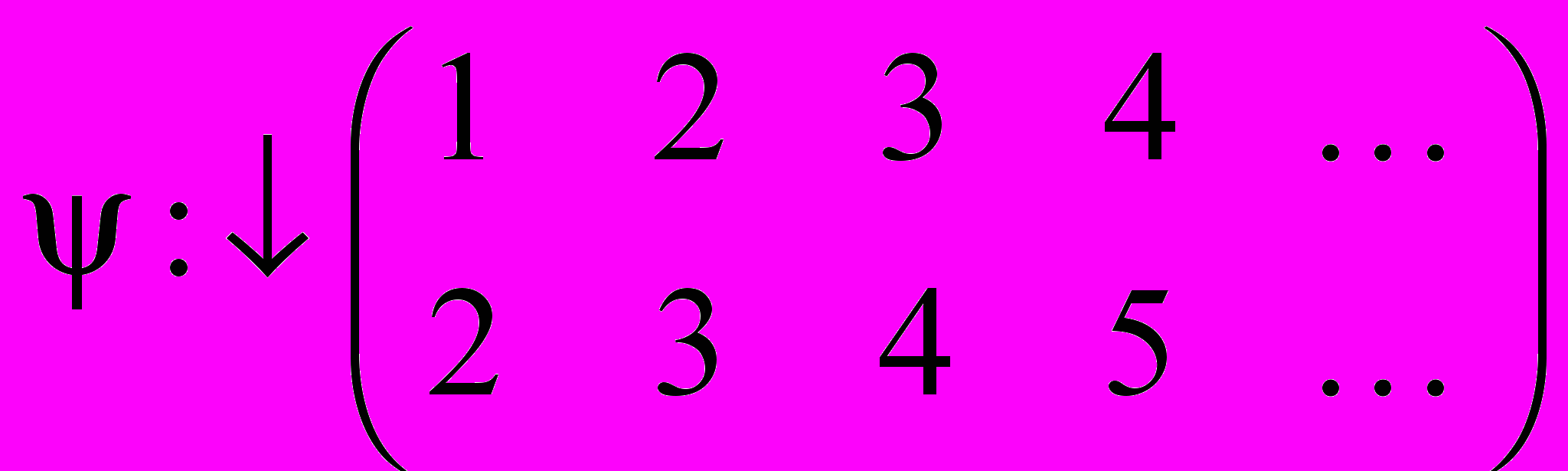Инъективность отображения при такой форме записи означает, что в нижней строке все элементы различны, а сюръективность означает, что все элементы данного множества в нижней строке таблички присутствуют. Так, из двух вышеприведенных примеров видно, что первое ото­бражение сюръективно, но не инъективно, а второе инъективно, но не сюръективно.

Чаще всего подобное изображение преобразования применяют к конечным множествам. В дальнейшем будем считать, что данное множество A есть множество всех натуральных чисел от 1 до n, расположенное в естественном порядке, а изображать будем только подстановки. Тогда в нижней строке будут находиться те же числа, что и в верхней, но записаны они будут в некоторой перестановке. У тождественной подстановки нижняя строка совпадает с верхней.

Как перемножить две подстановки, записанные в табличном виде? Объясним это на при­мере. Пусть, например, 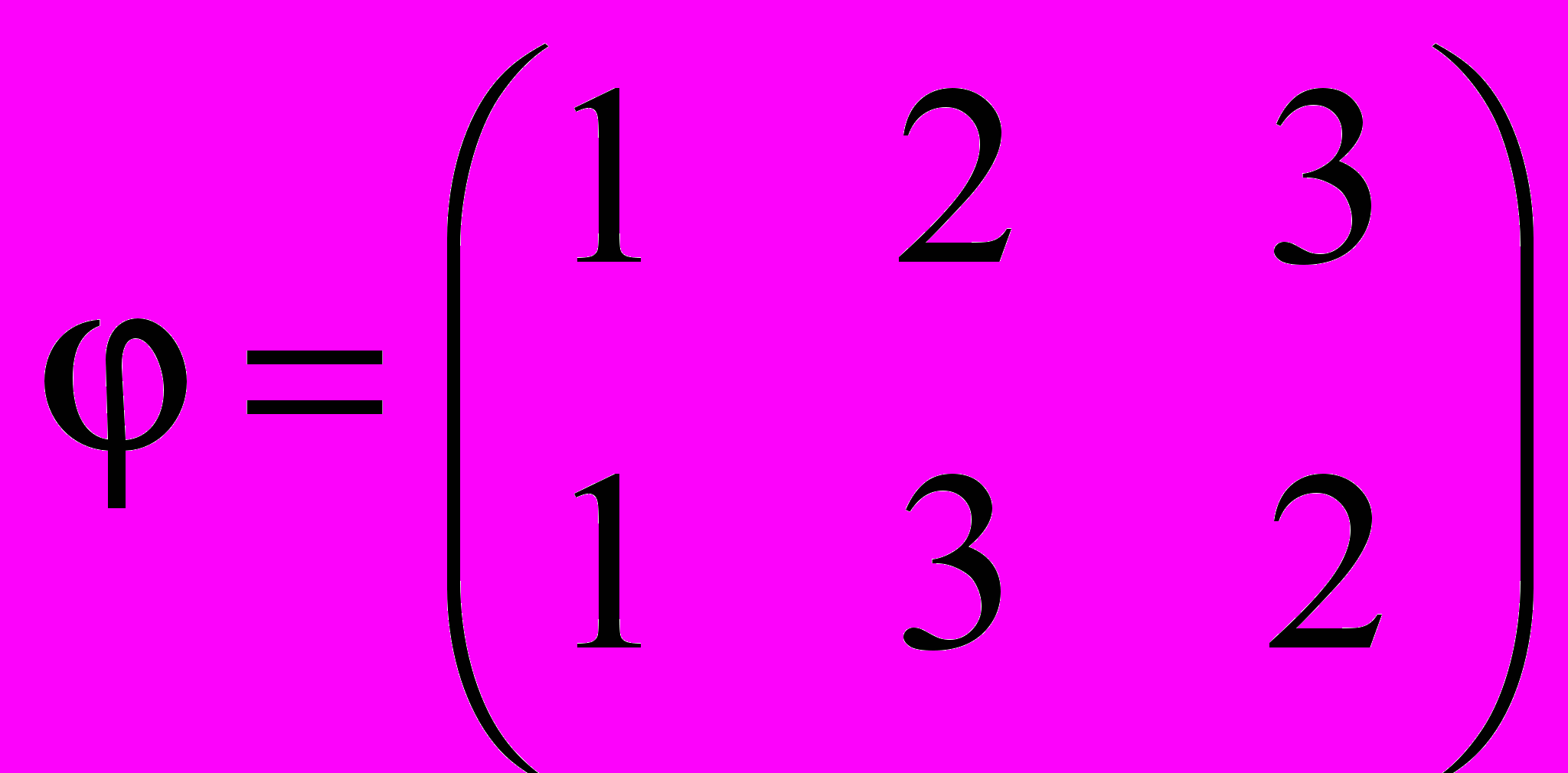, 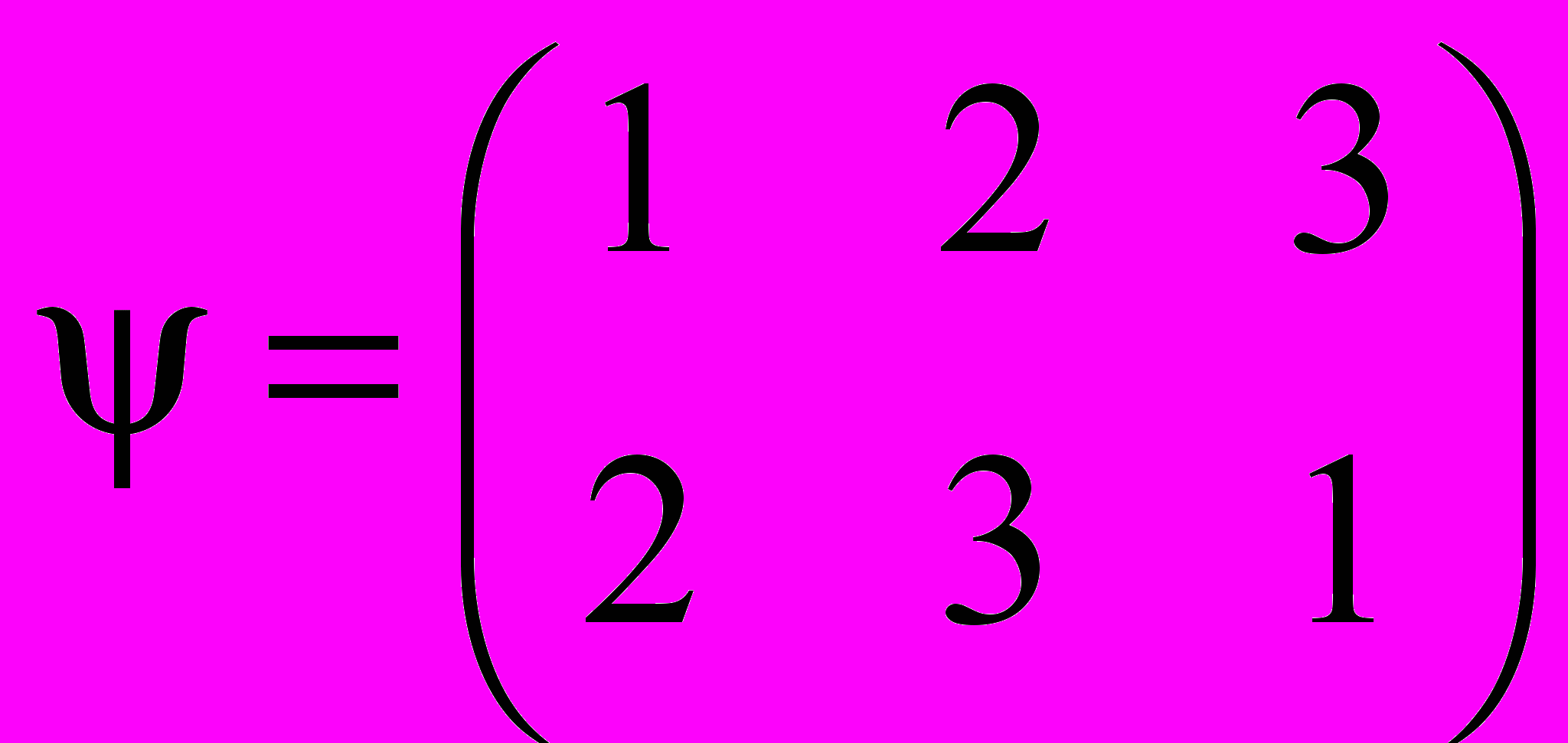. Не забудем, что перестановки (как и лю­бые отображения) перемножаются справа налево. Тогда

.

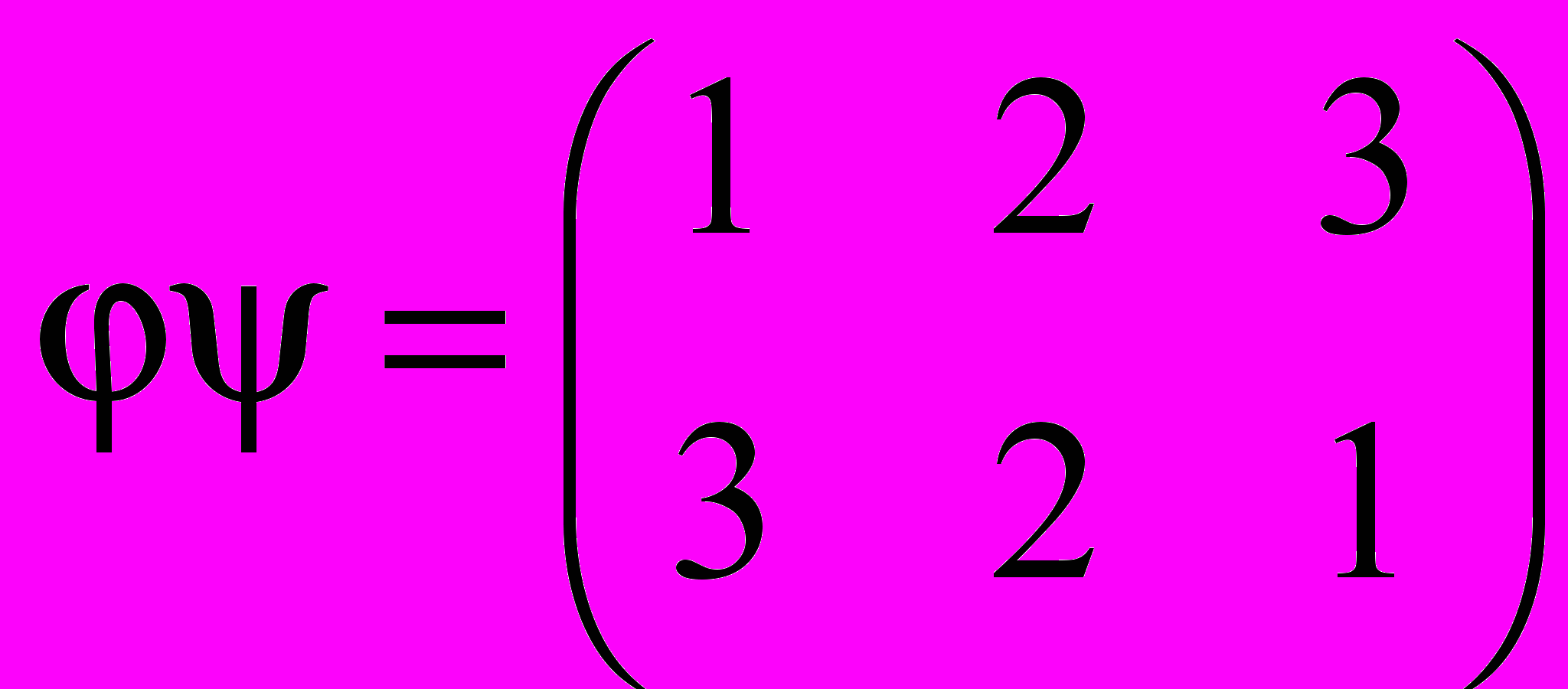Если мы перемножим те же подстановки в обратном порядке, то получим другой результат:

.


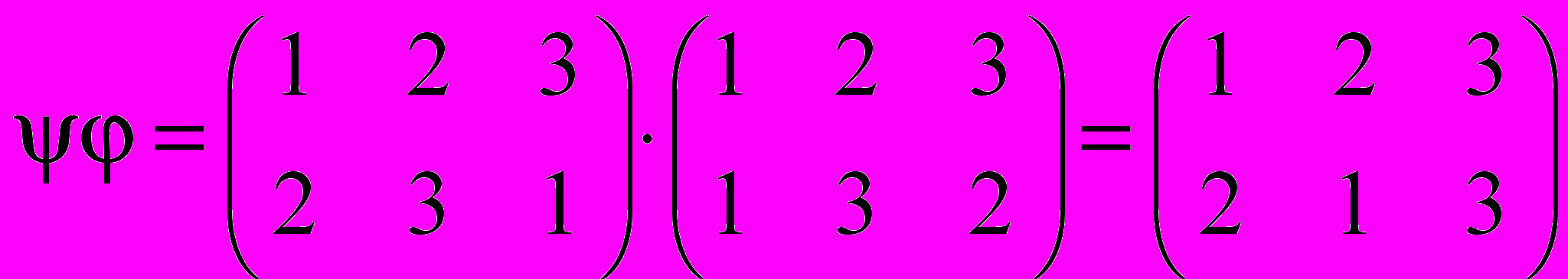Таким образом, умножение подстановок, вообще говоря, некоммутативно.

Определение. Неподвижным называется элемент, который данная подстановка переводит в себя (в тот же элемент). Все остальные элементы буду называть перемещаемыми.

Чтобы найти подстановку, обратную к данной, достаточно переставить строки изображаю­щей данную подстановку таблички (после этого можно, переставляя столбцы, расположить эле­менты верхней строки в нормальном порядке). Пример:

.

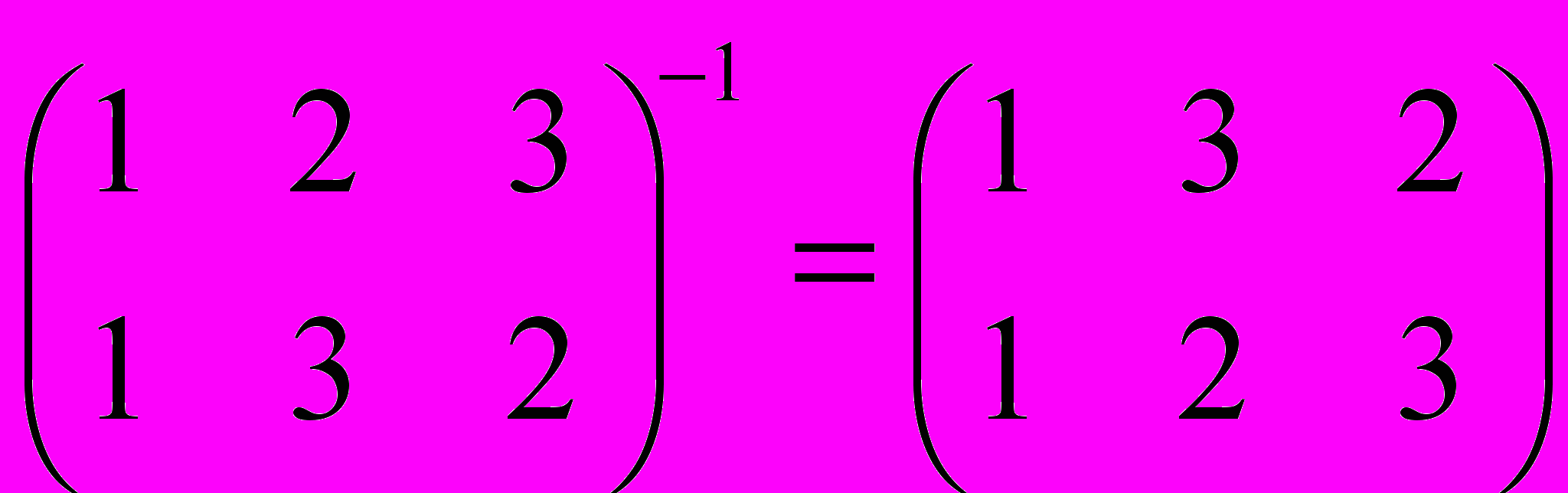Подстановки можно изображать в виде ориентированного графа.


6.1.7. Свойства подстановок

Если подстановка σ переставляет два элемента i и j, т. е. σ(i) = j, σ(j) = i, i ≠ j, а остальные элементы неподвижны, т. е. σ(k) = k при k ≠ i, j, то такая подстановка называется транспозициею (элементов i и j). Если вдобавок переставляемые элементы являются соседними, т. е. j = i + 1 или i = j + 1, то такую транспозицию назовём элементарною.

Если для двух элементов нижней строки σ(i) и σ(j) выполняются неравенства i < j, σ(i) > > σ(j), т. е. большее число стоит левее меньшего, то говорят, что эти два элемента нижней строки образуют инверсию. Подстановка называется чётною, если число инверсий в нижней строке её табличной записи чётно, и нечётною в противном случае.

Заметим, что любая транспозиция обратна самой себе: τ⁻¹ = τ (равносильно: τ² = ε_A).

Предложение 1. Умножение данной подстановки справа на транспозицию равносильно пе­рестановке соответствующих элементов нижней строки. В частности, умножение данной подста­новки справа на элементарную транспозицию переставляет соседние элементы.

Объясним на примере:

=.

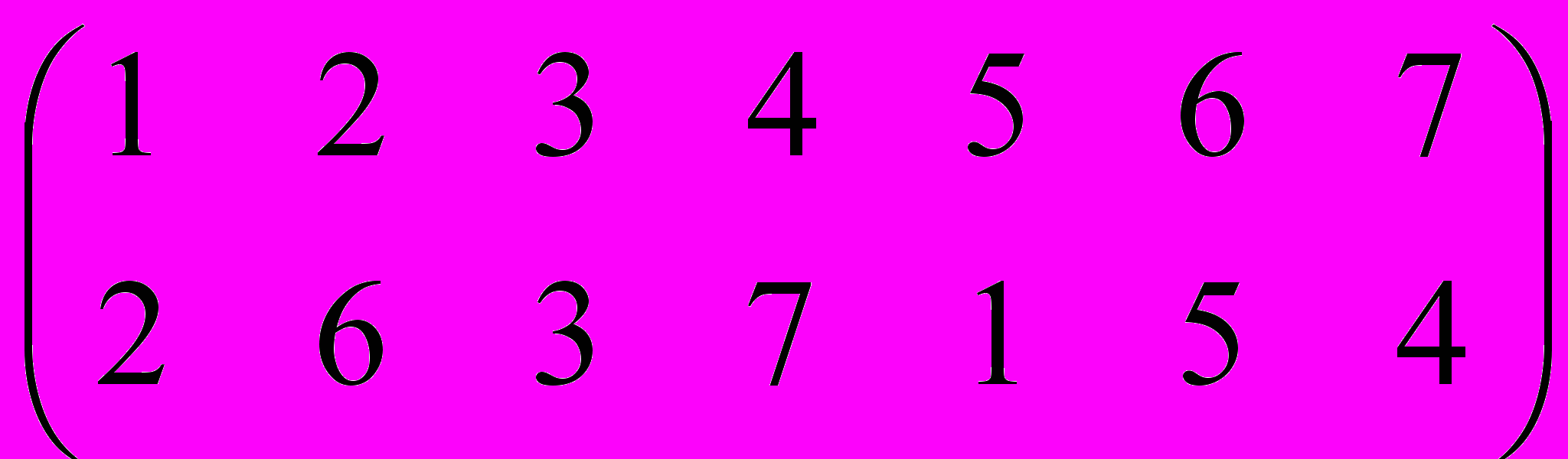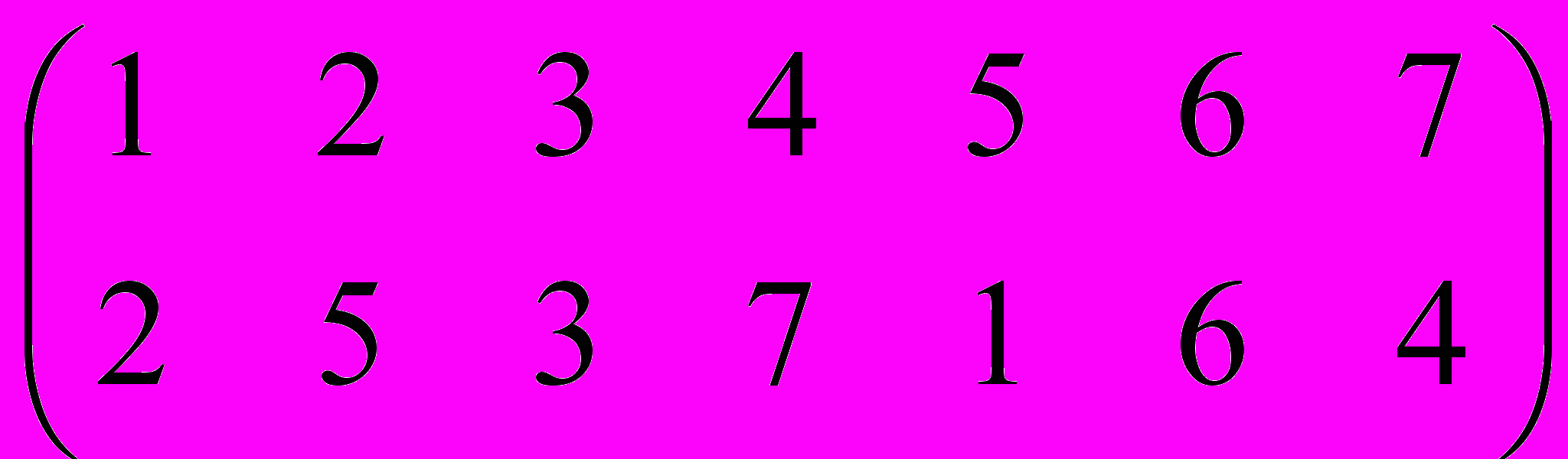
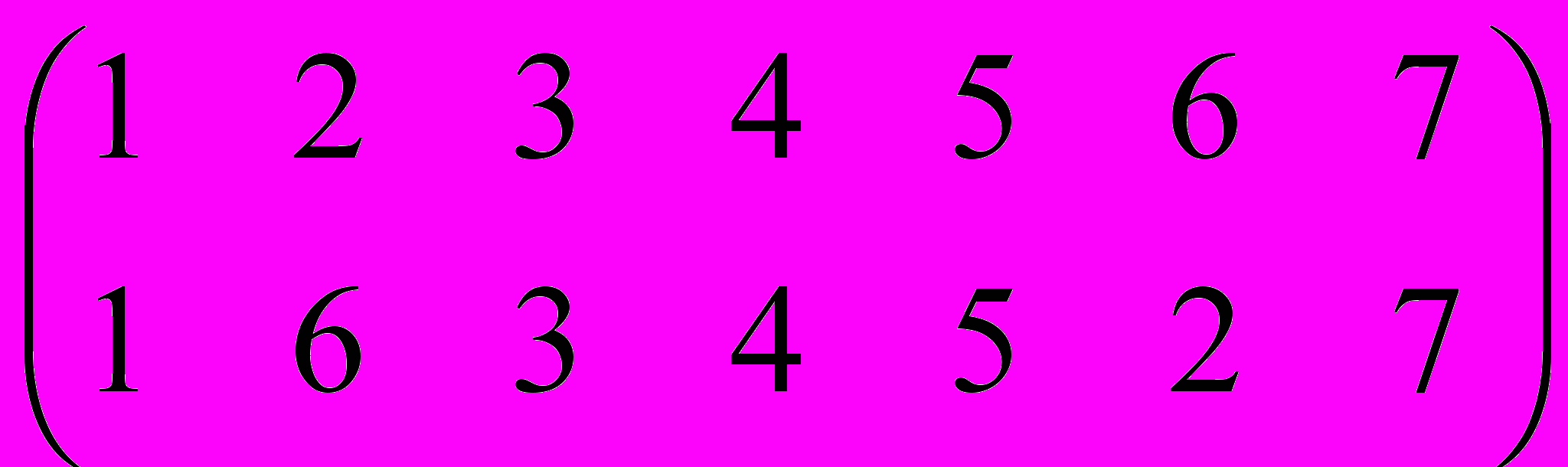В первом (левом) сомножителе по сравнению с исходной подстановкой (левой частью равенства) переставлены два элемента 5 и 6, а во втором (правом) сомножителе переставлены номера их по­зиций 6 и 2.

Предложение 2. Умножение данной подстановки справа на элементарную транспозицию меняет число инверсий на 1 (уменьшает, если соответствующие элементы образовывали инвер­сию, и увеличивает в противном случае).

Следовательно, умножение данной подстановки справа на элементарную транспозицию меняет чётность подстановки.

Предложение 3. Всякую нетождественную подстановку можно разложить в произведение элементарных транспозиций. При этом число сомножителей можно взять равным числу инверсий.

Доказательство индукцией по числу инверсий.

Если нет инверсий, то это тождественная подстановка. Если есть хотя бы одна инверсия, то не могут выполняться неравенства σ(1) < σ(2) < …  σ(n) (иначе σ = ε_A), а следовательно, для неко­торого k выполняется σ(k) > σ(k+1) (равенства не может быть в силу инъективности). Переставим эти элементы и получим новую подстановку σ₁, а для компенсации умножим справа σ₁ на соответ­ствующую элементарную транспозицию τ:


σ = σ₁τ.

В подстановке σ₁ будет уже на одну инверсию меньше. Если σ₁ = ε, то, значит, в подста­новке σ была единственная указанная инверсия, т. е. σ сама является элементарной транспозицией и равенство σ = σ является искомым разложением (из одного сомножителя); в этом случае пред­ложение доказано (база индукции). Если же σ₁ ≠ ε, то по предположению индукции σ₁ можно раз­ложить в произведение элементарных транспозиций:

σ₁ = τ₁τ₂…τ_s,

причем s равно числу инверсий в подстановке σ₁.

Имеем:

σ = σ₁τ = τ₁τ₂…τ_sτ.

Мы разложили подстановку σ в произведение s + 1 элементарной транспозиции, но в ней ровно столько же инверсий. Предложение доказано.

Предложение 4. Всякую транспозицию можно разложить в произведение нечётного числа элементарных транспозиций. Следовательно, всякая транспозиция нечётна.

Доказательство. Пусть дана какая-то транспозиция τ:

.

Рассмотрим пример, который покажет, как доказывать предложение в общем случае. До­пустим, необходимо переставить элементы 2 и 6. Проследим, как будет изменяться положение элементов в нижней строке:



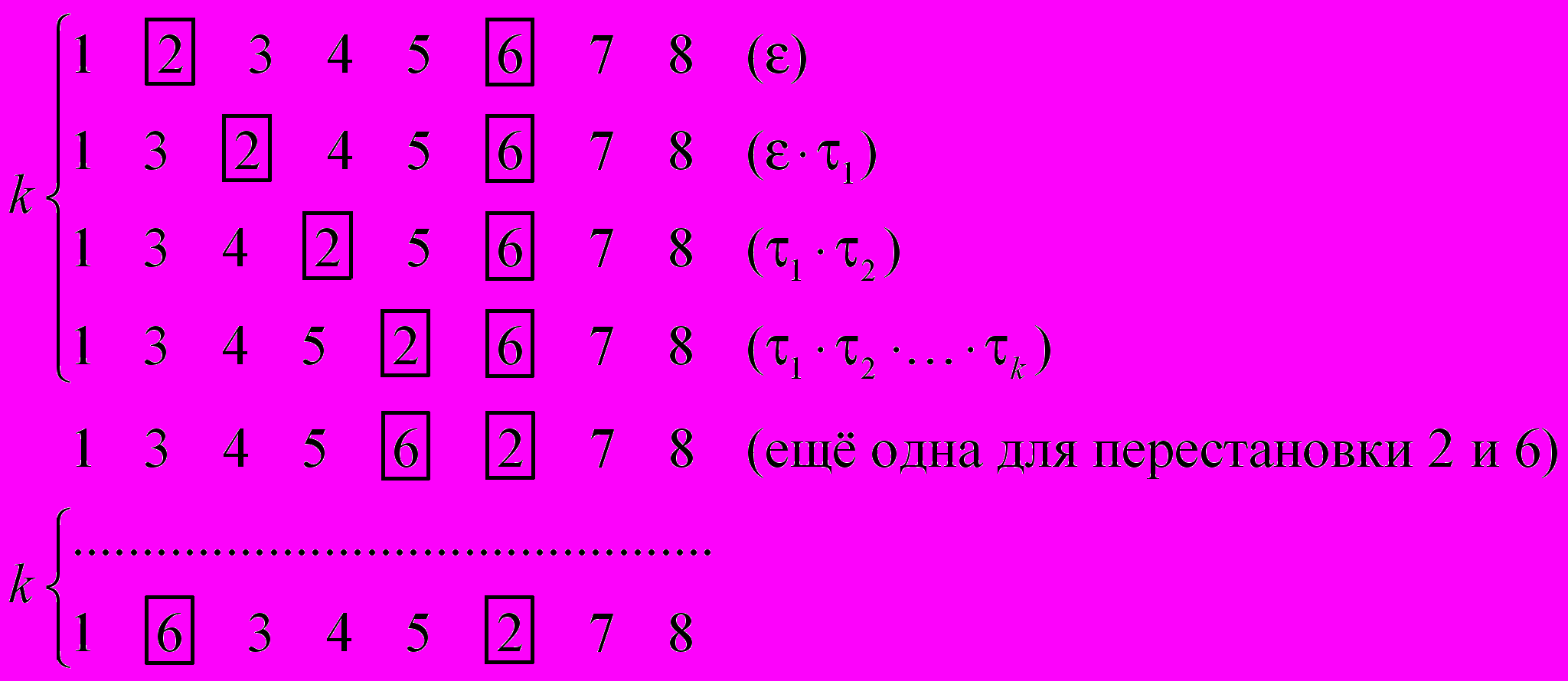
Итого: 2k + 1 элементарная транспозиция. Таким образом, мы разложили транспозицию элементов 2 и 6 в произведение нечётного числа элементарных транспозиций.

Предложение 5. Умножение справа на транспозицию меняет чётность подстановки.

Доказательство. Умножение справа на транспозицию равносильно умножению справа на произведение нечётного числа элементарных транспозиций (предложение 4). Умножение справа на одну элементарную транспозицию меняет число инверсий на единицу. В общей сложности число инверсий изменится на нечётное число, что означает изменение чётности подстановки.

Предложение 6. При любом разложении подстановки в произведение транспозиций число сомножителей имеет ту же чётность, что и сама данная подстановка.

Доказательство. Пусть

σ = τ₁τ₂…τ_s = τ₁τ₂…τ_s.


Если число сомножителей s чётно, то по предложению 5 чётное число раз переменится чёт­ность подстановки , т. е. подстановка σ чётна. Аналогично для нечётного s.

Предложение 7. Произведение двух подстановок одной чётности чётно. Произведение двух подстановок разной чётности нечётно.

Доказательство. Разложим обе подстановки произвольным образом в произведение транс­позиций. Допустим,

σ₁ = τ₁τ₂…τ_s – чётная подстановка;

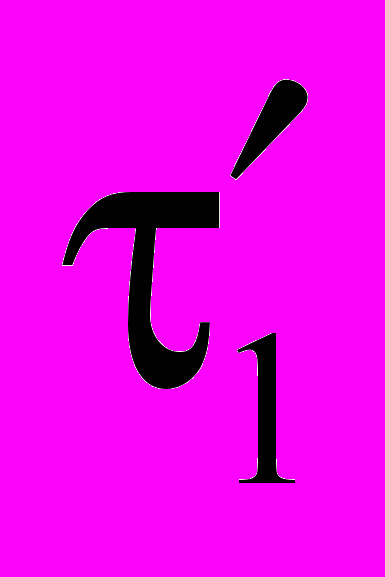
σ₂ = 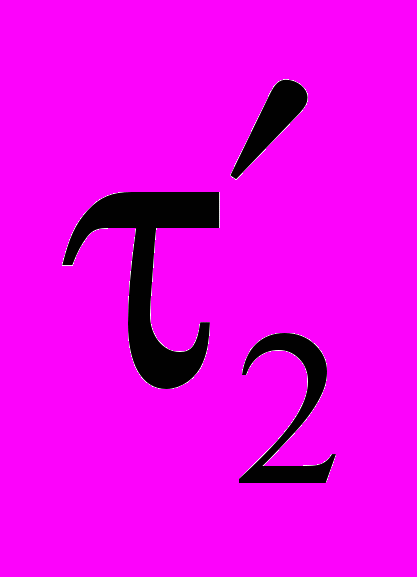… 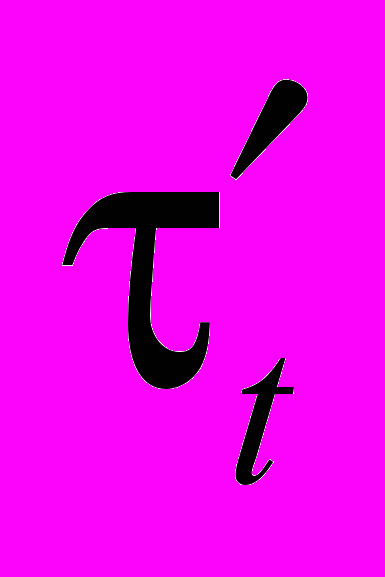– нечётная подстановка.

Из предложения 6 следует, что s чётно, а t нечётно.

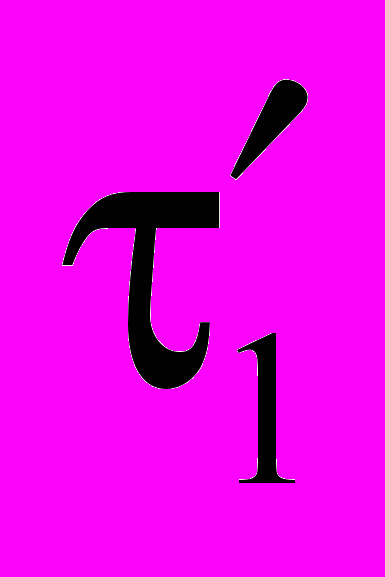
σ₁σ₂ = τ₁τ₂…τ_s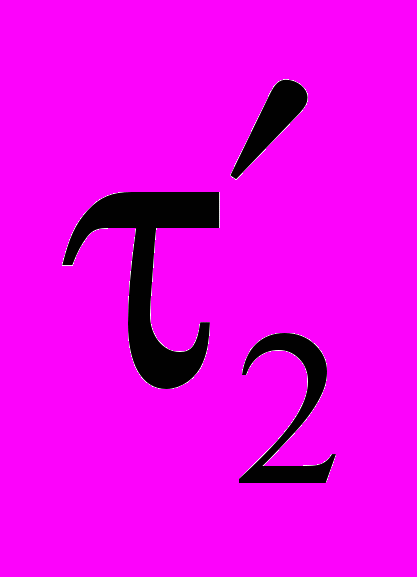…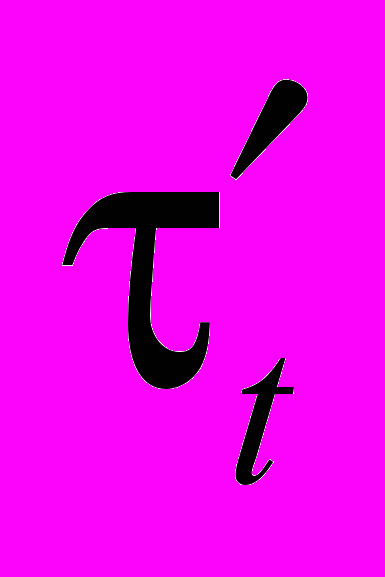. s + t нечётно, следовательно, по предложению 6 подстановка σ₁σ₂ не­чётна. Аналогично в других случаях.

Предложение 8. Обратная подстановка имеет ту же чётность, что и данная.

Доказательство. Пусть σ – данная подстановка, σ⁻¹ – обратная к σ. Рассмотрим произведе­ние:

σσ⁻¹ = ε. (1)

Необходимо доказать, что σ и σ⁻¹ имеют одну и ту же чётность. Допустим, σ и σ⁻¹ имеют разную чётность, тогда левая часть равенства (1) нечётна по предложению 7, а правая – чётна, чего не может быть.