1 семестр Информатика, ее предмет и задачи. Основные понятия информатики. Информация и формы ее представления

Вид материала

7. Внутреннее представление данных в памяти ЭВМ
7.1. Числа с фиксированной точкой.
7.2. Числа с плавающей точкой
7.4. Кодирование графической информации
7.5. Кодирование звуковой информации

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 22

7. Внутреннее представление данных в памяти ЭВМ

Информация в ЭВМ записывается в форме цифрового двоичного кода, т. к. элементы из которых строится память, могут находиться в двух устойчивых состояниях 0 и 1. Двоичное кодирование используется для представления как числовой, так и текстовой, графической, звуковой информации. Форматы представления данных в памяти компьютера определяют диапазоны значений, которые эти данные могут принимать, скорость их обработки, объем памяти, который требуется для хранения этих данных.

В ЭВМ используются следующие формы представления данных:

числа с фиксированной точкой;
числа с плавающей точкой;
символы.

7.1. Числа с фиксированной точкой.

Целые числа точно представляются в памяти компьютера и позволяют выполнять операции без погрешностей. Аппаратурой компьютеров поддерживается несколько форматов представления целых данных и множество операций над ними.

Целые числа в памяти компьютера всегда хранятся в формате с фиксированной точкой, что, безусловно, ограничивает диапазон чисел, с которыми может работать компьютер и требует учета особенностей организации арифметических действий в ограниченном числе разрядов. Рассмотрим подробнее это представление.

Все числа, которые хранятся в памяти компьютера, занимают определенное число двоичных разрядов. Это количество определяется форматом числа. Обычно для представления целых чисел используют несколько форматов. В IBM-совместимых ПК поддерживается три формата: байт (8 разрядов), слово (16 разрядов), двойное слово (32 разряда). Целые числа вписываются в разрядную сетку, соответствующую формату. Для целых чисел разрядная сетка имеет вид:

n-1	n-2	n-3		2	1	0
S			. . .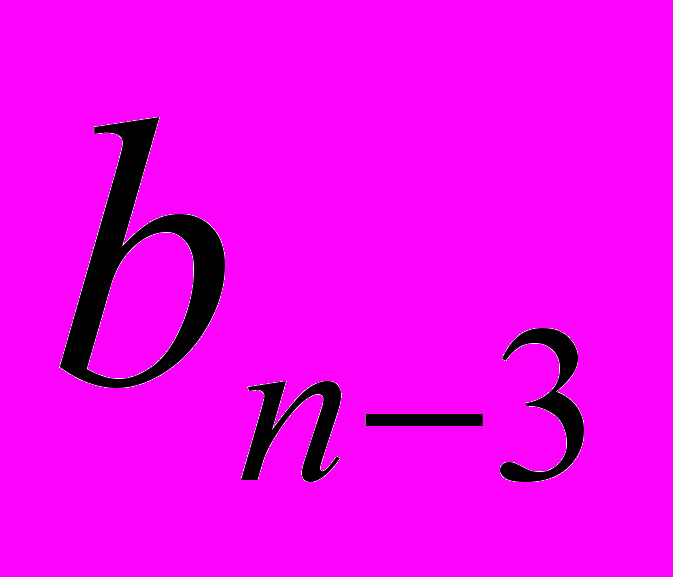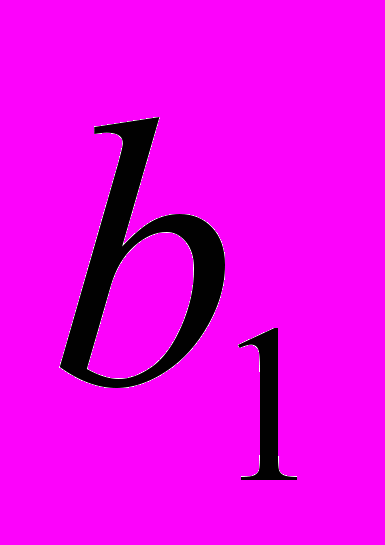

где

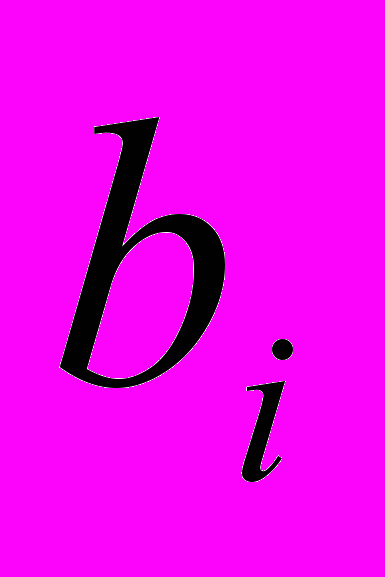- разряды двоичной записи целого числа, S - разряд, отведенный для представления знака числа. Для положительных чисел знак кодируется цифрой 0, а для отрицательных – цифрой 1 (прямой код). Разделитель между целой и дробной частью зафиксирован после

, дробной части нет. N - количество двоичных разрядов в разрядной сетке. Если количество разрядов в сетке оказывается больше, чем количество цифр в числе, то старшие разряды заполняются нулями. Например, число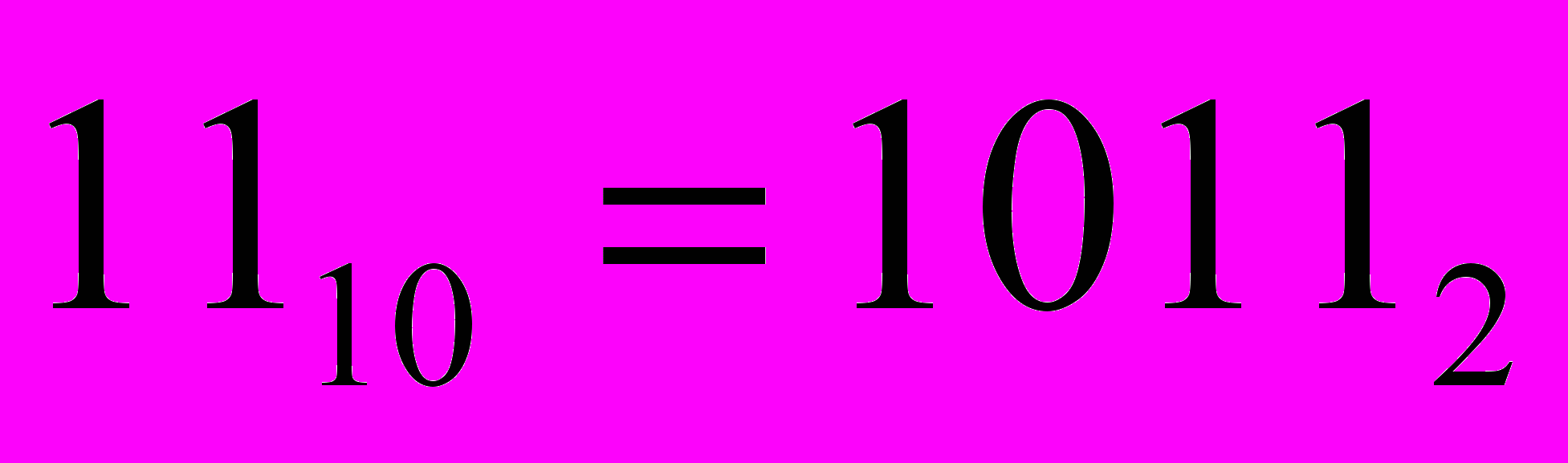

в формате байта (8 бит) запишется так:

7	6	5	4	3	2	1	1
0	0	0	0	1	0	1	1

знак

Для упрощения операций с отрицательными числами используются специальные (обратный и дополнительный) коды (см. выше).

7.2. Числа с плавающей точкой

Для представления вещественных чисел используется форма чисел с плавающей точкой. Такое представление основано на записи числа в экспоненциальном виде:

- нормальная форма. Нормальная форма представления чисел неоднозначна. Например, десятичное число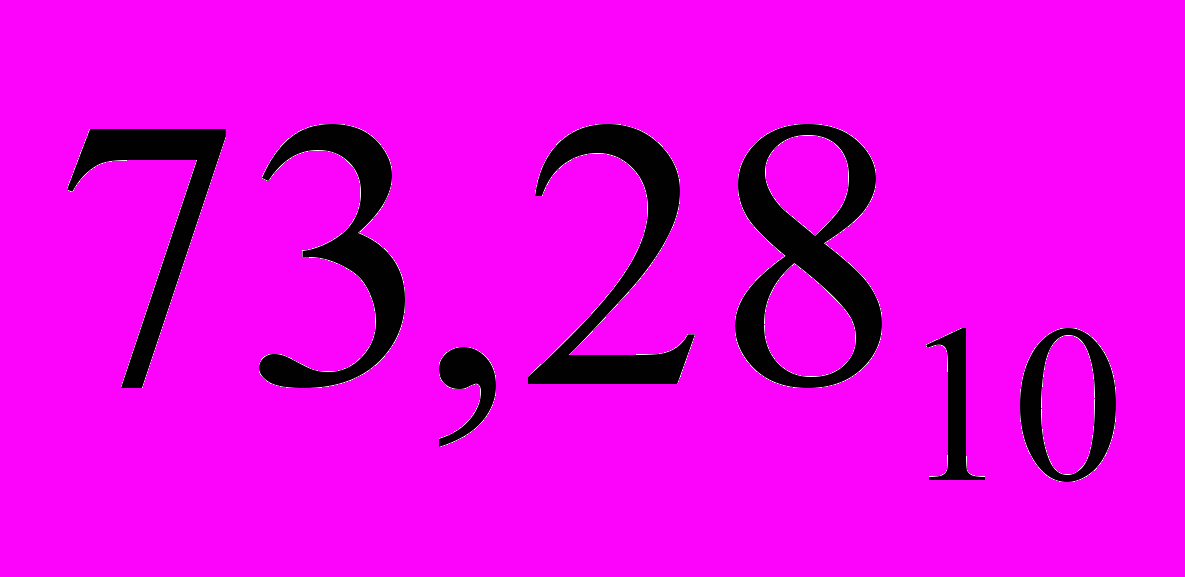

можно представить

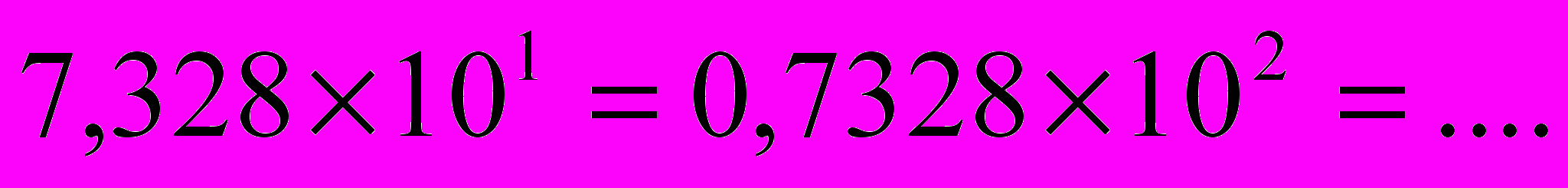Для однозначности используется нормализованная форма, в которой положение точки всегда задается перед первой значащей цифрой мантиссы, т.е. мантисса должна быть меньше 1 и первая значащая цифра – не ноль (0.7328 х 10²). В память ПК мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся). Следовательно, внутреннее представление вещественного числа сводится к представлению пары чисел: мантиссы и порядка. Таким образом часть разрядов памяти, отводимой под вещественное число используется для хранения порядка числа р, а остальные - разряды для хранения мантиссы:

Порядок числа и мантисса хранятся в двоичном коде. Точность вычислений зависит от длины мантиссы, а порядок числа определяет допустимый диапазон представления действительных чисел. В IBM-совместимых компьютерах используется три формата представления данных в форме с плавающей точкой (32 разряда, 64 разряда и 80 разрядов), позволяющие определить три диапазона для положительных вещественных чисел: от 1,5х10^-45 до 3,4х10³⁸, от 5х10^-324 до 1,7х10³⁰⁸и от 1,9х10^-4951 до 1,1х10⁴⁹³². Для представления положительных чисел в знаковый разряд записывается 0, а для отрицательных - 1.

В качестве примера рассмотрим внутреннее представление вещественного числа в 4-х байтовой ячейке памяти.

31			24	23			0
Знак	Порядок			Мантисса

В старшем бите первого байта хранится знак числа (0 –«+», 1 – «-»). Оставшиеся 7 бит отводятся под машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы (24 разряда).

В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. Следовательно, машинный порядок изменяется в диапазоне от 0 до 2⁷. Порядок может быть и положительным и отрицательным (-64 до 63).

Машинный порядок смещен относительно математического порядка и имеет только положительные значения. Минимальному математическому значению порядка соответствует 0: Мр=р+64.

В двоичной СС эта формула имеет вид:

Мр₂=р₂+100 0000₂

Пример: Записать внутреннее представление числа 250,1875 в форме с плавающей точкой.

Переведем число в 2-ю СС.

250,1875=1111 1010, 0011 0000 0000 0000₂ (24 значащие цифры)

2. Запишем в форме нормализованного числа с плавающей точкой

0, 1111 1010 0011 0000 0000 0000₂ х 10₂¹⁰⁰⁰

3. Вычислим машинный порядок в двоичной СС.

Мр₂=1000+100 0000= 100 1000

4. Запишем представление числа с учетом знака в 4-байтовой ячейке памяти:

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
0	1	0	0	1	0	0	0	1	1	1	1	1	0	1	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0
4 байт								3 байт								2 байт								1 байт

Особенности представления вещественных чисел в памяти ПК определяет свойства машинных чисел: при переводе дробной части десятичного числа в формат с плавающей точкой происходит его округление до количества разрядов, определяемых длинной мантиссы. Ограниченная длина мантиссы приводит к погрешности при выполнении операций – лишние разряды отсекаются или происходит округление чисел.

7.3. Символы

Текстовые данные рассматриваются как последовательность отдельных символов, каждому из которых ставится в соответствие двоичный код некоторого неотрицательного целого числа. Существуют разные способы кодирования символов. Наиболее распространенной до последнего времени была кодировка ASCII (American Standard Code for International Interchange). При использовании этой кодировки для представления символа используется 1 байт (8 разрядов). Таким образом, имеется возможность закодировать 256 различных символов.

Для отображения текстового документа с разбивкой его на строки, выравниванием и другими элементами форматирования, в него наряду с обычными символами включаются специальные (управляющие) символы.

В системе ASCII закреплены две таблицы кодирования базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная от 128 до 255. Первые 32 кода базовой таблицы, начиная с нулевого, содержат управляющие коды. Они не выводятся на экран, но с их помощью можно управлять выводом других данных. С 32 по 127 код размещены символы английского алфавита, цифры, знаки арифметических операций и т. п. Расширенная часть системы кодирования ASCII содержит национальные системы кодирования, т. е. коды с 128 по 255 будут содержать русский алфавит, а также символы псевдографики.

ASCII позволяет закодировать только 256 символов, но в некоторых языках символов больше, поэтому разрабатываются другие коды. Наиболее перспективным является Unicode. В этом коде каждый символ состоит из 16 битов (2 байта), что позволяет кодировать 65536 различных символов. Для каждого алфавита определены свои кодовые позиции. Например, 0100-017F – европейские латинские символы , 0400-04FF – кириллица и т. д. Около 29000 позиций пока не заняты, но зарезервированы для использования. Таким образом, Unicode допускает обмен данными на разных языках, каждому коду соответствует единственный символ, коды для разных языков не пересекаются.

На Unicode построена ОС Windows NT. У Windows95-98 16-битное наследство, поэтому вся внутренняя работа в этой ОС построена на использовании ANS-строк (ANSII – American National Standard Institute), в которых символ записан в один байт. ANSI-текст (или текст ASCII) - это текст без форматирования (с ним работает приложение «Блокнот» в Windows 9x).

Если для представления информации в разных информационных системах используются разные кодировки, то данные, подготовленные в одной системе, не смогут быть использованы в другой.

7.4. Кодирование графической информации

Способ кодирования графических изображений, отображаемых на экране, называют матричным. При этом экран рассматривается как двумерный массив отдельных точек (пикселов). Такой метод кодирования графической информации называется растровым. Для каждой точки рассматриваются ее линейные координаты и яркость, которые задаются в виде целых неотрицательных чисел. Общепринятым на сегодняшний день является представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета. Таким образом, для кодирования яркости любой точки будет достаточно одного байта, т. е. восьмиразрядного двоичного числа.

Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на основные составляющие. В качестве таких составляющих используют три цвета: красный (Red, R), зеленый (Green, G), синий (Blue, B). На практике считается, что любой цвет, видимый человеческим глазом, можно получить путем механического смешения этих трех цветов. Такая система кодирования называется системой RGB- по первым буквам основных цветов.

Если для кодирования яркости каждой из основных составляющих использовать по 256 значений (8 двоичных разрядов), то на кодирование одной точки придется затратить 24 разряда, при этом система кодирования обеспечивает однозначное определение 16,5 миллионов различных цветов. Режим представления цветной графики с использованием 24 разрядов называется полноцветным (True Color).

Каждому из основных цветов можно поставить в соответствие дополнительный цвет, т. е. цвет, дополняющий основной цвет до белого. Нетрудно заметить, что для любого из основных цветов дополнительным будет цвет, образованный суммой пары остальных основных цветов: голубой (Cyan, C), пурпурный (Magenta, M), желтый (Yellow, Y). Принцип декомпозиции произвольного цвета на составляющие компоненты можно применить не только для основных цветов, но и для дополнительных, т. е. любой цвет можно представить в виде суммы голубой, пурпурной и желтой составляющих. Такой метод кодирования принят в полиграфии, но там используется еще и четвертая краска – черная (Black, К). Поэтому данная система кодирования обозначается четырьмя буквами - CMYK. Для представления цветной графики в этой системе надо иметь 32 двоичных разряда. Такой режим тоже называется полноцветным (True Color).

Если уменьшить количество двоичных разрядов, используемых для кодирования цвета каждой точки, то можно сократить объем данных, но при этом диапазон кодируемых цветов заметно сокращается. Кодирование цветной графики 16-разрядными двоичными числами называется режимом High Color.

7.5. Кодирование звуковой информации

Приемы и методы работы со звуковой информацией пришли в вычислительную технику наиболее поздно. Поэтому эти методы работы еще не стандартизированы. Многие фирмы разработали свои корпоративные стандарты. Можно выделить два основных направления.

Метод частотных модуляций FM (Frequency Modulation).

По своей природе звук является непрерывным сигналом. Это колебания воздуха с определённой частотой и амплитудой. При преобразовании звука в электрический сигнал (например, при записи с помощью микрофона) происходит непрерывное фиксирование определённого напряжения электрического тока. Такой сигнал называется аналоговым:

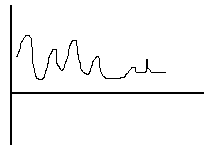
Для компьютерной обработки аналоговый сигнал нужно преобразовать в последовательность двоичных цифр, то есть дискретизировать и оцифровать.

Дискретизация - это превращение непрерывных электрических колебаний в числовую последовательность. Для этого измеряется амплитуда сигнала через равные промежутки времени, и полученные числовые значения кодируются в двоичной форме и записываются в память компьютера. Чем меньше промежуток времени, тем выше частота дискретизации и, соответственно, выше качество записи звука. Частота дискретизации измеряется в килогерцах.

1 кГц=1 тыс. измерений в секунду.

Наиболее распространёнными являются частоты 44,1 кГц и 48 кГц.

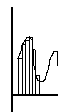
При воспроизведении звука производится обратная операция по превращению двоичных кодов в непрерывные электрические колебания. Эти функции по преобразованию звука выполняют два специальных устройства - аналого-цифровой и цифро-аналоговый преобразователи, которые располагаются на звуковой карте.

При таких преобразованиях неизбежны потери информации, связанные с методом кодирования, поэтому качество звукозаписи получается не вполне удовлетворительным. Но это достаточно компактный метод, он начал использоваться, когда ресурсов вычислительной техники было недостаточно.

Метод таблично-волнового синтеза (Wave-Table) состоит в следующем. Где-то в заранее подготовленных таблицах хранятся образцы звуков для различных музыкальных инструментов. В технике такие образцы называют сэмплами. Числовые коды выражают тип инструмента, номер его модели, высоту тона, продолжительность и интенсивность звука, динамику его изменения, параметры среды, в которой происходит звучание и др. Т .к в качестве образца использовались реальные звуки, то качество звука, полученного в результате синтеза получается достаточно высоким и приближается к качеству звучания реальных музыкальных инструментов.