1 семестр Информатика, ее предмет и задачи. Основные понятия информатики. Информация и формы ее представления
| Вид материала | Документы |
| 6. Кодирование информации 6.2. Понятие о специальном кодировании |
- 1. Основные понятия информатики. Определение понятия информатика. Предмет и задачи, 745.21kb.
- 1. Основные понятия информатики 2 Тема Предмет информатики, 1612.33kb.
- Вопросы к зачету по курсу лекций "Информатика" для студентов Iкурса кафедры аэту iсеместр., 18.81kb.
- Тематический план по дисциплине «Информатика и математика» для студентов 2 курса (набор, 46.52kb.
- Информация и информационные процессы, 276.11kb.
- Задачи и проблемы информатики 9 Инемного философии… 9 Использованная литература, 196.06kb.
- Защита данных комплекс мер, направленных на предотвращение потерь, воспроизведения, 85.23kb.
- Программа к вступительного экзамена в магистратуру по специальности 6М060200 Информатика, 50.03kb.
- Темы рефератов по истории информатики Шилов И. В. Эволюция понятия «информация», 19.62kb.
- Темы лекций. Неделя I: Предмет, объект, методы корпоративного управления. Основные, 54.05kb.
6. Кодирование информации
6.1. Цели кодирования
Кодирование – это переход от исходного представления информации удобного для восприятия человеком к представлению удобному для хранения, передачи и обработки информации с использованием вычислительной техники. Обратный процесс называется декодированием. При кодировании информации ставятся следующие цели:
- удобство физической реализации;
- удобство восприятия;
- высокая скорость передачи и обработки;
- уменьшение избыточности сообщений;
- надежность, т. е. защита от случайных искажений;
- сохранность, т. е. защита от несанкционированного доступа.
Эти цели могут противоречить друг другу: экономные сообщения неудобны для восприятия, их надежность уменьшается. Избыточные сообщения более надежны, но уменьшается скорость передачи информации и т.д.
На разных этапах обработки информации достигаются разные цели . Поэтому информация неоднократно преобразуется из вида удобного для восприятия человеком к виду удобному для обработки средствами вычислительной техники и наоборот.
6.2. Понятие о специальном кодировании
Для хранения чисел и выполнения операций над ними используют прямой, обратный и дополнительный коды.
- Прямой код
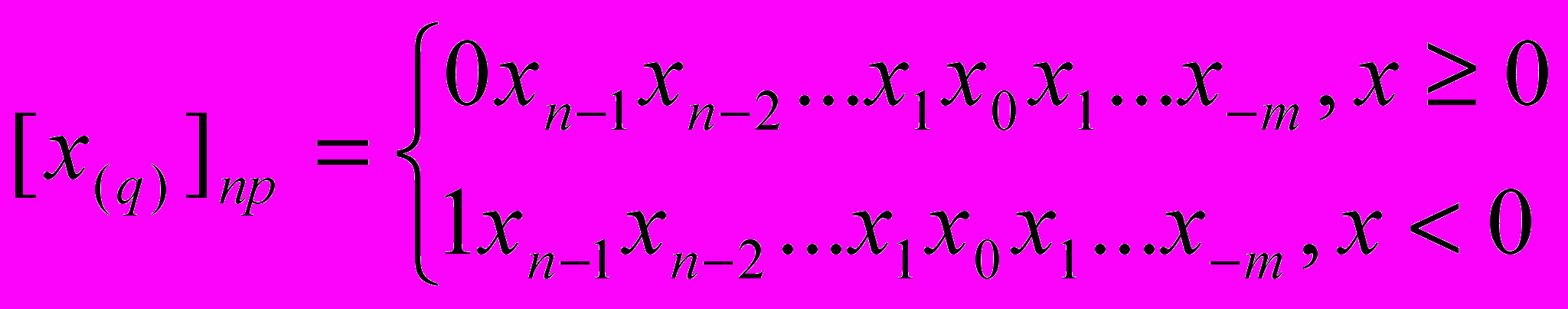
где
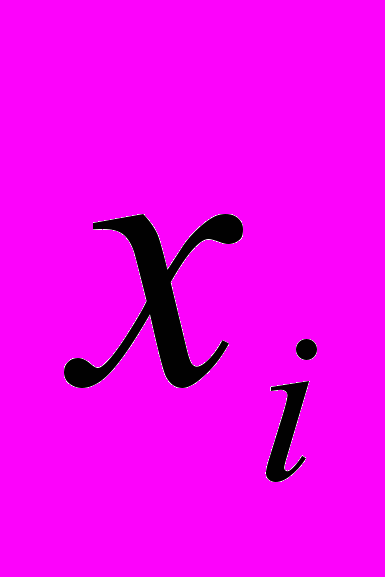 - значение цифры в i-ом разряде, q –основание системы счисления.
- значение цифры в i-ом разряде, q –основание системы счисления.Пример

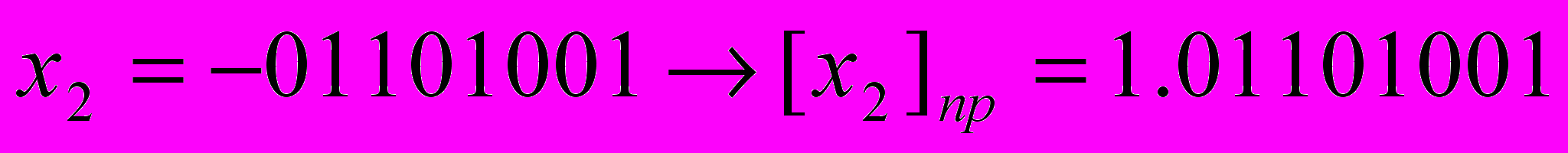
При таком представлении чисел реализация арифметических операций в ЭВМ должна предусматривать различные действия с модулями чисел в зависимости от знаков. Сложение чисел с одинаковыми знаками выполняется как обычно: числа складываются и сумме присваивается код знака слагаемых. При сложении чисел с разными знаками определяется большее по модулю число, из большего вычитается меньшее и результату присваивается знак большего по модулю числа.
Для упрощения таких операций в ЭВМ используются специальные коды, которые позволяют свести эту операцию к операции арифметического сложения: обратный и дополнительный.
- Обратный код
 ,
,где
 - инверсия цифры
- инверсия цифры 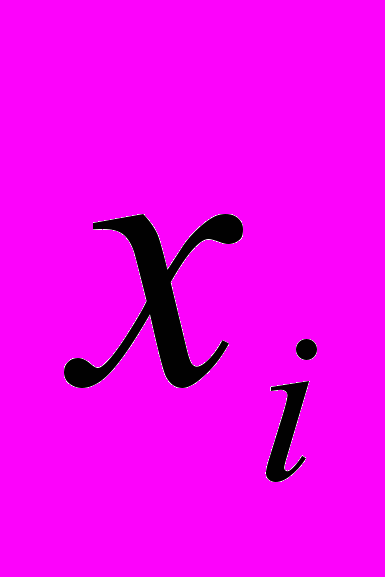 , определяется
, определяется  . Для двоичной СС инверсией 1 является 0 и наоборот.
. Для двоичной СС инверсией 1 является 0 и наоборот.Частное правило образования обратного кода для отрицательных двоичных чисел. Для преобразования прямого кода двоичного отрицательного числа в обратный код и наоборот необходимо знаковый разряд оставить без изменения, а в остальных разрядах 0 заменить на 1, а 1 на 0.
Пример.
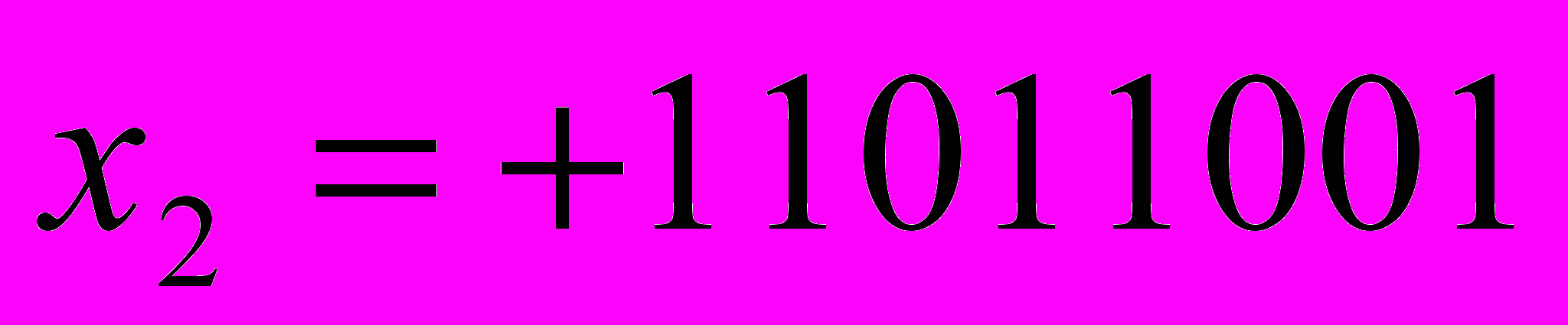 | 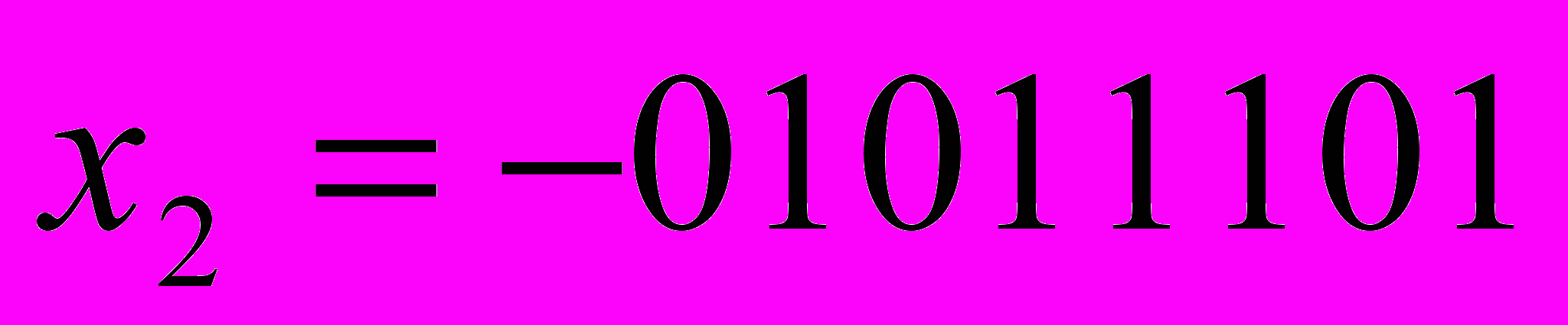 |
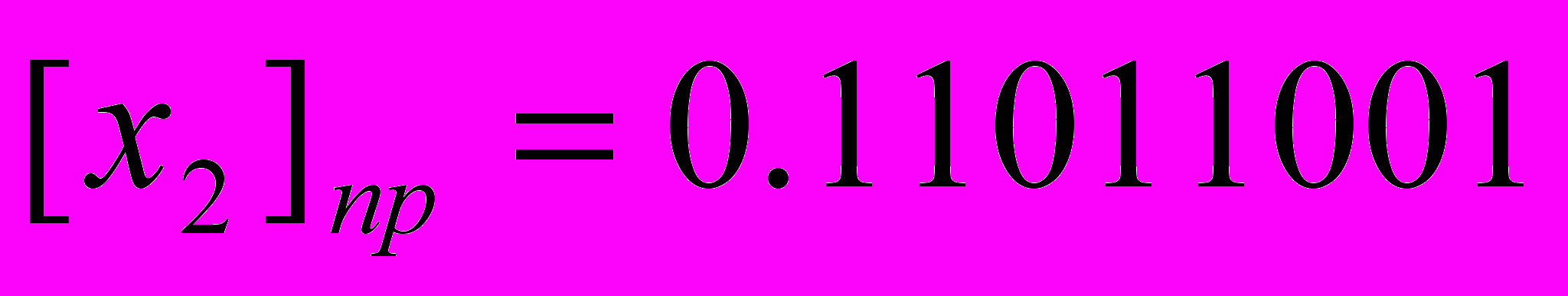 | 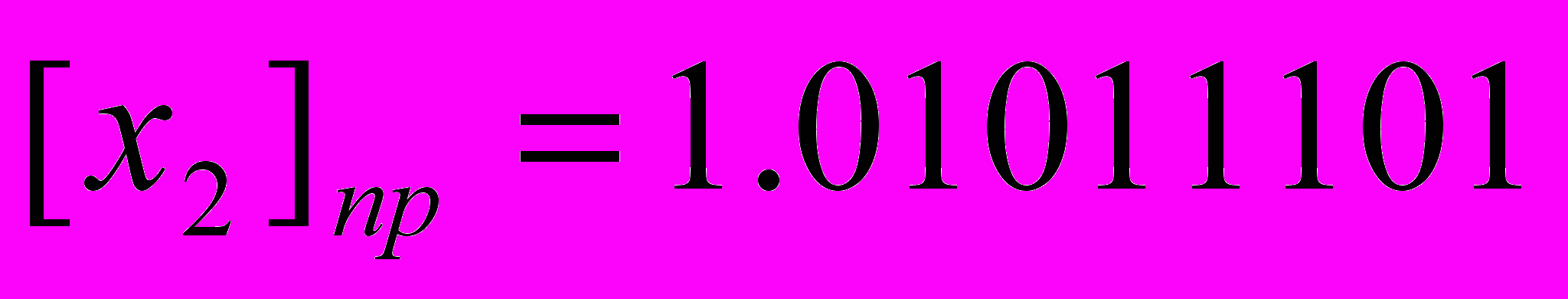 |
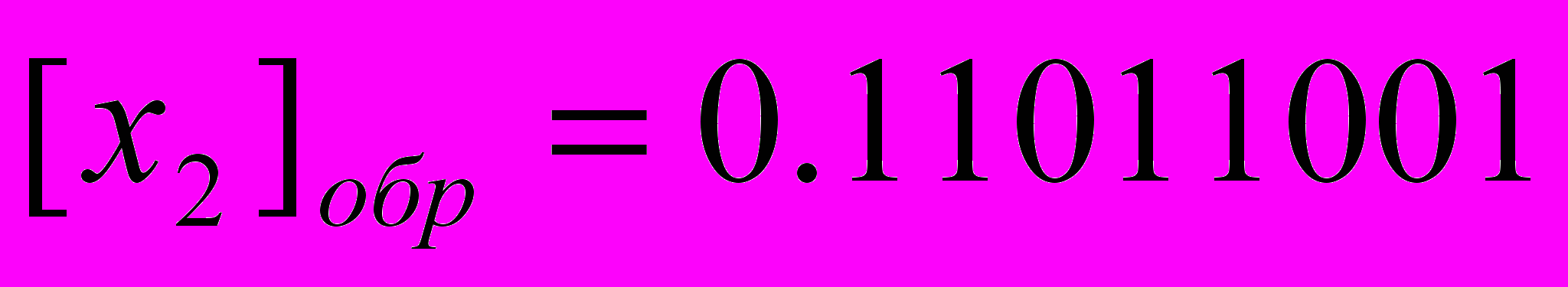 |  |
| | |
- Дополнительный код
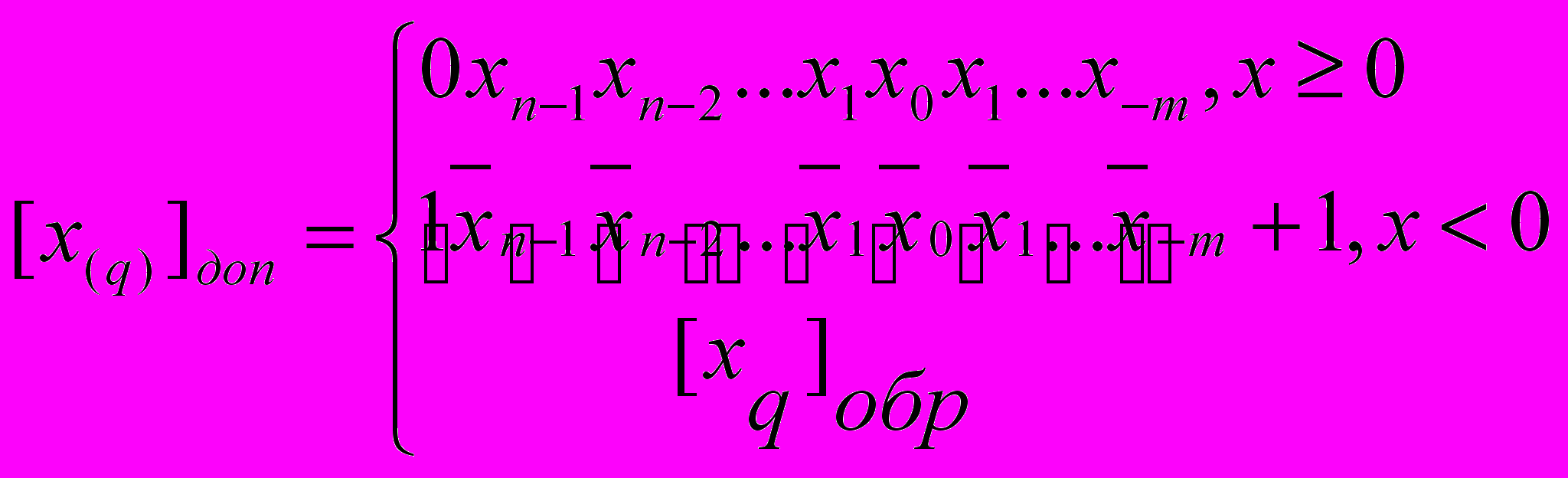
Таким образом, для преобразования прямого кода q-ичного отрицательного числа в дополнительный , надо преобразовать его в обратный код и в младший разряд добавить 1.
Пример
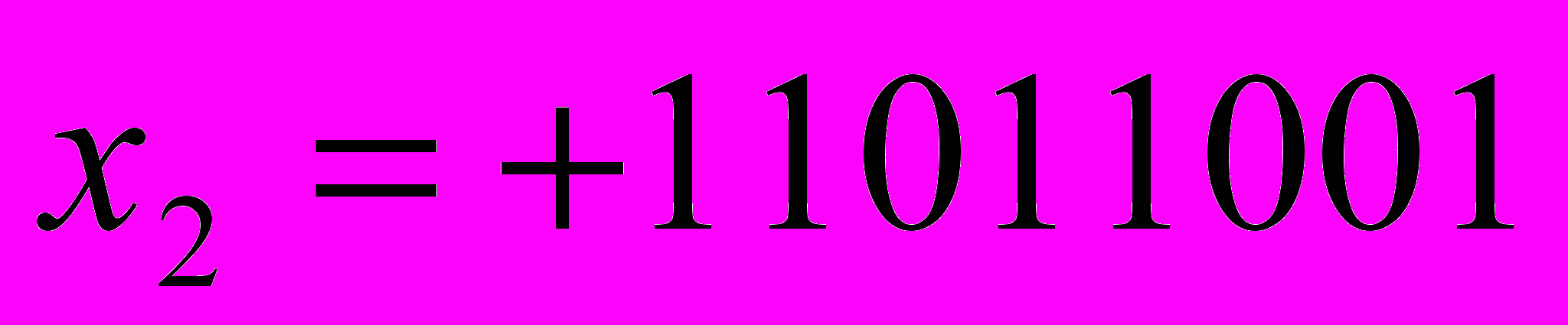 | 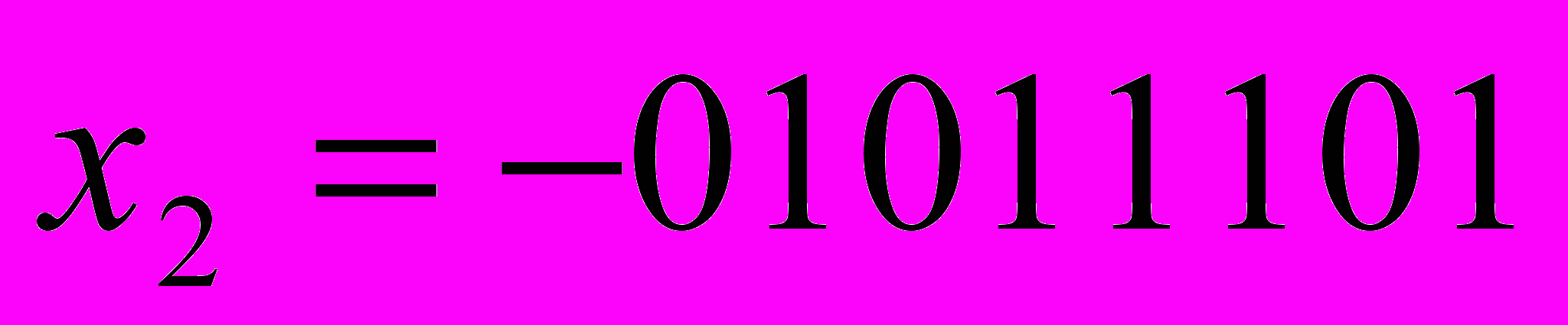 |
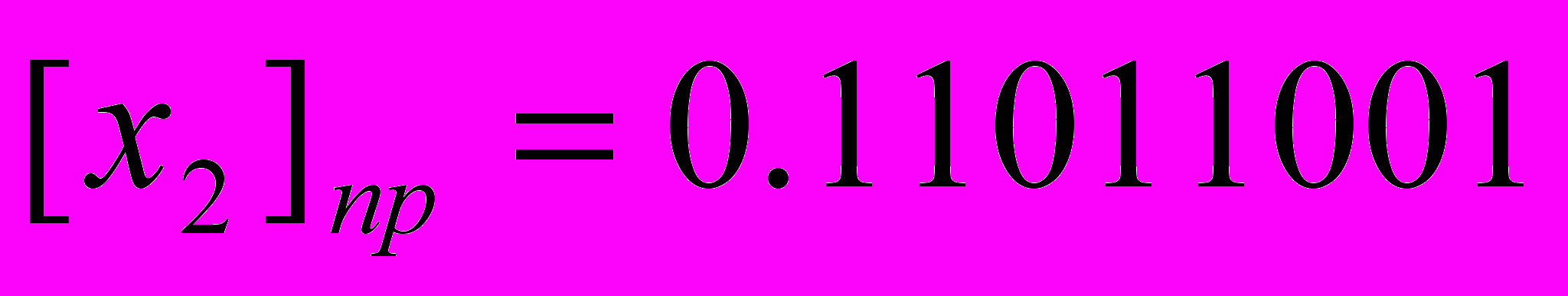 | 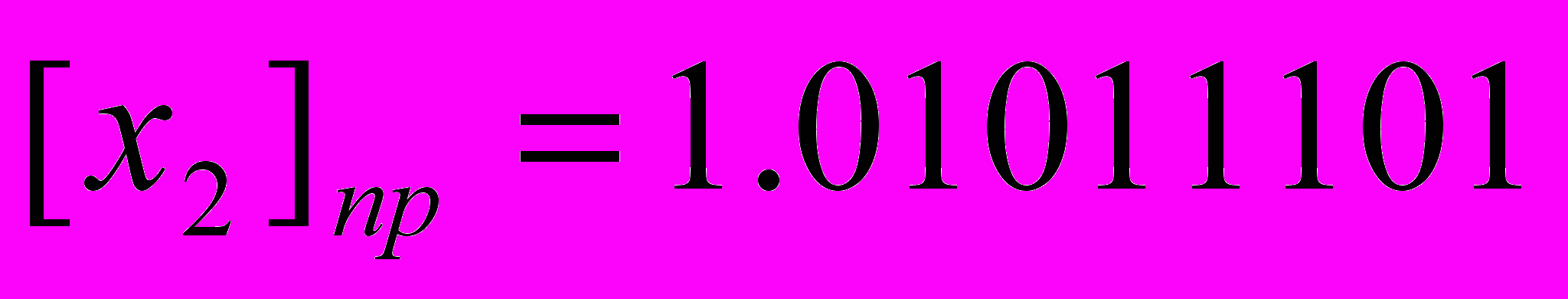 |
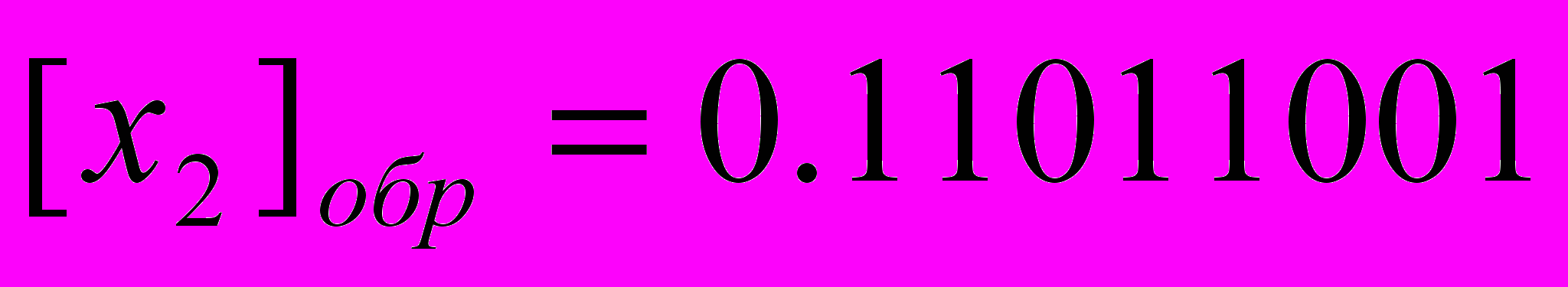 |  |
| | 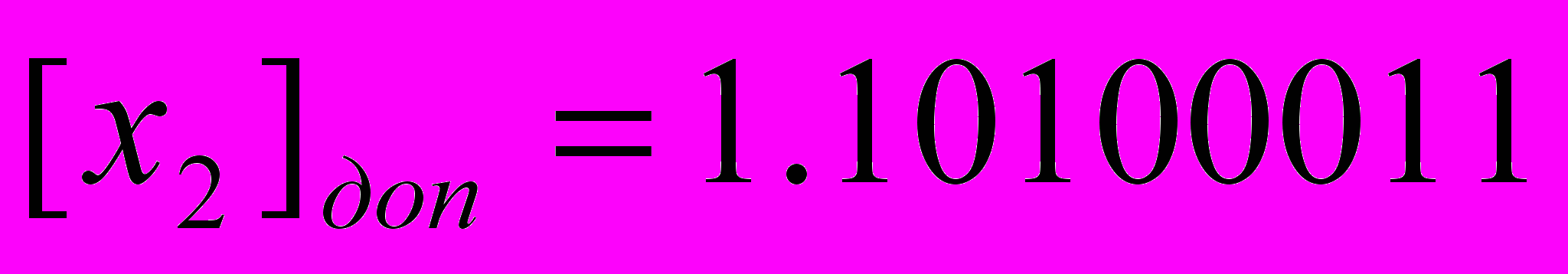 |
При выполнении операции сложения с помощью специальных кодов знаковые разряды участвуют в сложении также как цифровые разряды. Знаковые разряды и цифры переноса из старшего цифрового разряда складываются как одноразрядные двоичные коды. Если при этом формируется перенос из знакового разряда, то он добавляется в младший разряд результата при использовании обратного кода и отбрасывается при использовании дополнительного кода.
Пример.
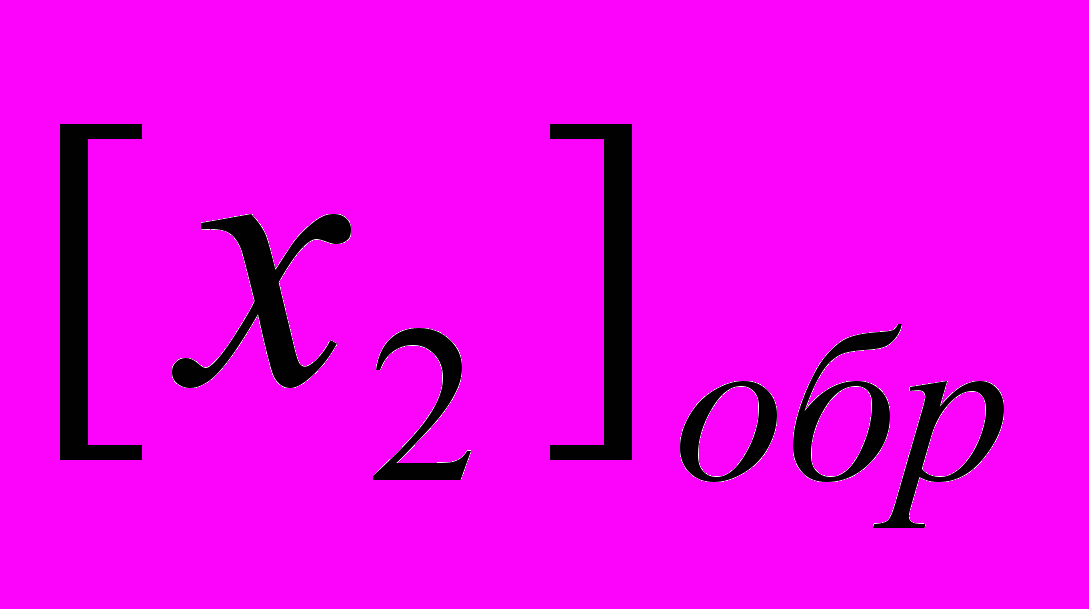 =0.1101 1001 =0.1101 1001 | 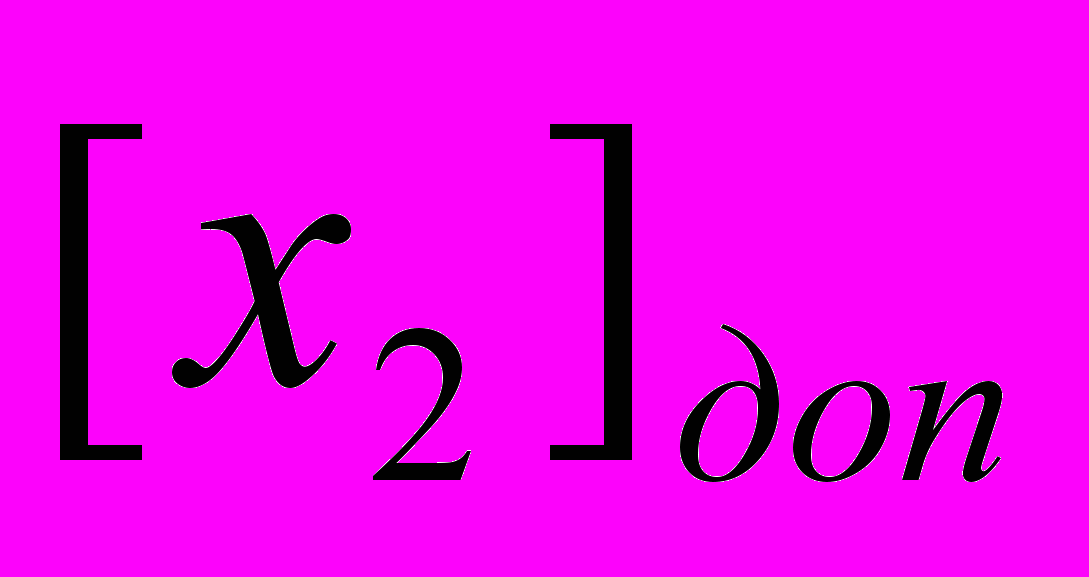 = 0.1101 1001 = 0.1101 1001 |
| + | + |
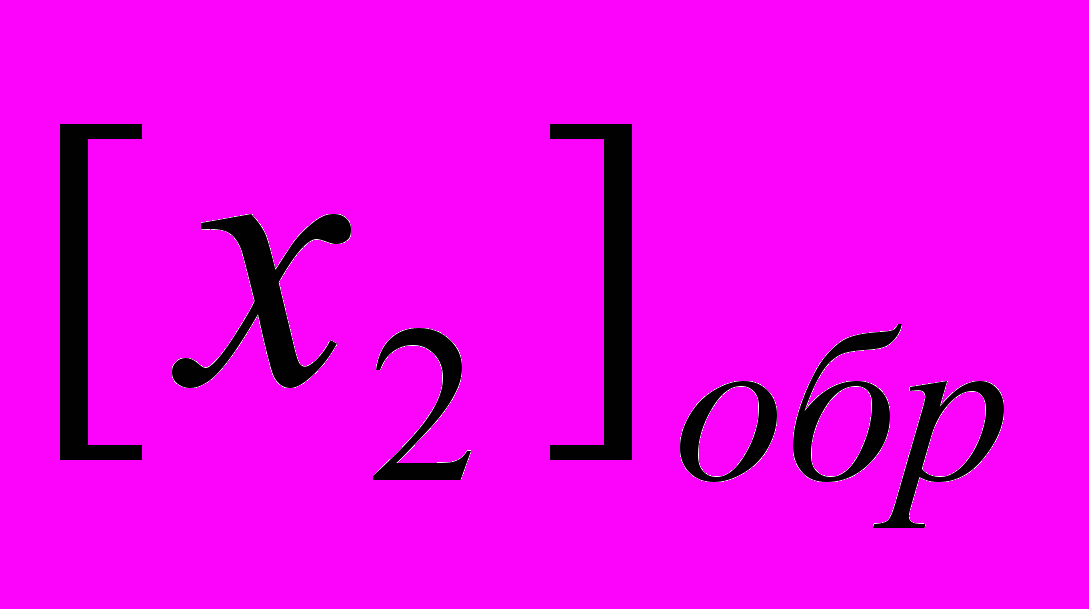 =1.1010 0010 =1.1010 0010 | 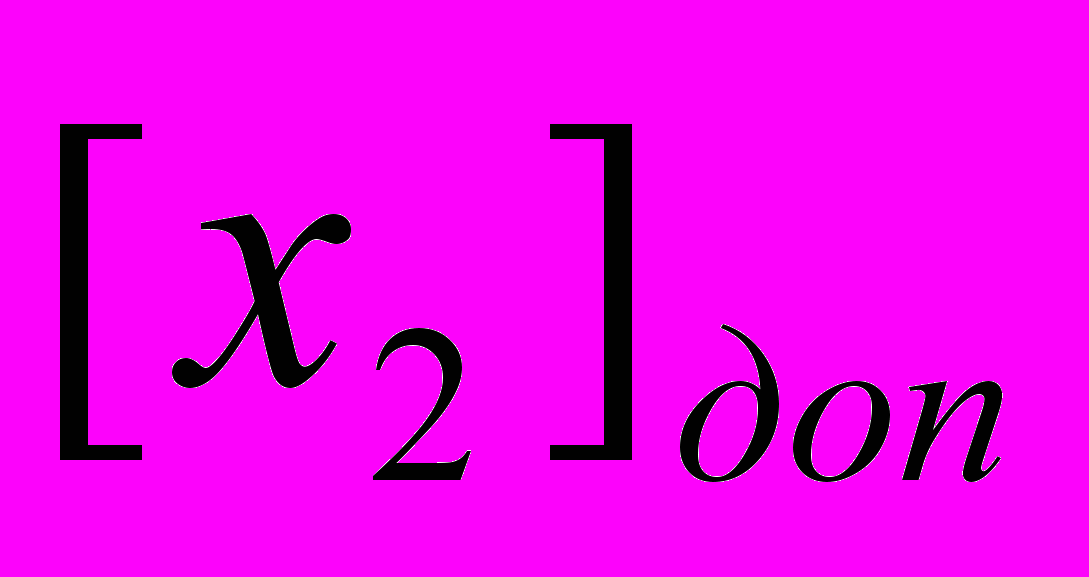 = 1.1010 0011 = 1.1010 0011 |
| = | = |
 10.0111 1011 10.0111 1011 | 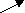 10.0111 1100 10.0111 1100 |
 +1 +1 | отбрасывается |
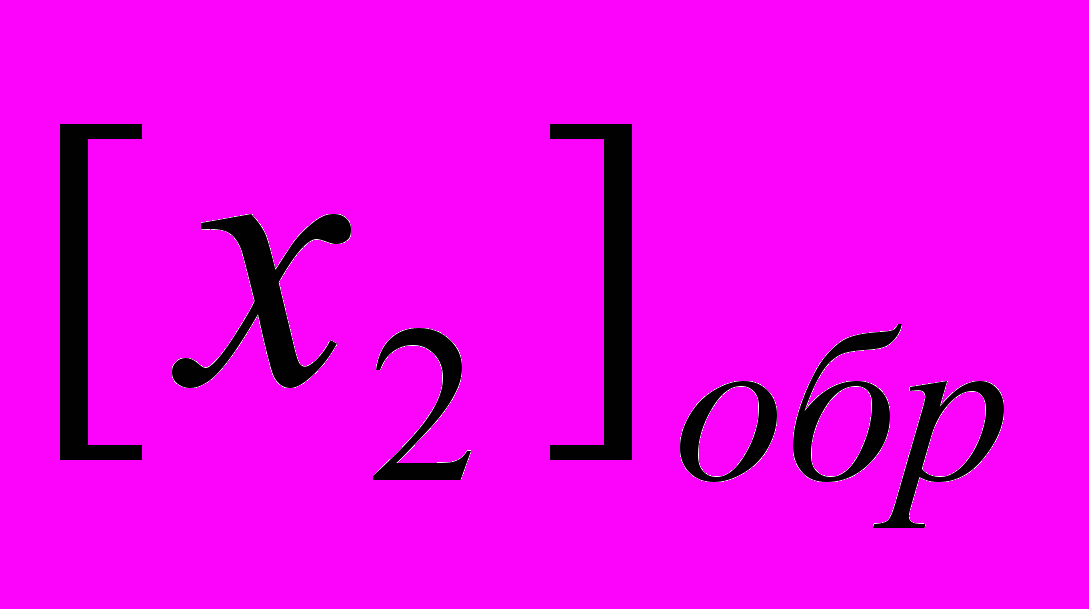 =0.0111 1100 =0.0111 1100 | 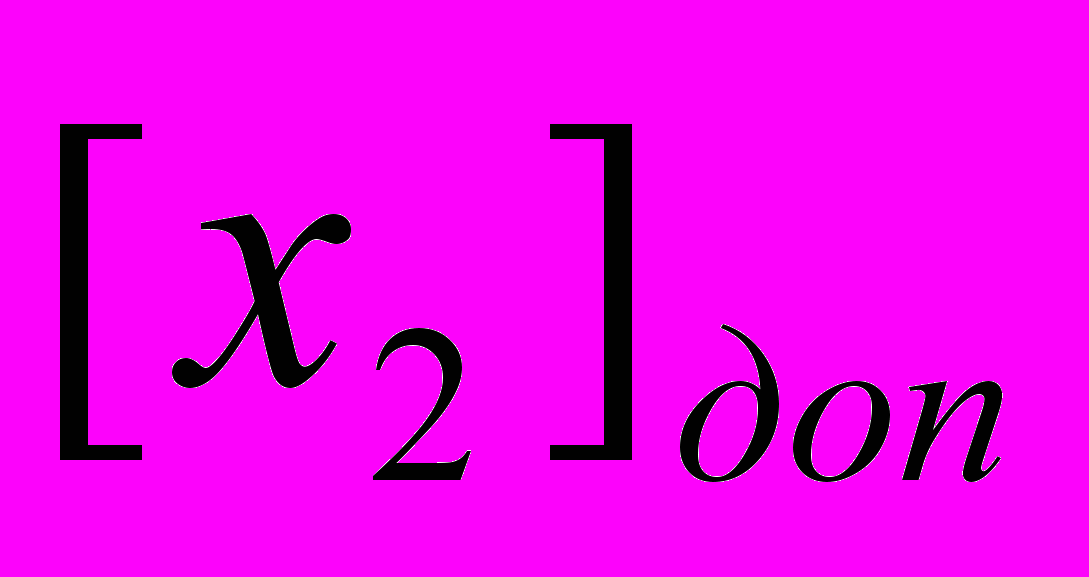 =0.0111 1100 =0.0111 1100 |
При выполнении алгебраического сложения, перед преобразованием прямых кодов слагаемых в специальные, их надо выровнять по количеству разрядов.
Пример 1.
Получить дополнительный код числа х= -1310
- х= -1310= -11012
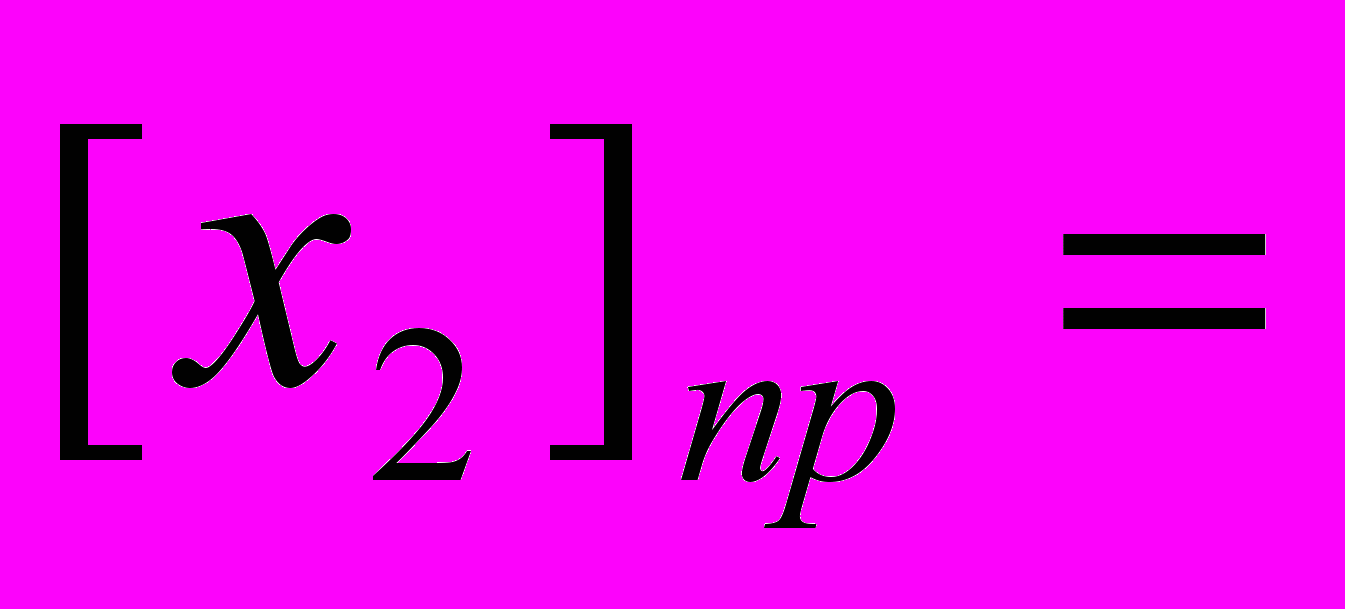 1.1101
1.1101
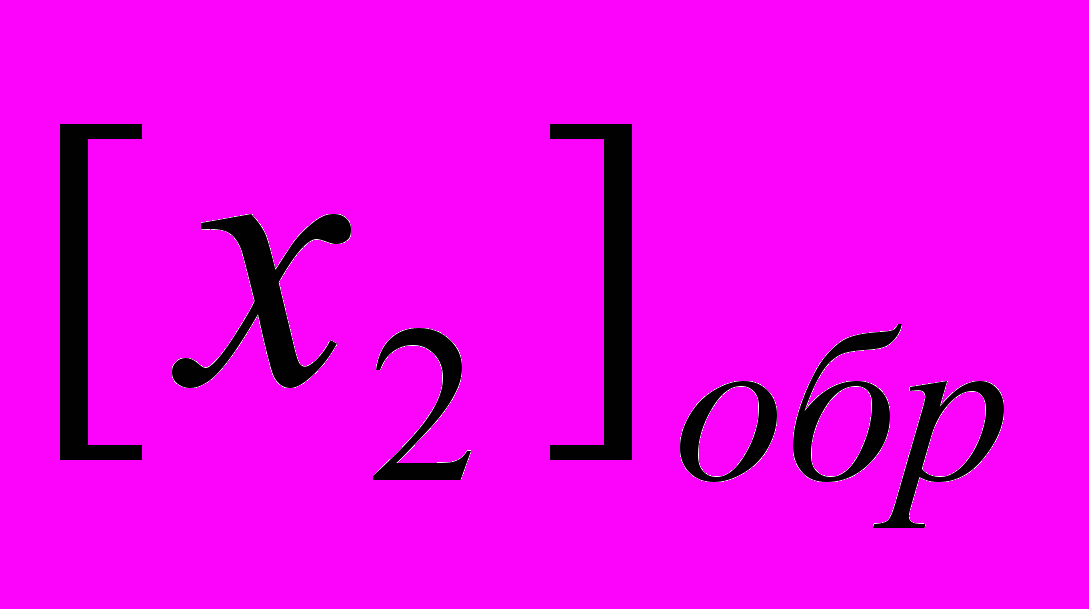 =1.0010
=1.0010
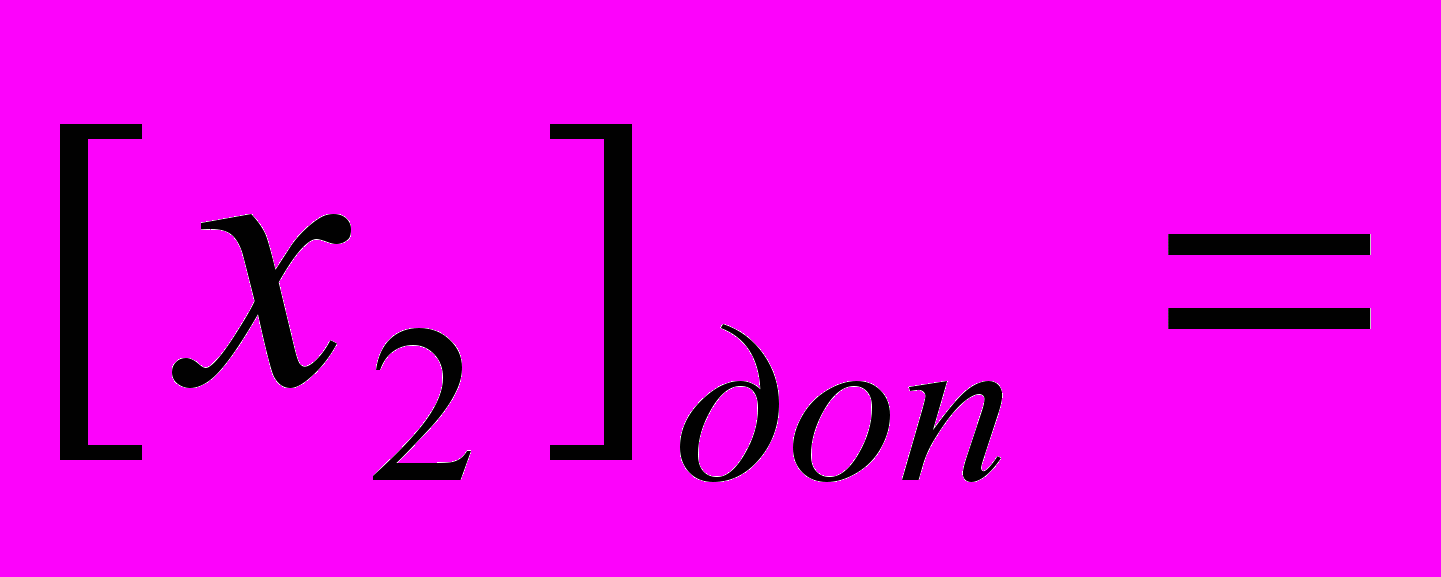 1.0011
1.0011
Пример 2.
Вычислить, используя дополнительные коды 710-310
| 1) | х= 710= 1112 | х= -310= -0112 |
| 2) | 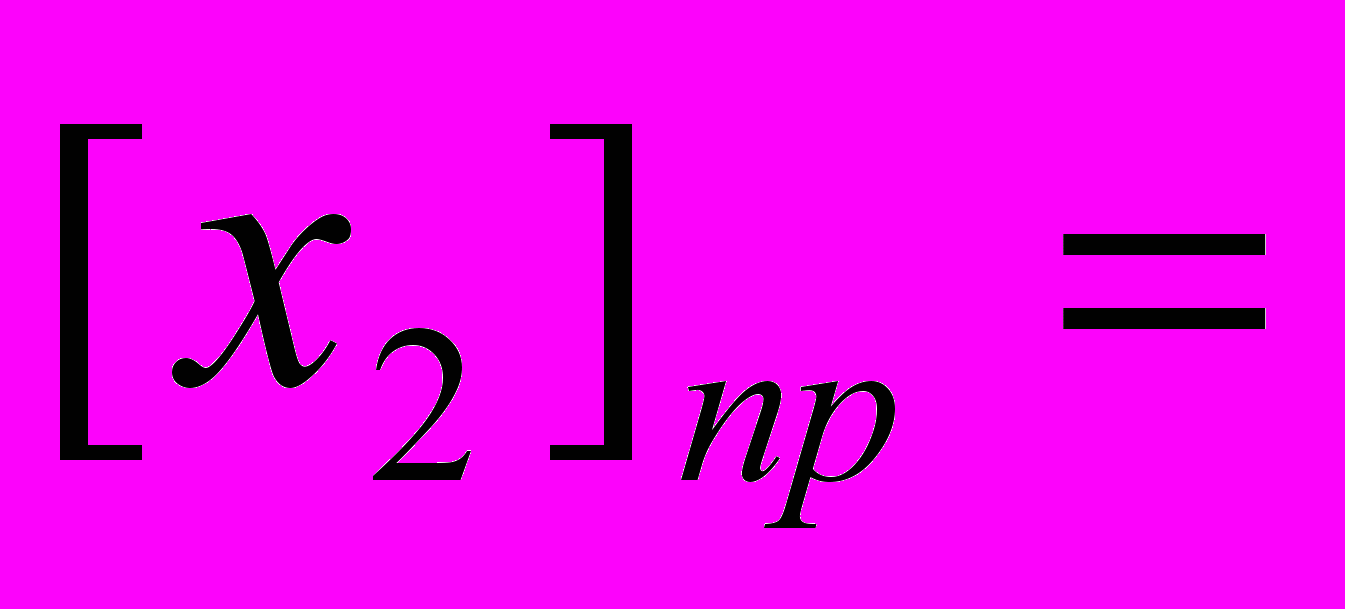 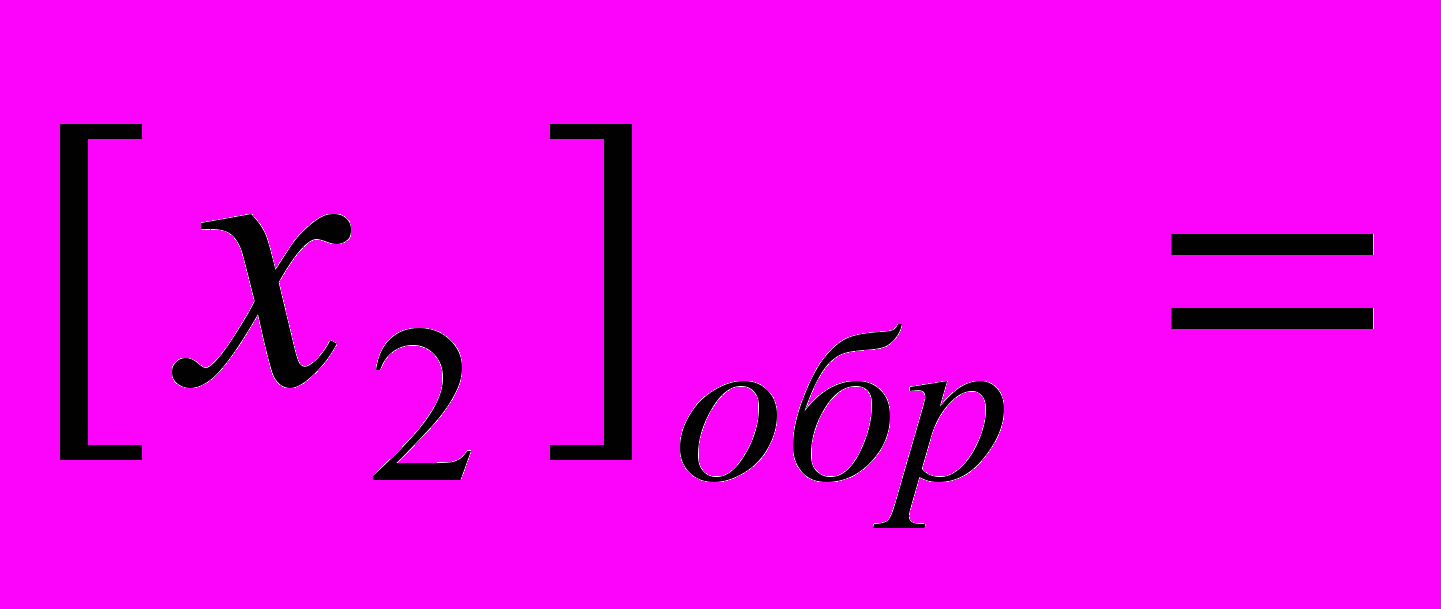 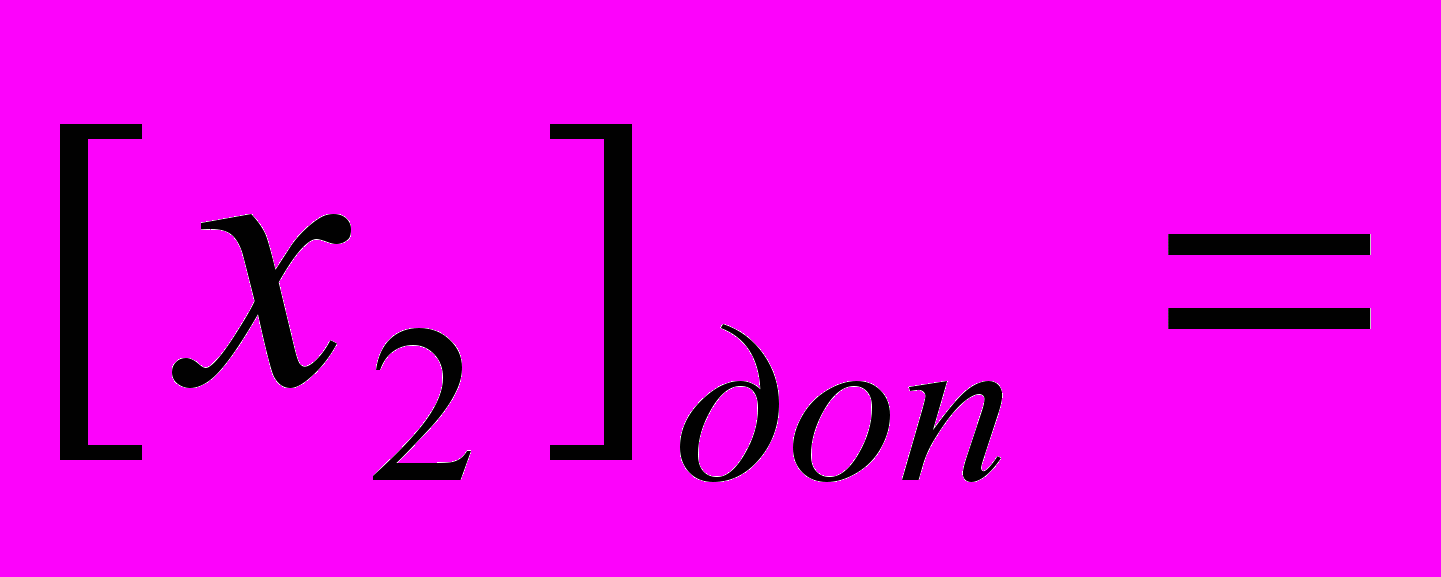 0.111 0.111 | 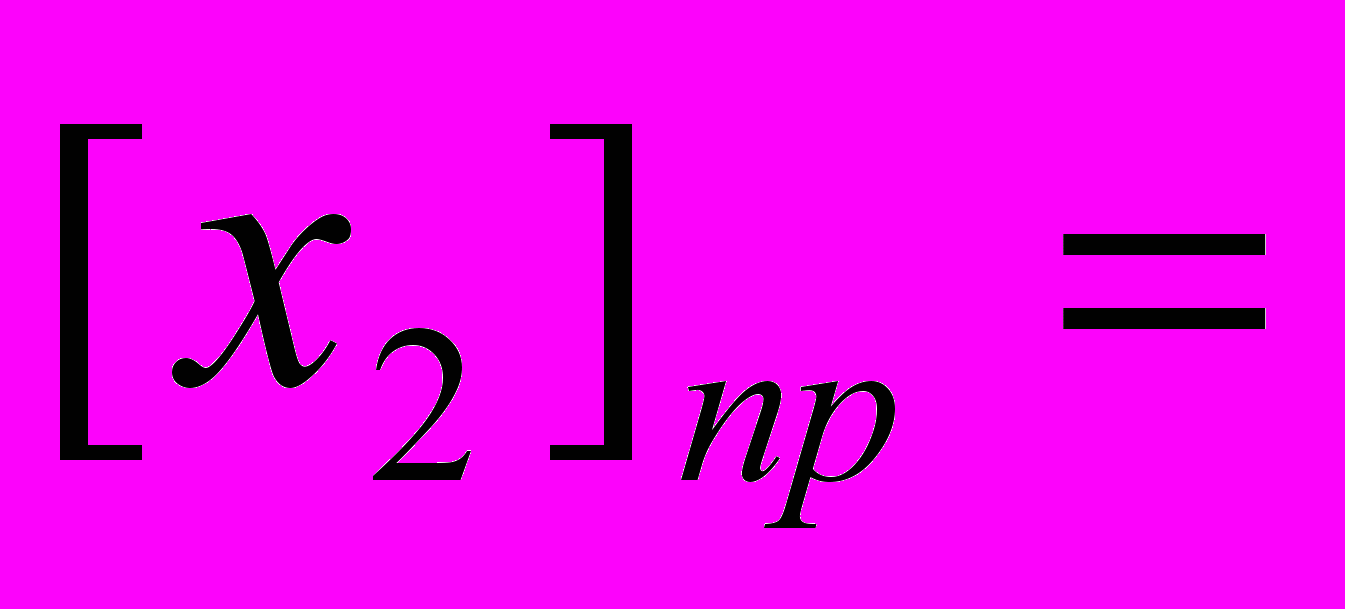 1.011 1.011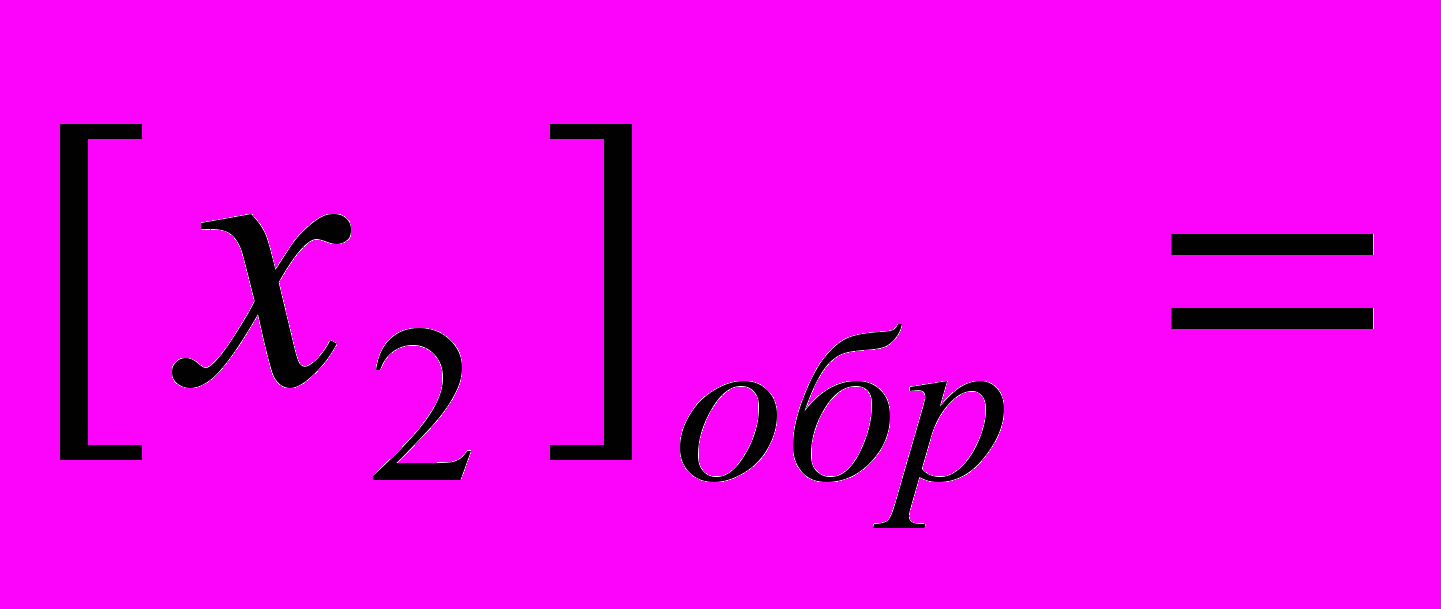 1.100 1.100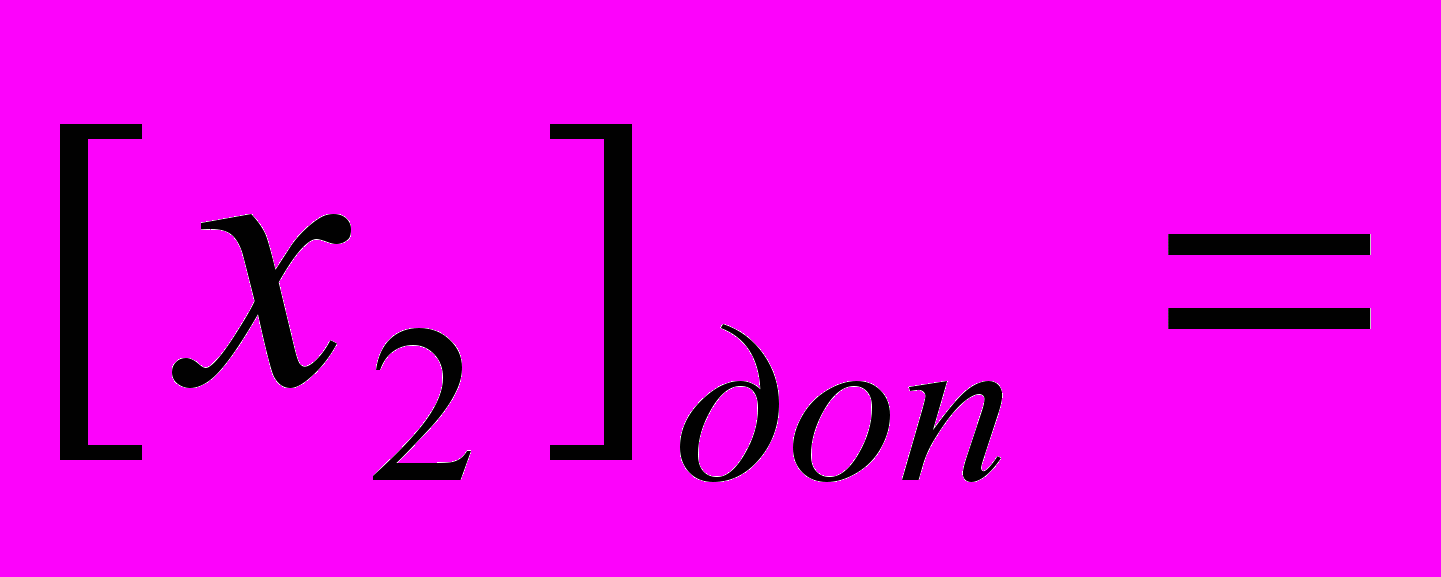 1.101 1.101 |
| 3) | 0.111 + 1.101 = 10.100 | |
| 4) | х= 1002=410 | |
Пример 3.
Вычислить, используя дополнительные коды 810-1310
| 1) | х= 810=10002 | х= -1310= -11012 |
| 2) | 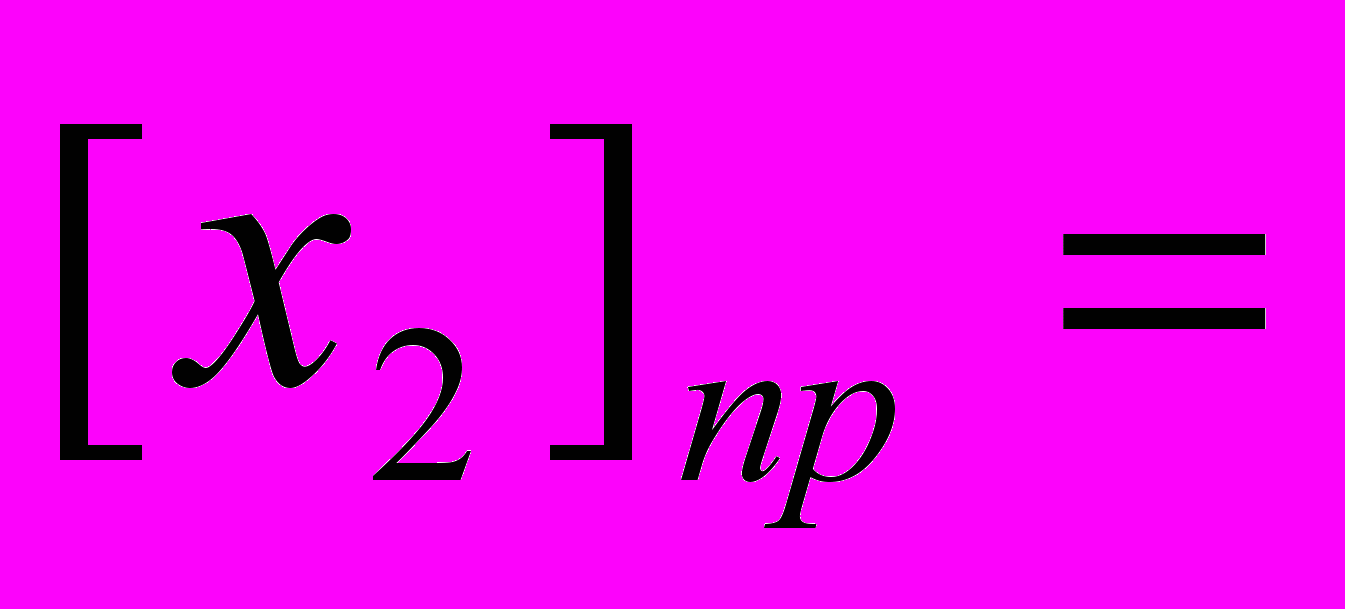 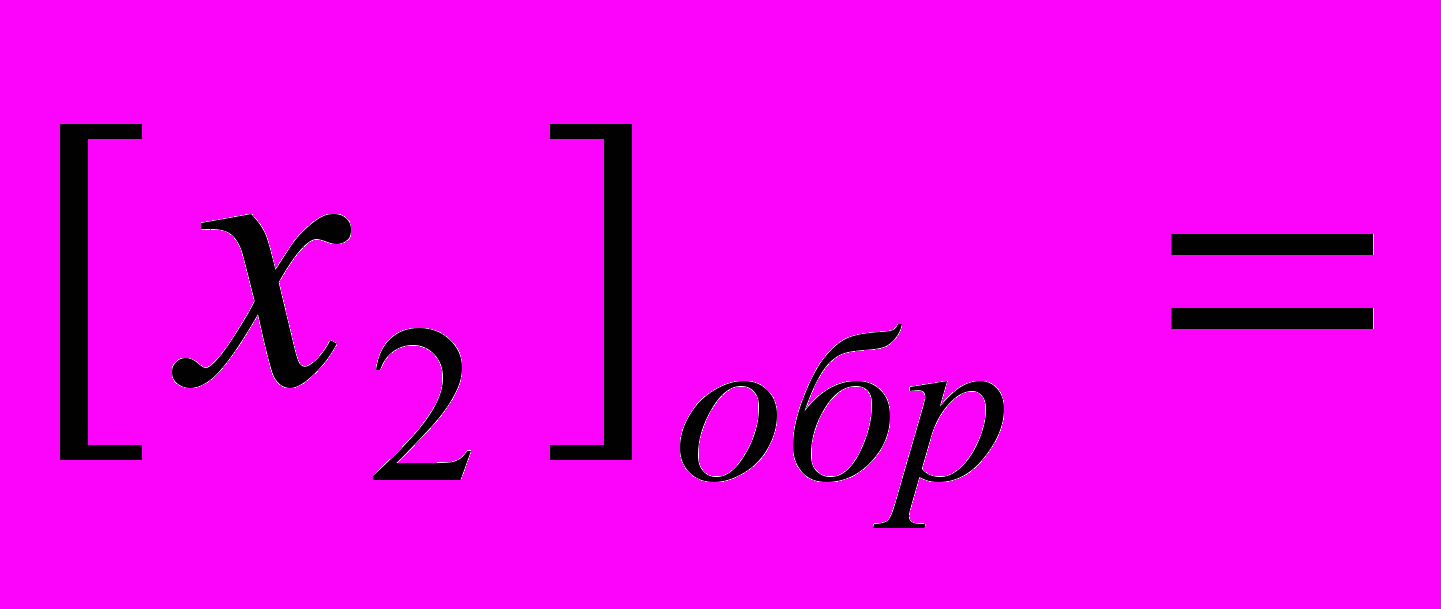 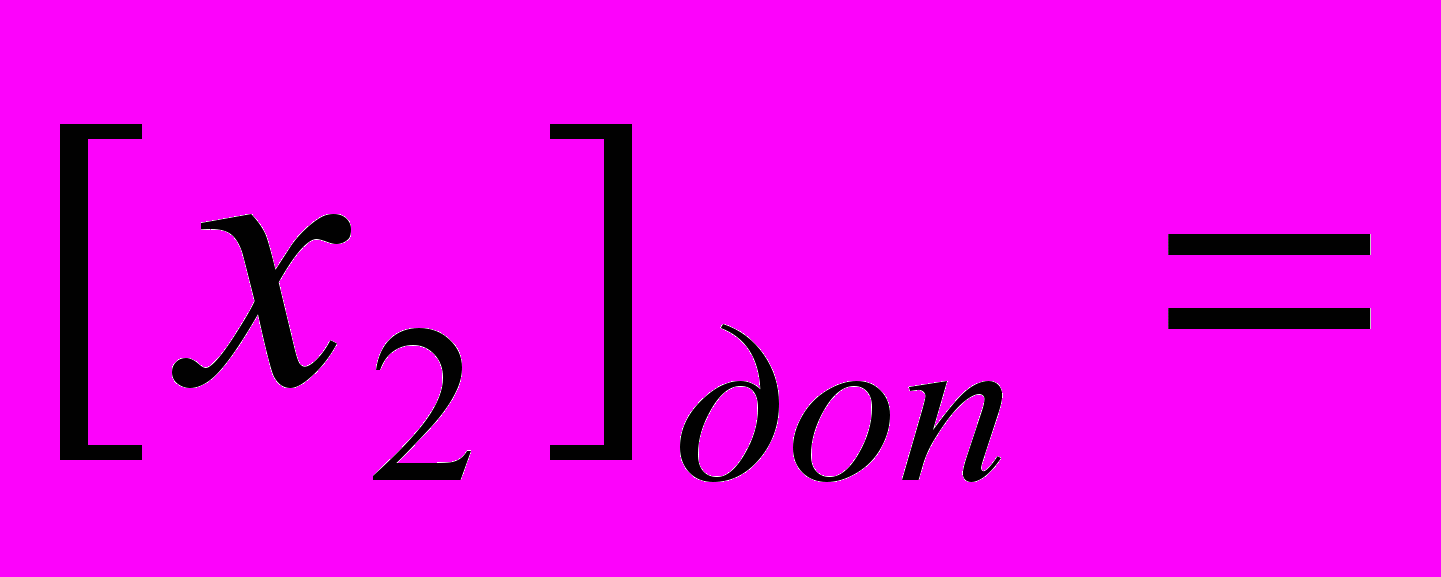 0.1000 0.1000 | 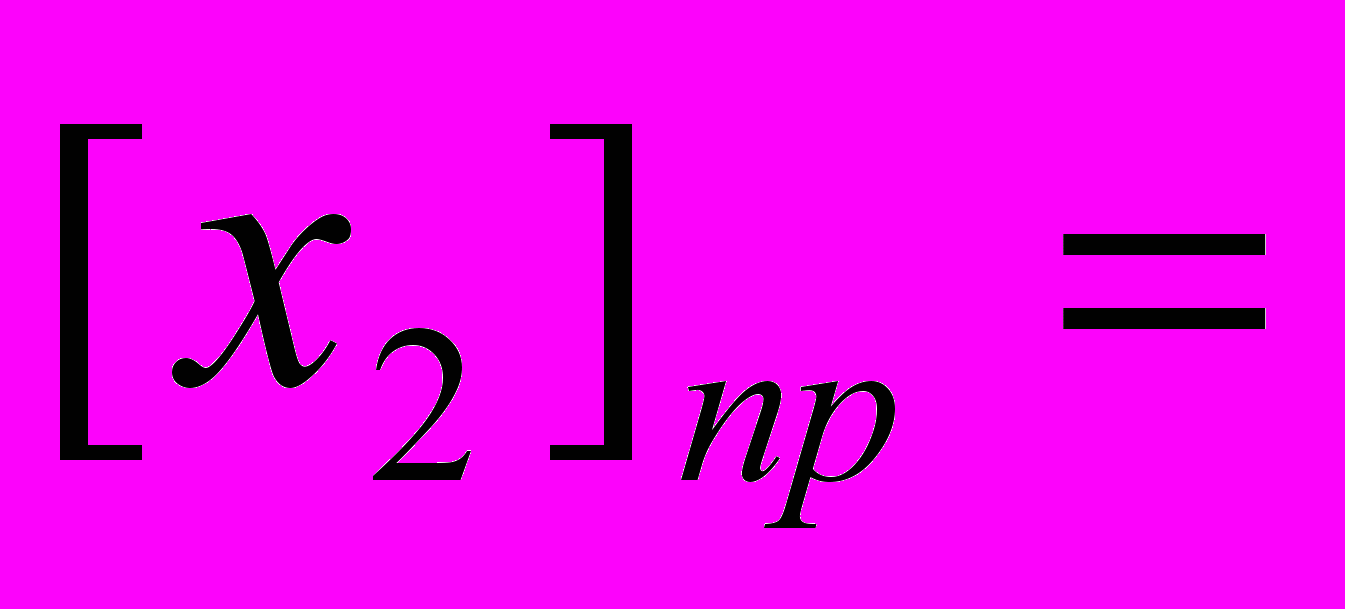 1.1101 1.1101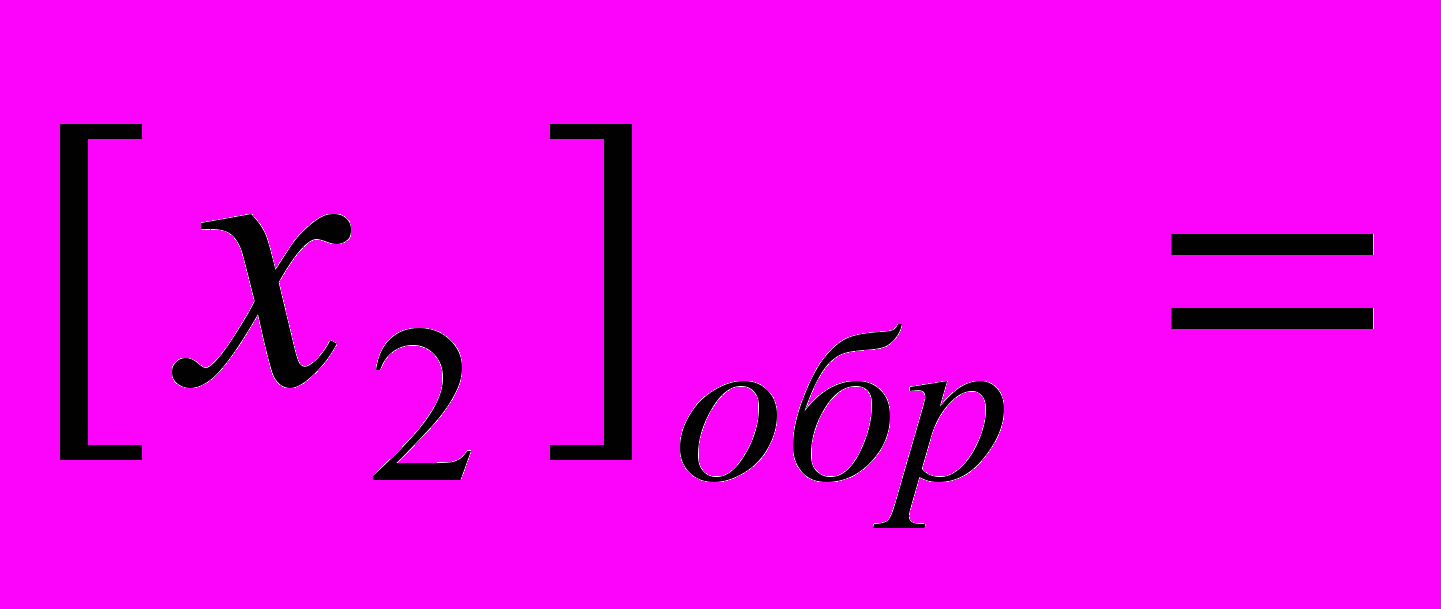 1.0010 1.0010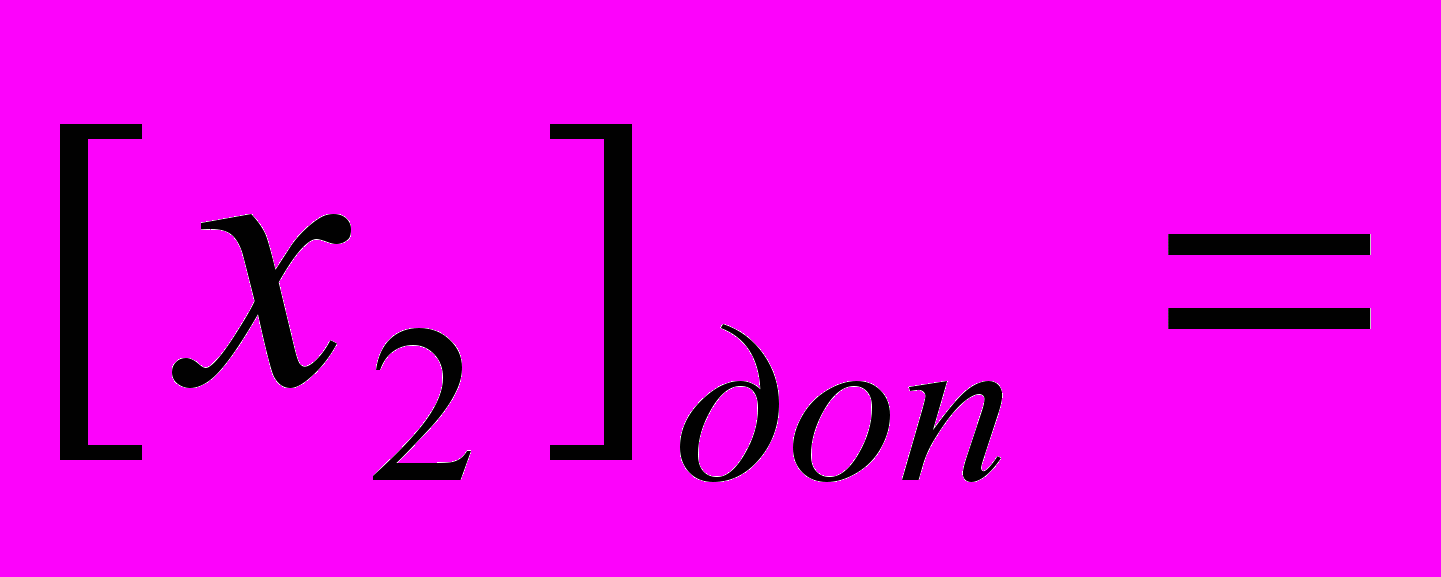 1.0011 1.0011 |
| 3) | 0.1000 + 1.0011 = 1.1011 В знаковом разряде стоит 1, следовательно, результат получен в дополнительном коде. | |
| 4) | 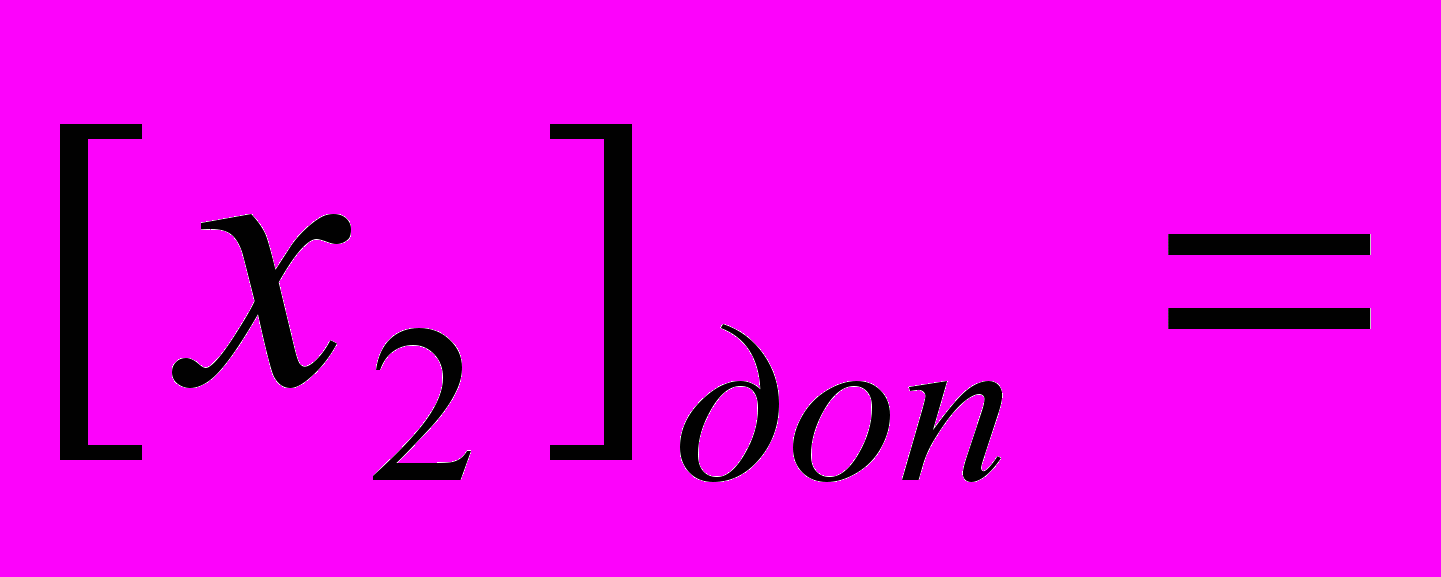 1.1011 1.1011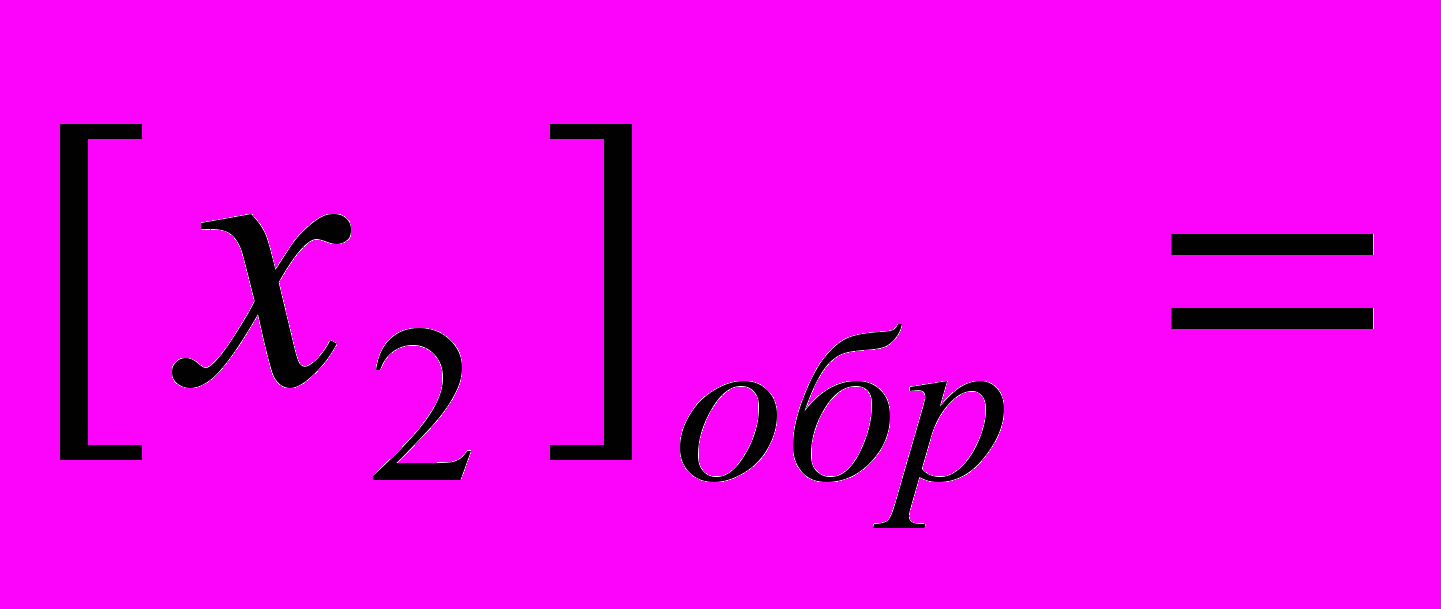 1.1011-1=1.1010 1.1011-1=1.1010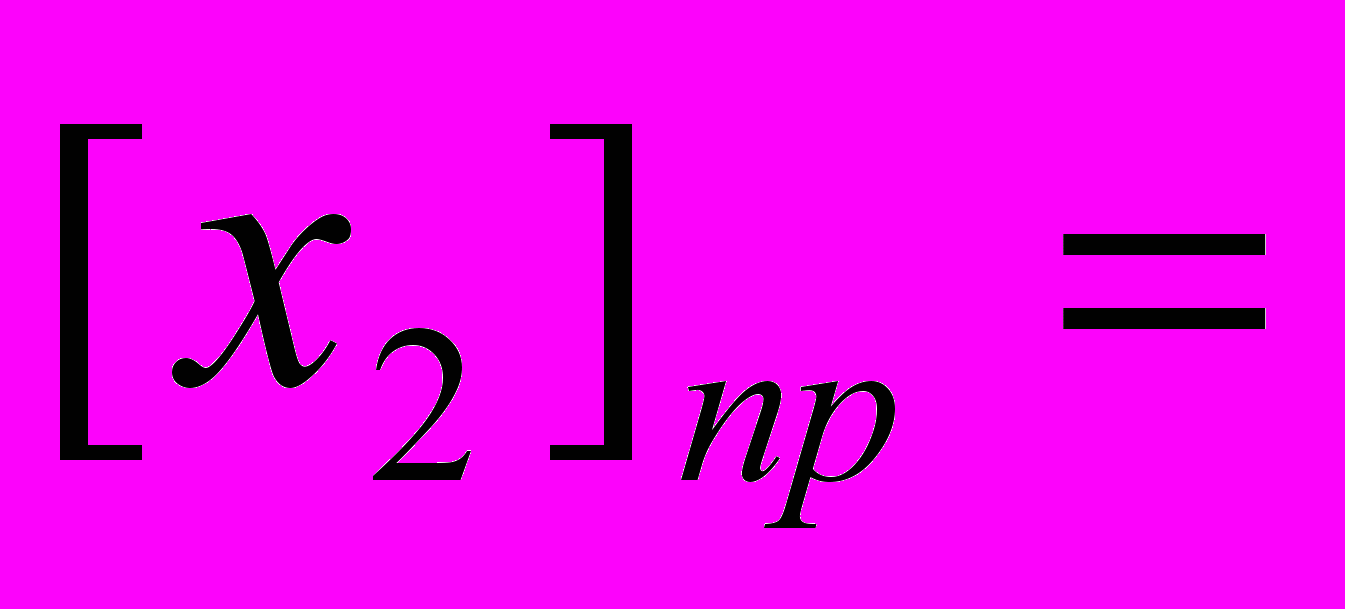 1.0101 1.0101В знаковом разряде стоит 1, следовательно, число отрицательное | |
| 5) | х= 1.01012= -510 | |
