1 семестр Информатика, ее предмет и задачи. Основные понятия информатики. Информация и формы ее представления
| Вид материала | Документы |
- 1. Основные понятия информатики. Определение понятия информатика. Предмет и задачи, 745.21kb.
- 1. Основные понятия информатики 2 Тема Предмет информатики, 1612.33kb.
- Вопросы к зачету по курсу лекций "Информатика" для студентов Iкурса кафедры аэту iсеместр., 18.81kb.
- Тематический план по дисциплине «Информатика и математика» для студентов 2 курса (набор, 46.52kb.
- Информация и информационные процессы, 276.11kb.
- Задачи и проблемы информатики 9 Инемного философии… 9 Использованная литература, 196.06kb.
- Защита данных комплекс мер, направленных на предотвращение потерь, воспроизведения, 85.23kb.
- Программа к вступительного экзамена в магистратуру по специальности 6М060200 Информатика, 50.03kb.
- Темы рефератов по истории информатики Шилов И. В. Эволюция понятия «информация», 19.62kb.
- Темы лекций. Неделя I: Предмет, объект, методы корпоративного управления. Основные, 54.05kb.
4. Качество информации
Качество информации – это характеристика информации, которая отражает степень ее полезности для пользователя.
Показатель качества – это одно из важнейших положительных свойств информации с точки зрения пользователя. Показатели качества являются количественными характеристиками положительных свойств информации.
Свойства информации
| № п/п | Ситуация, с которой сталкивается потребитель | Свойство |
| 1 | Часть информации соответствует запросу потребителя (релевантная), а часть нет (не релевантная). | Релевантность – способность информации соответствовать запросам пользователя |
| 2 | Информация релевантная, но ее недостаточно. | Полнота- свойство информации исчерпывающе для данного потребителя характеризовать отображаемый объект или процесс |
| 3 | Полученная информация может быть устаревшей, т. е. несвоевременной. | Своевременность – способность информации соответствовать нуждам потребителя в нужный момент времени. |
| 4 | Часть информации может содержать ошибки, т. е. недостоверна. Если пользователь обнаружил ошибки, то он будет считать эту информацию нерелевантной, т. е. ошибки должны быть скрытые. | Достоверность – свойство информации не иметь скрытых ошибок |
| 5 | Информация недоступна | Доступность – свойство информации, характеризующее ее возможность ее получения данным потребителем. |
| 6 | Информация подвержена нежелательному использованию и изменению со стороны других потребителей | Защищенность – свойство, характеризующее невозможность несанкционированного использования или изменения |
| 7 | Информация имеет неудобную форму или объем | Эргономичность - свойство, характеризующее удобство формы или объема информации с точки зрения данного потребителя |
Перечисленные свойства информации являются внешними, т. е. они характеризуют поведение информации при взаимодействии с другими объектами (пользователями). Кроме внешних, существуют внутренние свойства, которые органически присущи объекту и проявляют себя косвенным образом при взаимодействии данного объекта с другими. К таким свойствам относятся:
- количество (объем);
- структура, т. е. внутренняя организация информации.
По способу внутренней организации информацию делят на :
- Данные – простой логически неупорядоченный набор сведений;
- Логически упорядоченные структуры данных.
Упорядоченность достигается наложением на данные некоторой структуры, в результате чего получается структура данных.
5. Системы счисления
Система счисления (СС)– это совокупность приемов наименования и записи чисел. В любой СС для представления чисел используются некоторые числа, которые называются базисными числами, а все остальные числа получают в результате каких-либо операций над базисными числами. В современном мире наиболее распространено представление чисел 0. . .9.
СС различаются выбором базисных чисел и правилами образования из них остальных чисел. Например, в римской СС базисными являются: I (1),V(5), X (10), L (50), C(100), D (500), M (1000), а другие получаются путем сложения и вычитания базисных чисел. В римской СС каждый числовой знак имеет одно и тоже значение, т. е. значение числового знака не зависит от его расположения в записи числа: 146 – CXLVI.
Такая СС является непозиционной. В ней удобно записывать небольшие числа. Но выполнять операции над большими числами неудобно.
5.1. Позиционные системы счисления
В настоящее время для представления чисел используются позиционные СС. СС называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Количество цифр, используемых для изображения чисел в позиционной СС, называется ее основанием, т. е. если используется К цифр, то основание СС равно К. Число в позиционной СС можно представить следующим образом:
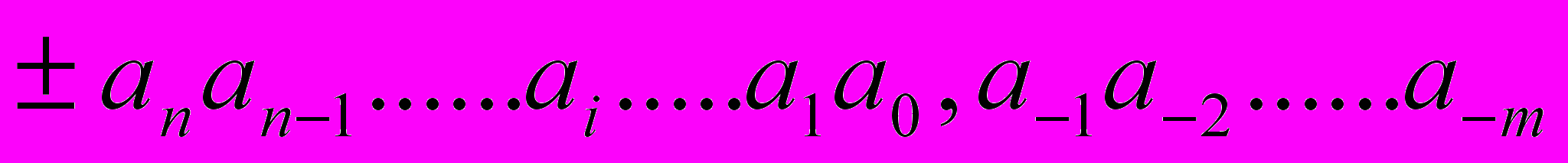

Позиции перенумерованные таким образом называют разрядами. Каждая из цифр принимает одно из значений
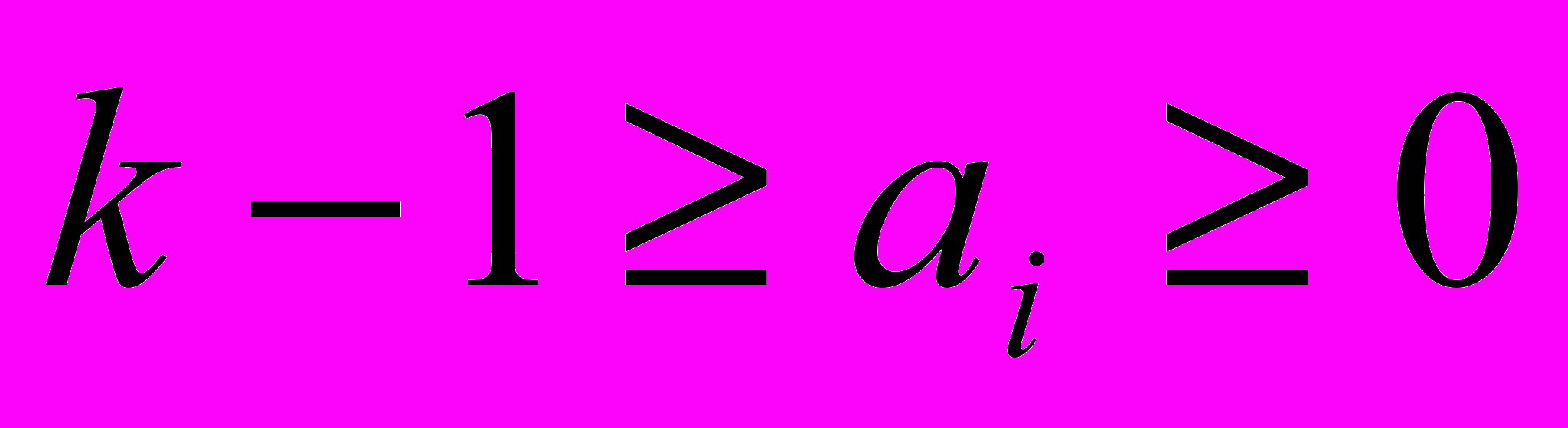 . K используется для количественной оценки каждого разряда числа. Т. е. число в k-ичной СС можно представить в виде полинома:
. K используется для количественной оценки каждого разряда числа. Т. е. число в k-ичной СС можно представить в виде полинома: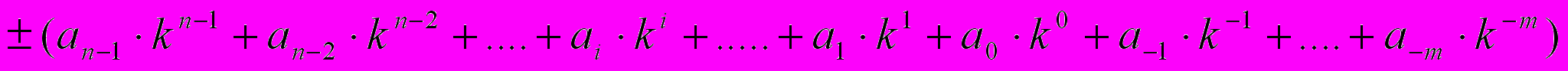
Примеры позиционных систем счисления:
- Десятичная СС. Используются цифры 0. . 9, тогда любое число может быть представлено как

Цифры 0. .9 называют базисными.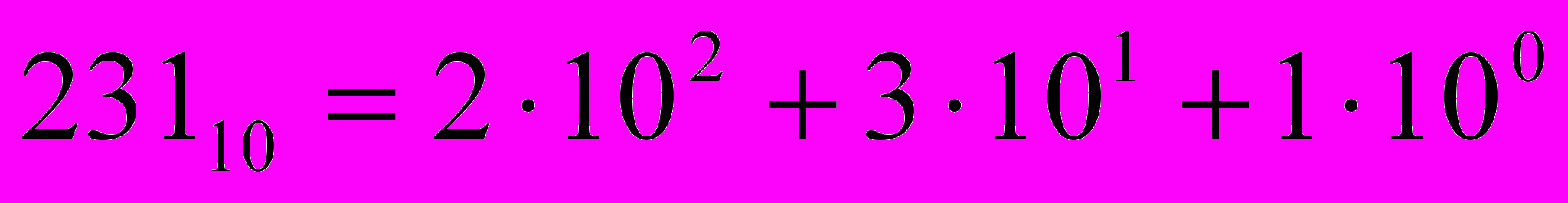
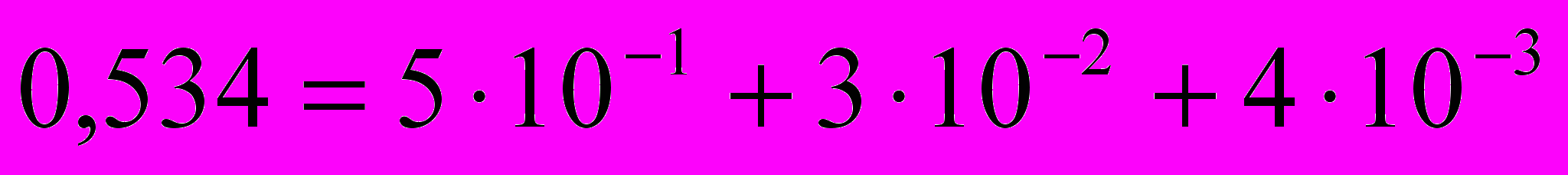
- Двоичная СС. Используются цифры 0 и1. Число в двоичной СС может быть представлено как
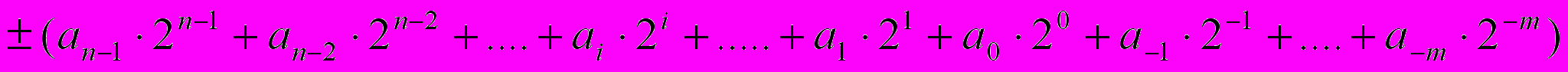

- Восьмеричная СС, в качестве базисных чисел используются цифры 0..7. Число представляется как
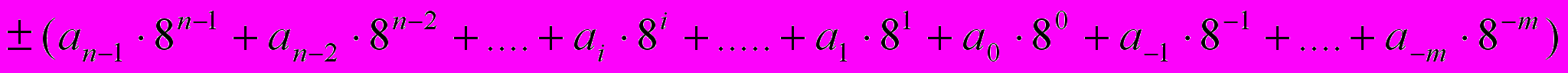

- Шестнадцатеричная СС, в качестве базисных чисел используются цифры 0..9, А, B,C, D, E, F . Число представляется как
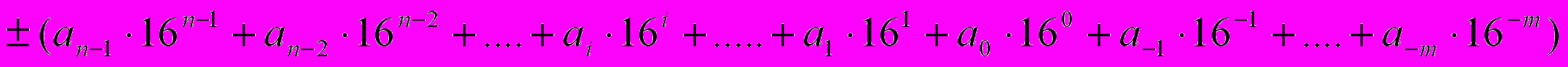
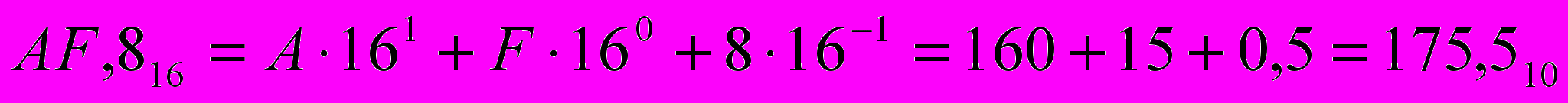
Арифметические действия в любой позиционной СС производятся по тем же правилам, что и в десятичной СС, т. к. все они основываются на правилах выполнения действий с соответствующими полиномами. При этом используются таблицы сложения и умножения, которые имеют место при данном основании СС.
Таблицы сложения и умножения в двоичной СС имеют вид:
| 0+0=0 | 0*0=0 |
| 0+1=1 | 0*1=0 |
| 1+0=1 | 1*0=0 |
| 1+1=10 | 1*1=1 |
Для физического представления чисел необходимы элементы, которые способны находиться в одном из нескольких устойчивых состояний. Число этих состояний должно быть равно основанию принятой СС, тогда каждое состояние будет представлять соответствующую цифру из алфавита данной СС. Для реализации десятичной системы СС потребуются элементы, имеющие 10 устойчивых состояний. Наиболее простыми с точки зрения технической реализации являются двухпозиционные элементы, способные находиться в одном из двух устойчивых состояний, например, электромагнитное реле (состояния «замкнуто»-«разомкнуто»), ферромагнитная поверхность (намагничена – размагничена), транзисторный ключ и т. д. Одно из этих состояний можно обозначить цифрой –0, а другое – 1.
С двоичной СС связаны и другие преимущества. Она обеспечивает максимальную помехоустойчивость в процессе передачи информации. В ней предельно просто выполняются арифметические и логические операции. Благодаря этому двоичная СС стала стандартом в современной вычислительной технике.
Недостатком двоичной СС является большое число разрядов двоичного кода.
5.2. Перевод чисел из одной СС в другую
При решении задач с помощью вычислительной техники исходные данные, как правило, задаются в десятичной СС, в этой же СС представляются и результаты, сами же операции выполняются в двоичной СС. Т. к. данные кодируются в двоичной СС, то возникает необходимость перевода чисел из десятичной СС в двоичную и наоборот.
Правило перевода из двоичной СС в десятичную можно сформулировать следующим образом: все цифры числа и основание СС заменяются их десятичными эквивалентами; число представляется в виде суммы произведений степеней на значения соответствующих позиций; затем производится арифметический подсчет.
Пример:
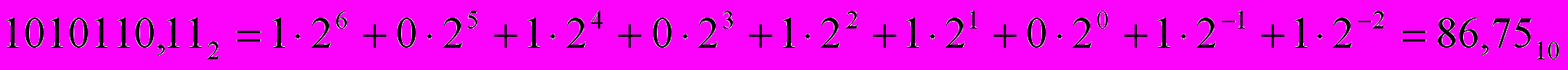
Правила перевода чисел из десятичную в двоичную различны для целой и дробной частей числа.
Для перевода целого числа (или целой части смешанного числа) используется алгоритм последовательного деления исходного числа на основание новой СС (т. е. на 2), действия производятся в старой СС (в десятичной). Деление прекращается, когда очередное частное от деления станет равно 0. Остатки от деления, выписанные в обратном порядке, образуют результат.
Пример:
| 11 | 2 | | | |
| 1  | 5 | 2 | | |
| | 1 | 2 | 2 | |
| | | 0 | 1 | 2 |
| |  | | 1 | 0 |
Таким образом,
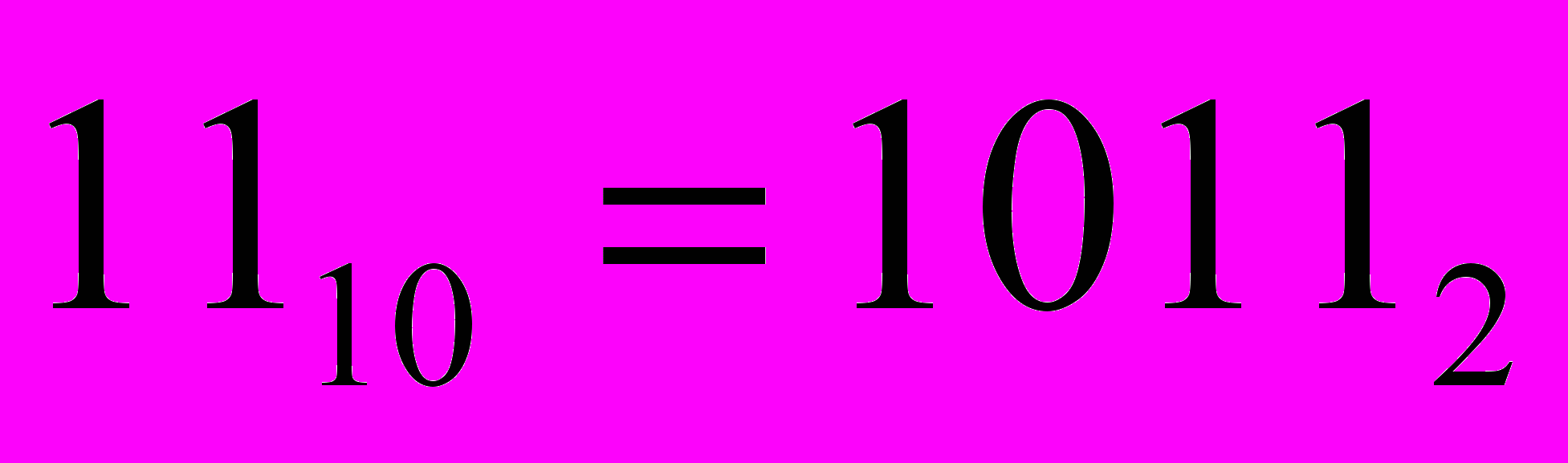
Для перевода дробной части числа используется алгоритм последовательного умножения на основание новой СС (на 2), действия производятся в старой СС (в десятичной), целые части чисел, полученные в результате умножения дают запись результата.
Пример:
| 0 | 875 |
| х | |
| | 2 |
| 1  | 75 |
| х | |
| | 2 |
| 1 | 5 |
| х | |
| | 2 |
| 1 | 0 |
Умножение прекращается, либо когда дробная часть становится равна 0, либо, когда будет получена требуемая точность представления числа.
| 0 | 7 |
| х | |
| | 2 |
| 1  | 4 |
| х | |
| | 2 |
| 0 | 8 |
| х | |
| | 2 |
| 1 | 6 |
. . . .
Аналогично переводятся позиционные числа и с другими основаниями СС.
5.3. Смешанные СС
В смешанных СС каждая цифра в СС с основанием Р записывается в виде цифры с основанием Q, (Q
Пример:
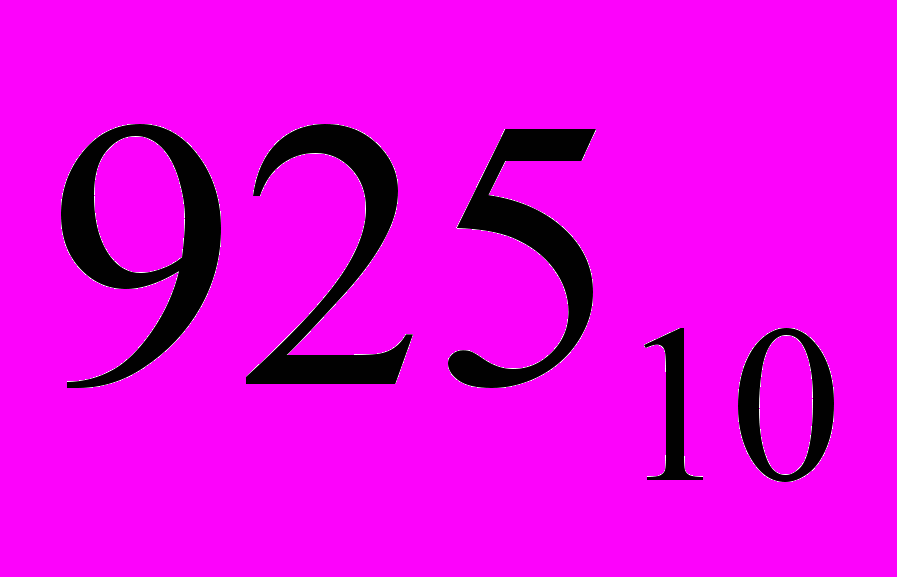 | = | 1001 | 0010 |  | (двоично-десятичная СС) |
| | | 9 | 2 | 5 | |
Аналогично рассмотренной двоично-десятичной СС можно использовать и другие смешанные СС при различных значениях P и Q (P- старшее основание СС, Q – младшее).
Отдельно рассматривается случай, когда
 , где l – целое положительное число. В этом случае запись числа в смешанной СС совпадает с изображением этого числа в СС с основанием Q. Например,
, где l – целое положительное число. В этом случае запись числа в смешанной СС совпадает с изображением этого числа в СС с основанием Q. Например, 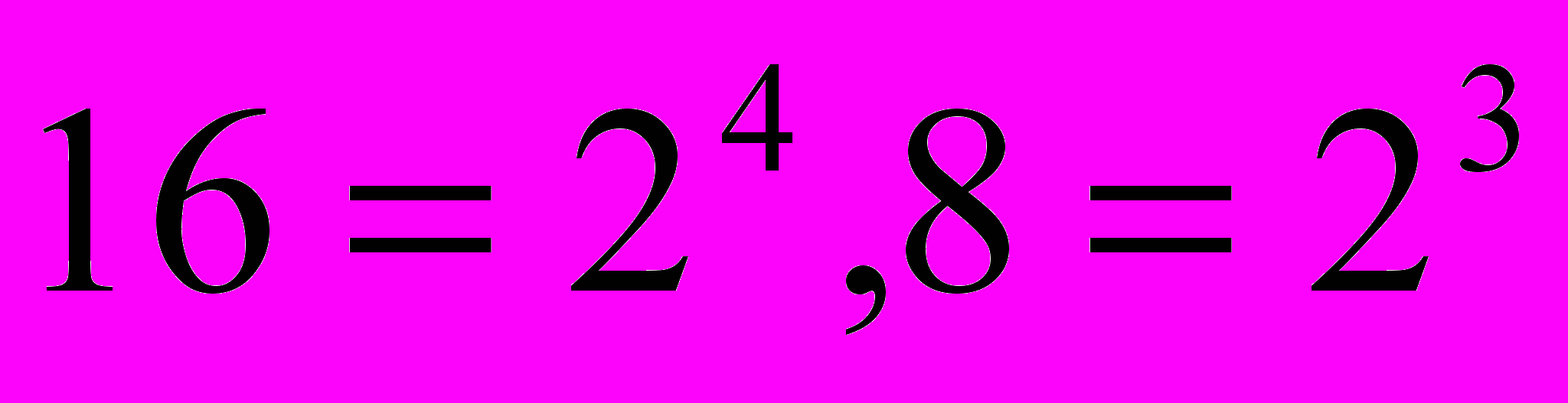 , т. е. запись шестнадцатеричного числа в смешанной двоично-шестнадцатеричной СС будет тождественна его записи в двоичной СС. Это свойство широко используется на практике для сокращенной записи чисел заданных в СС с небольшим основанием.
, т. е. запись шестнадцатеричного числа в смешанной двоично-шестнадцатеричной СС будет тождественна его записи в двоичной СС. Это свойство широко используется на практике для сокращенной записи чисел заданных в СС с небольшим основанием.Преобразование чисел из двоичной системы в восьмеричную и шестнадцатеричную
Для представления цифры в 16-чной СС понадобится 4 цифры двоичной СС, для представления цифры в 8-ной СС понадобится 3 цифры двоичной СС. Для перевода 8-чного числа в 2-чную СС надо заменить каждую цифру этого числа ее двоичным эквивалентом. Аналогично переводятся числа из 16-ой СС в двоичную.
Аналогично выполняются обратные преобразования
Таблица эквивалентов
| Десятичная, Восьмеричная (23), Шестнадцатеричная (24), | Двоичная |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 (A) | 1010 |
| 11 (B) | 1011 |
| 12 (C) | 1100 |
| 13 (D) | 1101 |
| 14 (E) | 1110 |
| 15 (F) | 1111 |
Примеры.
| 10 | 2->8 | 8 | 2->16 | 16 |
| 46,5 | 101 110,1 | 56,4 | 0010 0111,1000 | 2Е,8 |
| 21,5 | 010 101,1 | 25,4 | 0001 0101,1000 | 15,8 |
Аналогично можно выполнять преобразования чисел и для СС с основаниями 3 и 9, Они также связаны соотношением
 (9=32 )
(9=32 )| Десятичная, девятеричная | Троичная |
| 0 | 00 |
| 1 | 01 |
| 2 | 02 |
| 3 | 10 |
| 4 | 11 |
| 5 | 12 |
| 6 | 20 |
| 7 | 21 |
| 8 | 22 |
Для представления цифры в 9-ной СС понадобится 2 цифры троичной СС. Для перевода 9-чного числа в 3-чную СС надо заменить каждую цифру этого числа ее троичным эквивалентом.
Пример
| 9 | 3 |
| 345,3 | 10 11 12,10 |
