Исследование возможностей повышения частотной эффективности линий связи за счет использования сигналов с взаимной интерференцией символов

Вид материала

Содержание

Общая характеристика работы
2 статьи в журналах, входящих в перечень ВАК
Краткое содержание работы

Подобный материал:

^{На правах рукописи}

^{Мордвинов Александр Евгеньевич}

Исследование возможностей повышения частотной эффективности линий связи за счет использования сигналов с взаимной интерференцией символов

^{Специальность 05.12.04}

^{Радиотехника, в том числе системы и устройства телевидения}

^{АВТОРЕФЕРАТ}

^{диссертации на соискание ученой степени}

^{кандидата технических наук}

^{Москва 2008}

^{Работа выполнена на кафедре формирования колебаний и сигналов}

^{Московского энергетического института (технического университета).}

^{Научный руководитель: доктор технических наук, профессор}

^{Кулешов Валентин Николаевич}

^{Официальные оппоненты: доктор технических наук, профессор}

^{Немировский Михаил Семенович}

^{кандидат технических наук, доцент}

^{Борисов Виктор Алексеевич}

^{Ведущая организация: ФГУП «НИИ Космического приборостроения»}

^{Защита состоится “27” ноября 2008 г. в 15.30 на заседании диссертационного совета Д 212.157.05 при Московском энергетическом институте (техническом университет) по адресу: 111250, Москва, Красноказарменная ул., д. 17, аудитория А-402.}

^{Отзывы в двух экземплярах, заверенные печатью, просим направлять по адресу: 111250, Москва, Красноказарменная ул., д. 14, Ученый совет МЭИ (ТУ).}

^{С диссертацией можно ознакомиться в библиотеке Московского энергетического института (технического университета).}

^{Автореферат разослан « » октября 2008 г.}

^{Ученый секретарь}

^{диссертационного совета Д 212.157.05}

^{кандидат технических наук, доцент Т.И. Курочкина}

^{ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ}

^{Актуальность работы}

^{Одной из важнейших задач исследователей и инженеров в течение всей истории радиотехники и создания систем электрической связи была и остаётся задача поиска путей предельно возможного сокращения полосы частот в среде передачи сигналов и снижения мощности передающих устройств, при которой обеспечиваются необходимые скорость и верность передачи информации.}

^{Начиная с фундаментальных работ В.А.Котельникова и К.Шеннона, решением этой задачи занималось несколько поколений учёных и инженеров. Переход на цифровые методы передачи информации дает большое количество технических и эксплуатационных преимуществ по сравнению с аналоговой техникой, однако требует значительного расширения полосы частот, занимаемой в канале связи. В настоящее время выход находят в обработке передаваемого сообщения с целью сокращения его информационного объема. Хотя даже при полном исключении избыточности в исходном сообщении проблема “тесноты в эфире” остается актуальной. Это относится к космической связи, цифровому телевизионному и радиовещанию, передаче информации с бортов космических аппаратов и т.д.}

^{В различных вариантах задача построения максимально эффективных систем передачи информации рассматривалась и решалась в работах как отечественных учёных (А.А.Харкевич, В.И.Сифоров, Л.М.Финк, Л.С.Гуткин, В.И.Тихонов, П.И.Пенин, Л.И.Филиппов, Д.Д.Кловский, А.В.Михайлов, Д.Л.Коробков, Б.И.Николаев, В.И.Борисов, Ю.С.Шинаков, М.С.Немировский, В.Л.Банкет, В.М.Дорофеев и др.), так и зарубежных (А.Д.Витерби, Дж.Возенкрафт, И.Джекобс, Дж.Спилкер, Дж.Б.Андерсон, Д.Прокис, Б.Скляр и др.).}

^{В настоящее время в реальных системах связи эффективность передачи информации повышают за счет перехода к многопозиционным сигналам, использования помехоустойчивого кодирования и сокращения защитных частотных интервалов. При этом передача всегда ведется независимыми или не интерферирующими символами. Требование отсутствия интерференции символов в передаваемом сигнале ограничивает длительность тактового интервала следования символов. В то же время, если не требовать отсутствия межсимвольной интерференции, то частотная эффективность передачи информации может быть увеличена за счет уменьшения тактового интервала следования символов.}

^{Однако алгоритмы оптимальной или близкой к ней обработки сигналов в приёмниках при наличии интерференции символов, а, следовательно, и сами приёмники усложняются, причём с увеличением числа интерферирующих символов сложность приёмника увеличивается настолько быстро, что возникает вопрос не только о целесообразности его построения, но и о его практической реализуемости.}

^{При относительно низком уровне развития элементной базы цифровых устройств обработки принимаемых сигналов построение приёмников сигналов с интерферирующими символами, работающих в режиме реального времени, при достаточно больших скоростях передачи, оказывалось нецелесообразным уже при небольшом числе интерферирующих символов. Однако разработка и внедрение элементной базы цифровых устройств новых поколений существенно расширяет возможности реализации сложных алгоритмов обработки сигналов. Поэтому теоретический анализ возможностей повышения частотной эффективности передачи информации за счёт уменьшения тактового интервала и извлечения информации из потока интерферирующих символов приобретает практический интерес.}

^{Оценка возможности и практическая реализация возможного выигрыша в скорости передачи информации в жёстко ограниченной полосе частот особенно актуальны для спутниковых систем передачи информации, хотя и в других каналах связи они могут представлять значительный интерес.}

^{Цель работы.}^{Целью диссертации является исследование возможности увеличения частотной эффективности передачи информации за счет уменьшения тактового интервала следования символов, и в частности, анализ возможности использования этого способа в спутниковых системах связи.}

^{Для достижения поставленной цели должны быть решены следующие задачи:}

^{Исследование потенциальной помехоустойчивости передачи информации при интерференции символов, которая возникает из-за уменьшения тактового интервала следования символов, благодаря чему увеличивается скорость передачи информации.}
^{Исследование помехоустойчивости и сложности практически реализуемых подоптимальных алгоритмов приема сигналов с интерференцией символов.}
^{Исследование влияния на помехоустойчивость передачи информации линейных искажений, вносимых в передаваемый сигнал в трактах передатчика и приемника.}
^{Исследование влияния на помехоустойчивость передачи информации погрешностей в работе служебных систем приемника, таких как система символьной синхронизации и система синхронизации по несущему колебанию.}

^{Методы исследования.}^{В диссертационной работе используются: методы временного и спектрального анализа, теория радиотехнических цепей и сигналов, статистическая радиотехника, теория вероятностей и методы компьютерного имитационного моделирования.}

^{Научная новизна}^{диссертационной работы состоит в научном обосновании возможности увеличения частотной эффективности системы связи за счет уменьшения тактового интервала следования символов и в оценке достоинств и ограничений этого способа увеличения частотной эффективности.}

^{Конкретные новые научные результаты:}

^{Получены оценки потенциальной помехоустойчивости передачи данных с уменьшенным тактовым интервалом следования символов при использовании сигналов, спектры которых удовлетворяют определённым требованиям к электромагнитной совместимости.}
^{Установлена существенная зависимость потенциальной помехоустойчивости передачи данных с уменьшенным тактовым интервалом следования символов от требований к компактности спектральной плотности мощности передаваемого сигнала и уровню внеполосных излучений.}
^{Установлена существенная зависимость сложности оптимального приемника от выигрыша в частотной эффективности передачи данных и требований к спектральной плотности мощности.}
^{Исследованы структуры и свойства подоптимальных алгоритмов приема сигналов с интерференцией символов в системе передачи информации с уменьшенным тактовым интервалом следования символов и найдены условия близости эффективности их работы к эффективности оптимальных алгоритмов.}
^{Получены оценки влияния погрешностей работы систем фазовой и тактовой синхронизации приёмного устройства, а также линейных искажений, вносимых трактами передачи и приёма, на помехоустойчивость подоптимальных демодуляторов.}

^{Практическая ценность.}^{Создан комплекс компьютерных программ для оценки потенциальной помехоустойчивости передачи информации при интерференции символов, которая возникает при уменьшении тактового интервала следования символов, и для моделирования работы такой системы передачи информации. Разработаны программные реализации двух подоптимальных алгоритмов приема сигналов с интерференцией символов, на основе которых реализуется цифровая часть приёмника в такой системе передачи информации.}

^{Использование результатов работы.}^{Результаты работы были использованы при выполнении НИР на предприятии ФГУП ОКБ МЭИ в отделе ИТИС (Информационные Технологии и Связь).}

^{Апробация результатов работы.}Основные результаты работы были обсуждены на научно-технических конференциях и семинарах: на международных научно-технических конференциях студентов и аспирантов МЭИ 2006, 2007, 2008 гг.; на научной сессии РНТОРЭС им А. С. Попова 2008 г.; на научно-техническом семинаре РНТОРЭС им А. С. Попова «Системы синхронизации, формирования и обработки сигналов для связи и вещания» (г. Ярославль, 2008 г).

^{Публикации.}По теме диссертации опубликовано 8 печатных работ, из них 2 статьи в журналах, входящих в перечень ВАК, 3 тезисов докладов, 3 статьи в трудах семинаров и научных сессий.

^{Положения, выносимые на защиту.}

^{Теоретически обоснована возможность увеличения частотной эффективности системы связи за счет уменьшения тактового интервала следования символьных импульсов при заданной их форме, основанная на реализации оптимального приёма сигнала «в целом» с использованием алгоритма Витерби.}
^{Выявлена зависимость потенциальной помехоустойчивости передачи данных с уменьшенным тактовым интервалом следования символов от требований к компактности спектральной плотности мощности и уровню внеполосных излучений.}
^{Проанализирована зависимость сложности оптимального приемника от выигрыша в частотной эффективности передачи данных и требований к компактности спектральной плотности мощности передаваемого сигнала.}
^{Проведено сравнение рассматриваемого способа увеличения частотной эффективности передачи информации в системе связи со способом, основанным на переходе к многопозиционным сигналам, и показано что в ряде случаев рассматриваемый способ имеет ряд преимуществ.}
^{Проанализированы подоптимальные алгоритмы приема сигналов с интерференцией символов и найдены условия их близости к оптимальным алгоритмам.}
^{Проведён анализ влияния погрешностей в работе служебных систем приемника, таких как система символьной синхронизации и система синхронизации по несущему колебанию, а также влияния малых частотных искажений в тракте передачи на работу системы с рассматриваемым способом повышения частотной эффективности передачи информации.}

^{Объем и структура работы.}^{Диссертация состоит из введения, 4 глав, заключения, списка литературы, включающего 69 наименований и 3 приложений. Содержание работы изложено на 140 листах машинописного текста. Основное содержание работы включает 53 рисунка и 3 таблицы.}

^{КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ}

^{Во введении}^{обоснована актуальность темы, сформулирована цель и определены задачи диссертации, показаны научная новизна и практическая значимость работы.}

^{В первой главе}^{рассматривается модель системы передачи информации, определенны допущения, при которых будет проводиться ее анализ, определена модель канала связи, выполнен аналитический обзор публикаций, посвящённых решению задач повышения частотной эффективности передачи информации в цифровых каналах связи.}

^{Основными параметрами системы передачи информации являются ее частотная и энергетическая эффективность. Частотная эффективность определяется как отношение скорости передачи информации}^R^{к полосе частот занимаемой сигналом}^F₀^{. Энергетическая эффективность определяется отношением сигнал/шум на бит, требуемым для достижения заданной вероятности ошибки. Эти параметры зависят от вида модуляции, характеристик кода, типа канала связи и тех искажений, которые вносятся в сигнал во всем тракте передачи сигнала.}

^{В большинстве существующих систем передачи информации реализуется режим передачи статистически независимыми и не интерферирующими символами. Требование отсутствия интерференции символов в передаваемом сигнале приводит к тому, что минимальный период Т следования символов ограничен снизу величиной 1/(2}^F₀^{) и единственным способом увеличения частотной эффективности системы передачи информации является увеличение позиционности передаваемых символов. Такой способ увеличения частотной эффективности передачи информации хорошо изучен и приводит к одному из частотно эффективных методов модуляции: амплитудная, фазовая, амплитудно-фазовая. Среди этих видов модуляции, наилучшей энергетической эффективностью при заданной частотной эффективности обладает амплитудно-фазовая модуляция и в частности ее реализация с помощью КАМ сигналов. Поэтому все новые результаты, полученные в этой работе, сравниваются именно с этим видом модуляции.}

^{В тоже время, если отказаться от требования отсутствия интерференции символов, то тактовый интервал следования символов Т не будет ограничен снизу. При этом появляется возможность дополнительного увеличения частотной эффективности передачи информации за счет уменьшения тактового интервала следования символов Т.}

^{На целесообразность исследования возможности повышения частотной эффективности передачи информации за счет уменьшения тактового интервала следования символов Т обращал внимание К.А.Победоносцев, однако детально этот вопрос не был исследован в виду возникновения интерференции в большом количестве символов и усложнения алгоритмов демодуляции таких сигналов. В данной работе поставлена задача исследования этого пути повышения частотной эффективности передачи информации за счет уменьшения тактового интервала следования символов Т, поскольку за последние десятилетия характеристики цифровых устройств обработки сигналов вышли на качественно новый уровень и техническая реализация алгоритмов демодуляции таких сигналов стала возможной.}

^{Другая возможность увеличения частотной эффективности передачи информации возникает, если отказаться от статистической независимости передаваемых символов. Такой способ увеличения частотной эффективности передачи информации основан на управлении спектральными характеристиками формируемого сигнала через корреляционные связи в последовательности передаваемых символов. При этом способе из исходной некоррелированной последовательности символов получают последовательность коррелированных символов, которую передают по каналу связи. Последовательность коррелированных символов получают, при помощи дискретного фильтра с импульсной характеристикой конечной длительности.}

^{В ряде работ было показано, что при оптимизации отсчетов импульсной характеристики дискретного фильтра и определенных ограничениях на его амплитудно-частотную характеристику можно увеличить частотную эффективность передачи информации и при этом достичь лучшей помехоустойчивости по сравнению с КАМ сигналами. Основным недостатком данного подхода является то, что спектральная плотность мощности (СПМ) сигналов, формируемых с помощью таких фильтров, не может удовлетворить требованиям, предъявляемым в современных системах цифровой связи. А именно такие сигналы имеют высокую неравномерность СПМ (до 8 дБ), в пределах полосы частот, отведенной для передачи информации, и высокий уровень спектральной плотности мощности (достигающий примерно -25 дБ) вне занимаемой полосы частот.}

^{Во второй главе}^{проведено исследование возможности повышения частотной эффективности системы передачи информации путем уменьшения тактового интервала следования символов при неизменных прочих параметрах.}

^{Рассмотрен канал связи, информация по которому передается в виде последовательности независимых символов {}^a_k^{}, k = 0, 1, …, N – 1, каждый из которых выбирается из конечного числа M возможных значений (алфавита) и модулирует последовательность парциальных импульсов g(t-kT), следующих с тактовым интервалом T. При этих обозначениях передаваемый сигнал s(t) можно представить в виде:}

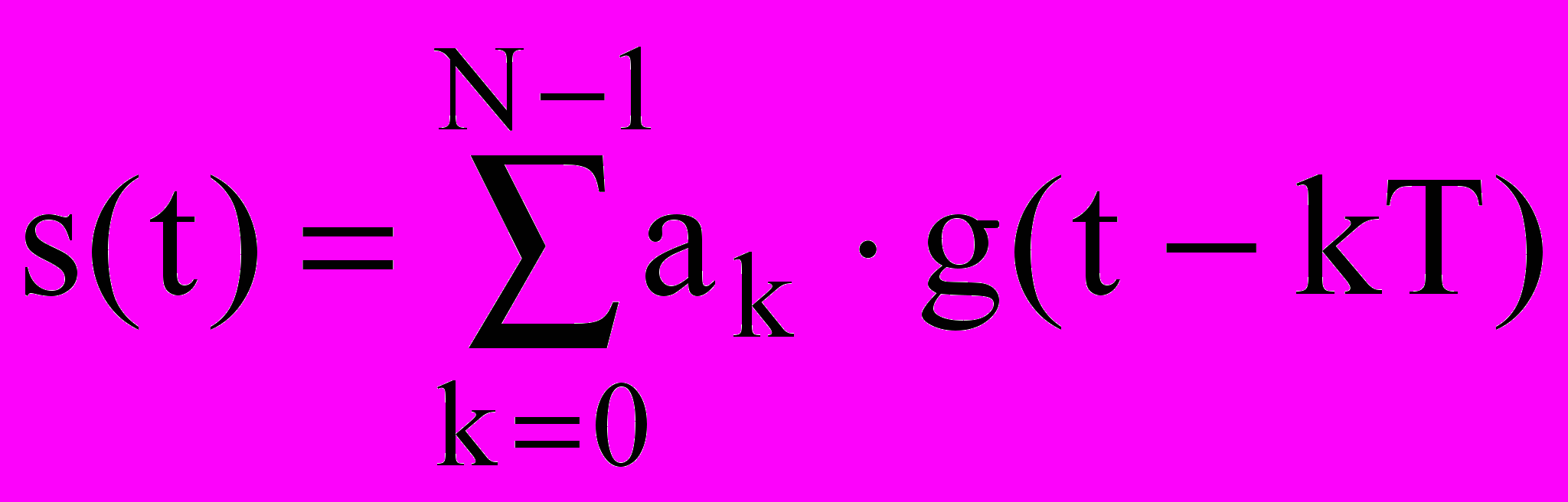^{. (1)}

^{Форма импульса}^g⁽^t^{) выбирается таким образом, чтобы СПМ сигнала}^s⁽^t^{) удовлетворяла заданным ограничениям. В качестве модели канала связи в работе выбран канал с аддитивным белым гауссовским шумом (АБГШ). В этой модели передаваемый сигнал}^s⁽^t^{) подвержен лишь воздействию АБГШ}ⁿ⁽^t^{). При этом принимаемый сигнал}^z⁽^t^{) можно представить в виде}^z⁽^t^{) =}^s⁽^t^{) +}ⁿ⁽^t^).

^{Известно, что оптимальный прием сигналов с интерференцией символов возможен только «в целом», когда принимается весь сигнал и выносится решение о принятой последовательности символов. Если интерференция символов в сигнале распространяется лишь на конечное число символов}^L^{, то наиболее экономичной реализацией приема «в целом» является использование алгоритма Витерби.}

^{При его использовании формируются величины}^z_k^{, которые представляют собой отсчеты свёртки входного сигнала и импульса}^g⁽^t^{) и определяются выражением}

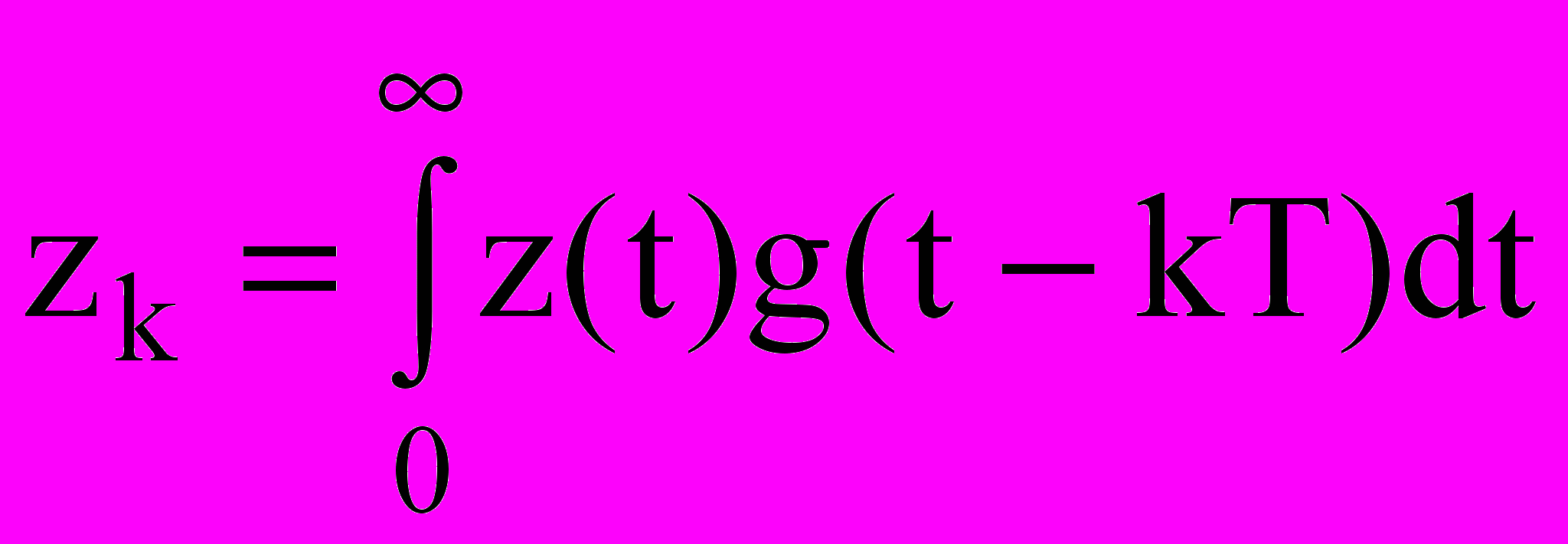^{. (2)}

^{Далее по первым}^L^{отсчетам}^z_k^{итеративно рассчитывается}^M^L^метрик^_n^L^{, соответствующих}^M^L^{возможным последовательностям символов {}^_n_,0^_n_,1^…^_n_,_L_-1^{}. Далее из каждых}^M^{последовательностей, которые имеют одинаковые символы {}^_n_,1^_n_,2^…^_n_,_L_-1^{} и различные символы}^_n_,0^{, приемник сохраняет только ту, которой соответствует меньшее значение метрики}^_n^L^{. Таким образом, “выживает” только}^M^L^-1^{последовательностей. На следующем шаге, при получении отсчета}^z_L^{, каждая выжившая последовательность продолжается одним из}^M^{возможных символов, после чего снова получается}^M^L^{последовательностей. Для каждой из них приемник вычисляет метрики}^_n^L⁺¹^{. И опять, из каждых}^M^{последовательностей, имеющих одинаковые символы {}^_n_,2^_n_,3^…^_n_,_L^{}, приемник оставляет только ту, которой соответствует меньшее значение метрики}^_n^L⁺¹^{. Эта процедура продолжается до тех пор, пока не будет принят весь сигнал. На последнем}^N^{-м шаге приемник из}^M^L^{возможных последовательностей выбирает ту, которой соответствует наименьшее значение метрики}^_n^N^{, и выносит ее в качестве решения. Метрики}^_n^k^{оцениваемых последовательностей вычисляются по формулам:}

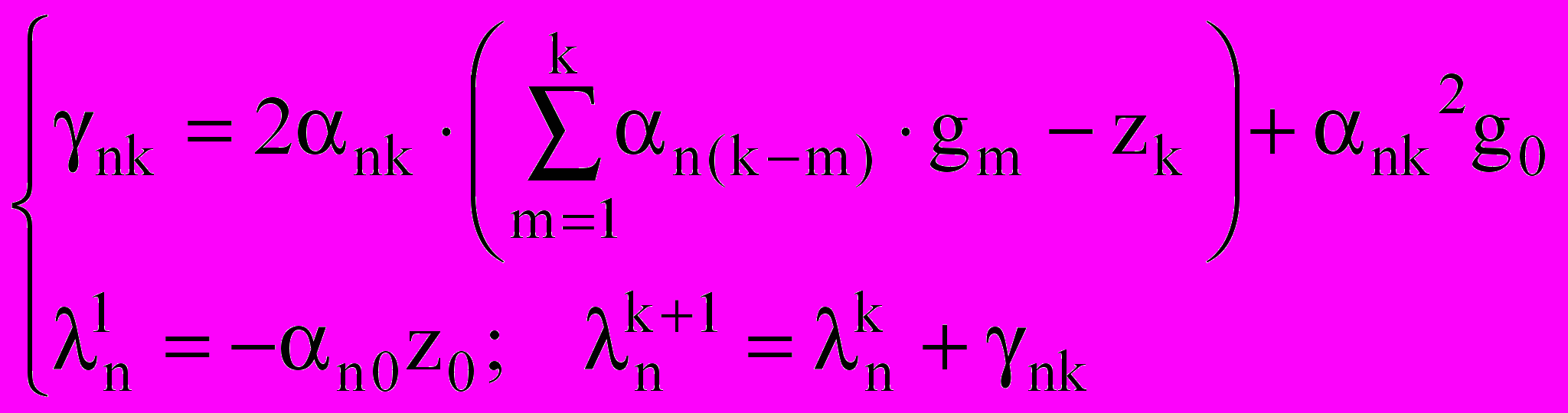
^k^{= 0, …,}^N^-1;ⁿ^{= 0, …,}^M^L-1^{– 1 . (3)}

Сложность приёмника, построенного на основе алгоритма Витерби, определяется числом M^L^-1 последовательностей, которые необходимо удерживать в каждый момент времени.

^{Помехоустойчивость оптимального способа приема сигналов при малых вероятностях ошибки оценивается при помощи приближенной формулы:}

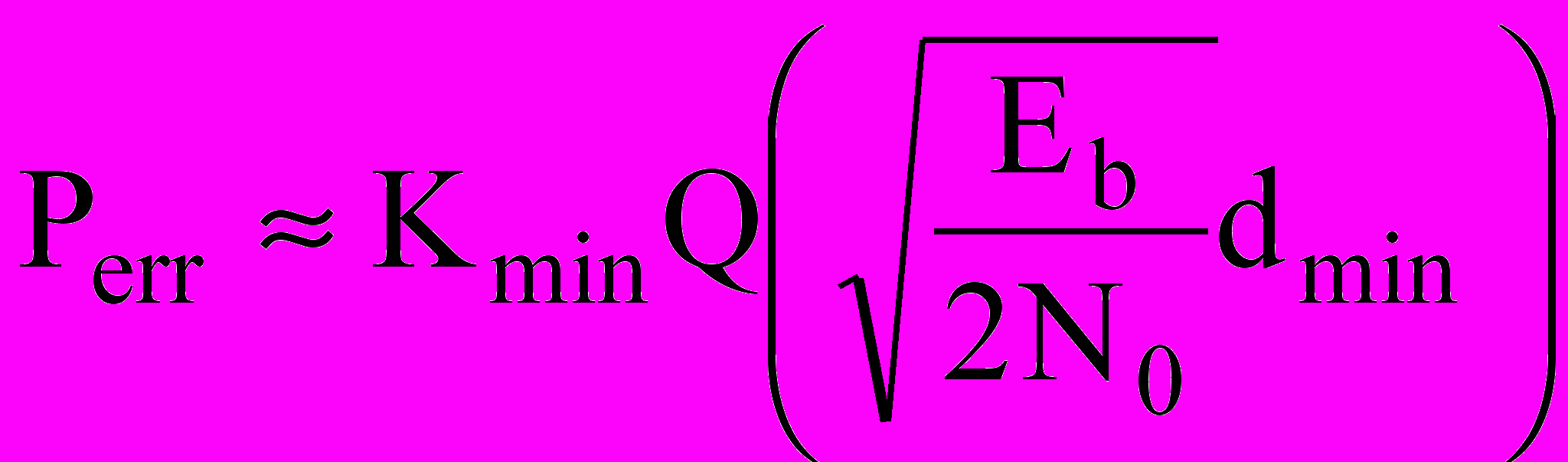^{, (4)}

^где^E_b^{– энергия, затрачиваемая, на передачу одного бита информации,}^N₀^{– СПМ шума}ⁿ⁽^t^),^d_min^{– минимальное евклидово расстояние между сигналами, возможными к передаче,}^K_min^{– константа, зависящая от количества сигналов, расположенных на минимальном расстоянии, и количества символов, в которых они различаются.}

^{Помехоустойчивость системы передачи информации с интерференцией символов оценивалась по величине минимального расстояния}^d_min^{. По этому параметру можно сравнивать различные способы передачи информации. Как видно из (4), при большем минимальном расстоянии требуется во столько же раз меньшее отношение сигнал/шум, необходимое для достижения той же вероятности ошибки.}

^{Для количественной оценки помехоустойчивости передачи информации с интерференцией символов были найдены минимальные расстояния для различных форм парциального импульса}^g⁽^t^{) и различных алфавитов передаваемых символов {}^a_k^{}. Форма парциального импульса задавалась при помощи формирующего фильтра, на вход которого подается дельта-импульс. В качестве формирующих рассмотрены два типа фильтров: фильтр типа квадратного корня из “приподнятого косинуса” и фильтр Баттерворта. При этом полоса}^F₀^,^{занимаемая сигналом, определялась по уровню АЧХ формирующего фильтра -3 дБ. Рассмотрены два алфавита передаваемых символов: двоичный и четверичный, при использовании которых передаваемые символы {}^a_k^{} выбираются из множеств {−1, +1} и {−3, −1, +1, +3} соответственно.}

^{На рис. 1 приведены зависимости минимального расстояния от скорости передачи информации}^R^{, нормированной к полосе частот, занимаемой сигналом}^F₀^{. На рис. 1,а эти зависимости построены для формирующего фильтра Баттерворта порядка}ⁿ^{, а на рис. 1,б – для формирующего фильтра типа квадратного корня из “приподнятого косинуса” с коэффициентом ската}^^{. Так же на рис. 1 кружочками отмечены минимальные расстояния, соответствующие КАМ сигналам.}

^{Видно, что на характер этих зависимостей тип используемого фильтра существенно не влияет. При небольшом увеличении нормированной скорости следования символов минимальное расстояние остается постоянным и равным 2 (0 дБ относительно минимального расстояния между сигналами КАМ-4)}

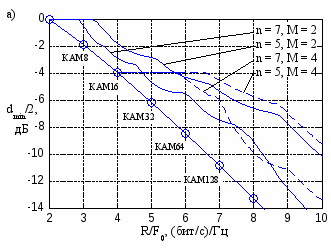
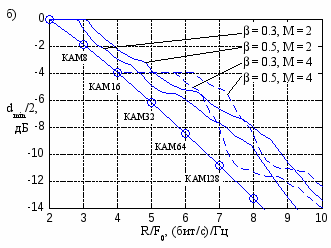
^{Рис. 1. Зависимости минимальных расстояний от нормированной скорости передачи информации.}

^{в случае двоичного алфавита передаваемых символов и 4/5 (−4 дБ) в случае четверичного алфавита передаваемых символов. Такие значения минимального расстояния соответствуют случаям передачи информации без интерференции символов. Из этого следует, что за счет уменьшения тактового интервала следования символов можно без потери в энергетической эффективности увеличить частотную эффективность передачи информации примерно на 40 – 60% в зависимости от используемого фильтра. При этом видно, чем компактней спектр сигнала, тем меньше выигрыш, достигаемый в частотной эффективности. При более значительном увеличении нормированной скорости следования символов минимальные расстояния монотонно убывают. Здесь также, чем компактней спектр сигнала, тем быстрее убывает минимальное расстояние.}

^{Сравнение найденных зависимостей с минимальными расстояниями КАМ сигналов показывает, что повышение частотной эффективности за счет уменьшения тактового интервала следования символов оказывается энергетически более эффективным, чем за счёт увеличения позиционности передаваемых сигналов. Выигрыш в помехоустойчивости по сравнению с КАМ сигналами лежит в пределах от 1 до 7 дБ в зависимости от формирующего фильтра, отношения}^R^/^F₀^{и алфавита передаваемых символов.}

^{В третьей главе}^{проведено исследование практически реализуемых алгоритмов приема сигналов с интерференцией символов.}

^{При описании алгоритма Витерби во второй главе}было сделано два предположения, которые могут существенно ограничить применение этого алгоритма на практике. Первое предположение касается конечности импульсной характеристики формирующего фильтра. Все используемые на практике формирующие фильтры, строго говоря, имеют импульсную характеристику бесконечной длительности, что приводит к бесконечному количеству интерферирующих символов. Но основной вклад в приращение _nk метрики _n^l (3) будет вносить лишь небольшое количество L символов, ближайших к рассматриваемому. Поэтому строить алгоритм Витерби можно так, как он строился бы, если бы приращение метрики зависело только от L символов, но при реальном расчете приращения метрики учитывать большее количество символов выжившей последовательности.

При помощи математического моделирования было показано, что с увеличением количества символов L, учитываемых при построении алгоритма, существенно увеличивается его помехоустойчивость. Начиная с некоторого значения L = L_min, результаты моделирования хорошо согласуются с теоретической оценкой помехоустойчивости для оптимального приема. При этом дальнейшее увеличение количества символов, учитываемых при построении алгоритма, практически не влияет на значение вероятности ошибки. Значения L_min были найдены для различных ^{форм парциального импульса и различных алфавитов передаваемых символов. Для моделей, описанных выше, они представлены в таблице 1.}

^{Таблица 1 – Значения}^L_min

R/F₀, (бит/с)/Гц	3	4	5	6	7	8
L_min при n = 5, M = 2	4	5	6	7	8	9
L_min при n = 7, M = 2	5	6	8	9	11	12
L_min при n = 5, M = 4	1	1	4	4	5	6
L_min при n = 7, M = 4	1	1	5	6	7	8
L_min при = 0.5, M = 2	4	5	6	7	7	8
L_min при = 0.3, M = 2	6	7	8	10	11	13
L_min при = 0.5, M = 4	1	1	4	4	5	6
L_min при = 0.3, M = 4	1	1	5	6	7	7

Второе предположение касается того, что решение о переданной последовательности символов выносится после приема всего сигнала. Для практики такое предположение неприемлемо, поскольку длительность сигнала может быть неограниченной. На практике удобнее, когда задержка решения фиксирована и не зависит от длины передаваемой последовательности символов. Поэтому был рассмотрен алгоритм Витерби с фиксированной задержкой решения. В этом алгоритме длины сохраняемых последовательностей ограничены величиной D. При этом после получения очередного отсчета ^z_k^{выносится окончательное решение о переданном символе}^a_k_-_D^.В работе были рассмотрены три способа принятия решения:

Решение принимается в пользу символа ^_n_,_k_-_D произвольно выбранной последовательности c номером n.
Решение принимается по совокупности символов ^_n_,_k_-_D всех сохраненных последовательностей по мажоритарному принципу.
Решение принимается в пользу символа ^_n_,_k_-_D той последовательности, которой соответствует наименьшее значение метрики _n^k.

При помощи математического моделирования показано, что при всех трех способах принятия решения характер зависимостей одинаков. А именно, при малой задержке решения и больших отношениях сигнал/шум E_b/N₀ возникает эффект ограничения минимально достижимой вероятности ошибки, т.е. вероятность ошибки практически не уменьшается с увеличением E_b/N₀ и выходит на некоторый постоянный уровень. С увеличением задержки решения постоянный уровень, на который выходит вероятность ошибки, снижается. При малых отношениях сигнал/шум вероятность ошибки практически не зависит от задержки решения.

Основное различие сравниваемых способов принятия решения заключается в величине задержки решения, требуемой для достижения того же результата. В общем, моделирование показало, что в случае принятия решения по символу произвольно выбранной последовательности и задержке решения D = 4L_min (при L_min < 11) или D = 5L_min (при L_min ≥ 11) эффект ограничения минимально достижимой вероятности ошибки либо отсутствует, либо постоянный уровень, на который выходит вероятность ошибки, лежит существенно ниже 10^-6. При принятии решения по мажоритарному принципу для достижения того же результата требуется задержка решения D = 3L_min (при L_min < 11) или D = 3.5L_min (при L_min ≥ 11). А при способе принятия решения по символу последовательности с минимальной метрикой требуется задержка решения D = 2.5L_min (при L_min < 11) или D = 3L_min (при L_min ≥ 11).

Также была рассмотрена возможность использования порогового алгоритма приема сигналов. Этот алгоритм относится к классу последовательных алгоритмов и в нем используется свойство метрик последовательностей заключающееся в том, что максимально правдоподобная последовательность содержится в некотором множестве наилучших последовательностей, т.е. тех которые имеют наименьшие значения метрик. Последовательность операций, выполняемых при реализации этого алгоритма, выглядит следующим образом:

При получении отсчета принятого сигнала z_k, каждая из N_k_-1 последовательностей, выживших на предыдущей итерации, продолжается одним из М возможных символов _k.
Для каждой обновленной последовательности вычисляются метрики _n^k по формулам (3).
Определяется последовательность, имеющая наименьшее значение метрики _min^k.
В качестве решения выносится символ _min_,_k_-_D последовательности, которой соответствует минимальное значение метрики.
Отсекаются все последовательности, метрики которых удовлетворяют следующему условию:

, n = 0, 1, …, MN_k_-1 – 1. (5)

Сложность порогового алгоритма, как и алгоритма Витерби, можно оценить по количеству последовательностей, сохраняемых после каждой итерации N_k, но в отличие от алгоритма Витерби, в пороговом алгоритме количество последовательностей, сохраняемых после каждой итерации N_k, является случайной величиной, среднее значение и дисперсия, которой существенно зависит от порога  и отношения сигнал/шум. От устанавливаемого порога  так же зависит помехоустойчивость алгоритма.

При помощи математического моделирования показано, что при правильном выборе , пороговый алгоритм достигает той же помехоустойчивости, что и алгоритм Витерби, при этом его средняя вычислительная сложность оказывается меньше чем у алгоритма Витерби. Для сигналов сформированных фильтром Баттерворта 7-ого порядка и двоичном алфавите передаваемых символов выигрыш в вычислительной сложности изменяется от 2 до 7 раз при изменении нормированной скорости передачи информации от 3 до 8 (бит/с)/Гц и вероятности ошибки 10^-5.

Однако пороговому алгоритму присущи некоторые недостатки. Пороговому алгоритму требуется больший объем памяти для хранения последовательностей и их метрик, чем для алгоритма Витерби. Для реализации указанного выигрыша в вычислительной сложности пороговому алгоритму требуется буферная память для хранения отсчетов z_k в течение периодов, когда сохранено большое количество последовательностей. В работе приводятся оценки для максимального количества сохраняемых последовательностей и требуемой длины буферной памяти. И последний недостаток это не постоянная задержка вынесения решения о переданных символах.

^{В четвертой главе}^{оценено влияние на помехоустойчивость передачи информации с интерференцией символов погрешностей в системах синхронизации и линейных искажений}в трактах передачи и приёма^{. Рассматривается модель, в которой используется формирующий фильтр Баттерворта 7-ого порядка и двоичный алфавит передаваемых символов.}

Для анализа влияния ^{погрешностей в системе синхронизации по несущему колебанию была рассмотрена модель системы связи, в которой передача информации осуществляется при помощи сигналов с интерференцией символов на квадратурных компонентах несущего колебания, т.е. передаваемый сигнал можно представить в виде}

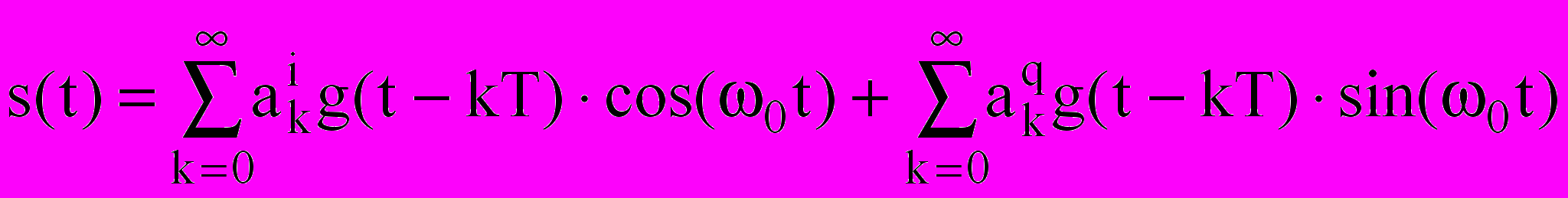. (6)

Сигнал (6) проходил канал связи, в котором искажался белым гауссовским шумом. В приемнике проходило восстановление несущего колебания и квадратурных компонент принятого сигнала, при этом считалось, что частота несущего колебания восстанавливается точно, а начальная фаза восстанавливается с ошибкой . Далее квадратурные компоненты обрабатывались не зависимо, с использованием алгоритма Витерби.

При помощи математического моделирования, показано, что с увеличением нормированной скорости передачи информации увеличивается чувствительность системы к ошибкам определения фазы несущего колебания. Например, для того чтобы потери в помехоустойчивости не превышали 1 дБ при вероятности ошибки 10^-5, ошибка  в определении фазы несущего колебания не должна превышать 1.7^о, 2.8^о, 3.9^о и 5.7^о при значениях R/F₀ равных 6 (бит/с)/Гц, 5 (бит/с)/Гц, 4 (бит/с)/Гц и 3 (бит/с)/Гц соответственно.

Для анализа влияния ^{погрешностей в системе символьной синхронизации рассмотрена модель, в которой появляется постоянная ошибка}

определения задержки сигнала в канале связи. Такая ошибка приводит к тому, что отсчеты z_k (2) формируются не в моменты времени kT, а в моменты времени kT+

. Было показано, что с увеличением нормированной скорости передачи информации увеличивается чувствительность системы к ошибкам определения задержки сигнала. Например, для того чтобы потери в помехоустойчивости не превышали 1 дБ при вероятности ошибки 10^-5, ошибка

не должна превышать 8.4%, 9.4%, 10.5% и 11.7% от периода следования символов Т при значениях R/F₀, равных 6 (бит/с)/Гц, 5 (бит/с)/Гц, 4 (бит/с)/Гц и 3 (бит/с)/Гц соответственно. Следует заметить, что передача информации при помощи КАМ сигналов обладает гораздо большей чувствительностью к ошибкам определения задержки сигнала, поскольку при таких ошибках в отсчетах КАМ сигнала возникает интерференция символов, которая не учитывается в алгоритме демодуляции и приводит к существенным потерям.

Рассмотрено влияние линейных искажений возникающих в частотно- избирательных цепях тракта передатчика и приемника. Предполагалось, что эти цепи могут быть описаны эквивалентными АЧХ фильтров Баттерворта, с полосами пропускания по уровню -3 дБ равными F_TX и F_RX соответственно для тракта передатчика и приемника. При помощи математического моделирования оценивался уровень потерь в помехоустойчивости возникающих вследствие прохождения сигнала через такие цепи. Проанализировано два варианта демодуляции сигнала. В первом варианте линейные искажения не учитываются при демодуляции сигнала, т.е. алгоритм приема строится, так как если бы искажения отсутствовали. Во втором варианте алгоритм приема строится с учетом сквозной импульсной характеристики всего тракта передачи сигнала.

Для первого варианта показано, что в случае сравнительно малых искажений, когда эквивалентные фильтры имеют пятый порядок и F_TX= F_RX = 1.8F₀ потери в отношении сигнал/шум, при котором обеспечивается вероятность ошибки 10^-5, составляют 0.2 дБ при R/F₀ = 4 (бит/с)/Гц. При R/F₀ = 6 (бит/с)/Гц, потери уже составляют 0.4 дБ. С уменьшением полос эквивалентных фильтров трактов передатчика и приемника до F_TX= F_RX = 1.6F₀ потери в отношении сигнал/шум возрастают до 0.6 дБ при R/F₀ = 4 (бит/с)/Гц, и до 1,0 дБ – при R/F₀ = 6 (бит/с)/Гц. При дальнейшем уменьшении полос эквивалентных фильтров потери в помехоустойчивости растут еще быстрее. При втором варианте демодуляции сигнала, подобный уровень искажений вообще не вызывает потерь.

Для второго варианта приема сигнала рассмотрен случай, когда эквивалентный фильтр тракта передатчика имеет пятый порядок и F_TX = 1.8 F₀, а эквивалентный фильтр тракта приемника имеет 10 порядок. Показано, что в случае F_RX = 1.2F₀ потери в отношении сигнал/шум при вероятности ошибки 10^-5 составляют менее 0.1 дБ при R/F₀ = 4 (бит/с)/Гц, а при R/F₀ = 6 (бит/с)/Гц они составляют примерно 0.2 дБ. С уменьшением полосы эквивалентного фильтра тракта приемника до F_RX = F₀ потери в отношении сигнал/шум возрастают до 0.8 дБ при R/F₀ = 4 (бит/с)/Гц, а при R/F₀ = 6 (бит/с)/Гц – до 1.3 дБ.

Заключение

Проведено исследование потенциальной помехоустойчивость рассматриваемого способа передачи информации. Оно позволило выявить существенную зависимость достижимого выигрыша в скорости передачи информации от требований к компактности спектральной мощности сигнала и уровню внеполосных излучений и получить количественные оценки этого выигрыша для сигналов, удовлетворяющих типовым требованиям.

Проанализированы несколько вариантов подоптимальных приёмников. Было показано, что сложность демодуляторов подоптимальных приёмников, обеспечивающих в заданных условиях работы помехоустойчивость, близкую к потенциальной, возрастает с увеличением желаемого выигрыша при заданных требованиях к спектру сигнала. При фиксированной величине желаемого выигрыша сложность демодулятора получается тем выше, чем выше требования к компактности спектра сигнала. Для типовых требований к спектрам сигналов получены количественные оценки сложности демодуляторов.

Исследовано влияние погрешностей систем фазовой и тактовой синхронизации на качество работы демодулятора сигналов с интерференцией символов. Проведённый анализ и сравнение исследуемого способа со способом, основанном на увеличении объёма алфавита в КАМ сигналах, показали, что эти факторы влияют на работу системы с интерференцией символов слабее, чем на работу системы с КАМ сигналами.

Оценено влияние линейных искажений в трактах передачи и приёма на работу демодулятора сигналов с интерференцией символов. Показано, что такая система обладает высокой чувствительностью к линейным искажениям сигнала. В тоже время, если учитывать линейные искажения сигнала в демодуляторе уровень потерь в энергетической эффективности можно минимизировать.

Приложения содержат программы для поиска минимального расстояния между сигналами с интерференцией символов и программы реализующие алгоритм Витерби и пороговый алгоритм.

Основные результаты диссертации опубликованы в работах:

Кулешов В. Н., Победоносцев К. А., Мордвинов А. Е. Повышение скорости передачи информации в линиях связи // – М.: Электросвязь, № 6, 2008, С. 27-28.
Кулешов В. Н., Победоносцев К. А., Мордвинов А. Е. Повышение скорости передачи информации в линиях связи за счёт использования сигналов с взаимной интерференцией символов // – М.: Вестник МЭИ, № 4, 2008, С. 86-93.
Мордвинов А. Е. (Научный руководитель Кулешов В. Н., консультант Победоносцев К. А.) Экспериментальная проверка станции космической связи с взаимной интерференцией символов // Двенадцатая науч.-техн. конф. студентов и аспирантов «РАДИОЭЛЕКТРОНИКА ЭЛЕКТРОТЕХНИКА И ЭНЕРГЕТИКА»: Тез. докл. – М.: Изд. МЭИ, 2006. Т.1. С. 59.
Мордвинов А. Е. (Научный руководитель Кулешов В. Н.) Метод увеличения скорости передачи информации // Тринадцатая науч.-техн. конф. студентов и аспирантов «РАДИОЭЛЕКТРОНИКА ЭЛЕКТРОТЕХНИКА И ЭНЕРГЕТИКА»: Тез. докл. – М.: Изд. МЭИ, 2007. Т.1. С. 28.
Мордвинов А. Е. (Научный руководитель Кулешов В. Н.) Повышение скорости передачи информации в линиях связи за счет использования сигналов с интерференцией символов // Тринадцатая науч.-техн. конф. студентов и аспирантов «РАДИОЭЛЕКТРОНИКА ЭЛЕКТРОТЕХНИКА И ЭНЕРГЕТИКА»: Тез. докл. – М.: Изд. МЭИ, 2008. Т.1. С. 27.
Кулешов В. Н., Победоносцев К. А., Мордвинов А. Е. Об одном способе увеличения скорости передачи информации // Труды РНТОРЭС имени А.С. Попова. Серия: Научная сессия, посвященная дню радио. Выпуск: LXIII. Москва, 2008. С. 143 -145.
Кулешов В. Н., Победоносцев К. А., Мордвинов А. Е. Повышение скорости передачи информации в линиях связи за счёт использования передачи данных с взаимной интерференцией символов // Труды РНТОРЭС имени А.С. Попова. Серия: Системы синхронизации, формирования и обработки сигналов для связи и вещания. Ярославль, июль 2008. С. 94 – 96.
Мордвинов А. Е. Алгоритмы подоптимального приема в линиях связи с увеличением скорости передачи информации за счет использования передачи данных с взаимной интерференцией символов // Труды РНТОРЭС имени А.С. Попова. Серия: Системы синхронизации, формирования и обработки сигналов для связи и вещания. Ярославль, июль 2008. С. 97 – 99.

Blog

Исследование возможностей повышения частотной эффективности линий связи за счет использования сигналов с взаимной интерференцией символов

Содержание