Geum.ru

Методические указания Екатеринбург 2006 утверждаю декан психологического факультета Глотова Г. А

Вид материалаМетодические указания
Наглядное пояснение основной концепции ФА с помощью
Единичная дисперсия
Подобный материал:
1   2   3   4   5   6

Наглядное пояснение основной концепции ФА с помощью

числового примера


По факторной матрице A, как это показано в табл.2, вычисляются общности. Общность hi2 первой переменной равна: 0,902 + 0,102 = 0,82. Тогда характерность определяется: 1-0,82 = 0,18. Таким же образом могут быть определены эти величины для всех переменных.

На рис. 12 единичная дисперсия каждой переменной изображена в виде прямоугольника, площадь которого равна единице. Единичная дисперсия с помощью методов факторного анализа разбивается на составляющие, одна из которых является дисперсией характерного фактора (затушевано), а другая - ее общностью (остальная часть площади прямоугольника). Общность каждой переменной далее расчленяется на доли дисперсии, связанные с отдельными факторами.

Таблица 2

Вычисление долей дисперсии по матрице А


А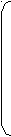= (аij)
А2= (аij2)
hi2
ui2

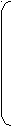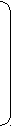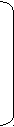0.90
0.10
0.81
0.01
0.82
0.18

0.80
0.05
0.64
0.0025
0.6425
0.3575

0.70
0.10
0.49
0.01
0.50
0.50

0.05
0.80
0.0025
0.64
0.6425
0.3575

0.10
0.70
0.01
0.49
0.50
0.50

0.05
0.50
0.0025
0.25
0.2525
0.7475

Суммы столбцов hi2 =
1.9550 + 1.4025 =

3.3575 2.6425

Полная дисперсия = hi2 + ui2 = 3.3575 + 2.6425

= 6.0000


Изобразим для наглядности структуру факторной матрицы A из табл.2 графически (рис.12).

В данном примере выделены два фактора. Доля дисперсии первого фактора изображена косой штриховкой, дисперсии второго фактора соответствует чистая площадка. Количественные соотношения между долями дисперсии взяты из табл.2. Например, единичная дисперсия первой переменной на 81% состоит из дисперсии первого фактора, на 1% – из дисперсии второго фактора и на 18% – из дисперсии характерного фактора. Аналогично из табл.2 берется распределение долей дисперсии других переменных.


Рис.12. Распределение долей единичных дисперсий переменных по факторам.

(доли соответствуют численным значениям табл.2)





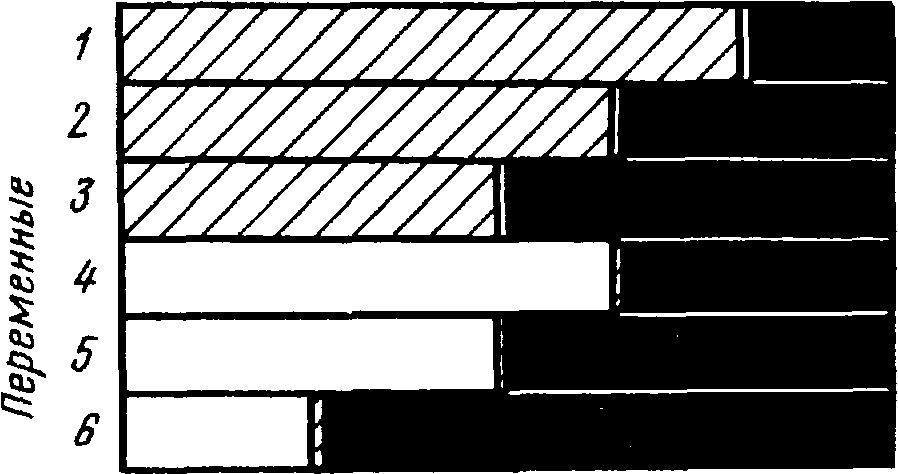
По рис.12 можно оценить, какая часть дисперсии каждой переменной объясняется факторами, выделенными в процессе анализа, и какая доля приходится на характерность. Также легко видеть, какие переменные с какими факторами связаны.

Если рассматривать лишь заштрихованные области, то видно, откуда первый фактор получает свою дисперсию.

Рассматривая только пустые клетки в прямоугольниках, определяем источники дисперсии второго фактора.

На рис.13 сопоставляются друг с другом доли дисперсии обоих факторов и суммарной характерности. В табл. 3 показано, как определяют доли дисперсии обоих факторов в процентах от полной дисперсии.

Таблица 3.

Доли дисперсии факторов в процентах от полной дисперсии

Вид дисперсии
Абс. значение
%

Полная дисперсия
6,0
100

Дисперсия 1 фактора
1,9550
32,58

Дисперсия второго фактора
1,4025
23,37

Суммарная общность
3,3575
55,95

Суммарная характерность
2,6425
44,04



Рис. 13. Процент полной дисперсии









Сумм. общность=55,95% Сумм. харак.=44,05


На рис.14 за 100% принята суммарная общность (сумма hi2 ) и показано соотношение дисперсий обоих факторов, отнесенных к hi2.


Рис. 14. Процент суммарной общности


1
2
3



4
5
6