Методические указания Екатеринбург 2006 утверждаю декан психологического факультета Глотова Г. А
| Вид материала | Методические указания |
- Учебно-методическое пособие Екатеринбург 2006 утверждаю декан психологического факультета, 1202.51kb.
- Учебно-методическое пособие Екатеринбург 2006 утверждаю декан психологического факультета, 4118.65kb.
- Программа курса Стандарт 020800 «Историко-архивоведение» Екатеринбург 2006 утверждаю, 234kb.
- Методические указания по выполнению выпускной квалификационной работы для студентов, 665.8kb.
- Программа специальной (Стандарт пд. Сд/ДС) Екатеринбург 2006 Утверждаю Декан физического, 73.92kb.
- Программа специальной (Стандарт пд. Сд/ДС) Екатеринбург 2006 Утверждаю Декан физического, 285.15kb.
- Программа дисциплины (Стандарт пд- сд ) Екатеринбург 2006 Утверждаю Декан экономического, 822.84kb.
- Программа дисциплины (Стандарт пд-сд) Екатеринбург 2006 Утверждаю Декан экономического, 316.67kb.
- Программа дисциплины (Стандарт пд-сд) Екатеринбург 2006 Утверждаю Декан экономического, 137.25kb.
- Программа дисциплины (Стандарт пд- сд /ДС/фтд/днм/сдм/нирм) Екатеринбург 2006 Утверждаю, 1309.1kb.
Общая характеристика факторного анализа как научного метода
Выше уже отмечалось, что одним из первых в рамках многомерного подхода был разработан метод факторного анализа. Долгое время в психологии он был практически единственным многомерным инструментом анализа данных и разработки тестовых методик (с его помощью созданы тесты Кетела, Айзенка, Векслера, Амтхауэра и т.д.). И сегодня, несмотря на возникновение других инструментов, он продолжает оставаться наиболее часто используемым многомерным методом.
Основные положения современного факторного анализа были сформулированы Терстоуном и Кеттеллом.
Исторически, на первых этапах развития факторные методы разрабатывались в целях определения основных свойств или «показателей» интеллекта – поиск основных видов умственных способностей, которые, как известно, варьируют от человека к человеку, являются переменными величинами. Это не случайно: использование ФА возможно лишь там, где существуют переменные величины. Только тогда, когда удастся уловить индивидуальные различия между людьми, т. е. вариацию изучаемого явления, можно применять факторный анализ для определения процессов, лежащих в основе изменений, обнаруженных экспериментально.
Приступая к изучению какой-то области явлений можно идти двояким путем.
- Можно выдвинуть гипотезу, касающуюся фундаментальных причин указанной вариации, и для ее проверки прибегнуть к факторному анализу. Такой ФА называется конфирматорным (проверочным).
- Можно собрать максимально возможное количество точных данных из интересующей нас области и без всяких гипотез использовать факторный анализ применительно к ним. В этом случае исходят из предположения, что методы факторного анализа позволяют обнаружить природу скрытых закономерностей, то есть выдвинуть и обосновать гипотезы.
Именно вторым способом ФА используется наиболее плодотворно – на ранних стадиях исследования и в тех областях, где лишь начинается научный поиск, где ещё не окончательно сформулированы законы и основные концепции, а также там, где трудно проводить эксперименты для оценки предложенных гипотез. Тэрстоун говорил: «Факторный анализ особенно полезен в пограничных областях науки». Такой ФА называется эксплораторным (разведочным).
Что представляет собой та «латентная структура», которая лежит в основе вариации изучаемых данных? Это система определенных влияний или факторов, которые определяют экспериментально установленную корреляцию. Слово фактор используется в другом смысле, чем это принято обычно: речь идет о математической величине, получаемой на основе наблюдений. О природе этих факторов не делается никаких априорных предположений. Они могут иметь общественный или физиологический характер, могут сильно коррелировать между собой или не коррелировать вообще, могут иметь простую или сложную внутреннюю структуру. Например, одни из них могут определяться влиянием внутренней секреции, а другие – опытом и подготовкой; одни могут быть врожденными, а другие – приобретенными; одни – относительно постоянными, а другие – быстроизменяющимися.
Основным предположением факторного анализа является следующее: явления в определенной области, несмотря на свою разнородность и изменчивость, могут быть описаны относительно небольшим числом факторов. Как можно прочувствовать это существо метода? Тэрстоун приводит упрощенный пример, в котором сложные психологические факторы заменены более известными и легко интерпретируемыми.
Представим себе, что в экспериментальной группе из нескольких сотен мальчиков одной возрастной категории проводятся 20 различных гимнастических упражнений, выполнение которых оценивается по какой-то шкале. Имея совокупности таких оценок, можно рассчитать все корреляции между двадцатью упражнениями с учетом качества их выполнения. В результате получим таблицу, имеющую 20 строк, 20 столбцов и включающую 190 коэффициентов корреляции (400-20)2), характеризующих существующие здесь зависимости. Но путем изучения такой таблицы коэффициентов корреляции трудно дойти до скрытой основы, до закономерностей экспериментально обнаруженных связей.
Но допустим, что, например, одно из упражнений требует в основном напряжения плечевого пояса, другое – чувства равновесия, третье – быстроты движений. При этом учтем, что многие упражнения, требующие в основном усилий плечевого пояса, могут в очень незначительной степени требовать чувства равновесия, и наоборот. Точно так же другие упражнения требуют в основном быстроты движений, но не требуют усилий плечевого пояса и т. д.
На этом примере мы видим, что обо всех коэффициентах корреляции можно судить по небольшому числу (в данном случае трем) основных параметров – факторов, которые называются: 1) чувство равновесия; 2) усилие плечевого пояса; 3) быстрота движения.
Но это – искусственный пример, где мы на основании жизненного опыта обоснованно предположили наличие объясняющих переменных. Факторный же анализ представляет собой метод, который позволяет выделить эти невидимые основные факторы, определяющие корреляции оценок в серии упражнений.
Но это еще не все. При помощи факторных методов можно определять, поддается ли обнаруженный фактор разложению на более простые элементы. Можно организовать, например, новый эксперимент, в котором изучается совокупность 20 упражнений на равновесие. После проведения факторного анализа может оказаться, что обнаруженный ранее фактор равновесия распадается на более элементарные единицы. Это могут быть какие-то частные ощущения равновесия, например в плоскости симметрии тела (отклонения вперед и назад) и в перпендикулярной к ней плоскости (отклонения в стороны). Таким образом, проводя новые факторные эксперименты, можно получить новую совокупность более элементарных факторов равновесия тела.
Итак, ФА позволяет выделить небольшое число скрытых переменных, объясняющих наблюдаемую корреляцию данных исследования, и добраться до элементарных факторов.
Приведем еще один пример рассуждений, приводящих к аналогичному выводу.
Пусть мы имеем множество коэффициентов корреляции, выражающих зависимости между множеством исходных переменных, например, между тестами. В соответствии с основным предположением ФА совокупность этих корреляций может быть описана при помощи некоторого – небольшого – числа общих для этих тестов факторов. Оценки отдельных переменных, полученные в ходе тестирования, могут быть экономно выражены в терминах этих общих факторов.
Поскольку для тестов такими факторами являются способности (понимаемые в широком смысле – как качества, необходимые для выполнения данного задания), каждая индивидуальная оценка, полученная за выполнение теста, теоретически определяется двумя обстоятельствами:
а) способностями, необходимыми для выполнения данного теста;
б) объемом этих способностей у данного индивида. Если предположить, что общие факторы (способности) некоррелированы, то описанная выше ситуация может быть выражена для q некоррелированных факторов с помощью следующего уравнения:
Sji = Cj1 X1 i + Cj2 X2 i + … + CjqXqi
где Sji – стандартная оценка человека i при выполнении теста j;
Cjq – содержание или нагрузка фактора q в тесте j;
Xqi – объем фактора (способности) q у обследуемого человека.
Как можно трактовать это уравнение с точки зрения психологии?
Все С имеют индекс j, а не i, так как относятся к тестам, а не к людям. Они показывают, в какой мере выполнение данного теста требует определенных способностей. Наоборот, все Х имеют индексы i а не j, так как относятся к отдельным обследуемым людям, а не к тестам. Они показывают, в какой степени данный человек обладает соответствующим качеством.
Первый член правой стороны уравнения показывает долю первого фактора (способности) при выполнении теста, второй – долю второго фактора, третий – третьего фактора, наконец, последующий – долю q-ro независимого фактора (вспомним пример Терстоуна про обучение мальчиков гимнастическим упражнениям).
Предположим, что способность (фактор) 1 является решающим условием выполнения j-го теста. Тогда коэффициент Сj1 будет положительным и высоким. Если одновременно человек i в достаточной степени наделен этой способностью, т. е. Х1i будет положительным и большим, то произведение обеих величин внесет существенный вклад в хорошую оценку выполнения теста.
Допустим, что способность 2 теперь совершенно не нужна для выполнения j-го теста. Тогда коэффициент Сj2 будет равен нулю. Если даже человек i щедро одарен этой способностью (стандартная оценка объема этой способности Х2i положительна и высока), произведение обоих коэффициентов будет равно нулю. Это означает, что для данного человека и данного теста эта способность не влияет на итоговую оценку.
Повторим еще раз: в основе такой интерпретации лежит предположение, что большое разнообразие поведения людей, например, в ситуации выполнения заданий может быть описано и объяснено при помощи ограниченного числа основных свойств (или способностей, или факторов – понятий в данном контексте являющихся синонимичными).
Подведем итог сказанному об общем характере метода ФА.
- Исследование начинается со сбора наблюдений о варьировании некоторого набора переменных1. Это могут быть, например, материалы нескольких десятков тестов, результаты опроса достаточно многочисленной группы людей, или какие-либо показатели экономической конъюнктуры, взятые за какой-то отрезок времени в рамках более длительного периода, и т. п.
- Рассчитываются все возможные корреляции между наблюденными переменными для определения того, существует ли между ними взаимосвязь и какова её мера2. Например, для группы переменных, относящихся к индивидуальным особенностям, можно констатировать, что оценки общительности положительно связаны с показателями здоровья, тогда как показатели интеллигентности никак не связаны с этими двумя переменными. Это означает, что интеллигентный человек не обязательно должен быть здоровым или общительным. На основе полученных коэффициентов корреляции и проводится ФА, выявляющий группы, в которые объединяются некоторые одинаково ведущие себя переменные.
- Кроме того, факторный анализ вскрывает основные общие факторы, влияющие на образование этих групп. Если, например, при изучении многочисленных черт личности выделяется группа переменных, каждая из которых включает элементы быстроты реакции, психической активности и реакции на различные стимулы, то на основе факторного анализа можно установить, что ковариация этих переменных вызвана каким-то одним фактором, который может быть сведен к функционированию щитовидной железы. Этот фактор непосредственно не входил в исследуемый набор переменных, но, несмотря на это, его влияние может быть количественно определено с помощью факторного анализа, а сам он при помощи содержательной интерпретации идентифицирован.
- Вскрытые факторы сами могут трактоваться как определенные переменные, представляющие собой как бы переменные более высокого порядка, которые могут использоваться для объяснения вариации более многочисленных, исходных переменных.
- Факторный анализ не требует предварительных гипотез, наоборот, он сам может служить методом выдвижения гипотез, а также выступать критерием гипотез, опирающихся на данные, полученные другими методами.
- Совокупность переменных, оказывающие существенное влияние в изучаемой области (то есть факторов), не выбирается по произволу исследователя, а выявляется в результате математического анализа данных.
- Факторный анализ не требует априорных предположений относительно того, какие переменные независимы, а какие зависимы. Этот вопрос, а так же вопрос о мере их связи решается в процессе дальнейших исследований.
- Важной особенностью ФА является то, что экспериментальная выборка, с которой он работает, не обязательно должна быть репрезентативна для соответствующей генеральной совокупности. В выборках, взятых с учетом каких-либо интересующих нас в данной области свойств, с гораздо большей вероятностью можно напасть на след скрытых закономерностей, лежащих в основе изучаемых явлений, по сравнению с выборками, для которых характерно стремление обеспечить случайный отбор из генеральной совокупности.
Благодаря этим свойствам ФА приобрел особое значение в психологии. Он, по мнению Кеттелла, самый лучший из существующих в настоящее время инструментов исследования.
Наиболее интересным для психологов является то, что существенным элементом этого метода является в большинстве случаев эксперимент. Не без основания в специальной литературе установился термин факторный эксперимент.
Сведения о матрицах, минимально необходимые для изучения ФА
Матрицей называется прямоугольная или квадратная таблица чисел, рассматриваемая безотносительно к тому, что именно представляют собой эти числа и существуют ли между ними какие-то заранее определенные зависимости. Вертикальный ряд чисел, расположенных в матрице одно над другим, называется столбцом, горизонтальный ряд чисел – строкой. Матрица, в которой число строк равно числу столбцов, называется квадратной. В тех случаях, когда нужно обозначить какие-либо элементы матрицы, им приписываются соответствующие индексы, первый из которых указывает номер строки, а второй – номер столбца, в котором находится данный элемент.

Схема 1. Квадратная матрица 4Х4
Таким образом, в квадратной матрице, показанной на схеме 1, символ а23 обозначает элемент, находящийся на пересечении второй строки и третьего столбца. Вся матрица обозначается буквой А. С обеих сторон матрица ограничивается двумя вертикальными линиями. О матрице, имеющей т строк и п столбцов, говорят, что ее порядок составляет т х п. Квадратная матрица п х п имеет порядок п.
Общий элемент матрицы записывается в виде аij где i (индекс строки) может принимать последовательные значения 1, 2, 3, ..., т, а j (индекс столбца) может принимать последовательные значения 1, 2, 3, ..., п.
Транспонирование матрицы
Это важное понятие, часто встречающееся в факторном анализе. Представим себе, что строки матрицы А становятся столбцами, в результате чего возникает новая матрица, которая будет транспонированной по отношению к А. Обозначим новую матрицу А'. Приведем пример транспонирования матрицы
А
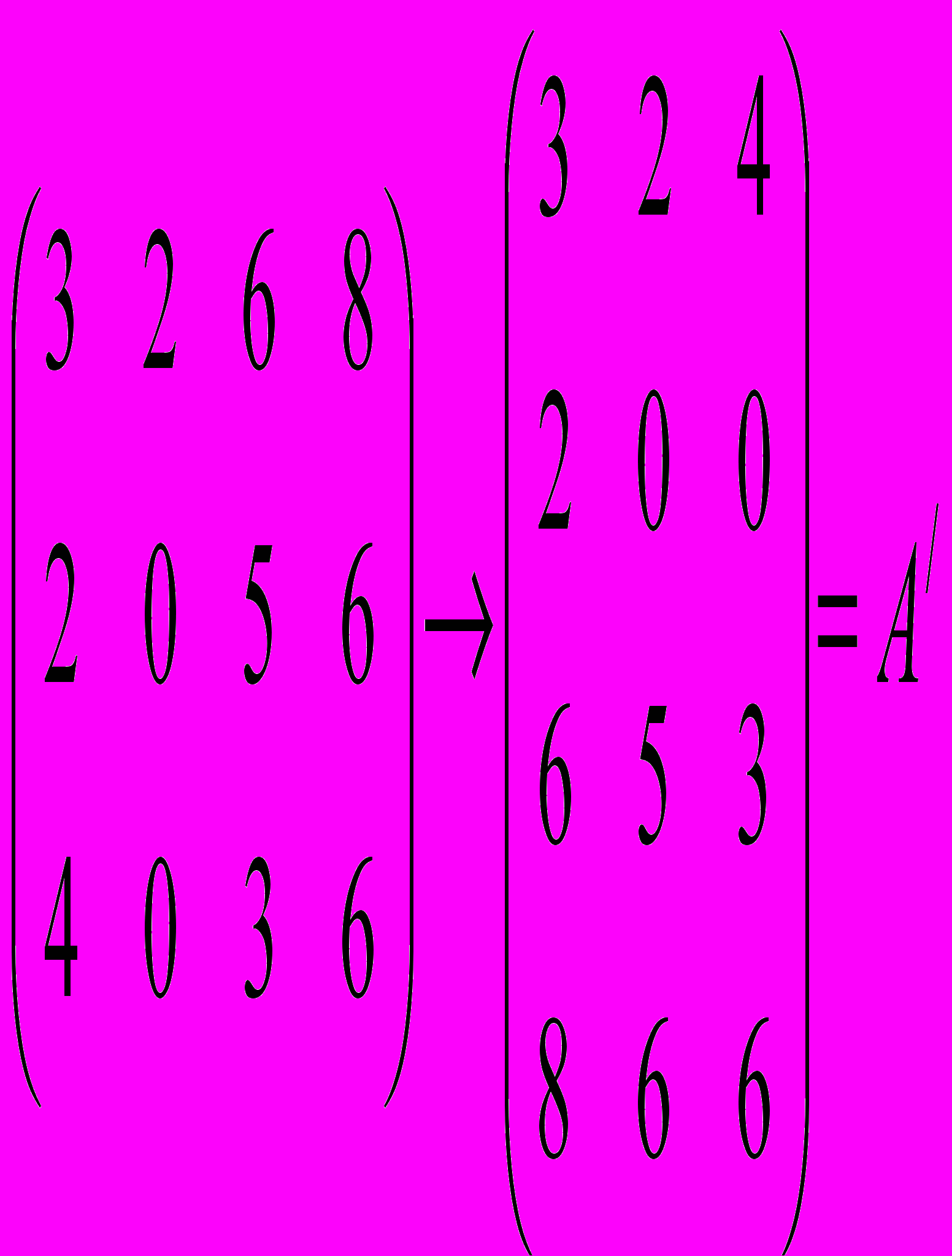
Схема 2. А/ - транспонированная матрица А
Симметрическая матрица
Е
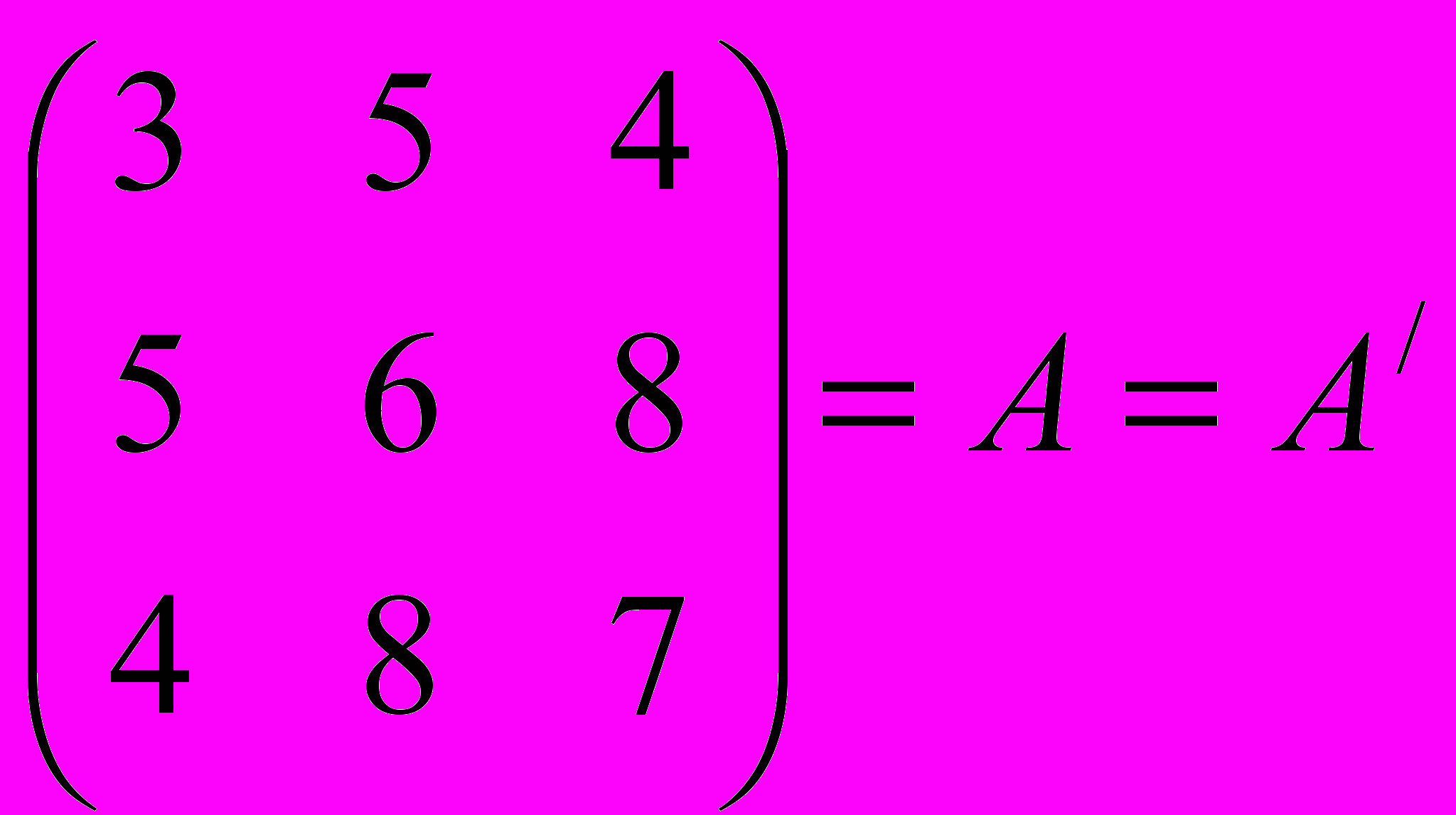
сли матрица А квадратная и совпадает с транспонированной к ней матрицей, то матрица А симметрична. Другими словами, квадратная матрица А симметрична, если А' = А. Пример симметрической матрицы дает схема 3.
Схема 3. Симметрическая матрица
Если элементами матрицы являются коэффициенты корреляции данной совокупности переменных, то эта матрица – симметрическая. В факторном анализе, как правило, встречаются именно такие ситуации.
Умножение матриц
Матрицы можно умножить друг на друга. Операция умножения часто встречается в факторном анализе и поэтому мы обсудим ее подробнее. Не вдаваясь глубоко в теорию вопроса, ограничимся описанием практических правил умножения матриц.
Правила эти гораздо сложнее правил умножения в арифметике. Первое отличие между умножением в арифметике и в матричной алгебре состоит в том, что при умножении матриц не действует закон коммутативности, в соответствии с которым произведение не зависит от порядка, в котором стоят сомножители. Если умножаются матрицы, их произведение в общем случае зависит от этого порядка. Другими словами, А В В А.
Для умножения матрицы А на матрицу В необходимо выполнение следующего условия: матрица А должна иметь столько столбцов, сколько строк в матрице В. Сам процесс умножения исходит из правила «строка на столбец». Это правило означает, что каждый элемент матрицы-произведения представляет собой сумму произведений от умножения элементов строки первой матрицы на соответствующие элементы столбца -второй матрицы.
Таким образом, элемент, стоящий на пересечении второй строки и третьего столбца матрицы С, образуется путем последовательного умножения элементов второй строки матрицы А на соответствующие элементы третьего столбца матрицы В и суммирования произведений. В приведенном примере каждый элемент матрицы-произведения представляет собой сумму двух произведений. Если бы матрица А имела 3 столбца, а матрица В – три строки, то каждый элемент матрицы-произведения являлся бы суммой трех произведений.
Матрица, представляющая собой произведение двух матриц, будет иметь всегда столько строк, сколько их было в первой матрице, и столько столбцов, сколько их было во второй матрице. Если матрица порядка (р х а) умножается на матрицу порядка (q х г), то их произведение будет иметь порядок (р х г).
Виды матриц, чаще всего встречающиеся в ФА
Диагональная матрица. Это квадратная матрица, в которой отличны от нуля только элементы, лежащие на главной диагонали. Главной диагональю называется линия, связывающая левый верхний угол с правым нижним углом матрицы. Диагональная матрица изображена на схеме 4.

Схема 4. Диагональная матрица
Скалярная матрица. Если все элементы диагональной матрицы равны между собой, то такая матрица называется скалярной.

Схема 5. Скалярная матрица
Единичная матрица. Это диагональная матрица, у которой все элементы главной диагонали равны единице. Единичная матрица выполняет в матричной алгебре ту же роль, что и единица в арифметике.

Схема 6. Единичная матрица
Обратная матрица. Выше уже была рассмотрена операция умножения матриц. В матричном исчислении существует операция, соответствующая делению в арифметике. Известна простая зависимость, которую можно представить в виде: X1/X =1. Эта зависимость означает, что произведение любого числа на обратное ему число равно единице. В матричной алгебре существует такая же связь.
ВАЖНЕЙШИЕ ПОНЯТИЯ И ТЕХНИКА ФАКТОРНОГО АНАЛИЗА
Два вводных примера

Пусть имеются четыре переменные, отдельные значения которых получены в результате наблюдения за рядом индивидуумов. Вычислим все парные коэффициенты корреляции, в итоге получим следующую корреляционную матрицу:
Визуальный анализ показывает, что корреляционная матрица является симметрической, т. е. наддиагональные элементы представляют собой зеркальное отражение поддиагональных относительно главной диагонали. При рассмотрении матрицы бросается в глаза тот факт, что все коэффициенты корреляции положительны. Кроме того, между первой и второй переменными имеется относительно тесная корреляционная связь, третья переменная с первыми двумя связана слабее, а четвертая практически не зависит от всех предыдущих. Следуя обычной процедуре корреляционного анализа можно было бы проверить значимость каждого коэффициента корреляции.
Целью факторного анализа является извлечение на поверхность величины, так называемого фактора, который бы по возможности точнее позволил воспроизвести наблюдаемые корреляции. Этот фактор и связанная с ним процедура вычислений вначале являются гипотетическими.
Обсудим подход к выявлению фактора и к процедуре вычислений.
Наблюдавшиеся коэффициенты корреляции можно в каждом случае воспроизвести с помощью следующего уравнения:
R+ F1 F/1
 A A/
A A/Вектор F1 = (0,90 0,80 0,50 0,05) представляет собой фактор. Матрица R+ является матрицей воспроизведенных коэффициентов корреляции. Используя правило умножения матриц, выполним действие F1 • F/1, в результате чего получим матрицу R+, отличающуюся от R диагональными элементами. Диагональные элементы матрицы R+ называются общностями. Например, элементы первого столбца корреляционной матрицы получаем следующим образом:
0,90 • 0,90=0,81; 0,80 • 0,90-0,720; 0,50 • 0,90-0,45; 0,05 • 0,90 = 0,045. И так далее.
Таким образом из чисел (0,90 0,80 0,50 0,05) получаем наблюдаемую корреляционную матрицу.
Как получаются численные значения элементов вектора F1, нас пока не интересует. Их называют факторными нагрузками. Они позволяют произвести численно-формальное объяснение наблюдаемых коэффициентов корреляции. Это дает основание предполагать, что за ними стоит фактор, который мог бы их причинно обусловливать.
Таким образом, мы на примере познакомились с основным уравнением факторного анализа: R+ = F1 • F/1 редуцированная корреляционная матрица равна произведению факторной матрицы на транспонированную.
За наблюдаемыми величинами всегда стоит фактор, но непосредственно для измерения он недоступен. Он гипотетичен. Факторный анализ устанавливает такие гипотетические факторы и из-за этого способ образования гипотез имеет всегда локальный характер.
При приведении корреляционной матрицы (1) к форме (2) возникают две проблемы.
Диагональные элементы матрицы R+ меньше единицы. Эти диагональные элементы называются общностями, а их определение составляет первую проблему ФА, проблему общности.
Второй проблемой является определение фактора F1. Это так называемая проблема факторов. Обе проблемы будут обсуждаться далее подробнее.
Обратимся еще раз к примеру, иллюстрирующему равенство (2). Десять (4+3+2+1 = 10) различных значений элементов (диагональных и поддиагональных) корреляционной матрицы приведены к четырем элементам вектора F1. Эти четыре значения содержат ту же самую информацию, что и вся корреляционная матрица. Таким образом достигается упрощение, причем объем информации сохраняется. Факторные нагрузки соответствуют коэффициентам корреляции, т. е. переменная 1 имеет много общего с фактором F1 (а1 = 0,90), переменная 2 – немного меньше (а2 = 0,80), переменная 3 – еще меньше (а3= 0,50). Переменная 4 почти не связана с фактором (а4 = 0,05).
Геометрически упрощение заключается в том, что единственная мера, а именно фактор F1, достаточна для отражения связей между переменными. Если каждую переменную представить в виде вектора, т. е., попросту говоря, в виде стрелки в пространстве, то в этом примере все стрелки примут одно направление, а именно направление фактора F1, который рассматривается как координатная ось одномерной системы координат. Длина стрелок зависит от длины факторных нагрузок (рис 5.).
Ф
 актор F1
актор F1 1
 .0
.0 0

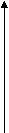 .9 перем.1
.9 перем.1 0
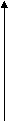 .8 перем.2
.8 перем.20
 .5 перем.3
.5 перем.3 0,05 перем.4
0,05 перем.40.0
Рис. 5. Геометрическая интерпретация матрицы A(2).
Второй пример. Пусть по результатам наблюдений за четырьмя переменными составлена корреляционная матица Rh, диагональные элементы которой заменяем общностями, которые предполагаются известными.

При просмотре корреляционной матрицы бросается в глаза, что первая и вторая переменные сильно коррелируют друг с другом. Можно говорить также о наличии корреляции между третьей и четвертой переменными. Между остальными переменными корреляция не проявилась. В таком случае, когда в корреляционной матрице существуют как бы обособленно два центра тяжести, не связанных друг с другом, для объяснения корреляции используют два фактора. Пусть первый фактор будет F1= (0,90 0,80 0,05 0,05), второй F2 =(0,05 0,05 0,80 0,70). В целом вся корреляционная матрица составляется с помощью двух факторов, и всю модель можно представить в виде равенства (3) F1 F2
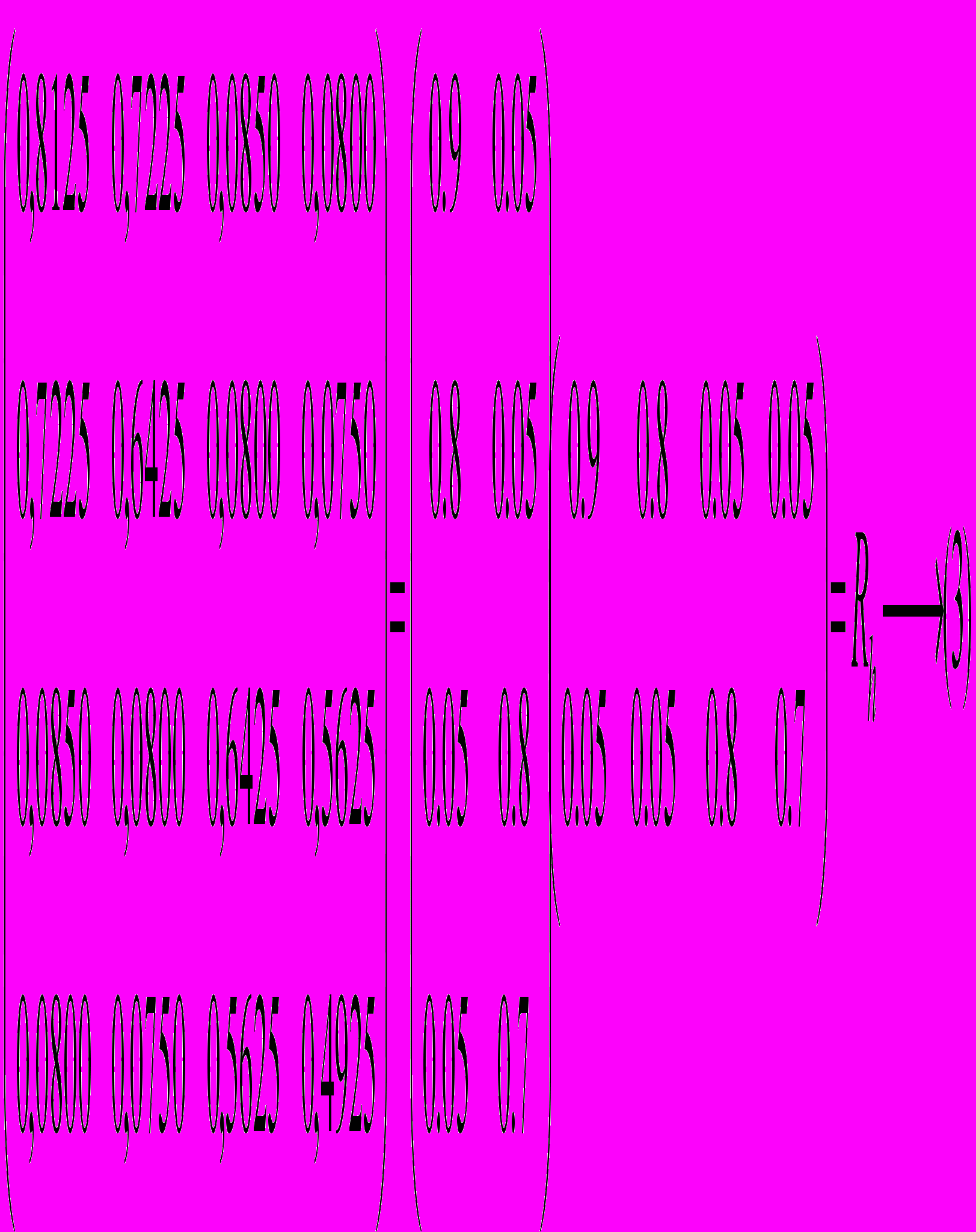 A A/
A A/ В равенстве (3) легко убедиться путем соответствующих вычислений. Первый элемент корреляционной матрицы равен: 0,8125 = 0,90 • 0,90+0,05 • 0,05, по тому же самому правилу умножения матриц получаем другие элементы.
При геометрической интерпретации векторы, соответствующие переменным, расположатся на плоскости. Координатные оси соответствуют факторам, векторы – переменным. Например, конец вектора 1 на рис.6 имеет координаты 0,90 (нагрузка первого фактора) и 0,05 (нагрузка второго фактора), которые берутся из матрицы А. Координатные оси являются факторами, на которые натянуто пространство, содержащее переменные.
F1
 1.0
1.0 0.9
0.9 0.8
0.80.5
 0.1
0.1

0.0 0.1 0.5 0.7 0.8 0.9 1.0 F2
Рис. 6. Геометрическая интерпретация матрицы А (3).
В этих двух примерах мы познакомились в первом приближении с рядом понятий и процедур, которые далее будут определены более подробно. Пока же назовем основные проблемы ФА и покажем схему их решения.
