Geum.ru

Методические указания Екатеринбург 2006 утверждаю декан психологического факультета Глотова Г. А

Вид материалаМетодические указания
Схема решения и основные проблемы факторного анализа.
Классификация факторов и связь между отдельными видами факторов
Важнейшие понятия ФА, связанные с дисперсией
Общая дисперсия
Суть основных проблем факторного анализа
Проблема вращения.
Подобный материал:
1   2   3   4   5   6

Схема решения и основные проблемы факторного анализа.

При проведении ФА все расчеты носят последовательный характер. Процедура выполнения вычислительных операций схематично представлена на рис.7. Четыре вертикальные стрелки соответствуют четырем основным проблемам, возникающим при проведении факторного анализа в тех местах схемы, куда указывают, стрелки.

Y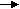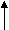ij



R



Rh



F



V



P




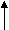
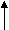
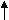
Проблема

общности



Проблема

факторов



Проблема вращения



Проблема оценки значений факторов





Рис. 7. Схема факторного анализа. Процедур вычислений начинается с матрицы исходных данных Y. Горизонтальные стрелки указывают последовательность отдельных этапов ФА; вертикальные стрелки – 4 основные проблемы ФА

  1. ФА начинается с Y – матрицы, исходных данных. По ней вычисляется корреляционная матрица R. По главной диагонали корреляционной матрицы затем проставляют оценки общностей и получают Rh. Это составляет проблему общности, которая состоит в установлении оценок hi2 Это самая первая проблема, которая возникает в ходе факторного анализа.
  2. Стрелка между Rh, и F указывает на проблему факторов. Из Rh, с помощью определенных способов извлекают факторы, получая в результате матрицу F.
  3. Столбцы матрицы F ортогональны и занимают произвольную позицию в отношении переменных, определяемую методом выделения факторов. Возможно большое число матриц F, которые будут одинаково хорошо воспроизводить Рh. Из них должна быть выбрана одна, что составляет проблему вращения. Решение проблемы вращения одним из нескольких способов приводит к матрице V.
  4. И наконец, последняя проблема касается оценки значений факторов для каждого индивидуума.

Классификация факторов и связь между отдельными видами факторов

Задачей факторного анализа является определение матрицы А. Матрица А называется факторным отображением или факторной матрицей, а ее элементы аij – факторными нагрузками.

ОПРЕДЕЛЕНИЕ. Факторная матрица – это матрица, столбцы которой состоят из нагрузок данного фактора на все переменные данной совокупности а строки – из факторных нагрузок данной переменной.

При ортогональных факторах, которые мы до сих пор исключительно и рассматривали, элементы принимают значения между -1 и + 1. Если факторы не ортогональны, то элементы могут принимать большие значения. Здесь мы ограничимся только этим замечанием.

Каждый фактор характеризуется столбцом, каждая переменная – строкой матрицы А. Если факторная нагрузка значительно больше или меньше нуля, то принята упрощенная форма записи в виде крестика (X) в соответствующем месте факторного отображения (рис.8). Выражение «значительно больше или меньше нуля» здесь означает не 0 в математическом смысле, обычно это значение по абсолютной величине превосходящее 0,3 или 0,4. При этом всеми другими нагрузками этого фактора пренебрегают, т. е. факторное отображение упрощается.

факторы

А B C U1 U2 U3 U4 U5 U6 U7 U8












































































































































































































































О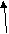бщие характерные факторы

факторы

Генеральный фактор


Рис. 8. Схематическое изображение факторной матрицы


Фактор называется генеральным (general factor), если все его нагрузки значительно отличаются от нуля. Следовательно, он имеет нагрузки от всех переменных и схематически такой фактор изображается столбиком А на рис. 4. Фактор называется общим, {common factor), если хотя бы две его нагрузки значительно отличаются от нуля. Столбики А, В, С на рис. 8 представляют такие общие факторы. Они имеют нагрузки от двух и более переменных. Они могут взаимно перекрываться, т. е. одни и те же переменные могут давать нагрузки на несколько факторов. Генеральный фактор является частным случаем общих факторов, так как он имеет более двух значимых нагрузок.

В противоположность этому факторы являются индивидуальными, если у них только одна нагрузка значительно отличается от нуля (см. столбики U1–U8 на рис.8). В этом случае говорят о характерных факторах {unique factors), которые представляют только одну переменную.

По аналогии с факторами можно провести классификацию переменных по числу достаточно высоких нагрузок. Число высоких нагрузок переменной на общие факторы называется ее сложностью {complexity}. Например, переменная 1 на рис. 8 имеет сложность два, переменная 4 – три.

Итак, столбец факторной матрицы характеризует фактор и его влияние на все переменные. Строка характеризует переменную и ее наполненность различными факторами – сложность и факторную структуру переменной.

Решающее значение в факторной матрице на рис.8 имеют общие факторы – А, В, С. Характерные факторы получаются автоматически, если общие факторы установлены.

Важнейшие понятия ФА, связанные с дисперсией

В факторном анализе используется ряд понятий и зависимостей, тесно связанных с дисперсией. Анализируется дисперсия переменных, представленных в факторной матрице.

Дисперсия – это квадрат стандартного отклонения о2. В широком смысле дисперсия представляет собой один из показателей вариации или рассеивания.

В факторном анализе необходимо различать отдельные компоненты дисперсии.

Полная (единичная) дисперсия переменной раскладывается на отдельные компоненты, которые представляют собой квадраты факторных нагрузок. Для наглядности это разложение графически представлено на рис.9.

Суммы квадратов нагрузок общих факторов и называются общей дисперсией или общностью (commonality) hi2. Общность представляет собой ту часть единичной дисперсии переменной, которая коррелирует с другими переменными – является общей для ряда переменных, то есть которую можно приписать общим факторам. Она равна квадрату коэффициента множественной корреляции между переменной и общими факторами.

Если из 1 вычесть hi2 ,то останется доля дисперсии, обозначаемая ui2, которая соответствует квадрату нагрузки определенного характерного фактора и называется характерностью. Она представляет собой часть единичной дисперсии переменной, которая не связана с общими факторами.

Характерность ui2 можно разбить на две составляющие, одна из которых, bi2, называется специфичностью, а другая, еi2, является дисперсией, обусловленной ошибкой, то есть является случайной, вызванной ошибками при организации измерений и неточностью наблюдений. Специфичность bi2 является той долей единичной дисперсии переменной, которая не связана с общими факторами, не может быть также сведена к ошибке и присуща лишь одной определенной переменной. Специфичность и общность образуют надежность ri2 (reliability). Надежность дополняет дисперсию ошибки до единицы. Общность не превышает надежности и равна ей только в случае нулевой специфичности.


Единичная (полная) дисперсия (по переменной i ) 2 =1 = 100%

Общность hi2
Характерность ui2

аi12
аi22
………………….
аi n2
Специфичность bi2
Дисперсия ошибки еi2

Надежность ri2
еi2


Рис 9. Составляющие полной дисперсии

Общая дисперсия или дисперсия общих факторов составляет ядро факторного анализа. Она может состоять из n компонентов – по числу общих факторов.

В связи с общей дисперсией и общими факторами вспомним о таком важном для факторного анализа понятии как факторная нагрузка (которую Тэрстоун называет также коэффициентом теста).

Факторная нагрузка – это мера «наполнения» переменной (теста) определенным фактором, мера, в соответствии с которой данный тест требуют для своего выполнения данного фактора, т. е. данного свойства или данной способности.

Факторная нагрузка – это коэффициент корреляции между данным тестом (переменной) и фактором. Чем выше эта корреляция, тем в большей степени, тест «наполнен» данным фактором и тем в большей степени является мерой этого фактора.

В терминах дисперсии факторная нагрузка интерпретируется следующим образом: квадрат каждой факторной нагрузки будет составлять ту долю общей дисперсии теста, которую можно приписать фактору, а сумма квадратов факторных нагрузок каждой строки редуцированной факторной матрицы равна общности данного теста (переменной).


Суть основных проблем факторного анализа

Теперь обсудим каждую из основных проблем ФА подробнее. Суть проблемы общности заключается в том, что значения общностей в редуцированной корреляционной матрице неизвестны, а для начала вычислений их необходимо иметь. На первый взгляд неразрешимая проблема решается так: до начала вычислений задаются некоторые приблизительные значения общностей (например, максимальный коэффициент корреляции по столбцу), а затем на последующих стадиях вычислений, когда уже имеются предварительные величины вычисленных факторных нагрузок, они уточняются. Таким образом, вычислительные алгоритмы ФА представляют собой последовательность итеративных (итерация – это математический термин, означающий результат применения какой-либо математической операции, получающийся в серии аналогичных операций) вычислений, где результаты каждого последующего шага определяются результатами предыдущих. С известной долей упрощения можно считать, что различные алгоритмы факторизации корреляционной матрицы в основном и отличаются тем, как конкретно решается данная проблема.

Суть проблемы факторов заключается в следующем. Основной смысл процедуры факторизации – переход от исходной матрицы данных к корреляционной матрице, далее к матрице факторных нагрузок и к геометрической интерпретации (построению факторных диаграмм – см., например, рис. 6 и 7). Напомним, что главная цель выделения первичных факторов в разведочном ФА состоит в определении минимального числа общих факторов, которые удовлетворительно воспроизводят (объясняют) корреляции между наблюдаемыми переменными. Начинают с однофакторной модели. Эта гипотеза оценивается с помощью какого-либо критерия оптимальности соответствия модели исходной корреляционной матрице. Если расхождение статистически значимо, то на следующем шаге оценивается модель с двумя факторами и т. д. Такой процесс подгонки модели под данные осуществляется до тех пор, пока с точки зрения используемого критерия соответствия расхождение не станет минимальным и будет оцениваться как случайное.

В современных компьютерных программах используются различные методы факторизации корреляционной матрицы, но наиболее часто используется метод главных компонент (= главных факторов, главных осей).

Первым результатом факторизации корреляционной матрицы является расчет статистических показателей для определения минимального числа факторов которые отражаются на экране в виде таблицы 1 (напомним, что максимальное число факторов равно числу переменных, и задача заключается в том, чтобы с помощью имеющихся формально-статистических критериев достаточности отсеять лишние).


Таблица 1

Статистические показатели для определения

минимального количества факторов


фактор
Собственное значение
% объясняемой дисперсии
Сумм. % объясняемой дисперсии

1
5,14
51,4
51,4

2
1,72
17,2
68,6

3
1,03
10,3
78,9

4
0,76
7,7
86,6

5
0,38
3,8
90,5

6
0,33
3,3
93,7

7
0,28
2,8
96,6

8
0,21
2,1
98,7

9
0,08
0,8
99,5

10
0,05
0,5
100


Первый важный показатель в этой таблице (второй столбец) – это величина собственного значения каждого фактора; факторы расположены в таблице по убыванию этой величины. Не очень строго говоря, этот показатель характеризует вес, значимость каждого фактора в найденном факторном решении3. Из таблицы видно, что от 1-го фактора к 10-му (всего было 10 переменных) величина собственного значения убывает более, чем в 100 раз.

Естественно возникает вопрос о том, какая величина данного показателя свидетельствует о значимом вкладе соответствующего фактора, и каков критерий для отсечения незначимых факторов. Часто в качестве такого критерия используют величину собственного значения, равную 1.0, то есть предполагают, что те факторы, у которых этот показатель меньше 1.0, не вносят значительного вклада в объяснение корреляционной матрицы.

Кроме анализа табличных величин полезно оценить динамику величины собственного значения визуально по графику. В большинстве статистических программ такая возможность пользователю предоставляется (см. рис. 10). Как предлагал Р. Кеттел, выделение факторов заканчивается, когда после резкого падения график фактически превращается в горизонтальную прямую линию. Несмотря на видимую простоту и ясность такого рецепта, следует отметить, что когда на графике имеется более чем один излом, то выделение горизонтального участка становится неоднозначным.



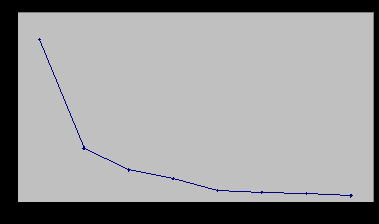
Рис. 10. Изменение величины собственного значения факторов: ось абсцисс – количество факторов; ось ординат – величина собственного значения


Не менее важный расчетный показатель значимости каждого фактора – процент объясняемой дисперсии переменных, содержащейся в корреляционной матрице (третий столбец в табл. 1). Естественно, что все 100% дисперсии будут объясняться только всеми десятью факторами. Однако известно, что при любых измерениях неизбежны разного рода случайные ошибки, и их вклад в общую дисперсию может оказаться значительным. Поэтому предполагается, что ряд выделенных факторов отражает влияние случайных процессов, никак не связанных с оценкой наблюдаемых переменных. Таким образом, формально задача заключается в том, чтобы, с одной стороны, выбрать некоторое минимальное количество факторов, которые бы, с другой стороны, объясняли достаточно большой процент всей дисперсии переменных. Ясно, что эти два требования в принципе взаимно противоречивы, и, следовательно, исследователь стоит перед выбором некоторой критической величины процента объясняемой дисперсии. Никаких точных рецептов по этому поводу не существует, но принято считать, что при хорошем факторном решении выбирают столько факторов, чтобы они в сумме (последний столбец таблицы) объясняли не менее 70–75%. По данным нашего примера оба статистических критерия свидетельствуют о достаточности 3-х факторов.

Однако, стоит подчеркнуть, что главным критерием для выделения минимального количества факторов будет их содержательная интерпретация, а к использованию формально-статистических критериев следует относиться с осторожностью.

Еще один способ решения проблемы факторов предложен В.М.Мельниковым и Л.Т.Ямпольским (Мельников В.М., Ямпольский Л.Т. Введение в экспериментальную психологию личности, с. 107-110). Для выбора лучшего факторного решения они предлагают опираться на пять взаимосвязанных критериев:
  1. Интерпретируемость факторов
  2. Гомогенность – свидетельство внутренней однородности выделенных факторов. Оценивается числом переменных, тесно связанных с фактором.
  3. Контрастность факторного решения. Оценивается по отношению связей между факторами и переменными внутри каждого фактора. Контрастность тем выше, чем связи между переменными, формирующими фактор, выше связей между факторами. Такое определение контрастности не требует ортогональности факторов.
  4. Устойчивость основной структуры факторов, то есть сохранность факторов с увеличением их числа.

Информационная надежность. Достигается за счет объединения в факторе большого числа взаимосвязанных переменных. Поскольку каждая переменная содержит ошибку измерения, оценка значения фактора становится более точной с ростом числа учитываемых переменных.

Проблема вращения. Одним из основных кажущихся парадоксов ФА как метода, обеспеченного солидным математическим аппаратом, является неоднозначность расчета факторных нагрузок по исходной корреляционной матрице. Фактически это означает следующее: любой алгоритм факторизации корреляционной матрицы дает какой-то один вариант расчета факторных нагрузок из целого множества эквивалентных.

Поясним сказанное, используя геометрическую интерпретацию результатов ФА. На рис.11 представлены две переменные (vl и v2) в пространстве двух ортогональных факторов (F1 и F2). Переменные изображены в виде векторов, а факторные нагрузки переменных на факторы геометрически представляют собой проекции данного вектора (переменной) на соответствующую координатную ось (фактор). Если мы осуществим произвольный поворот осей координат на какой-то угол, например, на 45 градусов вправо (новые оси – штрих-пунктирные линии на рис. 11), то расположение переменных в новой системе координат (F1'– F2') с математической точки зрения полностью эквивалентно исходному. Изменились лишь величины факторных нагрузок (сравните проекции переменной vl на оси F1 и F1', соответственно, до и после поворота). Таким образом, исходное факторное решение справедливо с точностью до любого угла поворота ортогональных факторных осей вокруг пучка векторов, образованного переменными vl и v2.

Естественно, возникает вопрос об оптимальном расположении переменных в пространстве факторных осей. Как было отмечено выше, эта проблема в принципе не имеет строгого математического решения. Она относится уже к содержательной интерпретации расположения переменных в факторном пространстве.




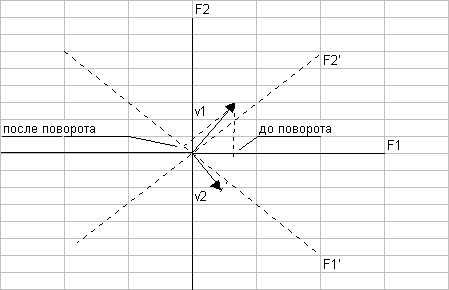
Рис. 11. Факторное пространство 2-х переменных в пространстве 2-х факторов:

Сплошные линии (F1 и F2) – до поворота; пунктирные линии (F1' и F2' ) – после по ворота.

Фактически суть проблемы состоит в следующем: какой набор факторных нагрузок (или какая геометрическая модель результатов ФА) будет более подходящим для интерпретации исследователем. Поскольку при повороте осей координат факторные нагрузки по одному фактору могут расти, а по другому – уменьшаться, то, соответственно, будет расти или уменьшаться вклад этих факторов в разные переменные. Из этого следует, что нужно искать такой вариант расположения переменных в факторном пространстве, который наилучшим образом соответствует ожиданиям исследователя, его предположениям о взаимосвязи и взаимозависимости исследуемых переменных. Как правило, при использовании ФА полагают, что существует одно оптимальное положение осей координат, соответствующее существенным для данного исследования и хорошо интерпретируемым факторам.

Описанный выше процесс поиска оптимальной факторной структуры получил название процедуры вращения факторов. По образному выражению Л. Терстоуна, цель исследователя заключается в поиске «простой структуры» или попытке объяснить большее число переменных меньшим числом факторов. С формальной точки зрения при поиске простой структуры следует иметь в виду следующее: целесообразно стремиться к получению для каждой переменной максимального числа больших факторных нагрузок по одним факторам и одновременно наибольшего количества минимальных факторных нагрузок по другим факторам. Следуя этому правилу, мы стремимся сделать так, чтобы одну группу переменных можно было в большей степени объяснить влиянием одних факторов, а другую – других. Таким образом, «простота» хорошего факторного решения заключается в том, что каждая переменная имеет наиболее простое факторное объяснение, т.е. характеризуется преобладающим влиянием некоторого одного фактора, и в меньшей степени связана с другими факторами. И наоборот: один фактор должен быть специфическим образом связан с одной группой переменных и не связан с другими переменными. В предельном случае самая простая структура получается тогда, когда все переменные располагаются на соответствующих факторных осях, т. е. имеют ненулевые факторные нагрузки только по одному фактору, а по остальным – нулевые. Возвращаясь к рис.11, укажем на результат вращения: после поворота факторных осей на 45 градусов вправо, нагрузка переменной vl по первому фактору резко уменьшилась и одновременно немного возросла по второму. Кроме того заметно уменьшилась нагрузка переменной v2 по второму фактору. Таким образом «простота» новой факторной структуры выразилась в доминирующем влиянии первого фактора на переменную v2, а второго фактора – на переменную vl.

Выделяют два класса методов вращения – методы ортогонального вращения, когда при повороте осей координат угол между факторами остается прямым (и, следовательно, остается верным предположение о некоррелированности факторов), и более общие методы косоугольного вращения, когда первоначальное ограничение о некоррелированности факторов снимается.

Методы ортогонального вращения: варимакс, квартимакс, эквимакс и биквартимакс. Варимакс – наиболее часто используемый на практике метод, цель которого – минимизировать количество переменных, имеющих высокие нагрузки на данный фактор, что способствует упрощению описания фактора за счет группировки вокруг него только тех переменных, которые с ним связаны в большей степени, чем остальные.

Квартимакс в определенном смысле противоположен варимаксу, поскольку минимизирует количество факторов, необходимых для объяснения данной переменной; поэтому он усиливает интерпретабельность переменных. Квартимакс-вращение приводит к выделению одного из общих факторов с достаточно высокими нагрузками на большинство переменных. Эквимакс и биквартимакс – это два схожих метода, представляющих собой своеобразную комбинацию варимакса, упрощающего описание факторов, и квартимакса, упрощающего описание переменных. Отметим, что выбор более подходящего метода вращения конечно же требует известного опыта использования ФА, однако специальные исследования X. Кайзера при прочих равных условиях свидетельствуют в пользу преимущественного применения варимакса.

Методы косоугольного вращения предполагают коррелированность факторов и, следовательно, возможность существования факторов более высокого порядка, объясняющих наблюдаемую корреляцию. Основное преимущество косоугольного вращения состоит в возможности проверки ортогональности получаемых факторов: если в результате вращения получаются действительно ортогональные факторы, то можно быть уверенным в том, что ортогональность им действительно свойственна, а не является следствием использования метода ортогонального вращения. В статистических программах наибольшую популярность получил метод облимин, по своей сути эквивалентный методу эквимакс при ортогональном вращении. В расчетах с помощью облимина используется специальный параметр (называемый в разных программах а или S), задающий степень косоугольности факторов при вращении. Большие отрицательные значения этого параметра соответствуют наиболее косоугольным решениям, а меньшие отрицательные значения – наиболее ортогональному решению.

Стоит особо отметить, что перед выполнением процедуры вращения следует указать количество факторов, в пространстве которых и производится вращение. Поэтому вопрос о минимальном количестве факторов следует решить (в первом приближении!) до того. После осуществления вращения и анализа факторных диаграмм можно еще раз вернуться к проблеме минимального количества факторов, чтобы затем еще раз выполнить вращение с другим количеством (меньшим или большим) факторов. Например, на основании использования ряда статистических критериев, описанных выше, мы начинаем проводить вращение с учетом наличия 4-х факторов, но в ходе анализа факторных диаграмм убеждаемся в избыточности третьего и четвертого факторов и окончательное вращение выполняем в 2-х факторном пространстве. Таким образом, вращение и анализ факторных диаграмм следует проводить несколько раз с учетом разного количества факторов, начиная, как правило, с избыточного количества.

Важно! Простая структура – существенный, но не основной критерий «хорошести» результатов ФА и, следовательно, единственности и оптимальности расположения исследуемых переменных в системе факторных координат. Главное – содержательный анализ полученных результатов.