Методическое пособие москва 2007 министерство образования российской федерации федеральное агенство по образованию
| Вид материала | Методическое пособие |
| 7.2. Функциональный и исторический анализ системы Предметный анализ Исторический анализ 7.3. Представление структур через матрицы связей |
- «Личное страхование», 397.08kb.
- Федеральное агенство по образованию министерство образования и науки российской федерации, 332kb.
- Министерство образования и науки российской федерации федеральное агенство по образованию, 529.84kb.
- Министерство образования и науки российской федерации федеральное агентство по образованию, 32.48kb.
- Российской Федерации Федеральное агентство по образованию обнинский государственный, 77.01kb.
- Российской Федерации Федеральное агентство по образованию обнинский государственный, 130.31kb.
- Российской Федерации Федеральное агентство по образованию обнинский государственный, 84.76kb.
- Российской Федерации Федеральное агентство по образованию обнинский государственный, 90.77kb.
- Российской Федерации Федеральное агентство по образованию обнинский государственный, 81.87kb.
- Учебное пособие Кемерово 2005 федеральное агенство по образованию российской федерации, 2102.39kb.
7.2. Функциональный и исторический анализ системы
Следующий шаг системного анализа - это исследование объекта, когда на основе результатов предметного (структурного) анализа проводится функциональный и исторический анализ. Правильное представление об объекте как системе можно получить, только если продолжить его структурное исследование на шаге первом – «включенность – целостность – делимость» (желательно оформлять, записывать результаты исследования). Обозначим шаги структурного анализа системы, как - предметный аспект, и дополним его функциональным и историческим исследованиями. Получим тогда следующую триаду (первый элемент является сверткой шага №1):
Итак.
I. Предметный анализ: Система выделяется как целостность. Далее определяют, из чего состоит система и как связаны компоненты системы (структурный анализ). Основа предметного исследования - целостность и делимость системы.
Далее надо установить место системы в надсистемах (включённость) и выявить её связи с элементами надсистем, как конкретные выражения включённости. Для этого надо ответить на вопросы:
- Из чего состоит надсистема, в которую входит наша система?
- Как в надсистеме наша система связана с другими системами (по сути каков "пучок связей" нашей системы с окружающими другими системами надсистемы)?
II. Функциональный анализ: Это анализ динамики связей, которые выявлены на этапе предметного анализа. Надо ответить (письменно!) на вопросы:
- Как работает данный компонент системы? (внутренние функции)?
- Как работает наша система в данной надсистеме? (внешняя функция)?
То есть, надо выявить перечень внутренних и внешних функций и указать, с какими компонентами какие функции связаны. В итоге это позволяет построить атлас структурно-функциональных схем системы и на его основе – атлас процессных схем.
III. Исторический анализ: тоже относится к динамике, но уже к другой - динамике развития системы: "Если ты хочешь понять что-либо, узнай, как оно возникло, и что его ждёт впереди". При этом, как минимум, строят жизненный цикл системы, разделяют его на несколько этапов:
- возникновение;
- становление;
- эволюция;
- разрушение или преобразование.
Для системы определяется, как она прошла предыдущие фазы, фиксируется её теперешнее состояние в цикле, то есть текущая стадия жизненного цикла, намечаются особенности её дальнейшего развития (прохождения последующих фаз), то есть по существу проводится агрегирование жизненного цикла в трехфазный цикл: генезис, праксис, прогноз.
7.3. Представление структур через матрицы связей
Поскольку понятие "связь" (вместе с понятием "структура", как "сумма связей") занимает ведущее место, следует упомянуть классический способ регистрации связей, принятый в большинстве дисциплин. Это регистрация связей с помощью матриц.
Чтобы построить квадратную матрицу связей между компонентами системы, следует взять список имён компонентов
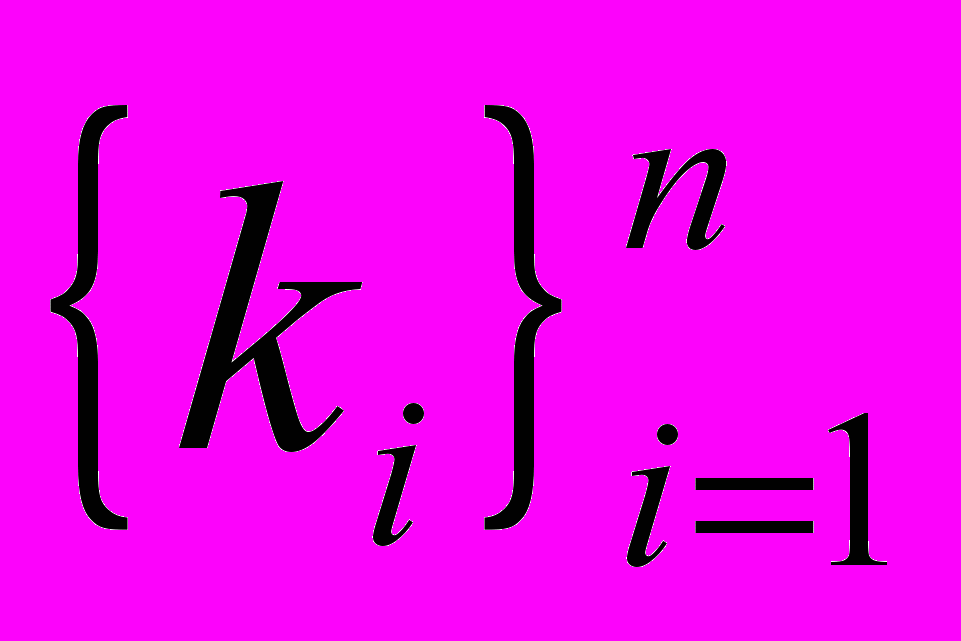и превратить эти имена (в заданном порядке) в имена строк таблицы и в имена столбцов этой же таблицы. Тогда получится n2 ячеек, в которые можно записывать сведения о наличии, либо отсутствии связи между любой парой компонентов.По поводу формы записи этих сведений могут быть приняты самые разные соглашения, например, если никакой связи cij между компонентом
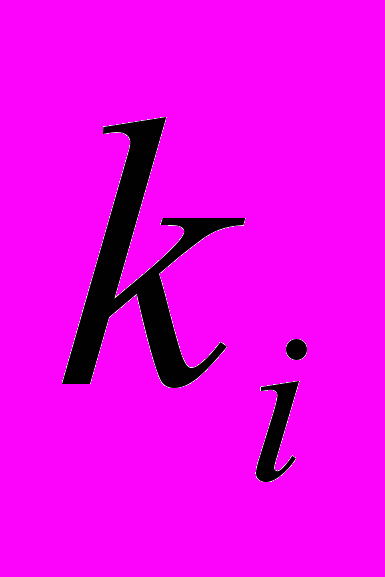и 
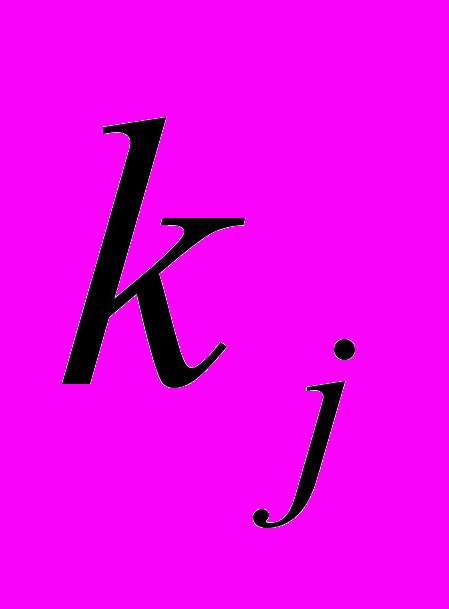нет, то ставят значение сij=0, если желают указать на ориентированность связи, то ставят значение cij=1, и cji=0, если связь "идёт" только от компонента 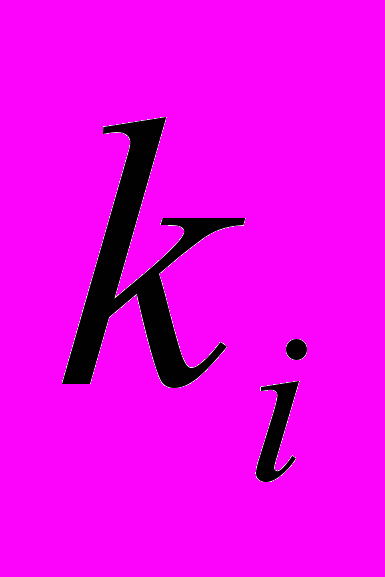названного в строке, к компоненту 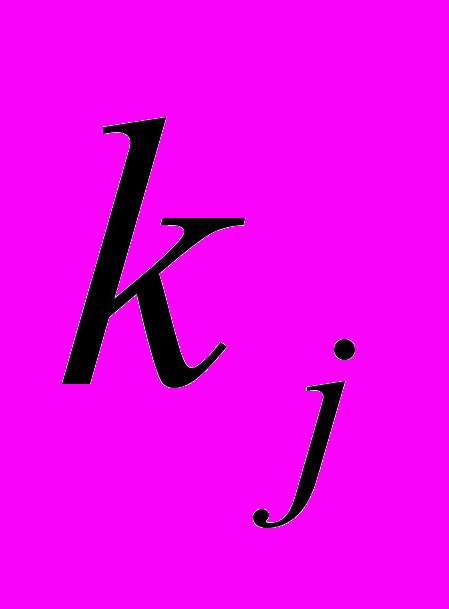, названному в столбце. Если никакое значение не проставлено (пробел), то это указывает просто на отсутствие информации о характере связи данных компонентов. Конечно, можно предложить ставить промежуточные значения, между 0 и 1 в клетках матрицы, если нет уверенности в том, что связь имеется наверняка. В этом случае промежуточные значения, например 0,75 говорят о том, что аналитик на три четверти уверен в наличии связи.Если какой-либо диагональный элемент такой матрицы равен 1, то это сигнализирует об особом типе связи (рефлексивной: элемент связан сам с собой). Если матрица
строится на одном множестве (списке, перечне) компонентов, или функций, то она имеет вид| | k1 | k2 | | kn |
| k1 | c11 | c12 | | c1n |
| k2 | c21 | c22 | | c2n |
| | | | | |
| kn | cn1 | cn2 | | cnn |
На основе матрицы
может быть построен граф структуры системы, вершинами которого являются компоненты системы 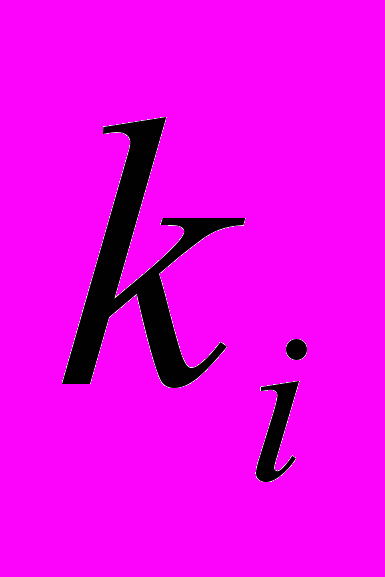, а дуги проводятся между теми компонентами, для которых значения cij=1.