Учебно-методический комплекс для студентов очного и заочного отделений Для специальности 080504 государственное и муниципальное управление

Вид материала

Учебно-методический комплекс

Содержание Как видим, показатели достаточно близки. 7.2. Таблицы смертности Интервальные показатели Кумулятивные показатели Графа 7. Общее число человеколет, прожитых в возрастном интервале Графа 8. Число человеколет, которое предстоит прожить после достижения точного возраста х Графа 9. Средняя продолжительность предстоящей жизни

Подобный материал:

• Учебно-методический комплекс для студентов специальности 080504 «Государственное, 816.03kb.
• Учебно-методический комплекс для студентов специальности 080504 «Государственное, 1310.34kb.
• Учебно-методический комплекс Для студентов, обучающихся по специальности 080504., 591.47kb.
• Учебно-методический комплекс для студентов специальности «Государственное и муниципальное, 852.85kb.
• Учебно-методический комплекс по дисциплине «Геополитика» для студентов специальности, 910.82kb.
• Учебно-методический комплекс для студентов, обучающихся по специальности 080504 «Государственное, 604.34kb.
• Учебно-методический комплекс для студентов специальности 080504 Государственное и муниципальное, 1331.5kb.
• Учебно-методический комплекс Дисциплина реклама в социально-культурной сфере ( цикл, 1250.21kb.
• Учебно-методический комплекс Для студентов отделений очного и заочного обучения. Специальность, 331.71kb.
• Учебно-методический комплекс уфа 2008 удк 330 ббк 65., 1042.22kb.

Как видим, показатели достаточно близки.

7.2. Таблицы смертности

Таблицы смертности (дожития) – это числовые модели смертности, служащие для характеристики ее общего уровня и возрастных особенностей в различных населениях. Они представляют собой систему упорядоченных по возрасту и взаимосвязанных между собой рядов чисел, которые в своей совокупности описывают процесс вымирания некоторого теоретического поколения с фиксированной начальной численностью (корень таблицы). Чаще всего корень таблицы смертности равен 100000.

В демографии различают таблицы смертности для реального и условного поколения.

В зависимости от шага временной шкалы различают полные (шаг равен 1 году) и краткие (шаг равен 5 или 10 годам) таблицы.

Показатели (функции) таблиц смертности делятся на интервальные и кумулятивные. Первые характеризуют смертность на данном этапе возраста, вторые – за весь период жизни до и после данного точного возраста.

Интервальные показатели таблицы смертности обозначаются с помощью соответствующего символа и двух нижних индексов. При этом правый индекс обозначает начало возрастного интервала, а левый его длину - _nS_x, (где S – любой символ, х – точный возраст (х) лет, т.е. начало возрастного интервала, n – длина возрастного интервала).

Кумулятивные показатели обозначаются с помощью соответствующего символа и правого нижнего индекса, обозначающего точный возраст - 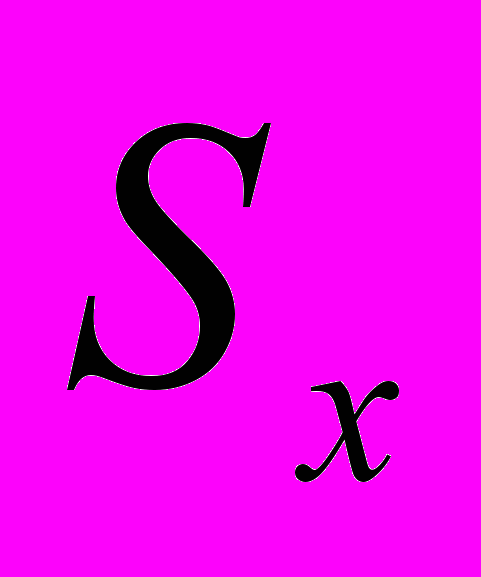(где S – любой символ, х – точный возраст х лет).

Показатели таблиц смертности связаны между собой определенными соотношениями. Исходным показателем является интервальная вероятность умереть в возрасте от х до(х+n) лет.

Рассмотрим основные функции полной таблицы смертности (см. таблицу 4.1):

• Графа 1. Возрастной интервал (х, х+1) год;
  
• Графа 2. Кумулятивный показатель числа доживающих до точного возраста х лет (l_x). Он равен вероятности того, что каждая единица исходной совокупности l₀ доживет до точного возраста х лет. Совокупность всех 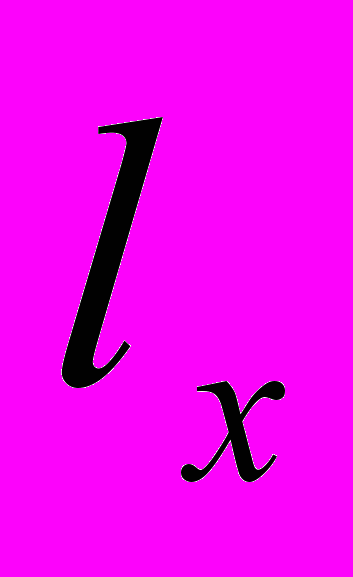называется порядком вымирания, а график, построенный на основе этих чисел, - линией дожития.
  
• Графа 3. Интервальная вероятность умереть в возрасте от х до (х+1) год, обозначаемая q_x. Каждое q_x представляет собой вероятность, что человек, достигший точного возраста х, не доживет до возраста (х+1) год. Эти вероятности рассчитываются на основе соответствующих повозрастных коэффициентов смертности реального населения.
  
• Графа 4. Интервальная вероятность остаться в живых в возрасте от х до (х+1) год. Каждое р_х представляет собой вероятность того, что человек, достигший точного возраста х лет, доживет и до возраста (х+1) год. Очевидно, что возможно одно из двух событий: дожить или не дожить, поэтому сумма q_x и р_х равна 1.
  
• Графа 5. Число умирающих на интервале возраста от х до (х+1) год - d_x. Это число также зависит от корня таблицы. Сумма d_x для всех возрастов равна l.
  
• Графа 6. Доля последнего года жизни умирающих на интервале возраста от х до (х+1) год, α_х . Каждый из d_x умирающих на возрастном интервале от х до (х+1) лет, прожил полные х лет плюс некоторую часть этого возрастного интервала. Средняя из этих долей и обозначается α_х.
  
• Графа 7. Общее число человеколет, прожитых в возрастном интервале от х до (х+1) лет, L_x. Каждый из тех, кто проживет полный возрастной интервал (х, х+1) лет, вносит в общее число человеколет (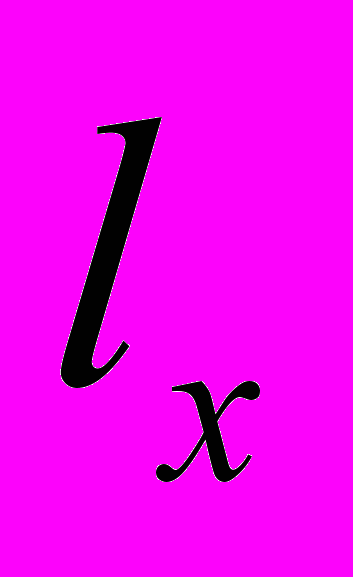-d_x) лет. Каждый же из тех, кто умрет на этом интервале возраста, вносит в L_x в среднем 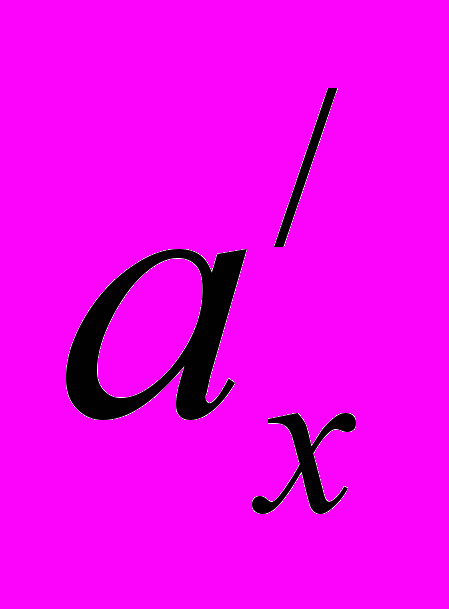часть этого интервала.
  
• Графа 8. Число человеколет, которое предстоит прожить после достижения точного возраста х лет, Т_х. Этот кумулятивный показатель равен сумме человеколет, прожитых на каждом возрастном интервале, начиная с возраста х лет, или
  
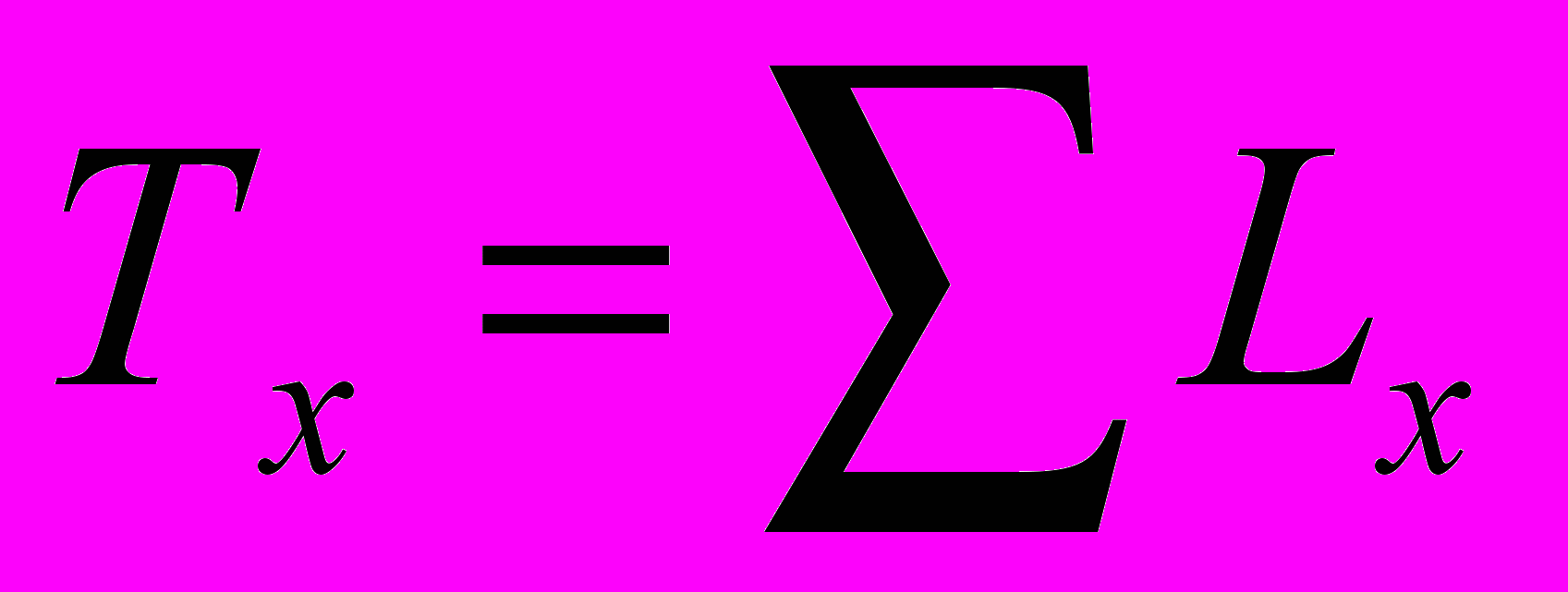
• Графа 9. Средняя продолжительность предстоящей жизни в возрасте х лет, 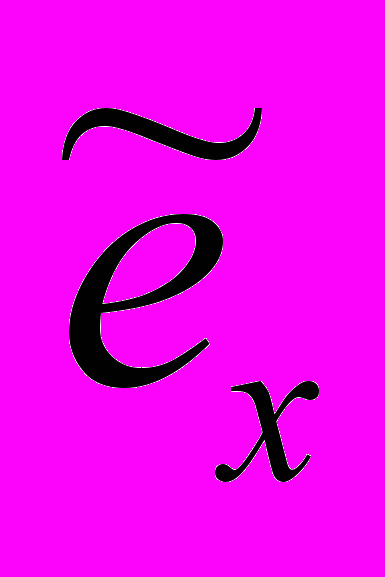. Это число показывает, сколько в среднем предстоит прожить человеку, достигшему возраста х лет, не зависит от корня таблицы. Как правило 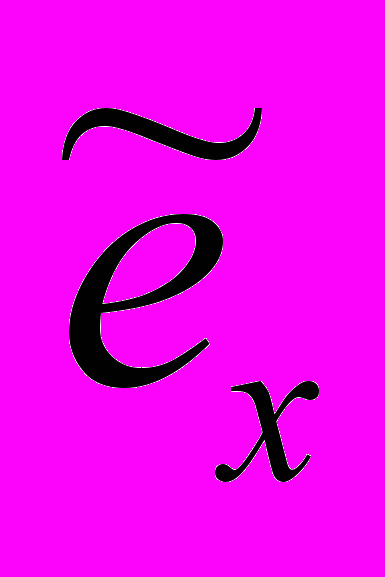убывает с возрастом. Единственное исключение представляет собой возраст 0 лет из-за высокой младенческой смертности. Это называется парадоксом младенческой смертности.
  

Таблица 7.1

Функции таблиц смертности

дИнтервал возраста (х, х+n) лет	Числа доживающих до точного возраста х лет	Вероятность умереть в возрасте (х, х+n) лет.	Вероятность остаться в живых в возрасте (х, х+n) лет	Числа умирающих на интервале возраста (х, х+n) лет	Доля последнего года жизни умирающих на интервале возраста (х, х+n) лет	Числа живущих на интервале возраста (х, х+n) лет	Число человеколет, прожитых после достижения точного возраста х лет	Средняя ожидаемая продолжительность предстоящей жизни в возрасте х лет
lx	nqx	nрх	ndx	nαх	nLx	Тх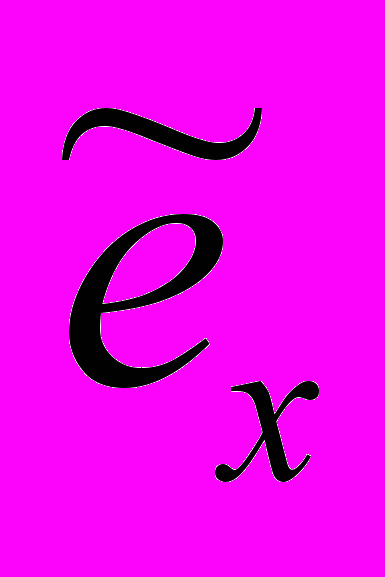
	100000		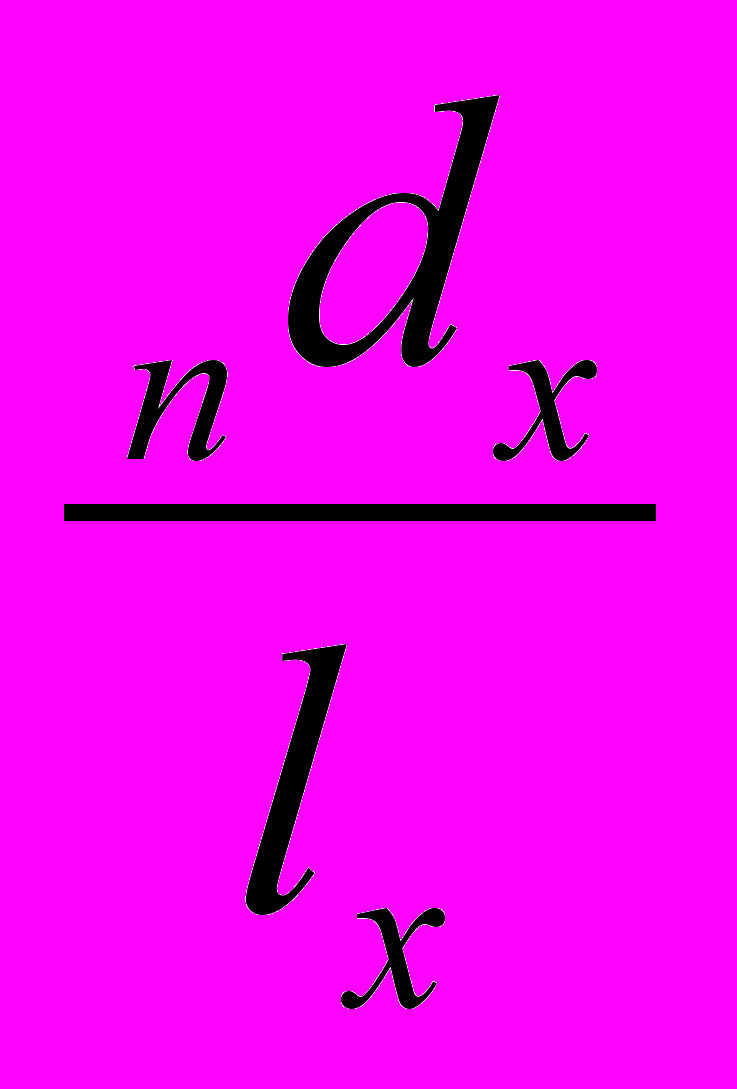		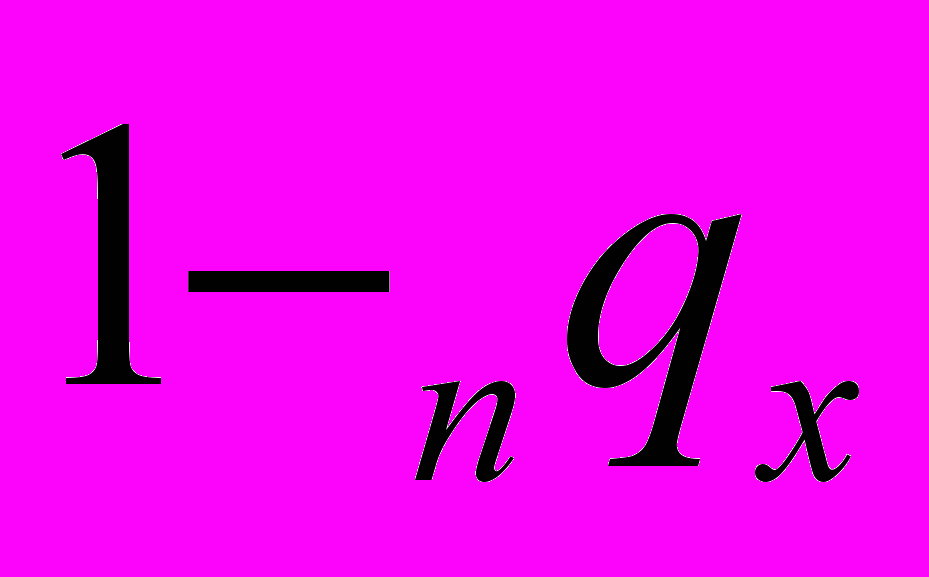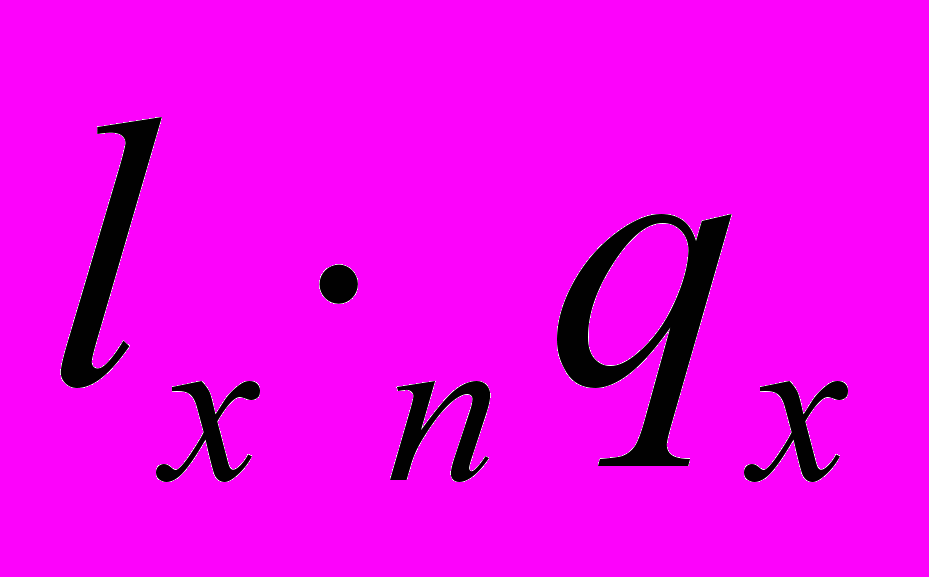0,10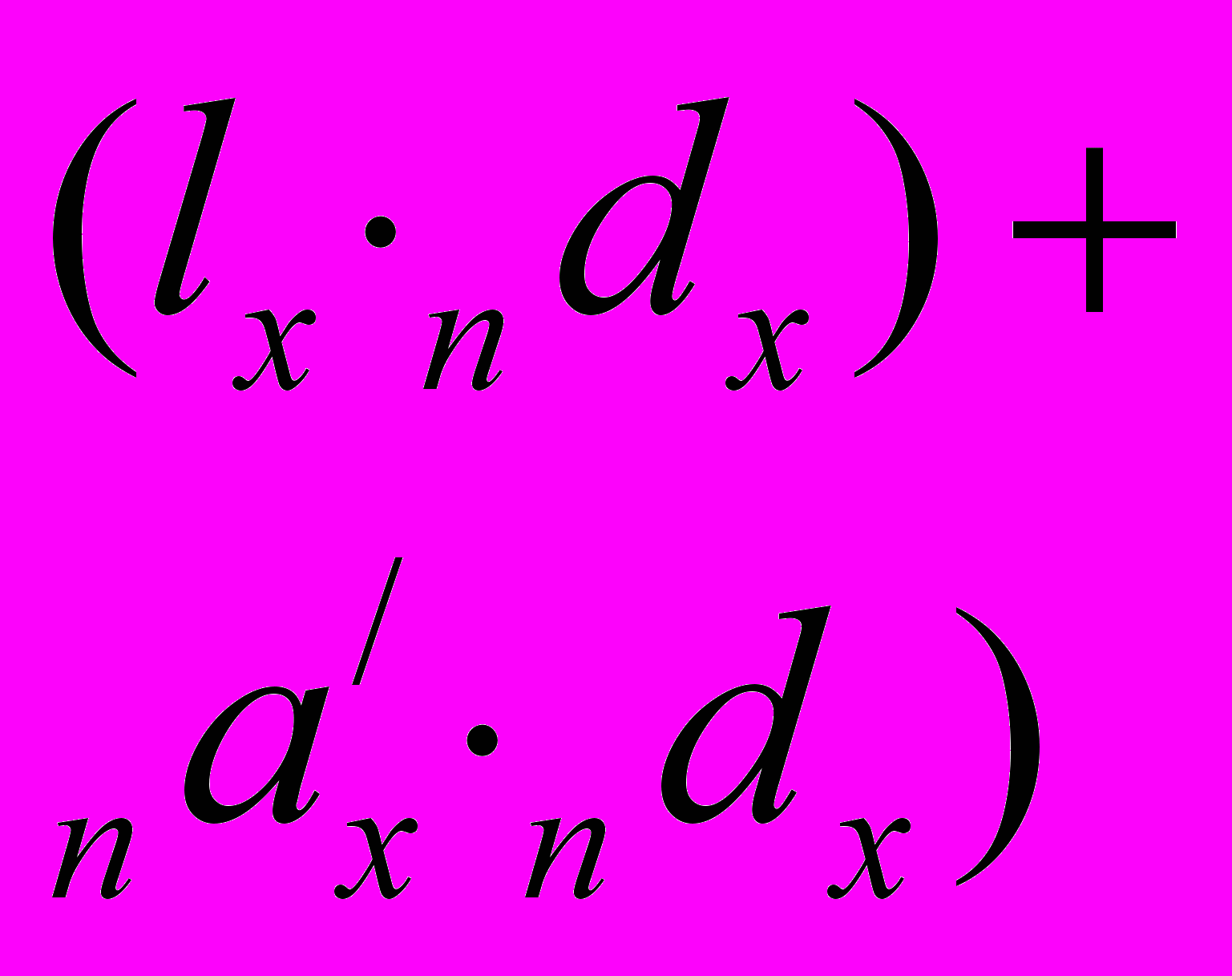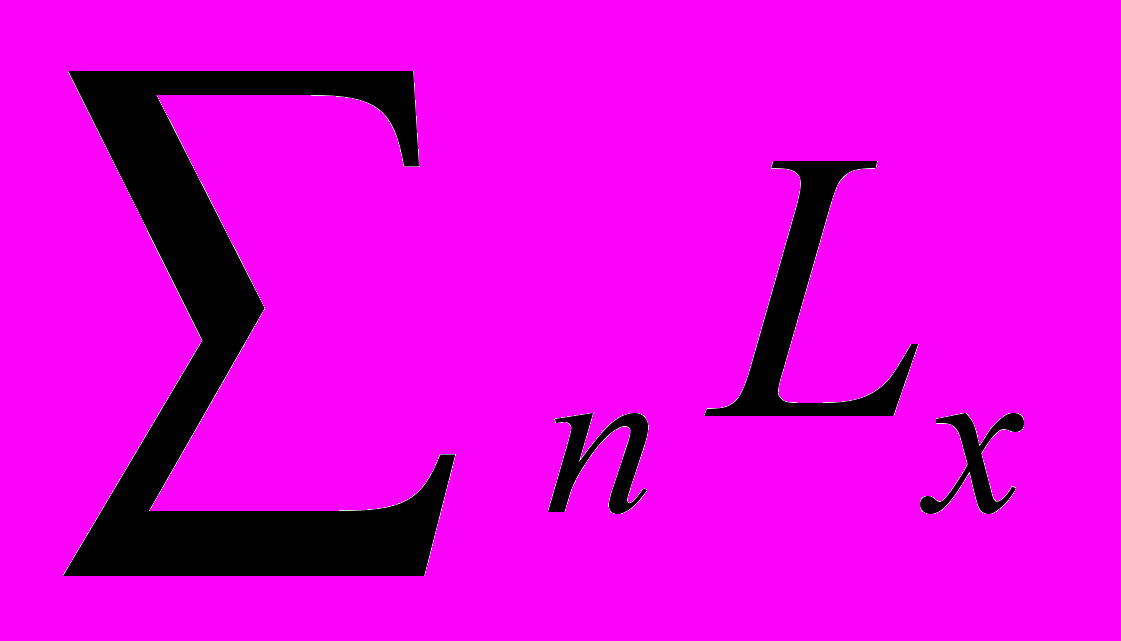
1-2	100000-d0		n		0,43
2-3		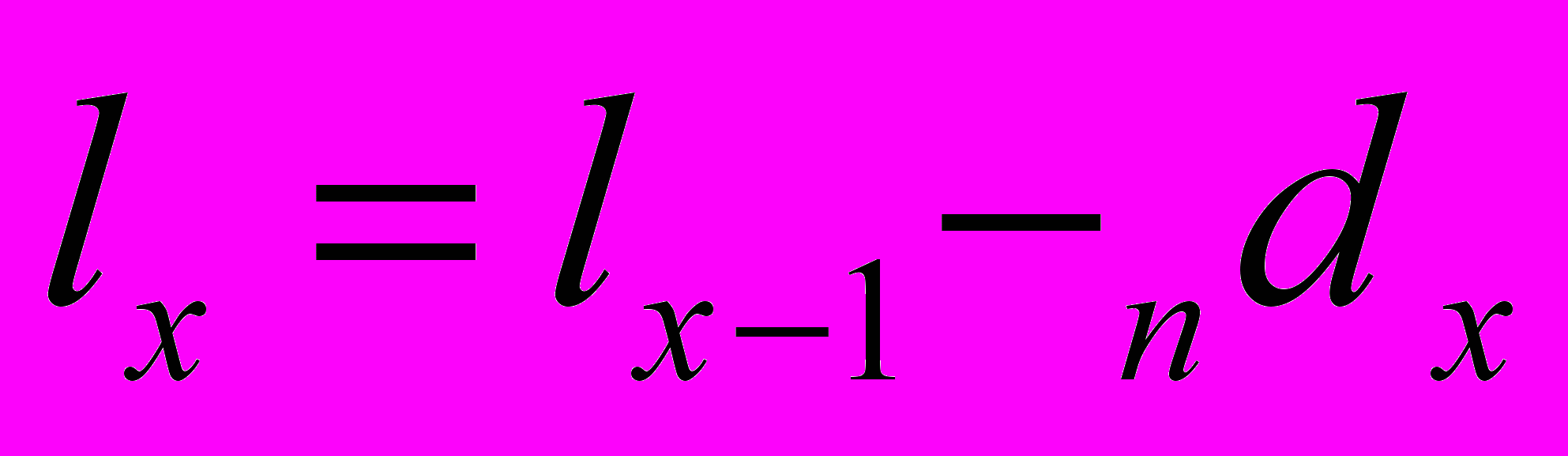			0,45
3-4					0,47
4-5					0,49
5-6					0,50