2 закон Ньютона (основне рівняння динаміки для тіла незмінної маси)

Вид материала

Закон

Содержание R – відстань від осі обертання.Динаміка матеріальної точки.

Подобный материал:

• Тема. Фізичне тіло І речовина. Маса тіла. Одиниці маси. Вимірювання маси тіл. Лабораторна, 374.64kb.
• З хімії для вступу на перший курс навчання до Вінницького національного технічного, 99.03kb.
• Програма нормативного курсу "Математична економіка" 5курс, "спеціаліст" "Математика", 67.55kb.
• План Вступ І. Визначення функціонального рівняння ІІ. Методи рішення функціональних, 228.44kb.
• Предмет Спецкурс "Вступ до фізики твердого тіла", 43.8kb.
• Відокремлення коренів рівняння, 189.57kb.
• Мова тіла вчителя на уроці, 31.32kb.
• Механика Ньютона Какими задачами ограничиваются возможности механики Ньютона? закон, 34.74kb.
• План Рівняння з відокремленими та відокремлюваними змінними Однорідні диференціальні, 199.1kb.
• Обчислювальні методи розв’язку нелінійних рівнянь, 310.67kb.

Кінематика.


Середня та миттєва швидкості:



Середнє та миттєве прискорення:



Миттєва швидкість і радіус-вектор точки при довільному русі:

;

Переміщення точки за проміжок часу [t₁, t₂] та пройдений нею шлях:



Нормальне, тангенціальне та повне прискорення:

,

R – радіус кривизни траєкторії.

Кутові швидкість та прискорення:



Зв’язок між лінійними та кутовими кінематичними величинами при обертанні навколо фіксованої осі:



R – відстань від осі обертання.


Динаміка матеріальної точки.


Основне рівняння динаміки:

.

2 закон Ньютона (основне рівняння динаміки для тіла незмінної маси):

.

Рівняння руху матеріальної точки в неінерціальній системі відліку:

.

Сили інерції:

.

Положення та рівняння руху центра мас системи:

.

Зміна імпульсу системи:



Робота та потужність сили:

.

Зміна повної механічної енергії системи:



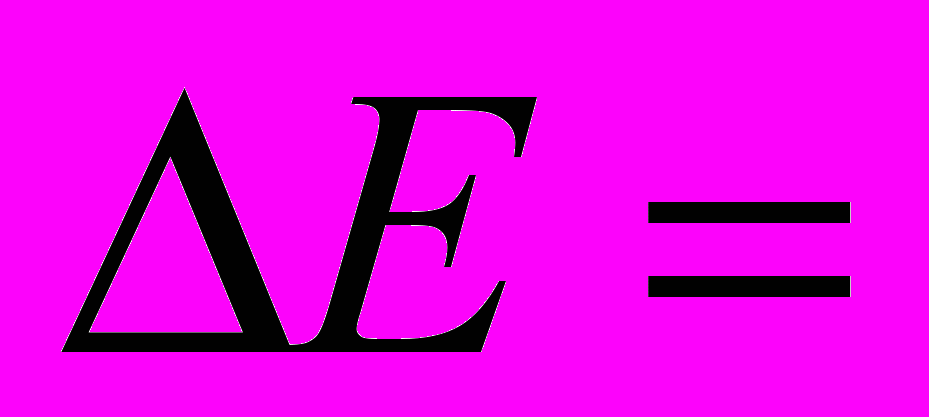
Зв’язок між консервативною силою та потенціальною енергією:



Градієнт у різних системах координат:

декартова:

циліндрична:

сферична:

Динаміка твердого тіла.


Рівняння моментів відносно осі:

.

Рівняння динаміки твердого тіла, що обертається навколо нерухомої осі:



Момент інерції протяжного тіла:

.

Теорема Гюйгенса – Штайнера:



Моменти інерції І_с деяких однорідних тіл:

Тіло	Вісь	Момент інерції Іо
Тонкий стержень довжини l	Перпендикулярна до стрижня	ml2/12
Суцільний циліндр (диск) радіуса R	Співпадає з віссю циліндра (диска)	mR2/2
Суцільна куля радіуса R	Проходить через центр кулі	2mR2/5

СТВ


Перетворення Лоренца:

.

Скорочення довжин й уповільнення часу:

.

Релятивістський закон перетворення швидкостей:

.

Імпульс релятивістської частинки з масою спокою m₀:

.

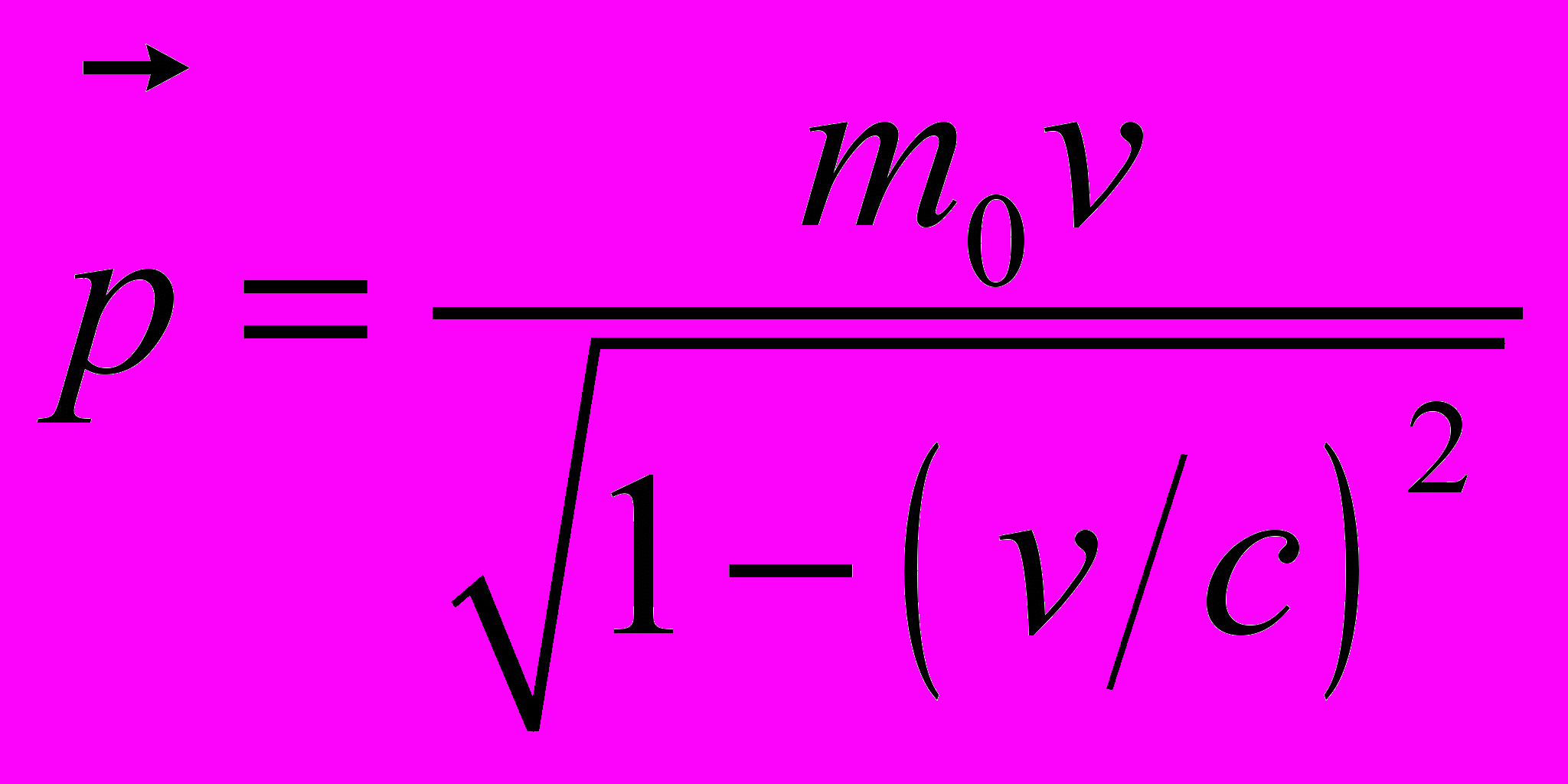
Рівняння динаміки релятивістської частинки:

Рівняння динаміки релятивістської частинки:



Повна енергія та енергія спокою релятивістської частинки:



Кінетична енергія релятивістської частинки:

.

Зв’язок між енергією та імпульсом релятивістської частинки:

.


Механічні коливання.


Зв’язок між параметрами гармонічних коливань:

.

Частота коливань матеріальної точки маси m під дією сили F =  kx:

.

Період гармонічних коливань і иласна частота фізичного маятника:

.

Зведена довжина фізичного маятника:

.

Частота вільних загасаючих коливань за наявності гальмівної сили F =  rv :

коефіцієнт загасання.

Амплітуда загасаючих коливань:

.

Характеристики загасання:

час релаксації

логарифмічний декремент загасання

добротність коливальної системи .

Енергія загасаючих коливань при слабкому загасанні (β << ₀) :

.

Відносна втрата енергії коливань за один період при слабкому загасанні:

.