Обчислювальні методи розв’язку нелінійних рівнянь
| Вид материала | Документы |
- Методи розв’язування нелінійних рівнянь та методи розв’язання систем лінійних алгебраїчних, 17.77kb.
- Зміст діючої програми для загальноосвітніх навчальних закладів. Зміст основних та додаткових, 169.77kb.
- Програма кандидатського іспиту зі спеціальності 01. 01. 02 Диференціальні рівняння, 94.14kb.
- Питання з курсу “Диференціальні рівняння”, 59.17kb.
- Нтд у сучасній теорії диференціальних рівнянь актуальними є питання якісної теорії, 101.01kb.
- Теоретичні питання з курсу „ Аналітична геометрія та лінійна алгебра, 24.09kb.
- Секція математичного аналізу та диференціальних рівнянь, 14.84kb.
- Програми розв’язку задач реалізовано в мові програмування Паскаль. Для учнів класів, 294.71kb.
- Тема: розв’язування тригонометричних рівнянь І нерівностей та обчислення похідної функції, 56.84kb.
- Тема: Методи розв’язування систем рівнянь, 38.35kb.
ЗМІСТ
Обчислювальні методи розв’язку нелінійних рівнянь 3
Методи хорд, дотичних, хорд-дотичних 3
Метод хорд 6
Метод дотичних 7
Метод хорд-дотичних 8
Метод ітерацій 8
Завдання. 9
Програмна реалізація методу 9
Метод половинного поділу 10
Завдання. 10
Програмна реалізація методу 10
МЕТОДИ ЛІНІЙНОЇ АЛГЕБРИ 12
Знаходження визначника матриці методом алгебраїчних доповнень 12
Розв’язок системи рівнянь методом Крамера 14
Розв’язок системи рівнянь методом Гауса 17
20
Знаходження визначника матриці методом Гауса 20
Знаходження оберненої матриці за допомогою 22
Розв’язок системи лінійних рівнянь 25
за допомогою методу Зейделя 25
ІНТЕРПОЛЮВАННЯ ФУНКЦІЙ 27
Інтерполяційний многочлен Лагранжа 27
Інтерполяційний многочлен Ньютона 30
ЧИСЕЛЬНЕ ІНТЕГРУВАННЯ ФУНКЦІЙ 35
Метод прямокутників 35
Метод трапецій 37
Метод Сімпсона 37
РОЗВ’ЯЗУВАННЯ ЗВИЧАЙНИХ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ 40
Метод Ейлера 40
Уточнений метод Ейлера 41
Метод Рунге-Кутта 4-го порядку 42
Обчислювальні методи розв’язку нелінійних рівнянь
Нехай задано рівняння з однією змінною
f(x)=0, (1)
де функція f(x) визначена і неперервна на деякому проміжку
Розв’язати рівняння - означає знайти множину його коренів, тобто таких значень x
Знайти точні значення коренів заданого рівняння можна лише для найпростіших функцій f(x); алгебраїчних многочленiв не вище четвертого степеня, деяких многочленiв степеня n5 і деяких трансцендентних функцій.
Універсальних методів для знаходження точних значень коренів алгебраїчних рівнянь степеня n5 і трансцендентних рівнянь не існує. Тому важливого значення набувають наближені методи знаходження коренів з достатньою для практики точністю. Задача знаходження коренів рівняння (1) вважається розв’язаною, якщо корені обчислені із наперед заданою точністю.
Знаходження наближених коренів рівняння (1) складається з двох етапів:
1) відокремлення коренів, тобто знаходження досить малих відрізків, на кожному з яких міститься один і тільки один корінь рівняння;
2) обчислення коренів з наперед заданою точністю.
До всіх представлених методів розроблені програмні реалізації на мові С. Для порівняння, завдання виконані також за допомогою пакету MathCad.
Методи хорд, дотичних, хорд-дотичних
В даному розділі реалізовані такі методи
I.метод хорд
II.метод дотичних
III.метод хорд-дотичних
Ці методи полягають у наближеній заміні на досить малому відрізку функції f(x) лінійною функцією, яка відповідає хорді, проведеній через дві задані точки (метод хорд), дотичною, проведеною в заданій точці (метод дотичних), або ж ці методи комбінуються (метод хорд-дотичних).
Метод хорд
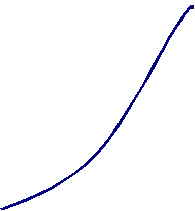
Якщо на інтервалі [a;b] неперервна функція F(x) задовольняє умову F(a)*F(b)<0, то корінь рівняння F(x)=0 наближено знаходиться за рекурентною формулою
xn=xn-1-
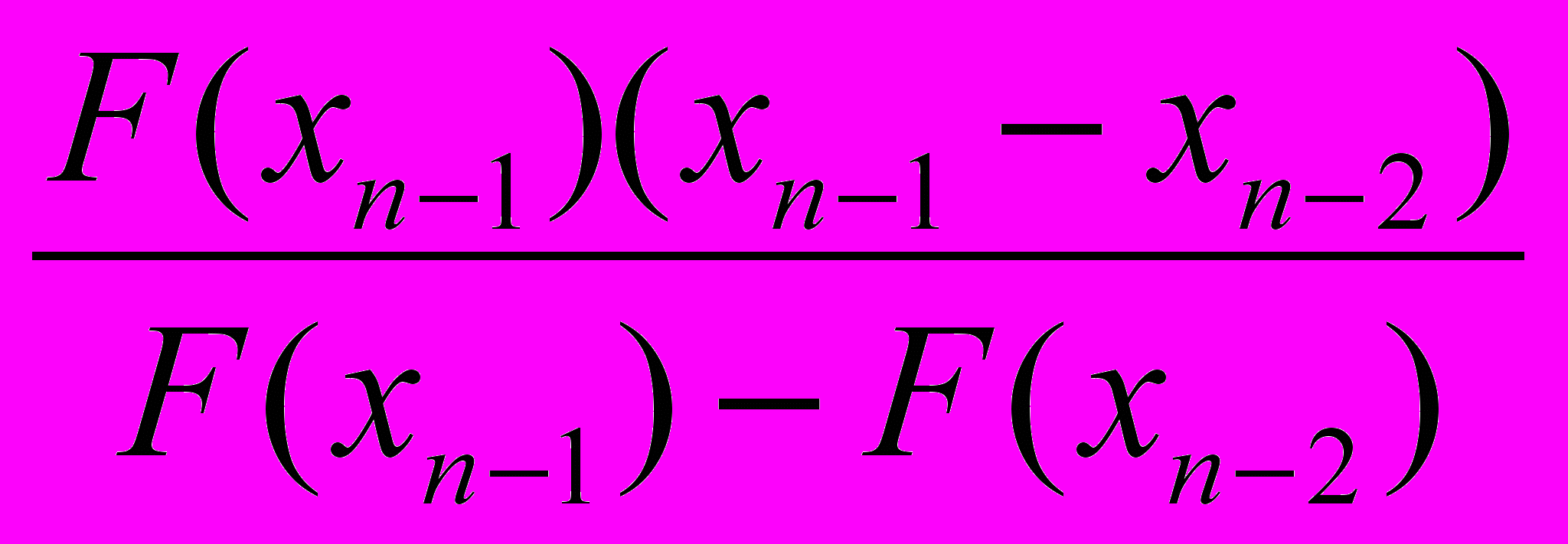 (2)
(2)Похибка обчислюється за формулою
|xn-xn-1|<
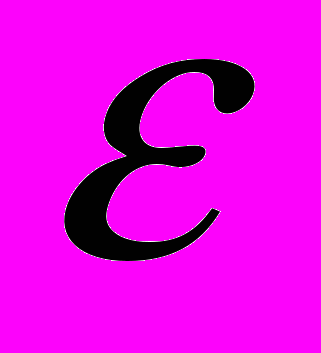 (3)
(3)Г






Xn-1
Xn
Xn-2
рафічна ілюстрація приведена на рис.1.
Метод дотичних
Корінь рівняння F(x)=0 обчислюється за ітераційною формулою
xk+1=xk-
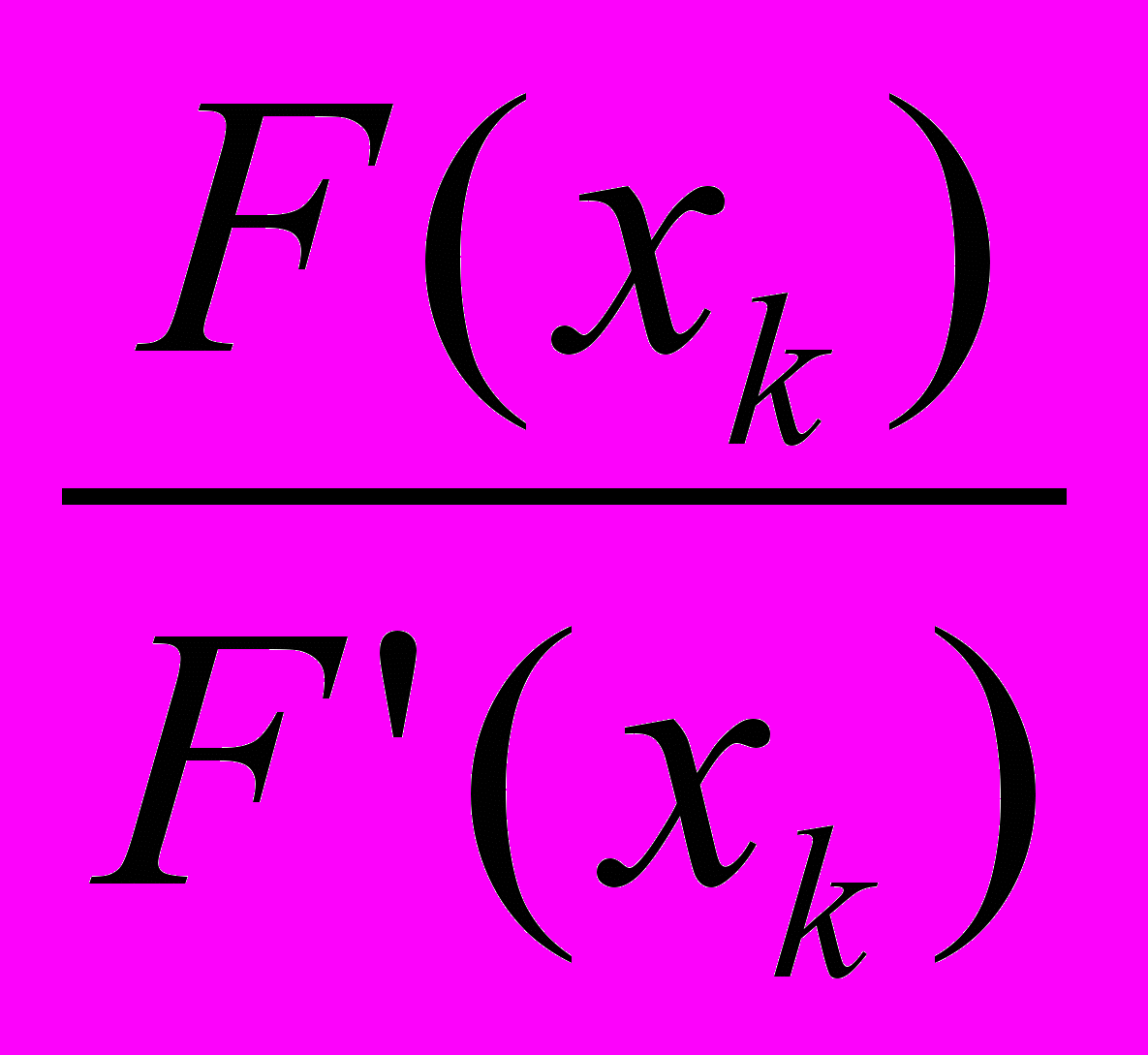 (4)
(4)Графічна ілюстрація приведена на рис.2.
Xk+1


Xk
рис.2
Метод хорд-дотичних
При використанні комбінованого методу хорд-дотичних уточнення інтервалу проводиться як методом хорд, так і методом дотичних. В залежності від знаку функції на кінцях уточненого інтервалу відбувається вибір наступного інтервалу. Графічна ілюстрація методу приведена на рис.3.