План Вступ І. Визначення функціонального рівняння ІІ. Методи рішення функціональних рівнянь Висновки
| Вид материала | Документы |
СодержаниеАх + хВ = у F (f (x), f (y), f (x + y)) = 0 При цьому вважають Застосовуючи послідовно підстановки |
- Обчислювальні методи розв’язку нелінійних рівнянь, 310.67kb.
- Методи розв’язування нелінійних рівнянь та методи розв’язання систем лінійних алгебраїчних, 17.77kb.
- Питання з курсу “Диференціальні рівняння”, 59.17kb.
- Нтд у сучасній теорії диференціальних рівнянь актуальними є питання якісної теорії, 101.01kb.
- План Лінійна однорідна система диференціальних рівнянь з постійними коефіцієнтами Лінійна, 186.96kb.
- Зміст діючої програми для загальноосвітніх навчальних закладів. Зміст основних та додаткових, 169.77kb.
- Методика та технологія реформування організаційного та функціонального змісту управління, 1154.04kb.
- Реалізуючи компетентнісний підхід, враховую два шляхи: зміст І методи навчання, 25.97kb.
- Рівняння 1 порядку, розв’язані відносно похідної. Загальні відомості. Розділення змінних, 69.48kb.
- План Рівняння з відокремленими та відокремлюваними змінними Однорідні диференціальні, 199.1kb.
План
Вступ
І. Визначення функціонального рівняння
ІІ. Методи рішення функціональних рівнянь
Висновки
Використана література
Вступ
І. Визначення функціонального рівняння
Функціональне рівняння — рівняння (лінійне чи нелінійне), у якому невідомим є елемент якого-небудь банахова простору, конкретного (функціонального) чи абстрактного, тобто рівняння виду:
Р (х) = у, (1.1)
де Р(х) — якийсь, взагалі говорячи, нелінійний оператор, що переводить елементи простору X типу В в елементи простору В того ж типу. Якщо функціональне рівняння містить ще і числовий (чи загальний функціональний) параметр λ, то замість (1) пишуть
Р (х; λ) = у,
де x ε X , y ε Y, λ ε Λ, Λ — простір параметрів.
Рівняннями виду (1) є конкретні чи абстрактні диференціальні рівняння, звичайні і з частковими похідними, інтегральні рівняння, інтегро-диференціальні рівняння, функціонально-диференціальні і більш складні рівняння математичного аналізу, а також системи алгебраїчних рівнянь, кінцеві і нескінченні, рівняння в кінцевих різницях і ін.
У лінійному випадку розглядаються функціональні рівняння 1-го роду
А х = у
і 2-го роду
х – λ А х = у,
де А — лінійний оператор з X в У,
λ — параметр.
При цьому формально функціональне рівняння 2-го роду може бути записане у виді рівняння 1-го роду
Т х = у ( Т=1 - λ А ).
Однак виділення тотожного оператора І виявляється доцільним, тому що оператор А може мати кращі властивості, чим оператор Т, що дозволяє повніше досліджувати розглянуте рівняння.
Функціональні рівняння розглядаються також і в інших просторах, наприклад, у просторах, нормованих елементами напівупорядкованих просторів.
Якщо рішення функціональних рівнянь є елементами простору операторів, то такі функціональні рівняння називаються операторними рівняннями, конкретними чи абстрактними. Тут також можуть бути алгебраїчні операторні рівняння, лінійні і нелінійні, диференціальні, інтегральні й інші операторні рівняння. Наприклад, нехай у нормованому кільці [Х] = [Х → X] лінійних операторів, що переводять простір X типу В в себе, розглядається звичайне диференціальне рівняння на нескінченному проміжку 0 ≤ λ ≤ ∞:
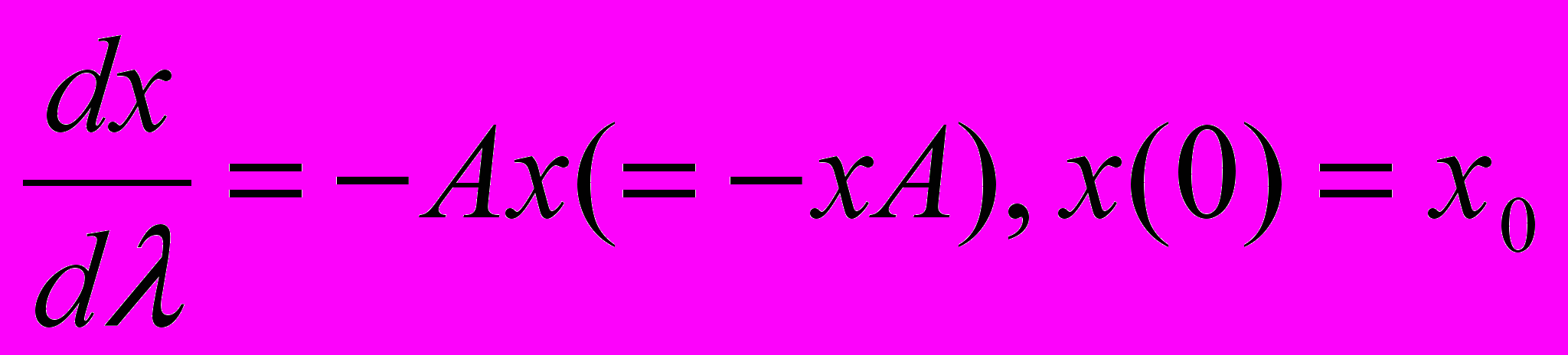 , (1.2)
, (1.2)де A, х0 ε [Х], х(λ) — абстрактна функція зі значеннями в банаховом просторі [Х].
Це рівняння є найпростішим абстрактним лінійним диференціальної операторним рівнянням, воно виходить, наприклад із застосування прямого методу варіації параметра до побудови операторів виду:
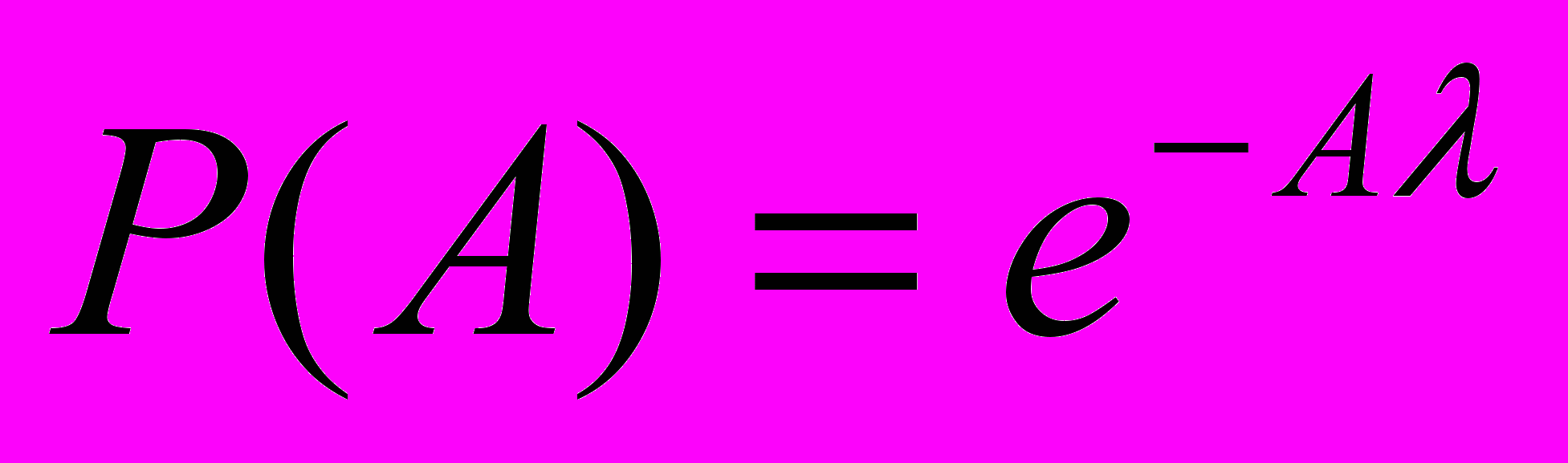 , 0 ≤ λ ≤ ∞,
, 0 ≤ λ ≤ ∞, зокрема проекторів
Р(А) ([Р (А)]2 = Р (А))
з одиничною нормою.
Проектори виду Р (А), Р (АС) і Р (СА), С ε [Х], застосовуються, наприклад, при побудові прямим методом варіації параметра явних і неявних псевдозворотніх операторів і псевдорішень лінійних функціональних рівнянь, а також власних елементів (власних підпросторів) оператора А. Зведення різних задач до задач для рівняння (2) і ін. є дуже зручним при розробці наближених методів рішення. Інтерес представляють також операторні рівняння виду:
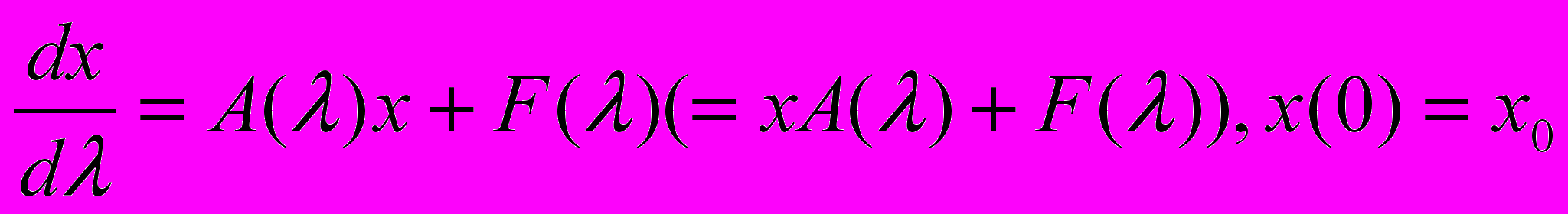
де А (λ), F(λ) — абстрактні функції зі значеннями з [X], і інші лінійні і нелінійні операторнi рівняння.
У деяких задачах, зв'язаних з диференціальними й інші рівняннями, приходиться досліджувати лінійні алгебраїчні операторні рівняння виду
Ах + хВ = у
і подібні ім. Тут х — шуканий, а А, В, у — задані лінійні оператори, що приймають, бути може, і нульові значення.
Під функціональним рівнянням у вузькому змісті цього слова розуміють рівняння, у яких шукані функції зв'язані з відомими функціями одного чи декількох перемінних за допомогою операції утворення складної функції. Наприклад, нехай
φi (x), i = 1, 2, . . ., n, — задані функції і Cі (x) = f (x, Cl, C2, . . ., Сn),
де Ψ — довільні постійні.
Виключення Cі з n + 1 рівняння виду
Ψ (φv (x)) = f (φv (x), Cl, C2, . . ., Сn),
v = 0, 1, 2, …, n, φ0 (x) = x,
приводить до функціонального рівняння виду
F [x, Ψ (x), Ψ ( φ1 (х)), Ψ ( φ2 (х))..., Ψ ( φn (х))] = 0, (1.3)
яке буде мати рішення:
Ψ (x) = f (x, Cl, C2, . . ., Сn).
Побудова функціонального рівняння являє собою пряму задачу функціонального числення, аналогічну з визначенням похідних вищого порядку в диференціальному численні.
Виключення Cі з n + 1 рівняння виду
Ψ v+1(х) = f (Ψ v(х), Cl, C2, . . ., Сn), v = 0, 1, 2, …, n,
Ψ0 (x) = x, Ψ1 (x) = Ψ (x), Ψ2 (x) = Ψ (Ψ1 (x)), …,
приводить до функціонального рівняння виду
F [x, Ψ (x), Ψ2 (х), ..., Ψ n+1(х)] = 0, (1.4)
яке буде мати рішення:
Ψ (x) = f (x, Cl, C2, . . ., Сn).
Іноді функціональні рівняння розрізняються за порядками і класами. Під порядком рівняння мається на увазі порядок шуканої функції, що входить у рівняння, а під класом рівняння — число даних функцій, до яких застосовується невідома функція. Так, рівняння (3) є функціональним рівнянням 1-го порядку і (n+1)-го класу. Рівняння (4) є функціональним рівнянням (n+1)-го порядку і 1-го класу.
Співвідношення (3) і (4) є тотожностями відносно х, рівняннями їхній називають остільки, оскільки шуканої є функція Ψ (х).
Рівняння (3) і (4) є функціональним рівнянням з одним незалежним перемінним. Можуть розглядатися функціональні рівняння з декількома незалежними перемінними, функціональні рівняння дробових порядків і інші, а також системи спільних функціональних рівнянь. При цьому функціональні рівняння чи системи функціональних рівнянь можуть містити в собі більше число істотних, істотно помітних між собою перемінних, чим шукана функція з максимальним числом перемінних.
До систем функціональних рівнянь приходять, наприклад, при визначенні довільних функцій, що входять в інтеграли рівнянь з частками похідними і задовольняючих умовам задачі. Якщо в інтеграл входить п довільних функцій, то, підкоряючи їхній п умовам, одержують п спільних функціональних рівнянь. Системи функціональних рівнянь у деяких випадках зручно записуються в більш короткому записі у виді векторного чи матричного функціонального рівняння.
Функціональні рівняння можна також розглядати як вираження властивості, що характеризує той чи інший клас функції. Hаприклад, функціональне рівняння:
f (x) = f (-x) (f (-x) = -f (x)) — характеризує клас парних (непарних) функцій;
функціональне рівняння:
f (х + 1) = f (x) — клас функцій, що мають період 1, і т.д.
Одними з найпростіших функціональних рівнянь є, наприклад, рівняння Коші
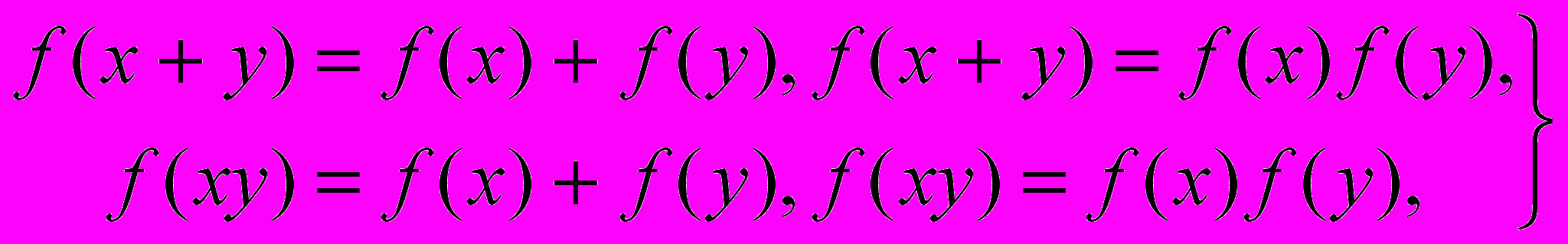 (1.5)
(1.5)безперервні рішення яких мають відповідно вид (у класі розривних функцій можуть бути й інші рішення):
f (x) = Cx, еСх, C ln x, хс (х > 0).
Функціональні рівняння (5) можуть служити засобом для визначення зазначених функцій при додатковій вимозі безперервності. Розглядаються також узагальнені функціональні рівняння Коші щодо трьох і більш невідомих функцій і інші, а також функціональні рівняння в комплексній області. Функціональні рівняння виду:
F (f (x), f (y), f (x + y)) = 0
і виду:
Ф (f (x), f (y), f (xy)) = 0
звуться відповідно теорема додавання і теорема множення функції f(t).
Найпростішими функціональними рівняннями, у яких шукана функція залежить від двох перемінних, є, наприклад, рівняння:
φ (х, у) + φ (у, z) = φ (х, z) і φ (x, у) φ (у, z) = φ(x, z),
рішення яких мають відповідно вид
φ (у, z) = Ψ (у) — Ψ (z) і φ (x, у) = Ψ (у) / Ψ (х),
де Ψ — довільна функція.
ІІ. Методи рішення функціональних рівнянь
Методи рішення функціональних рівнянь — методи перебування точних чи наближених рішень функціональних конкретних чи абстрактних рівнянь, тобто рівнянь виду
Р (х) = у, (2.1)
де Р (х) — якийсь, узагалі говорячи, нелінійний оператор, що переводить елементи простору X типу В (чи іншого типу) в елементи простору Y того ж типу. Точні рішення у виді аналітичних виражень виходять лише для деяких типів функціональних рівнянь, тому особливе значення мають наближені методи рішення.
Для перебування рішень загальних функціональних рівнянь виду (1) розвитий ряд методів, наприклад, метод нескінченних статечних рядів, метод послідовних наближень, метод Гальоркіна (метод моментів), метод дотичних гіпербол, метод Чебишева (дотичних парабол), метод Ньютона-Канторовича і його модифікації, метод найшвидшого спуска й ін., а також методи варіації параметра (прямі, ітераційні і комбіновані) визначених типів і їхні різні модифікації, у тому числі і з послідовною апроксимацією зворотного оператора. Загальні методи застосовуються до рішення різних конкретних функціональних рівнянь математичного аналізу. Крім того, існують спеціальні методи рішення конкретних функціональних рівнянь, у тому числі і чисельні методи, наприклад, метод сіток і інші. Метод варіації параметра, метод Ньютона-Канторовича і деякі інші з зазначених методів мають також і теоретичне значення, тому що з їх допомогою можна робити висновок про існування, одиничність і область розташування рішення функціональних рівнянь, не знаходячи самого рішення, що часом не менш важливо, чим фактичне знання рішення. Нижче як приклад розглядається прямий метод варіації параметра.
Нехай у банаховом просторі [Х] = [Х → X] лінійних обмежених операторів задане нелінійне операторне звичайне диференціальне рівняння на нескінченному проміжку:
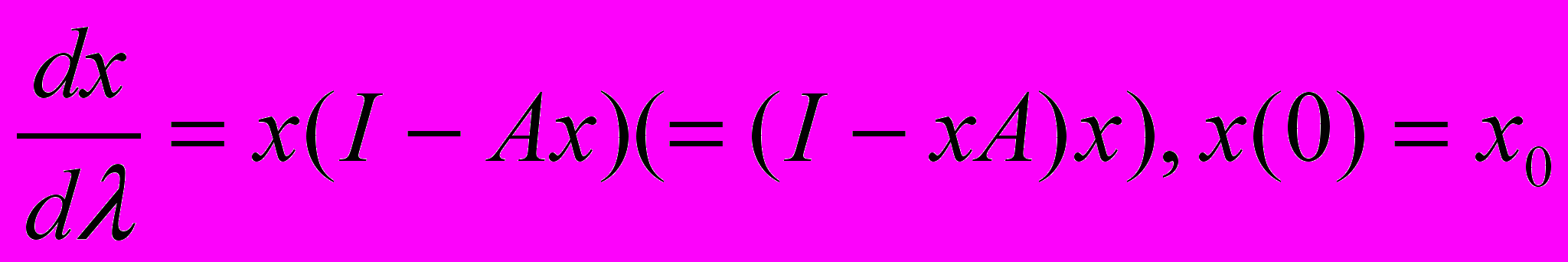 , (2.2)
, (2.2)де А , х0, І ε [Х] А, х0 - задані оператори,
І — тотожний оператор,
х(λ) — абстрактна функція зі значеннями з [X]
X — простір типу В.
До рішення рівняння (2.2) приводиться прямим методом варіації параметра задача побудови зворотного оператора А-1 для оборотного оператора А, рішення лінійного операторного рівняння виду:
І – Ах = 0
і інші задачі.
Якщо спектр оператора Ах0 (х0А) розташований у правій напівплощині, то задача (2.2) має єдине рішення:
х(λ), x(0) = x0,
 λ ε [ 0, ∞).
λ ε [ 0, ∞).Аналітичне застосування до задачі Коші (2.2) методів чисельного інтегрування звичайних диференціальних рівнянь приводить до цілого класу прямих методів варіації параметра рішення операторного рівняння (2.2), а отже, і рішення тих задач, що зводяться до задачі (2.2). Наприклад, метод Ейлера з нерівномірним кроком hk, приводить до наступного методу побудови оператора А -1:
x k + i = xk + hk xk (I — Axk) (+ hk (I — xk A) x k ),
k = 0, 1, 2 ... (2.3)
Кроки hk у формулі (2.3) вибирають різними способами. Коли спектр оператора:
I — Ax0 (I — x0A)
розташований на дійсній осі в інтервалі [ - р0, 0], 0 < р0 < ∞, дуже ефективним є наступний спосіб вибору кроків hk.
hk = 1/(1+ pk), pk +1 = pkLk , 4Lk = pk / (l + pk) ,
k = 0, 1, 2 ..., hk+1 = 4hk / (1 + hk)2. (2.4)
При цьому швидкість збіжності методу (2.3) має порядок вище, ніж 2k, норма нев'язання убуває за законом:
pk + 1 = pk2 / 4 (1 + pk).
Випадок інтервалу [0,
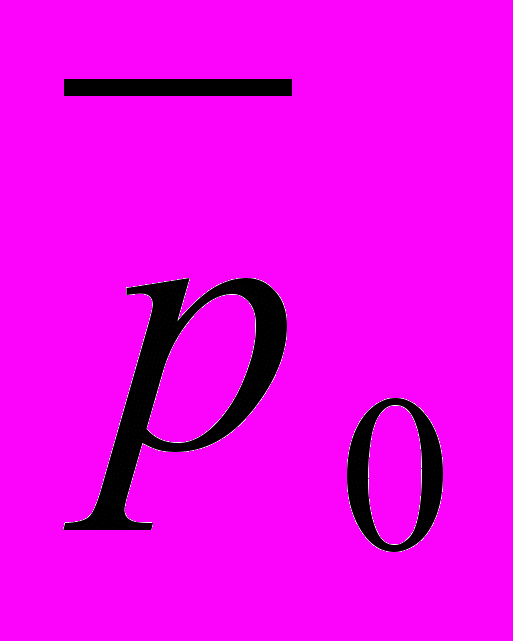 ], 0 <
], 0 < 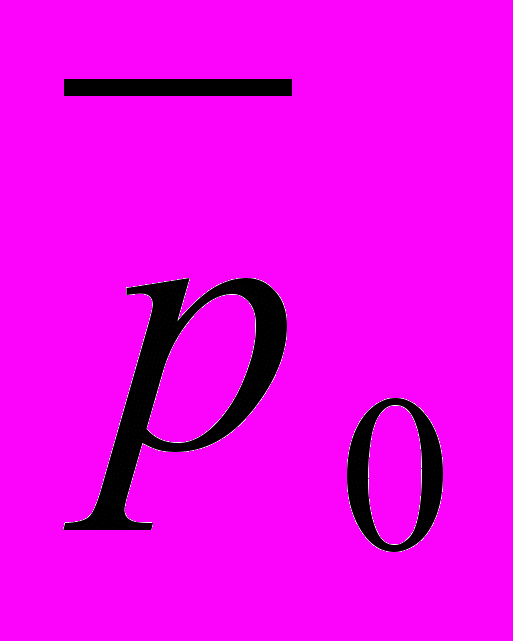 < 1, вигідно зводиться до розглянутого одного кроком методу (2.3) при
< 1, вигідно зводиться до розглянутого одного кроком методу (2.3) приh = 1/(l —
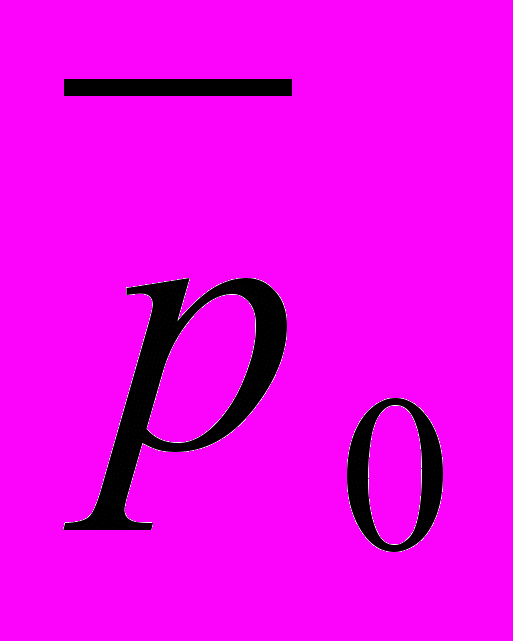 ), p0 =
), p0 = 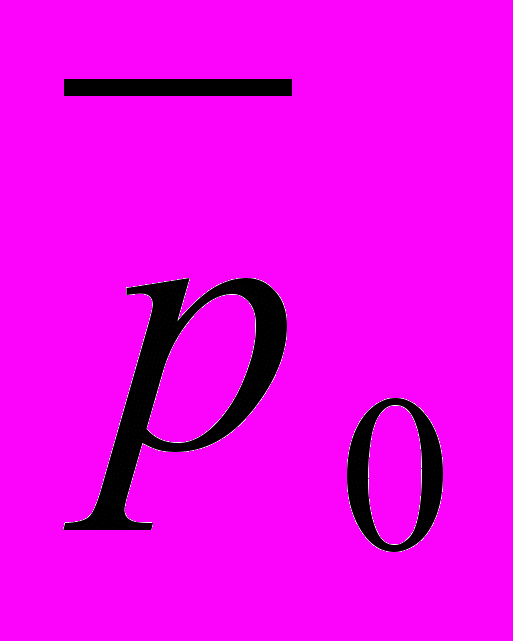 2 / 4 (1 —
2 / 4 (1 — 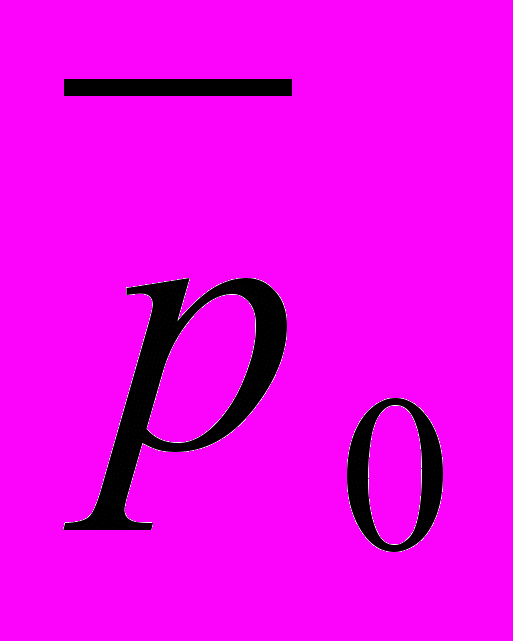 ).
).Щодо збіжності методу (2.3), (2.4) для конкретних операторних рівнянь можна висловити на підставі загальних фактів ті чи інші результати в залежності від того, який простір береться за основу.
До рішення задачі (2.2) зводяться також задача побудови проекторів виду:
Р (Ах0) (Р (х0А)), Р (К) = е –К λ│λ = ∞, К ε [Х],
[випадок, коли спектр оператора
I — Ax0 (I — x0A)
розташований в інтервалі [ - р0, 1]] і задача побудови псевдо-зворотних операторів х+( + х) для оператора А таких, що
I - Ax+ = Р (Ax0 ), І - +хА = Р (х0А), х+ = + х.
Для безпосередньої побудови проекторів Р (А ,х0) (Р (х0А)) метод (2.3), (2.4) можна переписати у виді:
Pk + 1 = Pk + hk Pk (Pk - I), k = 0, I, 2, ....,
P0 = I – Ax0 (P0 = I – x0A).
У залежності від розташування спектра і властивостей оператора A в якості х0 вибирають, наприклад, оператори I, А, А* чи ін.
До абстрактного лінійного функціонального звичайного диференціального рівняння (0 ≤ λ ≤ ∞)
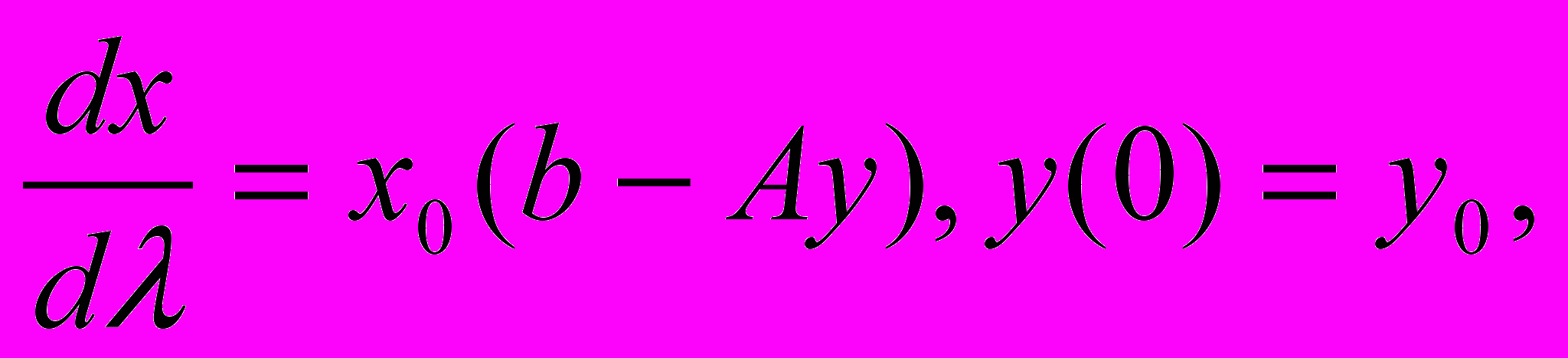 , (2.5)
, (2.5)де b, y0 ε X, x0, А ε [Х], у(λ) — абстрактна функція зі значеннями в X, зводиться прямим методом варіації параметра задача безпосередньої побудови псевдорiшення у+ лінійних функціональних рівнянь виду:
b - Ау+ = Р (Ах0) (b – Аy0), (2.6)
чи функціональних рівнянь
b - Ау+ = 0,
якщо
Р (Ах0) (b – Аy0) = 0.
До задачі (2.5) зводяться також і інші задачі, у тому числі задачі для диференціальних рівнянь звичайних і з частковими похідними, інтегральні рівняння й ін. Формула:
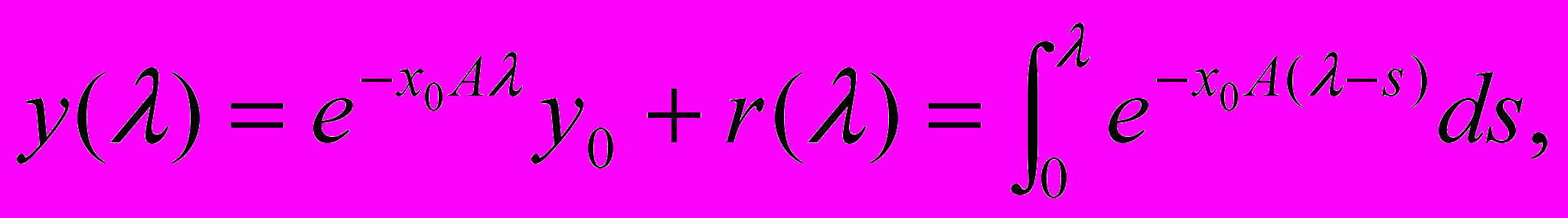
дає єдине рішення рівняння (2.5), що задовольняє умові y (0) = y0.
Застосування до задачі (2.5), наприклад, методу Ейлера з кроком hk+1 вперед приводить до наступного методу побудови псевдорішення у+ функціонального рівняння (2.6):
уk+1 = уk + hk+1 х0 (b – Ayk), k = 0, 1, 2, ... (2.7)
Кроки hk+1 вибирають, наприклад, через корені багаточленів Чебишева TN(t):
hj = 2[M + m — (M — m) tj]-1,
tj = cos[(2 μj — 1) π / 2N], j = 1, 2, ...,N, (2.8)
коли х0А — самосполучений оператор з ненульовою частиною спектра на відрізку [т, М], 0 < т ≤ М, РN = (μ1, μ2, ..., μN) — деяке упорядкування чисел 1, 2, ..., N для стійкості рахунка, N — порядок необхідного багаточлена. Метод (2.7), (2.8) дає оптимальну оцінку збіжності тільки на N-м кроці. При N = 2і (чи ≈ 2і) дуже ефективним є вибір кроків у (2.7) послідовно через корені багаточленів Чебишева
T2 (t) —T0 (t), T1(t), T1 (t), T2 (t), T2 (t), ... ,
…, Т2і –2 (t), Т2і –2 (t)
замість багаточлена TN (t), що істотно спрощує задачу упорядкування кроків hj і підвищує ефективність рахунка, особливо при великих N. У цьому випадку погрішність оптимально зменшується після уживання всіх упорядкованих коренів кожного багаточлена, що важливо для спрощення контролю рахунка. У випадку, якщо
Р (Ах0) (b – Ау0) = 0,
то Р (х0 А) ·(у+— у0) = 0;
при цьому, якщо Р (х0 А) — ортопроектор, то у+ - у0 є нормальним рішенням функціонального рівняння
А (у+ - у0) = b - Ау0.
З іншого боку, з (2.7) випливає
B — Ayk + 1 = Uk + 1 (b — Ау0),
Uk + 1 =
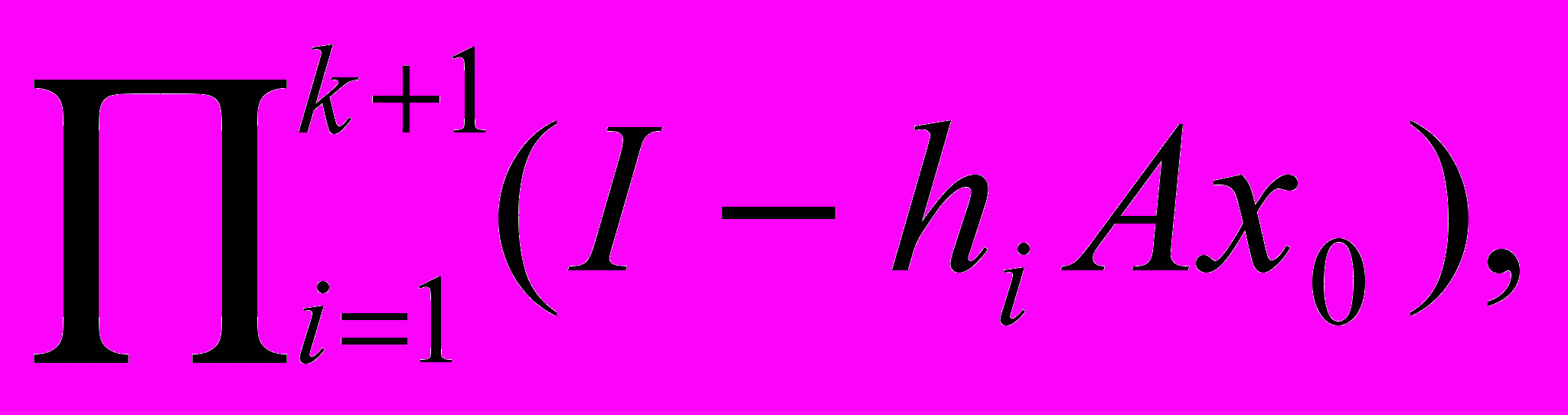 ,
,k = 0, 1, 2, ...
При цьому, якщо Р (Ах0) — проектор, тo
║Uk - P (Ax0) ║ ≤ 2qk/(l +q2k) → 0
при k → ∞ (q = ( √
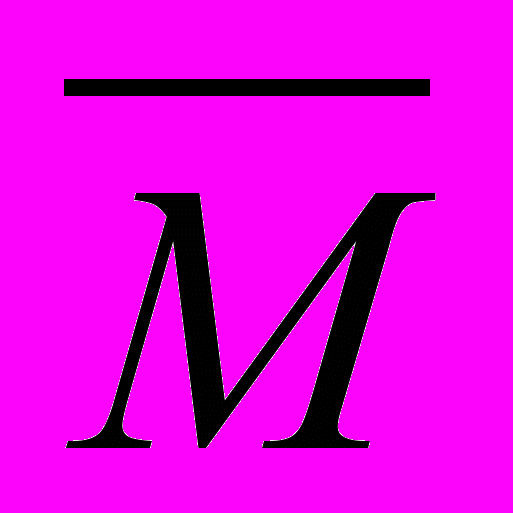 - √
- √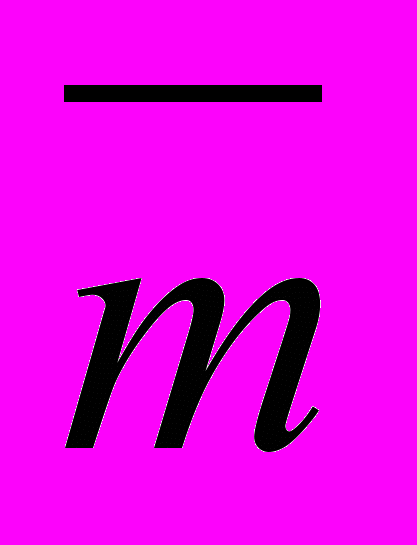 ) / (√
) / (√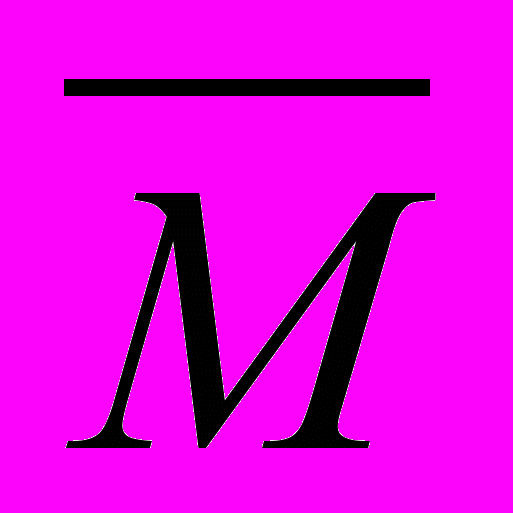 + √
+ √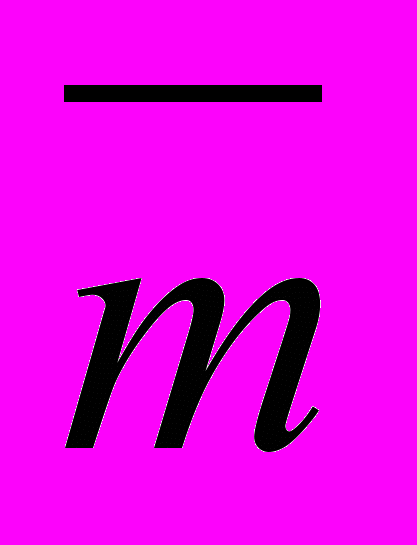 )).
)).Існують також прямі методи варіації параметра типу методу Eйлера, що використовують рекурентнi співвідношення для багаточленів Чебишева і близьких до них (без явного використання коренів цих багаточленів), з убуванням погрішності на кожнім кроці. Ці методи є багатокроковими і мають підвищену швидкість збіжності. Застосування до задачі (2.5) методу Ейлера з кроком hk+1 назад дає наступний ефективний клас методів
yk+1 = yk + hk+1 (I + hk+1 x0A) -1 x0 (b — Ау0),
k = 0, 1, 2, ...,
відкіля
b - Ayk+1 = Wk + 1 (b — Ay0),
Wk + 1 =
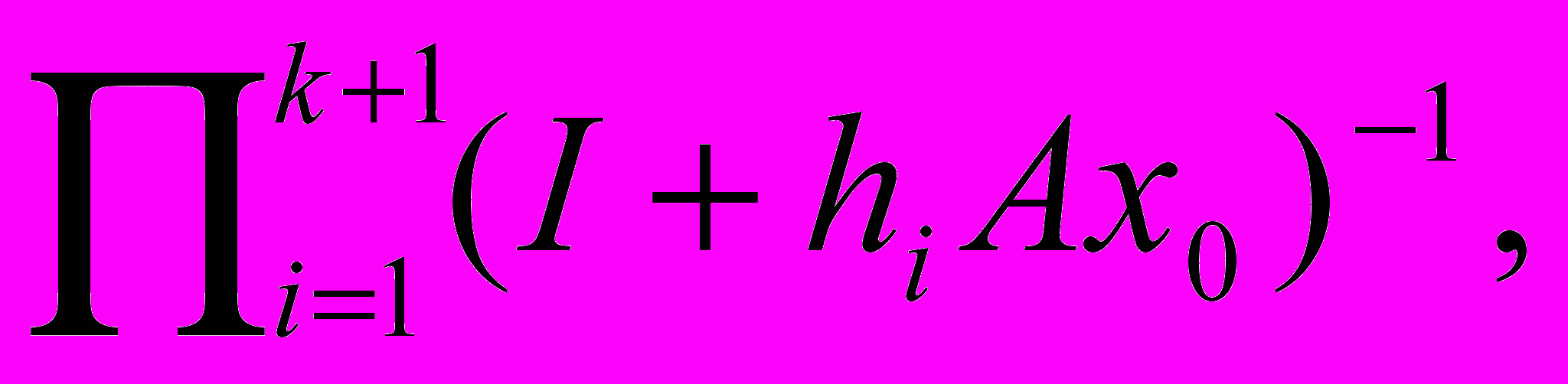 ,
,k = 0, 1, 2, ...
При цьому, якщо Р (Ах0) — проектор і hi > 0 такі, що для будь-якого i
║(I – P (Ax0)) (I + hi Ax0) -1║ ≤ ρi < 1,
тo ║Wk -Р (Ах0) ║ ≤
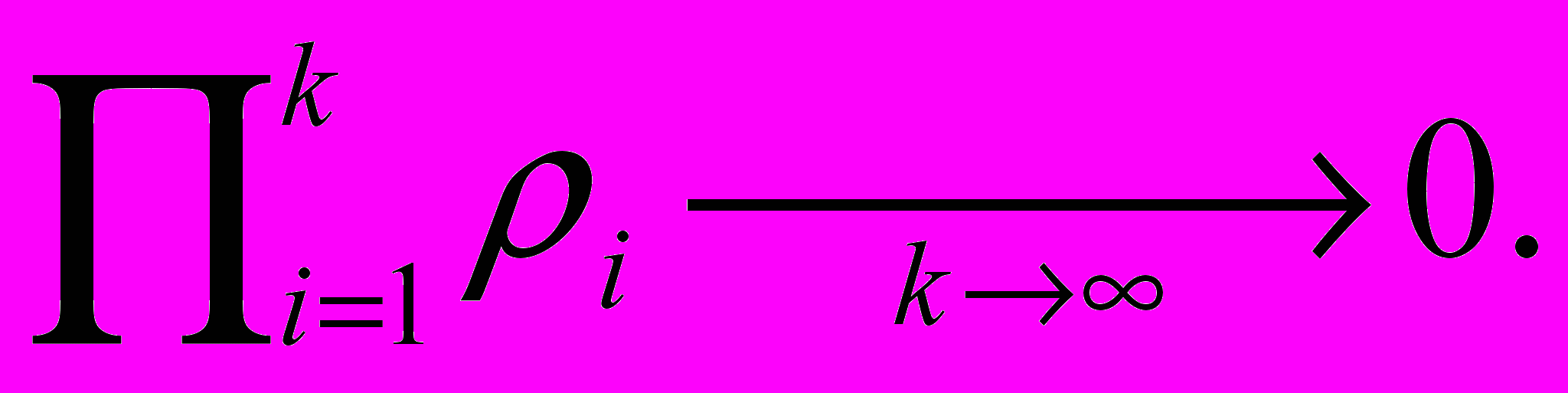
Існують аналогічні методи і для рішення нелінійних функціональних рівнянь і операторних рівнянь, а також методи з підвищеним ступенем точності типу методів Рунге-Кута s-гo порядку точності й інших типів.
Рішення функціональних рівнянь у вузькому змісті цього слова і систем таких рівнянь можуть бути як конкретними функціями, так і класами функцій, що залежать від довільних параметрів чи довільних функцій. У теорії функціональних рівнянь відомо мало загальних методів рішення таких рівнянь. Тому в кожнім окремому випадку необхідно, як правило, досліджувати ступінь спільності отриманого рішення.
Одним з більш-менш загальних методів рішення функціональних рівнянь є метод зведення їх до рішення рівнянь у кінцевих відмінностях. Нехай, наприклад, мається функціональних рівнянь n-го порядку і 1-го класу виду
F (x, φ (х), φ2 (х), ..., φn (x)) = 0, (2.9)
де функція F задана, функція φ(х) — шукана;
φ0 (х) = х, φl (x) = φ (x), φ2 (x) = φ (φ (х)), ...
При цьому вважають
x = uz, φ (x) = uz + 1.
Тут перехід від х к φ (х) заміняється введенням нового перемінного z і зміною z на 1 у функції uz. Після такої заміни рівняння (2.9) приймає вид
F (uz, uz + 1, ..., uz + n) = 0. (2.10)
Рішення рівняння (2.10) у кінцевих відмінностях n-го порядку дає вираження для uz через z і п довільних періодичної функцій Ci від z з періодом, рівним одиниці. Рішення функціональних рівнянь (2.9) у самому загальному виді представляється системою двох спільних рівнянь
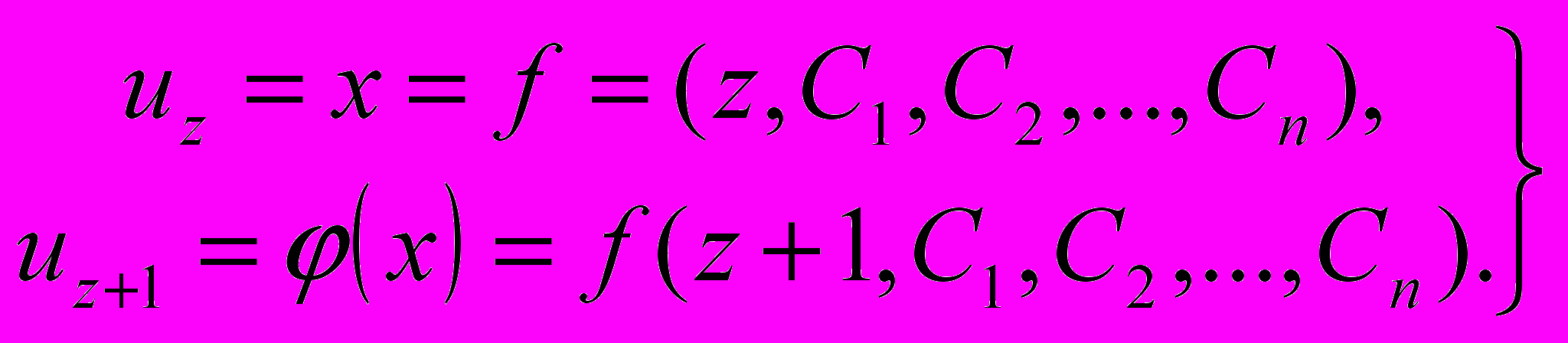 (2.11)
(2.11)Вибираючи в якості Ci їхні приватні значення, можна з (2.11) виключити z і одержати в такий спосіб приватне рішення рівняння (2.9). Наприклад, для функціонального рівняння 2-го порядку
φ [ φ (x)] + aφ (x) + bx = 0 (2.12)
загальне рішення (2.11) приймає вид
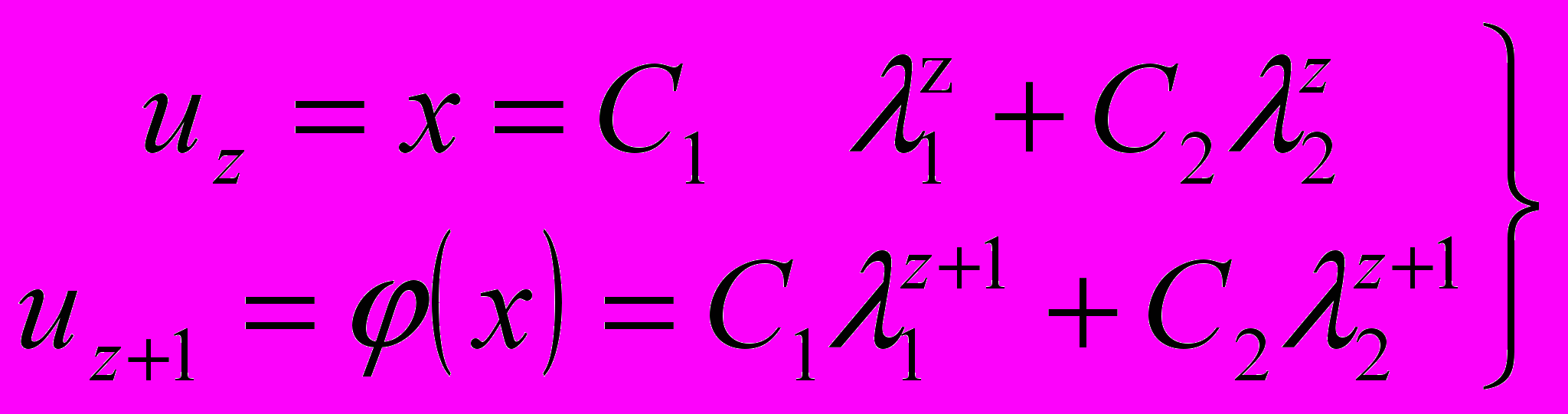 (2.13)
(2.13)де λ1 і λ2 — корені квадратного рівняння
λ.2 + aλ + b = 0,
C1 і C2 — довільні постійні періодичної функції з періодом, рівним одиниці. Якщо для C1 і C2 дати значення довільних постійних і виключити z з (2.13), то виходить повне рішення функціонального рівняння (2.12):
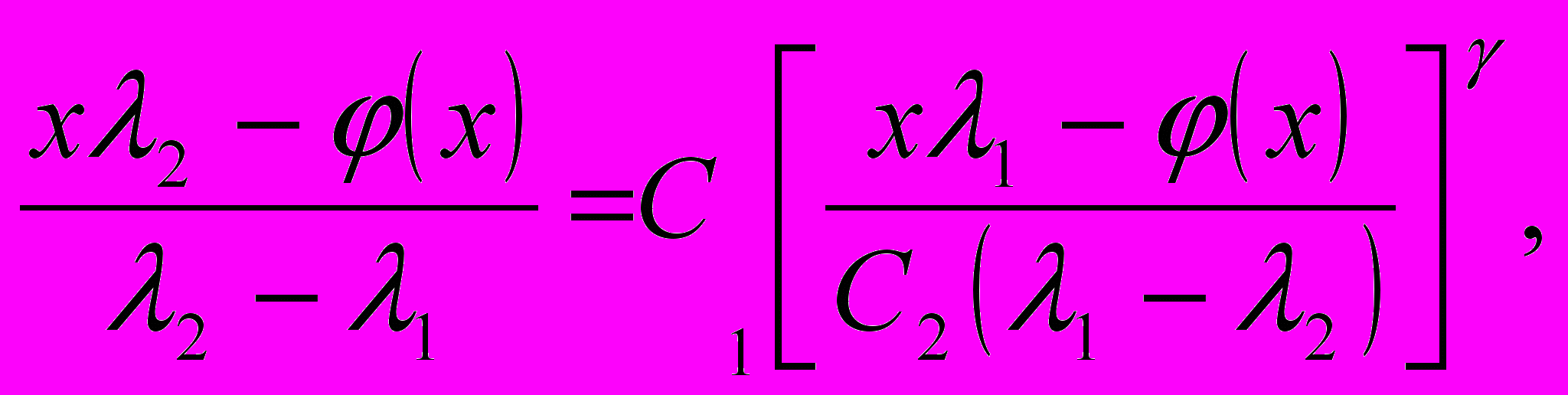
γ = ln λ1 / ln λ2.
Метод зведення до рівнянь у кінцевих відмінностях застосовується також і при рішенні прямих задач функціонального числення. Нехай, наприклад, задана функція
φ (х) = а + bх
і нехай потрібно побудувати вираження
φn (х) (φi (x) = φ (φi - 1 (х))).
При цьому вважають
φn (х) = un
і записують рівняння в кінцевих відмінностях
un + 1 = a + b un,
рішенням якого є
un = Cbn + a / (1 — b).
Звідси при n = 0 одержують
u0 = x = С + а / (1- b),
тобто C = х — а / (1- b).
Таким чином,
φn (х) = αn + βnx, аn = а (bn - 1) / (b - 1), βn = bn.
Тут же при бажанні можна записати i функціональне рівняння виду
φn (х) = βn – 1 φ (х) + αn – 1,
рішенням якого при будь-якому п є φ (х) і ін. Вирішуючи це функціональне рівняння тим же методом, можна побудувати й інші значення φ (х). Зокрема, для непарних п виходить ще одне дійсне рішення
φ (х) = - bx + а (1+ b) / (1 — b).
Для рішення функціональних рівнянь застосовується також метод підстановок. Нехай, наприклад, мається функціональне рівняння
f (x + y) + f (x - y) = 2f (x) cos y. (2.14)
Застосовуючи послідовно підстановки
x = 0, y = t; x =
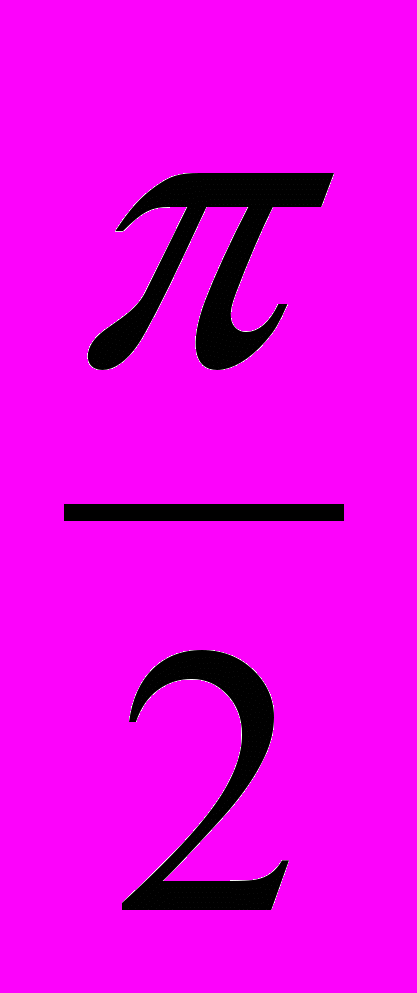 + t, y =
+ t, y = 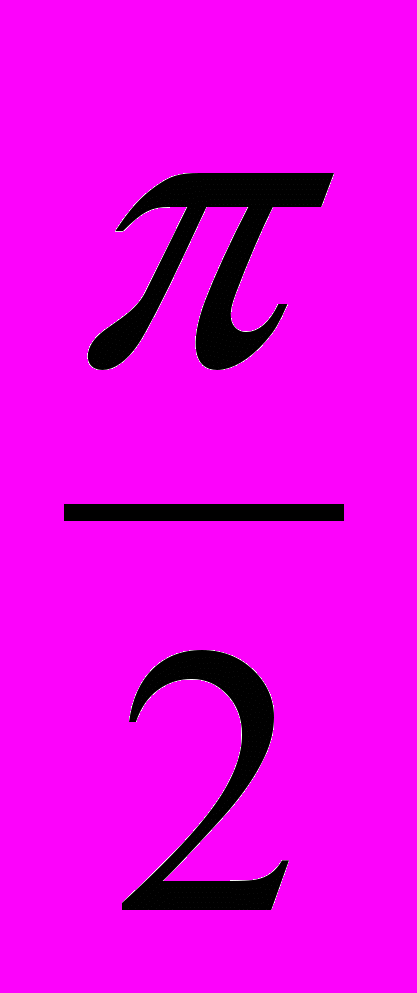 ; x =
; x = 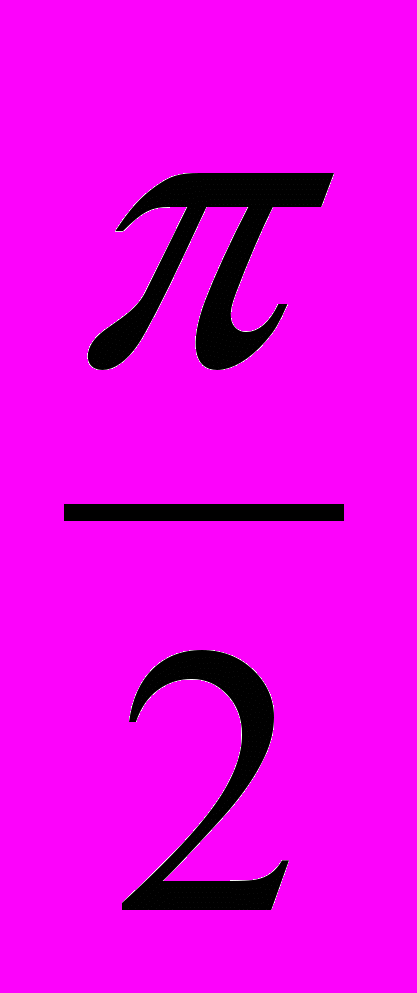 , y =
, y = 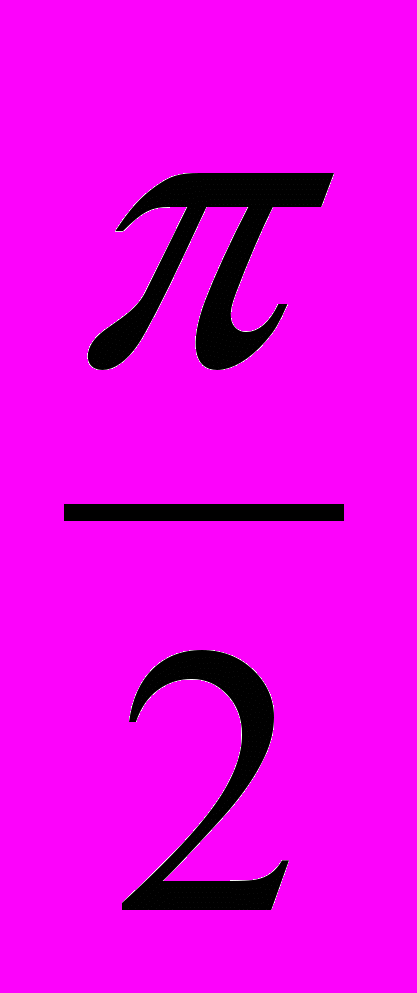 + t,
+ t,з (2.14) одержують відповідно рівняння
f (t) + f(- t) = 2a cos t, f (π + t) + f (t)= 0
і
f (π + t) + f ( - t) = 2b cos
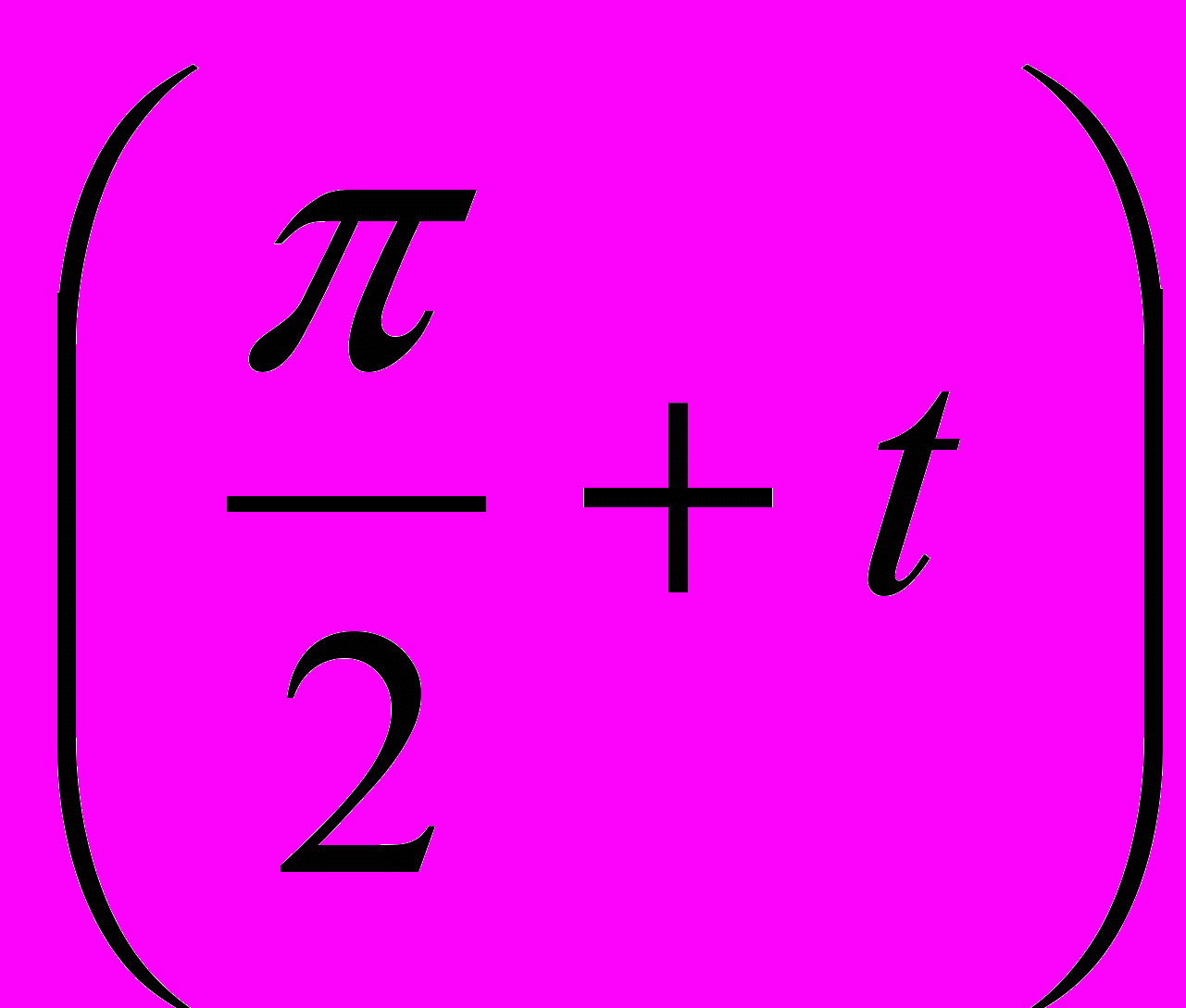 = - 2b sin t,
= - 2b sin t,де позначено f (0) = а, f (π /2) = b. Звідси шляхом вирахування із суми перших двох рівнянь третього рівняння одержують
2f (t) = 2a cos t +2b sin t.
Загальним рішенням вихідного функціонального рівняння (2.14) є функція
f (x) = a cos x + b sin x.
Цей метод застосуємо також і до інших рівнянь типу
H [f (x + y), f (x - y), f (х), х, y] = 0
при деяких припущеннях щодо функції H. До рівнянь інших типів застосовуються різні інші підстановки.
Метод підстановок застосовується і для зведення одних функціональних рівнянь до інших рівнянь того ж типу, зокрема до функціональних рівнянь з відомими рішеннями. Наприклад, функціональне рівняння
f ((x + y) / 2) = f (x) / 2 + f (y) / 2 (2.15)
може бути приведене до функціонального рівняння Коші
f (x + y) = f (x) + f (y) (2.16)
с безупинним рішенням
f (x) = Cx.
З цією метою підставляють у (2.15) х + у замість х і 0 замість у:
f ((x + y) / 2) = f (x + y) / 2 + a / 2, a = f (0).
Порівнюючи це з вихідним функціональним рівнянням (2.15), одержують функціональне рівняння виду
f (x + y) = f (x) + f (y) — a,
відкіля
φ (x + у) = φ (x) + φ (y), φ (x) = f (x) - а і φ (x) = Cx.
Рішенням є функція
f (x) = Cx + a.
Для зведення до інших функціональних рівнянь того ж типу застосовують також логарифмування й інші прийоми. Наприклад, рішення функціональних рівнянь
f (x + y) = f (x) f (y) (2.17)
шляхом логарифмування можна звести до рішення функціональних рівнянь (2.16). Безперервна функція f (х), що задовольняє функціональне рівняння (2.17), завжди строго позитивна, а функція φ (x) = ln f (x) — безупинна (як результат суперпозиції безупинних функцій) і задовольняє умові
φ (x + y) = φ (x) + φ (y), φ (x)=Cx.
Рішенням є функція
f (х) = еCх = ах.
У багатьох випадках для рішення функціональних рівнянь застосовується також метод зведення їх до диференціальних рівнянь. Наприклад, функціональне рівняння (2.14) можна звести до рівняння виду
fn (x) = — f (x).
До цього рівняння зводяться й інші функціональні рівняння. Цей метод дає лишe рішення, що належать класу диференцируємих функцій. Рішення, наприклад, функціональних рівнянь Коші (2.16) за умови диференцируємості функції f (х) можна знайти в такий спосіб. Диференціюючи (2.16) по х, одержують
f′ (x + y) = f′ (x),
і тому що y тут довільне, тo
f′ (x) = С.
Тоді інтегрування дає
f (x) = Cx + C1,
де С1 — нова постійна. Підставляючи знайдене вираження для f (x) знову у функціональних рівняннях (2.16), установлюють, що при всіх значеннях x i y повинне бути C1 = 0. Рішенням є функція
f (x) = Cx.
Для рішення функціональних рівнянь у ряді випадків застосовують також і метод ітерацій.
Висновки
Використана література
- Давиденко Д. Ф., в кн.: Математическое программирование и смежные вопросы. Вычислительные методы, М., 1976;
- Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977;
- Канторович Л. В., «Успехи матем. наук», 1956, т. 11, в. 6;
- Математическая энциклопедия: Гл. ред. И.М. Виноградов, т. 5. Слу – Я – М., «советская Энциклопедия», 1984.
