Сущность и методы управления инвестиционным портфелем содержание
| Вид материала | Реферат |
- Программа дисциплины "" Управление инвестиционным портфелем" для студентов магистратуры, 222.73kb.
- Методы измерения эффективности управления портфелем ценных бумаг, 67.04kb.
- «Оценка эффективности управления инвестиционным портфелем», 314.4kb.
- Темы вкр и назначение научных руководителей и рецензентов в спб филиале гу-вшэ 2006-2007, 195.71kb.
- 1. Сущность и содержание теории управления Понятие "управление". Содержание науки управления., 94.61kb.
- Программа дисциплины «Математика финансовых решений и управление инвестиционным портфелем», 235.92kb.
- Вобщем случае под инвестиционным портфелем понимают совокупность нескольких инвестиционных, 131.23kb.
- Учебно-методический комплекс по дисциплине управление качеством Специальность, 248.02kb.
- Г. А. Василевич, доктор юридических наук, профессор сущность конституции, 68.32kb.
- Темы курсовых работ по дисциплине: «Основы менеджмента» Необходимость и сущность управления, 90.42kb.
3.2 Формирование и оптимизация портфеля ценных бумаг
Формирование совокупного портфеля ценных бумаг банка будем проводить в несколько этапов. Первые два этапа включают в себя определение структуры оптимальных портфелей государственных облигаций и корпоративных акций. Третий этап является синтезом двух предыдущих и представляет собой определение конечной структуры общего портфеля. В завершении будет оценена эффективность применения моделей к данным рынкам путем определения полученного результата за период инвестирования.
Формирование оптимальной структуры портфеля государственных облигаций
Для формирования оптимальной структуры портфеля государственных облигаций будем использовать параметрическую модель Марковица. Эта методика оптимизирует структуру портфеля ценных бумаг на основе статистической информации.
В качестве периода накопления информации примем период с 1.06.2005г. по 30.11.2005г., который разобьем на 26 периодов длинной в одну неделю, т.е. значения показателей будем фиксировать каждую неделю периода накопления информации. Оптимальная структура портфеля формируется на декабрь 2005 г.
Для рассмотрения целесообразности включения в портфель были отобраны ОФЗ 25057, ОФЗ 25058, ОФЗ 26175, ОФЗ 26197, ОФЗ 27019, ОФЗ 27020, ОФЗ 27025, ОФЗ 27026, ОФЗ 28002, ОФЗ 46001, ОФЗ 46002, ОФЗ 46003, ОФЗ 46014, ОФЗ 46017, ОФЗ 46018, (итого 15 наименований). Примем эти ценные бумаги в качестве исходных для формирования оптимальной структуры портфеля государственных ценных бумаг (Приложение 1) .
Для обеспечения диверсификации портфеля ценных бумаг, количество ценных бумаг в портфеле должно быть не менее восьми. Портфель облигаций должен быть диверсифицирован по сроку до погашения облигаций. При отборе облигаций данные условия были соблюдены.
Исходными данными для реализации методики являются:
- курс облигаций за период накопления информации (Kit);
- рассчитанная на основе курса и календаря купонных выплат годовая эффективная доходность к погашению облигаций (rit).
Для решения задачи нахождения оптимальной структуры портфеля государственных облигаций воспользуемся моделью Марковица.
Параметрическая модель Марковица допускает эффективную статистическую оценку. Параметры этой модели можно оценить исходя из имеющихся статистических данных за прошлые периоды.
Математическое ожидание эффективной доходности каждой облигации (ri) вычисляется следующим образом:
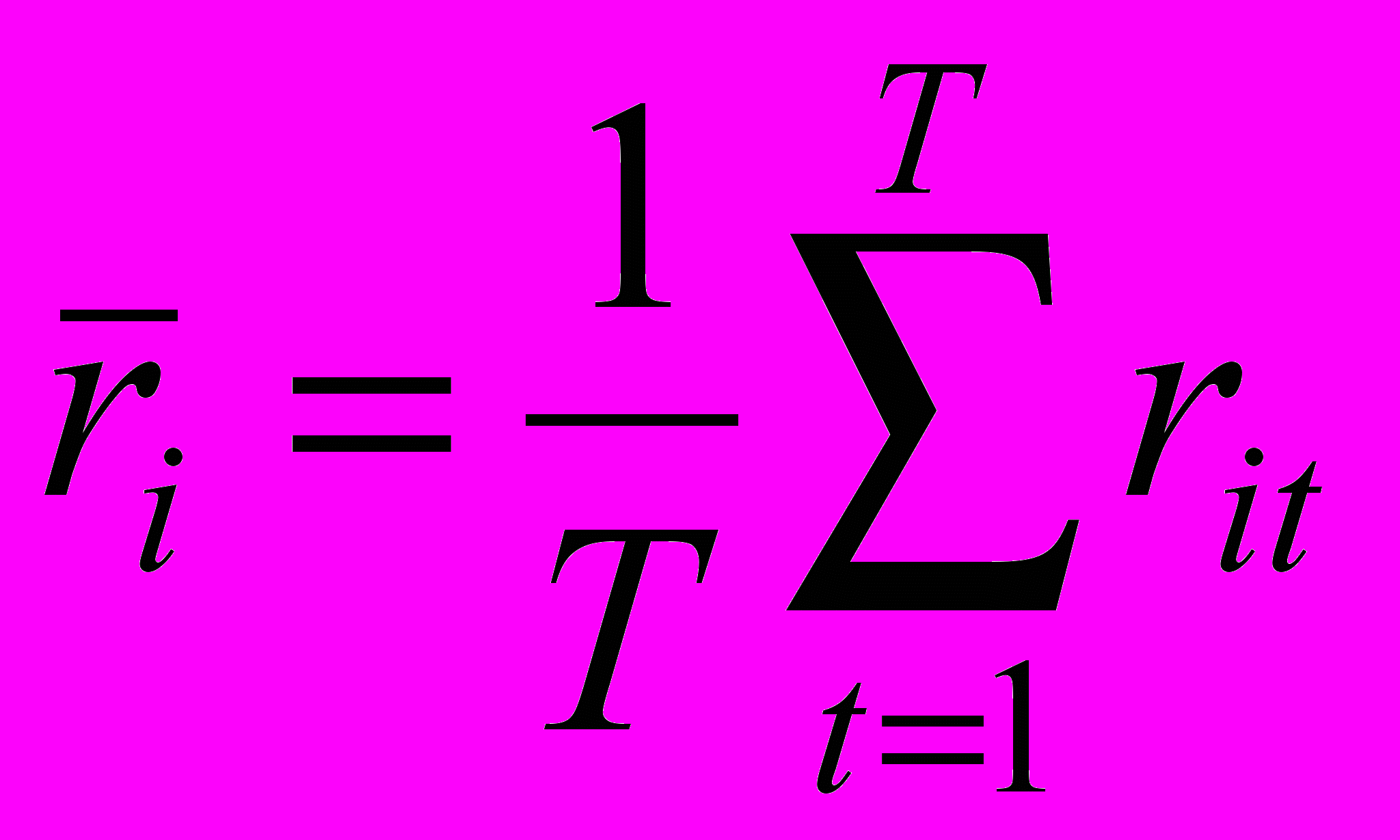. (22)где rit – эффективная доходность i-й облигации в период времени t, %, i = 1,…, 15;
t – номер периода диапазона накопления информации, t = 1, …, 26 ;
T – длительность периода накопления информации.
Стандартное отклонение эффективной доходности i-ой облигации (i) определяется по формуле37:
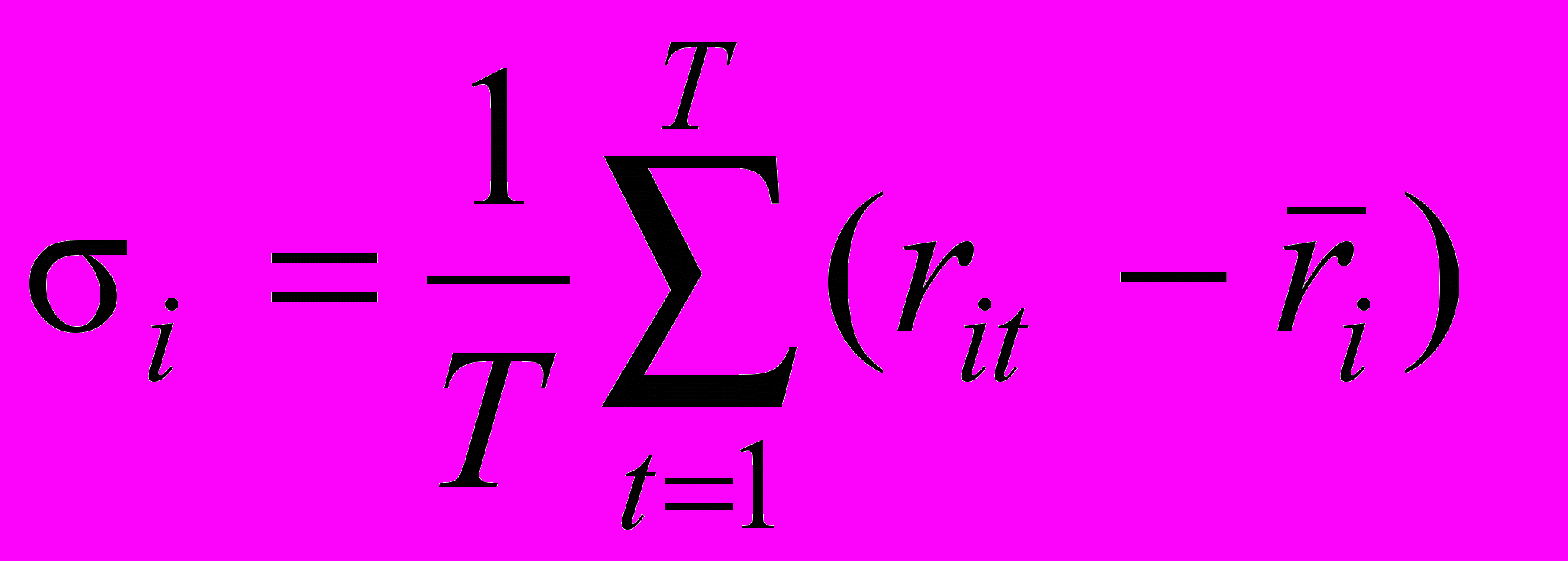, (23)Результаты вычисления математического ожидания и стандартного отклонения эффективной доходности каждой ценной бумаги представлены в таблице 4.
Ковариация между эффективными доходностями i-й и j-й облигаций (ij) определяется по формуле:
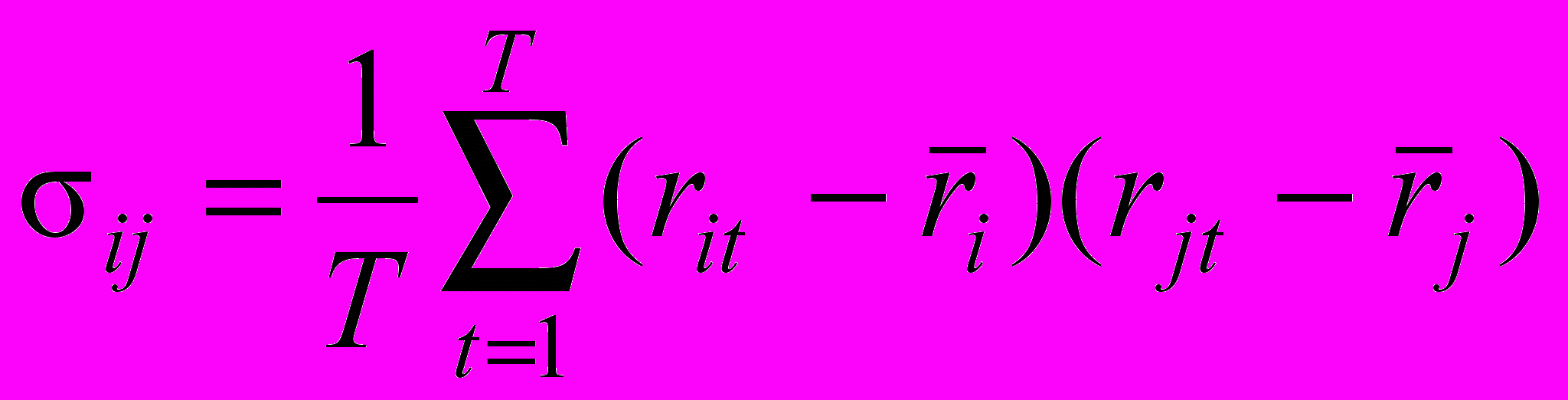, (24)где rit и rjt – эффективные доходности, соответственно, i-й и j-й облигации в период времени t, %;
ri и rj – соответственно, математические ожидания эффективных доходностей i-й и j-й облигации, %.
Таблица 3.2
Математическое ожидание и стандартное отклонение эффективной доходности облигаций
| Облигация | Показатель | |
| Математическое ожидание, % | Стандартное отклонение | |
| ОФЗ 25057 | 6,46 | 0,01 |
| ОФЗ 25058 | 6,15 | 0,02 |
| ОФЗ 26175 | 4,96 | 0,07 |
| ОФЗ 26198 | 6,82 | 0,01 |
| ОФЗ 27019 | 5,79 | 0,06 |
| ОФЗ 27020 | 5,68 | 0,09 |
| ОФЗ 27025 | 5,79 | 0,05 |
| ОФЗ 27026 | 6,38 | 0,00 |
| ОФЗ 28002 | 4,48 | 0,07 |
| ОФЗ 46001 | 6,12 | 0,04 |
| ОФЗ 46002 | 6,66 | 0,05 |
| ОФЗ 46003 | 6,53 | 0,06 |
| ОФЗ 46014 | 6,85 | 0,01 |
| ОФЗ 46017 | 6,9 | 0,01 |
| ОФЗ 46018 | 6,79 | 0,04 |
Совокупность ковариаций i-й и j-й облигаций дает ковариационную матрицу доходностей (таблица 3.3).
Следующий этап в определении оптимальной структуры портфеля – построение эффективного множества (рисунок 3.3). Это множество было построено при помощи метода линейного программирования, т.е. при заданном значении доходности портфеля, рассчитанной по формуле (17), минимизировалась величина риска, т.е. стандартного отклонения портфеля, полученного при помощи формулы (18).
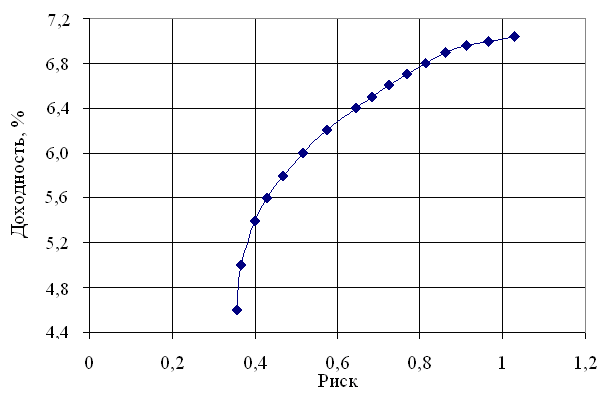
Рис.3.3 Эффективное множество портфелей ОФЗ
Для определения точки нахождения на эффективном множестве оптимального портфеля необходимо построить кривые безразличия. Так как это достаточно трудно осуществить на практике, ограничимся лишь простым выбором этой точки на графике, исходя из собственных предположений.
Так как банки являются достаточно консервативными организациями, не склонными к большому риску, то искомая точка должна находиться в левой части кривой – с меньшим риском. Начиная с некоторого момента, кривая приобретает все более пологий вид, что свидетельствует о том, что при
дальнейшем увеличении доходности риск увеличивается нарастающими
темпами. Поэтому, нами было принято решение считать целесообразным при формировании оптимального портфеля для данного инвестора портфель с доходностью 6% годовых.
Оптимальный портфель облигаций, таким образом, имеет структуру, представленную в таблице 3.3 и на рисунке 3.4
Таблица 3.3
Структура оптимального портфеля облигаций
-
Облигация
Доля
ОФЗ 25058
0,018
ОФЗ 26198
0,032
ОФЗ 46001
0,125
ОФЗ 46002
0,027
ОФЗ 46003
0,030
ОФЗ 46014
0,044
ОФЗ 46017
0,182
ОФЗ 46018
0,542
Риск портфеля, представленного в таблице 3.3, согласно формуле (18) и рисунку 3.3 составит величину p = 0,52.
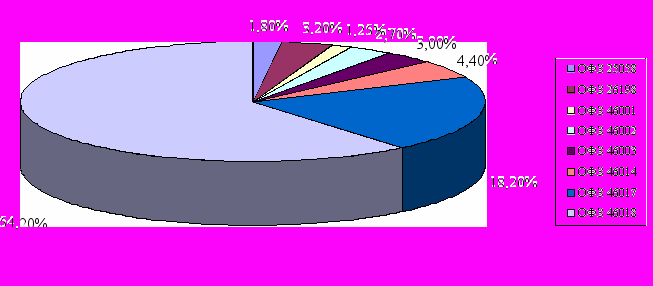
Рис. 3.4. Структура оптимального портфеля ОФЗ
Формирование оптимальной структуры портфеля акций
Для рассмотрения были отобраны наиболее ликвидные акции российского фондового рынка. Ликвидность была оценена по формуле расчета агрегированного показателя ликвидности38:
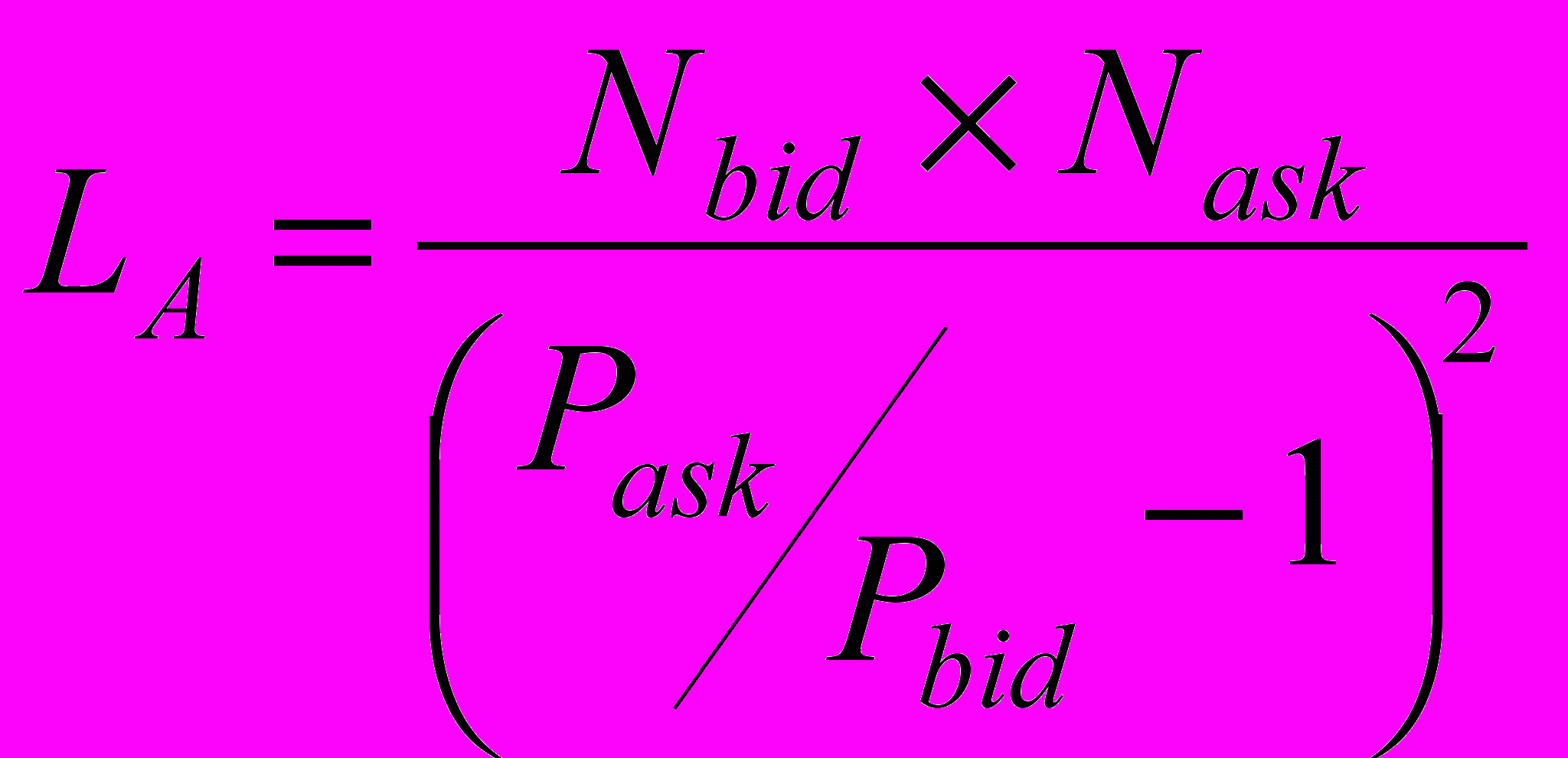, (25)где LA – агрегированный показатель ликвидности ценной бумаги;
Nbid, Nask – количество заявок на покупку и продажу соответственно, шт.;
Pbid, Pask – средняя цена покупки и продажи соответственно, руб.
Результаты сведены в таблицу 3.4. В этой таблице также приведены обозначения, принятые в РТС (тикеры), и которые будут применяться в дальнейшем для краткости.
Таблица 3.4
Список акций выбранных для рассмотрения
| Название эмитента | Тикеры (P – привилег.) | Агрегированный показатель ликвидности |
| "ЕЭС России" РАО | EESR, EESRP | 227 605,01 |
| "Сибнефть" | SIBN | 203 570,47 |
| "ЛУКОЙЛ "Нефтяная компания" | LKOH | 196 121,68 |
| "Сургутнефтегаз" | SNGS, SNGSP | 96 896,89 |
| "Ростелеком" | RTKM, RTKMP | 73 545,84 |
| "Газпром" | GSPBEX | 63 956,49 |
| "Мосэнерго" | MSNG | 59 818,43 |
| "Сбербанк России" | SBER | 30 339,70 |
| "Норильский никель" ГМК | GMKN | 11 928,16 |
| ООО УК "Нефтегазовые активы" | NGZANAG | 6 111,41 |
| ОАО “ТАГМЕТ" | TAMZ | 2 945,06 |
В качестве исходных данных приняты котировки акций в РТС, в качестве рыночного индекса – индекс РТС. Индекс РТС является единственным официальным индикатором Российской Торговой Системы. Индекс рассчитывается один раз в 30 минут в течение всей торговой сессии, начиная с 12:00 и заканчивая в 18:00. Значение индекса на 12:00 является значением открытия, на 18:00 – значением закрытия. Для расчетов фиксировалась значение индекса на момент закрытия торгов.
Для более точного регрессионного анализа за шаг расчет был принят один рабочий день. Доходность акций рассчитывалась по формуле (2).
Математическое ожидание рассчитывалось как арифметическое среднее на основе исторических данных. Результаты сведены в таблицу 3.5.
Коэффициент «бета» предоставляет информацию о том, как прибыль по акции изменяется в соответствии с динамикой рыночной прибыли. Положительное значение бета-коэффициента означает тенденцию акций повышаться в том же направлении, что и рынок; отрицательное значение «бета» указывает на тенденцию движения против рынка. Показатель «бета» больше единицы определяет акцию, которая проявляет тенденцию в пропорциональном отношении изменяться в большей степени, чем рынок. Доход по ней повышается еще больше в момент общего повышения доходности рынка и падает в большей степени в момент общего снижения дохода рынка. Бета-коэффициент меньше единицы характеризует акцию, доход по которой менее изменчив, чем рынок.
Таблица 3.5
Таблица коэффициентов
| | Бета | Альфа | R2 | СКО ошибки | Ошибка беты | Ошибка альфы | Математическое ожидание доходности, % |
| EESR | 0,496 | 0,0025 | 0,148 | 0,025 | 0,095 | 0,0023 | 11,6 |
| GSPBEX | 0,705 | 0,0001 | 0,022 | 0,024 | 0,095 | 0,0023 | 9,1 |
| LKOH | 0,481 | 0,0011 | 0,151 | 0,023 | 0,089 | 0,0021 | 8,5 |
| SBER | 0,840 | 0,0080 | 0,065 | 0,027 | 0,104 | 0,0025 | 28,1 |
| TAMZ | 0,581 | 0,0007 | 0,070 | 0,020 | 0,078 | 0,0019 | 8,8 |
| MSNG | 0,471 | 0,0000 | 0,079 | 0,023 | 0,088 | 0,0021 | 6,0 |
| RTKM | 0,714 | 0,0038 | 0,087 | 0,021 | 0,081 | 0,0019 | 17,2 |
| GMKN | 0,661 | 0,0008 | 0,060 | 0,025 | 0,097 | 0,0023 | 9,9 |
| SIBN | 0,698 | 0,0065 | 0,041 | 0,033 | 0,128 | 0,0031 | 23,0 |
| NGZANAG | 0,739 | 0,0039 | 0,147 | 0,015 | 0,056 | 0,0013 | 17,7 |
| SNGS | 0,936 | -0,0010 | 0,128 | 0,013 | 0,051 | 0,0012 | 9,4 |
| EESRP | 0,310 | 0,0082 | 0,007 | 0,092 | 0,358 | 0,0086 | 21,9 |
| SNGSP | 0,555 | 0,0009 | 0,202 | 0,019 | 0,074 | 0,0018 | 8,9 |
| RTKMP | 0,508 | 0,0059 | 0,039 | 0,025 | 0,098 | 0,0023 | 19,4 |
Основываясь на рисунке 3.5, можно сделать вывод о том, что в среднем у выбранных акций степень риска относительно невысока. Это следует из того, что коэффициент «бета» находится в пределах от 0 до 1. Хотя можно отметить, что простые акции «Сургутнефтегаза» лидировали в данной совокупности, и бета-коэффициент был всего лишь немногим меньше 1. Наиболее осторожный рост наблюдался у привилегированных акций РАО «ЕЭС России».
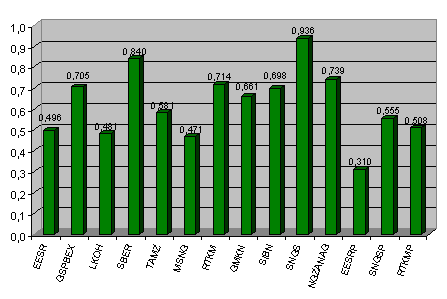
Рис. 3.5 – Бета-коэффициент акций
Для составления оптимального портфеля достаточно определения математического ожидания как арифметической средней прошлых доходностей (рисунок 3.6). Математическое ожидание не отражает действительный прогноз доходности акций, который проводится на основе всех воздействующих факторов, но оно достаточно для применения математических моделей построения оптимального портфеля ценных бумаг.
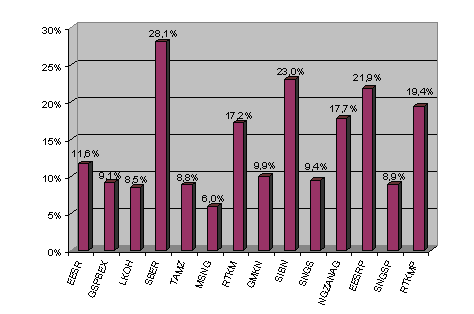
Рис. 3.6. Математическое ожидание доходности акций
Найдем теперь структуру оптимального портфеля акций. Для проведения расчетов необходимо задать безрисковую доходность. За безрисковую ставку примем ожидаемую доходность портфеля ОФЗ, рассчитанную ранее и равную 6% годовых. Хотя в рассчитанном портфеле государственных облигаций присутствует некоторая доля риска, с некоторыми допущениями доходность по нему можно принять в качестве безрисковой.
Ожидаемая доходность портфеля рассчитывается как взвешенное среднее математических ожиданий доходности входящих в него ценных бумаг, где в качестве весов взяты доли инвестиций, приходящихся на эти бумаги (формула 17).
На рисунке 3.7 отражена структура рассчитанного портфеля акций. Портфель состоит из непропорциональных частей: половина акций занимают 86,6% портфеля, другая половина – всего лишь 13,4%. Наибольшая доля выделена простым акциям Обществу с ограниченной ответственностью «Управляющая компания «Нефтегазовые активы» (ООО «УК «Нефтегазовые активы») – 28,8%.Компания «Ростелеком» представлена в портфеле двумя видами акций (простые – 13,6%, привилегированные – 15,5%), то наибольшая доля данного портфеля принадлежит акциям именно этой компании (29,1%).
.
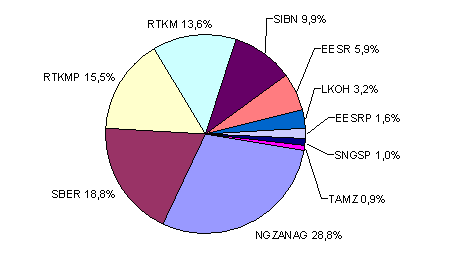
Рис. 3.7. Структура оптимального портфеля акций
Определение оптимальных портфелей государственных облигаций и акций не достаточно для составления конечного портфеля ценных бумаг. Необходимо также решить в каких пропорциях будут инвестироваться средства в эти портфели.
Для определения этих пропорций воспользуемся моделью Марковица, примененной при нахождении оптимального портфеля облигаций.
Характерной особенностью в данном случае будет то, что в качестве рассматриваемых единиц будут выступать не отдельные ценные бумаги, а сами портфели ценных бумаг. Поэтому интерес будет представлять динамика доходности портфелей, а динамика доходности отдельных их составляющих в расчет браться не будет.
При составлении портфеля акций тот факт, что цены были номинированы в долларах США, не влиял на конечный результат в виде доли ценной бумаги в портфеле. В данном случае при определении ковариаций с портфелем облигаций, выраженном в рублях, могут возникнуть расхождения. Поэтому возникает необходимость пересчета доходности акций, исходя из котировок акций в рублях.
Для решения задачи нахождения оптимальной структуры совокупного портфеля ценных бумаг будем использовать модель Марковица.
Для построения эффективного множества возможных портфелей необходимо вычислить математическое ожидание и ковариационную матрицу.
Доходность портфеля облигаций за месяц была найдена простым делением годовой доходности на 12. Недельная доходность портфеля акций была приведена к месячной путем умножения на количество недель.
Математическое ожидание доходности портфеля в данном случае рассчитано не как арифметическое среднее, а за него принята ожидаемая доходность, полученная в предыдущем параграфе. Она является более точной величиной.
Для составления ковариационной матрицы необходимо рассчитать среднеквадратическое отклонение доходности портфелей и коэффициент корреляции между ними (таблица 3.8).
Ковариации рассчитаны на основе формулы (18). Результаты сведены в таблице 3.9. Ковариации портфеля облигаций и портфеля акций равны среднеквадратическому отклонению, возведенному в квадрат, то есть дисперсии этих портфелей.
Таблица 3.8
Исходные данные для оптимизации совокупного портфеля
| Наименовании параметра | Портфель облигаций | Портфель акций |
| Математическое ожидание доходности, % | 1,333 | 26,600 |
| Среднеквадратическое отклонение | 0,071 | 36,802 |
| Коэффициент корреляции между портфелями | 0,168 | |
Таблица 3.9
Ковариационная матрица
| | Портфель облигаций | Портфель акций |
| Портфель облигаций | 0,00497 | 0,43710 |
| Портфель акций | 0,43711 | 1354,38 |
На основе этих данных возможно построить эффективное множество портфелей. Математическое ожидание доходности портфеля определяется как средневзвешенное доходностей, где в качестве веса выступает доля инвестиций к отдельную ценную бумагу (формула 17). Риск каждого портфеля определен по формуле (18). Результаты расчетов приведены в приложении 2. На основе этих данных возможно построить эффективное множество возможных совокупных портфелей ценных бумаг (рисунок 3.8).
Теперь необходимо определить местоположение оптимального портфеля, то есть выбрать приемлемое соотношение доходности и риска.
Так как банки являются организациями, не склонными к большому риску, то искомая точка должна находиться в левой части кривой – с меньшим риском. Начиная с некоторого момента, кривая приобретает все более пологий вид, что свидетельствует о том, что при дальнейшем увеличении доходности риск увеличивается нарастающими темпами. Поэтому, целесообразно за оптимальный портфель для данного инвестора принять портфель с доходностью 15,2%.
Таким образом, в данном портфеле облигации имеют 45%, а акции представлены 55%.
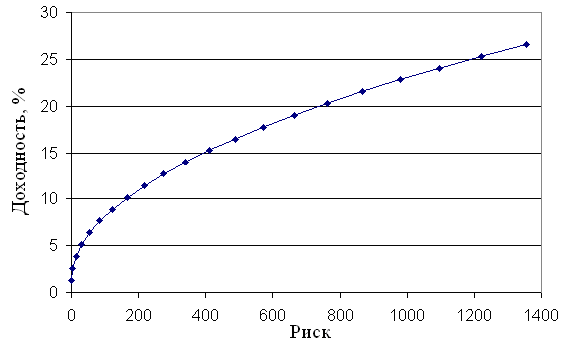
Рис. 3.8. Эффективное множество совокупных портфелей
До сих пор состав портфеля определялся в относительных величинах. Для последующей оценки результатов необходимы абсолютные значения. Поэтому необходимо определить количественный состав портфелей. Для этого необходимо выбрать сумму инвестируемых средств.
В период, когда Альфа-банк активно занимался операциями купли-продажи ценных бумаг, сумма инвестируемых средств доходила до 15% от валюты баланса. Валюта баланса составляла около 340 млн. рублей. Считаю целесообразным взять за размер инвестирования сумму в 5 млн. рублей, что составляет приблизительно 1,5% валюты баланса и соизмеримо с величиной статей отчетности.
Таким образом, учитывая, что 45% средств инвестируется в ОФЗ, а 55% – в акции, получим, что 2250 тыс. руб. должно быть направлено на покупку ОФЗ, а оставшаяся часть (2750 тыс. руб.) – на покупку акций.
Количество облигаций для покупки рассчитывается по формуле:
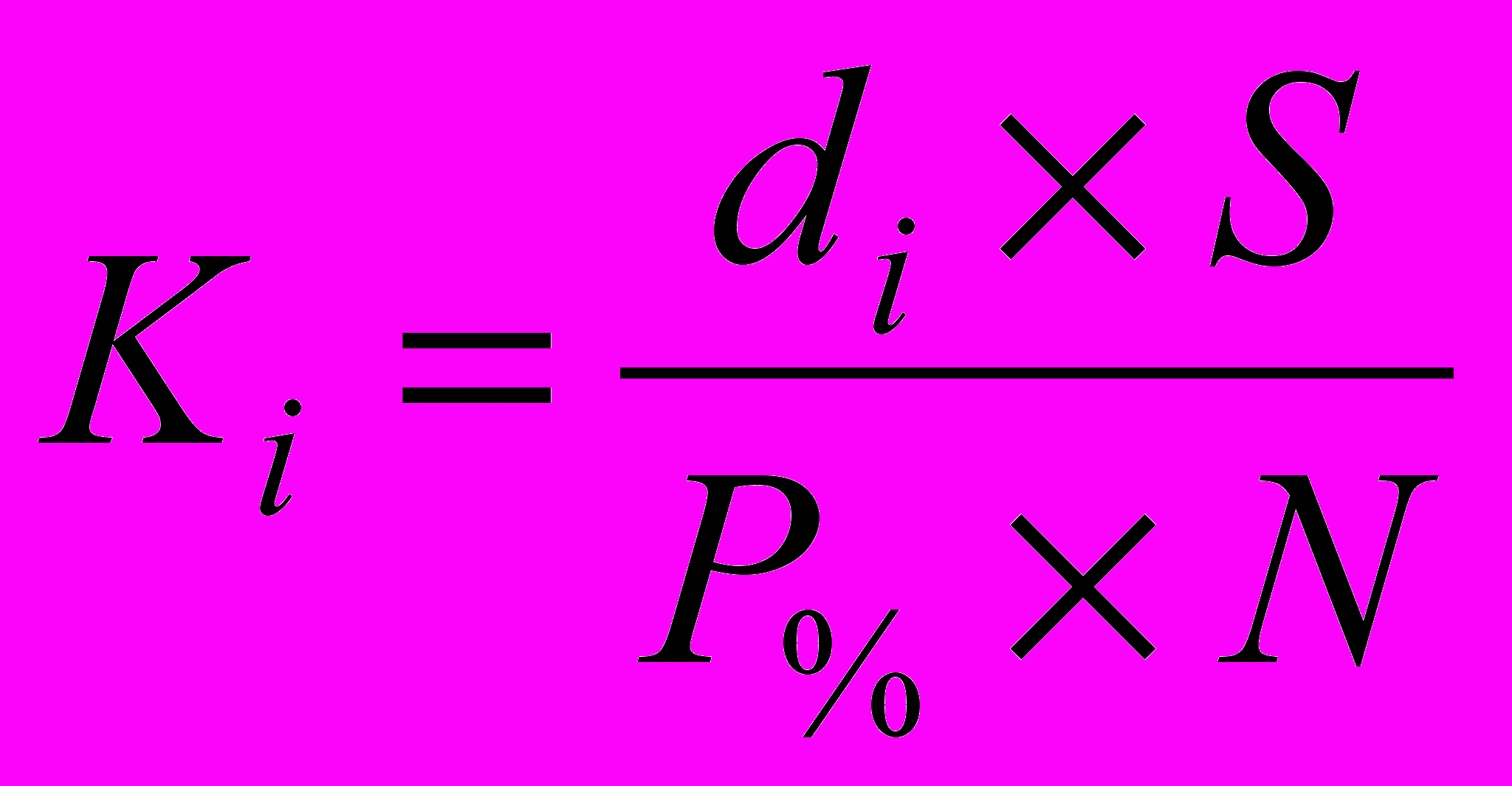, (26)где Ki – количество ценных облигаций, шт.;
di – доля портфеля, занимаемая облигацией;
S – сумма средств, инвестируемая в портфель, руб.;
P% – цена облигации, в % от номинала;
N – номинал облигации, руб.
Данные для расчета и результаты сведены в таблицу 3.10.
Таблица 3.10
Расчет количества облигаций для покупки
| Облигация | Доля инвестиций | Сумма инвестируемых средств, руб. | Цена на 01.12.05, % от номинала | Количество, шт. |
| ОФЗ 25058 | 0,018 | 40500 | 100,23 | 4063 |
| ОФЗ 26198 | 0,032 | 69750 | 95,36 | 7386 |
| ОФЗ 46001 | 0,125 | 283500 | 98,95 | 28364 |
| ОФЗ 46002 | 0,027 | 60750 | 97,79 | 6248 |
| ОФЗ 46003 | 0,030 | 67500 | 96,57 | 7116 |
| ОФЗ 46014 | 0,044 | 99000 | 96,66 | 10385 |
| ОФЗ 46017 | 0,182 | 411750 | 95,38 | 456 |
| ОФЗ 46018 | 0,542 | 1217250 | 91,76 | 137922 |
| Итого | 1,000 | 2250076 | | 201940 |
Так как количество облигаций округлялось до целого, сумма инвестируемых средств немного отличается от первоначальной. Таким образом, стоимость портфеля облигаций на 01.12.2005 составляет 2250076,42 руб.
Для определения количества акций, включаемого в портфель, необходимо их цены перевести в рубли, так как котировки акций в РТС выражены в долларах США. Курс доллара США на 01.12.2005, установленный ЦБ РФ, составлял 28,7792 рубля. Количество акций в портфеле определяется аналогично облигациям, но в знаменателе берется рыночная цена в рублях без номинала. В таблице 3.11 отражены результаты расчетов.
Таблица 3.11
Расчет количества акций для покупки в портфель
| Акция | Доля инвестиций | Сумма инвестируемых средств, руб. | Цена на 01.12.2005 | Количество, шт. | |
| в долларах США | в рублях | ||||
| EESRP | 0,016 | 44000 | 0,13 | 3,83 | 11781 |
| RTKMP | 0,155 | 426250 | 0,76 | 21,93 | 19468 |
| SBER | 0,188 | 517000 | 149,27 | 4295,94 | 120 |
| SIBN | 0,099 | 272250 | 1,82 | 52,44 | 5200 |
| RTKM | 0,136 | 374000 | 1,36 | 39,26 | 9513 |
| EESR | 0,059 | 162250 | 0,18 | 5,05 | 32130 |
| LKOH | 0,032 | 88000 | 15,76 | 453,77 | 193 |
| NGZANAG | 0,288 | 792000 | 9,05 | 260,56 | 3043 |
| SNGSP | 0,010 | 27500 | 0,24 | 6,78 | 4066 |
| TAMZ | 0,009 | 24750 | 0,74 | 21,31 | 1135 |
| Итого | 1,000 | 2728379 | | | 86649 |
Аналогично облигациям, количество акций округлялось до целого. Таким образом, стоимость портфеля акций на 01.12.2005 составляет 2728379,39 руб.