Б. В. Евтеев кандидат физико математических наук наук, доцент

Вид материала

Содержание

В.А. Коршунов
1. Поддержка выбора расположения распределительного склада методами решения транспортной задачи и учета полных общих затрат.
Пример 2. Размещение дополнительного оптового склада [1].
Таблица 1.2 Неравенство спроса и предложения
Таблица 1.3 Исходные данные для первого варианта
Таблица 1.4 Результаты решения задача для первого варианта
Таблица 1.5. Результаты решения задача для второго варианта
2. Определение логистических границ рынка
Таблица 2.1. Исходные данные
Таблица 2.2. Расчетные данные
Поиск решения
Таблица 2.3. Данные для построения диаграмм
Таблица 2.4. Матрица расстояний
3. Классическая транспортная задача.
Пример 3. Поддержка выбора наилучшего транспортного обслуживания школьников.
Таблица 3.1.Цены на билеты для различных маршрутов и типов автобусов
Таблица 3.2. Исходные данные и условия решения транспортной задачи
Таблица 3.3.Ответ
4. Поддержка выбора между использованием собственного или наемного склада.
Пример 4. Задача выбора собственного или наемного склада.
...
Полное содержание

Подобный материал:

Б И Б Л И О Т Е К А П Р Е Д П Р И Н И М А Т Е Л Я

Образовательный центр «ЗНАНИЕ»

Б.В. Евтеев, В.А. Коршунов

И Н Т Е Г Р И Р О В А Н Н А Я Л О Г И С Т И К А:

П О Д С И С Т Е М Ы С К Л А Д И Р О В А Н И Я

И Т Р А Н С П О Р Т И Р О В К И Г Р У З О В

В ПРАКТИКЕ МАЛОГО БИЗНЕСА

ПРАВИТЕЛЬСТВО МОСКВЫ

ДЕПАРТАМЕНТ ПОДДЕРЖКИ И РАЗВИТИЯ

МАЛОГО ПРЕДПРИНИМАТЕЛЬСТВА

МОСКОВСКИЙ ФОНД ПОДГОТОВКИ КАДРОВ

2004 г

Б.В. Евтеев – кандидат физико – математических наук наук, доцент

В.А. Коршунов – кандидат технических наук, доцент

«Интегрированная логистика: подсистемы складирования и транспортировки грузов» М., МСЭУ, с

Подготовлено при содействии Московского фонда подготовки кадров для слушателей курса «Логистика» предпринимателей, руководителей и специалистов малых предприятий.

.

 Б.В. Евтеев, Б.В. Коршунов 2004

 Издательство МСЭУ. 2004

Тираж 100 экз.

ВВЕДЕНИЕ

В предлагаемой учебно-методической разработке рассмотрены некоторые вопросы, относящиеся к таким функциональным областям логистики как складская и транспортная логистика.

«Генеральной идеей транспортно-грузового комплекса было создание центра распределения, в котором совмещались бы транспортные, складские и сбытовые функции при предоставлении клиентуре полного набора сопутствующих услуг. »[7]

Системный подход, являясь основным принципом логистики, во многом предопределяет возникновение новых тенденций развития и изменения логистических функций, например, изменение функций грузоперерабатывающих пунктов. «Эти изменения вызываются необходимостью применения таких способов повышения качества транспортного обслуживания, как доставка грузов «от двери к двери», а не от станции к станции, за счет применения контейнерных и комбинированных перевозок, технологических маршрутов и других современных способов транспортировки» [7].

В 1 Рассматривается задача выбора из двух вариантов расположения оптового склада наиболее подходящего варианта с точки зрения минимизации транспортных расходов, связанных с доставкой товаров со склада в магазины для розничной торговли. Поставленная задача сводится к транспортной задаче при помощи введения так называемой фиктивной торговой точки, с помощью которой уравновешиваются складские мощности и потребности магазинов в товарах. Требования совпадения этих показателей является одним из условий решения транспортной задачи. Существует достаточно большой выбор различных методов решения поставленной задачи. Однако цель данной разработки не знакомство с ними и их усвоение, а решение поставленных вопросов с помощью имеющихся возможностей разработанного программного обеспечения на их основе на примере возможностей приложения MS EXCEL.

В 2 рассматривается ситуация, связанная с использованием фирмами оптовых складов с целью оптимизировать общие издержки реализации продукции за счет уменьшения их транспортной составляющей. В итоге определяются логистические границы рынка для каждой фирмы, а также границы для места расположения оптового склада. В результате происходит территориальное разграничение на области, в каждой из которых у одной или нескольких фирм имеется преимущество перед другими фирмами. Полученные аналитические решения проиллюстрированы с помощью графических возможностей MS EXCEL.

В 3 решается классическая транспортная задача, на примере решения вопроса о выборе варианта наилучшего транспортного обслуживания школьников, средствами процессора электронных таблиц MS EXCEL

В 4 рассмотрено решение одной из известных задач «сделать или купить» на примере выбора одного из двух вариантов: использовать наемный склад, т.е. воспользоваться услугами складов общего пользования, или, если имеется такая возможность, использовать складские мощности собственного склада.

1. ПОДДЕРЖКА ВЫБОРА РАСПОЛОЖЕНИЯ РАСПРЕДЕЛИТЕЛЬНОГО СКЛАДА МЕТОДАМИ РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ И УЧЕТА ПОЛНЫХ ОБЩИХ ЗАТРАТ.

С целью удовлетворения возросшего спроса требуется решить задачу выбора наиболее подходящего места расположения дополнительного оптового склада. Для этого из нескольких возможных вариантов расположения склада требуется выбрать наилучший с точки зрения минимизации затрат, связанных с доставкой товаров в магазины для розничной торговли.

Формализация этой задачи показывает, что она относится к классу задач линейного программирования. Методы линейного программирования являются наиболее развитыми в области решения оптимизационных задач. Кроме этого, имеющееся программное обеспечение компьютеров предоставляет пользователю широкий выбор средств для решения упомянутых выше задач линейного программирования.

К компьютерным средствам такого рода, пользующимся достаточно большой популярностью среди широкого круга пользователей с разной степенью подготовки работы на компьютере, относится приложение MS EXCEL.

Пример 2. Размещение дополнительного оптового склада [1].

Фирма оптовый покупатель бытовой техники хочет открыть третий склад, который будет снабжать три розничных магазина “А”, “В” и “С”. Новый склад сможет поставлять 500 единиц товарных наборов в неделю. Руководство фирмы изучает два варианта размещения нового оптового склада. Транспортные расходы для варианта № 1 к магазинам “А”, “В” и “С” равны 6, 8 и 7 у.д.е. соответственно; для варианта № 2 , 10, 6 и 4 у.д.е. соответственно.

Начальные данные по уже существующей логистической системе поставок показаны в табл. 1.1.

Таблица 1.1

Удельные затраты на перевозки из складов в магазины, ограничения на спрос в магазинах и на объемы хранения на складах.

Места складов	Объемы поставок в магазины			Общий объем хранения на складе	Удельные транспортные расходы от складов к магазинам			Ограничения на общий объем хранения
Места складов	"А"	"В"	"С"		"А"	"В"	"С"	Xij = Вi
Склад №1	0	0	0	0	8	3	7	500
Склад №2	0	0	0	0	5	10	9	400
Ограничения на спрос магазина (Xij=Аj)	400	600	350

Какой из двух вариантов расположения нового оптового склада даст фирме наибольшую экономическую выгоду по критерию минимума транспортных расходов?

Решение.

В задачах транспортного типа удобно номеровать переменные не одним индексом, а двумя (x_ij), где первый индекс обозначает номер пункта отправки, а второй — номер пункта назначения.

Цены ресурсов также удобно записывать в виде матрицы, размерность которой должна совпадать с размерностью матрицы ограничений на переменные.

При указанных условиях оптимизационная модель записывается следующим образом:

Z = 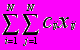→ Min (1.1)

при ограничениях

x_ij 0 , (1.2)

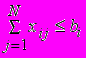i = 1,2,...,M (1.3.a)

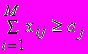j = 1,2,...,N , (1.3.b)

где c_ij— ставки переменных затрат выпуска по стратегии i для периода j, включая также затраты на хранение единицы продукции; a_j— cпрос за период j, b_i—лимиты производственных мощностей для выпуска по стратегии i.

Для указанных выше исходных данных общие соотношения перепишутся в следующем виде:

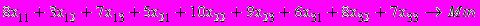,(1.4)

при ограничениях на складские мощности и потребности магазинов, которые записываются следующим образом:

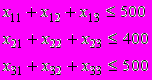(1.5.a)

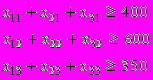(1.5.b)

x_ij 0 , (1.6)

При решении транспортных задач часто встречаются ситуации, когда спрос не равен предложению (для данной постановки логистической задачи предложение означает хранение на складе).

Таблица 1.2

Неравенство спроса и предложения

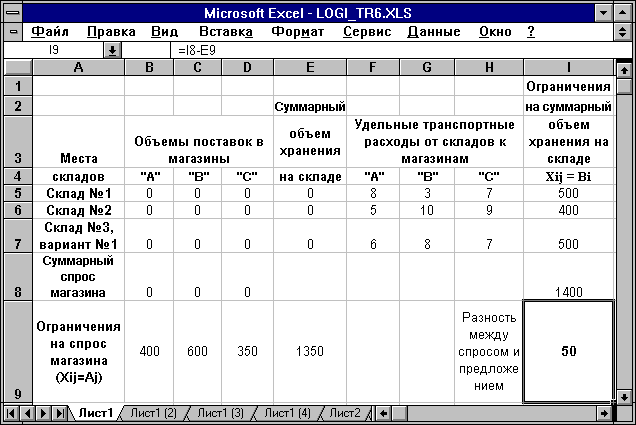
Рассматриваемый нами случай, как видно из данных, представленных в табл.1.2, обладает этими особенностями. Указанные исходные значения объемов хранения на трех складах показывают, что их суммарный объем превышает общий спрос в трех магазинах на 50 единиц, т.е. имеет место ситуация неравенства спроса и предложения.

Одним из методов решения транспортной задачи при неравенстве спроса и предложения является метод ввода фиктивного столбца или фиктивной строки.

В нашем случае вводится фиктивный столбец соответствующий четвертому магазину, с одновременным указанием нулевых значений всех удельных транспортных расходов для него, как это представлено в табл. 1.3.

Таблица 1.3

Исходные данные для первого варианта

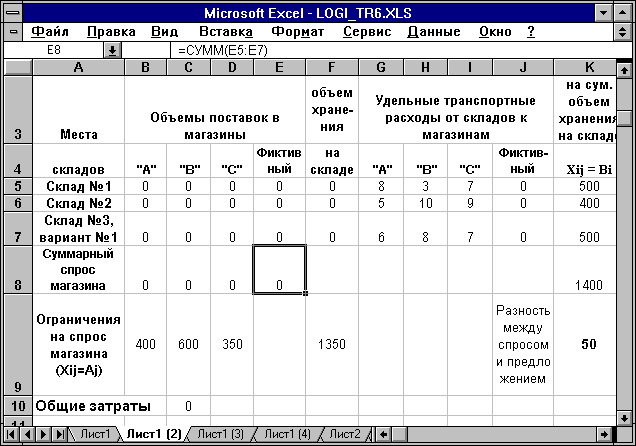
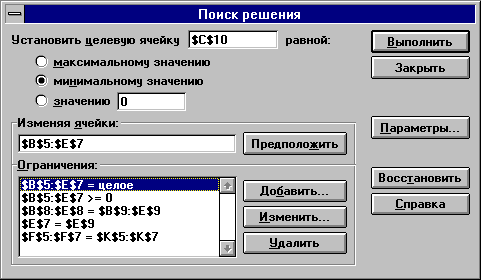
Рис. 1.1. Задание ограничений для решения задачи

Суммарный спрос этого фиктивного магазина совпадает с разностью между предложением и спросом, т.е. составляет 50 единиц.

Таблица 1.4

Результаты решения задача для первого варианта

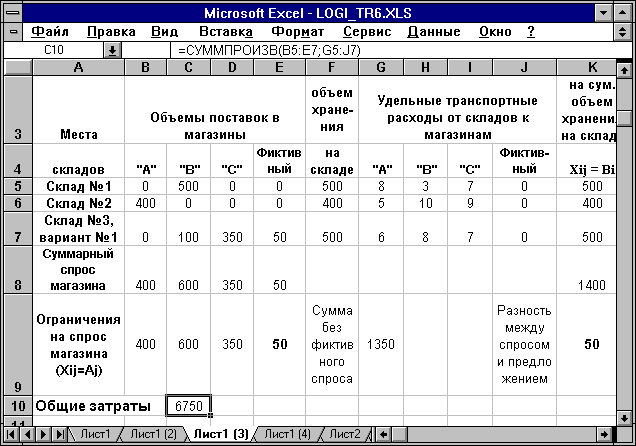
Таким образом, введение фиктивного магазина, с указанным выше спросом, позволило уравнять спрос и предложение, что в свою очередь является необходимым требованием транспортной задачи.

На рис. 1.1. показано, каким образом заполняются соответствующие поля при использовании опции Поиск решения.

Результаты решения транспортной задачи для первого и второго вариантов приведены в табл. 1.4. и табл. 1.5. соответственно.

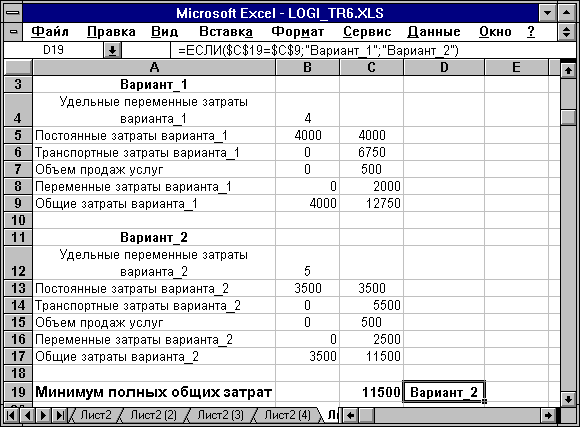
Итоговые результаты решения поставленной задачи представлены в табл. 1.6. В итоге оптимальным вариантом с точки

Таблица 1.5.

Результаты решения задача для второго варианта

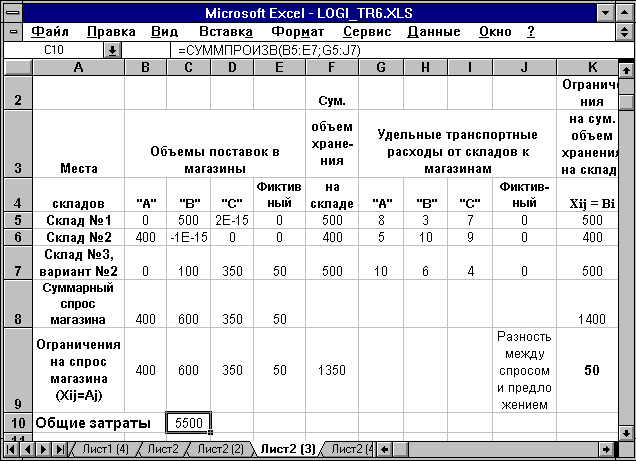
Таблица 1.6.

Результаты решения задачи для двух вариантов и выбор оптимального варианта

2. ОПРЕДЕЛЕНИЕ ЛОГИСТИЧЕСКИХ ГРАНИЦ РЫНКА

В дальнейшем, когда речь будет идти о границах рынка, подразумевается его территориальное разграничение на области, в каждой из которых у той или иной фирмы или у нескольких фирм имеется преимущество в реализации своей продукции. Это может проявляться в частности в том, что при примерно одинаковом уровне цен на эту продукцию прибыль от ее реализации у некоторых фирмы выше, чем у остальных.

Различные фирмы, продвигая свой товар на рынок, используют разнообразные приемы, позволяющие им постепенно наращивать сбыт собственной продукции. Это достигается не только увеличением сбыта в уже завоеванных сегментах рынка, но и посредством завоевания новых. При этом каждая фирма должна определить границы рынка, которые, как уже отмечалось выше, и определяют те области, где она будет иметь преимущество перед другими фирмами. Один из путей расширения этих границ – использование складских мощностей([5], [6]). При этом использование склада дает возможность фирме выгодно реализовывать свою продукцию не только в направлении удаления от неё, но и в направлении самой фирмы. Таким образом, если некоторая продукция реализуется несколькими фирмами, каждая из которых имеет сеть складов, то возникает задача определения для каждого пункта реализации этой продукции той фирмы, или нескольких фирм, у которой будут преимущества перед другими. Один из основных этапов решения этой задачи – ее решение для двух фирм. При этом мы ограничимся случаем, когда каждая из фирм использует один склад. Отметим, что при рассмотрении общего случая принципиальных затруднений не возникает.

С нашей точки зрения решение задачи целесообразно разбить на несколько случаев. Сначала решить задачу без использования складов фирмами. Потом рассмотреть случай использования склада одной фирмой, и, наконец, случай использования складов двумя фирмами. Все эти случаи проиллюстрированы на рис. 2.1.- рис. 2.3.

Таблица 2.1.

Исходные данные

Отметим, что цена продажи продукции зависит не только от ее себестоимости и затрат на транспортировку до места ее продажи, а и, учитывая анализ полной стоимости [4], от ряда других величин. Мы не будем стремиться учитывать все возможные зависимости, так как с нашей точки зрения существенные моменты рассматриваемой ситуации при этом не изменятся, а учтем лишь еще затраты связанные с функционированием складов.

Перечень используемых исходных данных, а также их обозначений приведен в табл. 2.1.

Хотелось бы обратить внимание на наличие двух видов транспортных тарифов приведенных в этой таблице. Их различие во многом предопределяет целесообразность использования складских мощностей для расширения границ рынка.

Таблица 2.2.

Расчетные данные

В табл. 2.2. приведены расчетные данные необходимые как для графического решения поставленной выше задачи, так и для нахождения ряда числовых характеристик необходимых для уточнения этого графического решения.

Сделаем необходимые пояснения для понимания результатов, приведенных в табл. 2.2.

Прежде всего, отметим, что все вычисления проводятся из расчета на единицу продукции, а минимальная цена, по которой каждая из фирм может продать свою продукцию без убытка, находится из следующих соотношений:

C_A = P_A +T_A*X (2.1.)

C_B = P_B +T_B*(S-X) (2.2.)

Здесь X обозначает расстояние от фирмы A до торговой точки реализации продукции. Значение X, при котором C_A = C_B, и определяет границу

Рис. 2.1. Графическое определение границ рынка без использования складов обеими фирмами

рынка. Она понимается в том смысле, что в точках, удаленных от фирмы A на расстояние меньшее, чем X , преимущество в реализации продукции будет у фирмы A. В то время как в точках, удаленных от фирмы A на расстояние большее, чем X, преимущество у фирмы B.

Отметим, что значение X, задающее границу рынка можно найти различными способами. Мы используем опцию Поиск решения с целью унификации нахождения границы рынка, а также других необходимых характеристик, и в двух других случаях. Для этого в ячейки C27 заносится целевая функция, представляющая собой разность правых частей соотношений (2.1.) и (2.2.), а в качестве изменяемой ячейки используется ячейка C28, которая в данном случае соответствует значению X.

Графическое решение задачи в первом случае с указанием границы рынка изображено на рис. 2.1.

Как уже отмечалось выше, одним из путей расширения рынка сбыта является использование складских мощностей с целью оптовых поставок продукции, после чего она поступает в розничную продажу. Сначала рассмотрим случай использования склада только одной из двух фирм. При этом фирма, использующая склад вынуждена нести дополнительные расходы, связанные с содержанием этого склада. При этом цена продажи продукции фирмой B вычисляется по приведенной ранее формуле (2.2), а цена реализации продукции фирмой A, которая обозначается через C_A_,_S , по формуле

C_A,S = P_A+D_A +T_O,A*Y+T_A*ABS(X-Y) , (2.3)

где ABS(X-Y) обозначает абсолютную величину разности X-Y, а Y – расстояние от склада до фирмы A. Границы рынка при этом находятся при тех же условиях, что и раньше:

C_A_,_S = C_B (2.4)

Уравнение (2.4) содержит две переменные величины X и Y. Поэтому, задавая значения одной из них, например, Y, мы ищем значение другой переменной. При этом, вообще говоря, не для любых фиксированных неотрицательных значений Y мы можем найти неотрицательные значения другой переменной X. Это объясняется, в частности, тем, что располагать склад фирмы A слишком близко к фирме B нецелесообразно. Причиной этому может послужить тот факт, что транспортные расходы даже оптовой поставки продукции фирмой A могут быть больше транспортных расходов розничной поставки продукции фирмой B, если при этом предполагать, что себестоимость самой продукции обеих фирм примерно одинаковая.

Таблица 2.3.

Данные для построения диаграмм

Таким образом, в этом случае возникает еще одна задача, связанная с нахождением границы для расположения склада фирмы A. Границу для расположения склада будем искать из следующих условий:

P_A + D_A+ T_O_,_A*Y = P_B+ T_B*(S-Y) (2.5)

Графическая иллюстрация результатов решения задачи во втором случае изображена на рис. 2.2.

Сделаем некоторые пояснения к изображенным на нем результатам. Во втором случае, в отличие от предыдущего, возможно несколько граничных значений рынка.

Рис. 2.2. Графическое определение границ рынка с использованием склада фирмой А

Поэтому на графике указывается максимальная из этих границ, хотя в рассмотренном конкретном случае она является единственной. Здесь мы не будем приводить варианты появления нескольких граничных значений, так как один из них приводится в третьем случае, который мы рассмотрим ниже.

Целевые функции, с помощью которых получены значения для максимальной границы рынка и границы склада занесены в ячейки C22 и C26, а сами значения границ в ячейки С23 и С24 соответственно.

Далее, для построения графика стоимости продукции фирмы A , используется встроенная функция MIN, с помощью которой из двух значений можно выбрать наименьшее значение.

Рис. 2.3. Графическое определение границ рынка с использованием складов обеими фирмами

Теперь перейдем к рассмотрению третьего случая, когда обе фирмы используют склады. Необходимые для этого случая пояснения уже были сделаны выше. Добавим лишь, что из представленных на рис. 2.3. графических результатов видно, что в данном случае рынок разбивается на четыре области, в двух из которых фирма А имеет преимущество перед фирмой В, а в оставшихся двух наоборот. В этом случае понятие границы рынка перестает быть однозначным и с его помощью можно разбить рынок на области, в которых одна из фирм имеет преимущество по отношению к другой.

Сделаем несколько пояснений к решению задачи разбиения множества торговых точек, в которых реализуется однотипная продукция двух фирм А и В по принципу преимущества одной из них. В этом случае удобно составить матрицу, столбцы которой обозначаются фирмами и торговыми точками, например, T(1), T(2), … , T(n), а строки обозначаются фирмами А и В. В ячейки этой матрицы заносятся неотрицательные числа, являющиеся расстояниями от фирмы, обозначающей строку до фирмы или торговой точки, обозначающей столбец. Случай заполнения матрицы по существующей схеме расположения фирм и торговых точек не вызывает затруднений. Случай же моделирования взаимного расположения фирм A и В и торговых точек T(1), T(2), … T(n) требует некоторых пояснений.

В дальнейшем, без ограничения общности можно считать, что торговые точки расположены на отрезке прямой, соединяющей точки А и В, причем порядок следования соответствует их удаленности от фирмы А.

В табл. 2.4. заносятся расстояния между фирмами и торговыми точками соответственно. Тогда при заполнении матрицы неотрицательными числами надо учитывать следующие требования.

Во-первых, S(1,1)=S(2,2)=0; S(1,2)=S(2,1)=S. Кроме этого, если все торговые точки различны, тогда для любых i и j должны выполнятся следующие соотношения: S(1,i)+S(i,2) = S(1,2) и S(1,i) ≠ S(1,j).

Таблица 2.4.

Матрица расстояний

	A	B	T(1)	T(2)	…	T(n)
A	S(1,1)	S(1,2)	S(1,3)	S(1,4)		S(1,n+2)
B	S(2,1)	S(2,2)	S(2,3)	S(2,4)		S(2,n+2)

. В заключение отметим, что полученные результаты можно обобщить на случай нескольких фирм, в результате чего рынок разбивается на области преимущества одних фирм перед другими

3. КЛАССИЧЕСКАЯ ТРАНСПОРТНАЯ ЗАДАЧА.

Транспорт – это необходимый компонент, как производственных процессов, так и процессов сферы обращения.

«Транспорт – это отрасль материального производства, осуществляющая перевозки людей и грузов. В структуре общественного производства транспорт относится к сфере производства материальных услуг. … Значительная часть логистических операций на пути движения материального потока от первичного источника сырья до конечного потребления осуществляется с применением различных транспортных средств. Затраты на выполнение этих операций составляют до 50% от суммы общих затрат на логистику» [4].

Таким образом, транспортная логистика – это одна из важнейших функциональных областей логистики. Минимизация затрат именно в этой области во многом предопределяет оптимизацию общих затрат

Далее приводится пример решения транспортной задачи с помощью MS EXCEL.

Пример 3. Поддержка выбора наилучшего транспортного обслуживания школьников.

В небольшом населенном пункте “А” есть школа, которую посещает ряд учеников; при этом 72 школьника живут вне пункта “А”, и возникает необходимость ежедневной доставки их к школе на автобусах.

Есть две основные автобусные остановки “В” и “С” (место “В” расположено между “А” и “С”). Число учеников, которых надо перевозить к школе на автобусах равняется: 42 на остановке “С”, 6  между “С” и “В”, 20  на остановке “В” и 4  между “А” и “В”.

Транспортное агенство, обслуживающее населенный пункт “А”, располагает двумя типами автобусов: вместимостью 35 и 50 мест. Агенством установлены следующие цены (в швейцарских франках) билетов в зависимости от отрезка пути и типа автобусов (см табл. 3.1).

Таблица 3.1.

Цены на билеты для различных маршрутов и типов автобусов

Маршруты	35 мест	50 мест
ВА	39	50,5
СА	54	68
СВ	45	57,5

Цены на билеты не пропорциональны расстояниям, так как постоянные затраты на перевозки школьников, как правило, превышают переменные затраты.

Найти количества автобусов соответствующих типов, которые надо использовать на каждом отрезке пути, чтобы суммарные затраты транспортного агенства стали минимальными.

Решение.

Ведем следующие обозначения для переменных, соответствующих числу автобусов, которые принимаются во внимание в каждом конкретном случае.

Маршруты	35 мест	50 мест
ВА	x₁₁	x₁₂
СА	x₂₁	x₂₂
СВ	x₃₁	x₃₂

Теперь можем сформулировать транспортную задачу линейной оптимизации с ограничениями.

Целевая (минимизируемая) функция примет тогда вид:

Min Z = 39 x₁₁+ 54 x₂₁+ 45 x₃₁+ 50,5 x₂₁+ 68 x₂₂+ 57,5 x₃₂(3.1)

при следующих ограничениях на переменные задачи.

Перевезти из пункта “С” в пункт “В” 48 школьников можно четырьмя вариантами:

1) 35-ти местными автобусами, курсирующими только по маршруту из пункта “С” в пункт “В”;

2) 50-ти местными автобусами, курсирующими только по маршруту из пункта “С” в пункт “В”;

3) 35-ти местными автобусами, курсирующими по маршруту из пункта “С” в пункт “А”;

4) 50-ти местными автобусами, курсирующими по маршруту из пункта “С” в пункт “А”;

Так как заранее неизвестно какой именно из этих четырех вариантов перевозок 48 школьников окажется наилучшим по критерию минимума общих затрат транспортного агенства, то все эти четыре возможности необходимо учесть (включить) в ограничении типа неравенства:

35 x₂₁+ 50 x₃₁+ 35 x₂₂+ 50 x₃₂ 48 (3.2)

Перевезти из пункта “В” в пункт “А” 72 школьников можно четырьмя вариантами:

1) 35-ти местными автобусами, курсирующими только по маршруту из пункта “В” в пункт “А”;

1) 50-ти местными автобусами, курсирующими только по маршруту из пункта “В” в пункт “А”;

3) 35-ти местными автобусами, курсирующими по маршруту из пункта “С” в пункт “А”;

4) 50-ти местными автобусами, курсирующими по маршруту из пункта “С” в пункт “А”;

Так как заранее неизвестно какой именно из этих четырех вариантов перевозок 72 школьников окажется наилучшим по критерию минимума общих

Таблица 3.2.

Исходные данные и условия решения транспортной задачи

затрат транспортного агенства, то все эти четыре возможности необходимо учесть (включить) в ограничении типа неравенства:

35 x₁₁+ 50 x₁₂+ 35 x₂₁+ 50 x₂₂ 72 (3.3)

Рис. 3.1. Задание ограничений транспортной задачи

Кроме этих специальных (уникальных) ограничений задачи необходимо учесть также универсальные:

1) все неизвестные задачи должны быть неотрицательными x_ij 0 ;

2) все неизвестные задачи должны быть целочисленными.

Для решения задачи в MS EXCEL используется опция Поиск решения. На рис. 3.1. показано, каким образом приведенные выше условия должны быть заданы в компьютере, чтобы можно было найти оптимальный вариант решения транспортной задачи.

Рис. 3.2. Окно ввода ограничений

На рис. 3.2. представлено дополнительное окно для ввода ограничений задачи.

Таблица 3.3.

Ответ. Минимальное значение функции общих затрат равно 107 франкам при таком из допустимых целочисленных решений, когда (см. табл. 3.3)

x₁₁= 1; x₂₁= 0; x₃₁= 0; x₁₂= 0; x₂₂= 1; x₃₂= 0; (3.4)

т.е. достаточно двух автобусов, один из которых (35-ти местный) перевозит школьников из пункта “В” в пункт “А”, а другой (50-ти местный)  из пункта “С” в пункт “А”.

Если исключить требование целочисленности переменных, то в качестве оптимального будет получено следующее решение (см. табл. 3.4)

x₁₁= 1; x₂₁= 0; x₃₁= 0; x₁₂= 0,48 ; x₂₂= 0,96 ; x₃₂= 0; (3.5)

т.е. решение (3.4) нельзя получить с помощью простого округления решения (3.5) до целых чисел (ни за счет отбрасывания целых частей, ни за счет их дополнения до единицы).

Таблица 3.4.

Результат решения задачи без требования
целочисленности решения

4. ПОДДЕРЖКА ВЫБОРА МЕЖДУ ИСПОЛЬЗОВАНИЕМ СОБСТВЕННОГО ИЛИ НАЕМНОГО СКЛАДА.

Неотъемлемым звеном любой логистической системы является склад. Более того складские расходы составляют значительную часть от общих расходов на поддержание функционирования самой логистической системы, а их минимизация в значительной степени способствует минимизации общих расходов.. «…проблемы, связанные с функционированием складов, оказывают значительное влияние на оптимизацию движения материальных потоков в логистической цепи и в конечном итоге на совокупные издержки обращения » [7].

Один из возможных путей решения этой задачи – использование системы поставок «точно в срок» (система ТВС). Ее применение позволяет значительно сократить объем запасов и потребность в складских мощностях. Однако не всякая ситуация допускает применение такой системы, в силу достаточно жестких требований к дисциплине поставок.

Более того, и система ТВС не обязательно предполагает исключение склада из своей структуры. Так, например, «В торговле система поставок ТВС может означать поставку товаров по одной из следующих схем:

склад предприятия оптовой торговли – торговый зал магазина;
склад готовой продукции завода – изготовителя – торговый зал магазина;
поле – торговый зал магазина» [4]

Наличие складских мощностей у предприятия вовсе не означает, что в любой ситуации оно должно использовать, в случае необходимости, именно их, а не пользоваться услугами других складов.

Причин тому может быть много, например, недостаточно развитая инфраструктура собственного склада по отношению к предъявляемым к ней требованиям или не подходящее его место расположения и т.д.

Поэтому, в силу сказанного выше, перед организацией может стоять вопрос о выборе варианта использования собственного или наемного склада.

Пример решения такой задачи приводится ниже.

Пример 4. Задача выбора собственного или наемного склада.

Дано. В табл. 1. представлены значения параметров затрат на собственном и на арендуемом (наемном) складах.

Найти значения грузооборота, при котором затраты содержания собственного склада и хранения в наемном складе совпадают. Решить задачу аналитически и графически.

Таблица 1.

alpha0,3Наименование параметра затрат хранения на складе	Символ	Значение
Число дней хранения на наемном складе за годСуточная стоимость грузовой площади наемного склада (в у.д.е. за 1 кв.м.)	N	365
Размер запаса в днях оборота	In	60
Число рабочих дней хранения на наемном складе за год	Nwork	250
Нагрузка на 1 кв. м. площади при хранении на наемном складе (в тоннах/кв. м.)	Etta	2
Постоянные затраты собственного склада (у.д.е./ год)	F2	30000
Удельная стоимость переработки на собственном складе	betta	4

Таблица 2.

Исходные и расчетные данные по использованию наемного склада

Таблица 3.

Исходные и расчетные данные по содержанию собственного склада

Рис. 1. Графическая иллюстрация решения задачи выбора между собственным и наемным складом

ЗАКЛЮЧЕНИЕ

В предлагаемой учебно-методической разработке затронуты некоторые вопросы, складской и транспортной логистики.

Целесообразность объединения этих вопросов и рассмотрения их вместе предопределена новыми взглядами на решение логистических проблем и тенденциями развития интегрированной логистики.

Задача выбора из двух вариантов расположения оптового склада наиболее подходящего варианта с точки зрения минимизации транспортных расходов, связанных с доставкой товаров со склада в магазины для розничной торговли сводится к транспортной задаче. Это достигается применением стандартного способа введения фиктивных переменных, в данном случае это так называемая фиктивная торговая точка, с помощью которой уравновешиваются складские мощности и потребности магазинов в товарах. Требования совпадения этих показателей является одним из условий решения транспортной задачи.

Существует довольно большое количество разнообразных подходов к решению задачи, связанной с минимизацией общих издержек реализации продукции. В данном случае основное внимание уделено транспортной составляющей этих издержек. Для ее возможного уменьшения рассматривается использование дополнительных складских мощностей, что позволяет повысить конкурентоспособность

В итоге определяются логистические границы рынка и границы для места расположения оптового склада, при помощи которых происходит разграничение на области, в каждой из которых у одной или нескольких фирм имеется преимущество перед другими фирмами. Графические возможности, предоставляемые компьютерными технологиями, позволяют наглядно проиллюстрировать полученные аналитические результаты.

Решение транспортной задачи, на примере выбора наилучшего варианта транспортного обслуживания школьников, средствами процессора электронных таблиц MS EXCEL, показывает, что в ряде случаев необходимо помочь компьютеру выбрать правильный вариант, что объясняется спецификой программного обеспечения.

Рассмотренное решение одной из известных задач «сделать или купить» имеющей самые разнообразные приложения иллюстрируется на примере выбора либо использования наемного склада, либо использования собственных складских мощностей.

Литература

Стивенсон В. Дж. Управление производством. М.: ООО “Издательство “Лаборатория базовых знаний””, ЗАО Издательство БИНОМ, 1998.
Кофман А., Анри-Лабордер А. Методы и модели исследования операций. Целочисленное программирование. — М.: Мир, 1977.
Гаджинский А.М. Практикум по логистике. 2-е изд., перераб. и доп. М.: издательско-торговый центр “Маркетинг”, 2001.
Гаджинский А.М. Логистика: Учебник для высших и средних специальных учебных заведений. 4-е изд., перераб. и доп..: Издательско-торговый центр “Маркетинг”, 2001.
Евтеев Б.В., Евтеев Е.Б. Границы рынка. // Современные аспекты экономики. —СПб, №11 (24), 2002, с. 150-154.
Евтеев Б.В., Евтеев Е.Б. Логистические границы рынка. Сборник научных работ. Выпуск 5. [По материалам 5-й научной конференции профессоров и преподавателей Института экономики и предпринимательства., 2 апреля 2002г.].- с.97—104. — М.: ИНЭП, 2002.
Интегрированная логистика накопительно-распределительных комплексов (склады, транспортные узлы, терминалы ): Учебник для транспортных вузов. / Под общ.ред. Л.Б.Миротина. – М.: Издательство «Экзамен», 2003.– 448 с.

Содержание.

ВВЕДЕНИЕ

ПОДДЕРЖКА ВЫБОРА РАСПОЛОЖЕНИЯ РАСПРЕДЕЛИТЕЛЬНОГО СКЛАДА МЕТОДАМИ РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ И УЧЕТА ПОЛНЫХ ОБЩИХ ЗАТРАТ
ОПРЕДЕЛЕНИЕ ЛОГИСТИЧЕСКИХ ГРАНИЦ РЫНКА
КЛАССИЧЕСКАЯ ТРАНСПОРТНАЯ ЗАДАЧА
ПОДДЕРЖКА ВЫБОРА МЕЖДУ ИСПОЛЬЗОВАНИЕМ СОБСТВЕННОГО ИЛИ НАЕМНОГО СКЛАДА

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

Blog