Измерение спектра и формы детерминированных сигналов

Вид материала

Документы

Содержание Частотная модуляция. Метод исчезающей несущей Анализ спектра сигналов Основными метрологическими характеристиками Анализаторы спектра последовательного действия Разрешающая способность Динамический диапазон Погрешность измерения уровней сигнала Цифровой анализ спектра Цифровые анализаторы спектра Анализаторы спектра на цифровых фильтрах Измерение нелинейных искажений

Подобный материал:

• Цифровая обработка сигналов, 25.15kb.
• Программа курса лекций (3 курс, 6 сем., 32 ч., диф зачет) Профессор Киричук Валерий, 72.05kb.
• Цифровая фильтрация, 139.58kb.
• Тема пространство и метрология сигналов физическая величина более точно определяется, 595.48kb.
• Обработка сигналов в радиотехнических системах, 126.5kb.
• Методические указания по выполнению лабораторной работы №2 по курсу "Цифровая обработка, 99.67kb.
• Измерение длины волны и ширины спектра лазерного излучения с помощью много лучевого, 102.41kb.
• Программа курса лекций, 51.42kb.
• Измерение фазового сдвига, 189.66kb.
• Цифровой вольтметр щ-304, 137.06kb.

ИЗМЕРЕНИЕ СПЕКТРА И ФОРМЫ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ


ИЗМЕРЕНИЕ ПАРАМЕТРОВ МОДУЛИРОВАННЫХ СИГНАЛОВ


В радиотехнических устройствах применяются ампли­тудная, частотная, фазовая, импульсная и комбинирован­ные виды модуляции. В первых трех видах модуляции амплитуда, частота или фаза синусоидального модулируе­мого сигнала изменяется по закону изменения модулирую­щего напряжения. При импульсной модуляции высота, частота повторения, длительность или временное положе­ние видеоимпульсов изменяются в соответствии с измене­нием модулирующего сигнала низкой частоты. Применя­ются и другие, более сложные виды модуляции — кодо-импульсная, дельта-модуляция и др.

Сигнал, модулированный по амплитуде, характеризуется коэффициентом модуляции М, по частоте, — девиацией частоты ∆f, по фазе, — индексом угловой модуляции ψ. Кроме того, все модулированные сигналы характеризу­ются глубиной модуляции, равной отношению данного коэффициента, девиации или индекса к максимальному значению, принимаемому за 100 %-ную модуляцию. Для оценки модуляции импульсов необходимо измерять пара­метры импульсов и их последовательностей.

Амплитудная модуляция. Сигнал, модулированный по амплитуде, записывается так:

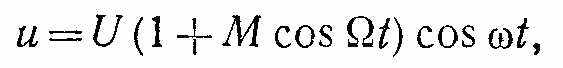(1)

где U — амплитуда немодулированного высокочастотного сигнала; 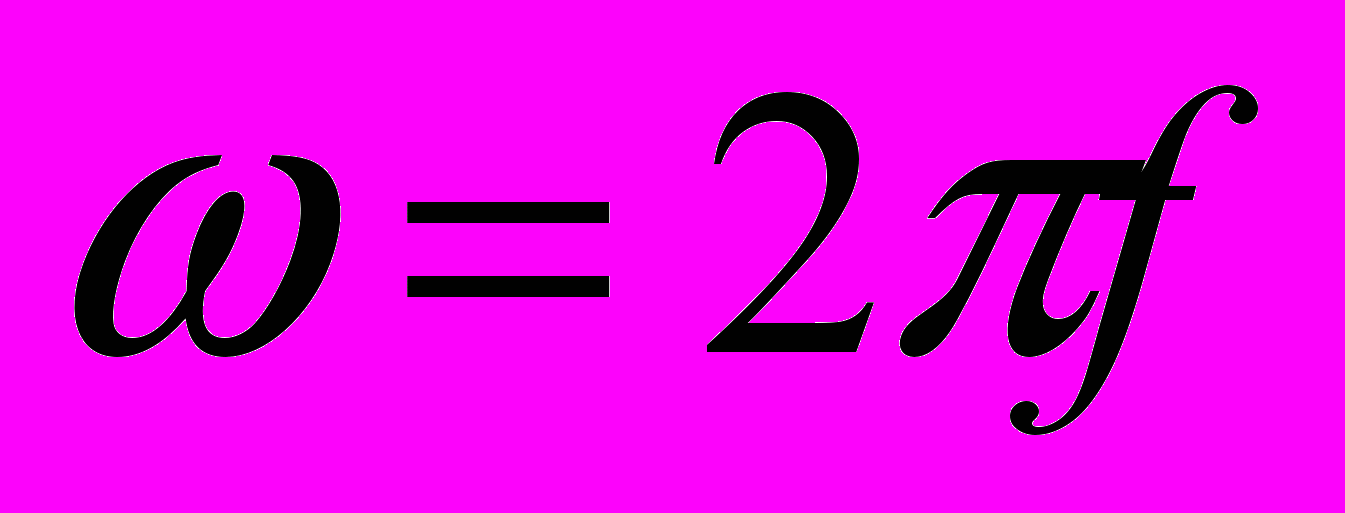; f — несущая частота; 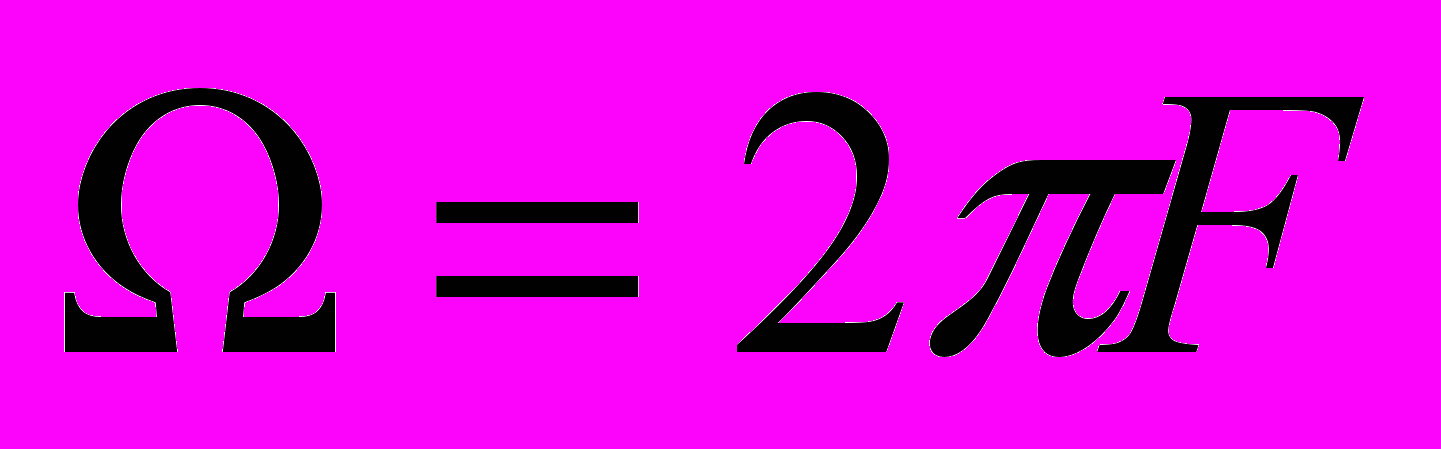; F — модулирующая частота; М — коэффициент амплитудной модуляции,

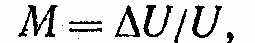(2)

∆U — приращение высокочастотного напряжения при мо­дуляции.

Обычно коэффициент модуляции выражается в процен­тах. При амплитудной модуляции коэффициент модуляции и ее глубина совпадают.

Н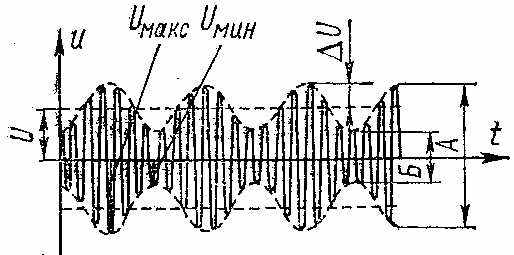а рисунке показан график, модулированного сиг­нала, соответствующий выражению (1); из графика сле­дует, что

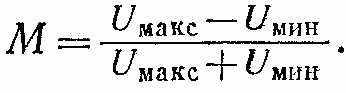(3)

Формулы (2) и (3) справедливы только для симмет­ричной модуляции. При несимметричной модуляции коэф­фициент модуляции измеряется раздельно «вверх» и «вниз» :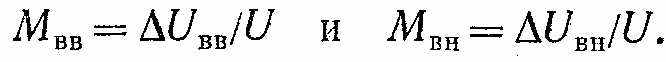



Коэффициент амплитудной модуляции измеряют двумя методами: осциллографическим и методом выпрямления (детектирования).

Осциллографический метод, в свою очередь, осуще­ствляют двумя способами: линейной или синусоидальной развертки.

При линейной развертке в канал вертикального отклоне­ния подают высокочастотный модулированный сигнал, частоту развертки устанавливают в 2-3 раза ниже модули­рующей частоты и синхронизируют модулирующим напряжением. На экране осциллографа появляется осциллограмма модулированного сигнала в виде у = f(t). Измерив с помощью масштабной сетки максимальное от­клонение луча А = 2U_макс и минимальное Б = 2U_мии, согласно формуле (3) получаем (в процентах)

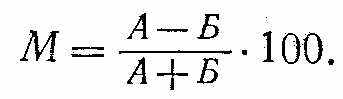(4)

В 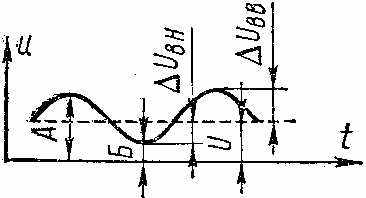канал вертикального отклонения можно подать выпрямленный (детектированный) сигнал, т. е. напряже­ние огибающей. Если осциллограф пропускает постоянный ток, то на экране появится осциллограмма вида рисунка справа, по которой также можно определить М. Размеры А и Б измеряют относительно линии развертки.

При синусоидальной развертке в канал вертикального отклонения подают модулированный сигнал, а в канал горизонтального отклонения — модулирующее напряже­ние. Верхняя огибающая модулированного сигнала опре­деляется выражением 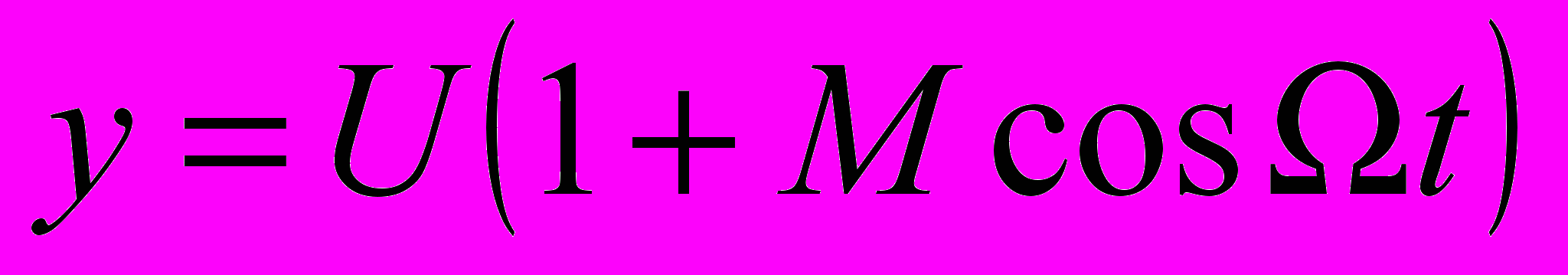. Отклонение по горизонтали х=UcosΩt. Подставляя из последнего выражения cosΩt в выражение для у, получаем у=U+Мх, т. е. верхняя огибающая имеет вид прямой линии с наклоном, определяемым значением М. Анало­гично, нижняя огибающая также прямая с наклоном —М.

О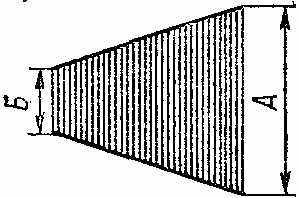сциллограмма представляет собой светящуюся плоскость трапецеидальной формы. Прямые, ограни­чивающие плоскость, являются фигурами Лиссажу, полу­чившимися за счет взаимодействия огибающих модулиро­ванного сигнала с модулирующим напряжением при отсут­ствии фазового сдвига между ними. Размеры А и Б соот­ветствуют максимальному и минимальному значениям мо­дулирующего напряжения, поэтому М вычисляется по фор­муле (4).

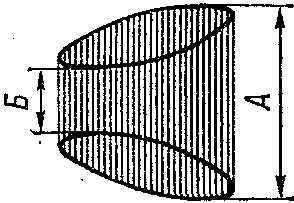
Усилители осциллографа или тракт модулирующего напряжения могут внести фазовый сдвиг между огибаю­щими и модулирующим напряжением. При этом прямые примут вид эллипсов. Коэффициент амплитуд­ной модуляции М вычисляется так же, как и раньше, только размеры А и Б измеряются между точками каса­ния горизонтальных прямых в местах максимального и минимального отклонений луча. Осциллограмма, изо­браженная на рисунке ниже, свидетельствует о наличии нелинейных искажений.

По виду фигуры, получающейся на экране осцилло­графа при отсутствии фазового сдвига и искажений, спо­соб синусоидальной развертки частот называют способом трапеции.

Осциллографический метод прост и удобен. Погрешность составляет 5—10%. Измерение коэффициента модуляции можно выполнять только на одной модулирующей частоте в процессе настройки, проверки или профилактики уст­ройств. В рабочих условиях при модуляции многочастот­ным сигналом можно только наблюдать непрерывно меняю­щуюся картину модулированного сигнала, но измерить его параметры невозможно.

Метод выпрямления (детектирования) позволяет изме­рять коэффициент амплитудной модуляции в процессе работы передатчика (генератора). Сущность метода заклю­чается в том, что высокочастотный модулированный сиг­нал детектируется, в результате чего выделяются постоянная составляющая, пропорциональная напряжению несу­щей U, и составляющая модулирующей частоты (огибаю­щая), амплитуды которой пропорциональны приращению сигнала при модуляции ∆U. Воспользовавшись форму­лой (2), можно определить М.

П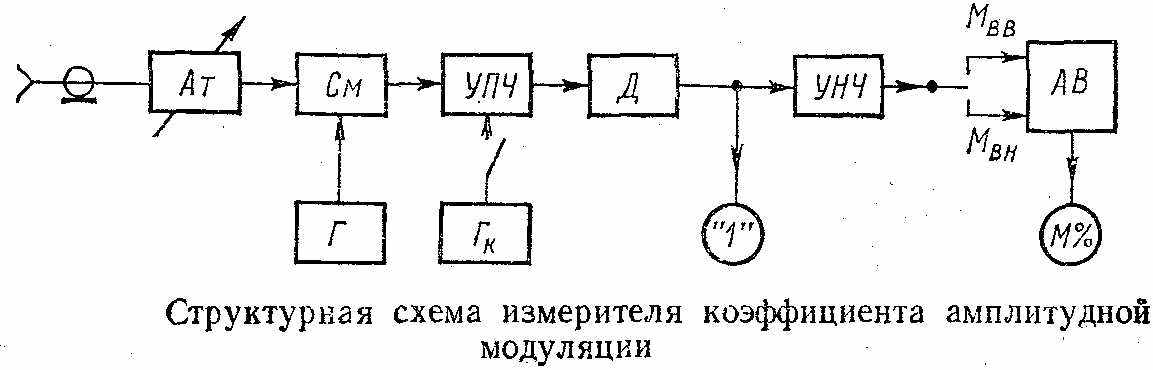риборы, основанные на этом методе, называют модулометрами, или измери­телями модуляции. Структур­ная схема такого прямо­показывающего прибора пред­став­ляет собой высоко­качественный супергетеро­динный радиоприем­ник амплитудно-модулированных сигналов соответствую­щего диапазона частот и особых пояснений не требует. Магнитоэлектрический индикатор, с помощью которого измеряется постоянная составляющая, выделен­ная детектором Д, пропорциональная напряжению несу­щей, всегда устанавливается на условную отметку «1», и тогда амплитудный (пиковый) вольтметр АВ с закрытым входом, измеряющий ∆U, можно градуировать непосред­ственно в процентах М. Переключая его вход, можно измерять М_вв и М_вн. Для установки напряжений несущей на «1» используют входной атеннюатор Aт, а для проверки тракта промежуточной частоты измерителя модуляции — калибровочный генератор Гк.

Частотная модуляция. Сигнал, модулированный по ча­стоте синусоидальным напряжением, записывается в таком виде:



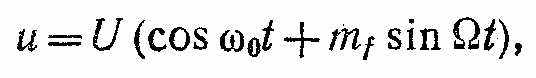
где U — амплитуда напряжения несущей частоты f₀; 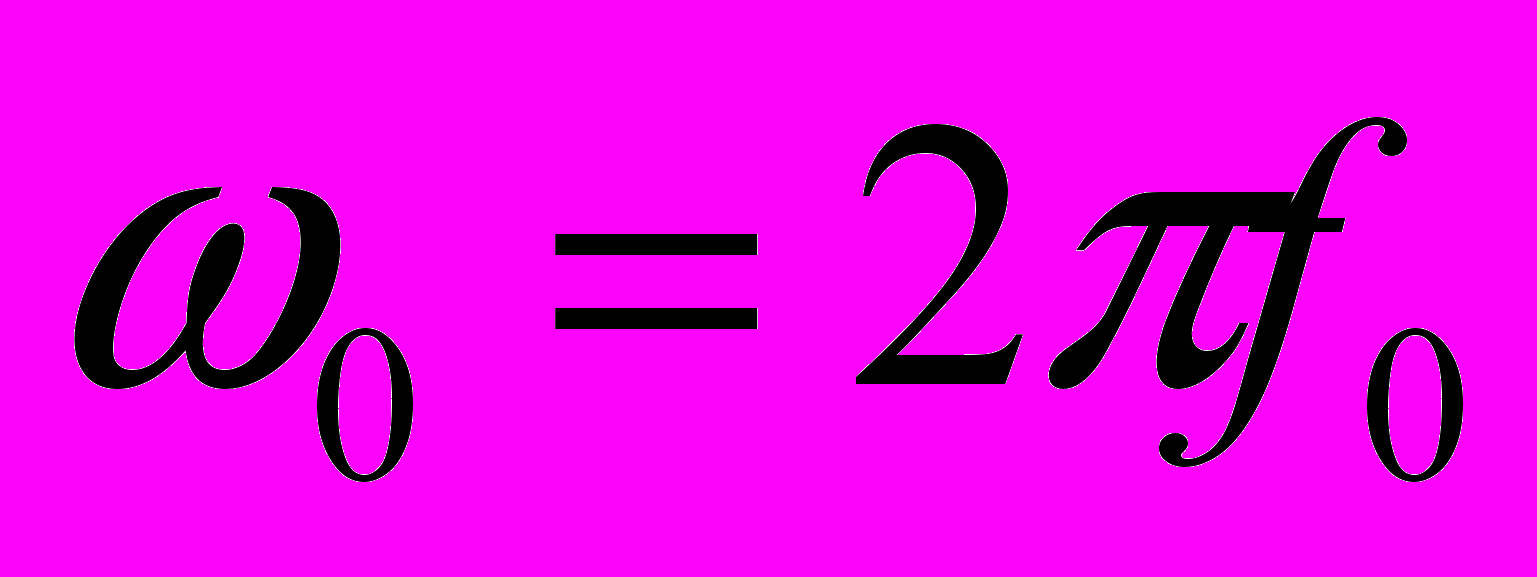; ; 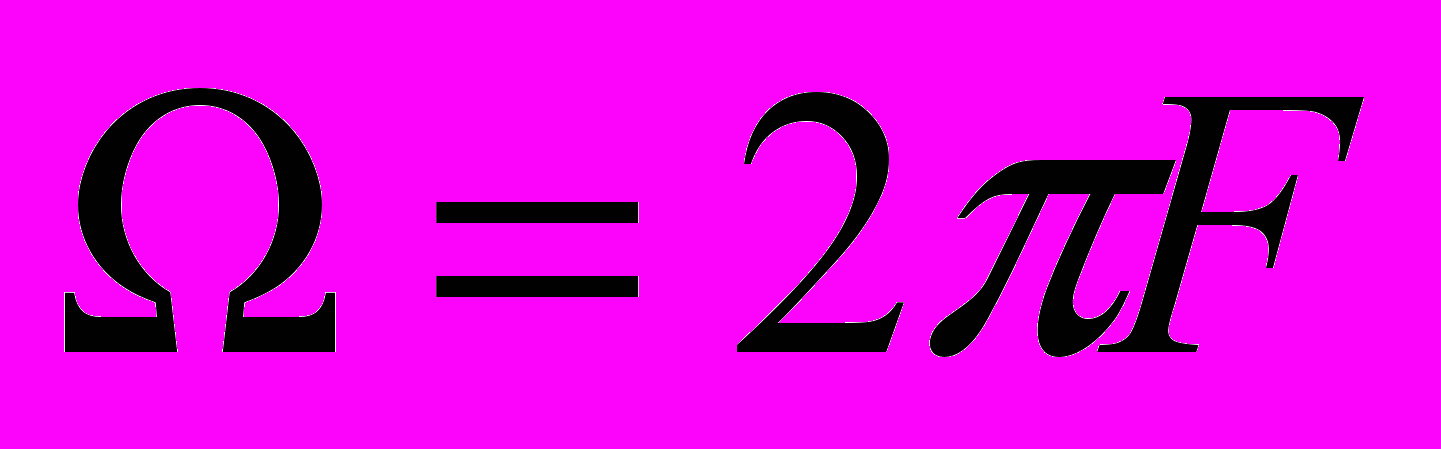F — частота модулирующего напряже­ния; m_f — индекс частотной модуляции,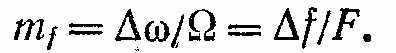



Здесь ∆f — отклонение высокой частоты при модуляции, или девиация частоты.

Мгновенное значение частоты частотно-модулированного сигнала f = f₀±∆f. Девиация частоты пропорциональна амплитуде модулирующего напряжения и не зависит от его частоты:

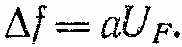(5)

Частота модулирующего напряжения определяет ско­рость изменения мгновенного значения девиации 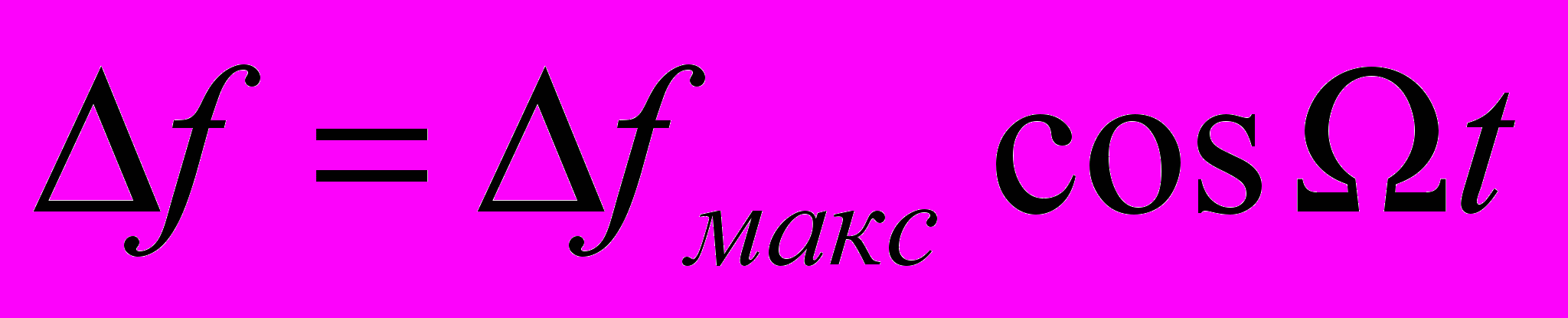, где ∆f_макс— максимальное значение де­виации, нормированное для данной системы связи или вещания. Например, для радиовещания с частотной моду­ляцией на ультракоротких волнах (УКВ ЧМ) ∆f_макс = ± 50 кГц; для звукового сопровождения телевизион­ных программ ∆f_макс = ± 75 кГц. В практике эксплуата­ции устройств с ЧМ в рабочих условиях измеряется девиа­ция частоты ∆f. Индекс модуляции m_f измеряется при кон­трольно-поверочных и регулировочных работах.

Для измерения девиации существует несколько методов, но практически используется метод частотного детектора. Сущность его состоит в том, что частотно-модулирован­ный сигнал преобразуется в амплитудно-модулированный и детектируется; в результате получается напряжение, пропорциональное напряжению модулирующей частоты. Как следует из выражения (5), шкалу амплитудного вольтметра можно градуировать непосредственно в едини­цах девиации частоты — килогерцах. Приборы, предназна­ченные для измерения девиации частоты, называются девиометрами.

Девиометр представляет собой высококачественный ка­либрованный радиоприемник частотно-модулированных сигналов, и его структурная схема подобна схеме модулометра. Отличие заключается в том, что после усилителя промежуточной частоты имеется амплитудный ограничитель, а вместо амплитудного детектора исполь­зуется частотный. Применяют частотные детекторы типа электронно-счетной схемы или на линии задержки. Вслед­ствие общности большинства узлов модулометра и девиометра они часто выпускаются в виде комбинированных приборов для измерения AM и ЧМ сигналов. Погрешность составляет 3—5 %.

Выражение для частотно-модулированного сигнала Мож­но представить в спектральной форме:

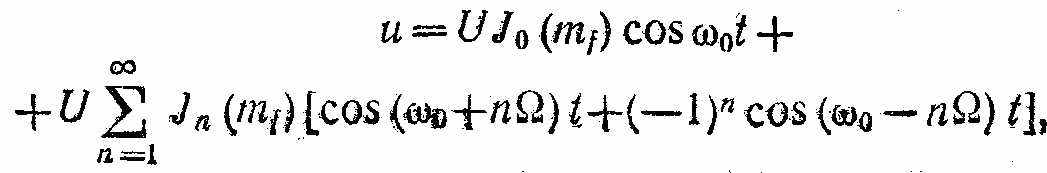(6)

где J₀(m_f) — функция Бесселя первого рода нулевого порядка аргумента, равного индексу частотной модуля­ции m_f; J_n () — то же n-го порядка; 2n — число боковых полос в частотно-модулирован­ном сигнале.

П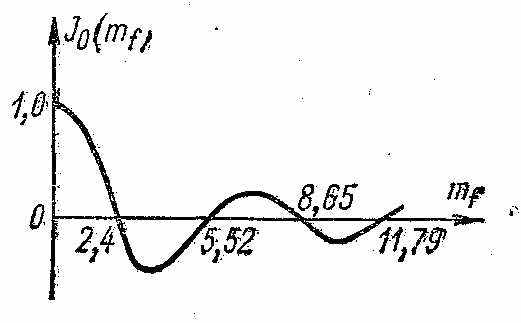ервое слагаемое в правой части формулы (6) представ­ляет собой напряжение, несу­щей частоты; амплитуда его ме­няется по закону изменения функции Бесселя, кривая кото­рой проходит через нулевые значения. При равен­стве индекса модуляции m_f зна­чениям корней Бесселевой функ­ции 2,4; 5,52; 8,65; 11,79; 14,93; 18,07 и так далее на­пряжение несущей в спектре частотно-модулированного колебания обращается в нуль, исчезает из спектра. На основе этого явления разработан метод измерения индек­са частотной модуляции, названный методом исчезающей несущей.

М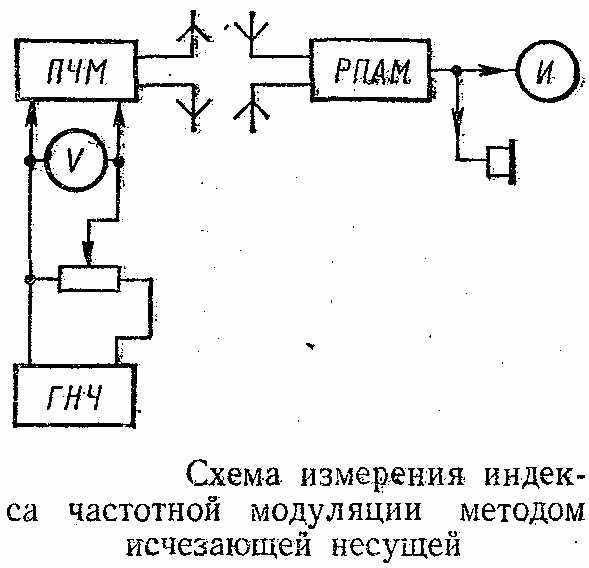етод исчезающей несущей реализуется с помощью схемы измерения, приведенной на рисунке. В нее входят: исследуемый генератор (передатчик) с частотной модуля­цией; генератор низкой частоты, являющийся источником модулирующих сигналов; высококачественный узкополосный радиоприемник соответствующего диапазо­на частот; элементы связи между передатчиком и при­емником; индикатор напря­жения несущей на выходе, приемника. Полоса пропу­скания приемника должна быть меньше удвоенного значения самой низкой мо­дулирующей частоты.

Измерение выполняют так. Радиоприемник сигна­лов с амплитудной модуляцией РПАМ настраивают на несу­щую частоту передатчика ПЧМ при отсутствии модуля­ции, и на индикаторе И устанавливают показание, близкое к максимальному. Радиоприемник регулируют на мини­мальную чувствительность. Затем постепенно повышают напряжение U_F генератора ГНЧ при выбранном значе­нии модулирующей частоты F. Показание индикатора при этом уменьшается и при некотором значении U_F1 исче­зает. Для точного определения момента исчезновения несущей увеличивают чувствительность приемника до воз­никновения собственных шумов. Полезно параллельно индикатору включить головные телефоны или громкогово­ритель. Уточненному значению U_F1 соответствует первый корень Бесселевой функции, равный 2,4, следовательно, m_f=∆f/F=2,4 и девиация частоты ∆f₁=m_f1F=2,4F. Продолжая увеличивать напряжение модуляции, на­ходят второе его значение, при котором снова исчезает показание индикатора. Это происходит при напряже­нии U_F2, которому соответ­ствует второй корень Бес­селевой функции, равный 5,52. Отсюда m_f2 = 5,52, а девиация ∆_f2 = 5.52F. Модулирующую частоту F нужно поддерживать по­стоянной. Результаты из­мерения удобно свести в таблицу (здесь F = 3 кГц = const).

UF , В	mf	∆f кГц
0 1 2 3 4 5 6 7 8 9	0 2,4 5,52 8,65 11,79 14,93 18,07 21,21 24,35 27,49	≈(0,002÷0,01) 7,2 16,56 25,95 35,37 44,79 54,21 63,63 73,05 82,47

П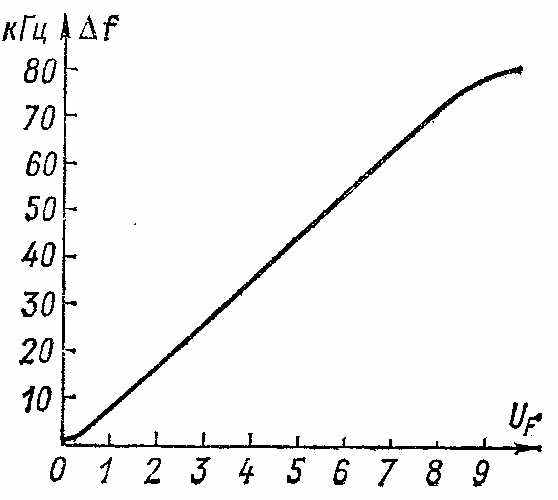о данным этой таблицы легко построить график, представляющий модуляционную характеристику передатчика. С помощью этого графика можно определить все промежуточные значения индекса m_f и напряжения U_F, а также границу линейного участка характеристики, за ко­торым начинаются нелинейные искажения. Иног­да характеристика не проходит через нуль (начало коорди­нат). Это свидетельствует о наличии паразитной частот­ной модуляции, вызванной собственными шумами в цепях передатчика или пульсациями питающего напряжения.

Точность определения девиации частоты методом исче­зающей несущей зависит от погрешности установки ча­стоты генератора модулирующего напряжения и намного превосходит точность измерения с помощью девиометров. Поэтому этот метод широко используется для первичной настройки и регулировки передатчиков, калибровки гене­раторов и в других случаях.

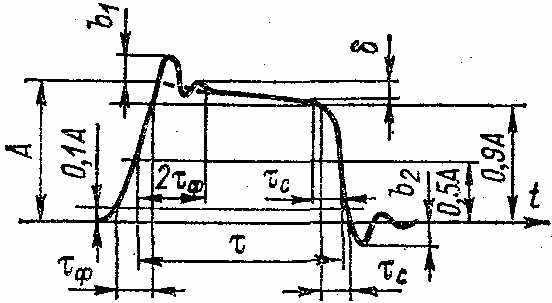
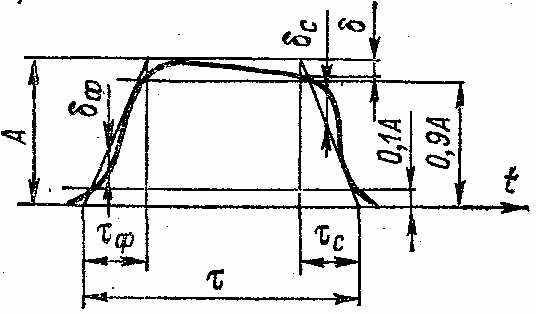
И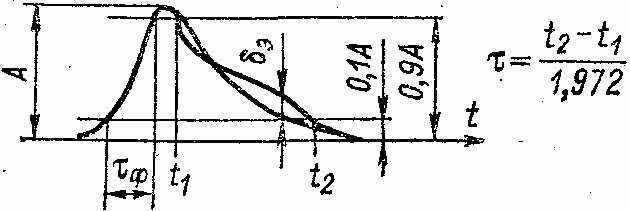мпульсная модуляция. В процессе прохождения им­пульсов через различные цепи и устройства, а также во время распространения радиоимпульсов между передающей и приемной антеннами форма их изменяется (искажается) и может принимать вид, представленный на рисунках. Искажения разделяются на амплитудные — неравномерность вершины импульса δ, выбросы на вершине b₁ и в паузе b₂, и временные — длительность фронта τ_ф и среза τ_с и связанная с ними длительность τ импульса на разных уровнях. В особо ответственных случаях рассматриваются нелинейности фронта δ_ф и среза δ_с и неэкспоненциальность среза δ_э. Импульсная последовательность характеризуетсячастотой повторения, длительностью временных интервалов между соседними импульсами и скважностью или коэффи­циентом заполнения. Представляет интерес мгновенное значение высоты импульса в заданный момент времени и изменения этого значения под влиянием различных факторов. Иногда интересуются интегральными параме­трами — обобщенными длительностью и высотой.

Все параметры импульсов напряжения, кроме интеграль­ных, можно измерять с помощью осциллографа. При изме­рении импульсов тока их сначала превращают в импульсы напряжения. Для этого в цепь, по которой передаются импульсы тока, включают вспомогательный резистор с не­большим сопротивлением, падение напряжения на котором и измеряют.

Осциллографический метод измерения параметров им­пульсов получил широкое распространение благодаря своей наглядности. Однако в ряде слу­чаев он не удовлетворяет требова­ниям точности, быстроты и удоб­ства измерения.

Диапазон временных парамет­ров импульсов простирается от до­лей наносекунды до единиц секунд. Измерение таких интервалов време­ни одним универсальным осцилло­графом невозможно. Для каждого конкретного случая нужно подбирать осциллограф, отвечающий по своим пара­метрам предстоящему измерению. Измерение длительно­стей осуществляют с помощью калиброванных меток и калиброванной развертки. Способ калиброванных меток пригоден для измерений импульсов любой формы при любой скважности.

С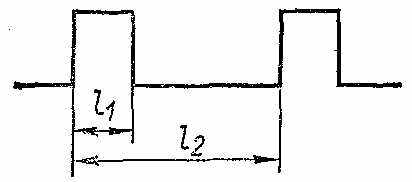пособ калиброванной развертки применяют, если форма импульсов близка к прямоугольной, а скважность неве­лика. В этом случае на осциллограмме устанавливают два соседних импульса и по масштабной сетке изме­ряют на экране осциллографа расстояния l₁ и l₂. Получен­ные данные позволяют вычислить длительность импульса 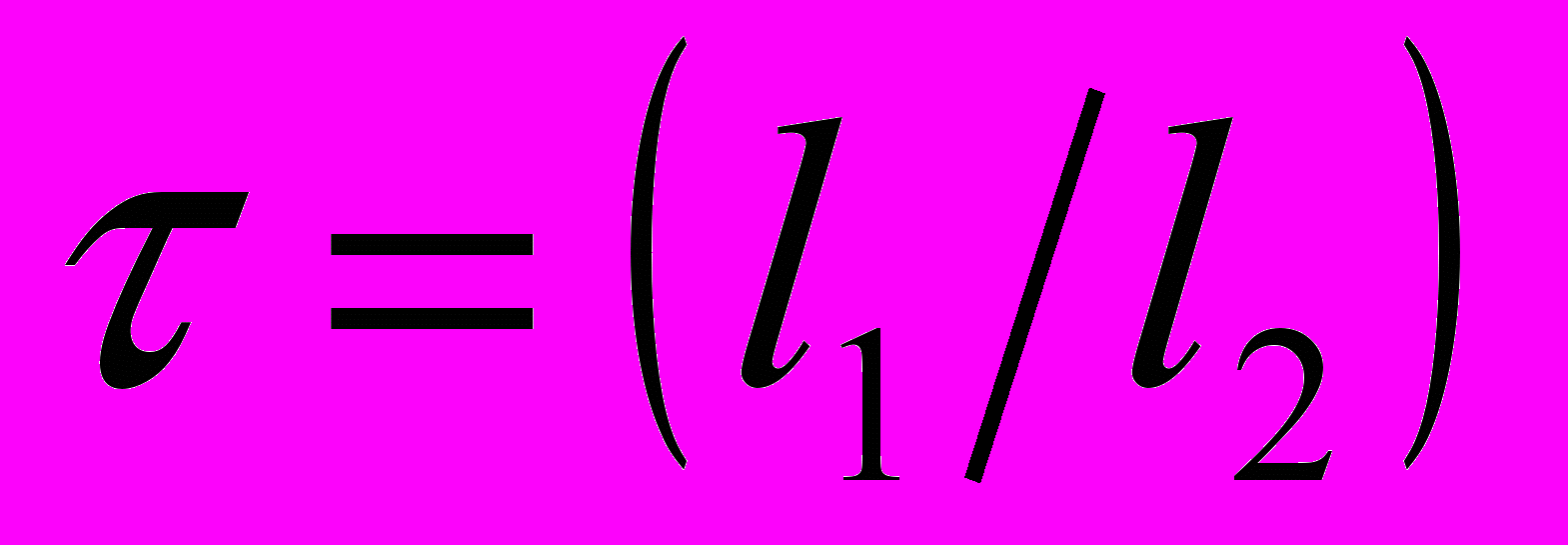Т_р и интервал между импульсами Т_р - τ =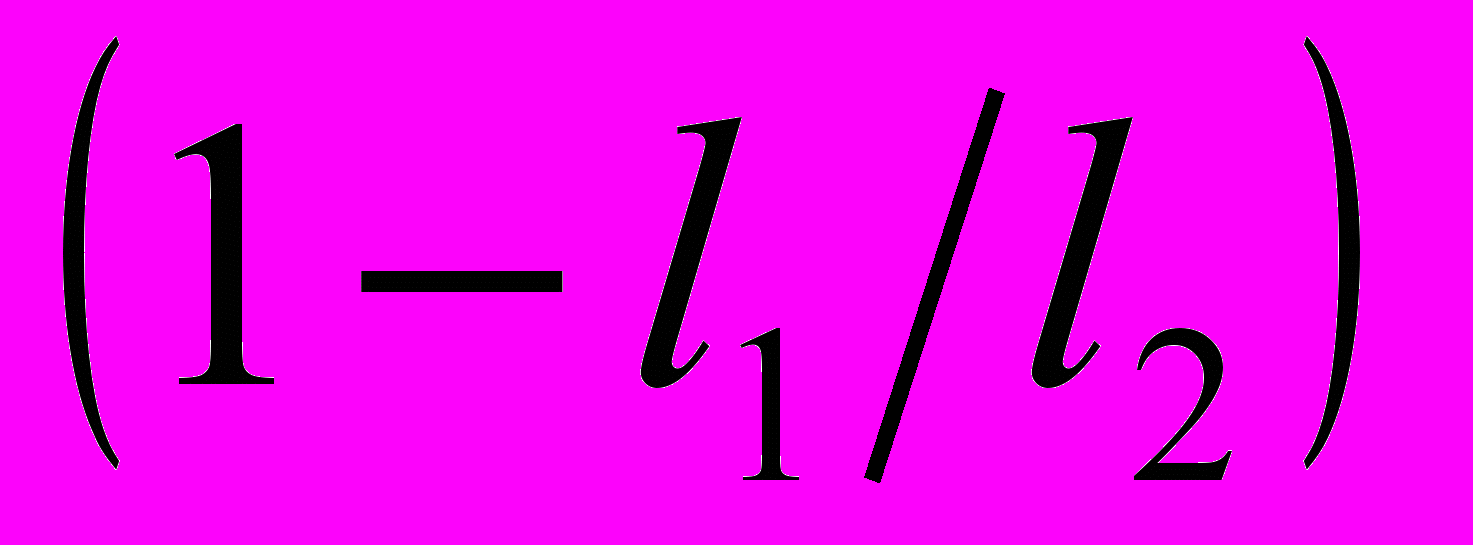Т_р, где Т_р — установленное калиброванное значение длительности развертки.

Измерение амплитудных параметров — высоты импуль­са, выбросов и спада плоской части выполняют с помощью осциллографа по известному калиброванному коэффициенту отклонения до вертикали. Параметры наносекундных импульсов измеряют с помощью- стробоскопических осцилло­графов.

Погрешность измерения осциллографическим методом составляет 5—10, в лучшем случае 2—4 %. Для более точных измерений импульсов выпускаются специализиро­ванные приборы, которые по способу отображения полу­ченных результатов измерения делятся на осциллографические и цифровые.

Осциллографические измерители временных и амплитуд­ных параметров отличаются от универсальных осциллогра­фов наличием дополнительных узлов, позволяющих выпол­нять амплитудные измерения сигнала на любом уровне от 0,1 до 0,9 его высоты через 0,1 и устанавливать произ­вольно уровень начала и конца измерения с погрешностью 1—3 %. Погрешность измерения временных пара­метров не превышает 10^-2— 10^-3 %, что достигается нали­чием точных калибраторов длительности, стабилизирован­ных кварцевыми резонаторами. Недостатком осциллогра-фических измерителей является сравнительно малая чув­ствительность.

Цифровые измерители временных интервалов основаны на методе дискретного счета, сущность которого заключа­ется в следующем. Измеряемый временной интервал запол­няется стабильными счетными импульсами известной дли­тельности, а их число иодсчитывается. электронным счет­чиком с выдачей результата в цифровой форме. Основными достоинствами цифровых измерителей являются: возмож­ность измерения параметров одиночных импульсов; быстро­действие; удобная индикация; вывод результатов измере­ния в электрическом коде; малая погрешность. Подробно метод дискретного счета рассматривается далее.

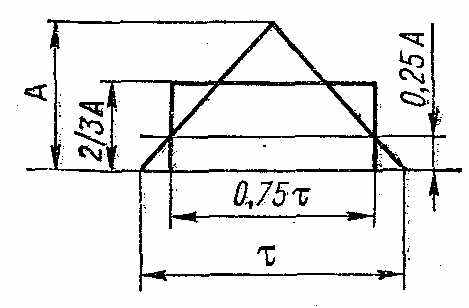
И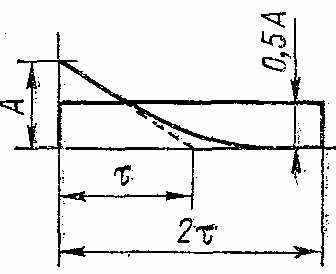нтегральные параметры измеряются приборами, в ко­торых измеряемая величина преобразуется в пропорцио­нальный ей аналоговый или дискретный сигнал. Обобщенные высота и длительность равны высоте и длительности эквивалентного импульса прямоугольной формы с равной площадью и энергией. На рисунках показаны для примера соотношения реальных и обобщенных высоты и длитель­ности треугольного и экспоненциального импульсов. При­боры, измеряющие интегральные параметры, позволяют сравнивать импульсные сигналы с энергетической точки зрения, что иногда бывает единственным критерием.

Исследование формы сигнала с помощью осциллографа позволяет получить зависимость напряжения от времени. Спектральное представление детерминированного сигнала в виде совокупности его частотных составляющих дает более полную информацию о его форме и, дополнительно, о качестве радиотракта, через который этот сигнал прошел. Измерение спектра используется для количественной оценки искажений импульсных сигналов, нелинейности радиотех­нических устройств и гармонических сигналов, параметров модулированных сигналов любого вида модуляции и для физических исследований.


АНАЛИЗ СПЕКТРА СИГНАЛОВ


В радиотехнических устройствах протекают электрические процессы, имеющие специфический характер. Реальный радиотехнический сигнал как физический объект аналитического и практического исследований достаточно сложен. Чтобы произвести анализ прохождения сигнала через радиотехнические цепи, необходимо его представить в удобной математической форме. В теории сигналов широкое при­менение нашли два способа математического и физического представления электри­ческих сигналов временной и спектральный. Такое представление возможно вслед­ствие принципа дуальности (двойственности, взаимосвязи) частоты и времени, по­скольку f= l/t. При временном способе анализа сигнал отражается непрерывной функци­ей времени или совокупностью элементарных импульсов, следующих друг за другом через определенные интервалы времени Спектральный способ основан на представлении (аппроксимации, декомпозиции) сигнала в виде суммы гармонических составляющих разных, обычно кратных друг другу частот

Процессы в электрических цепях получаются тем сложнее, чем более сложной является форма сигналов. В этих случаях часто становится эффективным и полезным спектральное представление сигналов


Общие сведения

Фундаментальная идея спектрального представления сигналов восходит к временам более чем 200-летней давности и принадлежит знаменитому фран­цузскому физику, математику и философу Фурье. В начале XIX в. Фурье удалось дока­зать оригинальную теорему, в которой он показал, что любое изменение во времени некоторой периодической функции можно представить в виде ко­нечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. В радиотехнике этой функ­цией может быть, в частности, ток или напряжение в некоторой электриче­ской цепи.

Столь простое представление сложного изменения во времени какой-либо фи­зической величины (в данном случае электрического сигнала) в виде суммы ряда простейших гармонических колебаний могло показаться на первый взгляд мате­матическим трюком. Но это не трюк. Несложный пример доказательства рассуж­дений Фурье показан на рис.

П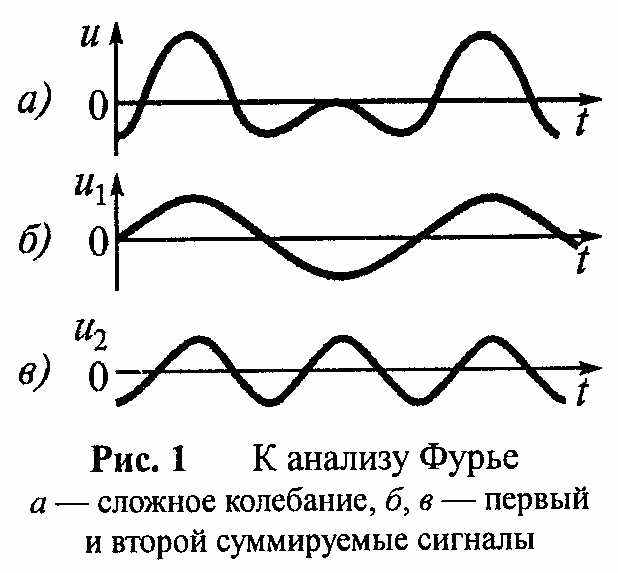усть периодическая, достаточно сложная по форме кривая напряжения u(t)— это сумма двух синусоид равной амплитуды, но разных частот и начальных фаз: основ­ной u₁(t) (первой гармоники) и удво­енной u₂(t) по отношению к ней час­тоты.

Д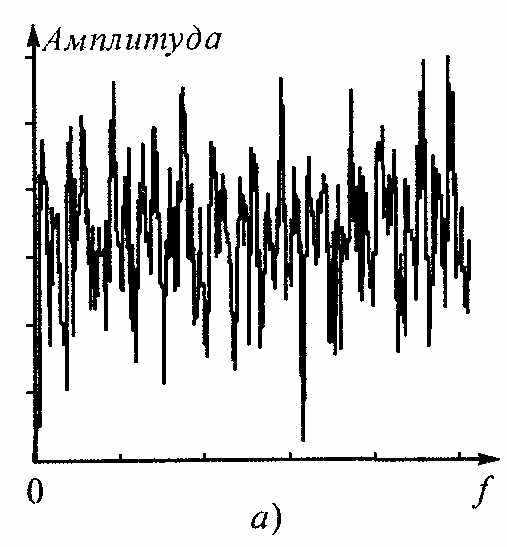ля периодических сигналов Фурье ввел разложение по различ­ным видам рядов — тригономет­рическим, комплексным и т.д.. Фурье также доказал, что непе­риодические (импульсные) сигна­лы можно описать с помощью двух его преобразований — прямого и обратного.

Итак, практически любой сигнал можно представить в виде суммы гар­монических составляющих, амплитуды и частоты которых могут быть опре­делены с помощью прямого преобразования Фурье. Этот спектр гармониче­ских составляющих можно изобразить графически, если по оси абсцисс от­кладывать обозначение частот, а по оси ординат — величины амплитуд гар­моник. На рис. наглядно показано временное и спектральное представ­ление достаточно сложного по форме сигнала.

А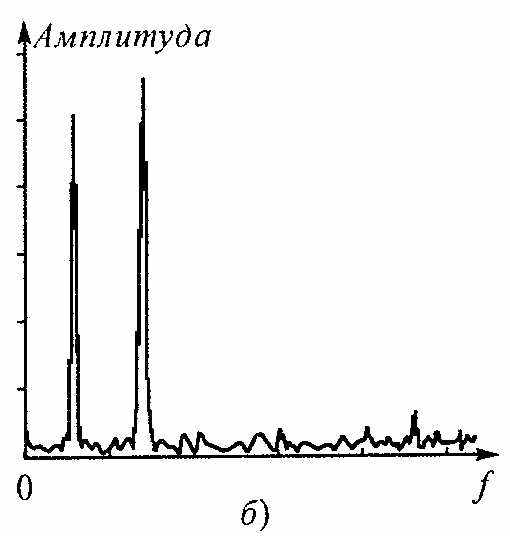нализ спектра включает измерение как амплитуд гармоник — спектр амплитуд, так и их начальных фаз — спектр фаз. Однако для многих практи­ческих задач достаточно знать лишь спектр амплитуд. Поэтому под анализом спектров обычно понимают нахождение спектра амплитуд исследуемого сигнала.

Автоматическое представление спектра сигналов осуществляется специ­альными приборами — анализаторами спектра.


Анализаторы спектра электрических сигналов можно классифицировать по ряду специфических признаков:

• по способу анализа — последовательные, параллельные (одновременные) и смешанные;

• по типу индикаторного устройства—осциллографические, с самописцем;

• по диапазону частот — низкочастотные, высокочастотные, сверхвысокочас­тотные, широкодиапазонные.

Большинство отечественных анализаторов спектра имеет обозначение С4 -.... Основными метрологическими характеристиками анализаторов являются: раз­решающая способность, время анализа и погрешности измерения частоты и ам­плитуды. Сущность этих понятий будет объяснена дальше. Отметим лишь, что метрологические характеристики анализатора определяются его схемой.

Для спектрального анализа непериодических сигналов (функций) исполь­зуют аппарат интегрального преобразования Фурье. При этом применяется известная формула прямого преобразования Фурье, характеризующая спек­тральную плотность непериодического (импульсного) сигнала:



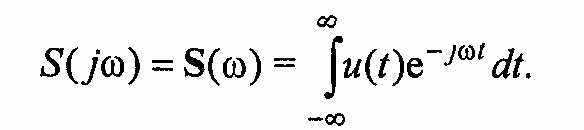
Однако есть одно обстоятельство, общее для всех схем анализаторов, ограничивающее точность анализа спектра сигнала. Преобразование Фурье широко применяют при аналитических исследованиях физических процес­сов, если выполняются условия Дирихле и абсолютной интегрируемости. Для реальных физических процессов эти условия обычно выполняются.

Преобразования Фурье предполагают, что процесс u(t) задан на всей оси времени от -∞ со до +∞. В частности, на интервале времени от -∞ до t₁ и от t₂ до +∞ считают u(t) = 0. Такая модель соответствует понятию конечно­сти во времени процесса, преобразуемого по Фурье. Спектр опреде­ляется всем закончившимся процессом, является функционалом всего про­цесса. Однако при измерениях наблюдают процессы на конечном интервале времени Т_a (времени анализа, наблюдения), т.е. не закончившиеся во време­ни. Это несоответствие позволяет устранить модель текущего частотного спектра, определяемого соотношением



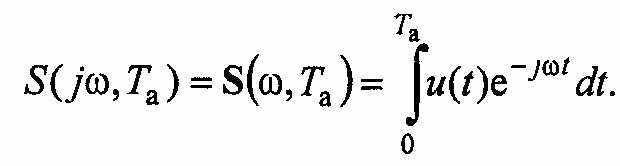
Иными словами, текущая спектральная плотность зависит от времени анализа и форма текущего спектра в общем случае отличается от истинного тем больше, чем меньше Т_a.

Отличие текущего спектра от спектра закончившегося процесса зависит от того, проявились ли за время анализа T_а все характерные особенности сигнала. Если исследуемый анализатором сигнал периодический с периодом следования Т, то необходимо, чтобы Т_a >>Т.

При измерении спектра нижний предел является конечным, т.е. интегри­рование (усреднение) производится в интервале от 0 до Т_a. За счет этого воз­никает погрешность определения составляющих спектра, связанная с мето­дом измерений, т. е. методическая погрешность. Эта погрешность для ряда технических применений не играет особой роли, в других случаях ее необхо­димо учитывать и исследовать.

Практически все приборы, применяемые для анализа спектра сигналов, можно условно разделить на аналоговые и цифровые. Несмотря на многие достоинства и возможности цифровых анализаторов, аналоговые анализато­ры еще широко применяются, особенно в верхней части высокочастотного и СВЧ диапазонов. Вместе с тем современные аналоговые анализаторы спек­тров содержат и цифровые устройства.

Практически во всех аналоговых анализаторах выделение гармонических составляющих сигнала производится узкополосными фильтрами. Этот метод реализуется двумя способами: параллельного и последовательного анализа сигнала. Основной элемент таких приборов — полосовой фильтр (высоко­добротный резонатор) с узкой полосой пропускания, служащий для выделения отдельных составляющих или узких диапазонов исследуемого спектра.


Параллельный анализ спектра


А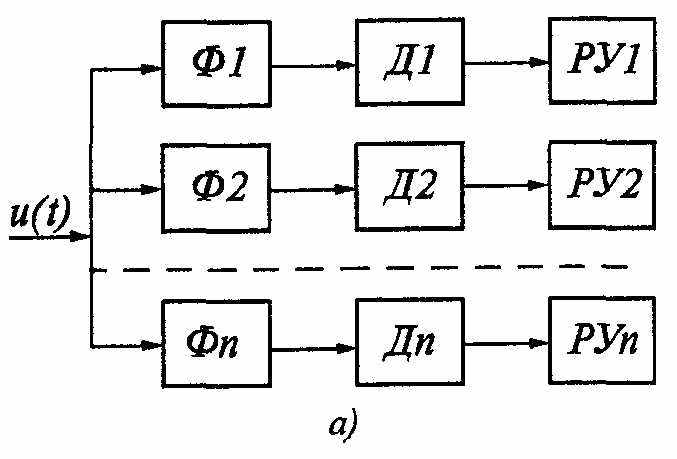нализаторы такого типа применяют в основном для анализа спектров одиночных импульсных сигналов. При параллельном анализе спектра сигнала применяют n полосовых фильтров Ф, каждый из которых настроен на опреде­ленную частоту.

Исследуемый сигнал u(t), спектр которого расположен в полосе частот ∆f_n подается одновременно на все фильтры. Фильтры имеют идент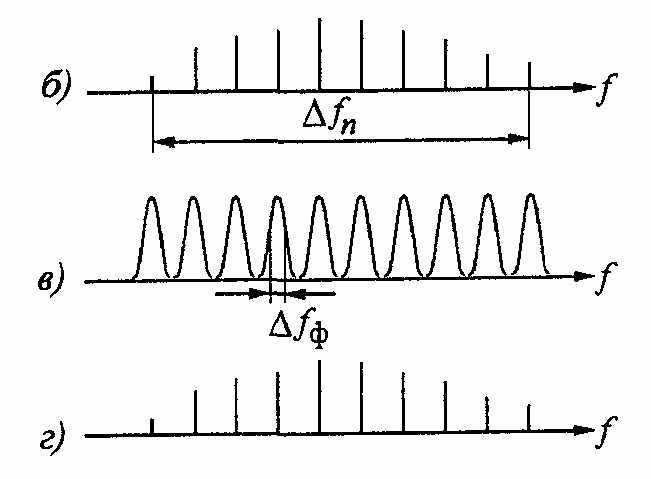ичные АЧХ с одинаковыми полосами пропускания ∆f_ф и настроены на опре­деленные частоты (рис. в). Сигналы на выходе фильтров определяются составляющими спектра анализируемого процесса (рис. г). Далее спек­тральные составляющие, после детектирования в детекторах Д поступают на регистрирующие устройства (РУ).

Полоса пропускания фильтра определяет статическую разрешающую способность анализатора (при условии время анализа 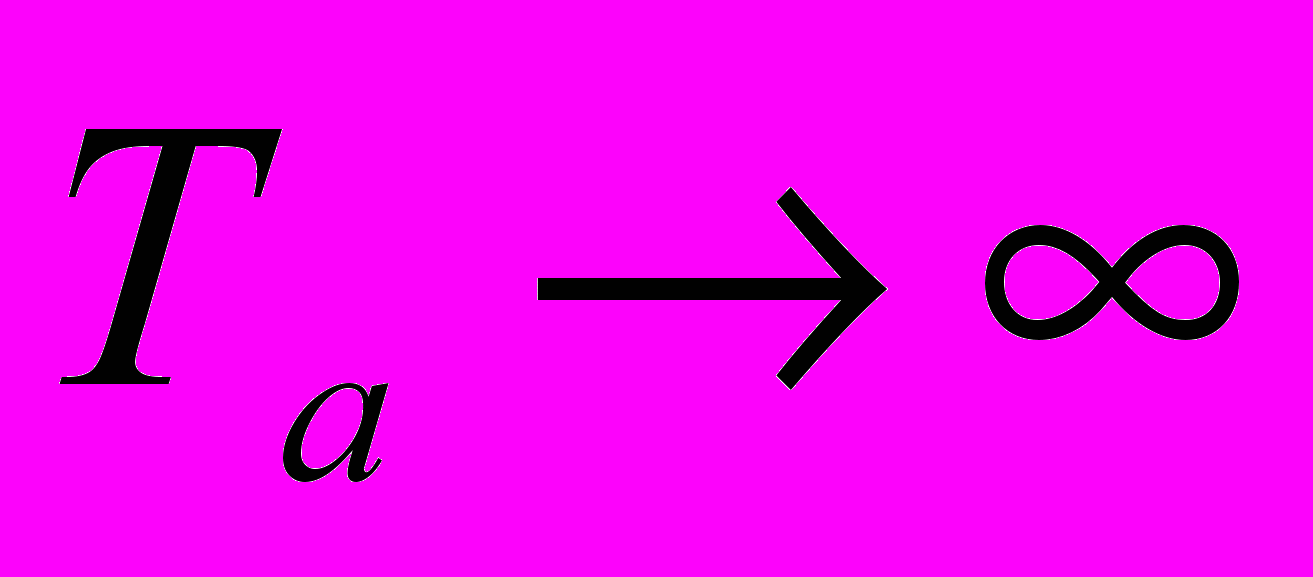, т. е. T_а — вели­ко). Разрешающая способность анализатора — способность различать со­ставляющие спектра с близкими частотами. Чем уже полоса пропускания фильтра, тем выше разрешающая способность. При широкой полосе пропус­кания несколько составляющих не будут разделяться. Если оценивать разре­шающую способность полосой частот ∆f_p, при которой возможно разделение ближайших составляющих, то при идеальной прямоугольной АЧХ фильтра можно полагать ∆f_p =∆f_ф ,. Для реальных фильтров ∆f_p=2∆f_ф. Если время ана­лиза Т_а мало, то имеет место динамическая разрешающая способность.

Необходимое время анализа для правильного воспроизведения спектра можно приблизительно оценить следующим образом. Время анализа при параллельном исследовании может быть принято примерно равным τ_у — времени установления напряжения на выходе фильтра с прямоугольной час­тотной характеристикой и рабочей полосой ∆f_ф (от уровня 0,1 до уровня 0,9 от установившегося значения). Из теории фильтров известно, что время ус­тановления τ_у = 0,86/(∆f_ф), следовательно, Т_а ≈ τ_у = 1/(∆f_ф).

Скорость параллельного анализа



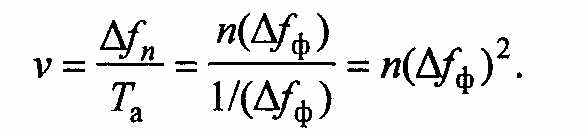
Скорость анализа резко снижается при сужении полосы пропускания фильтра. К достоинству анализаторов параллельного действия относится малое время анализа.

Погрешность при параллельном анализе определяют следующие основ­ные факторы: конечность времени установления колебаний на выходе фильт­ра и зависимость ее от полосы пропускания, различие характеристик фильт­ров, настроенных на разные частоты.